流体阻力系数——实验数据处理

流体阻力与阻力系数的实验研究引言：流体阻力是物体在流体中运动时所受到的阻碍力量。

研究流体阻力及阻力系数，对于理解物体在流体中的运动行为以及设计流体力学相关设备具有重要意义。

本实验旨在通过测量流体中运动物体所受的阻力，计算阻力系数，进一步探讨流体阻力的特性及影响因素。

一、实验介绍1. 实验目的：研究流体阻力及阻力系数。

2. 实验器材：流体介质、移动物体、测力传感器、电子天平、计时器、测速器等。

3. 实验原理：根据流体力学中的达西定律，物体在流体中受到的阻力与速度的平方成正比，并与物体形状、流体介质以及流体密度有关。

二、实验步骤1. 准备工作：a. 搭建流体管道系统，保证流体介质的自由流动。

b. 安装测力传感器于流体管道中，作为测量阻力的工具。

c. 放置测速器于流体管道中，记录物体的速度。

d. 校准测力传感器和测速器，确保实验数据的准确性。

2. 测量实验：a. 选取适当的流体介质，并确定起始速度。

b. 将移动物体放置在流体管道中，使其与流体介质接触。

c. 开始实验，记录物体所受的阻力、速度以及流体介质的相关数据。

d. 进行多组实验，改变流体介质或物体形状，以获得更多有关阻力的数据。

三、实验结果与分析1. 实验数据的收集与整理：a. 将测得的阻力、速度等数据整理成表格或图表。

b. 对数据进行初步的分析，发现其中的规律和差异。

2. 阻力系数的计算：a. 利用达西定律，通过阻力与速度的关系计算阻力系数。

b. 结合实验中所用的流体介质和物体形状，计算不同情况下的阻力系数。

3. 结果的解释与讨论：a. 分析实验数据，讨论阻力系数与流体介质、速度、物体形状之间的关系。

b. 探究流体阻力对物体运动的影响，以及如何降低阻力等应用方面的讨论。

四、实验结论1. 根据实验结果，得出流体阻力与物体速度的关系。

2. 讨论流体阻力系数与流体介质、物体形状以及速度之间的关系。

3. 强调流体阻力在物体运动中的重要性，并提出如何减小阻力的建议。

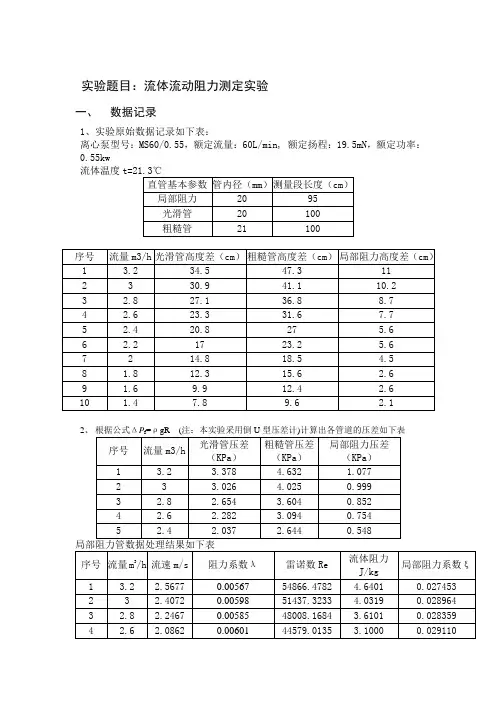
实验题目：流体流动阻力测定实验一、数据记录1、实验原始数据记录如下表：离心泵型号：MS60/0.55，额定流量：60L/min, 额定扬程：19.5mN，额定功率：0.55kw流体温度2、5 2.4 1.9258 0.00513 41149.8586 2.6487 0.024846 6 2.2 1.7653 0.0061 37720.7038 2.2759 0.029569 7 2 1.6048 0.00593 34291.5489 1.8149 0.028751 8 1.8 1.4443 0.00424 30862.3940 1.5304 0.020508 9 1.6 1.2838 0.00536 27433.2391 1.2164 0.025955 10 1.4 1.12340.005655 24004.08420.94180.0273820.00559绘制粗糙管路的双对数λ-Re 曲线如下图示：根据光滑管实验结果，对照柏拉修斯方程λ=0.3164/（Re0.25），计算其误差，计试验次数 阻力系数λ 雷诺数Re 柏拉修斯方程计算结果 误差1 0.016893 57609.8021 0.02042266 0.1728312 0.017215 54009.1895 0.02075485 0.1705553 0.017332 50408.5768 0.02111594 0.179198 4 0.017282 46807.9642 0.0215108 0.196595 0.018107 43207.3516 0.02194558 0.174914 6 0.017612 39606.7389 0.02242819 0.2147387 0.018552 36006.1263 0.02296902 0.1923038 0.019035 32405.5137 0.02358206 0.192819 9 0.019391 28804.901 0.02428678 0.201582 10 0.019954 25204.2884 0.02511122 0.205375 3 的流速2900d Vu π=（m/s ），雷诺数μρdu =Re ，流体阻力ρ1000⨯∆=P Hf，阻力系数22Lu d H f =λ，ξ=gu2f'Δ2ρP ，并以标准单位换算得光滑管数据处理结果如下表二、结果分析（1）光滑管结果分析：曲线表明，在湍流区内，光滑管阻力系数随雷诺数增大而减小，进入阻力平方区（也称完全湍流区）后，雷诺数对阻力系数的影响却越来越弱，阻力系数基本趋于不变。

流体流动阻力系数的测定实验报告一、实验目的：1、掌握测定流体流动阻力实验的一般实验方法。

2、测定直管的摩擦阻力系数λ及突然扩大管和阀门的局部阻力系数ξ。

3、验证湍流区内摩擦阻力系数λ为雷诺系数Re和相对粗糙度的函数。

4、将所得光滑管的λ—Re方程与Blasius方程相比较。

二、实验器材：流体阻力实验装置一套三、实验原理：1、直管摩擦阻力不可压缩流体（如水），在圆形直管中做稳定流动时，由于黏性和涡流的作用产生摩擦阻力；流体在流过突然扩大、弯头等管件时，由于流体运动的速度和方向突然变化，产生局部阻力。

影响流体阻力的因素较多，在工程上通常采用量纲分析方法简化实验，得到在一定条件下具有普遍意义的结果，其方法如下。

流体流动阻力与流体的性质，流体流经处的几何尺寸以及流动状态有关，可表示为△P=f (d, l, u,ρ,μ,ε)引入下列无量纲数群。

雷诺数Re=duρ/μ相对粗糙度ε/ d管子长径比l / d从而得到△P/(ρu2)=ψ(duρ/μ，ε/ d， l / d)令λ=φ（Re，ε/ d）△P/ρ=（l / d）φ（Re，ε/ d）u2/2可得摩擦阻力系数与压头损失之间的关系,这种关系可=△P/ρ=λ（l / d）u2/2用试验方法直接测定。

hf——直管阻力，J/kg式中，hfl——被测管长，md——被测管内径，mu——平均流速，m/sλ——摩擦阻力系数。

当流体在一管径为d的圆形管中流动时，选取两个截面，用U形压差计测出这两个截面间的静压强差，即为流体流过两截面间的流动阻力。

根据伯努利方程找出静压强差和摩擦阻力系数的关系式，即可求出摩擦阻力系数。

改变流速可测出不同Re下的摩擦阻力系数，这样就可得出某一相对粗糙度下管子的λ—Re关系。

（1）、湍流区的摩擦阻力系数在湍流区内λ=f（Re，ε/ d）。

对于光滑管，大量实验证明，当Re在3×103~105范围内，λ和Re的关系遵循Blasius关系式，即λ=0.3163 / Re0.25对于粗糙管，λ和Re的关系均以图来表示。

流体流动阻力的测定一、实验目的1．掌握测定流体流经直管、管件和阀门时阻力损失的一般实验方法。

2．测定直管摩擦系数λ与雷诺准数Re 的关系，验证在一般湍流区内λ与Re 的关系曲线，测定流体流经阀门时的局部阻力系数ξ。

4．学会倒U 形压差计的使用方法，识辨组成管路的各种管件、阀门，并了解其作用。

二、基本原理流体通过由直管、管件（如三通和弯头等）和阀门等组成的管路系统时，由于粘性剪应力和涡流应力的存在，要损失一定的机械能。

流体流经直管时所造成机械能损失称为直管阻力损失。

流体通过管件、阀门时因流体运动方向和速度大小改变所引起的机械能损失称为局部阻力损失。

1．直管阻力摩擦系数λ的测定流体在水平等径直管中稳定流动时，阻力损失为：2221u d l p p p h ff λρρ=-=∆=（1）即，22lu p d fρλ∆=（2）式中：λ—直管阻力摩擦系数，无因次；d —直管内径，m ；f p ∆—流体流经l 米直管的压力降，Pa; f h —单位质量流体流经l 米直管的机械能损失，J/kg ； ρ—流体密度，kg/m 3；l —直管长度，m ；u —流体在管内流动的平均流速，m/s 。

滞流(层流)时，Re 64=λ（3） μρdu =Re （4） 式中：Re —雷诺准数，无因次；μ—流体粘度，kg/(m·s)。

湍流时λ是雷诺准数Re 和相对粗糙度（ε/d ）的函数，须由实验确定。

由式（2）可知，欲测定λ，需确定l 、d ，测定f p ∆、u 、ρ、μ等参数。

l 、d 为装置参数（装置参数表格中给出），ρ、μ通过测定流体温度，再查有关手册而得，u 通过测定流体流量，再由管径计算得到。

例如本装置采用转子流量计测流量V （m 3/h ），且已经校核，则2900d Vu π=(5)f p ∆可用U 型管、倒置U 型管、测压直管等液柱压差计测定，或采用差压变送器和二次仪表显示。

（1）当采用倒置U 型管液柱压差计时gR p f ρ∆=(6)式中：R －水柱高度，m 。

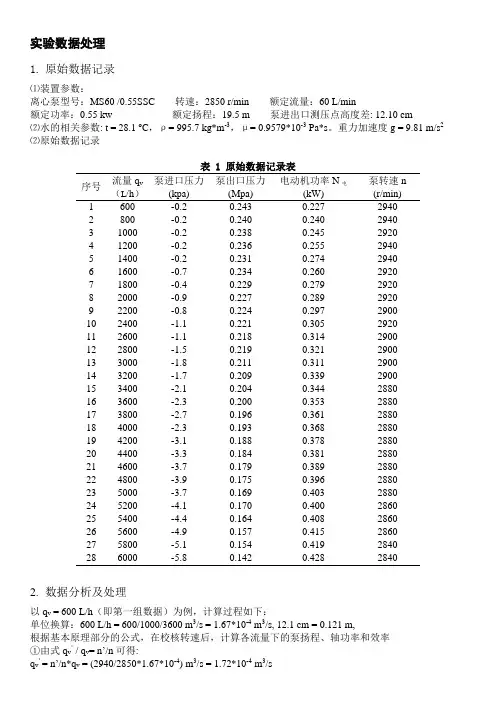
实验数据处理1.原始数据记录⑴装置参数：离心泵型号：MS60 /0.55SSC 转速：2850 r/min 额定流量：60 L/min额定功率：0.55 kw 额定扬程：19.5 m 泵进出口测压点高度差: 12.10 cm⑵水的相关参数: t = 28.1 o C，ρ= 995.7 kg*m-3，μ= 0.9579*10-3 Pa*s。

重力加速度g = 9.81 m/s2⑵原始数据记录表 1 原始数据记录表序号流量q v（L/h）泵进口压力(kpa)泵出口压力(Mpa)电动机功率N电(kW)泵转速n(r/min)1 600 -0.2 0.243 0.227 29402 800 -0.2 0.240 0.240 29403 1000 -0.2 0.238 0.245 29204 1200 -0.2 0.236 0.255 29405 1400 -0.2 0.231 0.274 29406 1600 -0.7 0.234 0.260 29207 1800 -0.4 0.229 0.279 29208 2000 -0.9 0.227 0.289 29209 2200 -0.8 0.224 0.297 290010 2400 -1.1 0.221 0.305 292011 2600 -1.1 0.218 0.314 290012 2800 -1.5 0.219 0.321 290013 3000 -1.8 0.211 0.311 290014 3200 -1.7 0.209 0.339 290015 3400 -2.1 0.204 0.344 288016 3600 -2.3 0.200 0.353 288017 3800 -2.7 0.196 0.361 288018 4000 -2.3 0.193 0.368 288019 4200 -3.1 0.188 0.378 288020 4400 -3.3 0.184 0.381 288021 4600 -3.7 0.179 0.389 288022 4800 -3.9 0.175 0.396 288023 5000 -3.7 0.169 0.403 288024 5200 -4.1 0.170 0.400 286025 5400 -4.4 0.164 0.408 286026 5600 -4.9 0.157 0.415 286027 5800 -5.1 0.154 0.419 284028 6000 -5.8 0.142 0.428 28402.数据分析及处理以q v = 600 L/h（即第一组数据）为例，计算过程如下：单位换算：600 L/h = 600/1000/3600 m3/s = 1.67*10-4 m3/s, 12.1 cm = 0.121 m,根据基本原理部分的公式，在校核转速后，计算各流量下的泵扬程、轴功率和效率①由式q v’ / q v= n’/n可得:q v’= n’/n*q v = (2940/2850*1.67*10-4) m3/s = 1.72*10-4 m3/s②扬程H = H0 + (p2 –p1)/（ρg）= 0.121+( 0.243*1000000+0.2*1000)/(9.81*995.7) = 25.02 m由式H’ / H = (n’/n)2可得:H’ = (n’/n)* H = [(2850/2940)2*23.26] m = 23.51 m③轴功率N = N电*0.95 = (0.227*0.95) = 0.216 kw由式N’ / N = (n’/n)3可得:N’= (n’/n)3*N = [(2850/2940)3*0.216] kw = 0.196 kwη= (q v Hρg/N) *100% = (1.67*10-4*25.02*995.7*9.81/0.216/1000)*100% = 18.93% η’ = (q v’H’ρg/N’) = (1.72*10-4*23.51*995.7*9.81/0.196/1000)*100% = 20.11%按此方法，对后面几组数据实施同样的计算，列出表格如下：表2 离心泵特性曲线数据处理表序号q v×10-4（m3/s)q v’×10-4（m3/s)H（m）H’（m）N（kW）N’（kW）η/% η/’%1 1.67 1.62 25.02 23.51 0.216 0.196 18.93 20.112 2.22 2.15 24.71 23.22 0.228 0.208 17.68 18.783 2.78 2.71 24.51 23.35 0.233 0.216 17.18 18.124 3.33 3.23 24.30 22.84 0.242 0.221 16.36 17.395 3.89 3.77 23.79 22.36 0.260 0.237 14.91 15.846 4.44 4.34 24.15 23.00 0.247 0.230 15.95 16.837 5.00 4.88 23.61 22.49 0.265 0.246 14.53 15.338 5.56 5.42 23.45 22.34 0.275 0.255 13.93 14.709 6.11 6.01 23.14 22.34 0.282 0.268 13.38 14.0210 6.67 6.51 22.86 21.78 0.290 0.269 12.87 13.5811 7.22 7.10 22.55 21.78 0.298 0.283 12.33 12.9212 7.78 7.64 22.70 21.92 0.305 0.289 12.14 12.7213 8.33 8.19 21.91 21.16 0.295 0.280 12.10 12.6814 8.89 8.74 21.69 20.95 0.322 0.306 10.99 11.5115 9.44 9.35 21.22 20.78 0.327 0.317 10.59 11.0216 10.00 9.90 20.83 20.40 0.335 0.325 10.13 10.5517 10.56 10.45 20.46 20.04 0.343 0.332 9.73 10.1318 11.11 11.00 20.12 19.70 0.350 0.339 9.39 9.7719 11.67 11.55 19.69 19.28 0.359 0.348 8.94 9.3120 12.22 12.09 19.30 18.90 0.362 0.351 8.70 9.0521 12.78 12.64 18.83 18.44 0.370 0.358 8.31 8.6522 13.33 13.19 18.44 18.05 0.376 0.365 7.99 8.3223 13.89 13.74 17.80 17.43 0.383 0.371 7.58 7.8924 14.44 14.39 17.94 17.82 0.380 0.376 7.70 7.9625 15.00 14.95 17.36 17.24 0.388 0.384 7.31 7.5526 15.56 15.50 16.70 16.58 0.394 0.390 6.91 7.1427 16.11 16.17 16.41 16.52 0.398 0.402 6.72 6.9028 16.67 16.73 15.25 15.36 0.407 0.411 6.12 6.28注：t是水的温度，q v是水的流量，N电是电动机功率，p1 是泵进口压力，p2是泵出口压力，n 是泵转速，ρ是水的密度，q V’是校核流量，H是扬程，H’是校核扬程，N是轴功率，N’是校核轴功率，η是效率，η’是校核效率。

流体流动阻力测定实验一、实验目的1．掌握测定流体流经直管、管件和阀门时阻力损失的一般实验方法。

2．测定直管摩擦系数λ与雷诺准数Re的关系，验证在一般湍流区内λ与Re 的关系曲线。

3．测定流体流经管件、阀门时的局部阻力系数ξ。

4．学会倒U形压差计和涡轮流量计的使用方法。

5．识辨组成管路的各种管件、阀门，并了解其作用。

二、基本原理流体通过由直管、管件（如三通和弯头等）和阀门等组成的管路系统时，由于粘性剪应力和涡流应力的存在，要损失一定的机械能。

流体流经直管时所造成机械能损失称为直管阻力损失。

流体通过管件、阀门时因流体运动方向和速度大小改变所引起的机械能损失称为局部阻力损失。

1．直管阻力摩擦系数λ的测定流体在水平等径直管中稳定流动时，阻力损失为：即，式中：λ—直管阻力摩擦系数，无因次；d —直管内径，m；—流体流经l米直管的压力降，Pa；hf—单位质量流体流经l米直管的机械能损失，J/kg；ρ—流体密度，kg/m3；l —直管长度，m；u —流体在管内流动的平均流速，m/s。

滞流（层流）时，式中：Re —雷诺准数，无因次；μ—流体粘度，kg/(m·s)。

湍流时λ是雷诺准数Re和相对粗糙度（ε/d）的函数，须由实验确定。

由式（2）可知，欲测定λ，需确定l、d，测定、u、ρ、μ等参数。

l、d 为装置参数（装置参数表格中给出），ρ、μ通过测定流体温度，再查有关手册而得， u通过测定流体流量，再由管径计算得到。

例如本装置采用涡轮流量计测流量V（m3/h）。

可用U型管、倒置U型管、测压直管等液柱压差计测定，或采用差压变送器和二次仪表显示。

根据实验装置结构参数l、d，指示液密度，流体温度 (查流体物性ρ、μ)，及实验时测定的流量V、压差，通过式(5)、(6)或(7)、(4) 和式(2)求取Re和λ，再将Re和λ标绘在双对数坐标图上。

2．局部阻力系数ξ的测定局部阻力损失通常有两种表示方法，即当量长度法和阻力系数法。

化工原理实验报告—流体流动阻力测定实验班级： 031112班小组：第六组指导老师：刘慧仙组长：陈名组员：魏建武曹然实验时间： 2013年10月18日目录一、实验内容 (1)二、实验目的 (1)三、实验基本原理 (1)1.直管阻力 (1)2.局部阻力 (3)四、实验设计 (3)1.实验方案 (3)2.测试点及测试方法 (3)原始数据 (3)测试点 (4)测试方法 (4)3.控制点及调节方法 (4)4.实验装置和流程设计 (4)主要设备和部件 (4)实验装置流程图 (4)五、实验操作要点 (5)六、实验数据处理和结果讨论分析 (6)实验数据处理 (6)1.实验数据记录表 (6)2.流体直管阻力测定实验数据整理表 (7)3.流体局部阻力测定实验数据整理表 (8)4.计算示例。

(9)结果讨论分析 (10)七、思考题 (11)实验一流体流动阻力的测定实验一、实验内容1.测定流体在特定材质和的直管中流动时的阻力摩擦系数，并确定和之间的关系。

2.测定流体通过阀门时的局部阻力系数。

二、实验目的1.了解测定流体流动阻力摩擦系数的工程定义，掌握测定流体阻力的实验方法。

2.测定流体流径直管的摩擦阻力和流经管件或局部阻力，确定直管阻力摩擦系数与雷诺数之间的关系。

3.熟悉压差计和流量计的使用方法。

4.认识组成管路系统的各部件、阀门并了解其作用。

三、实验基本原理流体管路是由直管、管件（如三通、肘管、弯头）、阀门等部件组成。

流体在管路中流动时，由于黏性剪应力和涡流的作用，不可避免地要消耗一定的机械能，流体在直管中流动的机械能损失为直管阻力；而流体通过阀门、管件等部件时，因流动方向或流动截面的突然改变导致的机械能损失称为局部阻力。

在化工过程设计中，流体流动阻力的测定或计算，对于确定流体输送所需推动力的大小，例如泵的功率、液位或压差，选择适当的输送条件都有不可或缺的作用。

1.直管阻力流体在水平的均匀管道中稳定流动时，由截面1流动至截面2的阻力损失表现为压力的降低，即①由于流体分子在流动过程中的运动机理十分复杂，影响阻力损失的因素众多，目前尚不能完全用理论方法来解决流体阻力的计算问题，必须通过实验研究掌握其规律。

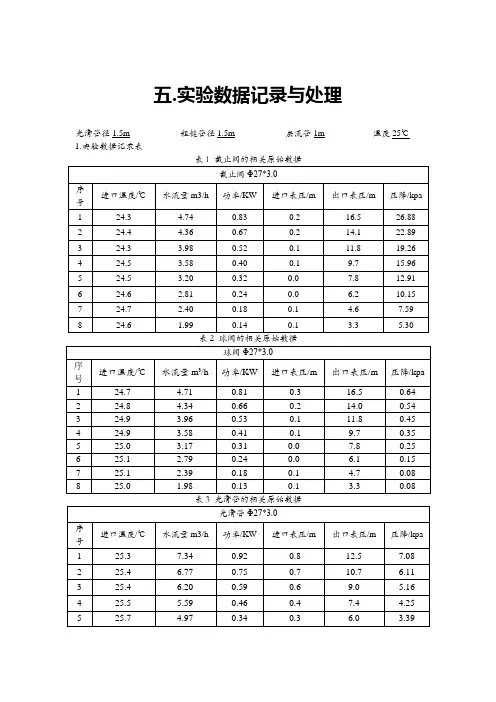
五.实验数据记录与处理光滑管径1.5m 粗糙管径1.5m 层流管1m 温度25℃1.实验数据记录表表1 截止阀的相关原始数据表7 层流的相关原始数据表8 相关的处理数据表直管阻力摩擦系数λ的测定流体在水平等径直管中稳定流动时, 阻力损失为:2***d *2u l p fρλ∆=湍流时的雷诺数为:μρdu R =e根据以上数据这里只作出光滑管和粗糙管的 ~Re 的的关系图由图可知: 光滑管在湍流区雷诺数与阻力系数呈反比的关系, 这与柏拉修斯式, 顾毓珍等公式基本相符由图可知: 粗糙管的阻力系数随着雷诺数的增大先增大后基本稳定的过程, 由于本实验处在完全湍流区, 区域内 , 对 均有影响, 且随着 的增大, 对 的影响越来越重要；相反, 对 的影响越来越弱。

可解释为, 一定时, 越大, 则层流底层相对越薄；当 增大到一定值后, 几乎所有的粗糙峰均暴露在湍流主体区内, 在大, 不变。

图1.流体阻力-离心泵联合实验流程1.水箱2、离心泵3、涡轮流量计4、层流水槽5、层流管6、截止阀7、球阀8、光滑管9、粗糙管10、突扩管11.孔板流量计12、流量调节阀排空排水入地沟图1 氧气吸收与解吸实验流程图1.氧气钢瓶9、吸收塔17、空气转子流量计2.氧减压阀10、水流量调节阀18、解吸塔3.氧压力表11.水转子流量计19、液位平衡罐4.氧缓冲罐12.富氧水取样阀20、贫氧水取样阀5.氧压力表13.风机21.温度计6.安全阀14.空气缓冲罐22.压差计7、氧气流量调节阀15.温度计23.流量计前表压计8、氧转子流量计16、空气流量调节阀24.防水倒灌阀。

流体流动阻力实验报告一、实验目的。

本实验旨在通过测量不同流速下流体通过不同形状截面管道时的流动阻力，探究流体流动阻力与流速、管道形状的关系，从而加深对流体力学的理解。

二、实验原理。

1. 流体流动阻力。

当流体通过管道流动时，由于管壁的摩擦力和管道内部的涡流等原因，会产生一定的阻力，称为流体流动阻力。

2. 流体流动阻力系数。

流体流动阻力系数与流速、管道形状等因素有关，通常用Reynolds数来表征，即Re=ρVD/μ，其中ρ为流体密度，V为流速，D为管道直径，μ为流体粘度。

不同形状的管道在不同流速下，其流动阻力系数也会有所不同。

三、实验装置。

1. 实验装置包括流速测量装置、管道系统、压力传感器、数据采集系统等。

2. 流速测量装置采用激光多普勒测速仪，能够准确测量流体通过管道的流速。

3. 管道系统包括不同形状截面的管道，用于测量不同形状管道的流动阻力。

四、实验步骤。

1. 将不同形状截面的管道依次连接到流速测量装置上，并通过数据采集系统记录流体通过管道的流速。

2. 调节流速测量装置，分别测量不同流速下流体通过不同形状管道的流速和压力。

3. 根据测得的数据，计算流体流动阻力系数，并绘制流速与流动阻力的关系曲线。

五、实验结果与分析。

1. 通过实验测得不同形状管道在不同流速下的流动阻力系数，发现在相同流速下，不同形状管道的流动阻力系数存在明显差异。

2. 经过分析发现，流体流动阻力系数与管道形状、流速等因素密切相关，其中流速对流动阻力系数的影响较大。

3. 实验结果与理论分析基本吻合，验证了流体流动阻力与流速、管道形状的关系。

六、实验结论。

1. 流体流动阻力与流速、管道形状密切相关，流速越大、管道形状越复杂，流动阻力越大。

2. 实验结果可为工程实践提供参考，对流体在管道内的流动阻力有一定的指导意义。

七、实验总结。

本实验通过测量不同形状管道在不同流速下的流动阻力系数，探究了流体流动阻力与流速、管道形状的关系，加深了对流体力学的理解。