圆心角与圆周角的专题练习
- 格式:doc
- 大小:60.50 KB
- 文档页数:4

圆心角圆周角练习题圆心角和圆周角是圆内角的一种特殊形式,它们在几何学中具有重要的地位。
本文将介绍关于圆心角和圆周角的一些练习题,帮助读者加深对这一概念的理解。
一、选择题1. 在同一个圆中,圆心角和对应的圆周角的关系是:A. 圆心角大于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角小于对应的圆周角2. 已知在同一个圆中,圆心角的度数为56°,则对应的圆周角的度数为:A. 56°B. 112°C. 224°3. 在圆O中,∠ACB是圆心角,则它所对应的圆周角的度数为:A. 30°B. 60°C. 120°4. 若∠ACD是圆O中的圆心角,且其度数为72°,则弧AB所对应的圆周角的度数为:A. 72°B. 144°C. 288°5. 在同一个圆中,圆心角和对应的弧所对应的圆周角之间的关系是:A. 圆心角小于对应的圆周角B. 圆心角等于对应的圆周角C. 圆心角大于对应的圆周角二、填空题1. 在同一圆中,一条弧的度数等于其所对应的圆周角的度数,则这条弧所对应的圆心角的度数为________。
2. 在圆O中,已知∠ACB是圆心角,则它所对应的圆周角的度数为________。
3. 在同一个圆中,圆心角的度数等于所对应的弧所对应的圆周角的度数,则该弧所对应的圆周角的度数为________。
三、解答题1. 在同一个圆中,圆心角和对应的圆周角的关系是什么?为什么?2. 已知在同一个圆中,圆心角的度数为60°,则对应的圆周角的度数是多少?并通过计算或推理进行解答。
3. 在圆O中,∠ACB是圆心角,则它所对应的圆周角的度数是多少?并通过计算或推理进行解答。
4. 若∠ACD是圆O中的圆心角,且其度数为90°,则弧AB所对应的圆周角的度数是多少?并通过计算或推理进行解答。
总结:本文通过选择题、填空题和解答题的形式,对圆心角和圆周角的概念进行了练习和探讨。

垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
推论:平分(非直径)弦的直径垂直于弦,并且平分弦所对的两条弧.练习:1.如图,在⊙O中,弦AB的长为8 cm.圆心O到AB的距离为3cm.求⊙O的半径.2.如图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,并且CD=4m,EM=6m.求⊙O的半径。
圆心角:顶点在圆心的角叫做圆心角。
圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等、所对的弦也相等.推论:(1)在同圆或等圆中,如果两条弧相等、那么它们所对的圆心角相等.所对的弦相等;(2)在同圆或等圆中,如果两条弦相等。
那么它们所对的圆心角相等,所对的优弧和劣弧分别相等.练习:1.如图,在⊙O中,AB=AC,∠ACB=60°,求证:AOB=∠BOC=∠AOC.圆周角:顶点在圆上,并且两边都与圆相交,所形成的角为圆周角。
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
推论:(1)同弧或等弧所对的圆周角相等;(2)半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径;(3)同弦或等弦所对的圆周角相等或互补;练习:1.如图,⊙O的直径AB为10 cm,弦AC为6cm,∠ACB的平分线交⊙O于点D,求BC,AD, BD的长。
2.如图,圆内接四边形ABCD的对角线AC、BD把它的4个内角分成8个角,这些角中哪些相等?为什么?如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆。
圆内接四边形性质:圆内接四边形的对角互补。
练习:1.如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,求∠ADE的度数。
2.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°,判断△ABC的形状,并证明你的结论.。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)试题1:在同圆中,同弦所对的圆周角 ( )A.相等 B.互补 C.相等或互补 D.互余试题2:如图3-63所示,A,B,C,D在同一个圆上,四边形ABCD的两条对角线把四个内角分成的8个角中,相等的角共有 ( )A.2对 B.3对 C.4对D.5对试题3:如图3-64所示,⊙O的半径为5,弦AB=,C是圆上一点,则∠ACB的度数是.试题4:如图,四边形 ABCD内接于⊙O,若∠BOD=100°,则∠DAB的度数为()A.50° B.80° C.100° D.130°试题5:如图是中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是() A.180° B.15 0° C.135° D.120°试题6:下列命题中,正确的命题个数是()①顶点在圆周上的角是圆周角;②圆周角度数等于圆心角度数的一半;③900的圆周角所对的弦是直径;④圆周角相等,则它们所对的弧也相等。
A、1个B、2个C、3个D、4个试题7:如图3-65所示,在⊙O中,∠AOB=100°,C为优弧ACB的中点,则∠CAB=.试题8:如图3-66所示,AB为⊙O的直径,AB=6,∠CAD=30°,则弦DC=.试题9:如图3-67所示,AB是⊙O的直径,∠BOC=120°,CD⊥AB,求∠ABD的度数.试题10:如图,已知AB是⊙O的直径,AD ∥ OC弧AD的度数为80°,则∠BOC=_________ 试题11:如图,⊙O内接四边形ABCD中,AB=CD则图中和∠1相等的角有______。

圆的定义圆心角圆周角训练题一、单选题(共17题;共34分)1.(2020九上·江苏月考)下列说法错误的是()A. 长度相等的两条弧是等弧B. 直径是圆中最长的弦C. 面积相等的两个圆是等圆D. 半径相等的两个半圆是等弧2.(2019九上·台安期中)下列说法中,不正确的个数是()①优弧一定比劣弧长;②面积相等的两个圆是等圆;③长度相等的弧是等弧;④经过圆心的一个定点可以作无数条弦;⑤经过圆内一定点可以作无数条直径.A. 1个B. 2个C. 3个D. 4个3.(2019九上·沭阳月考)下列命题:①直径相等的两个圆是等圆;②等弧是长度相等的弧;③圆中最长的弦是通过圆心的弦;④一条弦把圆分为两条弧,这两条弧不可能是等弧.其中真命题是( )A. ①③B. ①③④C. ①②③D. ②④4.(2019九上·贾汪月考)下列说法中,错误的是()A. 半圆是弧B. 半径相等的圆是等圆C. 过圆心的线段是直径D. 直径是弦5.(2018九上·下城期末)下列命题中是真命题的为()A. 弦是直径B. 直径相等的两个圆是等圆C. 平面内的任意一点不在圆上就在圆内D. 一个圆有且只有一条直径6.(2020九上·浙江期中)如图,是的直径,,,则的度数是().A. 52°B. 57°C. 66°D. 78°7.(2019九上·柳江月考)如图,AB是⊙O的直径,,∠COD=34°,则∠AOE的度数是( )A. 51°B. 56°C. 68°D. 78°8.(2019九上·邯郸月考)如图,AB是O的直径, ,∠BOC=40°,则∠AOE的度数为()A. 30°B. 40°C. 50°D. 60°9.(2019九上·余杭期中)如图,在△ABC中,∠C=90°,的度数为α,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E,则∠A的度数为()A. 45º-αB. αC. 45º+αD. 25º+α10.(2020九下·南召月考)如图,四边形ABCD内接于⊙O,AC平分∠BAD,则下列结论正确的是()A. AB=ADB. BC=CDC.D. ∠BCA=∠DCA11.(2020九上·无锡月考)在半径为的圆中,长度等于的弦所对的弧的度数为()A. B. C. 或 D. 或12.(2020·西湖模拟)如图,已知点A,B,C,D,E是⊙O的五等分点,则∠BAD的度数是()A. 36°B. 48°C. 72°D. 96°13.(2020·衢州模拟)如图,在⊙O中,=,∠A=40°,则∠B的度数是()A. 60°B. 40°C. 50°D. 70°14.(2020·乾县模拟)如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB 的度数是()A. 70°B. 80°C. 82°D. 85°15.(2019九上·龙湖期末)如图,在⊙O中,若点C是的中点,∠A=50°,则∠BOC=( )A. 40°B. 45°C. 50°D. 60°16.(2019九上·道外期末)如图,,是的直径,,若,则的度数是()A. 32°B. 60°C. 68°D. 64°17.(2019九上·光明期中)如图,已知AB是⊙O的直径,∠CBA=25°,则∠D的度数为()A. B. C. D.参考答案一、单选题1.【答案】A【解析】【解答】解:A、等弧就是指能完全重合的两段弧,所以长度相等的弧的度数不一定是等弧,故错误;B、直径是圆中最长的弦,正确;C、面积相等的两个圆是等圆,正确;D、半径相等的两个半圆是等弧,正确.故答案为:A.2.【答案】C【解析】【解答】在同圆或等圆中,优弧一定比劣弧长,所以①错误;面积相等的两个圆半径相等,则它们是等圆,所以②正确;能完全重合的弧是等弧,所以③错误;经过圆内一个定点可以作无数条弦,所以④正确;经过圆内一定点可以作无数条直径或一条直径,所以⑤错误.故答案为:C.3.【答案】A【解析】【解答】解:①直径相等的两个圆能重合,所以是等圆,①是真命题;②长度相等的弧不一定能重合,所以不一定是等弧,②是假命题;③圆中最长的弦是直径,通过圆心的弦是直径,③是真命题;④一条弦把圆分成两条弧,这两条弧可以是半圆,所以可能是等弧,④是假命题.故答案为:A.4.【答案】C【解析】【解答】解:A、半圆是弧,所以A选项的说法正确;B、半径相等的圆是等圆,所以B选项的说法正确;C、过圆心的弦为直径,所以C选项的说法错误;D、直径是弦,所以D选项的说法正确.故答案为:C.5.【答案】B【解析】【解答】解:弦不一定是直径,A是假命题;直径相等的两个圆是等圆,B是真命题;平面内的任意一点在圆上、圆内或圆外,C是假命题;一个圆有无数条直径,D是假命题;故选:B.6.【答案】C【解析】【解答】解:∵AB是⊙O的直径,,∠COD=38°,∴∠BOC=∠COD=∠DOE=38°.∴∠BOE=114°,∴∠AOE=180°-114°=66°.故答案为:C.7.【答案】D【解析】【解答】解:∵,∠COD=34°,∴∠BOC=∠COD=∠DOE=34°,∴∠AOE=180°-∠BOC-∠COD-∠DOE=180°-34°-34°-34°= 78° .故答案为:D.8.【答案】D【解析】【解答】解:∵,∠BOC=40°∴∠BOC=∠COD=∠EOD=40°∴∠BOE=120°∴∠AOE=180°-∠BOE=60°.9.【答案】A【解析】【解答】解:如图,连接CD,∵的度数为,∴∠DCE= ,∵BC=CD,∴∠CBD=∠BDC= ,∵∠C=90°,∴∠CBD+∠A=90°,∴,∴;故选择:A.10.【答案】B【解析】【解答】解:A.∵∠ACB与∠ACD的大小关系不确定,∴AB与AD不一定相等,故本选项错误;B.∵AC平分∠BAD,∴∠BAC=∠DAC,∴BC=CD,故本选项正确;C.∵∠ACB与∠ACD的大小关系不确定,∴与不一定相等,故本选项错误;D.∠BCA与∠DCA的大小关系不确定,故本选项错误。
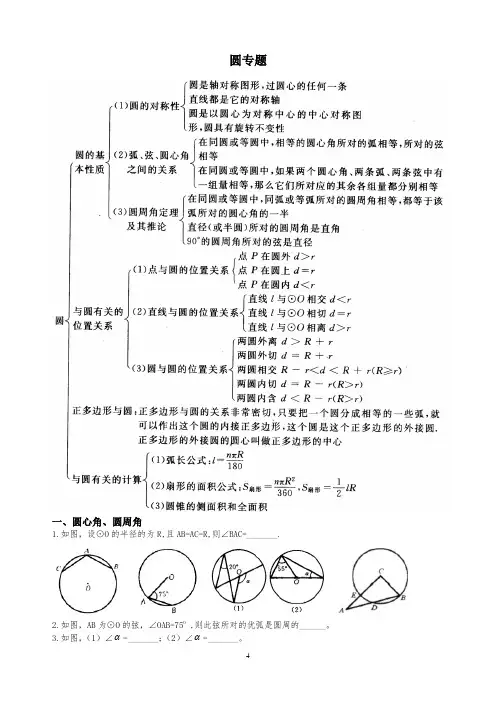
圆专题一、圆心角、圆周角1.如图,设⊙O的半径的为R,且AB=AC=R,则∠BAC=_______.2.如图,AB为⊙O的弦,∠OAB=75O ,则此弦所对的优弧是圆周的______。
4.如图,在△ABC 中,∠C 是直角,∠A=32O 18’ ,以点C 为圆心、BC 为半径作圆,交AB 于点D,交AC 于点E,则⋂BD 的度数是______。
5.如图,点O 是△ABC 的外心,已知∠ACB=100O ,则劣弧⋂AB 所对的∠AOB=______度。
6.如图,AB 是⊙O 的直径,CD 与AB 相交于点E, ∠ACD=60O , ∠ADC=50O ,则∠AEC=______度。
7.如图,以等腰△ABC 的边AB 为直径的半圆,分别交AC 、BC 于点D 、E,若AB=10, ∠OAE=30O,则DE=______。
8.在锐角△ABC 中,∠A=50O ,若点O 为外心,则∠BOC=_____;若点I 为内心,则∠BIC=______;若点H 为垂心,则∠BHC=________.9.若△ABC 内接于⊙O ,∠A=n O,则∠BOC=_______.10.如图,已知AB 和CD 是⊙O 相交的两条直径,连AD 、CB ,那么α和β的关系是( ) A.α=β B.β>21α C.β<21α D.β=2α 11.如图,在⊙O 中,弦AC 、BD 交于点E ,且⋂⋂⋂==CDBC AB ,若∠BEC=130O ,则∠ACD 的度数为( )A.15OB.30OC.80OD.105O12.如图,AB 为半圆的直径,AD ⊥AB,点C 为半圆上一点,CD ⊥AD,若CD=2,AD=3,求AB 的长。
13.如图,AO ⊥BO,AO 交⊙O 于点D ,AB 交⊙O 于点C, ∠A=27O,试用多种方法求⋂DC 、⋂BC 的度数。
14.求证:如果AB 和CD 为⊙O 内互相垂直的两条弦,那么∠AOC 和∠BOD 互补。

圆周角和圆心角的关系中考题目Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】圆周角和圆心角的关系-----中考链接能力提升题一.选择题(共12小题)1.(2013?自贡)如图,在平面直角坐标系中,⊙A经过原点O,并且分别与x轴、y轴交于B、C两点,已知B(8,0),C(0,6),则⊙A的半径为()A. 3 B.4 C.5 D.82.(2013珠海)如图,ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接AE,则∠AEB的度数为()A.36°B.46°C.27°D.63°3.(2013?湛江)如图,AB是⊙O的直径,∠AOC=110°,则∠D=()A.25°B.35°C.55°D.70°4.(2013?宜昌)如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()A.B.AF=BF C.OF=CF D.∠DBC=90°5.(2013?绥化)如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为()A. 4 B.5 C.6 D.76.(2013?苏州)如图,AB是半圆的直径,点D是的中点,∠ABC=50°,则∠DAB等于()A.55°B.60°C.65°D.70°7.(2013?日照)如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是()A.BD⊥AC B.AC2=2AB?AEC.△ADE是等腰三角形D.BC=2AD8.(2013?南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O的半径为()A. 4B.5 C.4 D.39.(2013?济南)如图,AB是⊙O的直径,C是⊙O上一点,AB=10,AC=6,OD⊥BC,垂足是D,则BD的长为()A. 2 B.3 C.4 D.610.(2013?临沂)如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是()A.75°B.60°C.45°D.30°11.(2013?红河州)如图,AB是⊙O的直径,点C在⊙O上,弦BD平分∠ABC,则下列结论错误的是()A. AD=DC B.C.∠ADB=∠ACB D.∠DAB=∠CBA12.(2013?黑龙江)如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么AB的值为()A. 3 B.2C.3D.2二.填空题(共6小题)13.(2013?淄博)如图,AB是⊙O的直径,,AB=5,BD=4,则sin∠ECB=_________ .14.(2013?黔西南州)如图所示⊙O中,已知∠BAC=∠CDA=20°,则∠ABO的度数为_________ .15.(2013?盘锦)如图,⊙O直径AB=8,∠CBD=30°,则CD= _________ .16.(2013?常州)如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= _________ .17.(2012?徐州)如图,已知AB是⊙O的直径,CD是弦,且CD⊥AB,AC=8,BC=6.则sin∠ABD=_________ .18.(2012?泰安)如图,在半径为5的⊙O中,弦AB=6,点C是优弧上一点(不与A,B重合),则cosC的值为_________ .三.解答题(共4小题)19.(2013?武汉)如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.(1)如图①,若∠BPC=60°.求证:AC=AP;(2)如图②,若sin∠BPC=,求tan∠PAB的值.20.(2013?温州)如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.(1)求证:∠B=∠D;(2)若AB=4,BC﹣AC=2,求CE的长.21.(2013?哈尔滨)如图,在△ABC中,以BC为直径作半圆O,交AB于点D,交AC于点E,AD=AE.(1)求证:AB=AC(2)若BD=4,BO=2,求AD的长.22.(2012?大庆)如图△ABC中,BC=3,以BC为直径的⊙O交AC于点D,若D是AC中点,∠ABC=120°.(1)求∠ACB的大小;(2)求点A到直线BC的距离.参考答案一.选择题(共12小题)1. C2. A.3. B.4. C.5. B.6. C.7. D.8. B.9. C.10. B.11. D.12. A.二.填空题(共6小题)13..14.50°.15. 4.16. 2.17..18..三.解答题(共4小题)19.解:(1)∵∠BPC=60°,∴∠BAC=60°,∵AB=AC,∴△ABC为等边三角形,∴∠ACB=∠ABC=60°,∴∠APC=∠ABC=60°,而点P是的中点,∴∠ACP=∠ACB=30°,∴∠PAC=90°,∴tan∠PCA==tan30°=,∴AC=PA;(2)过A点作AD⊥BC交BC于D,连结OP交AB于E,如图,∵AB=AC,∴AD平分BC,∴点O在AD上,连结OB,则∠BOD=∠BAC,∵∠BPC=∠BAC,∴sin∠BOD=sin∠BPC==,设OB=25x,则BD=24x,∴OD==7x,在Rt△ABD中,AD=25x+7x=32x,BD=24x,∴AB==40x,∵点P是的中点,∴OP 垂直平分AB,∴AE=AB=20x,∠AEP=∠AEO=90°,在Rt△AEO中,OE==15x,∴PE=OP﹣OE=25x﹣15x=10x,在Rt△APE中,tan∠PAE===,即tan∠PAB的值为.20.(1)证明:∵AB为⊙O的直径,∴∠ACB=90°,∴AC⊥BC,又∵DC=CB,∴AD=AB,∴∠B=∠D;(2)解:设BC=x,则AC=x﹣2,在Rt△ABC中,AC2+BC2=AB2,∴(x﹣2)2+x2=42,解得:x1=1+,x2=1﹣(舍去),∵∠B=∠E,∠B=∠D,∴∠D=∠E,∴CD=CE,∵CD=CB,∴CE=CB=1+.21.解:(1)连接BE,CD,∵BC是半圆O的直径,∴∠BDC=∠BEC=90°,∴∠ADC=∠AEB=90°,在Rt△ABE和Rt△ACD中,∵,∴△ABE≌△ACD,∴AB=AC.(2)∵BO=2,∴BC=4,在Rt△BDC中,CD==8,设AD=x,则AC=AB=x+4,在Rt△ADC中,82+x2=(x+4)2,解得:x=6.即AD=6.22.解:(1)连接BD,∵以BC为直径的⊙O交AC于点D,∴∠BDC=90°,∵D是AC中点,∴BD是AC的垂直平分线,∴AB=BC,∴∠A=∠C,∵∠ABC=120°,∴∠A=∠C=30°,即∠ACB=30°;(2)过点A作AE⊥BC于点E,∵BC=3,∠ACB=30°,∠BDC=90°,∴cos30°==,∴CD=,∵AD=CD,∴AC=3,∵在Rt△AEC中,∠ACE=30°,∴AE=×3=.。


B图2OBDCA图3圆中的角度计算专项训练圆心角定理推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等。
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。
圆周角定理推论:1.在同圆或等圆中,同弧或等弧所对的圆周角相等:相等的圆周角所对的弧也相等。
2.半圆或直径所对的圆周角是直角;90°的圆周角所对的弦是直径。
例1. 如图,点A、B、C在⊙O上,∠ACB=20°,则∠AOB的度数是()变式:如图,点A、B、C在⊙O上,AO∥BC,∠OAC=20°,则∠AOB的度数是()例2. 如图,若圆心角∠ABC=100°,则圆周角∠ADC=()变式:如图,若圆心角∠ABC=n°,则圆周角∠ADC=()小结:做题方法,数学定理练习:11. 如图2,在⊙O中,弦AD平行于弦BC,若80AOC=∠,则∠ABC 度, DAB∠= 度.2. 如图3,AB和CD都是⊙O的直径,50AOC=∠,则C∠的度数是3. 如图4,点A,B,C在⊙O上,80AOC=∠,则ABC∠的度数是5. 如图,已知AB是⊙O的直径,⌒ = ⌒ = ⌒ = ∠BOE=400,那么∠AOE =度例3.如图,已知AB是⊙O的直径, C,D 是⊙O上的两点,∠D=1300,则∠BAC= 度例2CD DE EBC图480_C_A_B_E_O_D例2”例1 例1”图7E 图96. 如图,AB为O ⊙的直径,C D ,是O⊙上两点,若50ABC =∠,则D ∠的度数为________.7. 如图,AB 是O ⊙的直径,点C 在O 上,连结OC ,BC ,若30OCB ∠=,则AO C ∠的度数为________.8. 如图所示,在⊙O 中,AB 是⊙O 的直径,∠ACB 的角平分线CD 交⊙O 于D ,则∠ABD =_____________度。

完整版)圆心角圆周角练习题知识点三:弧、弦、圆心角与圆周角1.定义圆心角为顶点在圆心的角。
2.在同圆或等圆中,弧、弦、圆心角之间的关系:两个圆心角相等,圆心角所对的弧相等(无论是优弧还是劣弧),圆心角所对的弦相等。
3.一个角是圆周角必须满足两个条件:(1)角的顶点在圆上;(2)角的两边都与圆有除顶点外的交点。
4.同一条弧所对的圆周角有两个。
5.圆周角定理:圆周角等于圆心角的一半。
6.圆周角定理的推论:(1)同弦或等弦所对的圆周角相等;(2)半圆或直径所对的圆周角相等;(3)90°的圆周角所对的弦是直径。
需要注意的是,“同弦或等弦”改为“同弧或等弧”结论就不一定成立了,因为一条弦所对的圆周角有两类,它们是相等或互补关系。
7.圆内接四边形定义为所有顶点都在圆上的多边形,圆心即为这个圆内接四边形的交点。
圆内接四边形的对角线相互垂直,且交点为对角线的中点。
夯实基础1.如果两个圆心角相等,则它们所对的弧相等,选项B正确。
2.不正确的语句为③,因为圆不一定是轴对称图形,只有圆上的任何一条直径所在直线才是它的对称轴。
3.错误的说法是D,相等圆心角所对的弦不一定相等。
4.根据圆心角的性质,∠A=2∠B,所以∠A=140°。
5.∠BAC与∠BCD互补,∠BCD与∠CBD相等,所以与∠BAC相等的角有2个,即∠CBD和∠ABD。
6.因为∠CAB为30°,所以∠ABC为60°,由正弦定理可得BC=5√3.7.根据圆周角定理,∠ACB=40°。
8.设∠A=3x,∠B=4x,∠C=6x,则∠D=360°-3x-4x-6x=120°。
9.∠DCE=∠A。
1、如图,AB是⊙O的直径,C,D是BE上的三等分点,∠AOE=60°,求证∠COE=80°。
证明:由三等分点的性质可知,BC=CD=DE,又∠AOE=60°,所以∠AOC=120°。
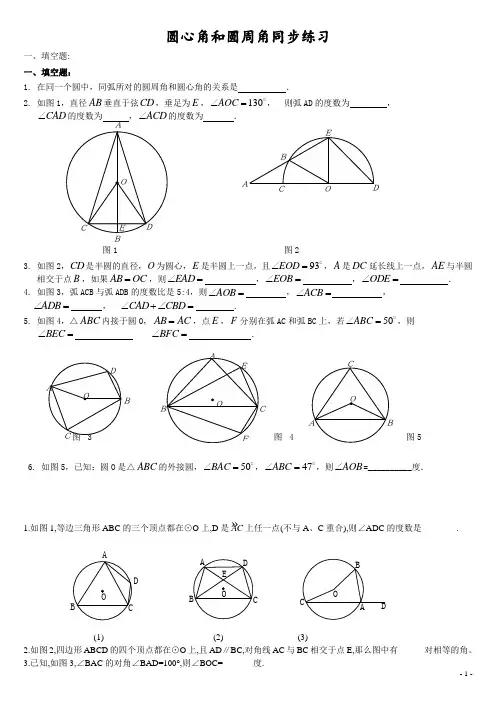
圆心角和圆周角同步练习一、填空题: 一、填空题:1. 在同一个圆中,同弧所对的圆周角和圆心角的关系是.2. 如图1,直径AB 垂直于弦CD ,垂足为E ,130AOC ∠=o, 则弧AD 的度数为 ,CAD ∠的度数为 ,ACD ∠的度数为 .图1 图23. 如图2,CD 是半圆的直径,O 为圆心,E 是半圆上一点,且93EOD ∠=o,A 是DC 延长线上一点,AE 与半圆相交于点B ,如果AB OC =,则EAD ∠= ,EOB ∠=,ODE ∠=.4. 如图3,弧ACB 与弧ADB 的度数比是5:4,则AOB ∠= ,ACB ∠=,ADB ∠= , CAD CBD ∠+∠= .5. 如图4,△ABC 内接于圆O ,AB AC =,点E ,F 分别在弧AC 和弧BC 上,若50ABC ∠=o,则BEC ∠= BFC ∠=.图图56. 如图5,已知:圆O 是△ABC 的外接圆,50BAC ∠=o,47ABC ∠=o,则AOB ∠=__________度.1.如图1,等边三角形ABC 的三个顶点都在⊙O 上,D 是»AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.DDCBAO(1) (2) (3)2.如图2,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BC 相交于点E,那么图中有______对相等的角。
3.已知,如图3,∠BAC 的对角∠BAD=100°,则∠BOC=_______度.A4.如图4,A 、B 、C 为⊙O 上三点,若∠OAB=46°,则∠ACB=_______度.BAA(4) (5) (6)5.如图5,AB 是⊙O 的直径, »»BC BD =,∠A=25°,则∠BOD 的度数为________.6.如图6,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.二、选择题:7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°DDCBA(7) (8) (9) (10)8.如图8,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( ) A.2对 B.3对 C.4对 D.5对9.如图9,D 是»AC 的中点,则图中与∠ABD 相等的角的个数是( ) A.4个 B.3个 C.2个 D.1个10.如图10,∠AOB=100°,则∠A+∠B 等于( )A.100°B.80°C.50°D.40°11.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( ) A.30° B.30°或150° C.60° D.60°或120°12.如图,A 、B 、C 三点都在⊙O 上,点D 是AB 延长线上一点,∠AOC=140°, ∠CBD 的度数是( ) A.40° B.50° C.70° D.110°三、解答题:13.如图,⊙O 的直径AB=8cm,∠CBD=30°,求弦DC 的长.BA14.如图,A 、B 、C 、D 四点都在⊙O 上,AD 是⊙O 的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC 的长.15.如图,在⊙O 中,AB 是直径,CD 是弦,AB ⊥CD.(1)P 是¼CAD上一点(不与C 、D 重合),试判断∠CPD 与∠COB 的大小关系, 并说明理由. (2)点P′在劣弧CD 上(不与C 、D 重合时),∠CP′D 与∠COB 有什么数量关系?请证明你的结论.16.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN 进攻.当甲带球部到A 点时,乙随后冲到B 点,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)答案:1.120°2.3 13.160°4.44°5.50°7.A 8.C 9.B 10.C 11.B 12.C 13.连接OC 、OD,则OC=OD=4cm,∠COD=60°,故△COD 是等边三角形,从而CD= 4cm. 14.连接DC,则∠ADC=∠ABC=∠CAD,故AC=CD.∵AD 是直径,∴∠ACD=90°, ∴AC 2+CD 2=AD 2,即2AC 2=36,AC 2. 15.(1)相等.理由如下:连接OD,∵AB ⊥CD,AB 是直径,∴»»BCBD ,∴∠COB= ∠DOB. ∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)∠CP′D+∠COB=180°.理由如下:连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠CP′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.16.迅速回传乙,让乙射门较好,在不考虑其他因素的情况下, 如果两个点到球门的距离相差不大,要确定较好的射门位置,关键看这两个点各自对球门MN的张角的大小,当张角越大时,射中的机会就越大,如图所示,则∠A<MCN=∠B,即∠B>∠A, 从而B处对MN的张角较大,在B处射门射中的机会大些.。

圆周角和圆心角的练习题一、选择题1.圆周角是24°,则它所对的弧是________ A.12°;B.24°;C.36°;D.48°.2.在⊙O中,∠AOB=84°,则弦AB所对的圆周角是________A.42°;B.138°;C.84°;D.42°或138°.3.如图,圆内接四边形ABCD的对角线AC,BD把四边形的四个角分成八个角,这八个角中相等的角的对数至少有___________.()A.1对;B.2对;C.3对;D.4对.4.如图,AC是⊙O的直径,AB,CD是⊙O的两条弦,且AB∥C D.如果∠BAC=32°,则∠AOD=___[ ] A.16°;B.32°;C.48°;D.64°.二、计算题6.如图,AD是△ABC外接圆的直径,AD=6cm,∠DAC=∠AB C.求AC的长.7.已知:△DBC和等边△ABC都内接于⊙O,BC=a,∠BCD=75°(如图).求BD 的长.8.如图,半圆的直径AB =13cm ,C 是半圆上一点,CD ⊥AB 于D ,并且CD =6cm .求AD 的长.、9.如图,圆内接△ABC 的外角∠MAB 的平分线交圆于E ,EC =8cm .求BE 的长.10.已知:如图,AD 平分∠BAC ,DE ∥AC ,且AB =a .求DE 的长.11.如图,在⊙O 中,F ,G 是直径AB 上的两点,C ,D,E 是半圆上的三点,如果弧AC 的度数为60°,弧BE 的度数为20°,∠CFA =∠DFB ,∠DGA =∠EG B .求∠FDG 的大小.12.如图,⊙O 的内接正方形ABCD 边长为1,P 为圆周上与A ,B ,C ,D 不重合的任意点.求PA 2+PB 2+PC 2+PD 2的值.13.如图,在梯形ABCD 中,AD ∥BC ,∠BAD =135°,以A 为圆心,AB 为半径作⊙A 交AD ,BC 于E ,F 两14.如图,⊙O 的半径为R ,弦AB =a ,弦BC ∥OA ,求AC 的长.15.如图,在△ABC 中,∠BAC ,∠ABC ,∠BCA 的平分线交△ABC 的外接圆于D ,E 和F ,如果,,分别为m °,n °,p °,求△ABC 的三个内角.16.如图,在⊙O 中,BC ,DF 为直径,A ,E 为⊙O 上的点,AB =AC ,EF =21DF .求∠ABD +∠CBE 的值.17.如图,等腰三角形ABC 的顶角为50°,AB =AC ,以数.第二页18.如图,AB是⊙O的直径,AB=2cm,点C在圆周上,且∠BAC=30°,∠ABD=120°,CD⊥BD于D.求BD的长.19.如图,△ABC中,∠B=60°,AC=3cm,⊙O为△ABC的外接圆.求⊙O的半径.20.以△ABC的BC边为直径的半圆,交AB于D,交AC于E,EF⊥BC于F,AB=8cm,AE=2cm,BF∶FC=5∶1(如图).求CE的长.21.已知等腰三角形的腰长为13cm,底边长为10cm,求它的外接圆半径.22.如图,△ABC中,AD是∠BAC的平分线,延长AD交△ABC的外接圆于E,已知AB=a,BD=b,BE=c.求AE的长.23.如图,△ABC中,AD是∠BAC的平分线,延长AD交△ABC的外接圆于E,已知AB=6cm,BD=2cm,BE=2.4cm.求DE的长.24.如图,梯形ABCD内接于⊙O,AB∥CD,的度数为60°,∠B=105°,⊙O 的半径为6cm.求BC的长.25.已知:如图,AB是⊙O的直径,AB=4cm,E为OB的中点,弦CD⊥AB于E.求CD的长.26.如图,AB为⊙O的直径,E为OB的中点,CD为过E点并垂直AB的弦.求∠ACE的度数.27.已知:如图,在△ABC中,∠C=90°,∠A=38°,以C为圆心,BC为半径作圆,交AB于D,求的度数.第三页28.如图,△ABC内接于圆O,AD为BC边上的高.若AB=4cm,AC=3cm,AD=2.5cm,求⊙O的半径.29.设⊙O的半径为1,直径AB⊥直径CD,E是OB的中点,弦CF过E点(如图),求EF的长.30.如图,在⊙O中直径AB,CD互相垂直,弦CH交AB于K,且AB=10cm,CH=8cm.求BK∶AK的值.31.如图,⊙O的半径为40cm,CD是弦,A为的中点,弦AB交CD于F.若AF=20cm,BF=40cm,求O点到弦CD的弦心距.32.如图,四边形ABCD内接于以AD为直径的圆O,且AD=4cm,AB=CB=1cm,求CD的长.三、证明题33.如图,已知△ABC内接于半径为R的⊙O,A为锐角.求证:ABCsin =2R 34.已知:如图,在△ABC 中,AD ,BD 分别平分∠BAC 和∠ABC ,延长AD 交△ABC 的外接圆于E ,连接BE .求证:BE =DE .35.如图,已知D 为等边三角形ABC 外接圆上的上的一点,AD 交BC 边于E .求证:AB 为AD 和AE 的比例中项.36.已知:如图,在△ABC 中,AB =AC ,以AB 为直径的圆交BC 于D .求证:D 为BC 的中点.第四页37.已知:如图,⊙O 是△ABC 的外接圆,AD ⊥BC 于D ,AE 平分∠BAC 交⊙O 于E .求证:AE 平分∠OA D .38.已知:如图,△ABC 的AB 边是⊙O 的直径,另两边BC 和AC 分别交⊙O 于D ,E 两点,DF ⊥AB ,交AB 于F ,交BE 于G ,交AC 的延长线于H .求证:DF 2=HF ·GF .39.已知:如图,圆内接四边形ABCD 中,BC =C D .求证:AB ·AD +BC 2=AC 2.40.已知:如图,AB 是半圆的直径,AC 是一条弦,D 是中点,DE ⊥AB 于E ,交AC 于F ,DB 交AC 于G .求证:AF =FG .41.如图,AB 是⊙O 的弦,P 是AB 所对优弧上一点,直径CD ⊥AB ,PB 交CD 于E ,延长AP 交CD 的延长线于F .求证:△EPF ∽△EO A .42.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,M为上一点,AM的延长线交DC于F.求证:∠AMD=∠FM C.43.已知:如图,AB,AC分别为⊙O的直径与弦,CD⊥AB于D,E为⊙O外一点,且AE=AC,BE交⊙O于F,连结ED,CF.求证:∠ACF=∠AE D.44.如图,⊙O的半径OD,OE分别垂直于弦AB和AC,连结DE交AB,AC于F,G.求证:AF2=AG2=DF·GE.45.如图,△ABC内接于圆,D是AB上一点,AD=AC,E是AC延长线上一点,AE=AB,连接DE交圆于F,延长ED交圆于G.求证:AF=AG.第五页46.已知:如图,⊙O的两条直径AB⊥CD,E是OD的中点,连结AE,并延长交⊙O于M,连结CM,交AB于F.求证:OB=3OF.47.已知:如图,△ABC是等边三角形,以AC为直径作圆交BC于D,作DE⊥AC 交圆于E.(1)求证:△ADE是等边三角形;(2)求S△ABC∶S△ADE.48.已知:如图,半径都是5cm的两等圆⊙O1和⊙O2相交于点A,B,过A作⊙O1的直径AC与⊙O2交于点D,且AD∶DC=3∶2,E为DC的中点.(1)求证:AC⊥BE;(2)求AB的长.一、填空题:1.如图1,等边三角形ABC 的三个顶点都在⊙O 上,D 是AC 上任一点(不与A 、C 重合),则∠ADC 的度数是________.DCBAO(1) (2) (3)2.如图2,四边形ABCD 的四个顶点都在⊙O 上,且AD ∥BC,对角线AC 与BC 相交于点E,那么图中有_________对全等三角形;________对相似比不等于1的相似三角形.3.已知,如图3,∠BAC 的对角∠BAD=100°,则∠BOC=_______度.4.如图4,A 、B 、C 为⊙O 上三点,若∠OAB=46°,则∠ACB=_______度.BAA(4) (5) (6)5.如图5,AB 是⊙O 的直径, BC BD ,∠A=25°,则∠BOD 的度数为________.第六页6.如图6,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______. 二、选择题:7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC 的度数是( ) A.50° B.100° C.130° D.200°DCBA(7) (8) (9) (10)8.如图8,A 、B 、C 、D 四个点在同一个圆上,四边形ABCD 的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对9.如图9,D 是AC 的中点,则图中与∠ABD 相等的角的个数是( )A.4个B.3个C.2个D.1个 10.如图10,∠AOB=100°,则∠A+∠B 等于( ) A.100° B.80° C.50° D.40°11.在半径为R 的圆中有一条长度为R 的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120°12.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )A.40°B.50°C.70°D.110°三、解答题:13.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.A14.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.15.如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值.16.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是CAD上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.第七页17.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素) 18.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢?。
圆的定义、圆心角、弧、弦和圆周角基础练习1、⊙O中,弦AB=12,⊙O半径为10,则O到AB的距离为.2、P为⊙O内一点,OP=4,⊙O半径为5,则过P点的最短弦长为,最长弦.3、如图1,⊙O中,弦CD⊥直径AB于E,AB=20,CD=16,则BE= .4、AB为⊙O直径,OD⊥弦AC于D,且OD=4,则弦BC= .5、如图2,将半径是2cm的圆形纸片折叠后圆弧恰好经过圆心O,则折痕AB= .6、半径为13的圆中,弦AB∥CD,且AB=10,CD=24,则AB与CD之间的距离为.7、如图3,AB为直径,B为弧BC的中点,∠A=35°,则∠BOD= .8、以等腰△ABC的腰AB为直径作⊙O交底边BC于点D,交AC于E,连接DE,若BC=8,则DE= .9、⊙O直径AB=8cm,C为⊙O上一点,∠BAC=30°,则BC= .10、如图4,⊙O半径OA⊥OB,D、E为⊙O上的点,则∠D+∠E= .11、如图5,∠ACB=20°,则∠OAB= .12、如图6,AB直径,∠BAC=20°,则∠D= .13、如图7,∠ABC=120°,则∠AOC= .14、如图8,AB为直径,∠COB=30°,则∠ADC= .15、如图9,OA⊥OB,∠A=38°,则∠F= .16、如图10,AB为直径,弦CD与AB相交于E,则∠AEC= .17、如图11,Δ ABC中,AB=AC,D是⊙O上的点,E在BD的延长线上且∠ADE=65°,则∠BOC= .18、已知⊙O是等边ΔABC 的外接圆,且⊙O半径为4,则ΔABC的边长是.19、如图12,∠BAC=30°,BC=2.4cm,则⊙O直径AB= .20、⊙O半径为10,OP=8,则点P在⊙O .(填内、上或外)21、如图13,⊙O的直径AB⊥弦CD于E,AB=10,CD=8,则BE= .22、如图14,⊙O的直径AB⊥弦CD,D=30°,CD= .23、如图15,∠ACB=45°,AB=4,⊙O的半径为.24、在ΔABC中,∠C=90°,AC=8,BC=6,则ΔABC的外接圆半径是.25、如图16,AB是⊙O的直径,CD⊥AB,∠CDB=35°,则∠CAD= .26、若AB是⊙O的弦,OA=6,∠AOB=120°,则AB= .27、如图17,∠COD=84°,AC平分∠OCD,则∠ABD+∠OCA= .28、如图18,AB为直径,∠BAC=50°,∠D= .29、如图19,AB直径,∠B=30°,OD⊥BC,∠BCD= .30、如图20,∠A=30°,OD⊥AB,则∠E= .31、如图21,∠BCD=58°,DC直径,则∠A= .CA P O DCEO AD B 32. 如图所示,OA 是圆O 的半径,弦CD ⊥OA 于点P ,已知OC=5,OP=3,则弦CD=_______。
圆心角与圆周角练习题一、选择题(每题3分,共30分)1. 在同圆或等圆中,如果圆心角相等,那么对应的圆周角:A. 相等B. 不相等C. 无法确定D. 可能相等2. 已知圆的半径为5,圆心角为30°,求圆周角的度数:A. 15°B. 30°C. 45°D. 60°3. 在圆中,圆心角的度数是圆周角度数的:A. 2倍B. 1/2倍C. 1/4倍D. 4倍4. 如果一个圆周角的度数是60°,那么它所对的圆心角是:A. 120°B. 60°C. 30°D. 180°5. 在同圆或等圆中,圆心角和圆周角的关系是:A. 相等B. 互补C. 互余D. 没有固定关系6. 已知圆的半径为10,圆心角为45°,求圆周角的度数:A. 22.5°B. 45°C. 90°D. 无法确定7. 圆心角和圆周角的关系可以用以下哪个公式表示:A. 圆心角= 2 × 圆周角B. 圆周角= 2 × 圆心角C. 圆心角 = 圆周角D. 圆周角 = 圆心角 / 28. 如果一个圆周角的度数是90°,那么它所对的圆心角是:A. 45°B. 90°C. 180°D. 270°9. 在圆中,圆心角和圆周角的度数之和:A. 总是等于180°B. 总是等于360°C. 总是小于360°D. 总是大于360°10. 已知圆的半径为8,圆心角为60°,求圆周角的度数:A. 30°B. 60°C. 90°D. 120°二、填空题(每题2分,共20分)11. 在同圆或等圆中,如果圆心角是圆周角度数的2倍,那么圆周角的度数是圆心角的________倍。
12. 圆心角的度数是圆周角度数的________倍。
圆----圆心角与圆周角练习题1.在⊙O中,同弦所对的圆周角()A.相等 B.互补 C.相等或互补 D.都不对2.如图,在⊙O中,弦AD=弦DC,则图中相等的圆周角的对数是()A.5对 B.6对 C.7对 D.8对3.下列说法正确的是()A.顶点在圆上的角是圆周角 B.两边都和圆相交的角是圆周角C.圆心角是圆周角的2倍 D.圆周角度数等于它所对圆心角度数的一半4.下列说法错误的是()A.等弧所对圆周角相等 B.同弧所对圆周角相等C.同圆中,相等的圆周角所对弧也相等. D.同圆中,等弦所对的圆周角相等5.如图4,AB是⊙O的直径,∠AOD是圆心角,∠BCD是圆周角.若∠BCD=25°,则∠AOD= .6.如图5,⊙O直径MN⊥AB于P,∠BMN=30°,则∠AON= .7.如图6,AB是⊙O的直径,⌒BC=⌒BD,∠A=25°,则∠BOD= .8.如图7,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M若∠BAC=60°∠ABC=50°,则∠CBM= ,∠AMB= .9.⊙O中,若弦AB长22cm,弦心距为2cm,则此弦所对的圆周角等于.10.如图8,⊙O中,两条弦AB⊥BC,AB=6,BC=8,求⊙O的半径.11.如图9,AB是⊙O的直径,FB交⊙O于点G,FD⊥AB,垂足为D,FD交AG于E.求证:EF·DE=AE·EG.12.如图,AB 是半圆的直径,AC 为弦,OD ⊥AB ,交AC 于点D ,垂足为O ,⊙O 的半径为4,OD=3,求CD 的长.13.如图,⊙O 的弦AD ⊥BC ,垂足为E ,∠BAD=∠α,∠CAD=∠β,且sin α=53,cos β=31,AC=2,求(1)EC 的长;(2)AD 的长.。
圆周角圆心角练习题一、选择题1. 圆周角定理指出,圆周角的度数是同弧所对圆心角的度数的______。
A. 1/2B. 2倍C. 3倍D. 4倍2. 若圆心角为40°,则同弧所对的圆周角为______。
A. 20°B. 40°C. 80°D. 120°3. 在圆中,若一条弦所对的圆心角为60°,则这条弦所对的圆周角是______。
A. 30°B. 45°C. 60°D. 90°4. 圆内接四边形ABCD中,若∠A=60°,则∠B的度数为______。
A. 60°B. 120°C. 180°D. 240°5. 已知圆的半径为5,圆心角为120°,那么这个圆心角所对的弧长为______。
A. 5πB. 10πC. 15πD. 20π二、填空题6. 若圆周角为45°,则同弧所对的圆心角为______。
7. 在圆中,若弦AB所对的圆心角为100°,则弦AB所对的圆周角为______。
8. 已知圆的半径为10,圆心角为150°,则这个圆心角所对的弧长为______。
9. 圆内接四边形ABCD中,若∠A=90°,则∠B的度数为______。
10. 若圆的半径为8,圆心角为90°,则这个圆心角所对的弧长为______。
三、简答题11. 解释什么是圆周角,并说明它与圆心角的关系。
12. 给出一个圆内接四边形的例子,并说明其对角互补的性质。
13. 解释如何计算一个圆心角所对的弧长。
14. 在圆中,如果知道圆周角的度数,如何计算同弧所对的圆心角的度数?15. 圆内接四边形的对角互补性质在实际问题中有哪些应用?四、解答题16. 已知圆的半径为6,圆心角为60°,求这个圆心角所对的弧长。
17. 在圆中,若弦AB所对的圆心角为120°,求弦AB所对的圆周角的度数。
(完整版)圆心角圆周角练习题知识点三:弧、弦、圆心角与圆周角1、圆心角定义:顶点在的角叫做圆心角2. 在同圆或等圆中,弧、弦、圆心角之间的关系:两个圆心角相等?圆心角所对的弧(都是优弧或都是劣弧)相等?圆心角所对的弦相等3、一个角是圆周角必须满足两个条件:(1)角的顶点在________;(2)角的两边都是与圆有除顶点外的交点。
4. 同一条弧所对的圆周角有__________个5.圆周角定理:1=2圆周角圆心角6.圆周角定理推论:(1)同弧或等弧所对的圆周角相等(2)半圆或直径所对的圆周角相等(3)90°的圆周角所对的弦是直径。
注意:“同弧或等弧”改为“同弦或等弦”结论就不一定成立了,因为一条弦所对的圆周角有两类,它们是相等或互补关系。
7. 圆内接四边形:定义:如果一个多边形的所有顶点都在圆上,这个多边形叫做,这个圆叫做。
性质:圆内接四边形的对角夯实基础1.如果两个圆心角相等,那么()A .这两个圆心角所对的弦相等;B .这两个圆心角所对的弧相等C .这两个圆心角所对的弦的弦心距相等;D .以上说法都不对2.下列语句中不正确的有()①相等的圆心角所对的弧相等②平分弦的直径垂直于弦③圆是轴对称图形,任何一条直径所在直线都是它的对称轴④长度相等的两条弧是等弧A.3个B.2个C.1个D.以上都不对3. 在同圆或等圆中,下列说法错误的是()A .相等弦所对的弧相等B .相等弦所对的圆心角相等C .相等圆心角所对的弧相等D .相等圆心角所对的弦相等4、如图,在⊙O 中,??AB AC ,∠B =70°,则∠A 等于.5、如图,在⊙O 中,若C 是?BD的中点,则图中与∠BAC 相等的角有() A.1个 B.2 个 C.3个 D.4个6、如图,若AB 是⊙O 的直径,AB=10cm ,∠CAB=30°,则BC= cm .7、如图,已知OA ,OB 均为⊙O 上一点,若∠AOB=80°,则∠ACB=()A.80°B.70°C.60°D.40°8、圆内接四边形ABCD,∠A,∠B,∠C的度数之比为3:4:6,则∠D的度数为()A.60 B.80 C.100 D.1209、已知如图,四边形ABCD内接于⊙O,若∠A=60°,则∠DCE =.题型一:利用圆心角圆周角定理求角度1、如图,AB是⊙O的直径,C,D是BE上的三等分点,∠AOE=60°,则∠COE是()A.40° B. 60° C. 80° D. 120 °2、如图,AB是⊙O的直径,BC⌒=BD⌒ ,∠A=25°,则∠BOD= .3、已知圆O的半径为5,弦AB的长为5,则弦AB所对的圆心角∠AOB= .4、在⊙O中,弦AB所对的劣弧为圆周的41,圆的半径等于12,则圆心角∠AOB=;弦AB的长为.5、如图,AB是⊙O的直径,点C在⊙O上,若∠A=40 o,则∠B 的度数为()A.80 oB.60 oC.50 oD.40 o6、如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为()OEDCBAODCBAA.50°B.60°C.70°D.80°7、如图,AB、CD是⊙O的两条弦,连接AD、BC,若∠BAD=60°,则∠BCD的度数为()A.40°B.50°C.60°D.70°8、如图,点A、B、C在⊙O上,∠AOC=60°,则∠ABC的度数是.9、如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=度.10、如图,⊙O的弦CD与直径AB相交,若∠BAD=50°,则∠ACD=..11、如图,AB是⊙O的直径,点C是圆上一点,∠BAC=70°,则∠OCB=.12、如图,在Rt △ABC 中,∠C=90°,∠A=26°,以点C 为圆心,BC 为半径的圆分别交AB 、AC 于点D 、点E ,则弧BD 的度数为()A .26°B .64°C .52°D .128°题型二:利用圆心角圆周角的性质定理求线段1、在⊙O 中,圆心角∠AOB =90°,点O 到弦AB 的距离为4,则⊙O 的直径的长为( )A.4B.82C.24D.162、如图,⊙O 是△ABC 的外接圆,∠B=60°,OP ⊥AC 于点P ,,则⊙O 的半径为()A .B .C .8D .123、如图,△ABC 内接于⊙O ,∠BAC=120°,AB=AC ,BD 为⊙O 的直径,AD=6,则DC= .题型三:利用弧、弦、圆心角、圆周角之间的关系证明弧相等,线段相等,角度相等1、如图,在⊙O 中,AB =AC ,∠ACB=60°,求证∠AOB =∠BOC =∠AOC .333B2.如图,在⊙O 中,C 、D 是直径AB 上两点,且AC=BD ,MC ⊥AB ,ND ⊥AB ,M 、N?在⊙O 上.(1)求证:?AM =?BN ;(2)若C 、D 分别为OA 、OB 中点,则?AM MN NB ==成立吗?3、如图,以⊙O 的直径BC 为一边作等边△ABC,AB 、AC 交⊙O 于D 、E,求证:BD=DE=EC4、如图,⊙O 的直径AB 为10cm ,弦AC 为6cm ,∠ACB 的平分线交⊙O 于D ,求BC ,AD ,BD 的长.5、如图,AB 是⊙O 的直径,C 是?BD的中点,CE ⊥AB 于 E ,BD 交CE 于点F .(1)求证:CF ﹦BF ;(2)若CD ﹦6, AC ﹦8,则⊙O 的半径为,CE 的长是.BA作业1、如图,AB 是⊙O 的直径,==,∠COD=34°,则∠AEO 的度数是()A .51°B .56°C .68°D .78°2、圆中有两条等弦AB=AE ,夹角∠A=88°,延长AE 到C ,使EC=BE ,连接BC ,如图.则∠ABC 的度数是()A .90°B .80°C .69°D .65°3. 如图所示⊙O 中,已知∠BAC=∠CDA=20°,则∠ABO 的度数为.B4. 如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,(1)求证:△ABC是等边三角形;(2)求圆心O到BC的距离OD.5、如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O 上一点,OD⊥AC,垂足为E,连接BD(1)求证:BD平分∠ABC;(2)当∠ODB=30°时,求证:BC=OD.。
初三数学圆周角和圆心角的关系试题1.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.【答案】160°【解析】由∠BAD=100°可得∠BAC的度数,再根据圆周角定理即可求得结果.∵∠BAD=100°∴∠BAC=80°∴∠BOC=160°.【考点】邻补角定理,圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.2.如图,AB是半圆O的直径,AC="AD,OC=2,∠CAB=30°," 则点O到CD的距离OE=____.【答案】【解析】由AC=AD,∠CAB=30°可得∠CDO的度数,即可得到∠EOD、∠COE的度数,判断出△COE的形状再结合勾股定理即可求得结果.∵AC=AD,∠CAB=30°,OA=OC∴∠CDO=75°,∠COD=60°∴∠EOD=15°∴∠COE=45°∴△COE为等腰直角三角形∵OC=2∴OE=.【考点】三角形内角和定理,勾股定理点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.3.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )A.50°B.100°C.130°D.200°【答案】A【解析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵∠BOC=100°∴∠BAC=50°故选A.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.4.如图,A、B、C、D四个点在同一个圆上,四边形ABCD的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对【答案】C【解析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.相等的角有∠ADB=∠ACB,∠BAC=∠BDC,∠CAD=∠CBD,∠ACD=∠ABC4对,故选C.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.5.如图,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A.4个B.3个C.2个D.1个【答案】B【解析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵D是弧AC的中点∴∠ABD=∠ACD=∠CBD=∠CAD故选B.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.6.如图, ,则∠A+∠B等于( )A.100°B.80°C.50°D.40°【答案】C【解析】连接CO并延长交圆于点D,根据圆周角定理即可得到结果.连接CO并延长交圆于点D由图可得∠A+∠B=∠AOD+∠BOD=∠AOB=50°故选C.【考点】圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.7.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120°【答案】B【解析】根据圆的性质可得这条弦与半径围成的三角形为等边三角形,再根据圆周角定理即可求得结果.由题意得这条弦与半径围成的三角形为等边三角形则该弦所对的圆周角的度数是30°或150°故选B.【考点】圆周角定理点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.8.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC="140°," ∠CBD的度数是( )A.40°B.50°C.70°D.110°【答案】C【解析】先求得弧ABC所对的圆周角的度数,再根据圆内接四边形的对角互补可得∠ABC的度数,即可求得结果.∵∠AOC=140°∴弧ABC所对的圆周角的度数为70°∴∠ABC=110°∴∠CBD=70°故选C.【考点】圆周角定理,圆内接四边形的性质点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.9.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.【答案】4cm【解析】连接OC、OD,根据圆周角定理可得∠COD=60°,即可得到△COD是等边三角形,根据等边三角形的性质即可求得结果.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD=4cm.【考点】圆周角定理,等边三角形的判定和性质点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.10.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.【答案】(1)相等;(2)∠CP′D+∠COB=180°【解析】(1)连接OD,根据垂径定理可得∠COB=∠DOB,再结合圆周角定理即可得到结果;(2)连接P′P,则可得∠P′CD=∠P′PD,∠P′PC=∠P′DC.即可得∠P′CD+∠P′DC=∠CPD,从而可以得到结果.从而∠CP′D+∠COB=180°.(1)连接OD,∵AB⊥CD,AB是直径,∴,∴∠COB= ∠DOB.∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠C P′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.【考点】垂径定理,圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.。
圆心角与圆周角 练习题1.圆周角是24°,则它所对的弧的度数是( ) A .12°;B .24°;C .36°;D .48°.2.在⊙O 中,∠AOB=84°,则弦AB 所对的圆周角是( )A .42°;B .138°;C .84°;D .42°或138°.3.如图,圆接四边形ABCD 的对角线AC ,BD 把四边形的四个角分成八个角,这八个角中相等的角的对数至少有( )A .1对;B .2对;C .3对;D .4对.4.如图,AC 是⊙O 的直径,AB ,CD 是⊙O 的两条弦,且AB ∥CD .如果∠BAC=32°,则∠AOD=( )A .16°;B .32°;C .48°;D .64°.5.直角三角形的斜边长是17,斜边上的高线长是120/17,求三角形外接圆半径长及各锐角的正切值.6.如图,AD 是△ABC 外接圆的直径,AD=6cm ,∠DAC=∠ABC .求AC 的长.7.已知:△DBC 和等边△ABC 都接于⊙O ,BC=a ,∠BCD=75°(如图).求BD 的长.8.如图,半圆的直径AB=13cm ,C 是半圆上一点,CD ⊥AB 于D ,并且CD=6cm .求AD 的长.、9.如图,圆接△ABC 的外角∠MAB 的平分线交圆于E ,EC=8cm .求BE 的长.10.已知:如图,AD 平分∠BAC ,DE ∥AC ,且AB=a .求DE 的长.11.如图,在⊙O 中,F ,G 是直径AB 上的两点,C ,D,E 是半圆上的三点,如果弧AC 的度数为60°,弧BE 的度数为20°,∠CFA=∠DFB ,∠DGA=∠EGB .求∠FDG 的大小.12.如图,⊙O 的接正方形ABCD 边长为1,P 为圆周上与A ,B ,C ,D 不重合的任意点.求PA2+PB2+PC2+PD2的值.13.如图,在梯形ABCD 中,AD ∥BC ,∠BAD=135°,以A 为圆心,AB 为半径作⊙A 交AD ,BC 于E ,F 两点,并交BA 延长线于G 求弧BF 的度数.14.如图,⊙O 的半径为R ,弦AB=a ,弦BC ∥OA ,求AC 的长.15.如图,在△ABC 中,∠BAC ,∠ABC ,∠BCA 的平分线交△ABC 的外接圆于D ,E 和F ,如果,,分别为m °,n °,p °,求△ABC 的三个角.16.如图,在⊙O 中,BC ,DF 为直径,A ,E 为⊙O 上的点,AB=AC ,EF=21DF .求∠ABD+∠CBE 的值.17.如图,等腰三角形ABC 的顶角为50°,AB=AC ,以AB 为直径作圆交BC 于点D ,交AC 于点E ,求弧BD ,弧DE ,弧AE 的度数.18.如图,AB 是⊙O 的直径,AB=2cm ,点C 在圆周上,且∠BAC=30°,∠ABD=120°,CD ⊥BD 于D .求BD 的长.19.如图,△ABC 中,∠B=60°,AC=3cm ,⊙O 为△ABC 的外接圆.求⊙O 的半径.20.以△ABC 的BC 边为直径的半圆,交AB 于D ,交AC 于E ,EF ⊥BC 于F ,AB=8cm ,AE=2cm ,BF ∶FC=5∶1(如图).求CE 的长.21.已知等腰三角形的腰长为13cm ,底边长为10cm ,求它的外接圆半径.22.如图,△ABC 中,AD 是∠BAC 的平分线,延长AD 交△ABC 的外接圆于E ,已知AB=a ,BD=b ,BE=c .求AE 的长.23.如图,△ABC 中,AD 是∠BAC 的平分线,延长AD 交△ABC 的外接圆于E ,已知AB=6cm ,BD=2cm ,BE=2.4cm .求DE 的长.24.如图,梯形ABCD 接于⊙O ,AB ∥CD ,的度数为60°,∠B=105°,⊙O 的半径为6cm .求BC 的长.25.已知:如图,AB 是⊙O 的直径,AB=4cm ,E 为OB 的中点,弦CD ⊥AB 于E .求CD 的长.26.如图,AB 为⊙O 的直径,E 为OB 的中点,CD 为过E 点并垂直AB 的弦.求∠ACE 的度数.27.已知:如图,在△ABC 中,∠C=90°,∠A=38°,以C 为圆心,BC 为半径作圆,交AB 于D ,求的度数.28.如图,△ABC 接于圆O ,AD 为BC 边上的高.若AB=4cm ,AC=3cm ,AD=2.5cm ,求⊙O 的半径.29.设⊙O 的半径为1,直径AB ⊥直径CD ,E 是OB 的中点,弦CF 过E 点(如图),求EF 的长.30.如图,在⊙O 中直径AB ,CD 互相垂直,弦CH 交AB 于K ,且AB=10cm ,CH=8cm .求BK ∶AK 的值.31.如图,⊙O 的半径为40cm ,CD 是弦,A 为的中点,弦AB 交CD 于F .若AF=20cm ,BF=40cm ,求O 点到弦CD 的弦心距.32.如图,四边形ABCD 接于以AD 为直径的圆O ,且AD=4cm ,AB=CB=1cm ,求CD 的长.33.如图,已知△ABC 接于半径为R 的⊙O ,A 为锐角.求证:A BCsin =2R34.已知:如图,在△ABC 中,AD ,BD 分别平分∠BAC 和∠ABC ,延长AD 交△ABC 的外接圆于E ,连接BE .求证:BE=DE .35.如图,已知D 为等边三角形ABC 外接圆上的上的一点,AD 交BC 边于E .求证:AB 为AD 和AE 的比例中项.36.已知:如图,在△ABC 中,AB=AC ,以AB 为直径的圆交BC 于D .求证:D 为BC 的中点.37.已知:如图,⊙O 是△ABC 的外接圆,AD ⊥BC 于D ,AE 平分∠BAC 交⊙O 于E .求证:AE 平分∠OAD .38.已知:如图,△ABC 的AB 边是⊙O 的直径,另两边BC 和AC 分别交⊙O 于D ,E 两点,DF ⊥AB ,交AB 于F ,交BE 于G ,交AC 的延长线于H .求证:DF2=HF ·GF .39.已知:如图,圆接四边形ABCD 中,BC=CD .求证:AB ·AD+BC2=AC2.40.已知:如图,AB 是半圆的直径,AC 是一条弦,D 是中点,DE ⊥AB 于E ,交AC 于F ,DB 交AC 于G .求证:AF=FG .41.如图,AB 是⊙O 的弦,P 是AB 所对优弧上一点,直径CD ⊥AB ,PB 交CD 于E ,延长AP 交CD 的延长线于F .求证:△EPF ∽△EOA .42.已知:如图,AB是⊙O的直径,弦CD⊥AB于E,M为上一点,AM的延长线交DC于F.求证:∠AMD=∠FMC.43.已知:如图,AB,AC分别为⊙O的直径与弦,CD⊥AB于D,E为⊙O外一点,且AE=AC,BE交⊙O于F,连结ED,CF.求证:∠ACF=∠AED.44.如图,⊙O的半径OD,OE分别垂直于弦AB和AC,连结DE交AB,AC于F,G.求证:AF2=AG2=DF·GE.45.如图,△ABC接于圆,D是AB上一点,AD=AC,E是AC延长线上一点,AE=AB,连接DE交圆于F,延长ED交圆于G.求证:AF=AG.46.已知:如图,⊙O的两条直径AB⊥CD,E是OD的中点,连结AE,并延长交⊙O于M,连结CM,交AB于F.求证:OB=3OF.47.已知:如图,△ABC是等边三角形,以AC为直径作圆交BC于D,作DE⊥AC交圆于E.(1)求证:△ADE是等边三角形;(2)求S△ABC∶S△ADE.48.已知:如图,半径都是5cm的两等圆⊙O1和⊙O2相交于点A,B,过A作⊙O1的直径AC与⊙O交于点D,且AD∶DC=3∶2,E为DC的中点.(1)求证:AC⊥BE;(2)求AB的长.阶段测试1.如图1,等边三角形ABC的三个顶点都在⊙O上,D是弧AC上任一点(不与A、C重合),则∠ADC的度数是________.2.如图2,四边形ABCD的四个顶点都在⊙O上,且AD∥BC,对角线AC与BC相交于点E,那么图中有_________对全等三角形;________对相似比不等于1的相似三角形.3.已知,如图3,∠BAC的对角∠BAD=100°,则∠BOC=_______度.4.如图4,A、B、C为⊙O上三点,若∠OAB=46°,则∠ACB=_______度.5.如图5,AB是⊙O的直径,弧 BC=弧BD,∠A=25°,则∠BOD的度数为________.6.如图6,AB是半圆O的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.7.如图7,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )A.50°B.100°C.130°D.200°8.如图8,A、B、C、D四个点在同一个圆上,四边形ABCD 的对角线把四个角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对9.如图9,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A.4个B.3个C.2个D.1个10.如图10,∠AOB=100°,则∠A+∠B等于( )A.100°B.80°C.50°D.40°11.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120°12.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC=140°, ∠CBD 的度数是( )A.40°B.50°C.70°D.110°13.如图,⊙O的直径AB=8cm,∠CB D=30°,求弦DC的长.14.如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC= ∠CAD,求弦AC的长.15.如图,AB为半圆O的直径,弦AD、BC相交于点P,若CD=3,AB=4,求tan∠BPD的值.16.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是弧CAD上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.17.在足球比赛场上,甲、乙两名队员互相配合向对方球门MN进攻.当甲带球部到A点时,乙随后冲到B,如图所示,此时甲是自己直接射门好,还是迅速将球回传给乙,让乙射门好呢?为什么?(不考虑其他因素)18.钳工车间用圆钢做方形螺母,现要做边长为a的方形螺母, 问下料时至少要用直径多大的圆钢?。