(完整版)SVAR模型制作过程
- 格式：doc
- 大小：538.10 KB
- 文档页数：9
下载文档原格式
合集下载
SVAR模型制作过程
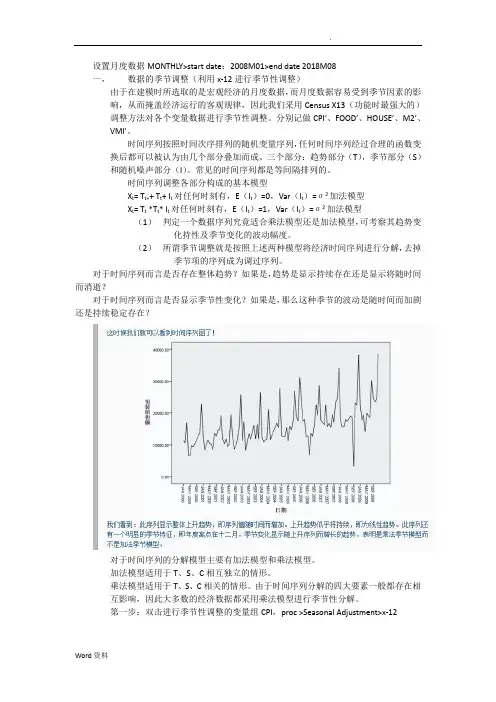
设置月度数据MONTHLY>start date：2008M01>end date 2018M08一，数据的季节调整（利用x-12进行季节性调整）由于在建模时所选取的是宏观经济的月度数据，而月度数据容易受到季节因素的影响，从而掩盖经济运行的客观规律，因此我们采用Census X13（功能时最强大的）调整方法对各个变量数据进行季节性调整。
分别记做CPI’、FOOD’、HOUSE’、M2’、VMI’。
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由几个部分叠加而成。
三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。
常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型X t= T t++ T t+ I t对任何时刻有，E（I t）=0，Var（I t）=σ2加法模型X t= T t *T t* I t对任何时刻有，E（I t）=1，Var（I t）=σ2加法模型（1）判定一个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
（2）所谓季节调整就是按照上述两种模型将经济时间序列进行分解，去掉季节项的序列成为调过序列。
对于时间序列而言是否存在整体趋势？如果是，趋势是显示持续存在还是显示将随时间而消逝？对于时间序列而言是否显示季节性变化？如果是，那么这种季节的波动是随时间而加剧还是持续稳定存在？对于时间序列的分解模型主要有加法模型和乘法模型。
加法模型适用于T、S、C相互独立的情形。
乘法模型适用于T、S、C相关的情形。
由于时间序列分解的四大要素一般都存在相互影响，因此大多数的经济数据都采用乘法模型进行季节性分解。
第一步：双击进行季节性调整的变量组CPI，proc >Seasonal Adjustment>x-12第二步：用Eviews软件进行季节调整的操作步骤：1，准备一个用于调整的时间序列（GDP）（注意：序列需同口径（当月或当季）、不变价、足够长）2，在Eviews中建立工作文件，导入序列数据3，序列图形分析（1）观察序列中的是否有季节性（2）是否有离群值或问题值（3）序列的趋势变动（是加法还是乘法模型）（加法模型主要适用于呈线性增长的数据序列，或者是围绕某一个中指波动的数据序列，如pmi数据序列）（乘法模型主要适用于呈指数级数增长的序列，如GDP、工业增加值，投资数据的名义值、实际值及物价的指数序列等。
s多方程第1题结构向量自回归模型svar-例9.1我国货币政策效应实证分析的var模型
1、结构向量自回归模型（SVAR ）（1）系统概述结构向量自回归模型（SVAR ）的结构（表达式）、识别与约束、估计、诊断检验（如滞后结构检验、残差检验等）及应用（如脉冲响应分析、方差分解等）、预测及评估。
（2）利用例题9.1中的数据，构建结构向量自回归模型，实现以上内容，分析结果。
结构V AR 模型(Structural V AR ，SV AR)，实际是指V AR 模型的结构式，即在模型中包含变量之间的当期关系。
1．两变量的SV AR 模型含有两个变量(k=2)、滞后一阶(p=1)的V AR 模型结构式可以表示为下式(9.1.8) 在模型(9.1.8)中假设：（1）随机误差u xt 和u zt 是白噪声序列，不失一般性，假设方差σx 2 = σz 2 =1 ； （2）随机误差u xt 和u zt 之间不相关，cov(u xt , u zt )=0 。
式(9.1.8)一般称为一阶结构向量自回归模型(SV AR(1))。
它是一种结构式经济模型，引入了变量之间的作用与反馈作用，其中系数c 12 表示变量z t 的单位变化对变量x t 的即时作用，γ21表示x t-1的单位变化对z t 的滞后影响。
虽然u xt 和u zt 是单纯出现在x t 和z t 中的随机冲击，但如果c 21 ≠ 0，则作用在x t 上的随机冲击u xt 通过对x t 的影响，能够即时传到变量z t 上，这是一种间接的即时影响；同样，如果c 12 ≠ 0，则作用在z t 上的随机冲击u zt 也可以对x t 产生间接的即时影响。
冲击的交互影响体现了变量作用的双向和反馈关系。
为了导出V AR 模型的简化式方程，将上述模型表示为矩阵形式该模型可以简单地表示为 (9.1.9)2．多变量的SV AR 模型p 阶结构向量自回归模型SV AR(p )为(9.1.13) 其中：10121111212021211221t t t t xtt t t t zt x c z x z u z c x x z u γγγγγγ----=++++=++++1,2,,t T=10121111212021211221t t t t xt t t t t ztx c z x z u z c x x z u γγγγγγ----=++++=++++10112111220121212211t t xt t t zt x x u c z z u c γγγγγγ---⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭0011t t t-=++C y ΓΓy u 1,2,,t T=01122t t t p t p t---=++++C y Γy Γy Γy u 121212012111k k k k c c c c c c --⎡⎤⎢⎥--⎢⎥=⎢⎥⎢⎥--⎣⎦C p i i kk i k i k i k i i i k i i i,,2,1,)()(2)(1)(2)(22)(21)(1)(12)(11 =⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=γγγγγγγγγΓ12t t t kt u u u ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦u可以将式(9.1.13)写成滞后算子形式(9.1.14)其中：C (L ) = C 0 -Γ1L -Γ2L 2 -… -Γp L p ，C (L )是滞后算子L 的k ⨯k 的参数矩阵，C 0≠I k 。
SVAR介绍[1]
![SVAR介绍[1]](https://img.taocdn.com/s1/m/25fcb5dc50e2524de5187eed.png)
约束条件，使得估计出的 VAR 模型对应的系数矩阵、对应的方差矩阵
等统计量的个数不少于 SVAR 模型中待求的未知量的个数。
我们知道，SVAR 模型与 VAR 模型有着内在的联系，而 SVAR 模
型的识别正是基于这种联系的基础上，欲通过对 VAR 模型的估计结
果，估计出 SVAR 模型中的待估计未知量。
(9.7)
基于以上定义，(9.3)就是一个 SVAR(1)模型的形式，其中各个变量的 结构性关系体现在了非单位矩阵的 Γ0 上。而以前我们介绍的简单 VAR 型，无一例外地都假设了当期变量Yt 的系数矩阵为单位阵。
9.1.2 SVAR 与缩减式 VAR 模型
进一步推导可以帮助我们认识到 SVAR 与 VAR 的内在联系和区
所以，(9.1)这个模型系统每个等式都是基于一定的经济理论基础 而建立起来的，并且这三个变量之间通过三个等式形成一个有机地动 态系统。这就是一个典型的 SVAR 模型，在整个系统中，每个变量除 了受各自的滞后项的影响，同时还包含了其它变量的即时（当期）的 影响。
注意，对于(9.1)这样的 SVAR 模型系统，每个等式不再能够使用 OLS 进行回归而获得无偏的估计结果了。这就是计量经济学科经常提 到的联立方程偏倚问题(simultaneous equation bias)。之所以会出现整个 问题，就是因为每个等式中的解释变量，通过整个系统的联系或者称 为传导，实际上是与各自等式中的随机扰动项具有相关性。而这违背 了 OLS 估计的根本假设要求之一。
第9章 结构向量自回归（SVAR）模型
本章内容：
1 SVAR 模型初步 2 SVAR 模型的基本识别方法 3 SVAR 模型的三种类型 4 SVAR 模型的估计方法总结 5 SVAR 与缩减 VAR 模型的脉冲响应及方差分解比较
SVAR模型制作过程
设置月度数据MONTHLY>start date：2008M01>end date 2018M08一，数据的季节调整（利用x-12进行季节性调整）由于在建模时所选取的是宏观经济的月度数据，而月度数据容易受到季节因素的影响，从而掩盖经济运行的客观规律，因此我们采用Census X13（功能时最强大的）调整方法对各个变量数据进行季节性调整。
分别记做CPI’、FOOD’、HOUSE’、M2’、VMI’。
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由几个部分叠加而成。
三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。
常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型X t= T t++ T t+ I t对任何时刻有，E（I t）=0，Var（I t）=σ2加法模型X t= T t *T t* I t对任何时刻有，E（I t）=1，Var（I t）=σ2加法模型（1）判定一个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
（2）所谓季节调整就是按照上述两种模型将经济时间序列进行分解，去掉季节项的序列成为调过序列。
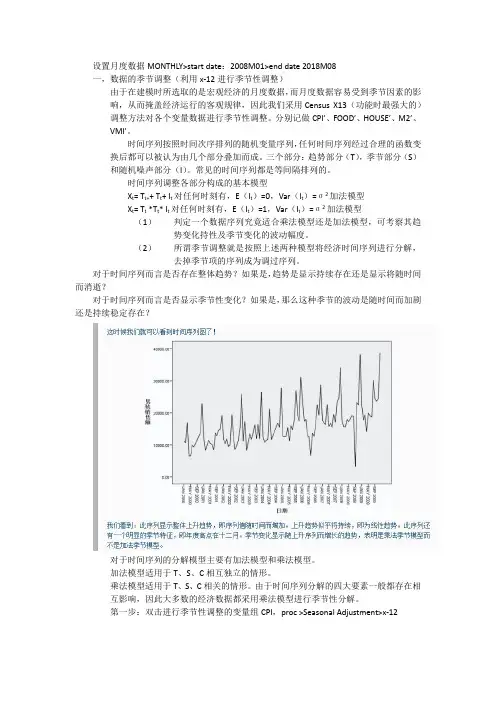
对于时间序列而言是否存在整体趋势？如果是，趋势是显示持续存在还是显示将随时间而消逝？对于时间序列而言是否显示季节性变化？如果是，那么这种季节的波动是随时间而加剧还是持续稳定存在？对于时间序列的分解模型主要有加法模型和乘法模型。
加法模型适用于T、S、C相互独立的情形。
乘法模型适用于T、S、C相关的情形。
由于时间序列分解的四大要素一般都存在相互影响，因此大多数的经济数据都采用乘法模型进行季节性分解。
第一步：双击进行季节性调整的变量组CPI，proc >Seasonal Adjustment>x-12第二步：用Eviews软件进行季节调整的操作步骤：1，准备一个用于调整的时间序列（GDP）（注意：序列需同口径（当月或当季）、不变价、足够长）2，在Eviews中建立工作文件，导入序列数据3，序列图形分析（1）观察序列中的是否有季节性（2）是否有离群值或问题值（3）序列的趋势变动（是加法还是乘法模型）（加法模型主要适用于呈线性增长的数据序列，或者是围绕某一个中指波动的数据序列，如pmi数据序列）（乘法模型主要适用于呈指数级数增长的序列，如GDP、工业增加值，投资数据的名义值、实际值及物价的指数序列等。
AB型SVAR模型公式
AB型SVAR模型公式第一部分经典论文解读第二部分操作步骤余结果解读1、单位根检验，季节调整2、最优滞后阶数得选择3、建立约束矩阵4、建模分析5、模型稳定性的检验6、进行脉冲响应7、方差分解在20世纪80年代，传统的联立方程模型曾经很流行。
这些结构模型越建越大，仿佛能够很好的反应样本的情况，但是对样本外的数据预测能力却很弱。
因此Sim（1980）提出了VAR模型。
简化的VAR 模型的脉冲效应函数并不是唯一的，并且不包含变量之间的当期影响。
经济学是一门不断发展的学问，经济学家试图将结构重新纳入VAR模型之中，并且考虑变量之间的当期影响。
以下是结构VAR模型的设定。
第一部分经典论文解读文章题目：人民币汇率变动对国内价格水平的传递效应文章来源：统计研究内容提要：本文运用长期约束的结构VAR，试图从一个崭新的视角实证考察人民币名义有效汇率对我国价格水平的传递效应。
文章特点在于考虑了汇率和价格可能都是受各种宏观经济因素影响的内生变量，以深入揭示两者之间的内在关系。
研究发现:(1)当发生汇率冲击时，人民币名义有效汇率对国内各价格水平的传递是不完全的，汇率变动对进口价格的影响强于对消费者价格的影响;(2)一旦考虑了经济体受到其他类型的宏观经济冲击后，估计的人民币汇率价格传递率则显得更为明显;(3)汇改后我国汇率传递效应趋于强化。
本文还分析了实证结果背后可能的深层次原因，并讨论相应的政策启示。
关键词:人民币名义有效汇率;汇率传递;宏观经济冲击;结构VAR结论与政策含义：本文采用基于Blanchard-Quah 识别方法的结构VAR，实证研究了1996 年1 月到2008 年10 月期间的人民币汇率价格传递效应。
研究发现:①当经济系统发生了汇率冲击，人民币名义有效汇率对我国消费者价格和进口价格的传递效应不完全，这与许多国内外同类研究结论一致。
②然而，当考虑了我国经济受其他宏观经济变量的冲击后，估计的人民币汇率价格的“传递”效应则显得更为迅速和强烈。
SVAR模型制作过程
设置月度数据MONTHLY>start date：2008M01>end date 2018M08一，数据的季节调整（利用x-12进行季节性调整）由于在建模时所选取的是宏观经济的月度数据，而月度数据容易受到季节因素的影响，从而掩盖经济运行的客观规律，因此我们采用Census X13（功能时最强大的）调整方法对各个变量数据进行季节性调整。
分别记做CPI’、FOOD’、HOUSE’、M2’、VMI’。
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由几个部分叠加而成。
三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。
常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型X t= T t++ T t+ I t对任何时刻有，E（I t）=0，Var（I t）=σ2加法模型X t= T t *T t* I t对任何时刻有，E（I t）=1，Var（I t）=σ2加法模型（1）判定一个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
（2）所谓季节调整就是按照上述两种模型将经济时间序列进行分解，去掉季节项的序列成为调过序列。
对于时间序列而言是否存在整体趋势？如果是，趋势是显示持续存在还是显示将随时间而消逝？对于时间序列而言是否显示季节性变化？如果是，那么这种季节的波动是随时间而加剧还是持续稳定存在？对于时间序列的分解模型主要有加法模型和乘法模型。
加法模型适用于T、S、C相互独立的情形。
乘法模型适用于T、S、C相关的情形。
由于时间序列分解的四大要素一般都存在相互影响，因此大多数的经济数据都采用乘法模型进行季节性分解。
第一步：双击进行季节性调整的变量组CPI，proc >Seasonal Adjustment>x-12第二步：用Eviews软件进行季节调整的操作步骤：1，准备一个用于调整的时间序列（GDP）（注意：序列需同口径（当月或当季）、不变价、足够长）2，在Eviews中建立工作文件，导入序列数据3，序列图形分析（1）观察序列中的是否有季节性（2）是否有离群值或问题值（3）序列的趋势变动（是加法还是乘法模型）（加法模型主要适用于呈线性增长的数据序列，或者是围绕某一个中指波动的数据序列，如pmi数据序列）（乘法模型主要适用于呈指数级数增长的序列，如GDP、工业增加值，投资数据的名义值、实际值及物价的指数序列等。
结构向量自回归(SVAR)模型操作步骤
0.05）说明（X外生于Y/ X不能Grange 引起Y ），简单地：当联合检验P值大 于0.05，则该被检验的因变量外生于系统（外生变量），
应重构VAR
9
最终VAR建模
记住VAR模型检验所得的滞后阶数 记住 VAR模型检验所得的外生变量 如果你幸运的话最初设置正确，你真历害，
不用再建模型了 如果不幸运，请利用所得信息
6
初始VAR模型检验
检验说明 对已构建的初始VAR做如：
一 AR根观察，以便确定模型的稳定性，模型不稳定则某些结果（如脉冲 响应函数的标准误差）不是有效的。
二 检验滞后阶数 三 因果关系检验（注：因果关系检验应在阶数确定后展开，如检验结果阶 数要更改，则用改正的阶数重新构建VAR后再行检验）
软件操做，请点VAR模型检验操作
23
③ 对VEC模型常数和趋势的说明在Cointegration栏 （下图）。必须从5个趋势假设说明中选择一个，也必须在 编辑框中填入协整关系的个数，应该是一个小于VEC模型 中内生变量个数的正数。
24
如果想强加约束于协整关系或(和)调整参数，用Restrictions 栏。注意：如果没在VAR Specification栏中单击 Impose Restrictions项，这一栏将是灰色的。
22
① 常数或线性趋势项不应包括在Exogenous Series 的编辑框中。对于VEC模型的常数和趋势说明应定义在 Cointegration栏中。
② 在VEC模型中滞后间隔的说明指一阶差分的滞 后。例如，滞后说明“1 2”将包括VEC模型右侧的变量 的 一 阶 差 分 项 的 滞 后 ， 即 VEC 模 型 是 两 阶 滞 后 约 束 的 VAR模型 。为了估计没有一阶差分项的VEC模型，指定 滞后的形式为：“0 0”。
应重构VAR
9
最终VAR建模
记住VAR模型检验所得的滞后阶数 记住 VAR模型检验所得的外生变量 如果你幸运的话最初设置正确，你真历害，
不用再建模型了 如果不幸运，请利用所得信息
6
初始VAR模型检验
检验说明 对已构建的初始VAR做如：
一 AR根观察，以便确定模型的稳定性，模型不稳定则某些结果（如脉冲 响应函数的标准误差）不是有效的。
二 检验滞后阶数 三 因果关系检验（注：因果关系检验应在阶数确定后展开，如检验结果阶 数要更改，则用改正的阶数重新构建VAR后再行检验）
软件操做，请点VAR模型检验操作
23
③ 对VEC模型常数和趋势的说明在Cointegration栏 （下图）。必须从5个趋势假设说明中选择一个，也必须在 编辑框中填入协整关系的个数，应该是一个小于VEC模型 中内生变量个数的正数。
24
如果想强加约束于协整关系或(和)调整参数，用Restrictions 栏。注意：如果没在VAR Specification栏中单击 Impose Restrictions项，这一栏将是灰色的。
22
① 常数或线性趋势项不应包括在Exogenous Series 的编辑框中。对于VEC模型的常数和趋势说明应定义在 Cointegration栏中。
② 在VEC模型中滞后间隔的说明指一阶差分的滞 后。例如，滞后说明“1 2”将包括VEC模型右侧的变量 的 一 阶 差 分 项 的 滞 后 ， 即 VEC 模 型 是 两 阶 滞 后 约 束 的 VAR模型 。为了估计没有一阶差分项的VEC模型，指定 滞后的形式为：“0 0”。
傅里叶红外光谱模型建立
傅里叶红外光谱模型建立
傅里叶红外光谱模型建立是在对样品进行红外光谱分析的过程中，根据样品的光谱特征来建立数学模型的过程。
该模型可以用于对未知样品的鉴定和定量分析。
建立傅里叶红外光谱模型的过程包括以下几个步骤：
1. 数据采集：通过红外光谱仪对一系列标准样品进行光谱采集，得到一系列光谱曲线。
2. 数据处理：将采集到的光谱曲线进行预处理，包括光谱去基线、光谱平滑等处理，以提高数据的质量。
3. 特征提取：对预处理后的光谱曲线进行特征提取，提取出与样品特征相关的光谱数据。
4. 模型建立：将提取到的特征作为输入变量，根据标准样品的已知性质（如成分、含量等）作为输出变量，通过数学方法建立起模型。
5. 模型评估：对模型进行评估，通过交叉验证等方法判断模型的预测能力。
6. 模型应用：将建立好的模型用于未知样品的分析，预测未知样品的性质和含量。
总之，建立傅里叶红外光谱模型的关键在于准确的数据处理和特征提取，以及有效的模型建立和评估。
结构向量自回归(SVAR)模型操作步骤课件
VS
模型适用性
在确定阶数后，需要检验模型是否适用于 数据，可以通过残差检验、单位根检验等 方法进行。
识别模型结构
结构识别
根据经济理论和数据特性，确定SVAR模型的结构，即变量之间的长期关系。常用的方法包括基于经济理论的约 束、基于数据的约束等。
约束检验
在确定了模型结构后，需要进行约束检验，以确保模型的有效性和准确性。常用的方法包括约束检验统计量、约 束检验图形等。
异方差性检验
通过GARCH等模型检验残差是否存在异方差性， 以判断模型是否合适。
诊断统计量
AIC和BIC值
01
通过比较不同模型的AIC和BIC值，选择具有较小值的模型，以
判断模型拟合优度。
FБайду номын сангаас计量
02
在约束性检验中，通过F统计量检验模型中各个约束是否显著，
以判断模型的有效性。
残差相关性检验
03
通过自相关图和偏自相关图检验残差是否存在相关性，以判断
应用场景
说明SVAR模型在宏观经济分析 、金融市场分析等领域的应用 场景和价值。
CHAPTER
04
SVAR模型的诊断与检验
残差诊断
残差图
通过绘制残差随时间变化的图形，可以直观地观 察残差的趋势和异常值。
残差正态性检验
通过统计检验方法，如Jarque-Bera检验，检验残 差是否符合正态分布假设。
整模型参数。
CHAPTER
05
SVAR模型的预测与应用
预测未来值
确定模型参数
通过估计SVAR模型的参数，可以 分析变量之间的动态关系，为预 测未来值提供依据。
预测时间序列数据
利用SVAR模型对时间序列数据进 行拟合，通过模型参数和历史数 据，预测未来的数值。
SVAR模型制作过程教学提纲
S V A R模型制作过程设置月度数据MONTHLY>start date：2008M01>end date 2018M08一，数据的季节调整（利用x-12进行季节性调整）由于在建模时所选取的是宏观经济的月度数据，而月度数据容易受到季节因素的影响，从而掩盖经济运行的客观规律，因此我们采用Census X13（功能时最强大的）调整方法对各个变量数据进行季节性调整。
分别记做CPI’、FOOD’、HOUSE’、M2’、VMI’。
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由几个部分叠加而成。
三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。
常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型X t= T t++ T t+ I t对任何时刻有，E（I t）=0，Var（I t）=σ2加法模型X t= T t *T t* I t对任何时刻有，E（I t）=1，Var（I t）=σ2加法模型（1）判定一个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
（2）所谓季节调整就是按照上述两种模型将经济时间序列进行分解，去掉季节项的序列成为调过序列。
对于时间序列而言是否存在整体趋势？如果是，趋势是显示持续存在还是显示将随时间而消逝？对于时间序列而言是否显示季节性变化？如果是，那么这种季节的波动是随时间而加剧还是持续稳定存在？对于时间序列的分解模型主要有加法模型和乘法模型。
加法模型适用于T、S、C相互独立的情形。
乘法模型适用于T、S、C相关的情形。
由于时间序列分解的四大要素一般都存在相互影响，因此大多数的经济数据都采用乘法模型进行季节性分解。
第一步：双击进行季节性调整的变量组CPI，proc >Seasonal Adjustment>x-12第二步：用Eviews软件进行季节调整的操作步骤：1，准备一个用于调整的时间序列（GDP）（注意：序列需同口径（当月或当季）、不变价、足够长）2，在Eviews中建立工作文件，导入序列数据3，序列图形分析（1）观察序列中的是否有季节性（2）是否有离群值或问题值（3）序列的趋势变动（是加法还是乘法模型）（加法模型主要适用于呈线性增长的数据序列，或者是围绕某一个中指波动的数据序列，如pmi数据序列）（乘法模型主要适用于呈指数级数增长的序列，如GDP、工业增加值，投资数据的名义值、实际值及物价的指数序列等。
SVAR模型制作过程
步骤：
第一：
利用图形确定常数项和趋势项Quick>seriesstatistic>unit root test
其中：
检验对象
Level（水平序列），1st difference（一阶差分序列），2st difference（二阶差分序列）
检验附加项
Intercept（常数项，漂移项），trend and intercept（趋势项和漂移项），none（无附加项）
（1）观察序列中的是否有季节性
（2）是否有离群值或问题值
（3）序列的趋势变动（是加法还是乘法模型者是围绕某一个中指波动的数据序列，如pmi数据序列）（乘法模型主要适用于呈指数级数增长的序列，如GDP、工业增加值，投资数据的名义值、实际值及物价的指数序列等。）（对数加法模型主要适用于同比增速呈线性增长的数据序列，如GDP、工业、投资及cpi的同比增速数据；伪加法模型则主要是对某些非负时间序列进行季节调整，他们具有这样的性质：在每一年中的相同月份出现接近与0的正值，在这些月份含有接近于0的季节因子，受这些小因子的影响，季节调整结果将出现偏差。在一年的特定时期，农产品产量就是这样的数据序列）
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由几个部分叠加而成。三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型
Xt=Tt++Tt+It对任何时刻有，E（It）=0，Var（It）=σ2加法模型
Xt=Tt*Tt*It对任何时刻有，E（It）=1，Var（It）=σ2加法模型
（1）判定一个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
第一：
利用图形确定常数项和趋势项Quick>seriesstatistic>unit root test
其中：
检验对象
Level（水平序列），1st difference（一阶差分序列），2st difference（二阶差分序列）
检验附加项
Intercept（常数项，漂移项），trend and intercept（趋势项和漂移项），none（无附加项）
（1）观察序列中的是否有季节性
（2）是否有离群值或问题值
（3）序列的趋势变动（是加法还是乘法模型者是围绕某一个中指波动的数据序列，如pmi数据序列）（乘法模型主要适用于呈指数级数增长的序列，如GDP、工业增加值，投资数据的名义值、实际值及物价的指数序列等。）（对数加法模型主要适用于同比增速呈线性增长的数据序列，如GDP、工业、投资及cpi的同比增速数据；伪加法模型则主要是对某些非负时间序列进行季节调整，他们具有这样的性质：在每一年中的相同月份出现接近与0的正值，在这些月份含有接近于0的季节因子，受这些小因子的影响，季节调整结果将出现偏差。在一年的特定时期，农产品产量就是这样的数据序列）
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由几个部分叠加而成。三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型
Xt=Tt++Tt+It对任何时刻有，E（It）=0，Var（It）=σ2加法模型
Xt=Tt*Tt*It对任何时刻有，E（It）=1，Var（It）=σ2加法模型
（1）判定一个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
VR模型制作阶段教程及规范课件
▪ 制作模型的时候一定要注意窗框玻璃片和墙
体窗洞的位置问题，每个窗洞的窗框和玻璃 图3 在同一面片用Blend材质表现，面片边缘于 窗洞内侧对齐，不能产生漏面或过大面的出 现。 （图2）
▪ Blend材质：玻璃材质放在第一层，Map
Channel为“4”；窗框材质放在第二层，Map Channel为“2”；黑白遮罩贴图放在第三层 mask位置；Map Channel为“1”； （图3）
一、模型的制作阶段，这个阶段制作环节比较重要，涉 及软件为MAX。制作的注意事项
▪重点区域为定点视点和浏览路径所能到达的区域范围（主体所在区域） ▪场景区域指重点表现区域外配楼所包含区域通俗的讲就是球天所能圈住
的除重点区域以外的所有区域。场景区域的大小根据项目来确定。
二、模型制作的步骤和规范
1.统一场景单位场景单位和场景尺寸均为米（Meters） （注：建筑部习惯米和厘米单位的制作，可以在最后模型整理烘焙前把 场景尺寸缩放到米和米的单位）
图1
▪ 玻璃体量模型——脚本可实现配楼大
小和高度的随机变化（用法见脚本说
明）(图2)
▪ 按玻璃体量区域塌陷模型，每个配楼
图2
物体不超过5000面，脚本可实现面数
限制。(图3) 图3
【植物】
植物贴图使用Alpha通道贴图（32位Tga格式）
▪ 贴图格式通道标准：32位Tga带Alpha通道贴图
▪ 贴图色彩、效果、种树： ▪ 植物贴图在素描关系上要与草地（草地稍稍偏亮）拉开距离，整体比草地深，局部点缀
模型
贴图
注：树坑模型摆放是注意主场景里面灯光主光的方向，摆对明暗面
【地形部分】
▪ 材质的制作规范
搜索非标准材质，提取物体和材质进行检查，批量强制改为标准 材质（由脚本辅助完成）
体窗洞的位置问题，每个窗洞的窗框和玻璃 图3 在同一面片用Blend材质表现，面片边缘于 窗洞内侧对齐，不能产生漏面或过大面的出 现。 （图2）
▪ Blend材质：玻璃材质放在第一层，Map
Channel为“4”；窗框材质放在第二层，Map Channel为“2”；黑白遮罩贴图放在第三层 mask位置；Map Channel为“1”； （图3）
一、模型的制作阶段，这个阶段制作环节比较重要，涉 及软件为MAX。制作的注意事项
▪重点区域为定点视点和浏览路径所能到达的区域范围（主体所在区域） ▪场景区域指重点表现区域外配楼所包含区域通俗的讲就是球天所能圈住
的除重点区域以外的所有区域。场景区域的大小根据项目来确定。
二、模型制作的步骤和规范
1.统一场景单位场景单位和场景尺寸均为米（Meters） （注：建筑部习惯米和厘米单位的制作，可以在最后模型整理烘焙前把 场景尺寸缩放到米和米的单位）
图1
▪ 玻璃体量模型——脚本可实现配楼大
小和高度的随机变化（用法见脚本说
明）(图2)
▪ 按玻璃体量区域塌陷模型，每个配楼
图2
物体不超过5000面，脚本可实现面数
限制。(图3) 图3
【植物】
植物贴图使用Alpha通道贴图（32位Tga格式）
▪ 贴图格式通道标准：32位Tga带Alpha通道贴图
▪ 贴图色彩、效果、种树： ▪ 植物贴图在素描关系上要与草地（草地稍稍偏亮）拉开距离，整体比草地深，局部点缀
模型
贴图
注：树坑模型摆放是注意主场景里面灯光主光的方向，摆对明暗面
【地形部分】
▪ 材质的制作规范
搜索非标准材质，提取物体和材质进行检查，批量强制改为标准 材质（由脚本辅助完成）
结构向量自回归(SVAR)模型操作步骤
方差分解
方差分解的基本思想
方差分解用于衡量模型中不同变量对内生变量变动的贡献程度。这种方法可以帮助我们理解不同变量在决定内生 变量变动时的相对重要性。
方差分解的步骤
首先，计算模型残差的方差；其次，将残差方差分解为各个变量冲击的贡献；最后，比较不同时期各个变量冲击 的贡献大小，以理解冲击的动态变化。
脉冲响应分析
脉冲响应函数
通过脉冲响应分析，可以观察到模型中 一个变量的冲击对其他变量的影响。这 种分析通常用于评估经济政策变动或突 发事件对经济系统的长期影响。
正交化脉冲响应函数
在某些情况下，为了更好地识别不同变量之 间的相互影响，可以使用正交化脉冲响应函 数。这种函数通过消除模型残差中的同期相 关性，提供更为准确的冲击响应估计。
在进行Johansen协整检验时，需要选择适当的滞后阶数和模型形式，以使检验结果更加准确。同时， 需要判断检验结果是否拒绝原假设，即是否存在协整关系。如果存在协整关系，则说明多个时间序列 数据之间存在长期均衡关系。
Granger因果检验
Granger因果检验是一种用于检验两 个时间序列数据之间是否存在因果关 系的检验方法。通过Granger因果检 验，可以判断一个时间序列数据是否 是另一个时间序列数据的原因。
结构向量自回归(SVAR)模型操作 步骤
目录
• 引言 • SVAR模型的建立 • SVAR模型的稳定性检验 • SVAR模型的估计结果分析 • SVAR模型的预测与决策应用 • 结论与展望
01 引言
SVAR模型的定义和重要性
定义
结构向量自回归（SVAR）模型是一种用于分析多个时间序列之间动态关系的 统计模型，特别适用于分析经济、金融等领域的多个变量之间的相互影响。
sav模型的原理和结构
sav模型的原理和结构
SVAR（Structural Vector Autoregression）模型，也被称为 SAV模
型（Structural Autoregressive Vector Autoregression），是一种
处理多变量动态模型的统计技术。
这种模型用于研究不同经济变量之
间的相互关系和因果关系。
SVAR模型结合了向量自回归（VAR）模型和经济结构变化的特性，以便更好地描述现实经济系统的动态特性。
SVAR模型的原理主要包括：
1. 多变量之间的长期均衡关系：通过估计不同方程（也就是变量），
然后检验这些方程之间的相互影响，了解各变量之间的长期均衡关系。
2. 经济结构变化：这种模型能考虑经济结构变化的影响，包括需求变动、生产函数变化、政策变化等。
它可以在一定程度上解释为何不同
变量之间会出现相互作用，即这些变量之间的动态关系如何随时间变化。
SVAR模型的结构主要包括：
1. SVAR模型的结构包含了完整的内生变量，这使得模型能捕捉到更多的信息。
2. 模型包含了结构的变动，如参数随时间变动的情况，这种特性使得
它更适合解释经济系统中可能存在的粘性因素。
SVAR模型需要使用特定的软件包（如SAC或SEU）进行估计和诊断，
如果使用计量经济学软件如Stata或R，可能需要利用该软件包中的专门函数来估计SVAR模型。
在选择模型和参数估计方法时，通常需要进
行模型的适应性检验和诊断，以确保估计结果的有效性和可靠性。
希望以上信息对你有帮助，可以咨询专业人士获取更多信息。
svar模型的起源、识别、估计与应用
svar模型的起源、识别、估计与应用以svar模型的起源、识别、估计与应用为标题，本文将介绍svar 模型的背景和原理、如何识别svar模型、如何估计svar模型参数以及svar模型在实际应用中的一些例子。
一、svar模型的起源与背景svar模型（Structural Vector Autoregression Model）是一种经济学中常用的时间序列分析方法，用于研究多个经济变量之间的关系。
svar模型可以用来分析变量之间的因果关系、冲击传导机制等。
svar模型的起源可以追溯到20世纪60年代，由于其简单而灵活的特点，逐渐成为经济学中的重要工具。
二、svar模型的识别在应用svar模型之前，首先需要识别模型的结构。
svar模型的结构识别是指确定模型中的内生变量和外生变量，以及它们之间的因果关系。
常用的结构识别方法有脉冲响应函数、方差分解和瞬时冲击反应函数等。
这些方法可以帮助研究者推断变量之间的因果关系，进而进行后续的分析。
三、svar模型的估计svar模型的估计是对模型参数进行求解的过程。
常用的估计方法有最小二乘法（OLS）和贝叶斯方法。
最小二乘法是一种经典的估计方法，通过最小化残差平方和来估计模型的参数。
贝叶斯方法则是一种基于贝叶斯统计理论的估计方法，可以提供参数的后验分布。
根据实际情况和研究目的，选择合适的估计方法非常重要。
四、svar模型的应用svar模型在经济学领域有着广泛的应用。
首先，svar模型可以用来分析宏观经济变量之间的关系，比如GDP、通胀率、利率等。
通过建立svar模型，可以研究这些变量之间的因果关系，对经济政策的制定提供参考。
其次，svar模型还可以用于分析金融市场的波动和冲击传导机制。
通过估计svar模型，可以研究金融市场变量之间的关系，预测市场的变动趋势。
此外，svar模型还可以应用于其他领域，比如医学、环境科学等，用于分析变量之间的关系和相互影响。
svar模型是一种重要的时间序列分析方法，用于研究变量之间的关系。
（完整版）SVAR模型制作过程
（完整版）SVAR模型制作过程设置⽉度数据MONTHLY>start date：2008M01>end date 2018M08⼀，数据的季节调整（利⽤x-12进⾏季节性调整）由于在建模时所选取的是宏观经济的⽉度数据，⽽⽉度数据容易受到季节因素的影响，从⽽掩盖经济运⾏的客观规律，因此我们采⽤Census X13（功能时最强⼤的）调整⽅法对各个变量数据进⾏季节性调整。
分别记做CPI’、FOOD’、HOUSE’、M2’、VMI’。
时间序列按照时间次序排列的随机变量序列，任何时间序列经过合理的函数变换后都可以被认为由⼏个部分叠加⽽成。
三个部分：趋势部分（T），季节部分（S）和随机噪声部分（I）。
常见的时间序列都是等间隔排列的。
时间序列调整各部分构成的基本模型X t= T t++ T t+ I t对任何时刻有，E（I t）=0，Var（I t）=σ2加法模型X t= T t *T t* I t对任何时刻有，E（I t）=1，Var（I t）=σ2加法模型（1）判定⼀个数据序列究竟适合乘法模型还是加法模型，可考察其趋势变化持性及季节变化的波动幅度。
（2）所谓季节调整就是按照上述两种模型将经济时间序列进⾏分解，去掉季节项的序列成为调过序列。
对于时间序列⽽⾔是否存在整体趋势？如果是，趋势是显⽰持续存在还是显⽰将随时间⽽消逝？对于时间序列⽽⾔是否显⽰季节性变化？如果是，那么这种季节的波动是随时间⽽加剧还是持续稳定存在？对于时间序列的分解模型主要有加法模型和乘法模型。
加法模型适⽤于T、S、C相互独⽴的情形。
乘法模型适⽤于T、S、C相关的情形。
由于时间序列分解的四⼤要素⼀般都存在相互影响，因此⼤多数的经济数据都采⽤乘法模型进⾏季节性分解。
第⼀步：双击进⾏季节性调整的变量组CPI，proc >Seasonal Adjustment>x-12第⼆步：⽤Eviews软件进⾏季节调整的操作步骤：1，准备⼀个⽤于调整的时间序列（GDP）（注意：序列需同⼝径（当⽉或当季）、不变价、⾜够长）2，在Eviews中建⽴⼯作⽂件，导⼊序列数据3，序列图形分析（1）观察序列中的是否有季节性（2）是否有离群值或问题值（3）序列的趋势变动（是加法还是乘法模型）（加法模型主要适⽤于呈线性增长的数据序列，或者是围绕某⼀个中指波动的数据序列，如pmi数据序列）（乘法模型主要适⽤于呈指数级数增长的序列，如GDP、⼯业增加值，投资数据的名义值、实际值及物价的指数序列等。