第3章-介质波导

导波光学教学大纲课程编号：课程名称：导波光学学时学分：48 (教学课时48)先修课程：光电子技术、电磁场理论、物理光学一.课程教学目标：本课程是信息工程（光电信息工程）专业的一门专业必修课。

要求学生学习和掌握波导波光学的基本原理，并对基本的波导结构利用所掌握的知识进行解算。

二.教学内容及基本要求：第一章介质光波导基础理论--电磁场基础知识回顾（4学时）1.1介质光波导（2学时）介绍介质光波导的基本概念、类型等1.2电磁场基本理论回顾（2学时）麦克斯韦方程的积分表达形式、微分表达形式、物理意义，坡印亭矢量及其物理意义、电磁场的波动方程的推导、物理意义第二章理想平板介质光波导（6学时）2.1平板光波导光波特征方程的推导及讨论（截止波长、模式）（2学时）2.2平板光波导的电磁理论求解（2学时）2.3平板光波导中的场分布、归一化参数，MTALAB仿真（2学时）第三章三层平板介质波导（8学时）3.1.用电磁场理论解释均匀三层波导中TE波、TM波的电磁场的分布情况（2学时）3.2.模式方程、模的介质条件、归一化参量(2学时)3.3.模式方程的解传播常数近似方程的推导课题练习（2学时）3.4.利用马卡梯里模型对两个独立的三层平板波导求解其波导方程，课堂讨论（2学时）第四章四层平板介质光波导（6学时）4.1 四层平板波导TE波和TM波的模式方程推导（2学时）4.2 分支波导（2学时）4.3 习题课（2学时）第五章光纤的基础知识（6学时）5.1 光纤传导基本原理，光纤衰减基本原理（2学时）5.2 单模光纤工作原理、高斯光束、结构、截止波长（2学时）5.3 光纤中的色散（从多模光纤的色散，到带宽分析）（2学时）掌握部分：光的导光条件，数值孔径、接收角的物理含义和计算方法、光纤衰减的计算方法和解决方案，光纤的色散机理和对抗措施，带宽与色散的关系第六章光纤的波导技术（12学时）6.1 光纤中的麦克斯韦方程及亥姆霍茨方程的推导（2学时）6.2 利用麦克斯韦方程求光纤中电磁场的分量（2学时）6.3 单模阶跃型折射率光纤中的各个模式及其物理意义的讨论（2学时）6.4 单模阶跃型折射率光纤中场分布及MATLAB数值仿真（2学时）6.5 多模光纤的特征方程及其MATLAB数值求解（2学时）6.6 多模光纤中的场分布及其MATLAB仿真（2学时）第七章光波导的调制（6学时）简要介绍光波调制的种类和基本概念，重点阐述电光调制的基本原理7.1 、7.2 光波调制的基本概念、调制器的性能（2学时）7.3 电光调制的基本原理（2学时）7.4 集成光波导在光纤陀螺中的应用（2学时）。

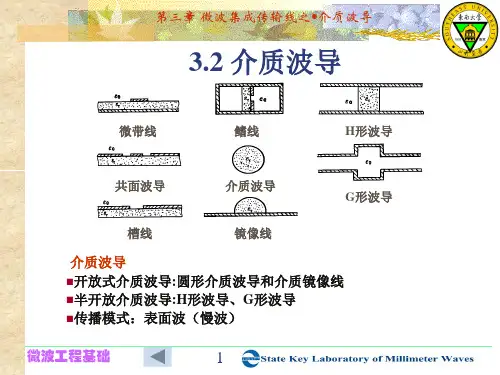
介质波导法介质波导法是一种在介质中传播电磁波的方法。

在介质波导中，电磁波通过界面反射来限制在介质内传播。

这种波导结构在许多应用中都得到广泛应用，如光纤通信和微波技术等。

介质波导法涉及到一些关键的概念，例如全内反射和波导模式。

首先，全内反射是指当光线从光密介质射入光疏介质时，当入射角大于临界角时，光线将完全被反射，不再继续传播到光疏介质中。

这种特性是光纤通信中的核心机制之一。

波导模式是介质波导的电磁场分布的一种特定形式。

它是波导中电磁场的准静态解决方案，且具有特定的传播常数。

波导模式的特点是只有特定的频率和传播常数下才能在波导中传播。

这些模式通过波导的物理尺寸和介质参数来确定。

介质波导的设计和分析可以使用一些数学方法和物理原理。

其中，麦克斯韦方程组是描述电磁波的重要工具，它们将电场和磁场之间的关系进行了描述。

此外，电磁波的传播可以使用亥姆霍兹方程进行建模，该方程描述了电磁波在波导中的传播行为。

在实际的介质波导应用中，波导结构的设计和特性分析是非常重要的。

例如，在光纤通信中，波导的损耗和色散特性是需要进行详细研究的。

波导损耗是指光能量在波导中传输时的衰减，这会导致信号的衰减和干扰。

波导色散是因为介质的色散特性而导致信号在波导中传播速率随着频率的变化而变化。

为了实现较低的波导损耗和色散特性，波导的结构和材料选择也是需要仔细考虑的。

例如，在光纤通信中，选择较低损耗和较低色散的材料非常重要。

传统的光纤一般由硅或玻璃制成，这些材料具有低损耗和较低色散特性，使其成为光纤通信中的首选。

除了光纤通信，介质波导法还在微波技术中得到广泛应用。

例如，微波集成电路中的传输线和器件常常使用介质波导结构来实现信号的传输和分配。

在微波波导中，微波信号的传播速率和功率耗散也是需要考虑的因素。

总而言之，介质波导法是一种广泛应用于光纤通信和微波技术等领域的方法。

通过对介质波导的设计和分析，我们可以实现优化的波导结构，从而实现更高效、低损耗的信号传输。

电磁场与电磁波总结第1章 场论初步一、矢量代数A •B =AB cos θA B ⨯=AB e AB sin θA •(B ⨯C ) = B •(C ⨯A ) = C •(A ⨯B ) A ⨯ (B ⨯C ) = B (A •C ) – C •(A •B ) 二、三种正交坐标系 1. 直角坐标系矢量线元 x y z =++l e e e d x y z矢量面元 =++S e e e x y z d dxdy dzdx dxdy 体积元 d V = dx dy dz单位矢量的关系 ⨯=e e e x y z ⨯=e e e y z x ⨯=e e e z x y 2. 圆柱形坐标系矢量线元 =++l e e e z d d d dz ρϕρρϕl 矢量面元 =+e e z dS d dz d d ρρϕρρϕ 体积元 dV = ρ d ρ d ϕ d z 单位矢量的关系 ⨯=⨯⨯=e e e e e =e e e e zz z ρϕϕρρϕ3. 球坐标系矢量线元 d l = e r d r + e θ r d θ + e ϕ r sin θ d ϕ 矢量面元 d S = e r r 2sin θ d θ d ϕ 体积元 dv = r 2sin θ d r d θ d ϕ 单位矢量的关系 ⨯=⨯⨯=e e e e e =e e e e r r r θϕθϕϕθcos sin 0sin cos 0 001x r y z z A A A A A A ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ϕϕϕϕϕsin cos sin sin cos cos cos cos sin sin sin cos 0x r y z A A A A A A ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦θϕθϕθϕθθϕθϕθϕϕsin 0cos cos 0sin 010r r z A A A A A A ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦θϕϕθθθθ三、矢量场的散度和旋度 1. 通量与散度=⋅⎰A S Sd Φ 0lim∆→⋅=∇⋅=∆⎰A S A A Sv d div v2. 环流量与旋度=⋅⎰A l ld Γ maxn 0rot =lim∆→⋅∆⎰A lA e lS d S3. 计算公式∂∂∂∇=++∂∂∂⋅A y x zA A A x y z11()∂∂∂∇=++∂∂∂⋅A zA A A z ϕρρρρρϕ 22111()(sin )sin sin ∂∂∂∇=++∂∂∂⋅A r A r A A r r r r ϕθθθθθϕx y z ∂∂∂∇⨯=∂∂∂e e e A x y z x y z A A A ∂∂∂∇⨯=∂∂∂e e e A z z z A A A ρϕρϕρρϕρ sin sin ∂∂∂∇⨯=∂∂∂e e e A r r zr r r A r A r A ρϕθθθϕθ 4. 矢量场的高斯定理与斯托克斯定理⋅=∇⋅⎰⎰A S A SV d dV⋅=∇⨯⋅⎰⎰A l A S lSd d四、标量场的梯度 1. 方向导数与梯度00()()lim∆→-∂=∂∆l P u M u M u llcos cos cos ∂∂∂∂=++∂∂∂∂P uu u ulx y zαβγ cos ∇⋅=∇e l u u θ grad ∂∂∂∂==+∂∂∂∂e e e +e n x y zu u u uu n x y z2. 计算公式∂∂∂∇=++∂∂∂e e e xy z u u uu x y z1∂∂∂∇=++∂∂∂e e e z u u u u z ρϕρρϕ 11sin ∂∂∂∇=++∂∂∂e e e r u u uu r r r zθϕθθ 五、无散场与无旋场1. 无散场 ()0∇⋅∇⨯=A =∇⨯F A2. 无旋场 ()0∇⨯∇=u =∇F u六、拉普拉斯运算算子 1. 直角坐标系22222222222222222222222222222222∂∂∂∇=++∇=∇+∇+∇∂∂∂∂∂∂∂∂∂∂∂∂∇=++∇=++∇=++∂∂∂∂∂∂∂∂∂A e e e x x y y z zy y y x x x z z z x y zu u u u A A A x y zA A A A A A A A A A A A x y z x y z x y z，，2. 圆柱坐标系22222222222222111212⎛⎫∂∂∂∂∇=++ ⎪∂∂∂∂⎝⎭∂∂⎛⎫⎛⎫∇=∇--+∇-++∇ ⎪ ⎪∂∂⎝⎭⎝⎭A e e e z z u u uu zA A A A A A A ϕρρρρϕϕϕρρρρρϕρρϕρρϕ3. 球坐标系22222222111sin sin sin ⎛⎫∂∂∂∂∂⎛⎫∇=++ ⎪ ⎪∂∂∂∂∂⎝⎭⎝⎭u u uu r r r r r r θθθϕθϕ ⎪⎪⎭⎫⎝⎛∂∂+-∂∂+∇+⎪⎪⎭⎫⎝⎛∂∂--∂∂+∇+⎪⎪⎭⎫ ⎝⎛∂∂-∂∂---∇=∇ϕθθθϕθϕθθθθϕθθθθϕϕϕϕθθθϕθθA r A r A r A A r A r A r A A r A r A r A r A r r r r r 222222222222222222sin cos 2sin 1sin 2sin cos 2sin 12sin 22cot 22e e e A 七、亥姆霍兹定理如果矢量场F 在无限区域中处处是单值的，且其导数连续有界，则当矢量场的散度、旋度和边界条件（即矢量场在有限区域V ’边界上的分布）给定后，该矢量场F 唯一确定为()()()=-∇+∇⨯F r r A r φ其中 1()()4''∇⋅'='-⎰F r r r r V dV φπ1()()4''∇⨯'='-⎰F r A r r r V dV π第2章 电磁学基本规律一、麦克斯韦方程组 1. 静电场基本规律真空中方程：d ⋅=⎰SE S qεd 0⋅=⎰lE l 0∇⋅=E ρε 0∇⨯=E 场位关系：3''()(')'4'-=-⎰r r E r r r r V q dV ρπε =-∇E φ 01()()d 4π''='-⎰r r |r r |V V ρφε介质中方程：d ⋅=⎰D S Sqd 0⋅=⎰lE l ∇⋅=D ρ 0∇⨯=E极化：0=+D E P ε e 00(1)=+==D E E E r χεεεε 极化电荷：==⋅P e PS n n P ρ =-∇⋅P P ρ2. 恒定电场基本规律电荷守恒定律：0∂∇⋅+=∂J tρ传导电流： =J E σ 与运流电流：ρ=J v恒定电场方程：d 0⋅=⎰J S Sd 0l⋅=⎰E l 0∇⋅=J 0∇⨯E =3. 恒定磁场基本规律真空中方程：0 d ⋅=⎰B l lI μ d 0⋅=⎰SB S 0∇⨯=B J μ 0∇⋅=B场位关系：03()( )()d 4π ''⨯-'='-⎰J r r r B r r r VV μ =∇⨯B A 0 ()()d 4π'''='-⎰J r A r r r V V μ 介质中方程：d ⋅=⎰H l lId 0⋅=⎰SB S ∇⨯=H J 0∇⋅=B磁化：0=-BH M μ m 00(1)=+B H =H =H r χμμμμ 磁化电流：m =∇⨯J M ms n =⨯J M e4. 电磁感应定律d d ⋅=-⋅⎰⎰S E l B S ld dt ∂∇⨯=-∂BE t5. 全电流定律和位移电流全电流定律： d ()d ∂⋅=+⋅∂⎰⎰D H l J S l S t ∂∇⨯=+∂DH J t 位移电流： d =DJ d dt6. Maxwell Equationsd ()d d d d d 0∂⎧⋅=+⋅⎪∂⎪∂⎪⋅=-⋅⎪∂⎨⎪⋅=⎪⎪⋅=⎪⎩⎰⎰⎰⎰⎰⎰⎰D H J S B E S D S B S l S l SSV Sl t l t V d ρ 0∂⎧∇⨯=+⎪∂⎪∂⎪∇⨯=-⎨∂⎪∇⋅=⎪⎪∇⋅=⎩D H J B E D B t t ρ ()() ()()0∂⎧∇⨯=+⎪∂⎪∂⎪∇⨯=-⎨∂⎪∇⋅=⎪⎪∇⋅=⎩E H E H E E H t t εσμερμ 二、电与磁的对偶性e m e m e m e e m m e e m mm e 00∂∂⎫⎧∇⨯=-∇⨯=⎪⎪∂∂⎪⎪∂∂⎪⎪∇⨯=+∇⨯=--⎬⎨∂∂⎪⎪∇=∇=⎪⎪⎪⎪∇=∇=⎩⎭⋅⋅⋅⋅B D E H D B H J E J D B D B t t &t t ρρ m e e m ∂⎧∇⨯=--⎪∂⎪∂⎪∇⨯=+⇒⎨∂⎪∇=⎪⎪∇=⎩⋅⋅B E J D H J D B tt ρρ 三、边界条件 1. 一般形式12121212()0()()()0⨯-=⨯-=⋅-=⋅-=e E E e H H J e D D e B B n n S n Sn ρ2. 理想导体界面 和 理想介质界面111100⨯=⎧⎪⨯=⎪⎨⋅=⎪⎪⋅=⎩e E e H J e D e B n n Sn S n ρ 12121212()0()0()0()0⨯-=⎧⎪⨯-=⎪⎨⋅-=⎪⎪⋅-=⎩e E E e H H e D D e B B n n n n 第3章 静态场分析一、静电场分析1. 位函数方程与边界条件位函数方程： 220∇=-∇=ρφφε电位的边界条件：121212=⎧⎪⎨∂∂-=-⎪∂∂⎩s nn φφφφεερ 111=⎧⎪⎨∂=-⎪∂⎩s const nφφερ（媒质2为导体） 2. 电容定义：=qC φ两导体间的电容：=C q /U任意双导体系统电容求解方法：2211⋅⋅===⋅⋅⎰⎰⎰⎰D S E S E lE lS S d d qC Ud d ε 3. 静电场的能量N 个导体： 112==∑ne i i i W q φ 连续分布： 12=⎰e VW dV φρ 电场能量密度：12D E ω=⋅e二、恒定电场分析1. 位函数微分方程与边界条件位函数微分方程：20∇=φ边界条件：121212=⎧⎪⎨∂∂=⎪∂∂⎩nn φφφφεε 12()0⋅-=e J J n 1212[]0⨯-=J J e n σσ 2. 欧姆定律与焦耳定律欧姆定律的微分形式： =J E σ 焦耳定律的微分形式： =⋅⎰E J VP dV3. 任意电阻的计算2211d d 1⋅⋅====⋅⋅⎰⎰⎰⎰E l E l J SE SSSU R G Id d σ （L R =σS ）4. 静电比拟法：C —— G ，ε —— σ2211⋅⋅===⋅⋅⎰⎰⎰⎰D S E S E lE lS S d d qC Ud d ε 2211d d d ⋅⋅===⋅⋅⎰⎰⎰⎰J S E SE lE lS S d I G Uσ三、恒定磁场分析1. 位函数微分方程与边界条件矢量位：2∇=-A J μ 12121211⨯⨯⨯A A e A A J n s μμ()=∇-∇=标量位：20m φ∇= 211221∂∂==∂∂m m m m n nφφφφμμ 2. 电感定义：d d ⋅⋅===⎰⎰B S A l SlL IIIψ=+i L L L3. 恒定磁场的能量 N 个线圈：112==∑Nm j j j W I ψ 连续分布：m 1d 2A J =⋅⎰V W V 磁场能量密度：m 12H B ω=⋅ 第4章 静电场边值问题的解一、边值问题的类型● 狄利克利问题：给定整个场域边界上的位函数值()=f s φ ● 纽曼问题：给定待求位函数在边界上的法向导数值()∂=∂f s nφ● 混合问题：给定边界上的位函数及其向导数的线性组合：2112()()∂==∂f s f s nφφ ● 自然边界：lim r r φ→∞=有限值二、唯一性定理静电场的惟一性定理：在给定边界条件（边界上的电位或边界上的法向导数或导体表面电荷分布）下，空间静电场被唯一确定。

222n E --e22122e 1e1eg TE sin n n cos n cos n 2E E t α-+αα==e22122e 1e 12e 1e r TEsin n n cos n sin n cos n E r α-+ααα==对称的平板介质波导示意图对称的平板介质波导中光波的反射和传输22将上式代入前一式中，沿着波导传播的光波必须满足：[]θθθcos 21)1cos 2()2cos(2d BC BC BC BC AB =+-=+=+[])2(2cos 22πφθm d k =-πφθπm dn m m =-cos 22λπθπφm dn -=cos 22对称平板介质波导中m=0,1,2三个模式的电场分布图m=0时，电场的峰值在波导层中的中心，只有一个峰值，这就是单模。

虽然有部分电场泄漏到限制层中，但是比较少，并且呈指数衰减。

m=1,2时，分别有两个和三个峰值，并且呈指数衰减=12时分别有两个和三个峰值求解这一波动方程，可得：式中A 和B 为常数。

)exp()]exp()exp([),(t i t B t A t z E x ωββ+-=x 模，则有：TE 模：存在，且只是x 的函数，与22022β>k n 而不是虚数。

所以在有源区外衰减的波导模式传播，要求：22022β>k n 2212k n >β这正是前面介绍过的光波导的条件。

在垂直方向±d/2的区域内光场呈指数衰减，这种场称之为消失场。

这种衰减不是由于介质1和3的光学吸收所引起的，而是由12n n >则有：21222222)2()2(R rd Kd Y X =+=+这就是一个半径为的园方程。

将两式联立求解：⎩⎨⎧==+XX Y R Y X tan 222偶阶TE 模式本征方程图解（该图为λ=0.9μm 时的情形）47，要想使半导体激光器以低阶偶横模的方。

)(40NA λ奇阶TE模式本征方程图解（该图为λ=0.9μm时的情形）52偶阶和奇阶TE模式本征方程的图解53 4.6矩形介质波导七种条形介质波导结构示意图54矩形介质波导的结构和折射率分布示意图，周围介质折射矩形波导芯区截面为矩形，折射率为n矩形波导芯区截面为矩形折射率为周围介质折射1(a)和(b)矩形波导的折射率分布示意图,（c)-(e)脊形波导的折射率分布示意图。

《半导体光电学》课后习题第一章半导体中光子-电子的相互作用思考与习题1、在半导体中有哪几种与光有关的跃迁，禾I」用这些光跃迁可制造出哪些类型的半导体光电子学期间。

2、为什么半导体锗、硅不能用作为半导体激光器的有源介质，面却是常用的光探测器材料？3、用量子力学理论证明直接带隙跃迁与间接带隙跃迁半导体相比其跃迁几率大。

4、什么叫跃迁的K选择定则？它对电子在能带间的跃迁速率产生什么影响？5、影响光跃迁速率的因素有哪些？6推导伯纳德-杜拉福格条件，并说明其物理意义。

7、比较求电子态密度与光子态密度的方法与步骤的异同点。

8、在半导体中重掺杂对能带结构、电子态密度、带隙、跃迁几率等带来什么影响？9、什么叫俄歇复合？俄歇复合速率与哪些因素有关？为什么在叹「-总汗7沁等长波长激光器中，俄歇复合是影响其阀值电流密度、温度稳定性与可靠性的重要原因？10、比较严格k选择定则与其受到松弛情况下增益-电流特性的区别。

11、带尾的存在对半导体有源介质增益特性产生哪些影响？12、证明式（1.7-20）。

13、说明图1.7-5和图1.7-6所依据的假设有何不同？并说明它们各自的局限性。

第二章异质结思考与习题1、什么是半导体异质结？异质结在半导体光电子器件中有哪些作用？2、若异质结由n型（「< ■ 1■）和P型半导体（丨缺邛）结构，并有匚.二，* 「，⑺匚讥，试画出np能带图。

3、同型异质结的空间电荷区是怎么形成的？它与异质结的空间电荷形成机理有何区别？4、推导出pn异质结结电容C!与所加正向偏压的关系，匸1的大小时半导体光电子器件的应用产生什么影响？5、用弗伽定律计算：和丿-:挖半导体当x=0.4时的晶格常数，并求出GaAs的晶格失配率。

6探讨在Si衬底上生GaAs异质结的可能性。

7、用」''半导体作为激射波长为工用〉可且光激光器的有源材料，计算其中AlAs的含量。

8、由经验得出，当y = 2-16(1 -X)时皿血-出歹l-y能与很好的晶格匹配，试求出激射擅长为时的x，y值.9、为了减少载流子激光器有源区中泄漏，能否无限制地增加异质结势垒高度，为什么？10、如取有源层与限制层带隙差AR t=°-25^°45cV,相对折射率齐/云丘为有源层的折射率)为•，试设计入-护氷匸的可见光半导体激光器，即求出有源层G町3加和限制层Gai_y Al y As的合理组分.第三章平板介质光波导理论思考与习题1、论述光波导致应在异质结激光器中的作用，在垂直于异质结平而方向上的光波导是怎样形成的？2、要想在激射波长为1.3um的双异质结激光器中得到基横模。

3-1一根以聚四氟乙烯 2.10r ε=为填充介质的带状线，已知其厚度b =5mm ，金属导带厚度和宽度分别为0t =、W =2mm ，求此带状线的特性阻抗与其不出现高次模式的最高频率。

解: 由于/2/50.40.35W b ==>，由公式20(0.35/)e W W b b W b ⎧=-⎨-⎩/0.35/0.35W b W b <> 得中心导带的有效宽度为：2e W W mm ≈=，077.3Z ==Ω带状线的主模为TEM 模，但若尺寸不对也会引起高次模，为抑止高次模，带状线的最短工作波长应满足：1010max(,)cTE cTM λλλ>102 5.8cTE mm λ==mmb r cTM 5.14210==ελ所以它的工作最高频率GHz cf 20105.1410338=⨯⨯==-λ3-2对于特性阻抗为50Ω的铜导体带状线，介质厚度b =0.32cm ，有效相对介电常数2.20r ε=，求线的宽度W 。

若介质的损耗角正切为0.001，工作频率为10GHz ，计算单位为dB/λ的衰减，假定导体的厚度为t =0.01mm 。

解:074.2120==<和030)0.4410.830x π=-=，所以由公式00,1200.85120x W b ⎧<⎪=⎨>⎪⎩其中，0.441x =- 计算宽度为(0.32)(0.830)0.266W bx cm ===。

在10GHz ，波数为1310.6k m -== 由公式)(/2tan 波TEM m Np k d δα=介电衰减为m Np k d /155.02)001.0)(6.310(2tan ===δα在10GHz 下铜的表面电阻为0.026s R =Ω。

于是，根据公式300002.710120,30()/0.16120,s r c s R Z A b t Np m R B Z b επα-⎧⨯<⎪-⎪=⎨>⎪⎪⎩其中2121ln()W b t b tA b t b t tπ+-=++-- 0.414141(0.5ln )(0.50.7)2b t WB W t W tππ=++++得出的导体的衰减为mNp A t b Z R r s c /122.0)(30107.203=-⨯=-πεα因为 4.74A =。