平面直角坐标系中的作图题

专题06 平面直角坐标系考点一、平面直角坐标系例1、（2020·山东威海市·中考真题）如图①，某广场地面是用A．B．C三种类型地砖平铺而成的，三种类型地砖上表面图案如图②所示，现用有序数对表示每一块地砖的位置：m n位置恰第一行的第一块（A型）地砖记作(1,1)，第二块（B型）地时记作(2,1)…若(,)好为A型地砖，则正整数m，n须满足的条是__________．【答案】m、n同为奇数或m、n同为偶数【分析】几何图形，观察A型地砖的位置得到当列数为奇数时，行数也为奇数，当列数为偶数，行数也为偶数的，从而得到m、n满足的条件．【详解】解：观察图形，A型地砖在列数为奇数，行数也为奇数的位置上或列数为偶数，行数也为偶数的位置上，若用（m，n）位置恰好为A型地砖，正整数m，n须满足的条件为m、n同为奇数或m、n 同为偶数，故答案为：m、n同为奇数或m、n同为偶数．【点睛】本题考查了坐标表示位置：通过类比点的坐标考查解决实际问题的能力和阅读理解能力．分析图形，寻找规律是关键．考点二、坐标方法的简单应用例2、（2020·甘肃金昌市·中考真题）如图，在平面直角坐标系中，OAB ∆的顶点A ，B 的坐标分别为，(4,0)，把OAB ∆沿x 轴向右平移得到CDE ∆，如果点D 的坐标为，则点E 的坐标为__________．【答案】(7,0)【分析】根据B 点横坐标与A 点横坐标之差和E 点横坐标与D 点横坐标之差相等即可求解．【详解】解：由题意知：A 、B 两点之间的横坐标差为：431-=，由平移性质可知：E 、D 两点横坐标之差与B 、A 两点横坐标之差相等，设E 点横坐标为a ，则a -6=1，∴a=7，∴E 点坐标为(7,0) ．故答案为：(7,0) ．【点睛】本题考查了图形的平移规律，平移前后对应点的线段长度不发生变化，熟练掌握平移的性质是解决此题的关键.达标检测1．点(﹣4，2)所在的象限是（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】B【分析】根据第二象限的点的横坐标是负数，纵坐标是正数解答．【详解】解：点（-4，2）所在的象限是第二象限．故选：B ．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．2．已知点P 的坐标为(3,4)--，则点P 到y 的距离为（ ）A ．3-B ．3C ．4D ．4-【答案】B【分析】根据点到y 轴的距离等于横坐标的长度解答．【详解】解：∴点P 的坐标为（-3，-4），∴点P 到y 轴的距离为3．故选：B ．【点睛】本题考查了点的坐标，熟记点到y 轴的距离等于横坐标的长度是解题的关键．3．在平面直角坐标系中，下列各点位于第三象限的是（ ）A ．(0,3)B ．(2,1)-C ．(1,2)-D ．(1,1)-- 【答案】D【分析】根据各象限内点的坐标特征对各选项分析判断后利用排除法求解．【详解】解：A 、(0，3)在y 轴上，故本选项不符合题意；B 、(−2，1)在第二象限，故本选项不符合题意；C 、(1，−2)在第四象限，故本选项不符合题意；D 、(-1，-1)在第三象限，故本选项符合题意．故选：D ．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解题的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．4．下列语句正确的是（ ）A ．在平面直角坐标系中，(3,5)-与(5,3)-表示两个不同的点B ．平行于x 轴的直线上所有点的横坐标都相同、C ．若点(,)P a b 在y 轴上，则0b =D ．点(3,4)P -到x 轴的距离为3【答案】A【分析】根据平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点逐一判断即可得.【详解】A.在平面直角坐标系中， (−3，5) 与 (5，−3) 表示两个不同的点，此选项正确；B.平行于 x 轴的直线上所有点的纵坐标都相同，此选项错误；C.若点 P (a ，b ) 在 y 轴上，则a =0 ，此选项错误；D.点 P (−3，4) 到 x 轴的距离为4，此选项错误；故选：A.【点睛】本题主要考查坐标与图形的性质，解题的关键是掌握平行与坐标轴的直线上点的坐标特点、坐标的概念、坐标轴上点的坐标特点及点到坐标轴的距离等知识点.5．将点A （2，1）向下平移2个单位长度得到点A ′，则点A ′的坐标是（ ）A ．（0，1）B ．（2，﹣1）C ．（4，1）D ．（2，3） 【答案】B【分析】让点A 的横坐标不变，纵坐标减2即可得到平移后点A ′的坐标．【详解】解：将点A （2，1）向下平移2个单位长度得到点A ′，则点A ′的坐标是（2，1-2），即（2，-1）．故选：B．【点睛】本题考查坐标与图形变化-平移，关键是要熟记：上下平移只改变点的纵坐标，上加下减．6．如图，货船A与港口B相距35海里，我们用有序数对（南偏西40°，35海里）来描述货船B相对港口A的位置，那么港口A相对货船B的位置可描述为（）A．（南偏西50°，35海里）B．（北偏西40°，35海里）C．（北偏东50°，35海里）D．（北偏东40°，35海里）【答案】D【分析】根据方位角的概念并结合平行线的性质，可得答案．【详解】解：过点B作BD∴AC，∴∴1=∴A=40°∴港口A相对货船B的位置可描述为（北偏东40°，35海里），故选：D．【点睛】本题考查了方向角的知识点，解答本题的关键是理解确定一个点的位置需要两个量应该是方向角，一个是距离．7．在平面直角坐标系中，将点A（x，y）向左平移3个单位长度，再向上平移5个单位长度后与点B（﹣3，2）重合，则点A的坐标是（）A．（2，5）B．（0，﹣3）C．（﹣2，5）D．（5，﹣3）【答案】B【分析】根据向左平移，横坐标减，向上平移纵坐标加列方程求出x、y，然后写出即可．【详解】解：∴点A（x，y）向左平移3个单位长度，再向上平移5个单位长度后与点B（﹣3，2）重合，∴x﹣3＝﹣3，y+5＝2，解得x＝0，y＝﹣3，所以，点A的坐标是（0，﹣3）．故选：B．【点睛】本题考查了坐标平移变化规律；明白向左平移，横坐标减，向上平移纵坐标加是关键．8．象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏，如图，若表示棋子“馬”和“車”的点的坐标分别为（3，2），（﹣3，0），则表示棋子“炮”的点的坐标为（）A．（1，2）B．（0，2）C．（2，1）D．（2，0）【答案】B【分析】根据棋子“馬”和“車”的点的坐标可得出原点的位置，进而得出答案．【详解】根据棋子“馬”和“車”的点的坐标可建立直角坐标系，如图所示：故棋子“炮”的点的坐标为：(0，2)．故选：B ．【点睛】本题主要考查了坐标确定位置，正确得出原点的位置建立直角坐标系是解题关键． 9．在直角坐标系中，点P （m ，2—2m ）的横坐标与纵坐标互为相反数，则P 点在（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】D【分析】根据m +2-2m =0计算m 的值，后判定横坐标，纵坐标的正负求解即可【详解】∴点P （m ，2—2m ）的横坐标与纵坐标互为相反数，∴m +2-2m =0，∴m =2，∴2-2m =-2，∴点P 位于第四象限，故选D【点睛】本题考查了坐标与象限的关系，利用相反数的性质构造等式计算m 的值是解题的关键． 10．如图，在平面直角坐标系中，已知点()2,1M ，()1,1N -，平移线段MN ，使点M 落在点()1,2M '-处，则点N 对应的点N '的坐标为（ ）A ．()2,0-B ．()0,2-C ．()1,1-D ．()3,1--【答案】A【分析】 根据()2,1M 平移后得到()1,2M '-，确定其平移规律是向左平移3个单位，后向上平移1个单位，根据规律确定点N 的平移坐标即可．【详解】∴()2,1M 平移后得到()1,2M '-，∴其平移规律是向左平移3个单位，后向上平移1个单位，∴()1,1N -，∴平移后的坐标为（1-3，-1+1）即()2,0-，故选A ．【点睛】本题考查了坐标系中点的坐标平移，准确确定平移方向和平移距离，并熟记左减右加，上加下减的计算法则是解题的关键．二、填空题11．己知(82,1)P m m -+点在x 轴上，则点P 的坐标为___．【答案】(10,0)【分析】根据x 轴上点的横坐标为0列方程求出m 的值，然后求解即可．【详解】解：点(82,1)P m m -+在x 轴上，10m ∴+=，解得1m =-，828210m ∴-=+=，∴点P 的坐标为(10,0)．故答案为：(10,0)．【点睛】本题考查了点的坐标，熟记x 轴上点的横坐标为0是解题的关键．12．如图，点A 在射线OX 上，2OA =．若将OA 绕点O 按逆时针方向旋转30到OB ，那么点B 的位置可以用()2,30︒表示．若将OB 延长到C ，使5OC =，再将OC 按逆时针方向继续旋转45︒到OD ，那么点D 的位置可以用____表示．【答案】（5，75°）【分析】直接利用已知点的意义，进而得出点D 的位置表示方法．【详解】解：如图所示：由题意可得：OD =OC =5，∴AOD =75°，故点D 的位置可以用：（5，75°）表示．故答案为：（5，75°）．【点睛】此题主要考查了坐标确定位置，正确得出坐标的意义是解题关键．13．已知点()2,3A --，将点A 先向右平移4个单位长度，再向上平移6个单位长度，得到A '，则A '的坐标为_________．【答案】()2,3【分析】根据平移规律左减右加，上加下减，进行平移计算即可；【详解】∴()2,3A --，向右平移4个单位长度，向上平移6个单位长度∴()24,36A '-+-+∴()2,3A '故答案为：()2,3【点睛】本题主要考查了平面直角坐标系坐标的平移变化，熟悉掌握坐标的变化规律是解题的关键．14．平面直角坐标系中，点(P 到x 轴的距离是_________．【答案】2【分析】根据点到x 轴的距离是纵坐标的绝对值，可得答案．【详解】解：点P （2）到x 轴的距离是|2|=2，故答案为：2．【点睛】本题考查了点的坐标，利用点到x 轴的距离是纵坐标的绝对值是解题关键．15．把点(2,3)-的向上平移4个单位长度，再向左平移3个单位长度，得到的点的坐标为________．【答案】（-5，7）【分析】根据点的平移方法可得把点（-2，3）的横坐标减3，纵坐标加4，然后计算即可．【详解】解：点（-2，3）向上平移4个单位长度单位再向左平移3个单位长度所到达点的坐标为（-2-3，3+4），即（-5，7），故答案为：（-5，7）．【点睛】此题主要考查了点的平移，关键是掌握横坐标，右移加，左移减；纵坐标，上移加，下移减．16．全英羽毛球公开赛混双决赛，中国组合鲁恺/ 黄雅琼，对阵马来西亚里约奥运亚军陈炳顺/吴柳萤，鲁恺/黄雅琼两名小将的完美配合结果获胜．如图是羽毛球场地示意图，x轴平行场地的中线，y轴平行场地的球网线，设定鲁恺的坐标是（3，1），黄雅琼的坐标是（0，－1），则坐标原点为__________．【答案】O1【分析】根据黄雅琼的位置即可确定坐标原点的位置．【详解】∴鲁恺的坐标是（3，1），黄雅琼的坐标是（0，−1），∴坐标原点为O1，故答案为：O1．【点睛】本题考查了坐标确定位置的知识，解题的关键是能够了解（0，−1）在坐标原点的下面一个单位，17．在平面直角坐标系中，孔明做走棋的游戏，其走法是：棋子从原点出发，第1步沿x轴向右走1个单位长度，第2步向右走2个单位长度，第3步向上走1个单位长度，第4步向右走1个单位长度，…，依此类推，第n步的走法是：当n能被3整除时，则向上走1个单位长度：当n被3除，余数为1时，则向右走1个单位长度：当n被3除，余数为2时，则向右走2个单位长度，当走完第6步时，棋子所处位置的坐标是，当走完第7步时，棋子所处位置的坐标是 ，当走完第2021步时，棋子所处位置的坐标是 ． 【答案】A 6（6，2），A 7（7，2），（2021，673） 【分析】设走完第n 步，棋子的坐标用A n 来表示．列出部分A 点坐标，发现规律“A 3n （3n ，n ），A 3n +1（3n +1，n ），A 3n +2（3n +3，n ）”，根据该规律即可解决问题． 【详解】解：设走完第n 步，棋子的坐标用A n 来表示．观察，发现规律：A 0（0，0），A 1（1，0），A 2（3，0），A 3（3，1），A 4（4，1），A 5（6，1），A 6（6，2），A 7（7，2），…， …，∴A 3n （3n ，n ），A 3n +1（3n +1，n ），A 3n +2（3n +3，n ）． ∴2021=673×3+2， ∴A 2021（2021，673）．故答案为：A 6（6，2），A 7（7，2），（2021，673）． 【点睛】本题考查了规律型中的点的坐标，解题的关键是发现规律“A 3n （3n ，n ），A 3n +1（3n +1，n ），A 3n +2（3n +3，n ）”．本题属于基础题，难度不大，解决该题型题目时，根据棋子的运动情况，罗列出部分A 点的坐标，根据坐标的变化发现规律是关键．18．如图，四边形AOBC 是正方形，曲线123CPP P ⋅⋅⋅叫做“正方形的渐开线”，其中弧1CP ，弧12PP ，弧23P P ，弧34P P 的圆心依次按点A ，O ，B ，C 循环，点A 的坐标为()2,0，按此规律进行下去，则点2021P 的坐标为______．【答案】()4044,0 【分析】由题意可知，正方形的边长为2，每旋转一次半径增加2，每次旋转的角度为90°，据此解【详解】解：由题意可知：正方形的边长为2，∴A（2，0），B（0，2），C（2，2），P1（4，0），P2（0，﹣4），P3（﹣6，2），P4（2，10），P5（12，0），P6（0，-12）…可发现点的位置是四个一循环，每旋转一次半径增加2，P在x轴正半轴，2021÷4=505……1，故点2021OP的长度为2021×2+2=4044，即：P2021的坐标是（4044，0），故答案为：（4044，0）．【点睛】本题考查了直角坐标系内点的坐标运动变化规律，解题的关键是理解A点的坐标除符合变化之外，还由旋转半径确定，而且每旋转一次半径增加2．三、解答题19．在平面直角坐标系中描出下列各组点，并将各组内的点用线段依次连接起来．（-5，0），（-4，3），（-3，0），（-2，3），（-1，0），（-5，0）【答案】见解析【分析】将坐标表示的点分别在坐标系中标出来，然后用线段依次连接起来即可．【详解】解：如图所示：本题考查了平面直角坐标系中的作图，正确地将点在坐标系中标出来是解题的关键．20．如图所示，在平面直角坐标系中点()30A -,，()5,0B ，()3,4C ，()2,3D -．（1）求四边形ABCD 的面积（2）点P 为y 轴上一点，且ABP △的面积等于四边形ABCD 的面积的一半，求点P 的坐标．【答案】（1）23；（2）90,4⎛⎫ ⎪⎝⎭或90,4⎛⎫- ⎪⎝⎭． 【分析】（1）分别过C 、D 作x 轴的垂线，垂足分别为E 、F ，分别计算AF 、DF 、BE 的长，根据三角形面积公式、梯形面积公式分别解得32ADF S =△，4BCE S =△，352CEFD S =梯形即可解题；（2）设()0,P b ，根据题意，结合三角形面积公式及绝对值的性质化简解题即可． 【详解】解：（1）分别过C 、D 作x 轴的垂线，垂足分别为E 、F ，因为()30A -，，()B 5，0，()34C ，，()23D -，， 所以1AF =，34DF CE ==，25BE EF ==，所以131322ADF S =⨯⨯=△， 所以12442BCE S =⨯⨯=△，所以()353452CEFD S =+⨯=梯形，所以33542322ABCD S ++==四边形．（2）设()0P b ，则有123=22ABP ABCD S S =△四边形 即11238222AB OP b ⨯⨯=⨯⨯=解得：23||8b = 所以238b =± 所以点P 的坐标为904⎛⎫ ⎪⎝⎭，或904⎛⎫- ⎪⎝⎭，． 【点睛】本题考查坐标与图形的性质、三角形面积、绝对值的性质等知识，是重要考点，难度较易，掌握相关知识是解题关键．21．在平面直角坐标系中，完成以下问题：（1）请在坐标系中标出点(3,2)A 、(2,3)B -；（2）若直线l 经过点B 且//l y 轴．点C 是直线l 上的一个动点，请画出当线段AC 最短时的简单图形，此时点C 的坐标为 ；（3）线段AC 最短时的依据为 ．【答案】（1）见详解；（2）画图见详解，C （﹣2,2）；（3）点到直线的距离垂线段最短 【分析】(1)根据点坐标的定义直接在坐标系中标出点即可；（2）根据点到直线的距离垂线段最短即可判断点C 的坐标； （3）依据点到直线的距离垂线段最短． 【详解】(1)A,B 两点如下图；（2）AC 最短时的图形如下图所示，此时C 点坐标为：（﹣2,2）； （3）点到直线的距离垂线段最短．【点睛】本题考查了平面直角坐标系中点的坐标问题，及对点到直线的距离垂线段最短的理解与应用，解题关键在于理解应用点到直线的距离垂线段最短．22．如图，在直角坐标系中，已知A （﹣1，4），B （﹣2，1），C （﹣4，1），将ABC 向右平移3个单位再向下平移2个单位得到111A B C △，点A 、B 、C 的对应点分别是点A 1、B 1、C 1．（1）画出111A B C △；（2）直接写出点A 1、B 1、C 1的坐标； （3）直接写出111A B C △的面积．【答案】（1）见解析；（2）A 1（2，2），B 1（1，﹣1），C 1（﹣1，﹣1）；（3）3． 【分析】（1）直接利用平移的性质得出对应点位置，画出图形即可； （2）利用（1）中图形，利用平移的性质得出对应点坐标； （3）利用三角形面积公式可得出答案． 【详解】解：（1）如图所示：111A B C △，即为所求；（2）由平移的性质结合图形可得：A 1（2，2），B 1（1，﹣1），C 1（﹣1，﹣1）； （3）111A B C △的面积为：12×2×3＝3．【点睛】本题考查的是平移的性质，图形与坐标，三角形面积的计算，掌握以上知识是解题的关键． 23．在边长为的方格纸中有一个ABC ．（1）作出ABC 的高CD ，并求出ABC 面积；（2）将ABC 向上平移3个单位，再向左平移2个单位，得到111A B C △，请画出111A B C △； （3）请任意写出一组平移前后两个三角形中平行且相等的线段．【答案】（1）8，画图见解析；（2）画图见解析；（3）11//A B AB ，11A B AB =． 【分析】（1）直接作高，得到高的长度，利用三角形面积公式计算即可.（2）图形的平移关键是点的平移.按平移的法则确定了A 、B 、C 平移后的对应点A 1、B 1、C 1位置，连接即可得到111A B C △；（3）根据平移前后，对应线段(不在同一直线上的)互相平行且相等，举例即可. 【详解】 （1）1144822ABC S AB CD =⨯⨯=⨯⨯=△． 如图所示：（2）先将点A ，B ，C 分别向上平移3个单位，再向左平移2个单位确定点1A ，1B ，1C ，再连接11A B ，11B C ，11AC ，此时111A B C △即为所求．（3）11//A B AB ，11//AC AC ，11//B C BC ．三组线段任写一组． 【点睛】本题主要考查了图形的平移，图形的平移实质是点的平移，正确的确定对应点的位置是正确作图的关键，同时平移前后，对应线段(不在同一直线上的)互相平行且相等这一平移性质的运用.24．综合与探究．如图1，在平面直角坐标系中，点O ，A 的坐标分别为()0,0，()02,，将线段OA 沿x 轴方向向右平移，得到线段CB ，点O 的对应点C 的坐标为3,0，连接AB ．点P 是y 轴上一动点．（1）请你直接写出点B 的坐标____________．（2）如图1，当点P 在线段OA 上时（不与点O 、A 重合），分别连接BP ，CP ．猜想BPC ∠，ABP ∠，OCP ∠之间的数量关系，并说明理由．（3）①如图2，当点P 在点A 上方时，猜想BPC ∠，ABP ∠，OCP ∠之间的数量关系，并说明理由．②如图3，当点P 在y 轴的负半轴上时，请你直接写出BPC ∠，ABP ∠，OCP ∠之间的数量关系．【答案】（1）()3,2；（2）BPC ABP OCP ∠=∠+∠，理由见解析；（3）（3）①BPC OCP ABP ∠=∠-∠，理由见解析；②BPC ABP OCP ∠=∠-∠．【分析】（1）根据平移的规律即可求解；（2）过点P 作//PD AB ，得到BPD ABP ∠=∠，再证明//PD OC ，得到CPD PCO ∠=∠，即可得到BPC BPD CPD ABP OCP ∠=∠+∠=∠+∠；（3）①过点P 作//PE AB ，得到BPE ABP ∠=∠，再证明//PE OC ，得到EPC OCP ∠=∠，即可证明BPC BPD CPD ABP OCP ∠=∠+∠=∠+∠；②过点P 作//PF AB ，得到BPF ABP ∠=∠，再证明//PF OC ，得到FPC OCP ∠=∠，即可证明BPC FPB FPC ABP OCP ∠=∠-∠=∠-∠． 【详解】解:（1）∴线段OA 沿x 轴方向向右平移，得到线段CB ，点O 的对应点为C 坐标为（3,0）， ∴点A （0,2）的对应点B 的坐标为（3,2）， 故答案为：()3,2；（2）BPC ABP OCP ∠=∠+∠，理由如下： 如图1，过点P 作//PD AB ， ∴BPD ABP ∠=∠， 由平移可知，//AB OC ， 又//PD AB ， ∴//PD OC ， ∴CPD PCO ∠=∠，∴BPC BPD CPD ABP OCP ∠=∠+∠=∠+∠；∠=∠-∠，理由如下：（3）①BPC OCP ABPPE AB，如图2，过点P作//∠=∠，∴BPE ABPAB OC，又∴//PE OC，∴//∠=∠，∴EPC OCP∠=∠-∠=∠-∠．∴BPC EPC EPB OCP ABP∠=∠-∠，理由如下：②BPC ABP OCPPF AB，如图3，过点P作//∠=∠，∴BPF ABPAB OC，又∴//PF OC，∴//∠=∠，∴FPC OCP∠=∠-∠=∠-∠．∴BPC FPB FPC ABP OCP 【点睛】本题考查了平面直角坐标系中平移的规律、平行线的性质与判定等知识，熟知相关知识点并根据题意灵活应用是解题关键．25．在平面直角坐标系xOy 中描出下列两组点，分别将每组里的点用线段依次连接起来． 第一组：()3,3A -、()4,3C ；第二组：()2,1D --、()2,1E -．（1）直接写出线段AC 与线段DE 的位置关系；（2）在（1）的条件下，线段AC ，DE 分别与y 轴交于点B ，F ．若点M 为射线OB 上一动点（不与点O ，B 重合）．①当点M 在线段OB 上运动时，连接AM 、DM ，补全图形，用等式表示CAM ∠、AMD ∠、MDE ∠之间的数量关系，并证明．②当ACM △与DEM △面积相等时，求点M 的坐标．【答案】（1）线段AC 与线段DE 的位置关系；AC∥DE ，证明见详解；（2）AMD ∠=CAM∠+MDE ∠，证明见详解；（3）M （0，1711）． 【分析】（1）AC∥DE ，由()3,3A -、()4,3C 两点纵坐标相同，-3≠4，可得AC∥x 轴，由()2,1D --、()2,1E -两点纵坐标相同，-2≠2，可得DE∥x 轴，利用平行同一直线两直线平行可得AC∥DE ； （2）AMD ∠=CAM ∠+MDE ∠，过M 作MN∥AC ，内错角相等得∴CAM =∴AMN ，由AC∥DE ，可得MN∥DE ，内错角相等∴NMD =∴MDE ，可证AMD ∠=CAM ∠+MDE ∠；（3）由AC ∴y 轴于B ，DE ∴y 轴于F ，求出B （0，3），F （0，-1），,可确BF =4，设OM =m ，MB =3-m ，MF =4-（3-m ）=m +1，AC =7，DE =4，用含m 的式子表示S ∴ACM =()1732m ⨯⨯-，S ∴DEM =()1412m ⨯⨯+，当ACM △与DEM △面积相等时，可列方程()()1173=4122m m ⨯⨯-⨯⨯+，解之即可． 【详解】解：（1）直接写出线段AC 与线段DE 的位置关系；AC∥DE∴()3,3A -、()4,3C 两点纵坐标相同，-3≠4∴AC∥x 轴，∴()2,1D --、()2,1E -两点纵坐标相同，-2≠2∴DE∥x 轴，∴AC∥DE ，（2）AMD ∠=CAM ∠+MDE ∠过M 作MN∥AC ，∴∴CAM =∴AMN ，∴AC∥DE ，∴MN∥DE ，∴∴NMD =∴MDE ，∴∴AMD =∴AMN +∴NMD =∴CAM +∴MDE ，∴AMD ∠=CAM ∠+MDE ∠，（3）∴AC ∴y 轴于B ，DE ∴y 轴于F ，∴B （0，3），F （0，-1），,∴BF =OB +OF =3+1=4，设OM =m ，∴MB =3-m ，MF =4-（3-m ）=m +1，∴AC =4-（-3）=7，DE =2-(-2)=4，S ∴ACM =()117322AC MB m ⨯⋅=⨯⨯-，S ∴DEM =()114122DE MF m ⨯⋅=⨯⨯+， 当ACM △与DEM △面积相等时，即()()1173=4122m m ⨯⨯-⨯⨯+， 整理得21744m m -=+， 解得1711m =， ∴M （0，1711）．【点睛】本题考查画图，平行线的判定与性质，角的互相关系，三角形面积，一元一次方程，掌握画图技巧，平行线的判定与性质，角的和差关系，三角形面积求法，一元一次方程的解法是解题关键．26．已知，在平面直角坐标系中，AB ⊥x 轴于点B ，点A (a ，b )+|b ﹣3|＝0，平移线段AB 使点A 与原点重合，点B 的对应点为点C ．（1）a ＝ ，b ＝ ，点C 坐标为 ；（2）如图1，点D (m ，n )是射线CB 上一个动点．①连接OD ，利用OBC ，OBD ，OCD 的面积关系，可以得到m 、n 满足一个固定的关系式，请写出这个关系式： ；②过点A 作直线1⊥x 轴，在l 上取点M ，使得MA ＝2，若CDM 的面积为4，请直接写出点D 的坐标 ．（3）如图2，以OB 为边作⊥BOG ＝⊥AOB ，交线段BC 于点G ，E 是线段OB 上一动点，连接CE 交OG 于点F ，当点E 在线段OB 上运动过程中，OFC FCG OEC∠+∠∠的值是否发生变化？若变化请说明理由，若不变，求出其值．【答案】（1）6，3，（0，-3）；（2）①m -2n ＝6；②（2，-2）或（4，-1）；（3）不变，理由见解析【分析】（1）利用非负数的性质求解即可．（2）①如图1，过点D 分别作DM x ⊥轴于点M ，DN y ⊥轴于点N ，连接OD ，利用面积法求解即可．②如图11-中，设直线AM 交y 轴于T ，连接DT ，CM ，CM '．分两种情形：当点M 在点A 的左侧时，设(,3)2m D m -，根据4CDM CTD MTD CTD S S S S ∆∆∆∆=+-=，构建方程求解，当点M '在点A 的右侧时，同法可得．（3）OFC FCG OEC∠+∠∠的值不变，值为2．利用平行线的性质，三角形的外角的性质证明即可．【详解】解：（1）|3|0b -=，60a ∴-=，30b -=，6a ∴=，3b =，3AB OC ==，且C 在y 轴负半轴上，(0,3)C ∴-，故答案为：6，3，(0,3)-．（2）①如图1-1，过点D 分别作DM x ⊥轴于点M ，DN y ⊥轴于点N ，连接OD ．AB x ⊥轴于点B ，且点A ，D ，C 三点的坐标分别为：(6,3)，(,)m n ，(0,3)-， 6OB ∴=，3OC =，MD n =-，ND m =，192BOC S OB OC ∆∴=⨯=， 又BOC BOD COD S S S ∆∆∆=+1122OB MD OC ND =⨯+⨯ 116()322n m =⨯⨯-+⨯⨯ 332m n =-， ∴3392m n -=，26m n ∴-=， m ∴、n 满足的关系式为26m n -=．故答案为：26m n -=．②如图12-中，设直线AM 交y 轴于T ，连接DT ，DM ，CM '．当点M 在点A 的左侧时，设(,3)2m D m -，4CDM CTD MTD CTD S S S S ∆∆∆∆=+-=， ∴11164(33)4642222m m ⨯⨯+⨯⨯-+-⨯⨯=， 解得2m =，(2,2)D ∴-， 当点M '在点A 的右侧时，同法可得(4,1)D -，综上所述，满足条件的点D 的坐标为(2,2)-或(4,)1-．故答案为：(2,2)-或(4,)1-．（3）OFC FCG OEC∠+∠∠的值不变，值为2．理由如下： 线段OC 是由线段AB 平移得到，//BC OA ∴，AOB OBC ∴∠=∠，又BOG AOB ∠=∠，BOG OBC ∴∠=∠，根据三角形外角性质，可得2OGC OBC ∠=∠，OFC FCG OGC ∠=∠+∠，22OFC FCG FCG OBC ∴∠+∠=∠+∠2()FCG OBC =∠+∠2OEC =∠， ∴22OFC FCG OEC OEC OEC∠+∠∠==∠∠． 【点睛】本题属于几何变换综合题，主要考查了非负数，坐标与图形，平行线的性质以及平移的性质，解决问题的关键是作辅助线，运用面积法，角的和差关系以及平行线的性质进行求解．。

四年级垂线练习题作图作图是数学学习中的重要环节之一，通过作图可以更直观地理解和解决问题。

本文将为四年级学生提供一些垂线练习题，并详细介绍如何进行图形的作图。

1. 作图题一：画一个直角三角形ABC，其中∠ACB为直角，AB=5cm，BC=4cm。

解答：步骤一：用尺子在一张纸上画一条5cm的线段AB，作为直角三角形的直角边。

步骤二：再用尺子在点B上方和下方分别画出两条长度为4cm的线段。

步骤三：连接上述两条线段和点B，得到直角三角形ABC。

2. 作图题二：在平面直角坐标系中，作一个矩形，其中一条边与x轴重合，且矩形的长是4cm，宽是3cm。

解答：步骤一：用尺子在一张纸上画一条长度为4cm的线段AB，作为矩形的一条边。

步骤二：在点B上方和下方分别用尺子画出两条长度为3cm的线段。

步骤三：连接上述两条线段和点A，得到矩形。

3. 作图题三：画一个正方形，边长为6cm。

解答：步骤一：用尺子在一张纸上画一条长度为6cm的线段。

步骤二：以该线段为边，依次在两个端点上方和下方分别画出两条长度也为6cm的线段。

步骤三：连接上述两条线段，得到正方形。

4. 作图题四：作一个等边三角形，边长为8cm。

解答：步骤一：用尺子在一张纸上画一条长度为8cm的线段AB，作为等边三角形的一条边。

步骤二：以点A为圆心，以8cm为半径画一个圆弧。

步骤三：再以点B为圆心，以8cm为半径画一个圆弧。

步骤四：连接上述两个圆弧的交点和两个端点，得到等边三角形。

通过以上几个作图题的解答，我们能够发现，作图的关键在于准确地测量和刻画线段的长度，以及妥善地使用尺子和直尺来进行作图。

在实际操作过程中，同学们应该注意保持手的稳定，使线段和直角边的绘制更加准确。

总结：作图是数学学习中非常重要的一部分，通过作图能够更直观地理解和解决问题。

在进行作图的过程中，我们需要准确地测量和刻画线段的长度，合理地使用尺子和直尺，并保持手的稳定。

相信通过反复的练习和实践，同学们能够变得更加熟练和娴熟地进行作图，提高数学学习的效果。

人教版七年级数学下册第七章第一节平面直角坐标系习题（含答案)在平面直角坐标系中，有(2,2)A a -+，(3,4)B a -，(4,)C b b -三点． （1）当ABx 轴时，求A 、B 两点间的距离；（2）当CD x ⊥轴于点D ，且3CD =时，求点C 的坐标． 【答案】（1）1；（2）点C 的坐标为(1,3)-、(7,3)-- 【解析】 【分析】 （1）根据ABx 轴可知点,A B 的纵坐标一样解得a 的值，再求解B 的横坐标，最后即可求得两点间的距离；（2）根据CD x ⊥轴于点D ，且3CD =，即(4,)C b b -的纵坐标3b =±，即可得出点C 的坐标.【详解】 解：（1）由AB x 轴可得，24a +=，即2a =，∴31a -=-，∴A 、B 两点间的距离为1(2)1---=． （2）由题意得||3b =，即3b =或3-， ∴41b -=-或47b -=-， ∴点C 的坐标为(1,3)-、(7,3)-- 【点睛】本题主要考查坐标于图形的性质，熟练掌握性质是关键.92．如下图所示，在直角坐标系中，第一次将△OAB 变换成11OA B ，第二次将11OA B，第三次将22OA B变换成22OA B，已知A(1,2)，OA B△变换成33A(2,2)，2A(4,2)3A(8,2)，B(2,0)，1B(4,0)，2B(8,0)，3B(16,0)．1（1）观察每次变换前后的三角形有何变化，找出规律，按此规律再将33OA B 变换成44OA B，则4A的坐标为，4B的坐标为．．（2）可以发现变换过程中123A,A,A……An的纵坐标均为（3）按照上述规律将△OAB进行n次变换得到n n△，则可知A n的坐标OA B为，n B的坐标为．（4）线段nOA的长度为．【答案】（1）(16，2)；(32，0)；（2）2；（3）(2n，2)；(2n+1，0)；（4【解析】【分析】（1）根据A1、A2、A3和B1、B2、B3的坐标找出规律，求出A4的坐标、B4的坐标；（2）根据A1、A2、A3的纵坐标找出规律，根据规律解答；（3）根据将△OAB进行n次变换得到△OA n B n的坐标变化总结规律，得到答案；（4）根据勾股定理计算．【详解】（1）∵A1（2，2），A2（4，2）A3（8，2），∴A4的坐标为（16，2），∵B1（4，0），B2（8，0），B3（16，0），∴B4的坐标为（32，0），故答案为：（16，2）；（32，0）；（2）变换过程中A1，A2，A3……A n的纵坐标均为2，故答案为：2；（3）按照上述规律将△OAB进行n次变换得到△OA n B n，则可知A n的坐标为（2n，2），B n的坐标为（2n+1，0）故答案为：（2n，2）；（2n+1，0）；（4）∵A n的横坐标为2n，B n﹣1的横坐标为2n，∴A n B n﹣1⊥x轴，又A n的纵坐标2，由勾股定理得，线段OAn【点睛】本题考查的是坐标与图形、图形的变换、图形的变化规律，正确找出变换前后的三角形的变化规律、掌握勾股定理是解题的关键．93．对于平面直角坐标系x O y中的点P(a，b)，若点P′的坐标为(a+kb，k≠)，则称点P′为点P的“k属派生点”.例如：P(1，ka+b)(其中k为常数，且04)属派生点为P′(1+2×4，2×1+4)，即P′(9，6).(1)点P(-2，3)的“2属派生点”P′的坐标为__________.(2) 若点P的“3属派生点”P′的坐标为（6，2），求点P的坐标；(3) 若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值.【答案】（1）(4，-1)；（2）P（0，2）；（3）2k=±【解析】【分析】（1）根据“k属派生点”计算可得；（2）设点P的坐标为（x、y），根据“k属派生点”定义及P′的坐标列出关于x、y的方程组，解之可得；（3）先得出点P′的坐标为（a，ka），由线段PP′的长度为线段OP长度的2倍列出方程，解之可得．【详解】（1）点P(-2，3)的“2属派生点”P′的坐标为（-2+3×2，-2×2+3），即(4，-1)，故答案为：(4，-1)；（2）设点P的坐标为（x、y），由题意知3632x yx y+⎧⎨+⎩＝＝，解得：2xy⎧⎨⎩＝＝，即点P的坐标为（0，2），故答案为：（0，2）；（3）∵点P 在x 轴的正半轴上， ∴b=0，a ＞0．∴点P 的坐标为（a ，0），点P ′的坐标为（a ，ka ） ∴线段PP ′的长为P ′到x 轴距离为|ka|． ∵P 在x 轴正半轴，线段OP 的长为a ， ∴|ka|=2a ，即|k|=2， ∴k=±2．【点睛】此题考查坐标与图形的性质，熟练掌握新定义并列出相关的方程和方程组是解题的关键．94．如图，网格图中的每小格均是边长是1的正方形，ABC ∆与A B C '''∆的顶点均在格点上，请完成下列各题：（1）在平面直角坐标系中画出与ABC ∆关于x 轴对称的111A B C ∆，并写出将111A B C ∆沿着x 轴向右平移几个单位后得到A B C '''∆；（2）在x 轴上求作一点P ，使得PC PB '-的值最大。

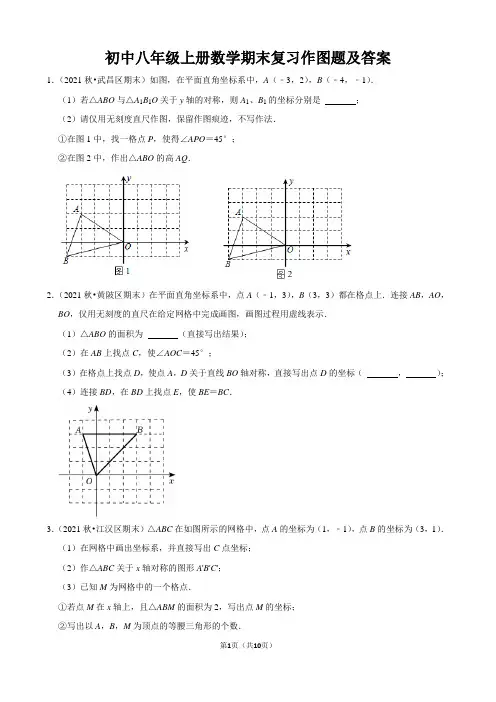
初中八年级上册数学期末复习作图题及答案1．（2021秋•武昌区期末）如图，在平面直角坐标系中，A（﹣3，2），B（﹣4，﹣1）．（1）若△ABO与△A1B1O关于y轴的对称，则A1、B1的坐标分别是；（2）请仅用无刻度直尺作图，保留作图痕迹，不写作法．①在图1中，找一格点P，使得∠APO＝45°；②在图2中，作出△ABO的高AQ．2．（2021秋•黄陂区期末）在平面直角坐标系中，点A（﹣1，3），B（3，3）都在格点上．连接AB，AO，BO，仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．（1）△ABO的面积为（直接写出结果）；（2）在AB上找点C，使∠AOC＝45°；（3）在格点上找点D，使点A，D关于直线BO轴对称，直接写出点D的坐标（，）；（4）连接BD，在BD上找点E，使BE＝BC．3．（2021秋•江汉区期末）△ABC在如图所示的网格中，点A的坐标为（1，﹣1），点B的坐标为（3，1）．（1）在网格中画出坐标系，并直接写出C点坐标；（2）作△ABC关于x轴对称的图形A'B'C'；（3）已知M为网格中的一个格点．①若点M在x轴上，且△ABM的面积为2，写出点M的坐标；②写出以A，B，M为顶点的等腰三角形的个数．4．（2021秋•武汉期末）如图，在平面直角坐标系中，点A（0，4），点B（3，0），AB＝5．请按要求用无刻度的直尺作图（横纵坐标均为整数的点称为格点）．（1）在图1中将线段AB向左平移5个单位得线段CD（点A的对应点为C），并直接写出四边形ABDC 的面积为；（2）在图1中作出∠ABO的平分线BM，P为BM上的格点，则P点有个；（3）在图2中过O作AB的垂线ON，Q为ON上的格点，写出Q点的坐标为．5．（2021秋•汉阳区期末）在平面直角坐标系的网格中，横、纵坐标均为整数的点叫做格点．例如：A（0，4），B（4，2）都是格点．请仅用无刻度的直尺在网格中完成下列画图，保留连线的痕迹．（1）画出线段AB关于x轴对称的线段EF；（2）在x轴上找一点P，使AP+BP最小；（3）连接AP，BP，画出△APB关于y轴对称的△AP′B′．6．（2021秋•硚口区期末）如图是由小正方形组成的6×6网格．每个小正方形的顶点叫做格点，点A，B，C均是格点，仅用无刻度的直尺在给定网格中按要求画图（画图过程用虚线表示）．（1）在图1中，画一个以AB为腰的等腰△ABD；（2）①在图2中，画一个以AB为腰，以A为直角顶点的等腰Rt△ABE；②在图2中，画AB延长线上的点F，使得∠CF A＝45°．（3）在图3中，画AB的垂直平分线．7．（2021秋•青山区期末）如图，在8×7的网格中，横、纵坐标均为整数的点叫做格点，如A（1，4）、B （6，4）、C（3，0）都是格点，且BC＝5．请用无刻度直尺在给定网格中画出下列图形，并保留作图痕迹．（画图过程用虚线表示，画图结果用实线表示）．（1）过点A作AD∥BC，且AD＝BC；（2）画△ABC的高BE，并直接写出E点坐标；（3）在AB上找点P，使∠BCP＝45°：（4）作点P关于AC的对称点Q．8．（2021秋•江夏区期末）如图，在平面直角坐标系中，点A（3，3），B（5，1），C（﹣2，﹣3）．（1）在图中画出△ABC关于y轴对称的△A1B1C1，并直接写出点A1，B1，C1的坐标．（2）求△ABC的面积．9．（2021秋•洪山区期末）如图，网格中的每个小正方形的顶点称作格点．点A、C、G、H在格点上，将点A先向右移动5格，再向上移动2格后得到点B，仅用无刻度的直尺在给定网格中按下列步骤完成画图，保留画图过程的痕迹，并回答问题：（1）在网格中标注点B，并连接AB；（2）在网格中找格点D，使得GD∥AB且GD＝AB；（3）在网格中找格点E，使得CE⊥AB，垂足为F；（4）在线段GH上找一点M，使得∠AMG＝∠BMH．10．（2021秋•江岸区期末）如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点，△ABC的顶点在格点上．请选择适当的格点，用无刻度的直尺在网格中完成下列画图，保留连线的痕迹，不要求说明理由．（1）如图1，作△ABC的中线AD；（2）如图2，作△ABC的高线CE；（3）如图3，点F是AC与网格线的交点，请在BC上作一点H，使FH∥AB；（4）如图4，直线a和直线b在网格线上，点A和点H在两条直线的两侧，请在直线a上作一点M，直线b上作一点N，使AM+MN+NH的值最小．参考答案与试题解析一．解答题（共10小题）1．【解答】解：（1）如图，△A1B1O即为所求，则A1、B1的坐标分别（3，2），（4，﹣1）；（2）①如图1在，点P即为所求（答案不唯一，（2，2），（﹣3，3）也满足条件）；②如图2中，线段AQ即为所求．2．【解答】解：（1）△ABO的面积，故答案为：6；（2）如图所示：（3）如图所示，D（3，﹣1）；故答案为：3；﹣1；（4）如图所示．3．【解答】解：（1）如图，（2）如图，△A'B'C'为所作；（3）①设M（t，0），∵△ABM的面积为2，∴|t﹣2|×2＝2，解得t＝0或t＝4，∴M点坐标为（0，0）或（4，0）②以A，B，M为顶点的等腰三角形的个数为13．4．【解答】解：（1）如图1，∵将线段AB向左平移5个单位得线段CD，∴AC＝BD＝5，∵AB5，∴CD＝AB＝5，∴AB＝BD＝CD＝AC，∴四边形ABDC是菱形，∴四边形ABDC的面积＝BD•OA＝5×4＝20；故答案为：20；（2）作射线BC，由（1）知，四边形ABDC是菱形，∴BC平分∠ABO，∴射线BM与射线BC是同一条射线，由图知满足条件的P点有4个，故答案为：4；（3）如图2，过点（4，3），（0，0）作直线，则OQ⊥AB，Q（4，3）或（﹣4，﹣3），故答案为：（4，3）或（﹣4，﹣3）．5．【解答】解：（1）如图，线段EF即为所求；（2）如图，点P即为所求；（3）如图所示，△AP′B′即为所求．6．【解答】解：（1）如图1中，△ABD即为所求；（2）①如图2中，△ABE即为所求；②如图2中，∠AFC即为所求；（3）如图，直线PQ即为所求．7．【解答】解：（1）如图，线段AD即为所求；（2）如图，线段BE即为所求；（3）如图，点P即为所求；（4）如图，点Q即为所求．8．【解答】解：（1）如图，△A1B1C1即为所求．并直接写出点A1（﹣3，3），B1（﹣5，1），C1（2，﹣3）．故答案为：（﹣3，3），（﹣5，1），（2，﹣3）；（2）S△ABC＝6×76×52×27×4＝11．9．【解答】解：（1）如图，线段AB即为所求；（2）如图，线段DG即为所求；（3）如图，线段CE，点F即为所求；（4）如图，点M即为所求．10．【解答】解：（1）如图1中，线段AD即为所求；（2）如图2中，线段CE即为所求；（3）如图3中，线段FH即为所求；（4）如图4中，点M，点N即为所求．。

一、平面几何1. 画一个圆，半径为3cm。

2. 画一个等边三角形，边长为4cm。

3. 画一个长方形，长为5cm，宽为3cm。

4. 画一个平行四边形，相邻两边长分别为4cm和6cm。

5. 画一个梯形，上底长为3cm，下底长为5cm，高为2cm。

6. 画一个正五边形，边长为4cm。

7. 画一个圆，圆心为点O，半径为2cm，画圆上的任意两点A和B。

8. 画一个直线，经过点P(2,3)和点Q(4,5)。

9. 画一个射线，起点为点R，经过点S(1,2)。

10. 画一个角，顶点为点T，一个边为射线UT，另一个边为射线VT。

二、立体几何1. 画一个正方体，边长为3cm。

2. 画一个长方体，长为4cm，宽为2cm，高为3cm。

3. 画一个圆柱，底面半径为2cm，高为4cm。

4. 画一个圆锥，底面半径为3cm，高为5cm。

5. 画一个球，半径为2cm。

6. 画一个棱锥，底面为正三角形，边长为4cm，高为5cm。

7. 画一个棱柱，底面为矩形，长为3cm，宽为2cm，高为4cm。

8. 画一个球冠，底面半径为3cm，高为2cm。

9. 画一个球缺，底面半径为3cm，高为2cm。

10. 画一个椭球体，长轴为4cm，短轴为2cm，焦距为1cm。

三、坐标系1. 在平面直角坐标系中，画出点A(2,3)和点B(4,5)。

2. 在平面直角坐标系中，画出直线y=2x。

3. 在平面直角坐标系中，画出射线x=3。

4. 在平面直角坐标系中，画出圆x^2+y^2=9。

5. 在平面直角坐标系中，画出椭圆x^2/4+y^2/9=1。

6. 在空间直角坐标系中，画出点P(2,3,4)和点Q(4,5,6)。

7. 在空间直角坐标系中，画出直线x=2。

8. 在空间直角坐标系中，画出球面x^2+y^2+z^2=16。

9. 在空间直角坐标系中，画出椭球面x^2/4+y^2/9+z^2/16=1。

10. 在空间直角坐标系中，画出直线x+y+z=3。

四、三角函数1. 画y=sin(x)在[0, 2π]范围内的图像。

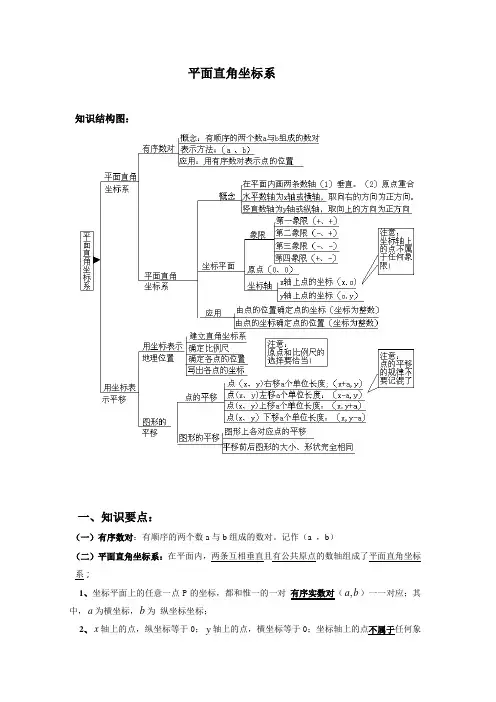
平面直角坐标系知识结构图：一、知识要点：（一）有序数对：有顺序的两个数a与b组成的数对。

记作（a ，b）（二）平面直角坐标系：在平面内，两条互相垂直且有公共原点的数轴组成了平面直角坐标系；a,）一一对应；其1、坐标平面上的任意一点P的坐标，都和惟一的一对有序实数对（b中，a为横坐标，b为纵坐标坐标；2、x轴上的点，纵坐标等于0；y轴上的点，横坐标等于0；坐标轴上的点不属于任何象限（三）四个象限的点的坐标具有如下特征：1、点P （y x ,）所在的象限 横、纵坐标x 、y 的取值的正负性；2、点P （y x ,）所在的数轴 横、纵坐标x 、y 中必有一数为零； （四）在平面直角坐标系中，已知点P ),(b a ，则 1、点P 到x 轴的距离为b ； 2、点P 到y 轴的距离为a ；3、点P 到原点O 的距离为PO ＝ 22b a +（五）平行直线上的点的坐标特征：1、在与x 轴平行的直线上， 所有点的纵坐标相等；点A 、B 的纵坐标都等于m ；2、在与y 轴平行的直线上，所有点的横坐标相等；点C 、D 的横坐标都等于n ；（六）对称点的坐标特征：1、点P ),(n m 关于x 轴的对称点为),(1n m P -， 即横坐标不变，纵坐标互为相反数；象限 横坐标x纵坐标y第一象限 正 正 第二象限 负 正 第三象限 负 负 第四象限正负P （b a ,）abxy OXYA BmXYC Dn2、点P ),(n m 关于y 轴的对称点为),(2n m P -， 即纵坐标不变，横坐标互为相反数；3、点P ),(n m 关于原点的对称点为),(3n m P --，即横、纵坐标都互为相反数；关于x 轴对称 关于y 轴对称 关于原点对称（七）两条坐标轴夹角平分线上的点的坐标的特征：1、若点P （n m ,）在第一、三象限的角平分线上，则n m =，即横、纵坐标相等；2、若点P （n m ,）在第二、四象限的角平分线上，则n m -=，即横、纵坐标互为相反数；在第一、三象限的角平分线上 在第二、四象限的角平分线上（八）利用平面直角坐标系绘制区域内一些点分布情况平面图过程如下：1、建立坐标系，选择一个适当的参照点为原点，确定x 轴、y 轴的正方向；2、根据具体问题确定适当的比例尺，在坐标轴上标出单位长度；3、在坐标平面内画出这些点，写出各点的坐标和各个地点的名称。

人教版2023中考数学二轮复习专题之平面直角坐标系一、单选题1．（2022八上·沈北新期中）在平面直角坐标系中，下列坐标所对应的点位于第三象限的是（）A．（﹣1，2）B．（1，2）C．（2，﹣1）D．（-1，-3）2．（2022八上·电白期中）若点P（a，b）在第四象限，则点Q（﹣a，b﹣1）在（）A．第一象限B．第二象限C．第三象限D．第四象限3．（2022八上·太原期中）在如图所示的平面直角坐标系中，点P的坐标为（）A．(2，3)B．(−2，3)C．(3，−2)D．(−2，−3)4．（2022八上·常熟月考）如图，正方形ABCD的边长为4，点A的坐标为（﹣1，1），AB平行于x轴，则点C的坐标为（）A．（3，1）B．（﹣1，1）C．（3，5）D．（﹣1，5）5．（2022九上·和平期中）如图，菱形ABCD对角线交点与坐标原点O重合，点A(−2，5)，则点C的坐标为（）A．(5，−2)B．(2，−5)C．(2，5)D．(−2，−5)6．（2022九上·萧山期中）如图，在正方形网格中，线段AB绕点O旋转一定的角度后与线段CD重合(C、D均为格点，A的对应点是点C)，若点A的坐标为(−1，5)，点B的坐标为(3，3)，则旋转中心O点的坐标为（）A．(1，1)B．(4，4)C．(2，1)D．(1，1)或(4，4)7．（2022八上·西安期中）如图，在平面直角坐标系中，点A的坐标是(−3，0)，点B的坐标是(0，4)，点C是OB上一点，将△ABC沿AC折叠，点B恰好落在x轴上的点B′处，则点C的坐标为（）A．(32，0)B．(0，32)C．(52，0)D．(0，52)8．（2022八上·杭州期中）已知点A的坐标为(a+1，3−a)，下列说法正确的是（）A．若点A在y轴上，则a=3B．若点A在一三象限角平分线上，则a=1C．若点A到x轴的距离是3 ，则a=±6D．若点A在第四象限，则a的值可以为-29．（2022七下·康巴什期末）我们规定：在平面直角坐标系xOy中，任意不重合的两点M(x1，y1)，N(x2，y2)之间的折线距离为d(M，N)=|x1−x2|+|y1−y2|，例如图①中，点M(−2，3)与点N(1，−1)之间的折线距离为d(M，N)= |−2−1|+|3−(−1)|=3+4=7．如图②，已知点P(3，−4)若点Q的坐标为(t，2)，且d(P，Q)=10，则t的值为（）A．−1B．5C．5或−13D．−1或7 10．（2022七下·纳溪期末）在平面直角坐标系中，对于点P（x，y），我们把点P′（﹣y+1，x+1）叫做点P伴随点．已知点A1的伴随点为A2，点A2的伴随点为A3，点A3的伴随点为A4，…，这样依次得到点A1，A2，A3，…，A n，…若点A1的坐标为（2，4），点A2021的坐标为（）A．（3，﹣1）B．（﹣2，﹣2）C．（﹣3，3）D．（2，4 ）二、填空题11．（2022八上·瑞安月考）在平面直角坐标系中，点(1，-2)向左平移2个单位后的坐标为。

平面直角坐标系一、选择题1. (2018 山东省东营市)在平面直角坐标系中，若点P（m﹣2，m+1）在第二象限，则m的取值范围是（）A．m＜﹣1 B．m＞2C．﹣1＜m＜2 D．m＞﹣1【答案】C【解析】∵点P（m﹣2，m+1）在第二象限，∴，解得﹣1＜m＜2．故选：C．2. (2018 山东省济宁市)如图，在平面直角坐标系中，点A，C在x轴上，点C的坐标为（﹣1，0），AC=2．将Rt△ABC先绕点C顺时针旋转90°，再向右平移3个单位长度，则变换后点A的对应点坐标是（）A．（2，2）B．（1，2）C．（﹣1，2）D．（2，﹣1）【答案】A【解析】∵点C的坐标为（﹣1，0），AC=2，∴点A的坐标为（﹣3，0），如图所示，将Rt△ABC先绕点C顺时针旋转90°，则点A′的坐标为（﹣1，2），再向右平移3个单位长度，则变换后点A′的对应点坐标为（2，2），故选：A．3. (2018 山东省青岛市)如图，将线段AB绕点P按顺时针方向旋转90°，得到线段A'B'，其中点A、B的对应点分别是点A'、B'，则点A'的坐标是（）A．（﹣1，3）B．（4，0）C．（3，﹣3）D．（5，﹣1）【答案】D【解析】画图如下：则A'（5，﹣1），故选：D．4. (2018 山东省泰安市)如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，△ABC经过平移后得到△A1B1C1，若AC上一点P（1.2，1.4）平移后对应点为P1，点P1绕原点顺时针旋转180°，对应点为P2，则点P2的坐标为（）A．（2.8，3.6）B．（﹣2.8，﹣3.6）C．（3.8，2.6）D．（﹣3.8，﹣2.6）【答案】A【解析】由题意将点P向下平移5个单位，再向左平移4个单位得到P1，∵P（1.2，1.4），∴P1（﹣2.8，﹣3.6），∵P1与P2关于原点对称，∴P2（2.8，3.6），故选：A．5. (2018 山东省潍坊市)在平面直角坐标系中，点P（m，n）是线段AB上一点，以原点O为位似中心把△AOB 放大到原来的两倍，则点P的对应点的坐标为（）A．（2m，2n）B．（2m，2n）或（﹣2m，﹣2n）C．（m，n）D．（m，n）或（﹣m，﹣n）【答案】B【解析】点P（m，n）是线段AB上一点，以原点O为位似中心把△AOB放大到原来的两倍，则点P的对应点的坐标为（m×2，n×2）或（m×（﹣2），n×（﹣2）），即（2m，2n）或（﹣2m，﹣2n），故选：B．6. (2018 山东省潍坊市)在平面内由极点、极轴和极径组成的坐标系叫做极坐标系．如图，在平面上取定一点O称为极点；从点O出发引一条射线Ox称为极轴；线段OP的长度称为极径．点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度（规定逆时针方向转动角度为正）来确定，即P（3，60°）或P （3，﹣300°）或P（3，420°）等，则点P关于点O成中心对称的点Q的极坐标表示不正确的是（）A．Q（3，240°）B．Q（3，﹣120°）C．Q（3，600°）D．Q（3，﹣500°）【答案】D【解析】∵P（3，60°）或P（3，﹣300°）或P（3，420°），由点P关于点O成中心对称的点Q可得：点Q的极坐标为（3，240°），（3，﹣120°），（3，600°），故选：D．7. (2019 山东省滨州市)在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点B，则点B的坐标是（）A．（﹣1，1）B．（3，1）C．（4，﹣4）D．（4，0）【答案】A【解析】∵将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点B，∴点B的横坐标为1﹣2＝﹣1，纵坐标为﹣2+3＝1，∴B的坐标为（﹣1，1）．故选：A．8. (2019 山东省滨州市)已知点P（a﹣3，2﹣a）关于原点对称的点在第四象限，则a的取值范围在数轴上表示正确的是（）A．B．C．D．【答案】C【解析】∵点P（a﹣3，2﹣a）关于原点对称的点在第四象限，∴点P（a﹣3，2﹣a）在第二象限，∴，解得：a＜2．则a的取值范围在数轴上表示正确的是：．故选：C．9. (2019 山东省青岛市)如图，将线段AB先向右平移5个单位，再将所得线段绕原点按顺时针方向旋转90°，得到线段A′B′，则点B的对应点B′的坐标是（）A．（﹣4，1）B．（﹣1，2）C．（4，﹣1）D．（1，﹣2）【答案】D【解析】将线段AB先向右平移5个单位，点B（2，1），连接OB，顺时针旋转90°，则B'对应坐标为（1，﹣2），故选：D．10. (2019 山东省枣庄市)在平面直角坐标系中，将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，则点A′的坐标是（）A．（﹣1，1）B．（﹣1，﹣2）C．（﹣1，2）D．（1，2）【答案】A【解析】∵将点A（1，﹣2）向上平移3个单位长度，再向左平移2个单位长度，得到点A′，∴点A′的横坐标为1﹣2＝﹣1，纵坐标为﹣2+3＝1，∴A′的坐标为（﹣1，1）．故选：A．二、填空题11. (2018 山东省威海市)如图，在平面直角坐标系中，点A1的坐标为（1，2），以点O为圆心，以OA1长为半径画弧，交直线y=x于点B1．过B1点作B1A2∥y轴，交直线y=2x于点A2，以O为圆心，以OA2长为半径画弧，交直线y=x于点B2；过点B2作B2A3∥y轴，交直线y=2x于点A3，以点O为圆心，以OA3长为半径画弧，交直线y=x于点B3；过B3点作B3A4∥y轴，交直线y=2x于点A4，以点O为圆心，以OA4长为半径画弧，交直线y=x于点B4，…按照如此规律进行下去，点B2018的坐标为．【答案】：（22018，22017）【解析】：由题意可得，点A1的坐标为（1，2），设点B1的坐标为（a，a），，解得，a=2，∴点B1的坐标为（2，1），同理可得，点A2的坐标为（2，4），点B2的坐标为（4，2），点A3的坐标为（4，8），点B3的坐标为（8，4），……∴点B2018的坐标为（22018，22017），故答案为：（22018，22017）．12. (2018 山东省潍坊市)如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D 在x轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置，B'C′与CD相交于点M，则点M的坐标为．【答案】：（﹣1，）【解析】如图，连接AM，∵将边长为1的正方形ABCD绕点A逆时针旋转30°得到正方形AB'C′D′，∴AD=AB′=1，∠BAB′=30°，∴∠B′AD=60°，在Rt△ADM和Rt△AB′M中，∵，∴Rt△ADM≌Rt△AB′M（HL），∴∠DAM=∠B′AM=∠B′AD=30°，∴DM=ADtan∠DAM=1×=，∴点M的坐标为（﹣1，），故答案为：（﹣1，）．13. (2019 山东省东营市)如图，在平面直角坐标系中，△ACE是以菱形ABCD的对角线AC为边的等边三角形，AC＝2，点C与点E关于x轴对称，则点D的坐标是．【答案】：（，0）【解析】：如图，∵△ACE是以菱形ABCD的对角线AC为边的等边三角形，AC＝2，∴CH＝1，∴AH＝，∵∠ABO＝∠DCH＝30°，∴DH＝AO＝，∴OD＝﹣﹣＝，∴点D的坐标是（，0）．故答案为：（，0）．14. (2019 山东省济宁市)已知点P（x，y）位于第四象限，并且x≤y+4（x，y为整数），写出一个符合上述条件的点P的坐标．【答案】：（1，﹣2）（答案不唯一）．【解析】∵点P（x，y）位于第四象限，并且x≤y+4（x，y为整数），∴x＞0，y＜0，∴当x＝1时，1≤y+4，解得：0＞y≥﹣3，∴y可以为：﹣2，故写一个符合上述条件的点P的坐标可以为：（1，﹣2）（答案不唯一）．故答案为：（1，﹣2）（答案不唯一）．15. (2019 山东省临沂市)在平面直角坐标系中，点P（4，2）关于直线x＝1的对称点的坐标是．【答案】（﹣2，2）【解析】∵点P（4，2），∴点P到直线x＝1的距离为4﹣1＝3，∴点P关于直线x＝1的对称点P′到直线x＝1的距离为3，∴点P′的横坐标为1﹣3＝﹣2，∴对称点P′的坐标为（﹣2，2）．故答案为：（﹣2，2）．三、作图题16. (2017 山东省枣庄市) 如图，在平面直角坐标系中，已知△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）．（1）请在图中，画出△ABC向左平移6个单位长度后得到的△A1B1C1；（2）以点O为位似中心，将△ABC缩小为原来的，得到△A2B2C2，请在图中y轴右侧，画出△A2B2C2，并求出∠A2C2B2的正弦值．【解析】（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C2，即为所求，由图形可知，∠A2C2B2=∠ACB，过点A作AD⊥BC交BC的延长线于点D，由A（2，2），C（4，﹣4），B（4，0），易得D（4，2），故AD=2，CD=6，AC==2，∴sin∠ACB===，即sin∠A2C2B2=．17. (2015 山东省枣庄市) 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．（1）画出△ABC向下平移4个单位长度得到的△A1B1C1，点C1的坐标是；（2）以点B为位似中心，在网格内画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2：1，点C2的坐标是；（3）△A2B2C2的面积是平方单位．【解析】（1）如图所示：C1（2，﹣2）；故答案为：（2，﹣2）；（2）如图所示：C2（1，0）；故答案为：（1，0）；（3）∵A2C22=20，B2C=20，A2B2=40，∴△A2B2C2是等腰直角三角形，∴△A2B2C2的面积是：×20=10平方单位．故答案为：10．。

题型专项(六) 网格作图题网格作图题是对图形变换的综合考查，在网格中可以同时考察平移、旋转、轴对称、中心对称等几种图形变换．此类题目属于图形的操作问题，在网格中进行图形变换的操作时，图形的每一个顶点都是关键点，可以将图形的变换操作转化为点的变换操作．此类题目属中档题，复习时注意练习即可．1．如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(2，－1)，B(3，－3)，C(0，－4)．(1)画出△ABC关于原点O成中心对称的△A1B1C1；(2)画出△A1B1C1关于y轴对称的△A2B2C2.解：(1)△A1B1C1如图所示．(2)△A2B2C2如图所示．2．在如图所示的方格纸中，每个小正方形的边长都是1，△ABC和△A1B1C1成中心对称．(1)请在图中画出对称中心O；(2)在图中画出将△A1B1C1沿直线DE平移5格得到的△A2B2C2；(3)要使△A2B2C2与△CC1C2重合，需将△A2B2C2绕点C2顺时针旋转，则至少要旋转90度．解：(1)如图，点O即为所求．(2)如图，△A2B2C2即为所求．3．山区一模)如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(－4，3)，B(－3，1)，C(－1，3)．(1)请按下列要求画图：①将△ABC先向右平移4个单位长度，再向上平移2个单位长度，得到△A1B1C1，画出△A1B1C1；②△A2B2C2与△ABC关于原点O中心对称，画出△A2B2C2；(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称，请直接写出对称中心M点的坐标(2，1)．解：(1)①如图：△A1B1C1即为所求．②如图：△A2B2C2即为所求．4．拟)在下列网格图中，每个小正方形的边长均为1个单位．在Rt△ABC中，∠C＝90°，AC＝3，BC＝4.(1)试在图中作出△ABC以A为旋转中心，沿顺时针方向旋转90°后的图形△AB1C1；(2)若点B的坐标为(－3，5)，试在图中画出直角坐标系，并标出A，C两点的坐标；(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2，并标出B2，C2两点的坐标．解：(1)△AB1C1如图所示．(2)如图所示，A(0，1)，C(－3，1)．(3)△A2B2C2如图所示，B2(3，－5)，C2(3，－1)．5．如图，在平面直角坐标系中，点A、B、C的坐标分别为(－1，3)、(－4，1)、(－2，1)，先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是(1，2)，再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2.(1)画出△A1B1C1；(2)画出△A2B2C2；(3)求出在这两次变换过程中，点A经过点A1到达点A2的路径总长．解：(1)如图，△A1B1C1即为所求．(2)如图，△A2B2C2即为所求．(3)OA1＝42＋42＝42，点A 经过点A 1到达A 2的路径总长为52＋12＋90·π·42180＝26＋22π. 6．拟)如图，在平面直角坐标系中，已知△ABC 的三个顶点的坐标分别为A(－1，1)，B(－3，1)，C(－1，4)．(1)画出△ABC 关于y 轴对称的△A 1B 1C 1；(2)将△ABC 绕着点B 顺时针旋转90°后得到△A 2BC 2，请在图中画出△A 2BC 2，并求出线段BC 旋转过程中所扫过的面积(结果保留π)．解：(1)如图所示，△A 1B 1C 1即为所求．(2)如图所示，△A 2BC 2即为所示， 线段BC 旋转过程中所扫过的面积S ＝90×13π360＝13π4. 7．龙区二模)如图，△ABC 三个顶点的坐标分别为A(1，1)，B(4，2)，C(3，4)．(1)请画出将△ABC 先向左，再向下都平移5个单位长度后得到的△A 1B 1C 1；(2)请画出将△ABC 绕O 按逆时针方向旋转90°后得到的△A 2B 2C 2；(3)在x 轴上求作一点P ，使△PAB 周长最小，请画出△PAB 并直接写出点P 的坐标．解：(1)如图，△A 1B 1C 1即为所求．(2)如图，△A 2B 2C 2即为所求．(3)如图，△PAB 即为所求，P(2，0)．8．拟)图中的小方格都是边长为1的正方形，△ABC 的顶点和O 点都在正方形的顶点上．(1)以点O 为位似中心，在方格图中画出将△ABC 放大为原来的2倍得到的△A ′B ′C ′；(2)△A ′B ′C ′绕点B ′顺时针旋转90°，画出旋转后得到的△A ″B ′C ″，并求边A ′B ′在旋转过程中扫过的图形面积．解：(1)如图，△A′B′C′即为所求．(2)如图，△A″B′C″即为所求．S＝90360π(22＋42)＝14π·20＝5π.。