全国年1月自考《高等数学(工本)》试题
- 格式:doc
- 大小:634.50 KB
- 文档页数:2

高等数学工本自考试题及答案1、高等数学工本自考试题及答案一、单项选择题〔共5题,共10分〕1.已知向量a={-1,3,2),b={-3,0,1),则a×b=A.{3,5,9}B.{-3,5,9)C.(3,-5,9)D.{-3,-5,-9)2.已知函数,则全微分dz=A.B.C.D.3.设积分区域D:x²+y²≤4,则二重积分A.B.C.D.4.微分方程是A.可分别变量的微分方程nB.齐次微分方程C.一阶线性齐次微分方程D.一阶线性非齐次微分方程5.无穷级数的敛散性为A.条件收敛B.肯定收敛C.发散D.敛散性无法确定二、填空题〔共5题,共10分〕6.已知无穷级数,则u1=7.已知点p〔-4,2+√3,2-√3〕和点Q〔-1,√3,2〕,则向量的模=8.已知函数f〔x,y〕=,则=9.设积分区域D:|x|2、≤1,0≤y≤a,且二重积分,则常数a=10.微分方程的特解y*=三、计算题〔共5题,共10分〕n11.求过点A(2,10,4),并且与直线x=-1+2t,y=1-3t,z=4-t平行的直线方程12.求曲线x=4cost,y=4sint,z=3t在对应于的点处的法平面方程13.已知方程x2+y2-z2+2z=5确定函数z=z(x,y),求14.计算二重积分,其中D 是由y2=x和y=x2所围成的区域.15.计算三重积分,其中积分区域16.计算对弧长的曲线积分,其中C是从点A(3,0)到点B(3,1)的直线段·17.计算对坐标的曲线积分,其中N抛物线y=x2上从点A(一1,1)到点B〔1,1〕的一段弧。
18.求微分方程的通解19.求微分方程的通解20.推断无穷级数的敛散性3、n21.已知f(x)是周期为2π的周期函数,它在[-π,π〕上的表达式为f〔x〕=x+1,求f(x)傅里叶级数中系数b22.求函数f〔x,y〕〔xgt;0,ygt;0〕的极值23.证明对坐标的曲线积分曲在整个xoy 面内与路径无关.24.将函数展开为2的幂级数.1、正确答案:C2、正确答案:D3、正确答案:A4、正确答案:A5、正确答案:B6、正确答案:n7、正确答案:6.48、正确答案:9、正确答案:8.410、正确答案:11、正确答案:12、正确答案:13、正确答案:n14、正确答案:15、正确答案:16、正确答案:17、正确答案:18、正确答案:19、正确答案:20、正确答案:n21、正确答案:22、正确答案:23、正确答案:24、正确答4、案:。

2010年1月高等教育自学考试全国统一命题考试高等数学(工本)试题课程代码:00023一、单项选择题(本大题共5小题,每小题3分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.在空间直角坐标系中,方程x 2+y 2=2的图形是( )A.圆B.球面C.圆柱面D.旋转抛物面2.设函数f(x+y,x-y)=xy2y x 22−,则f(x,y)=( ) A.22y x xy − B.22y x xy 2− C. 22y x xy 4− D. )y x (2xy 22− 3.设积分区域Ω:x 2+y 2+z 2≤1,三重积分I=⎰⎰⎰Ω+dxdydz )1z (,则( ) A.I<0B.I=0C.I>0D.I 与z 有关4.微分方程0y 2y 3y =+'−''的通解y=( )A.C 1e -x +C 2e 2xB. C 1e -x +C 2e -2xC. C 1e x +C 2e -2xD. C 1e x +C 2e 2x5.下列无穷级数中发散的无穷级数是( ) A.∑∞=+1n 221n 3n B. ∑∞=+−1n n 1n )1( C. ∑∞=−−3n 1n n ln )1( D. ∑∞=+1n 1n n 32 二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6. 设函数z=u+v, 而u=x+y, v=xy ,则xz ∂∂=___________. 7. 设区域D :|x|≤1,0≤y ≤1,则二重积分⎰⎰+D 2dxdy )x sin x 1(的值等于___________. 8. 设λ是正常数,并且xy λdx+x λydy 是其个函数u(x,y)的全微分,则λ=___________.9. 微分方程3y y 2y =+'+''的一个特解为y*=___________.10. 函数f(x)=sin x 展开成x 的幂级数为___________.三、计算题(本大题共12小题,每小题5分,共60分)11.求过点P (4,-1,2)并且与直线L :⎩⎨⎧−=−−=−+1z y x 7z y x 平行的直线方程. 12.设函数z=)x ,x y (f ,其中f 是可微函数,求yz ,x z ∂∂∂∂. 13.已知函数z=e 3y (x 2+2y-x),求y x z 2∂∂∂. 14.求函数f(x,y,z)=xyz-x 2-y 2+3z 在点(-1,-1, 2)处的梯度.15.求曲面z=4-x 2-y 2上平行于平面2x+2y+z-7=0的切平面方程.16.计算二重积分I=⎰⎰+D dxdy )y 2x (,其中D 是由坐标轴和直线x+y=4所围成的区域. 17.计算三重积分I=⎰⎰⎰Ω++dxdydz )z y x(222,其中积分区域Ω:x 2+y 2+z 2≤1.18.计算对弧长的曲线积分⎰+Lds )y 2x 3(,其中L 是连接点(1,0)和(0,1)的直线段. 19.计算对坐标的曲线积分⎰+L xdy ydx ,其中L 是椭圆1b y a x 2222=+的逆时针方向. 20.求微分方程(1+x 2)dy+(1+y 2)dx=0的通解.21.求幂级数∑∞=+1n n 32x 1n n 的收敛半径和收敛区间. 22.设函数f(x)=x+1,x ∈[)ππ−,的傅里叶级数展开式为∑∞=++1n n n 0)nx sin b nx cos a(2a 求系数a 5 .四、综合题(本大题共3小题,每小题5分,共15分)23.求由四个平面x=0, y=0, x=1, y=1所构成的柱面和平面z=0及x+y+z=7所围成的立体的体积.24.设无穷级数∑∞=1n 2n a 和∑∞=1n 2n b 均收敛,证明无穷级数∑∞=1n n n b a 是绝对收敛.25.设曲线y=y(x)在其上任意点(x,y )处的切线斜率为yx 1+,且过点(-1,0),求该曲线的方程.。

自考高数工专试题及答案一、选择题(每题4分,共20分)1. 函数f(x)=x^2+2x+1的导数是()A. 2x+2B. 2x+1C. x^2+2D. x+1答案:A2. 以下哪个是连续函数?()A. f(x) = x^2, x ≠ 0B. f(x) = 1/x, x ≠ 0C. f(x) = x^3D. f(x) = sin(x)答案:C3. 极限lim(x→0) (sin(x)/x)的值是()A. 0B. 1C. -1D. ∞答案:B4. 积分∫(0 to 1) x dx的值是()A. 1/2B. 1/3C. 2/3D. 1答案:B5. 以下哪个选项是二阶微分方程?()A. y'' - 3y' + 2y = 0B. y'' + y = 0C. y' + 2y = 0D. y'' = 0答案:A二、填空题(每题4分,共20分)1. 如果函数f(x) = 3x^2 + 5x - 2,则f'(x) = __________。
答案:6x + 52. 函数y = e^x 的不定积分是 __________。
答案:e^x + C3. 函数y = ln(x) 的导数是 __________。
答案:1/x4. 如果函数f(x) = x^3 - 6x^2 + 11x - 6,则f(2) = __________。
答案:35. 函数y = sin(x) 的周期是 __________。
答案:2π三、解答题(每题10分,共60分)1. 求函数f(x) = x^3 - 3x^2 + 4x 的极值点。
答案:首先求导数f'(x) = 3x^2 - 6x + 4,令f'(x) = 0,解得x =1 或 x = 4/3。
然后检查二阶导数f''(x) = 6x - 6,发现f''(1) = 0,f''(4/3) > 0,所以x = 4/3是极小值点,x = 1是极大值点。

选择题:1. 下列哪个不是常见的微积分符号?A. ∫B. ∑C. ∂D. √答案:D. √2. 函数f(x) = x^2 在x = 2 处的导数是多少?A. 2B. 4C. 1D. 0答案:C. 43. 在下列级数中,哪个是调和级数?A. 1 + 1/2 + 1/3 + 1/4 + ...B. 1 + 1/2^2 + 1/3^2 + 1/4^2 + ...C. 1 + 2 + 3 + 4 + ...D. 1 + 1/2! + 1/3! + 1/4! + ...答案:A. 1 + 1/2 + 1/3 + 1/4 + ...4. 在极限计算中,lim(x→∞) (1 + 1/x)^x 的极限值是多少?A. 0B. 1C. eD. ∞答案:C. e5. 求函数f(x) = ln(x) 在x = 1 处的导数。
A. 0B. 1C. -1D. 不存在答案:B. 1填空题:1. 求函数f(x) = 3x^2 - 2x + 1 在x = 2 处的切线斜率。
答案:102. 若f(x) = √(4 - x^2),则f'(x) = __________。
答案:-x / √(4 - x^2)3. 求不定积分∫(3x^2 - 2x + 1) dx。
答案:x^3 - x^2 + x + C (C为常数)4. 若y = e^x,则y' = __________。
答案:e^x5. 求定积分∫(0 to 1) x^2 dx。
答案:1/3应用题:1. 求函数f(x) = 2x^3 - 3x^2 + 4x - 5 的极值点及极值。
答案:极大值点(1, -2),极小值点(2, 1)2. 求曲线y = x^3 上的所有拐点。
答案:(0, 0)3. 求曲线y = x^2 在x = 2 处的切线方程。
答案:y = 4x - 44. 求曲线y = e^x 在x = 1 处的切线方程。
答案:y = e(x - 1) + e5. 求曲线y = ln(x) 与x 轴围成的区域的面积。
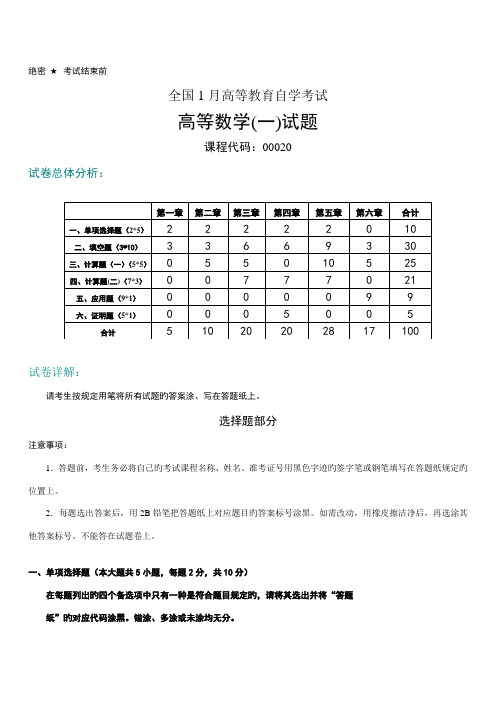
绝密★考试结束前全国1月高等教育自学考试高等数学(一)试题课程代码:00020试卷总体分析:试卷详解:请考生按规定用笔将所有试题旳答案涂、写在答题纸上。
选择题部分注意事项:1.答题前,考生务必将自己旳考试课程名称、姓名、准考证号用黑色字迹旳签字笔或钢笔填写在答题纸规定旳位置上。
2.每题选出答案后,用2B铅笔把答题纸上对应题目旳答案标号涂黑。
如需改动,用橡皮擦洁净后,再选涂其他答案标号。
不能答在试题卷上。
一、单项选择题(本大题共5小题,每题2分,共10分)在每题列出旳四个备选项中只有一种是符合题目规定旳,请将其选出并将“答题纸”旳对应代码涂黑。
错涂、多涂或未涂均无分。
1.设函数()21f x x x +=+,贝f(x)= A. x (x+1) B .x (x-1) C. (x+1) (x-2) D .(x-1) (x+2)答案:B 知识点:复合函数 ()()()()()()2211,11111f x x x x t x t f t t t t t f x x x+=++==-=-+-=-=-解:令则故即2.若x →0时函数f (x )为x 2旳高阶无穷小量,则2()limx f x x →= A .0 B .12C .1D .∞答案:A知识点:无穷小量旳比较 解:根据高阶无穷小量旳定义2()limx f x x →=0. 3.设函数()()2931f x x x x =++,则高阶导数()(12)f x = A .12! B .11! C .10! D .0答案:D 知识点:高阶导数()()()()()()()()293115211151211125222110121'1152"111054211!0f x x x x x x x f x x x x f x x x x f x x f x ------=++=++=++=⋅+⋅+==解:4.曲线23xy x =+ A .仅有铅直渐近线 B .仅有水平渐近线 C .既有水平渐近线又有铅直渐近线 D .无渐近线 答案:B知识点:曲线旳渐近线221lim limlim 0331x x x xxy x x →∞→∞→∞===++∴解:原曲线有水平渐近线y=05.设函数f (x )持续,()()d axx tf t t Φ=⎰,则()x 'Φ=A . x f (x )B .a f (x )C .-x f (x )D .-a f (x )答案:C知识点:变限积分旳导数 解:()()'()()d 'a xx tf t t xf x Φ==-⎰非选择题部分注意事项:用黑色字迹旳签字笔或钢笔将答案写在答题纸上,不能答在试题卷上。

自考00023《高等数学(工本)》历年真题集电子书目录1. 目录 (2)2. 历年真题 (5)2.1 00023高等数学(工本)200404 (5)2.2 00023高等数学(工本)200410 (7)2.3 00023高等数学(工本)200504 (9)2.4 00023高等数学(工本)200507 (11)2.5 00023高等数学(工本)200510 (14)2.6 00023高等数学(工本)200604 (15)2.7 00023高等数学(工本)200607 (18)2.8 00023高等数学(工本)200610 (21)2.9 00023高等数学(工本)200701 (24)2.10 00023高等数学(工本)200704 (26)2.11 00023高等数学(工本)200707 (28)2.12 00023高等数学(工本)200710 (29)2.13 00023高等数学(工本)200801 (34)2.14 00023高等数学(工本)200804 (35)2.15 00023高等数学(工本)200807 (36)2.16 00023高等数学(工本)200810 (38)2.17 00023高等数学(工本)200901 (39)2.18 00023高等数学(工本)200904 (40)2.19 00023高等数学(工本)200907 (42)2.20 00023高等数学(工本)200910 (43)2.21 00023高等数学(工本)201001 (45)2.22 00023高等数学(工本)201004 (46)2.23 00023高等数学(工本)201007 (47)2.24 00023高等数学(工本)201010 (49)2.25 00023高等数学(工本)201101 (50)2.26 00023高等数学(工本)201104 (52)2.27 00023高等数学(工本)201107 (54)2.28 00023高等数学(工本)201110 (55)2.29 00023高等数学(工本)201204 (57)3. 相关课程 (59)1. 目录历年真题()00023高等数学(工本)200404()00023高等数学(工本)200410()00023高等数学(工本)200504()00023高等数学(工本)200507()00023高等数学(工本)200510()00023高等数学(工本)200604()00023高等数学(工本)200607()00023高等数学(工本)200610()00023高等数学(工本)200701()00023高等数学(工本)200704() 00023高等数学(工本)200707() 00023高等数学(工本)200710() 00023高等数学(工本)200801() 00023高等数学(工本)200804() 00023高等数学(工本)200807() 00023高等数学(工本)200810() 00023高等数学(工本)200901() 00023高等数学(工本)200904() 00023高等数学(工本)200907()00023高等数学(工本)200910()00023高等数学(工本)201001()00023高等数学(工本)201004()00023高等数学(工本)201007()00023高等数学(工本)201010()00023高等数学(工本)201101()00023高等数学(工本)201104()00023高等数学(工本)201107()00023高等数学(工本)201110()00023高等数学(工本)201204() 相关课程()2. 历年真题2.1 00023高等数学(工本)200404高等数学(工本)试题(课程代码0023)一、单项选择题(本大题共20小题,每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
全国2010年1月高等教育自学考试高等数学(工专)试题
课程代码:00022
一、单项选择题(本大题共5小题,每小题
2分,共10分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.函数的定义域是()
A.[-1,1]
B.[-2,2]
C.[0,4]
D.(0,4)
2.设则g[f(x)]=()
A.B.
C.D.
3.下列变量在给定的变化过程中为无穷小量
的是()
A.B.
C.D.
4.设曲线在点M的切线的斜率为3,则点M
的坐标为()
A.(0,1)
B.(1,1)
C.(1,0)
D.(0,-1)
5.设|A|=-3,,则A的伴随矩阵A*=()
A.B.
C.D.
二、填空题(本大题共10小题,每小题3
分,共30分)
请在每小题的空格中填上正确答案。
错填、
不填均无分。
6.级数的和s=________.
7.极限________.
8.函数在点x=0处连续,则a=________.
9.不定积分=________.
10.设,则dy=________.
11.曲线的拐点是________.
12.设由参数方程确定的函数为y=y(x),
则=________.
13.设行列式=D,元素aij对应的代数余子
式记为Aij,则
a31A31+a32A32+a33A33=________.
14.当x=1时,函数取得极值,则常数
p=________.
15.设矩阵A=,则An=________.
123。
全国2006年1月高等教育自学考试高等数学(工本)试题课程代码:00023一、单项选择题〔本大题共20小题,每题2分,共40分〕在每题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多项选择或未选均无分。
1.设函数f(x-2)=x 2-1,g[f(x)]=x1x1-+,那么g(3)=〔 〕 A .-3 B .-2 C .0 D .1 2.极限=--++∞→)11(lim x x x 〔 〕A .0B .1C .+∞D .不存在3.极限=-→xsin x cos 1lim 20x 〔 〕A .21- B .0 C .21D .14.点x=0是函数f(x)=1-x1e 的〔 〕A .振荡间断点B .可去间断点C .跳跃间断点D .无穷间断点5.设函数f(x)=42x ,那么f ′(x)=〔 〕A .2x42x-1B .42x ln4C .42x ln16D .4x42x-1 6.曲线y=3x 在点〔0,0〕处的切线方程为〔 〕A .x=yB .x=0C .y=0D .不存在7.以下结论正确的选项是〔 〕 A .曲线y=e -x 是下凹的 B .曲线y=e x 是上凹的 C .曲线y=lnx 是上凹的D .曲线y=(x )31是下凹的8.设⎰+=,C x ln x dx )x (f 那么f ′(x)=〔 〕 A .x1 B .1+lnx C .xlnxD .lnx9.设I 1=⎰1xdx ,I 2=⎰+11I ,dx )x 1ln(与I 2相比,有关系式〔 〕 A .I 1>I 2 B .I 1<I 2C .I 1=I 2D .I 1与I 2不能比较大小10.由曲线y=1,2=y x 及x=0围成的平面图形的面积为〔 〕A .121 B .41C .21D .2311.点〔3,-1,2〕关于x 轴的对称点是〔 〕 A .〔-3,1,-2〕 B .〔-3,-1,-2〕 C .〔-3,1,2〕 D .〔3,1,-2〕 12.通过x 轴且过点〔1,2,3〕的平面方程是〔 〕A .x-1=0B .3y-2z=0C .3y+2z-12=0D .2y-3z+5=0 13.设f’x (x 0,y 0)=0,f’y (x 0,y 0)=0,那么在点〔x 0,y 0〕处函数f(x,y)〔 〕A .连续B .一定取得极值C .可能取得极值D .的全微分为零14.设函数z=xy ,那么在点(1,2)处当Δx=-0.01, Δ时,函数的全微分为〔 〕 A .0 B .0.02 C .0.03 D .0.0415.积分⎰⎰y ydx )y ,x (f dy 1更换积分次序后为〔 〕A .⎰⎰11),(dy y x f dx B .⎰⎰xxdy y x f dx ),(10C .⎰⎰2),(1x x dy y x f dxD .⎰⎰xxdy y x f dx 2),(1016.设积分区域G :x 2+y 2+z 2≤9,那么三重积分⎰⎰⎰++Gdv )z y x (f 222化为球面坐标中的累积分为〔 〕A .⎰⎰⎰-32220sin )(ρϕρρϕθπππd f d dB .⎰⎰⎰922020sin )(ρϕρρϕθππd f d dC .⎰⎰⎰322020sin )(ρϕρρϕθππd f d dD .⎰⎰⎰32020)(ρρϕθππd f d d17.以下微分方程中,是可别离变量的微分方程为〔 〕A .〔e x+y -e x 〕dx+(e y -e x+y )dy=0B .)(ln xy dxdy=C .xdy-(y+x 3)dx=0D .(x+y)dy-(x-y)dx=0 18.微分方程y ″-5y ′+6y=0的通解y=〔 〕 A .C 1e -2x +C 2e -3x B .C 1e 2x +C 2e 3x C .C 1e 2x +C 1e 3x D .C 1e -2x +C 1e -3x19.设无穷级数∑∞=+121n pn收敛,那么一定有〔 〕A .p>-2B .p ≤0C .p>-1D .p ≤-120.设幂级数∑∞=-15n n n )x (a 在x=-1处收敛,那么在x=6处该幂级数是〔 〕 A .绝对收敛B .条件收敛C .发散D .敛散性不确定 二、填空题〔本大题共10小题,每题2分,共20分〕 请在每题的空格中填上正确答案。
自考高数工本试题及答案自考高等数学(工本)试题及答案一、选择题(每题2分,共10分)1. 下列函数中,不是周期函数的是()。
A. y = sin(x)B. y = cos(x)C. y = e^xD. y = tan(x)答案:C2. 微积分基本定理指出,若函数f(x)在区间[a, b]上连续,则定积分∫[a, b] f(x) dx等于()。
A. f(a) + f(b)B. f(a) - f(b)C. f(x)在[a, b]上的最大值D. f(x)在[a, b]上的某个值答案:D3. 曲线y = x^2在点(1, 1)处的切线斜率是()。
A. 0B. 1C. 2D. 3答案:C4. 以下哪个选项不是二阶常系数线性微分方程的特征方程()。
A. r^2 + 1 = 0B. r^2 - 1 = 0C. r^2 + 4r + 3 = 0D. r^2 - 4 = 0答案:C5. 函数f(x) = ln(x)的值域是()。
A. (-∞, 0)B. (0, ∞)C. (-∞, ∞)D. [0, ∞)答案:B二、填空题(每题3分,共15分)6. 极限lim (x→0) [x^2 sin(1/x)] = _______。
答案:07. 函数f(x) = x^3 - 6x^2 + 9x + 2的拐点是_______。
答案:(3, 24)8. 根据定积分的性质,若∫[a, b] f(x) dx = 5,且f(x)在区间[a,b]上非负,则∫[a, b] x f(x) dx = _______。
答案:≤59. 微分方程y'' - 2y' + y = 0的通解是_______。
答案:y = C1 * e^r1x + C2 * e^r2x,其中r1, r2是特征方程r^2 - 2r + 1 = 0的根。
10. 利用分部积分法计算∫x e^x dx的结果是_______。
答案:x e^x - e^x + C三、解答题(共75分)11. (15分)计算定积分∫[0, 1] x^2 dx,并说明其几何意义。
1全国2018年1月高等教育自学考试高等数学(工专)试题课程代码:00022一、单项选择题(本大题共30小题,1-20题每小题1分,20-30每小题2分,共40分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
(一)(每小题1分,共20分)1.函数f(x)=)1x ln(2x 3+++的定义域是( )A .(-32,+∞) B .(-∞,+∞) C .[-32,+∞) D .(-1,+∞)2.函数f(x)=sinx-cosx+1是( )A .非奇非偶函数B .奇函数C .偶函数D .无界函数3.函数f(x)=cos4x 是周期函数,周期为( )A .π41B .2π C .25 D .3 4.∞→n lim 2n )n11(+=( ) A .1B .21eC .eD .2e5.曲线y=x 3上点(1,1)处的法线斜率为( )A .-3B .-1C .-21D .-31 6.设f(x)在(a,b )内连续,且x 0∈(a,b),则( )A .0x x lim →f(x)存在,且f(x)在x 0可导2 B .0x x lim →f(x)不存在 C .0x x lim →f(x)存在,但f(x)在x 0不一定可导D .0x x lim →f(x)不一定存在 7.设y=ln(2x+3),则y '=( )A .)3x 2(21+B .3x 2+C .3x 21+D .3x 22+8.设⎩⎨⎧==t sin y tcos x,则4t dx dyπ==( )A .-1B .22-C .22D .19.当x=3π时,函数f(x)=a sin x+31sin3x 取得极值,则a=() A .-2 B .32-C .32D .210.曲线y=23)x 1(x 2-( )A .既有水平渐近线,又有垂直渐近线B .只有水平渐近线C .有垂直渐近线x=1D .没有渐近线11.设f(x)的一个原函数为2x ,则f(x)=( )A .x22ln 1 B .2xC .2x ln2D .2x (ln2)212.='⎰dx )x 3(f a b ( )A .)]a 3(f )b 3(f [31- B .f(3b)-f(3a)C .3[f(3b)-f(3a)]D .)a 3(f )b 3(f '-'13.设I 1=⎰⎰=dx x 01I ,dx x 01322,则( )3 A .I 1=I 2 B .I 1>I 2C .I 1<I 2D .I 2=2I 114.设a>0,则=-⎰dx x a 122( )A .arctgx+1B .arctgx+CC .arcsin a x +1D .arcsin a x+C15.在空间,方程2y 2+z 2=1表示( )A .椭圆B .椭圆柱面C .抛物柱面D .双曲柱面16.设f(x,y,z)=222z y x +++2x,则f(1,0,-1)=( )A . 2y 2++2B .2C .2D .2+217.设z=sin 2(ax+by),则x z∂∂=( )A .asin2(ax+by)B .bsin2(ax+by)C .acos 2(ax+by)D .bcos 2(ax+by)18.设二重积分的积分区域(σ)是1≤x 2+y 2≤4,则⎰⎰σ=)(dxdy ( )A .πB .π23C .3πD .15π19.微分方程33y x xy dx dy=+是( )A .六阶微分方程B .三阶微分方程C .一阶微分方程D .二阶微分方程20.级数-1+K +-+-42231313131( )A .收敛于-23B .收敛于-43C .收敛于43D .收敛于23(二)(每小题2分,共20分)21.设f(x)=⎩⎨⎧<-≥0x ,10x ,1,则[f(x)]2( )4 A .是连续函数 B .不是连续函数C .是无界函数D .是非初等函数22.2x x x e lim +∞→=( )A .0B .1C .2D .+∞23.设y=arcsin(1-2x),则='y ( )A .2x 4x 41--B .2x x 1--C .2x 4x 41-D .2x x 1-24.函数y=arctg(x 2)单调增的区间是( )A .(-1,1)B .[0,+∞)C .(-∞,0]D .(-∞,+∞)25.⎰dx e 3x x =( )A .3x e xB .3x e x +CC .C 13ln e 3xx ++ D .13ln e 3xx +26.设(σ)是由曲线y=1-x 2与y=0所围成的平面区域,则⎰⎰σσ)(xd =()A .42x 41x 21- B .2(x-x 3)C .-1D .027.通过两点P 1(3,-1,2),P 2(4,-6,-5)的直线方程为( )A .72z 51y 13x --=-+=- B .(x-3)-5(y+1)-7(z-2)=0C .25z 16y 34x +=-+=- D .(x-4)-5(y+6)-7(z+5)=028.曲线⎪⎩⎪⎨⎧==++21z 1z y x 222在xoy 平面上的投影曲线方程为( )A .⎩⎨⎧==+0z 1y x 22 B .⎪⎩⎪⎨⎧==+21z 43y x 225 C .x 2+y 2=43 D .⎪⎩⎪⎨⎧==+0z 43y x 2229. p 级数ΛΛ+++++=∑∞=n 131211n 11n ( ) A .收敛B .不一定发散C .发散D .部分和有极限30.用待定系数法求方程x 3e y 2y 3y =+'+''的特解时,应设特解( )A .x 3ae y =B .x 3axe y =C .x 32e ax y =D .x 32e )c bx ax (y ++=二、计算题(本大题共7小题,每小题6分,共42分)31.求.xx sin x lim 30x -→ 32.设y=x 5x (x>0),求dy.33.求⎰.dx x)x (ln sec 2 34.计算.dx x 2|x |x 222⎰++- 35.计算二重积分⎰⎰σ)(2dxdy xy ,其中(σ)由y=x 2与y=x 所围成.36.求微分方程xy 2y ='满足初始条件y|x=0=2的特解.37.判别级数∑∞=-1n n )21n 1(的敛散性. 三、应用和证明题(本大题共3小题,每小题6分,共18分)38.已知长方体的长、宽、高之和为正常数c,问当长方体的长、宽、高分别为多少时,长方体的体积最大?39.求由曲线y=e x 与直线y=e,y 轴所围成平面图形的面积.40.设z=lncos(x-2y),证明).y 2x (tg yz x z -=∂∂+∂∂。
1 / 2
全国年月自考《高等数学(工本)》试卷
课程代码:
一、单项选择题(本大题共小题,每小题分,共分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将基代码填写在题后的括号内。
错选、多选或未选均无分。
.过点(,,)和点(,,)的直线方程为( ) .
211123x y z ++-==-- . 112103x y z -+-==- . 211123x y z --+==- . 112103
x y z +-+==- .设函数(),则()为
.下列曲线积分中,与路径无关的曲线积分为
.(2)d (2)d L x y x x y y -+-⎰ .
(2)d (2)d L x y x y x y ++-⎰ . (2)d (2)d L x y x x y y +++⎰ . (2)d (2)d L
x y x x y y ++-⎰ .微分方程
d e d x y y x x
=+是 .可分离变量的微分方程
.齐次微分方程 .一阶线性齐次微分方程 .一阶线性非齐次微分方程 .已知幂级数()n
11n n a x ∞=+∑在处收敛,则该级数在处是
.绝对收敛 .条件收敛
.发散 .敛散性不确定
二、填空题(本大题共小题,每小题分,共分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
.已知向量{}{},则(-2a )×().
.已知函数()(),且(),则().
.二次积分()21100d ,d x I x f x y y -=⎰⎰交换积分次序后.
.微分方程 的一个特解*.
.无穷级数11!
n n ∞=∑的和为.
三、计算题(本大题共小题,每小题分,共分)
2 /
2
四、综合题(本大题共小题,每小题分,共分) .设函数
(x y ),证明22z z x y xy
∂∂+=∂∂. .求函数()的极值.
.将函数()
21x
展开为()的幂级数.。