2016年成人高考高起点文科数学真题及答案1

绝密★启封并使用完毕前试题类型：2016年普通高等学校招生全国统一考试文科数学注意事项：1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页.2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成，答在本试题上无效.4.考试结束后，将本试题和答题卡一并交回.第Ⅰ卷一. 选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设集合{1,3,5,7}A =，{|25}B x x =≤≤，则AB =（A ）{1,3}（B ）{3,5}（C ）{5,7}（D ）{1,7}(2)设(12i)(i)a ++的实部与虚部相等，其中a 为实数，则a=（A ）－3（B ）－2（C ）2（D ）3（3）为美化环境，从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中，余下的2种花种在另一个花坛中，则红色和紫色的花不在同一花坛的概率是 （A ）13（B ）12（C ）13（D ）56（4）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知5a =，2c =，2cos 3A =，则b= （A ）2（B ）3（C ）2（D ）3（5）直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为（A ）13（B ）12（C ）23（D ）34（6）若将函数y =2sin (2x +π6)的图像向右平移14个周期后，所得图像对应的函数为 （A ）y =2sin(2x +π4) （B ）y =2sin(2x +π3) （C ）y =2sin(2x –π4) （D ）y =2sin(2x –π3)（7）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3，则它的表面积是（A ）17π （B ）18π （C ）20π （D ）28π（8）若a>b>0，0<c<1，则（A ）log a c <log b c （B ）log c a <log c b （C ）a c <b c （D ）c a >c b（9）函数y =2x 2–e |x |在[–2,2]的图像大致为（A ）（B ）（C ）（D ）（10）执行右面的程序框图，如果输入的0,1,x y ==n =1,则输出,x y 的值满足（A ）2y x =（B ）3y x =（C ）4y x =（D ）5y x =（11）平面α过正文体ABCD —A 1B 1C 1D 1的顶点A 11//CB D α平面,ABCD m α=平面，11ABB A n α=平面，则m ，n 所成角的正弦值为（A ）32（B ）22（C ）33（D ）13 （12）若函数1()sin 2sin 3f x x -x a x =+在(),-∞+∞单调递增，则a 的取值范围是（A ）[]1,1-（B ）11,3⎡⎤-⎢⎥⎣⎦（C ）11,33⎡⎤-⎢⎥⎣⎦（D ）11,3⎡⎤--⎢⎥⎣⎦第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题，每个试题考生都必须作答.第(22)题~第(24)题为选考题，考生根据要求作答.二、填空题：本大题共3小题，每小题5分（13）设向量a =(x ，x +1)，b =(1，2)，且a ⊥b ，则x = .（14）已知θ是第四象限角，且sin(θ+π4)=35，则tan(θ–π4)= . （15）设直线y=x +2a 与圆C ：x 2+y 2-2ay -2=0相交于A ，B 两点，若，则圆C 的面积为 。

2016年成人高等学校专升本招生全国统一考试真题高等数学（一）第Ⅰ卷（选择题，共40分）一、选择题（1-10小题，每小题4分，共40分）1. limx→03sin x 2x =（ ） A.23 B.1 C. 32 D. 32. 若函数y =2x +sin x ,则y′=（ ）A.1−cos xB.1+cos xC. 2−cos xD.2+cos x3.设函数y =e x−2,则dy =（ ）A.e x−3dxB.e x−2dxC.e x−1dxD.e x dx4.设函数y =(2+x)3,则y′=（ ）A.(2+x)2B.3(2+x)2C. (2+x)4D.3 (2+x)45.设函数y =3x +1,则y′′=（ ）A.0B.1C.2D.36.d dx ∫e t dt x 0=( ).A.e xB. e x −1C.e x−1D.e x+17. ∫xdx =( ).A 、2x 2+CB 、x 2+C C 、12x 2+CD 、x +C 8. ∫2sin x dx =π20（ ）A. 12B. 1C.2D.39.设函数 z =3x 2y ，则ðz ðy =（ ）A.6yB.6xyC.3xD.3x 210.幂级数∑1n x n ∞n=1的收敛半径为（ ） A.0 B.1 C.2 D.+∞二、填空题（11-20小题，每小题4分，共40分）11. lim x→0(1+x )2x=12.设函数y =x 3，则y ′=13.设函数y =(x −3)4，则dy =14.设函数y =sin(x −2)，则y ′′=15.∫12x dx =16. ∫x 71−1dx =17. 过坐标原点与直线x−13=y+12=z−3−2 垂直的平面方程为 .18.设函数z =3x +y 2，则dz =19.微分方程y′=3x 2的通解为y =20.设区域D =*(x,y)|0≤x ≤1,0≤y ≤1+，则∬2dxdy = .三、解答题（21-28题，共70分）21.若函数f (x )= 在x =0处连续，求a .22. lim x→01−e x sin x23.求曲线y =x 3−3x +5的拐点24.计算∫(x −e x )dxsin xx ,x ≠0a ,x =025.设函数z=x2sin y+ye x，求∂z.∂x26.设D为曲线y=x2与直线y=x所围成的有界平面图形，求D绕x轴旋转一周所得旋转体的体积Vdxdy,其中D为由曲线y=x2与直线y=1所围成的有界平面区27.求∬(x3+y)D域.28.求微分方程y′′−y′−2y=e x的通解。

2016年成人高等学校招生全国统一考试数学试题一、选择题：本大题共17小题，每小题5分，共85分（1）设集合A={0,1}，B={0,1，2}，则Ａ∩Ｂ=（ ）（Ａ）｛0,1｝（Ｂ）｛0,2｝（Ｃ）｛1,2｝（Ｄ）｛0,1，2，｝（2）函数y =sin cos x x 的最小正周期是（ ） （Ａ）2π（Ｂ）π（Ｃ）π2（Ｄ）4π（3）在等差数列}{n a 中，132,6a a ==，则7a =（ ）（Ａ）14（Ｂ）12（Ｃ）10 （Ｄ）8（4）设甲：x ＞1；乙：2e ＞1，则（ ）（Ａ）甲是乙的必要条件，但不是乙的充分条件。

（Ｂ）甲是乙的充分条件，但不是乙的必要条件。

（Ｃ）甲不是乙的充分条件，也不是乙的必要条件 （Ｄ）甲是乙的充分必要条件。

（5）不等式231x -≤的解集是（ ）（Ａ）｛|13x x ≤≤｝（Ｂ）｛|12x x x ≤-≥或｝（Ｃ）｛|12x x ≤≤｝ （Ｄ）｛|23x x ≤≤｝（6）下列函数中，为偶函数的是（ ）（Ａ）2log y x = （Ｂ）2y x x =+（Ｃ）4y x =（Ｄ）2y x =（7）点（2,4）关于直线y x =的对称点的坐标是（ ）（Ａ）（-2,4） （Ｂ）（-2，-4） （Ｃ）（4,2） （Ｄ）（-4，-2）（8）将一颗骰子抛掷一次，得到的点数为偶数的概率为（ ） （Ａ）23（Ｂ）12（Ｃ）13（Ｄ）16（9）在△ABC 中，若AB=3，A=45°，C=30°，则BC=（ ）（Ａ） （Ｄ）（10）下列函数张中，函数值恒为负值的是（ D ）（Ａ）y x =（Ｂ）21y x =-+ （Ｃ）2y x = （Ｄ）21y x =--（11）过点（0,1）且与直线10x y ++=垂直的直线方程为（ ）（Ａ）y x =（Ｂ）21y x =+ （Ｃ）1y x =+ （Ｄ）1y x =-（12）设双曲线221169x y -=的渐近线的斜率为k ，则︱k ︱=（ ） （Ａ）916（Ｂ）34（Ｃ）43 （Ｄ）169（13）2364+19log 81=（ ）（Ａ）8 （Ｂ）10 （Ｃ）12 （Ｄ）14（14）tan α=3，则tan()4πα+=（ ） （Ａ）2 （Ｂ）12（Ｃ）-2 （Ｄ）-4（15）函数21ln(1)1y x x =-+-的定义域为（ ） （Ａ）｛x ︱＜-1或x ＞1｝（Ｂ）R（Ｃ）｛x ︱-1＜x ＜1｝（Ｄ）｛x ︱＜1或x ＞1｝（16）某同学每次投蓝投中的概率25，该同学投篮2次，只投进1次的概率为（ ）（Ａ）625（Ｂ）925（Ｃ）1225（Ｄ）35（17）曲线342y x x =-+在点（1，-1）处的切线方程为（ ） （Ａ）0x y +=（Ｂ）0x y -=（Ｃ）20x y --=（Ｄ）20x y +-=二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

2016年成人高考专升本考试《高等数学》真题(总分150, 考试时间150分钟)一、选择题：1～10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的。

1.A 0B 1C 2D 3该问题分值: 4答案:C2.A -1B 0C 1D 2该问题分值: 4答案:C3. 设函数y=2+sinx，则y/=A cosxB -cosxC 2+cosxD 2-cosx该问题分值: 4答案:A4. 设函数y=ex-1+1，则dy=A exdxB ex-1dxC (ex+1)dxD (ex-1+1)dx该问题分值: 4答案:B5.A 1B 3C 5D 7该问题分值: 4答案:B6.A π/2+1B π/2C π/2-1D 1该问题分值: 4答案:A7.A 4x3+4xB 4x3+4C 12x2+4xD 12x2+4该问题分值: 4答案:D8.A -1B 0C 1D 2该问题分值: 4答案:C9. 设函数z=x2+y，则dz=A 2xdx+dyB x2dx+dyC x2dx+ydyD 2xdx+ydy该问题分值: 4答案:A10.A 1/2B 1C 3/2D 2该问题分值: 4答案:D填空题填空11-20小题。

每小题4分，共40分。

11.该问题分值: 4答案:-1/312. 设函数y=x2-ex，则y/=该问题分值: 4答案:2x-ex13. 设事件A发生的概率为0.7，则A的对立事件非A发生的概率为该问题分值: 4答案:0.314. 曲线y=lnx在点（1，0）处的切线方程为该问题分值: 4答案:y=x-115.该问题分值: 4答案:ln|x|+arctanx+C16.该问题分值: 4答案:cosx17.该问题分值: 4答案:cosx18. 设函数z=sin(x+2y),则αz/αx=该问题分值: 4答案:cos(x+2y)19. 已知点（1,1）是曲线y=x2+alnx的拐点，则a=该问题分值: 4答案:220. 设y=y(x)是由方程y=x-ey所确定的隐函数，则dy/dx=该问题分值: 4答案:1/（1+ey）解答题21-28题，共70分。

绝密★启封并使用完毕前试题类型：2016年普通高等学校招生全国统一考试文科数学注意事项：1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页，第Ⅱ卷3至5页.2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置.3.全部答案在答题卡上完成，答在本试题上无效.4.考试结束后，将本试题和答题卡一并交回.第Ⅰ卷选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.（1）设集合，，则（A ）{1,3} （B ）{3,5} （C ）{5,7} （D ）{1,7}(2)设的实部与虚部相等，其中a 为实数，则a=（A ）－3 （B ）－2 （C ）2 （D ）3（3）为美化环境，从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中，余下的2种花种在另一个花坛中，则红色和紫色的花不在同一花坛的概率是（A ） （B ） （C ）32 （D ） （4）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知，，，则b=（A ） （B ） （C ）2 （D ）3（5）直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到的l 距离为其短轴长的41，则该椭圆的离心率为（A ）31 （B ）21 （C ）32 （D ）43 （6）若将函数y =2sin (2x +6π)的图像向右平移41个周期后，所得图像对应的函数为（A ）y =2sin(2x +4π) （B ）y =2sin(2x +3π) （C ）y =2sin(2x –4π) （D ）y =2sin(2x –3π ) ) （7）如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是328π，则它的表面积是（A）17π （B）18π （C）20π （D）28π（8）若a>b>0，0<c<1，则（A）log a c<log b c （B）log c a<log c b （C）a c<b c （D）c a>c b（9）函数y=2x2–e|x|在[–2,2]的图像大致为（A）（B）（C）（D）（10）执行右面的程序框图，如果输入的n=1,则输出的值满足（A）（B）（C）（D）（11）平面过正方体ABCD—A1B1C1D1的顶点A，,，，则m，n所成角的正弦值为（A）（B）（C）（D）（12）若函数在单调递增，则a的取值范围是（A ） （B ） （C ） （D ）第II 卷本卷包括必考题和选考题两部分.第(13)~(21)题为必考题，每个试题考生都必须作答.第(22)~(24)题为选考题，考生根据要求作答.二、填空题：本大题共4小题，每小题5分（13）设向量a =(x ，x +1)，b =(1，2)，且a b ，则x =（14）已知θ是第四象限角，且sin(θ+)=，则tan(θ–)=.（15）设直线y=x +2a 与圆C ：x 2+y 2-2ay -2=0相交于A ，B 两点，若32AB ，则圆C 的面积为（16）某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料。

成人高考成考数学(文科)(高起本)复习试题(答案在后面)一、单选题（本大题有12小题，每小题7分，共84分）1.下列哪个数是有理数？A. √2B. πC. -3/4D. e2.已知函数f(x) = 2x^3 - 3x^2 - 12x + 1，那么f(x)在区间[-2, 3]上的最大值是：A. 17B. 25C. 33D. 413、如果一个数的小数点向左移动2位，则这个数缩小了原来的（）倍。

A、100B、10C、1/100D、1/104、若函数f(x)满足f(1) = 4, f’(1) = 2, x > 0。

若存在一个常数c，使得对于任意x > 0，都有f(x) ≥ cx^2，则c的最大值是（A、0B、1C、2D、45、一元二次方程的判别式为零时，该方程的实数根的情况是（）A. 方程有两个相等的实数根B. 方程没有实数根C. 方程有两个非相等的实数根D. 以上都不正确6.等差数列2, 5, 8, 11, … 的第 20 项是多少？A. 59B. 61C. 65D. 677、直线l过点（1, 3）且与双曲线x 22−y21=1一条渐近线平行，则（）。

A. 直线l无斜率B. 直线l的斜率为±√2C. 直线l的斜率为-1或-√2D. 直线l的斜率为±1解析：双曲线x 22−y21=1的渐近线方程为y=±√22x，又直线l过点（1, 3），故当直线l 与渐近线y=√22x 平行时，直线l 的斜率为√22（舍去）；当直线l 与渐近线y=-√22x 平行时，直线l 的斜率为-√22；当直线l 与渐近线垂直时，直线l 的斜率不存在。

综上可知：直线l 的斜率为-1或-√2。

选C 。

8、在多项式x 2+2x +1中，x 2+2x 的系数是（ ）。

A. -1B. 1C. -2D. 29、一个多项式函数的最小项是关于x 的3次幂，则该多项式函数的次数至少是（ ）次。

A 、4B 、3C 、2D 、110、已知函数 f(x) = ax^3 + bx^2 + cx 在 x=x ₀ 处取得极值，且 f’(x ₀) = 0，则关于函数 f(x) 的极值说法正确的是：A. f(x) 在 x=x ₀ 处一定有极大值或极小值B. 若 f’(x ₀) 是正的或负的，则 f(x) 在 x=x ₀ 处有极大值或极小值C. f(x) 在 x=x ₀ 处没有极值，导数等于零不一定有极值点出现D. 函数是否存在极值与变量 x ₀ 有关，所以需要通过实际代入求解来确定极值的存在性。

2016年成人高等学校招生全国统一考试数学试题一、选择题：本大题共17小题，每小题5分，共85分（1）设集合A={0,1}，B={0,1，2}，则Ａ∩Ｂ=（ ）（Ａ）｛0,1｝ （Ｂ）｛0,2｝ （Ｃ）｛1,2｝ （Ｄ）｛0,1，2，｝（2）函数y =sin cos x x 的最小正周期是（ ） （Ａ）2π（Ｂ）π （Ｃ）π2 （Ｄ）4π（3）在等差数列}{n a 中，132,6a a ==，则7a =（ ）（Ａ）14 （Ｂ）12 （Ｃ）10 （Ｄ）8（4）设甲：x ＞1；乙：2e ＞1，则（ ）（Ａ）甲是乙的必要条件，但不是乙的充分条件。

（Ｂ）甲是乙的充分条件，但不是乙的必要条件。

（Ｃ）甲不是乙的充分条件，也不是乙的必要条件（Ｄ）甲是乙的充分必要条件。

（5）不等式231x -≤的解集是（ ）（Ａ）｛|13x x ≤≤｝ （Ｂ）｛|12x x x ≤-≥或｝（Ｃ）｛|12x x ≤≤｝ （Ｄ）｛|23x x ≤≤｝（6）下列函数中，为偶函数的是（ ）（Ａ）2log y x = （Ｂ）2y x x =+ （Ｃ）4y x = （Ｄ）2y x =（7）点（2,4）关于直线y x =的对称点的坐标是（ ）（Ａ）（-2,4） （Ｂ）（-2，-4） （Ｃ）（4,2） （Ｄ）（-4，-2）（8）将一颗骰子抛掷一次，得到的点数为偶数的概率为（ ）（Ａ）23 （Ｂ）12（Ｃ）13 （Ｄ）16 （9）在△ABC 中，若AB=3，A=45°，C=30°，则BC=（ ）（Ａ） （Ｂ） （Ｄ）（10）下列函数张中，函数值恒为负值的是（ ）（Ａ）y x = （Ｂ）21y x =-+ （Ｃ）2y x = （Ｄ）21y x =--（11）过点（0,1）且与直线10x y ++=垂直的直线方程为（ ）（Ａ）y x = （Ｂ）21y x =+ （Ｃ）1y x =+ （Ｄ）1y x =-（12）设双曲线221169x y -=的渐近线的斜率为k ，则︱k ︱=（ ） （Ａ）916 （Ｂ）34 （Ｃ）43 （Ｄ）169 （13）2364+19log 81=（ ）（Ａ）8 （Ｂ）10 （Ｃ）12 （Ｄ）14（14）tan α=3，则tan()4πα+=（ ） （Ａ）2 （Ｂ）12 （Ｃ）-2 （Ｄ）-4（15）函数21ln(1)1y x x =-+-的定义域为（ ） （Ａ）｛x ︱＜-1或x ＞1｝ （Ｂ）R（Ｃ）｛x ︱-1＜x ＜1｝（Ｄ）｛x ︱＜1或x ＞1｝ （16）某同学每次投蓝投中的概率25，该同学投篮2次，只投进1次的概率为（ ） （Ａ）625 （Ｂ）925 （Ｃ）1225（Ｄ）35 （17）曲线342y x x =-+在点（1，-1）处的切线方程为（ ）（Ａ）0x y += （Ｂ）0x y -=（Ｃ）20x y --= （Ｄ）20x y +-=二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

2016成人高考数学试题及答案【篇一：2016年成人高等学校招生全国统一考试数学试题】p class=txt>一、选择题：本大题共17小题，每小题5分，共85分（1）设集合a={0,1}，b={0,1，2}，则Ａ∩Ｂ=（）（Ａ）｛0,1｝（Ｂ）｛0,2｝（Ｃ）｛1,2｝（Ｄ）｛0,1，2，｝（2）函数y?sinxcosx的最小正周期是（）（Ａ）（Ｂ）? （Ｃ）2?（Ｄ）4?（3）在等差数列{an}中，a1?2,a3?6，则a7?（）（Ａ）14（Ｂ）12 （Ｃ）10 （Ｄ）8（4）设甲：x＞1；乙：e2＞1，则（）（Ａ）甲是乙的必要条件，但不是乙的充分条件。

（Ｂ）甲是乙的充分条件，但不是乙的必要条件。

（Ｃ）甲不是乙的充分条件，也不是乙的必要条件（Ｄ）甲是乙的充分必要条件。

（5）不等式2x?3?1的解集是（）（Ａ）｛x|1?x?3｝（Ｂ）｛x|x??1或x?2｝（Ｃ）｛x|1?x?2｝（Ｄ）｛x|2?x?3｝（6）下列函数中，为偶函数的是（）（Ａ）y?log2x （Ｂ）y?x2?x （Ｃ）y? （Ｄ）y?x2（7）点（2,4）关于直线y?x的对称点的坐标是（）（Ａ）（-2,4）（Ｂ）（-2，-4）（Ｃ）（4,2）（Ｄ）（-4，-2）4x?2（8）将一颗骰子抛掷一次，得到的点数为偶数的概率为（）（Ａ）（Ｂ）（Ｃ）（Ｄ）（Ａ）（Ｂ）（Ｄ）（10）下列函数张中，函数值恒为负值的是（ d ）（Ａ）y?x （Ｂ）y??x2?1 （Ｃ）y?x2 （Ｄ）y??x2?1（11）过点（0,1）且与直线x?y?1?0垂直的直线方程为（）（Ａ）y?x （Ｂ）y?2x?1 （Ｃ）y?x?1 （Ｄ）y?x?1x2y2（12）设双曲线??1的渐近线的斜率为k，则︱k︱=（）16923121316（Ａ）93416 （Ｂ）（Ｃ）（Ｄ） 1643923（13）64+log181=（）9（Ａ）8（Ｂ）10 （Ｃ）12 （Ｄ）14（14）tan?=3，则tan(??)=（） 4121（15）函数y?ln(x?1)2?的定义域为（） x?1?（Ａ）2（Ｂ）（Ｃ）-2 （Ｄ）-4（Ａ）｛x︱＜-1或x＞1｝（Ｂ）r（Ｃ）｛x︱-1＜x＜1｝（Ｄ）｛x︱＜1或x＞1｝（16）某同学每次投蓝投中的概率，该同学投篮2次，只投进1次的概率为（） 25（Ａ）69 （Ｂ） 2525（Ｃ）12 25（Ｄ） 35（17）曲线y?x3?4x?2在点（1，-1）处的切线方程为（）（Ａ）x?y?0（Ｂ）x?y?0（Ｃ）x?y?2?0（Ｄ）x?y?2?0二、填空题：本大题共4小题，每小题4分，共16分，把答案填在题中横线上。

2016年高考文科数学真题及答案全国卷1注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷 一. 选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.（1）设集合{}1,3,5,7A =,{}25B x x =,则AB =（A ）{1,3} （B ）{3,5} （C ）{5,7} （D ）{1,7} 【答案】B考点：集合的交集运算【名师点睛】集合是每年高考中的必考题,一般以基础题形式出现,属得分题.解决此类问题一般要把参与运算的集合化为最简形式再进行运算,如果是不等式解集、函数定义域及值域有关数集之间的运算,常借助数轴进行运算.(2) 设()()12i i a ++的实部与虚部相等,其中a 为实数,则a= （A ）－3 （B ）－2 （C ）2 （D ）3 【答案】A 【解析】试题分析：i a a i a i )21(2))(21(++-=++,由已知,得a a 212+=-,解得3-=a ,故选A. 考点：复数的概念及复数的乘法运算【名师点睛】复数题也是每年高考必考内容,一般以客观题形式出现,属得分题.高考中复数考查频率较高的内容有：复数相等,复数的几何意义,共轭复数,复数的模及复数的乘除运算,这类问题一般难度不大,但容易出现运算错误,特别是2i 1=-中的负号易忽略,所以做复数题要注意运算的准确性.（3）为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是 （A ）13 （B ）12 （C ）23 （D ）56【答案】A 考点：古典概型【名师点睛】作为客观题形式出现的古典概型试题,一般难度不大,解答常见错误是在用列举法计数时出现重复或遗漏,避免此类错误发生的有效方法是按照一定的标准进行列举.（4）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c.已知a =2c =,2cos 3A =,则b=（A （B （C ）2 （D ）3 【答案】D 【解析】试题分析：由余弦定理得3222452⨯⨯⨯-+=b b ,解得3=b （31-=b 舍去）,故选D. 考点：余弦定理【名师点睛】本题属于基础题,考查内容单一,根据余弦定理整理出关于b 的一元二次方程,再通过解方程求b.运算失误是基础题失分的主要原因,请考生切记！（5）直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为（A ）13 （B ）12 （C ）23 （D ）34 【答案】B 【解析】试题分析：如图,由题意得在椭圆中,11OF c,OB b,OD 2b b 42===⨯= 在Rt OFB ∆中,|OF ||OB||BF ||OD |⨯=⨯,且222a b c =+,代入解得22a 4c =,所以椭圆得离心率得1e 2=,故选B.考点：椭圆的几何性质【名师点睛】求椭圆或双曲线离心率是高考常考问题,求解此类问题的一般步骤是先列出等式,再转化为关于a,c 的齐次方程,方程两边同时除以a 的最高次幂,转化为关于e 的方程,解方程求e .（6）若将函数y =2sin (2x +π6)的图像向右平移14个周期后,所得图像对应的函数为 （A ）y =2sin(2x +π4) （B ）y =2sin(2x +π3) （C ）y =2sin(2x –π4) （D ）y =2sin(2x –π3) 【答案】D考点：三角函数图像的平移【名师点睛】函数图像的平移问题易错点有两个,一是平移方向,注意“左加右减“,二是平移多少个单位是对x 而言的,不用忘记乘以系数.（7）如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是（A ）17π （B ）18π （C ）20π （D ）28π 【答案】A 【解析】考点：三视图及球的表面积与体积【名师点睛】由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键. x（8）若0a b >>,01c <<,则（A ）log a c <log b c （B ）log c a <log c b （C ）a c <b c （D ）c a >c b 【答案】B 【解析】试题分析：由01c <<可知log c y x =是减函数,又0a b >>,所以log log c c a b <．故选B.本题也可以用特殊值代入验证. 考点：指数函数与对数函数的性质【名师点睛】比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数单调性进行比较,若底数不同,可考虑利用中间量进行比较.（9）函数22xy x e =-在[]2,2-的图像大致为（A ）（B ）（C ）（D ）【答案】D考点：函数图像与性质【名师点睛】函数中的识图题多次出现在高考试题中,也可以说是高考的热点问题,这类题目一般比较灵活,对解题能力要求较高,故也是高考中的难点,解决这类问题的方法一般是利用间接法,即由函数性质排除不符合条件的选项.（10）执行右面的程序框图,如果输入的0,1,x y ==n =1,则输出,x y 的值满足 （A ）2y x = （B ）3y x = （C ）4y x = （D ）5y x =结束【答案】C 【解析】试题分析：第一次循环：0,1,2x y n ===,第二次循环：1,2,32x y n ===, 第三次循环：3,6,32x y n ===,此时满足条件2236x y +≥,循环结束,3,62x y ==,满足4y x =．故选C考点：程序框图与算法案例【名师点睛】程序框图基本是高考每年必考知识点,一般以客观题形式出现,难度不大,求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果. （11）平面α过正文体ABCD —A 1B 1C 1D 1的顶点A 11//CB D α平面,ABCD m α=平面,11ABBA n α=平面,则m ,n 所成角的正弦值为（A （B）2 （C （D ）13【答案】A考点：平面的截面问题,面面平行的性质定理,异面直线所成的角.【名师点睛】求解本题的关键是作出异面直线所成角,求异面直线所成角的步骤是：平移定角、连线成形,解形求角、得钝求补.（12）若函数1()sin 2sin 3f x x -x a x =+在(),-∞+∞单调递增,则a 的取值范围是 （A ）[]1,1-（B ）11,3⎡⎤-⎢⎥⎣⎦（C ）11,33⎡⎤-⎢⎥⎣⎦（D ）11,3⎡⎤--⎢⎥⎣⎦【答案】C考点：三角变换及导数的应用【名师点睛】本题把导数与三角函数结合在一起进行考查,有所创新,求解关键是把函数单调性转化为不等式恒成立,再进一步转化为二次函数在闭区间上的最值问题,注意与三角函数值域或最值有关的问题,要注意弦函数的有界性. 第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答. 二、填空题：本大题共3小题,每小题5分（13）设向量a =(x ,x +1),b =(1,2),且a ⊥b ,则x = .【答案】23- 【解析】试题分析：由题意, 20,2(1)0,.3x x x ⋅=++=∴=-a b 考点：向量的数量积及坐标运算【名师点睛】全国卷中向量大多以客观题形式出现,属于基础题.解决此类问题既要准确记忆公式,又要注意运算的准确性.本题所用到的主要公式是：若()()1122,,,x y x y ==a b ,则1122x y x y ⋅=+a b .（14）已知θ是第四象限角,且sin(θ+π4)=35,则tan(θ–π4)=. 【答案】43- 【解析】试题分析：由题意sin sin 442θθπππ⎡⎤⎛⎫⎛⎫+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦3cos 45θπ⎛⎫=-= ⎪⎝⎭, 因为2222k k θ3ππ+<<π+π()k ∈Z ,所以722444k k θ5ππππ+<-<π+()k ∈Z , 从而4sin 45θπ⎛⎫-=- ⎪⎝⎭,因此4tan 43θπ⎛⎫-=- ⎪⎝⎭．故填43-． 考点：三角变换【名师点睛】三角函数求值,若涉及到开方运算,要注意根式前正负号的取舍,同时要注意角的灵活变换.（15）设直线y=x +2a 与圆C ：x 2+y 2-2ay -2=0相交于A ,B 两点,若,则圆C 的面积为【答案】4π 考点：直线与圆【名师点睛】注意在求圆心坐标、半径、弦长时常用圆的几何性质,如圆的半径r 、弦长l 、圆心到弦的距离d 之间的关系：2222l r d ⎛⎫=+ ⎪⎝⎭在求圆的方程时常常用到. （16）某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料.生产一件产品A 需要甲材料1.5kg,乙材料1kg,用5个工时；生产一件产品B 需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A 的利润为2100元,生产一件产品B 的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A 、产品B 的利润之和的最大值为元. 【答案】216000 【解析】试题分析：设生产产品A 、产品B 分别为x 、y 件,利润之和为z 元,那么1.50.5150,0.390,53600,0,0.x y x y x y x y +⎧⎪+⎪⎪+⎨⎪⎪⎪⎩ ①目标函数2100900z x y =+.取得最大值.解方程组10390053600x y x y +=⎧⎨+=⎩,得M 的坐标(60,100).所以当60x =,100y =时,max 210060900100216000z =⨯+⨯=. 故生产产品A 、产品B 的利润之和的最大值为216000元. 考点：线性规划的应用【名师点睛】线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有：纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合.本题运算量较大,失分的一个主要原因是运算失误.三.解答题：解答应写出文字说明,证明过程或演算步骤.（17）.（本题满分12分）已知{}n a 是公差为3的等差数列,数列{}n b 满足12111==3n n n n b b a b b nb +++=1，，,.（I ）求{}n a 的通项公式； （II ）求{}n b 的前n 项和. 【答案】（I ）31n a n =-（II ）131.223n --⨯（II ）由（I ）和11n n n n a b b nb +++= ,得13n n b b +=,因此{}n b 是首项为1,公比为13的等比数列.记{}n b 的前n 项和为n S ,则111()313.122313nn n S --==-⨯- 考点：等差数列与等比数列【名师点睛】等差、等比数列各有五个基本量,两组基本公式,而这两组公式可看作多元方程,利用这些方程可将等差、等比数列中的运算问题转化解关于基本量的方程（组）,因此可以说数列中的绝大部分运算题可看作方程应用题,所以用方程思想解决数列问题是一种行之有效的方法.（18）.（本题满分12分）如图,在已知正三棱锥P -ABC 的侧面是直角三角形,PA =6,顶点P 在平面ABC 内的正投影为点E ,连接PE 并延长交AB 于点G . （I ）证明G 是AB 的中点；（II ）在答题卡第（18）题图中作出点E 在平面PAC 内的正投影F （说明作法及理由）,并求四面体PDEF 的体积．PABD CGE【答案】（I ）见解析（II ）作图见解析,体积为43试题解析：（I ）因为P 在平面ABC 内的正投影为D ,所以.AB PD ⊥因为D 在平面PAB 内的正投影为E ,所以.AB DE ⊥ 所以AB ⊥平面PED ,故.AB PG ⊥又由已知可得,PA PB =,从而G 是AB 的中点.（II ）在平面PAB 内,过点E 作PB 的平行线交PA 于点F ,F 即为E 在平面PAC 内的正投影.理由如下：由已知可得PB PA ⊥,⊥PB PC ,又//EF PB ,所以EF PC ⊥,因此EF ⊥平面PAC ,即点F 为E 在平面PAC 内的正投影.连接CG ,因为P 在平面ABC 内的正投影为D ,所以D 是正三角形ABC 的中心. 由（I ）知,G 是AB 的中点,所以D 在CG 上,故2.3=CD CG 由题设可得⊥PC 平面PAB ,⊥DE 平面PAB ,所以//DE PC ,因此21,.33==PE PG DE PC 由已知,正三棱锥的侧面是直角三角形且6=PA ,可得2, 2.==DE PE 在等腰直角三角形EFP 中,可得 2.==EF PF 所以四面体PDEF 的体积114222.323=⨯⨯⨯⨯=V 考点：线面位置关系及几何体体积的计算【名师点睛】文科立体几何解答题主要考查线面位置关系的证明及几何体体积的计算,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,要防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.（19）（本小题满分12分）某公司计划购买1台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图：频数记x 表示1台机器在三年使用期内需更换的易损零件数,y 表示1台机器在购买易损零件上所需的费用（单位：元）,n 表示购机的同时购买的易损零件数.（I ）若n =19,求y 与x 的函数解析式；（II ）若要求“需更换的易损零件数不大于n ”的频率不小于0.5,求n 的最小值；（III ）假设这100台机器在购机的同时每台都购买19个易损零件,或每台都购买20个易损零件,分别计算这100台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买19个还是20个易损零件？【答案】（I ）)(,19,5700500,19,3800N x x x x y ∈⎩⎨⎧>-≤=（II ）19（III ）19 （Ⅱ）由柱状图知,需更换的零件数不大于18的概率为0.46,不大于19的概率为0.7,故n 的最小值为19.（Ⅲ）若每台机器在购机同时都购买19个易损零件,则这100台机器中有70台在购买易损零件上的费用为3800,20台的费用为4300,10台的费用为4800,因此这100台机器在购买易损零件上所需费用的平均数为4050)104500904000(1001=⨯+⨯. 比较两个平均数可知,购买1台机器的同时应购买19个易损零件.考点：函数解析式、概率与统计【名师点睛】本题把统计与函数结合在一起进行考查,有综合性但难度不大,求解关键是读懂题意,所以提醒考生要重视数学中的阅读理解问题.（20）（本小题满分12分）在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C ：22(0)y px p =>于点P ,M 关于点P 的对称点为N ,连结ON 并延长交C 于点H .（I ）求OH ON； （II ）除H 以外,直线MH 与C 是否有其它公共点？说明理由.【答案】（I ）2（II ）没有【解答】试题分析：先确定),(2t p t N ,ON 的方程为x tp y =,代入px y 22=整理得0222=-x t px ,解得01=x ,p t x 222=,得)2,2(2t p t H ,由此可得N 为OH 的中点,即2||||=ON OH .（II ） 把直线MH 的方程x tp t y 2=-,与px y 22=联立得04422=+-t ty y ,解得t y y 221==,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其它公共点.（Ⅱ）直线MH 与C 除H 以外没有其它公共点.理由如下：直线MH 的方程为x tp t y 2=-,即)(2t y p t x -=.代入px y 22=得04422=+-t ty y ,解得t y y 221==,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其它公共点.考点：直线与抛物线【名师点睛】高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试内容,主要由求值、求方程、求定值、最值、求参数取值范围等几部分组成；解析几何中的证明问题通常有以下几类：证明点共线或直线过定点；证明垂直；证明定值问题.其中考查较多的圆锥曲线是椭圆与抛物线,解决这类问题要重视方程思想、函数思想及化归思想的应用.（21）（本小题满分12分）已知函数()()()22e 1x f x x a x =-+-．(I)讨论()f x 的单调性；(II)若()f x 有两个零点,求a 的取值范围.【答案】见解析(II)()0,+∞ 【解析】试题分析：(I)先求得()()()'12.x f x x e a =-+再根据1,0,2a 的大小进行分类确定()f x 的单调性；(II)借助第一问的结论,通过分类讨论函数单调性,确定零点个数,从而可得a 的取值范围为()0,+∞.试题解析： (I)()()()()()'12112.x x f x x e a x x e a =-+-=-+(i)设0a ≥,则当(),1x ∈-∞时,()'0f x <；当()1,x ∈+∞时,()'0f x >.所以在(),1-∞单调递减,在()1,+∞单调递增.(ii)设0a <,由()'0f x =得x =1或x =ln(-2a). ①若2e a =-,则()()()'1x f x x e e =--,所以()f x 在(),-∞+∞单调递增. ②若2e a >-,则ln(-2a)<1,故当()()(),ln 21,x a ∈-∞-+∞时,()'0f x >； 当()()ln 2,1x a ∈-时,()'0f x <,所以()f x 在()()(),ln 2,1,a -∞-+∞单调递增,在()()ln 2,1a -单调递减. ③若2e a <-,则()21ln a ->,故当()()(),1ln 2,x a ∈-∞-+∞时,()'0f x >,当()()1,ln 2x a ∈-时,()'0f x <,所以()f x 在()()(),1,ln 2,a -∞-+∞单调递增,在()()1,ln 2a -单调递减.考点：函数单调性,导数应用【名师点睛】本题第一问是用导数研究函数单调性,对含有参数的函数单调性的确定,通常要根据参数进行分类讨论,要注意分类讨论的原则：互斥、无漏、最简；第二问是求参数取值范围,由于这类问题常涉及到导数、函数、不等式等知识,越来越受到高考命题者的青睐,解决此类问题的思路是构造适当的函数,利用导数研究函数的单调性或极值破解.请考生在22、23、24题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号（22）（本小题满分10分）选修4-1：几何证明选讲如图,△OAB 是等腰三角形,∠AOB =120°.以O 为圆心,12OA 为半径作圆. (I)证明：直线AB 与O 相切； (II)点C ,D 在⊙O 上,且A ,B ,C ,D 四点共圆,证明：AB ∥CD .O DCB A【答案】(I)见解析(II)见解析在Rt AOE ∆中,12OE AO =,即O 到直线AB 的距离等于圆O 的半径,所以直线AB 与⊙O 相切． E O'DC OBA（Ⅱ）因为2OA OD =,所以O 不是,,,A B C D 四点所在圆的圆心,设'O 是,,,A B C D 四点所在圆的圆心,作直线'OO ．由已知得O 在线段AB 的垂直平分线上,又'O 在线段AB 的垂直平分线上,所以'OO AB ⊥． 同理可证,'OO CD ⊥．所以//AB CD ．考点：四点共圆、直线与圆的位置关系及证明【名师点睛】近几年几何证明题多以圆为载体命制,在证明时要抓好“长度关系”与“角度关系的转化”,熟悉相关定理与性质.该部分内容命题点有：平行线分线段成比例定理；三角形的相似与性质；四点共圆；圆内接四边形的性质与判定；切割线定理.（23）（本小题满分10分）选修4—4：坐标系与参数方程在直角坐标系x O y 中,曲线C 1的参数方程为cos 1sin x a ty a t =⎧⎨=+⎩（t 为参数,a ＞0）．在以坐标原点为极点,x 轴正半轴为极轴的极坐标系中,曲线C 2：ρ=4cos θ.（I ）说明C 1是哪一种曲线,并将C 1的方程化为极坐标方程；（II ）直线C 3的极坐标方程为0θα=,其中0α满足tan 0α=2,若曲线C 1与C 2的公共点都在C 3上,求a ．【答案】（I ）圆,222sin 10a ρρθ-+-=（II ）1试题解析：⑴ cos 1sin x a t y a t=⎧⎨=+⎩ （t 均为参数）,∴()2221x y a +-= ① ∴1C 为以()01，为圆心,a 为半径的圆．方程为222210x y y a +-+-= ∵222sin x y y ρρθ+==，,∴222sin 10a ρρθ-+-= 即为1C 的极坐标方程⑵ 24cos C ρθ=：,两边同乘ρ得22224cos cos x y x ρρθρρθ==+=，224x y x ∴+=,即()2224x y -+= ②3C ：化为普通方程为2y x =,由题意：1C 和2C 的公共方程所在直线即为3C①—②得：24210x y a -+-=,即为3C∴210a -=,∴1a =考点：参数方程、极坐标方程与直角坐标方程的互化及应用【名师点睛】“互化思想”是解决极坐标方程与参数方程问题的重要思想,解题时应熟记极坐标方程与参数方程的互化公式及应用.（24）（本小题满分10分）,选修4—5：不等式选讲已知函数()123f x x x =+--.（I ）在答题卡第（24）题图中画出()y f x =的图像；（II ）求不等式()1f x >的解集．【答案】（I ）见解析（II ）()()11353⎛⎫-∞+∞ ⎪⎝⎭，，，试题解析：⑴如图所示：考点：分段函数的图像,绝对值不等式的解法【名师点睛】不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等.解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式.。

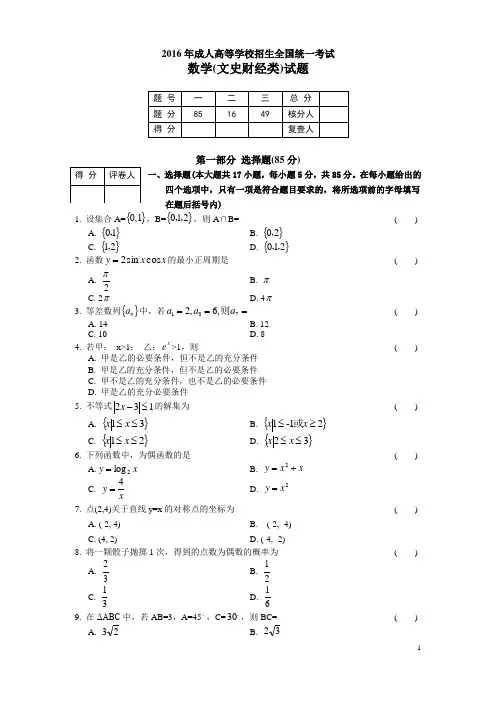
2016年成人高等学校招生全国统一考试数学(文史财经类)试题第一部分 选择题(85分)一、选择题(本大题共17小题，每小题5分，共85分。

在每小题给出的 四个选项中，只有一项是符合题目要求的，将所选项前的字母填写 在题后括号内)1. 设集合A=}{1,0，B=}{210，，，则A ∩B=( )A. }{10，B. }{20，C. }{21，D. }{210，，2. 函数x x y cos sin 2=的最小正周期是( )A.2πB. πC. 2πD. 4π3. 等差数列}{n a 中，若===731,6,2a a a 则( )A. 14B. 12C. 10D. 84. 若甲： x>1； 乙：xe >1，则 ( )A. 甲是乙的必要条件，但不是乙的充分条件B. 甲是乙的充分条件，但不是乙的必要条件C. 甲不是乙的充分条件，也不是乙的必要条件D. 甲是乙的充分必要条件5. 不等式132≤-x 的解集为( )A. }{31≤≤x xB. }{21-1≥≤x x 或C. }{21≤≤x xD. }{32≤≤x x6. 下列函数中，为偶函数的是( )A.x y 2log =B. x x y +=2C. xy 4=D. 2x y = 7. 点(2,4)关于直线y=x 的对称点的坐标为( )A. (-2, 4)B. (-2, -4)C. (4, 2)D. (-4, -2) 8. 将一颗骰子抛掷1次，得到的点数为偶数的概率为( )A.32B.21 C. 31D. 619. 在ΔABC 中，若AB=3，A=45。

，C=。

30，则BC=( )A. 23B. 32C.3D.22 10. 下列函数中，函数值恒为负值的是( )A. x y =B. 12+=x yC. 3x y = D. 12--=x y 11. 过点（0,1）且与直线x+y+1=0垂直的直线方程为( )A. x y =B. 12+=x yC. 1+=x yD. 1-=x y12. 设双曲线191622=-y x 的渐近线的斜率为k ，则k =( )A. 169B. 43C. 34D. 91613. =+81log 649132( )A. 8B. 10C. 12D. 14 14. 若3tan =α，则⎪⎭⎫⎝⎛+4tan πα=( )A. 2B.21 C. -2D. -4 15. 函数()111ln 2-+-=x x y 的定义域为( )A. }{11〉〈-x x x 或B. RC. }{11〈〈-x xD. }{11〉〈x x x 或16. 某同学每次投篮投中的概率为52，该同学投篮2次，只投中1次的概率为 ( )A.256 B. 259C. 2512D. 5317. 曲线243+-=x x y 在点(1，-1)处的切线方程为( )A. x +y =0B. x -y =0C. x -y -2=0`D. x +y -2=0第二部分 非选择题(65分)二、填空题(本大题共4小题，每小题4分，共16分。