非对称损失函数的质量特性值优化选择

{品质管理品质知识}质量损失函数质量损失函数日本质量管理学家田口玄一（Taguchi）认为产品质量与质量损失密切相关，质量损失是指产品在整个生命周期的过程中，由于质量不满足规定的要求，对生产者、使用者和社会所造成的全部损失之和。

田口用货币单位来对产品质量进行度量，质量损失越大，产品质量越差；反之，质量损失越小，产品质量越好。

一、质量特性产品质量特性是产品满足用户要求的属性，包括产品性能、寿命、可靠性、安全性、经济性、可维修性和环境适应性等。

（与前描述是否一致）（一）质量特性分类田口先生为了阐述其原理，对质量特性在一般分类的基础上作了某些调整，分为计量特性和计数特性，如图1所示。

1、望目特性。

设目标值为m，质量特性y围绕目标值m波动，希望波动愈小愈好，则y就被称为望目特性，例如加工某一轴件图纸规定φ10±0.05(mm)，加工的轴件的实际直径尺寸y就是望目特性，其目标值m=10(mm)。

2、望小特性。

不取负值，希望质量特性y愈小愈好，波动愈小愈好，则y 被称为望小特性。

比如测量误差，合金所含的杂质、轴件的不圆度等就属于望小特性。

3、望大特性。

不取负值，希望质量特性y愈大愈好，波动愈小愈好，则y 被称为望大特性。

比如零件的强度、灯泡的寿命等均为望大特性。

（二）质量特性波动产品在贮存或使用过程中，随着时间的推移，发生材料老化变质、磨损等现象，引起产品功能的波动，我们称这种产品由于使用环境，时间因素，生产条件等影响，产品质量特性y偏离目标值m，产生波动。

引起产品质量特性波动的原因称为干扰源。

主要有以下三种类型：1、外干扰（外噪声）使用条件和环境条件（如温度，湿度，位置，输入电压，磁场，操作者等）的变化引起产品功能的波动，我们称这种使用条件和环境条件的变化为外干扰，也称为外噪声。

2、内干扰（内噪声）材料老化现象为内干扰，也称为内噪声。

3、随机干扰（产品间干扰）在生产制造过程中，由于机器、材料、加工方法、操作者、计测方法和环境（简称5MIE）等生产条件的微小变化，引起产品质量特性的波动，我们称这种在生产制造过程中出现的功能波动为产品间波动。

《基于深度学习的锂电池RUL预测》一、引言随着社会科技水平的持续进步，锂电池因其高能量密度、长寿命和环保特性，在电动汽车、移动设备等领域得到了广泛应用。

然而，锂电池的可靠性、安全性及维护成本等问题也日益凸显。

因此，对锂电池剩余使用寿命（RUL）的预测显得尤为重要。

本文将探讨基于深度学习的锂电池RUL预测方法，以期望提高锂电池的使用效率，降低维护成本，并为后续研究提供理论依据和实践指导。

二、锂电池RUL预测的重要性锂电池的RUL预测是电池管理系统的重要组成部分，其准确性直接影响到电池的使用寿命、安全性以及维护成本。

通过准确预测锂电池的RUL，可以提前发现潜在的安全隐患，避免因电池故障导致的经济损失和人员伤害。

此外，RUL预测还能帮助实现电池的合理调配和使用，提高电池的整体使用寿命。

三、深度学习在锂电池RUL预测中的应用随着深度学习技术的不断发展，其在锂电池RUL预测中得到了广泛应用。

深度学习能够从海量数据中提取有价值的信息，对电池性能进行准确预测。

在锂电池RUL预测中，常用的深度学习模型包括循环神经网络（RNN）、长短期记忆网络（LSTM）和卷积神经网络（CNN）等。

这些模型能够处理时间序列数据、图像数据等多种类型的数据，从而实现对锂电池RUL的准确预测。

四、基于深度学习的锂电池RUL预测方法基于深度学习的锂电池RUL预测方法主要包括数据采集、数据预处理、模型构建和模型评估四个步骤。

首先，需要收集锂电池的运行数据，包括电压、电流、温度等参数；其次，对数据进行预处理，包括数据清洗、特征提取等；然后，构建深度学习模型，如RNN、LSTM或CNN等；最后，对模型进行评估和优化，以实现对锂电池RUL的准确预测。

五、实践案例分析以某电动汽车企业为例，该企业采用基于深度学习的锂电池RUL预测方法，对电池进行实时监控和预测。

首先，该企业收集了大量电池运行数据，包括电压、电流、温度等参数；然后，利用深度学习模型对数据进行处理和分析，实现对电池性能的准确预测；最后，根据预测结果制定合理的维护计划，提高了电池的使用寿命和安全性。

各损失函数的优缺点-概述说明以及解释1.引言1.1 概述概述部分的内容：引言是对文章主题的简要介绍，本文将探讨各种损失函数的优缺点。

在机器学习和数据分析中，损失函数是评估模型性能的重要指标之一，它用于衡量预测结果与实际值之间的差异。

通过选择合适的损失函数，可以优化模型的训练过程，并使得预测结果更加准确。

本文将重点介绍三种常见的损失函数：损失函数A、损失函数B和损失函数C。

每种损失函数都有自己独特的优点和缺点，通过分析它们的特性，我们可以更好地了解何时选择哪种损失函数。

在正文部分，我们将详细介绍损失函数A、损失函数B和损失函数C 的优缺点。

对于每一种损失函数，我们将分别列出它们的优点和缺点，并且说明它们在不同场景下的适用性。

最后，结论部分将总结各种损失函数的优缺点，并给出选择损失函数的建议。

通过深入理解各种损失函数的特性，我们可以在实际应用中更加智能地选择和优化损失函数，从而提高模型的性能和预测准确度。

1.2文章结构1.2 文章结构本文将针对不同的损失函数进行分析，包括损失函数A、损失函数B 和损失函数C。

每个损失函数都有其独特的优点和缺点。

下面将展示各个损失函数的优缺点，并对选择损失函数提出一些建议。

首先，我们将介绍第一个损失函数A的优缺点。

接下来，我们将讨论第二个损失函数B的优缺点。

最后，我们将探讨第三个损失函数C的优缺点。

通过对这些损失函数的详细分析，我们可以更好地理解它们的适用场景和限制，从而为选择合适的损失函数提供指导。

在结论部分，我们将总结每个损失函数的优缺点，并提出相应的建议。

这些建议将帮助读者在实际应用中选择适合的损失函数，以达到最佳的模型性能。

通过对不同损失函数的深入研究，我们可以更好地了解这些损失函数的特性，从而在实际问题中取得更好的效果。

1.3 目的本文的目的是对各种常见损失函数进行全面分析，探讨它们各自的优点和缺点。

通过比较不同损失函数的性质和特点，我们旨在帮助读者更好地理解和选择适合自己问题的损失函数。

质量损失函数
质量损失函数是一个损失函数，用来衡量模型在预测过程中拥有的质量，它衡量的是模型的准确性。

质量损失函数由质量指标组成，这些指标可以是数据准确性、预测准确性、生产效率等。

质量损失函数的基本原理是：实际的预测结果与模型期望结果之间的差距，而这个差距应该尽可能的小，从而提升模型预测的效率和准确性。

用来计算质量损失函数的公式可以是任意函数，通常可以用均方差（MSE）来衡量质量损失。

MSE是一种平均偏差的可量化衡量，它表示模型输出值与真实值之间的差距。

另外，贝叶斯损失函数也可以用来衡量质量损失，它是一种按比例降低异常结果的方法，能够较好地衡量模型的质量。

在实际的机器学习和数据挖掘系统中，质量损失函数是一个重要的概念，它能够帮助模型追求更大的精度和准确性。

模型的优化过程需要连续更新质量损失函数，以获得更好的预测结果，这就决定了质量损失函数在机器学习和数据挖掘中的重要性。

质量损失函数日本质量管理学家田口玄一（Taguchi）认为产品质量与质量损失密切相关，质量损失是指产品在整个生命周期的过程中，由于质量不满足规定的要求，对生产者、使用者和社会所造成的全部损失之和。

田口用货币单位来对产品质量进行度量，质量损失越大，产品质量越差；反之，质量损失越小，产品质量越好。

一、质量特性产品质量特性是产品满足用户要求的属性，包括产品性能、寿命、可靠性、安全性、经济性、可维修性和环境适应性等。

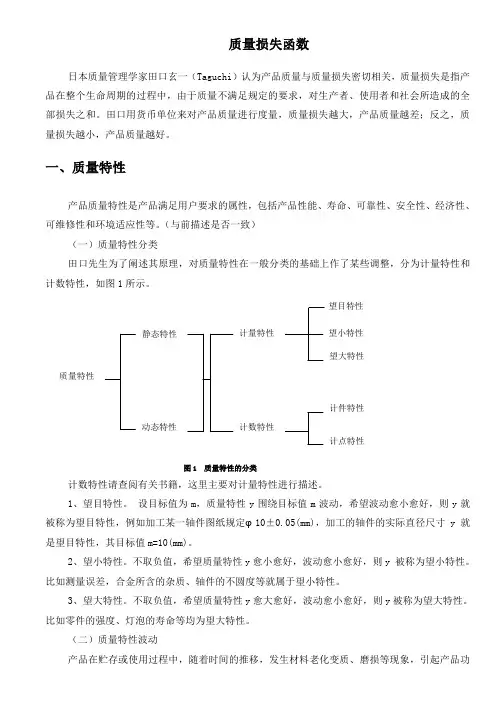
（与前描述是否一致）（一）质量特性分类田口先生为了阐述其原理，对质量特性在一般分类的基础上作了某些调整，分为计量特性和计数特性，如图1所示。

图1 质量特性的分类计数特性请查阅有关书籍，这里主要对计量特性进行描述。

1、望目特性。

设目标值为m，质量特性y围绕目标值m波动，希望波动愈小愈好，则y就被称为望目特性，例如加工某一轴件图纸规定φ10±0.05(mm)，加工的轴件的实际直径尺寸y就是望目特性，其目标值m=10(mm)。

2、望小特性。

不取负值，希望质量特性y愈小愈好，波动愈小愈好，则y 被称为望小特性。

比如测量误差，合金所含的杂质、轴件的不圆度等就属于望小特性。

3、望大特性。

不取负值，希望质量特性y愈大愈好，波动愈小愈好，则y被称为望大特性。

比如零件的强度、灯泡的寿命等均为望大特性。

（二）质量特性波动产品在贮存或使用过程中，随着时间的推移，发生材料老化变质、磨损等现象，引起产品功能的波动，我们称这种产品由于使用环境，时间因素，生产条件等影响，产品质量特性y偏离目标值m，产生波动。

引起产品质量特性波动的原因称为干扰源。

主要有以下三种类型：1、外干扰（外噪声）使用条件和环境条件（如温度，湿度，位置，输入电压，磁场，操作者等）的变化引起产品功能的波动，我们称这种使用条件和环境条件的变化为外干扰，也称为外噪声。

2、内干扰（内噪声）材料老化现象为内干扰，也称为内噪声。

3、随机干扰（产品间干扰）在生产制造过程中，由于机器、材料、加工方法、操作者、计测方法和环境（简称5MIE）等生产条件的微小变化，引起产品质量特性的波动，我们称这种在生产制造过程中出现的功能波动为产品间波动。

损失函数改进⽅法总览损失函数改进⽅法总览https:///u014380165/article/details/76946358这篇博客主要列个引导表，简单介绍在深度学习算法中损失函数可以改进的⽅向，并给出详细介绍的博客链接，会不断补充。

1、Large Marge Softmax LossICML2016提出的Large Marge Softmax Loss（L-softmax）通过在传统的softmax loss公式中添加参数m，加⼤了学习的难度，逼迫模型不断学习更具区分性的特征，从⽽使得类间距离更⼤，类内距离更⼩。

核⼼内容可以看下图：详细了解可以参看：2、Center LossECCV2016提出的center loss是通过将特征和特征中⼼的距离和softmax loss⼀同作为损失函数，使得类内距离更⼩，有点L1，L2正则化的意思。

核⼼内容如下图所⽰：详细了解可以参看：3、Angular Softmax LossCVPR2017提出的A-softmax loss（angular softmax loss）⽤来改进原来的softmax loss，并将A-softmax loss⽤于⼈脸识别，这就是SphereFace，作者还是Large margin softmax loss的原班⼈马。

A-softmax loss简单讲就是在large margin softmax loss的基础上添加了两个限制条件||W||=1和b=0，使得预测仅取决于W和x之间的⾓度。

核⼼思想可以参看下⾯这个图。

详细了解可以参看：4、Focal LossFocal loss是Facebook的RBG和Kaiming⼤神在ICCV2017的best paper，主要是改进了⽬标检测（object detection）算法的效果，在COCO 数据集上的AP和速度都有明显提升。

核⼼思想在于概括了object detection算法中proposal-free⼀类算法准确率不⾼的原因在于：类别不均衡。

第三次作业（第5章——第6章）一、判断题1、评审的目的在于及早查出和补救产品设计中的缺陷。

（√）2、质量功能展开所用的基本工具是“质量屋”。

（√）3、过程能力一般用6δ来表示，6δ越大，即过程质量波动越大，过程能力越高。

（×）4、“将正常判为异常”的错误，这种虚发警报的错误叫做第二类错误，概率一般记为α。

（√）5、三次设计的重点是系统设计。

（×）6、计量数据取值可以通过某种量具、仪器等的测定得到，它们只能取非负整数。

（×）7、“将异常判为正常”的错误，这种漏发警报的错误叫做第二类错误，概率一般记为β。

（√）8、参数设计实质上是质量优化设计，是质量设计的核心。

（√）9、在产品开发的不同阶段，有不同的评价内容和重点。

规划、方案、构思阶段，主要是对产品质量目标进行评价，称为B评价。

（×）10、分析用控制图与控制用控制图的过程实际上就是不断进行质量改进的过程。

（√）二、填空：1、田口将产品的设计过程分成三个阶段，即系统设计、参数设计和容差设计。

三次设计的重点在参数设计。

2、质量损失函数L(y)=K(y-m)²。

3、生产者风险常取a=0.05 ，其含义是如果供需双方认可，那么在100批合格的交验产品中，生产者要承担的风险是平均有5批被判为不合格而拒收。

4、控制图判断异常的准则有两条：点子出界就判断异常；界内点排列不随机判断异常。

5、用社会损失来度量质量，将质量与经济性紧密结合起来，使质量变成一种可量化度量的量，这是田口玄一对质量工程学的重大贡献之一。

6、产品质量设计的职能：产品质量信息的收集分析；产品质量目标的制定；产品质量评价活动；产品质量成本分析：产品设计评审。

7、设计评审的目的：纠正设计质量至善论；打破产品设计垄断；防止产品设计的片面性。

8、过程能力指数的值越大，说明过程能力越能满足技术要求，产品质量越有保证。

9、X图可以观察产品质量特性值分布的集中趋势和中心位置，从而控制平均值的变化。

非对称自动寻优算法非对称自动寻优算法（Asymmetric Automatic Tuning Algorithm，简称AATA）是一种用于优化计算机系统性能的算法。

与传统的对称自动寻优算法不同，非对称自动寻优算法通过动态调整系统各个组件的参数，使其能够在不同的工作负载下实现最佳性能。

在计算机系统中，各个组件的参数设置对系统性能有着重要的影响。

传统的对称自动寻优算法通常采用试错的方式，在不同的参数组合下进行测试，然后根据测试结果调整参数。

这种方法的问题在于，它忽略了不同组件之间的相互影响，可能导致参数调整的局部最优解，并不能达到系统的最佳性能。

非对称自动寻优算法则通过考虑各个组件之间的相互关系，从整体上优化系统性能。

该算法基于对系统的建模，通过数学模型和算法模拟，找到使系统性能最优的参数组合。

与传统的试错方法相比，非对称自动寻优算法能够更快地找到最佳解，并且可以在不同的工作负载下自动适应。

非对称自动寻优算法的核心思想是通过动态调整系统各个组件的参数来优化系统性能。

在算法运行过程中，首先对系统进行建模，将系统的各个组件和参数进行抽象和描述。

然后，通过数学模型和算法模拟，计算出每个组件参数的最佳值。

最后，将这些最佳值应用到实际系统中，实现系统性能的优化。

为了实现非对称自动寻优算法，需要解决以下几个关键问题：1. 参数建模：对系统各个组件和参数进行抽象和描述，建立数学模型。

这需要深入了解系统的架构和组件之间的相互关系，以及参数对系统性能的影响。

2. 算法设计：设计合适的算法，通过数学模型和算法模拟，计算出每个组件参数的最佳值。

这需要考虑到参数之间的相互关系，以及参数调整的优化目标。

3. 参数调整：将计算得到的最佳参数应用到实际系统中，实现系统性能的优化。

这需要考虑到系统的实际运行环境和工作负载，在动态调整参数的过程中保持系统的稳定性和可靠性。

非对称自动寻优算法在实际应用中有着广泛的用途。

例如，在大规模数据中心中，通过对服务器、网络设备和存储系统等各个组件的参数进行优化，可以提高整个数据中心的性能和效率。

损失函数超参数调试方法
调试损失函数的超参数是优化模型性能的重要步骤。

损失函数的超参数包括学习率、正则化参数、优化器类型等。

以下是一些常见的方法来调试损失函数的超参数：
1. 网格搜索，网格搜索是一种常见的超参数调试方法，它通过遍历给定的超参数组合来寻找最佳的超参数组合。

这种方法的缺点是计算成本高，特别是在超参数空间较大的情况下。

2. 随机搜索，与网格搜索相比，随机搜索在超参数空间中随机采样，这样可以更快地找到较好的超参数组合。

随机搜索的优点在于它可以在有限的计算资源下找到较好的超参数组合。

3. 贝叶斯优化，贝叶斯优化是一种基于贝叶斯方法的序列模型优化方法，它通过构建超参数与性能之间的概率模型来选择下一个要尝试的超参数组合。

这种方法在高维超参数空间中表现良好。

4. 自适应优化，一些优化器（如Adam）具有自适应学习率的特性，可以根据损失函数的表现自动调整学习率。

这种方法可以减少手动调试超参数的工作量。

5. 交叉验证，交叉验证是评估模型性能和选择超参数的重要工具。

通过将数据集分成训练集和验证集，可以在不同超参数下比较
模型的性能，从而选择最佳的超参数组合。

总的来说，调试损失函数的超参数是一个复杂而耗时的过程，
需要结合实际问题和计算资源来选择合适的调试方法。

同时，需要
注意避免过拟合和欠拟合，以及了解不同超参数对模型性能的影响，才能找到最佳的超参数组合。

【科普】质量方法论之质量损失函数质量损失是指企业在生产、经营过程和活动中，由于产品的质量问题而导致的损失，即由于质量低劣而产生的内、外部损失。

质量损失的存在在于资源的潜力没能得到充分的发挥，是质量改进的机会所在。

质量损失可分为两种形式：有形损失和无形损失。

有形损失指由于内部故障而直接发生的费用，如返工、低效的人机控制、丧失机会等而引起的低工作效率而造成的资源和材料的浪费等。

无形损失是指由于顾客不满意而发生的未来销售的损失，如因顾客不满意而失去顾客，丧失信誉，从而失去更多销售机会或增值机会所造成的损失。

无形损失不是实际的费用支出，常常难以统计和定量，并且它对组织的影响大且长久，因而，它是一种很重要的损失。

质量损失函数：日本质量管理专家田口玄一给出了质量损失函数的表达式——一个“二次方程式”及其平衡的条件。

其中：L(x)——质量损失，m——质量特性标准，x——质量特性值, k——常数，一般可以由“机能界限”确定。

应用损失函数在实践中最重要的运用，在于协助我们通过过程的改善而持续减少目标值的变异，并非仅仅追求符合逻辑。

现在举个例子：某个工厂人员的产出，以每小时多少元来计算，而损失函数所显示的，是产出以室内通风条件而改变的情形。

厂内工作的每个人，都有自己的损失函数。

为了简化说明，假设每个人的损失函数均为一条抛物线，其底部一点代表产出值最大时的通风条件，把所有人员的损失函数进行叠加，公司整体的损失函数也必然是一条抛物线。

如果通风条件偏离这个最佳水准，就会有额外损失发生。

该抛物线与横轴相切时，切点的左右各有一小段与横轴几近重合。

也就是说，有最适点偏离一小短距离，损失小到可以忽略不计。

因此，当室内通风条件稍稍偏离均衡点，发生的损失可以忽略不计。

但是远离均衡点时，总是有人必须支付这损失。

如果我们能够导出有具体数字的损失函数，我们就可以计算出最有均衡点，在均衡点中最适合的通风条件如何，以及达到要求的费用支出是多少。

损失函数设计损失函数在机器学习研究中拥有重要作用，它可以帮助研究人员记录与预测准确度相关的性能指标，并帮助它们在实践中快速改进模型。

一个有效损失函数的设计是一项复杂的任务，也是机器学习和深度学习的一个核心挑战。

本文将介绍损失函数的概念，以及损失函数设计中的常见技术：损失函数的可视化，损失函数的反向传播，损失函数的正则化和正则化参数等。

最后，将介绍几个示例，帮助读者理解损失函数设计的实际应用。

一、损失函数概念损失函数是机器学习中一个重要的概念。

它是度量预测值与实际值之间偏差的一种方法，其中更小的偏差意味着模型的性能更高。

例如，常见的损失函数有均方误差（MSE），均方根误差（RMSE），平均绝对偏差（MAE）等。

损失函数通常使用梯度下降法进行优化，以最小化损失函数值，实现模型参数优化。

由于损失函数大多数时候是非凸函数，因此梯度下降法可以帮助实现最小化损失函数值。

二、损失函数设计技术损失函数设计技术主要有以下几种：（1）损失函数的可视化利用可视化技术可以清楚地查看损失函数的变化情况，并比较不同的损失函数模型，以帮助研究人员选择最佳损失函数。

可视化技术可以帮助研究人员更好地了解损失函数的性能，也可以帮助研究人员发现和改进模型表现中的缺陷。

（2）损失函数的反向传播反向传播（Backpropagation）是一种利用反馈机制来更新和优化网络参数的机器学习方法。

它可以帮助研究人员快速改进模型的性能，从而降低损失函数的值。

（3）损失函数的正则化正则化是指在损失函数中添加正则化参数，以防止模型过拟合。

正则化可以帮助模型更好地泛化，也可以降低损失函数的值。

三、损失函数设计的实例（1）最小平方误差（MSE）最小平方误差（MSE）是一种常用的损失函数，它可以度量实际值和预测值之间的偏差，它可以用来判断模型的预测精度。

计算公式为：MSE=∑（y_i-y_i）^2/n其中，y_i是实际值，y_i是预测值，n是样本数量。

（2）均方根误差（RMSE）均方根误差（RMSE）是一种度量预测值与真实值之间偏差的方法，它是MSE的平方根。

六西格玛工具箱之质量损失函数六西格玛工具箱之质量损失函数质量特性的波动(即产品性能相对设计目标值的偏离)是引起质量损失和质量问题的原因，田口博士建立了质量损失函数，以描述质量损失与质量波动之间的关系。

质量损失QL(Quality Loss)是质量特性y的函数。

不同的产品和不同的质量特性对应不同的质量损失曲线。

当产品性能恰好为目标值m时，质量损失最小，相对值可定义为零。

产品性能偏离目标值越远，质量损失越大。

质量损失函数L(y)的图象为一条曲线，在y=m处有极小值零。

假定L(y)在y=m处存在二阶导数，可将L(y)在y=m处展开成泰勒级数，考虑L(y)=0，L,(m)=0，并忽略高阶无穷小，L(y)可简化为式中k=L,,(m)/2!为不依赖于y的常数。

因此质量损失函数的图像在y=m附近近似地等于一条抛物线。

j(y)为一批产品的性能概率分布密度函数，其均值为μ，标准差为σ，则这批产品的质量损失的数学期望为?????? 当随机变量y服从正态分布N(μ，σ2)时，由(1-8)式可得 ?????? ??????可见质量损失的数学期望L与产品性能方差σ2、平均波动的平方(μ-m)2和损失系数k有关。

?????? σ2和(μ-m)2决定了曲线j(y)的形状与位置，而k 则决定了质量损失函数L(y)的形状。

健壮设计的目标有两个，一个目标是使[s2+(m-m)2]最小，即曲线j(y)很陡且均值接近m，另一个目标是使k最小，即曲线L(y)很平坦，从而使产品的质量损失最小。

六西格玛工具箱之因果图因果图又叫“石川馨图”，也称为鱼刺图、特性要因图等。

它是利用“头脑风暴法”，集思广益，寻找影响质量、时间、成本等问题的潜在因素，然后用图形形式来表示的一种十分有用的方法，它揭示的的是质量特性波动与潜在原因的关系。

因果图有三个显著的特征: 是对所观察的效应或考察的现象有影响的原因的直观的表示; 这些可能的原因的内在关系被清晰地显示出来; 内在关系一般是定性的和假定的。

日本质量管理学家田口玄一(Taguchi)认为产品质量与质量损失密切相关，质量损失是指产 品在整个生命周期的过程中，由于质量不满足规定的要求，对生产者、使用者和社会所造成的全 部损失之和。

田口用货币单位来对产品质量进行度量，质量损失越大，产品质量越差；反之，质 量损失越小，产品质量越好。

产品质量特性是产品满足用户要求的属性，包括产品性能、寿命、可靠性、安全性、经济性、 可维修性和环境适应性等。

(与前描述是否一致)(一)质量特性分类田口先生为了阐述其原理，对质量特性在普通分类的基础上作了某些调整，分为计量特性和计数特性，如图 1 所示。

计数特性请查阅有关书籍，这里主要对计量特性进行描述。

1、望目特性。

设目标值为 m ，质量特性 y 环绕目标值 m 波动，希翼波动愈小愈好，则 y 就 被称为望目特性，例如加工某一轴件图纸规定φ 10±0.05(mm)，加工的轴件的实际直径尺寸 y 就 是望目特性，其目标值 m=10(mm)。

2、望小特性。

不取负值，希翼质量特性 y 愈小愈好，波动愈小愈好，则y 被称为望小特性。

比如测量误差，合金所含的杂质、轴件的不圆度等就属于望小特性。

3、望大特性。

不取负值，希翼质量特性 y 愈大愈好，波动愈小愈好，则 y 被称为望大特性。

比如零件的强度、灯泡的寿命等均为望大特性。

(二)质量特性波动产品在贮存或者使用过程中，随着时间的推移，发生材料老化变质、磨损等现象，引起产品功 能的波动，我们称这种产品由于使用环境，时间因素，生产条件等影响，产品质量特性 y 偏离目 标值 m ，产生波动。

引起产品质量特性波动的原因称为干扰源。

主要有以下三种类型：望目特性望小特性望大特性质量特性计件特性动态特性 计数特性计点特性计量特性 静态特性1、外干扰(外噪声)使用条件和环境条件(如温度，湿度，位置，输入电压，磁场，操作者等)的变化引起产品 功能的波动，我们称这种使用条件和环境条件的变化为外干扰，也称为外噪声。

损失函数和优化算法
在机器学习中，损失函数和优化算法是两个非常重要的概念。

损失函数是用来衡量模型预测值与真实值之间的差异的函数。

它可以帮助我们评估模型的性能，并指导模型的优化。

常见的损失函数包括均方误差（MSE）、交叉熵（CE）等。

选择合适的损失函数对于模型的训练非常重要，因为不同的任务可能需要不同的损失函数。

优化算法是用来最小化损失函数的算法。

它可以帮助我们找到模型的最优参数，从而提高模型的性能。

常见的优化算法包括随机梯度下降（SGD）、Adagrad、Adadelta 等。

选择合适的优化算法对于模型的训练也非常重要，因为不同的优化算法可能适用于不同的任务和数据集。

在实际应用中，我们通常会将损失函数和优化算法结合起来使用。

具体来说，我们会先定义一个损失函数，然后使用优化算法来最小化这个损失函数。

在训练过程中，我们会不断地计算损失函数的值，并根据优化算法的规则来更新模型的参数，直到损失函数的值达到最小。

总之，损失函数和优化算法是机器学习中非常重要的概念，它们可以帮助我们评估模型的性能并找到最优的模型参数。

在实际应用中，我们需要根据具体的任务和数据集来选择合适的损失函数和优化算法。