余弦值对应表

常用正余弦值表
正弦和余弦是三角函数中最常见的两个函数。

它们的值可以通过查表或使用计算器等工具进行计算。

下面是常用正余弦值表的一部分：
表格1：正弦值表
角度（度）正弦值
0°0
30°0.5
45°0.707
60°0.866
90°1
120°0.866
135°0.707
150°0.5
180°0
...
注意：上述角度是以度为单位的，正弦值是对应角度的正弦值。

对于其他角度，可以通过插值或使用三角函数公式进行计算。

表格2：余弦值表
角度（度）余弦值
0°1
30°0.866
45°0.707
60°0.5
90°0
120°-0.5
135°-0.707
150°-0.866
180°-1
...
同样，上述角度是以度为单位的，余弦值是对应角度的余弦值。

对于其他角度，可以使用类似的方法进行计算。

请注意，这只是常用正余弦值表的一部分，实际上正弦和余弦的值是连续变化的。

在实际使用中，可以使用计算器或计算机软件来获得更准确的正余弦值。

希望以上的回答对您有所帮助！如需更多信息，请随时提问。

正弦余弦值对照表正弦余弦值对照表：1. 0的正弦余弦值：正弦值：0；余弦值：1。

2. 30°的正弦余弦值：正弦值：0.5；余弦值：0.866。

3. 45°的正弦余弦值：正弦值：0.7071；余弦值：0.7071。

4. 60°的正弦余弦值：正弦值：0.866；余弦值：0.5。

5. 90°的正弦余弦值：正弦值：1；余弦值：0。

6. 120°的正弦余弦值：正弦值：0.866；余弦值：-0.5。

7. 135°的正弦余弦值：正弦值：0.7071；余弦值：-0.7071。

8. 150°的正弦余弦值：正弦值：0.5；余弦值：-0.866。

9. 180°的正弦余弦值：正弦值：0；余弦值：-1。

10. 210°的正弦余弦值：正弦值：-0.5；余弦值：-0.866。

正弦值：-0.7071；余弦值：-0.7071。

12. 240°的正弦余弦值：正弦值：-0.866；余弦值：-0.5。

13. 270°的正弦余弦值：正弦值：-1；余弦值：0。

14. 300°的正弦余弦值：正弦值：-0.866；余弦值：0.5。

15. 315°的正弦余弦值：正弦值：-0.7071；余弦值：0.7071。

16. 330°的正弦余弦值：正弦值：-0.5；余弦值：0.866。

17. 360°的正弦余弦值：正弦值：0；余弦值：1。

正弦余弦值对照表是由数学中的正弦定理衍生出来的，它是一种可以表达正弦和余弦值之间关系的表格。

正弦余弦表是采用近似三角函数来求得直角三角形锐角中角度和对边之间的对应关系，以便更准确地确定直角三角形各边和锐角的大小。

下面是正弦余弦值对照表：1. 0°的正弦余弦值：正弦值：0；余弦值：1。

2. 30°的正弦余弦值：正弦值：0.5；余弦值：0.866。

正弦值：0.7071；余弦值：0.7071。

高中完整的三角函数值表弧度制在高中数学学习中，三角函数是一个非常重要的概念，它在数学和物理等领域都有着广泛的应用。

而在学习三角函数时，理解三角函数值表是至关重要的一步。

本文将详细介绍高中完整的三角函数值表，以弧度制为单位。

正弦函数的值表正弦函数是三角函数中最基本的一个函数，其定义域为实数集，值域为[-1, 1]。

下表展示了常见角度对应的正弦函数值（保留四位小数）：弧度（rad）0π/6π/4π/3π/22π/33π/45π/6π正弦值0.00000.50000.70710.86601.00000.86600.70710.50000.0000余弦函数的值表余弦函数也是三角函数中常见的一个函数，其定义域为实数集，值域为[-1, 1]。

下表展示了常见角度对应的余弦函数值（保留四位小数）：弧度（rad）0π/6π/4π/3π/22π/33π/45π/6π余弦值1.00000.86600.70710.50000.0000-0.5000-0.7071-0.8660-1.0000正切函数的值表正切函数在三角函数中也有着重要的作用，其定义域为实数集，值域为实数集。

下表展示了常见角度对应的正切函数值（保留四位小数）：弧度（rad）0π/6π/4π/3π/22π/33π/45π/6π正切值0.00000.57741.00001.7321不定义-1.7321-1.0000-0.5774-0.0000通过上述三角函数值表，我们可以更加直观地理解不同角度对应的三角函数值，为我们在数学和物理问题中的运用提供了重要参考。

希望本文内容对您有所帮助。

常见三角函数表值查表
三角函数是数学中的重要概念，在许多数学问题中都有广泛的应用。

为了方便计算和使用，我们通常会使用三角函数的表格来查找特定角度对应的数值。

在这篇文章中，我们将详细介绍常见三角函数（正弦、余弦、正切）的表值，并讨论如何有效地利用这些表值来解决数学问题。

正弦函数表值
正弦函数是一个周期函数，其定义域为实数集，值域为[-1, 1]。

下表列出了常见角度的正弦函数值：
角度（度）030456090
正弦值00.50.7070.8661
余弦函数表值
余弦函数也是一个周期函数，其定义域为实数集，值域为[-1, 1]。

下表列出了常见角度的余弦函数值：
角度（度）030456090
余弦值10.8660.7070.50
正切函数表值
正切函数是一个奇函数，其定义域为实数集，值域为实数集。

下表列出了常见角度的正切函数值：
角度（度）030456090
正切值00.5771 1.732无穷
如何利用表值
查表是解决三角函数问题的一种有效方法。

例如，如果要
计算30度的正弦函数值，只需在正弦函数表中查找30度对
应的值即可找到答案0.5。

通过巧妙地利用这些表值，我们可
以快速解答各种与三角函数有关的问题。

总结
通过本文，我们介绍了常见三角函数（正弦、余弦、正切）的表值，并讨论了如何利用这些表值来解决数学问题。

三角函数的表值对于数学学习和实际问题求解都具有重要意义，希望本文能为读者提供帮助。

如果要进一步了解三角函数的性质和应用，建议继续学习相关内容。

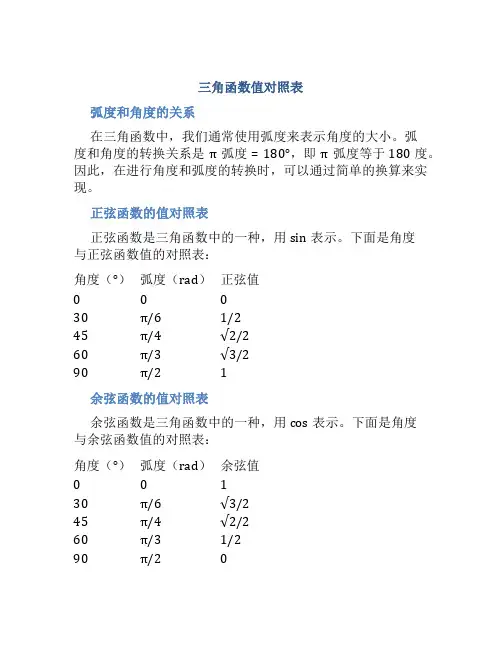
三角函数值对照表
弧度和角度的关系
在三角函数中，我们通常使用弧度来表示角度的大小。

弧
度和角度的转换关系是π 弧度 = 180°，即π 弧度等于180度。

因此，在进行角度和弧度的转换时，可以通过简单的换算来实现。

正弦函数的值对照表
正弦函数是三角函数中的一种，用sin表示。

下面是角度
与正弦函数值的对照表：
角度（°）弧度（rad）正弦值
000
30π/61/2
45π/4√2/2
60π/3√3/2
90π/21
余弦函数的值对照表
余弦函数是三角函数中的一种，用cos表示。

下面是角度
与余弦函数值的对照表：
角度（°）弧度（rad）余弦值
001
30π/6√3/2
45π/4√2/2
60π/31/2
90π/20
正切函数的值对照表
正切函数是三角函数中的一种，用tan表示。

下面是角度与正切函数值的对照表：
角度（°）弧度（rad）正切值
000
30π/6√3/3
45π/41
60π/3√3
90π/2未定义
总结
通过以上对照表可以清晰地显示出不同角度下三角函数的值，对于理解三角函数在不同角度下的表现具有重要意义，也方便我们在数学计算中的应用。

熟练掌握三角函数值的对照表有助于提高数学运算效率，希望对您有所帮助。

正弦余弦正切值对照表高中正弦余弦正切值对照表1. sin(0°) = 0, cos(0°) = 1, tan(0°) = 02. sin(30°) = 0.5, cos(30°) = 0.866, tan(30°) = 0.5773. sin(45°) = 0.707, cos(45°) = 0.707, tan(45°) = 14. sin(60°) = 0.866, cos(60°) = 0.5, tan(60°) = 1.7325. sin(90°) = 1, cos(90°) = 0, tan(90°) = 无限大从数学层面上讲，正弦函数（sin）是每个极度（omnik）的角度将其值变成一条正弦曲线，而余弦函数（cos）是每个极度倾向于变成一条余弦曲线。

正切函数（tan）则是极角轴上变换程度跟随一条正切曲线。

下面我们将表述几个关键点：1. 当角度为0°时，有正弦值为0，余弦值为1，正切值为0，也就是说x轴的正方向和y轴的正方向垂直，所以正切值为0。

2. 当角度为30°时，有正弦值为0.5，余弦值为0.866，正切值为0.577，此时正切值就表示x轴和y轴的变形程度，向左倾斜了30°，正切值即0.577。

3. 当角度为45°时，有正弦值为0.707，余弦值为0.707，正切值为1，我们可以推断出数学中45度就是一个直角，所以正弦值和余弦值是完全相等的，自然正切就等于1。

4. 当角度为60°时，有正弦值为0.866，余弦值为0.5，正切值为1.732，此时正切值表示了x轴和y轴的变形程度，向左倾斜了60°，正切值等于1.732。

5. 当角度为90°时，有正弦值为1，余弦值为0，正切值为无限大，由于90°代表一个垂直，即x轴改变了90°，y轴完全不动，所以正切值此时正好成为正无穷大。

常见三角函数值表高清
在数学中，三角函数是研究角与其它两边之间关系的一门重要学科。

常见的三角函数包括正弦函数、余弦函数和正切函数等。

下面是一个常见三角函数值表，帮助大家快速查阅各个角度对应的三角函数值。

角度（度）正弦值余弦值正切值
0°010
30°1/2√3/21/√3
45°√2/2√2/21
60°√3/21/2√3
90°10无穷
120°√3/2-1/2-√3
135°√2/2-√2/2-1
150°1/2-√3/2-1/√3
180°0-10
通过这个高清的三角函数值表，可以方便地获取各角度下的正弦值、余弦值和正切值。

三角函数在数学和物理等领域有着广泛的应用，掌握这些数值对于解决问题和理解相关理论非常重要。

希望这个表格对大家有所帮助！。

初中常用的三角函数值表
在初中数学学习中，三角函数是一个非常重要的概念。

三角函数在数学中起到了非常关键的作用，它们与角度的关系紧密联系在一起。

我们常用的三角函数包括正弦函数、余弦函数和正切函数，它们在初中阶段被广泛讨论和运用。

了解三角函数值的表格对于解题和理解三角函数的性质非常有帮助。

正弦函数值表
正弦函数是三角函数中的一个重要概念，它表示一个角的正弦值。

正弦函数的值域在-1到1之间变化，下表列出了一些常见角度对应的正弦函数值：
角度0°30°45°60°90°
正弦值01/2√2/2√3/21
余弦函数值表
余弦函数是另一个常用的三角函数，它表示一个角的余弦值。

余弦函数的值域也在-1到1之间，下表列出了一些常见角度对应的余弦函数值：
角度0°30°45°60°90°
余弦值1√3/2√2/21/20
正切函数值表
正切函数是三角函数中的另一个重要概念，它表示一个角的正切值。

正切函数的值可以是任意的实数，下表列出了一些常见角度对应的正切函数值：
角度0°30°45°60°90°
正切值0√3/31√3无穷大
通过上述三角函数的值表，我们可以看到不同角度对应的正弦、余弦和正切函数值的关系。

这些数学概念在几何学、物理学等领域中有着广泛的应用，掌握它们有助于我们更深入地理解数学知识。

在初中阶段，三角函数值表是一个重要的学习工具，帮助我们更好地理解和运用三角函数的性质和特点。

高中三角函数表在高中数学学习中，三角函数是一个非常重要的概念。

其中最基础的三个三角函数，即正弦、余弦和正切函数，在解决各种数学问题中起着重要的作用。

三角函数表是一种方便查找各种角度对应三角函数值的工具。

通过三角函数表，我们可以快速地得到各种角度对应的正弦、余弦、正切值，从而简化数学运算。

正弦函数表正弦函数通常用符号sin表示，对于一个给定的角度θ，它的正弦值就是三角形中对边与斜边的比值。

在高中数学中，我们经常需要求解各种角度对应的正弦值。

下面是一个正弦函数的部分表格：角度（度）正弦值00300.545√2/260√3/2901余弦函数表余弦函数通常用符号cos表示，对于一个给定的角度θ，它的余弦值就是三角形中邻边与斜边的比值。

余弦函数在解决各种几何问题和物理问题中经常会用到。

下面是一个余弦函数的部分表格：角度（度）余弦值0130√3/245√2/2600.5900正切函数表正切函数通常用符号tan表示，对于一个给定的角度θ，它的正切值就是三角形中对边与邻边的比值。

正切函数在解决各种几何和物理问题中也是非常重要的。

下面是一个正切函数的部分表格：角度（度）正切值0030√3/345160√390无穷大三角函数表中还包括了其他角度的数值，通过这些数值可以在数学计算中快速准确地得到各种角度的正弦、余弦和正切值。

三角函数表的使用可以简化复杂的数学运算，并且有助于理解三角函数之间的关系，为进一步学习数学打下坚实的基础。

希望这份三角函数表对大家的数学学习有所帮助。

常用三角函数表值查表在数学和物理学中，三角函数是一组描述角度和长度关系的函数。

常用的三角函数包括正弦函数（sine）、余弦函数（cosine）和正切函数（tangent）。

这些函数在各种科学和工程领域中经常被使用，因此了解它们的数值表值是很有用的。

本文将提供常用三角函数的表值，帮助读者快速查找常见角度的三角函数值。

以下是常见角度的正弦、余弦和正切值的表格：角度正弦值余弦值正切值0°01030°1/2√3/2√3/345°√2/2√2/2160°√3/21/2√390°10undefined120°√3/2-1/2-√3135°√2/2-√2/2-1150°1/2-√3/2-√3/3180°0-10通过查阅上述表格，我们可以快速获得常见角度的三角函数表值。

需要注意的是，在表格中有一些特殊的角度，如90°和180°，它们的正弦值和余弦值分别为1和-1，而正切值在这些角度处是未定义的。

调用三角函数时，我们通常会使用弧度而不是角度作为输入参数。

下面的表格列出了一些常见角度对应的弧度值：角度弧度0°0 30°π/6 45°π/4 60°π/3 90°π/2 120°2π/3 135°3π/4 150°5π/6 180°π通过将角度转换为弧度，我们可以使用标准的数学函数库来计算三角函数的值。

常用的编程语言通常提供了这些函数，例如Python中的math库和JavaScript中的Math对象。

除了上述常见角度的三角函数值之外，我们还可以通过使用三角函数的性质来计算其他角度的值。

例如，正弦函数是一个周期函数，其周期为360°或2π弧度。

因此，对于角度θ，我们可以使用以下公式计算正弦函数的值：sin(θ) = sin(θ mod 360°)其中。

sin tan cos三角函数表前言在数学领域中，三角函数是一类非常重要的函数，其中最常见的三个是正弦函数（sin）、余弦函数（cos）和正切函数（tan）。

它们在数学运算、物理学和工程学中都有广泛的应用。

本文将介绍sin、tan、cos三角函数的基本定义、性质和常用数值范围，以及它们在实际问题中的应用。

正弦函数sin正弦函数是最基础的三角函数之一，通常表示为sin(x)，其中x为自变量（弧度）。

正弦函数的定义域为实数集，值域为[-1, 1]。

正弦函数在二维平面上表示了单位圆上的点的y 坐标。

若角度为x度，则sin(x)表示单位圆上与对应角度相对应的点的y坐标值。

余弦函数cos余弦函数是另一个常见的三角函数，通常表示为cos(x)，其中x为自变量（弧度）。

余弦函数的定义域也为实数集，值域为[-1, 1]。

余弦函数在二维平面上表示了单位圆上的点的x坐标。

若角度为x度，则cos(x)表示单位圆上与对应角度相对应的点的x坐标值。

正切函数tan正切函数是第三个常见的三角函数，通常表示为tan(x)，其中x为自变量（弧度）。

正切函数的定义域为实数集，但在特定点上会有无定义的情况（如π/2 + nπ）。

正切函数的值域为实数集，即它可以取任意实数值。

三角函数表下面是一些常见角度下sin、tan、cos函数的数值表：角度（度）正弦值sin余弦值cos正切值tan0010300.5√3/2√3/345√2/2√2/2160√3/20.5√39010无定义应用举例三角函数在数学、物理、工程等领域有广泛的应用。

例如，在物理学的力学中，三角函数可以用来描述物体受到的力和受力方向之间的关系；在工程学中，三角函数可以用来分析电路中的交流信号波形等。

因此，熟练掌握三角函数的性质和应用是非常重要的。

总结本文介绍了三角函数sin、tan、cos的定义、性质和常用数值范围，以及它们在实际问题中的应用。

通过学习和掌握三角函数的基本知识，读者可以更好地理解数学和物理问题，提高解决问题的能力。

高中数学三角函数值表
在高中数学学科中，三角函数是一个非常重要的内容，它包括正弦函数、余弦函数、正切函数等。

为了帮助高中生更好地掌握三角函数的数值，下面列出了常见角度对应的三角函数值表，供学生参考。

正弦函数值表
角度（度）角度（弧度）正弦值
000
30π/60.5
45π/4√2 / 2
60π/3√3 / 2
90π/21
余弦函数值表
角度（度）角度（弧度）余弦值
001
30π/6√3 / 2
45π/4√2 / 2
60π/30.5
90π/20
正切函数值表
角度（度）角度（弧度）正切值
000
30π/6√3 / 3
45π/41
60π/3√3
90π/2不存在
通过以上数值表，我们可以看到不同角度对应的三角函数值，这些数值对于解决三角函数相关的问题非常有用。

高中生们在学习三角函数时，可以利用这些数值表进行练习和验证，在加深对三角函数的理解的同时，也提高了解题的效率。

希望学生们能够充分利用这些数值表，掌握好三角函数的相关知识，取得优异的学习成绩！。

高中物理 - 三角函数值表格在高中物理学习过程中，三角函数是一个重要的数学工具，常常用于描述物理问题中的各种关系。

三角函数包括正弦、余弦、正切等函数，它们的数值在一定角度范围内是固定的，可以通过表格的形式进行整理和查阅。

正弦函数值表格正弦函数是一个周期函数，其值在每个周期内都是循环的。

下表列出了正弦函数在0°至360°范围内的取值：角度（度）正弦值00300.5450.707600.8669011200.8661350.7071500.51800210-0.5225-0.707240-0.866270-1300-0.866315-0.707330-0.53600余弦函数值表格余弦函数也是一个周期函数，其值同样在每个周期内循环变化。

下表是余弦函数在0°至360°范围内的取值：角度（度）余弦值01300.866450.707600.5900120-0.5135-0.707150-0.866180-1210-0.866225-0.707240-0.527003000.53150.7073300.8663601正切函数值表格正切函数的周期性比正弦、余弦函数更强，其在0°至360°范围内的取值如下：角度（度）正切值00300.57745160 1.73290无穷大120-1.732135-1150-0.57718002100.5772251240 1.732270无穷大300-1.732315-1330-0.5773600这些三角函数的数值表格可以帮助高中物理学生更好地理解三角函数的性质和变化规律，有助于解决实际物理问题中的计算和分析。

读者在学习过程中可以通过表格查找需要的数值，加深对三角函数的理解。

常用三角函数值对照表图解正弦函数（Sin）正弦函数是三角函数中的一个基本函数，通常表示为Sinθ。

下面是常见角度的正弦函数值对照表：角度（度）角度（弧度）正弦值00030π/61/245π/4√2/260π/3√3/290π/21从上表可以看出，随着角度的增大，正弦函数值也在增大，最大值为1。

余弦函数（Cos）余弦函数是另一个重要的三角函数，通常表示为Cosθ。

下面是常见角度的余弦函数值对照表：角度（度）角度（弧度）余弦值00130π/6√3/245π/4√2/260π/31/290π/20与正弦函数相反，余弦函数随着角度增大，其值逐渐减小，最终趋近于0。

正切函数（Tan）正切函数是三角函数中的另一个重要函数，通常表示为Tanθ。

下面是常见角度的正切函数值对照表：角度（度）角度（弧度）正切值00045π/4190π/2无穷大1353π/4-1180π0由于正切函数在π/2和3π/2处有奇点，所以值会趋近于无穷大或负无穷大。

Cot、Sec 和 Csc 函数除了正弦、余弦和正切函数外，还有它们的倒数函数，即余切函数（Cot）、正割函数（Sec）和余割函数（Csc）。

它们的值可以通过对应的三角函数值求倒数得到。

函数定义值Cotθ1/Tanθ1/0或无穷大Secθ1/Cosθ1/1或1Cscθ1/Sinθ1/0或无穷大综上所述，通过常用三角函数的值对照表图解，我们可以更直观地理解角度与三角函数之间的关系，这对于数学分析和实际应用都具有重要意义。

常用的三角函数值对照表
正弦函数（Sine Function）
正弦函数是三角函数中的一种，通常用sin表示。

在数学中，正弦函数的定义如下：
$$ \\sin(\\theta) = \\frac{对边}{斜边} $$
下表是常用角度的正弦值对照表：
角度（度）0°30°45°60°90°
正弦值00.50.7070.8661
余弦函数（Cosine Function）
余弦函数是三角函数中的一种，通常用cos表示。

在数学中，余弦函数的定义如下：
$$ \\cos(\\theta) = \\frac{邻边}{斜边} $$
下表是常用角度的余弦值对照表：
角度（度）0°30°45°60°90°
余弦值10.8660.7070.50
正切函数（Tangent Function）
正切函数是三角函数中的一种，通常用tan表示。

在数学中，正切函数的定义如下：
$$ \\tan(\\theta) = \\frac{对边}{邻边} $$
下表是常用角度的正切值对照表：
角度（度）0°30°45°60°90°
正切值00.5771 1.732∞
以上是常用的三角函数值对照表，这些数值在解决各种数学和物理问题中经常会被用到。

三角函数是数学中非常重要的概念，对于理解波动、振动、周期性等现象具有重要意义。

希望这份对照表能帮助您更好地理解和应用三角函数。