《第九章多室模型》word版
- 格式：doc
- 大小：294.50 KB
- 文档页数：10
下载文档原格式
合集下载
多室模型名词解释(一)
多室模型名词解释(一)多室模型名词解释什么是多室模型多室模型是一种用于描述系统内部组织结构和交互关系的模型。
它将一个系统划分为多个相互独立的“房间”或“室”，每个房间都有自己的功能和责任，并通过门户进行通信和交互。
多室模型可以帮助开发人员更好地理解系统的结构和内部逻辑，提高系统的可维护性和可扩展性。
主要名词解释以下是与多室模型相关的一些重要名词的解释和示例说明：1. 房间（Room）房间是系统中的一个功能模块或单元，每个房间都有自己的职责和功能。
房间之间通过门户进行通信和交互。
示例：在一个在线商城系统中，可以将用户管理、商品管理、订单管理等功能划分为不同的房间。
2. 门户（Gateway）门户是房间之间进行通信和交互的接口，它定义了房间之间可以进行的操作和数据传递方式。
示例：在一个客户关系管理系统中，可以定义一个名为“CustomerGateway”的门户，用于房间之间的用户信息传递和管理。
3. 通信（Communication）通信是房间之间进行信息传递和交流的过程。
通过门户，房间可以发送和接收消息，以实现各种功能和操作。
示例：在一个社交媒体平台中，用户房间可以通过消息门户向好友房间发送私信，实现用户之间的即时通信。
4. 调度器（Scheduler）调度器是多室模型中的一个组件，用于协调和控制房间之间的交互和执行顺序。
它可以根据规则和策略来安排房间的执行顺序和时间。
示例：在一个任务调度系统中，调度器可以根据任务的优先级和时间约束，安排各个任务房间的执行顺序和时间点。
总结多室模型是一种用于描述系统内部组织结构和交互关系的模型。
通过将系统划分为多个相互独立的房间，并通过门户进行通信和交互，我们可以更好地理解系统的结构和内部逻辑，提高系统的可维护性和可扩展性。
在多室模型中，房间、门户、通信和调度器等名词扮演着重要的角色，它们相互配合，共同构建出一个完整的系统。
生物药剂与药物动力学(附习题及答案)
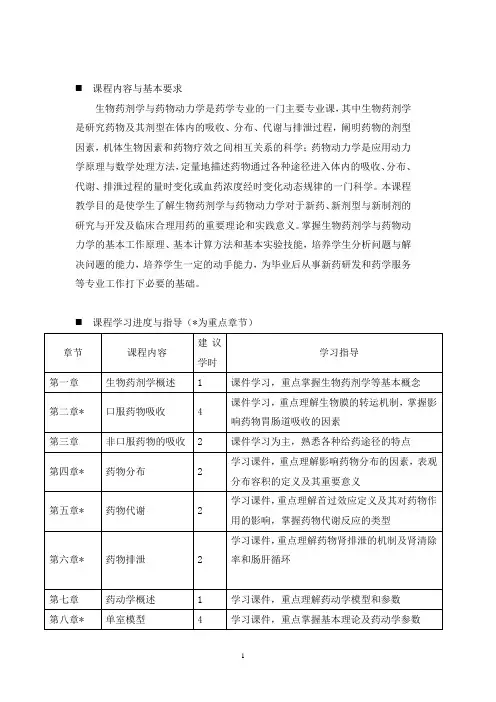
⏹课程内容与基本要求生物药剂学与药物动力学是药学专业的一门主要专业课，其中生物药剂学是研究药物及其剂型在体内的吸收、分布、代谢与排泄过程，阐明药物的剂型因素，机体生物因素和药物疗效之间相互关系的科学；药物动力学是应用动力学原理与数学处理方法，定量地描述药物通过各种途径进入体内的吸收、分布、代谢、排泄过程的量时变化或血药浓度经时变化动态规律的一门科学。
本课程教学目的是使学生了解生物药剂学与药物动力学对于新药、新剂型与新制剂的研究与开发及临床合理用药的重要理论和实践意义。
掌握生物药剂学与药物动力学的基本工作原理、基本计算方法和基本实验技能，培养学生分析问题与解决问题的能力，培养学生一定的动手能力，为毕业后从事新药研发和药学服务等专业工作打下必要的基础。
⏹课程学习进度与指导（*为重点章节）第九章多室模型 1 学习课件，理解多室模型特点和识别方法第十章* 多剂量给药 3 学习课件，重点掌握稳态血药浓度的计算第十一章非线性药物动力学 2 学习课件，重点理解特点，机制和识别方法第十二章统计矩分析 1 学习课件，掌握MRT含义及计算第十三章* 药物动力学在临床药学中的应用3 学习课件，重点掌握给药方法设计方法第十四章* 药物动力学在新药研究中的应用3 学习课件，重点掌握第一章生物药剂学概述一、学习目标掌握生物药剂学的定义，剂型因素与生物因素的含义。
熟悉生物药剂学的研究内容和进展，了解生物药剂学研究在新药开发中的作用。
二、学习内容生物药剂学的定义与研究内容；剂型因素与生物因素的含义。
三、本章重点、难点生物药剂学的概念；剂型因素与生物因素的含义。
四、建议学习策略通读教材后观看视频,并复习相关药剂药理知识帮助理解.五、习题一、名词解释1、生物药剂学（Biopharmacutics）2、吸收(absorption)3、分布(distribution)4、代谢 (metabolism) 5、排泄 (excretion) 6、转运 (transport) 7、处置 (disposition) 8、消除 (elimination) 二、简答题1．简述生物药剂学研究中的剂型因素。
生物药剂学与药物动力学(生物制药专业)-已修订
生物制药专业《生物药剂学与药物动力学》课程教学大纲课程名称：生物药剂学与药物动力学课程代码：05101902 课程类型：限制性专业课总学时：54 学分：3实验（训）学时：12 自主学习学时：4考核方式：分散一、课程教学目标生物药剂学是生物制药专业的一门主要专业课程。
它是研究药物及其剂型在体内的吸收、分布、代谢、排泄过程，阐明药物的剂型因素，机体生物因素和药物疗效间相互关系，并应用动力学原理与数学处理方法，定量描述药物在体内动态变化规律的学科。
它的基本目的是：对体内过程进行定量描述，正确评价药剂质量，设计合理剂型、处方及生产工艺，为临床合理用药提供科学依据，使药物发挥最佳治疗作用。
通过本课程的教与学，力求使理论与实际相结合，不仅培养学生具有生物药剂与药物动力学的基本理论、基本知识和基本技能，而且培养学生独立分析和解决问题的能力及严谨的科学作风。
为从事药学及临床药学工作，保证药品质量，合理用药，充分发挥药效，降低毒副反应，以及研究探讨新剂型和新制剂，更好地为卫生保健事业服务打下良好的基础。
二、教学内容与学时分配第一章绪论[目的要求]1.掌握生物药剂学的定义与研究内容；2.掌握剂型因素与生物因素的含义；3.熟悉药物的体内过程；4.了解生物药剂学研究在新药开发中的作用。
[教学内容]1.生物药剂学的定义；2.药物的体内过程；3.生物药剂学研究内容；4.生物药剂学的发展；5.生物药剂学与相关学科的关系。
[教学方法] 课堂讲授法[讲课时数] 3学时第二章口服药物的吸收[目的要求]1.了解生物膜的结构2.掌握药物通过生物膜的转运机制3.熟悉胃肠道的结构、功能4.掌握影响药物消化道吸收的生理因素、药物因素和剂型因素5.熟悉口服药物制剂作用快慢的主要原因[教学内容]1.药物的膜转运与胃肠道吸收2.影响药物吸收的生理因素3.影响药物吸收的物理化学因素4.剂型因素对药物吸收的影响5.口服药物吸收与制剂吸收与制剂设计[教学方法] 讲授法，实验[讲课时数] 15学时，课堂讲授学时9，实验学时6。
药代动力学离线作业
浙江大学远程教育学院《药代动力学》课程作业（必做）姓名：学号：年级：学习中心：—————————————————————————————第一章生物药剂学概述一、名词解释1．生物药剂学；2．剂型因素；3．生物因素；4．药物及剂型的体内过程二、问答题1．生物药剂学的研究工作主要涉及哪些内容？2．简述生物药剂学研究对于新药开发的作用。
第二章口服药物的吸收一、名词解释1．细胞通道转运；2．被动转运；3．溶出速率；4．载体媒介转运；5．促进扩散；6．ATP驱动泵；7．多药耐药；8．生物药剂学分类系统；9．药物外排转运器；10.多晶型二、问答题1．简述促进扩散的特点，并与被动转运比较两者的异同。
2．简述主动转运的分类及特点。
3．简述生物药剂学中讨论的生理因素对药物吸收的影响。
4．已知某药物普通口服固体剂型生物利用度只有5%，与食物同服生物利用度可提高近一倍。
试分析影响该药物口服生物利用度的因素可能有哪些，拟采用哪些方法改善之。
5.药物的溶出速率对吸收有何意义？影响其溶出速率的因素有哪些？6．影响Ⅱ型药物口服吸收的理化因素有哪些？如何改善该类药物的口服生物利用度？第三章非口服药物的吸收一、填空题1．药物经肌内注射有吸收过程，一般____药物通过毛细血管壁直接扩散，水溶性药物中分子量______的可以穿过毛细血管内皮细胞膜上的孔隙快速扩散进入毛细血管，分子量____的药物主要通过淋巴系统吸收。
2．体外评价药物经皮吸收速率可采用______或______扩散池。
3．为达到理想的肺部沉积效率，应控制药物粒子的大小，其空气动力学粒径范围一般为______.4．蛋白多肽药物经黏膜给药的部位主要包括______、______、______等。
5．影响离子导入的因素有______、______等。
6．药物溶液滴入结膜内主要通过______、______途径吸收。
二、问答题1．采用什么给药途径可避免肝首过效应？试结合各给药途径的生理学特点说明其避免首过效应的原理。
专业基础课-《生物药剂学与药代动力学》课程教学大纲
《生物药剂学与药代动力学》课程教学大纲适用对象：药学专业学生（学分：2 ；学时： 36小时）一、课程的性质和任务：《生物药剂学与药物动力学》是研究药物及其制剂在生物体内的动态过程并应用数学分析手段来处理的一门课程。
主要内容包括药物在生物体内吸收、分布、代谢和排泄过程及其影响因素。
采用隔室模型、非线性动力学或统计矩分析药物体内过程，并将药物动力学参数应用于新药研发。
生物药剂学和药物动力学。
二者既相互独立又相互联系，生物药剂学是解析药物体内过程的机制的学科，而药物动力学是定量描述药物体内过程的学科。
本课程要求学生掌握影响药物体内吸收、分布、代谢和排泄四个过程的生理因素和剂型因素。
计算药物动力学参数的方法。
熟悉生物药剂学原理在制剂设计尤其是缓控释制剂中的应用。
了解药物的生物利用度和药物动力学在临床药学和新药研发中的应用。
教材选用刘建平主编《生物药剂学与药物动力学》（第5版），人民卫生出版社2016年出版。
二、教学内容和要求（含每章教学目的、基本教学内容和教学要求）：三、课程的重点和难点：1、各种药代动力学模型的定义,使用,和参数的计算。
2、不同的剂量和给药方案计算。
四、参考性教学时间安排：五、实践（实验）教学环节（含实验项目、实践内容）：六、教材和主要参考书：《Basic Pharmacokinetics》，Michael C. Makoid, Phillip J. Vuchetich，Umesh V. Banakar. The Virtual University Press刘建平.《生物药剂学与药物动力学》第5版。
北京：人民卫生出版社，2016七、其他说明：注：1、表格不够可自行添加。
2、范文可参见教务处主页上教学大纲一栏中土木系教学大纲。
多室模型-药代动力学
005 Nhomakorabea10
15
t
根据图初步判断此药不是单室模型（因其不成 直线），故可能是二室或三室模型。
二、用残差平方和与加权残差平方和判断
n
残差平方和： SUM (Ci Cˆi )2 i 1 n
权重残差平方和： Re Wi (Ci Cˆi )2 i 1
Ci ：实测血药浓度值； Ci’：按某一模型计算出来的理论血药浓度值； Wi：权重系数，通常取实测值平方的倒数，如果 数据在高浓度的准确性比低浓度大，则Wi=1，Re 也就可以用SUM计算。
CL V
式中Vβ为二室模型总表观分布容积。而我们讨 论的模型只从中央室消除，所以总体清除率的 公式可以写成：
CL V k10Vc
又因为
k10
k21
A B
A B A B
AB
又因为
AUC A B
所以
CL k10 Vc
A B A B
X0 A B
▪ 以lgCr→t作图亦为一条直线即残数线,根据残数 线的斜率b2和截距a2分别可求出α和A以及分布相 的生物半衰期t1/2(α)。
b2 2.303
2.303b2
A lg 1 a2
t1/ 2( )
0.693
注意
此药物属几室模型？
一、作图判断 二、 用残差平方和与加权残差平方和判断 三、 用拟合度（r2）进行判断 四、 AIC 法 五、 F 检验
一、作图判断
lgC
lgC
lgC
8
6
4
2
将此直线外推至与纵轴相交，得截距（lgB）， 即可求出B。
lg B a1
B lg 1 a1
15
t
根据图初步判断此药不是单室模型（因其不成 直线），故可能是二室或三室模型。
二、用残差平方和与加权残差平方和判断
n
残差平方和： SUM (Ci Cˆi )2 i 1 n
权重残差平方和： Re Wi (Ci Cˆi )2 i 1
Ci ：实测血药浓度值； Ci’：按某一模型计算出来的理论血药浓度值； Wi：权重系数，通常取实测值平方的倒数，如果 数据在高浓度的准确性比低浓度大，则Wi=1，Re 也就可以用SUM计算。
CL V
式中Vβ为二室模型总表观分布容积。而我们讨 论的模型只从中央室消除，所以总体清除率的 公式可以写成：
CL V k10Vc
又因为
k10
k21
A B
A B A B
AB
又因为
AUC A B
所以
CL k10 Vc
A B A B
X0 A B
▪ 以lgCr→t作图亦为一条直线即残数线,根据残数 线的斜率b2和截距a2分别可求出α和A以及分布相 的生物半衰期t1/2(α)。
b2 2.303
2.303b2
A lg 1 a2
t1/ 2( )
0.693
注意
此药物属几室模型？
一、作图判断 二、 用残差平方和与加权残差平方和判断 三、 用拟合度（r2）进行判断 四、 AIC 法 五、 F 检验
一、作图判断
lgC
lgC
lgC
8
6
4
2
将此直线外推至与纵轴相交，得截距（lgB）， 即可求出B。
lg B a1
B lg 1 a1
第九章 二室模型
A、B、α、β、t1/2(α)、 t1/2(β)、Vc、k21、k10、k12、AUC、 CL.
第二节 静脉滴注
模型的建立
k0
Central compartment
k21
k10
k12
Peripheral compartment
k0
K12 XC K 21 K10
XP
dXc k k21 Xp k12 Xc k10 Xc 0 dt
第一节 静脉注射
模型的建立
Dose k21
Central compartment
k12
Peripheral compartment
k10
K10 药物从中央室消除的一级速度常数 K12 药物从中央室向周边室转运的一级速度常数
模型参数
K21 药物从周边室向中央室转运的一级速度常数
X0
XC
K10
dXc dt
第三节
模型的建立
血管外给药
X0
The site of absorption
ka
Central compartment
k21
k12
Peripheral compartment
k10
dXa kaXa dt
dXc kaXa (k12 k10 ) Xc k21 Xp dt
dXp k12 Xc k21 Xp dt
2.模型参数 （1）k12、k21、k10
L (ka ) M (ka ) k21 L ka M ka
k10
k21
k12 k21 k10
Vc
ka FX0 (k21－ ) L Vc ka
第九章 多室模型
第九章多室模型一．填空题1．双室模型静脉注射血药浓度与时间的关系可表示为（）。
2．双室模型静脉注射的混杂参数有（）。
3．双室模型血管外给药与静脉注射给药相比，药物进入中央室前后的主要区别是（1）（2）。
4．双室模型血管外给药的体内过程可分为三个部分。
5．混杂参数与模型参数之间的关系为（）。
二．是非题1．α和β分别代表分布相和消除相的特征。
（）2．双室模型中k10、α、β、A、B等均称为混杂参数。
（）3．AIC值愈大，则该模型拟合愈好。
（）4．根据双室模型血管外给药血药浓度经时曲线可用残数法分解求出基本参数。
（）5．Loo-Riegelman法是求双室模型的吸收速度常数的经典方法。
（）三．计算题1.静脉注射氨吡酮后由血药浓度数据获得该药的药动学方程如下：C = 4.62 e-8.94t + 0.64-0.19t (C单位为μg/ml，t单位为h)求：V C，k12，k21，k10，t1/2(β)及静脉注射后3小时的血药浓度。
2. 静脉注射100 mg某药后, 测得血药浓度数据如下:求: α, β, A, B, k12，k21，k10，t1/2(β), CL, V, AUC。
3．已知茶碱的α = 6.36 h-1, β= 0.157 h-1，k10 = 0.46 h-1，k21= 2.16 h-1，V C = 0.1421 L /kg。
某60 kg体重受试者以656mg/(kg·h)速度静脉滴注, 计算滴注10h的血药浓度。
4．口服某双室模型药物500mg，设F=1，测得不同时间的血药浓度如下：t (h) 0.5 1.0 1.5 2.0 2.5 3.0 4.0 5.0 7.0 9.0 11.0 13.0 C(μg/ml) 3.71 4.93 5.5 5.7 5.6 5.33 4.8 4.1 3.1 2.2 1.8 1.4 试求该药的β，M，α，L，k a，N等基本参数5．已知某药物按单室模型处理，R e1 = 0.00402，自由度df1 = 5；按双室模型处理，R e2 = 0.000477, df2 = 3。
《生物药剂学与药物动力学》教学大纲设计(2011.7.18)
《生物药剂学与药物动力学》教学大纲【概要】课程名称：生物药剂学与药物动力学英文名称：bioparmaceutics and pharmacokinetics课程性质：专业课面向专业：药学本科、药物制剂本科、药学（营销方向）本科选用教材：《生物药剂学与药物动力学》(第四版),刘建平主编出版单位：人民卫生出版社总学时：72学时（理论课40学时，实验课32学时）【前言】生物药剂学与药物动力学是药学专业的一门专业课程。
药物动力学（Pharmacokinetics）是应用动力学原理与数学处理方法，定量描述药物在体内动态变化规律的学科。
药物通过各种途径进人体内，其吸收、分布、代谢和排泄，即ADME过程均存在“量时”变化或“血药浓度经时”变化，对这一动态变化过程规律进行定量描述即为药物动力学的基本任务。
生物药剂学（Biopharmaceutics；Biopharmacy）是研究药物的剂型因素、生物因素与药效（包括疗效、副作用和毒性）关系的一门科学。
主要研究药物在体内的量变规律及影响这种量变规律的因素。
为剂型设计、制备工艺与临床合理用药提供依据，以保证临床用药的高效性和安全性。
生物药剂学在保证药品质量、新药开发和临床合理用药等方面具有重要作用。
本大纲通过对药学本科生课程教学的基本要求，通过本课程的教学、实验等方式进行教学。
根据生物药剂学与药物动力学课程的特点，贯彻理论与实践相结合的原则，使学生具有生物药剂学与药物动力学的基本理论、基本知识和技术，培养基础知识踏实、专业知识雄厚技术能力精湛的全面发展的高质量药学人才。
为从事新药研究开发、合理制药、保证安全用药等工作，更好地为卫生保健事业服务打下良好的基础。
通过本课程的教与学，力求使理论与实际相结合，不仅培养学生具有生物药剂学与药物动力学的基本理论、基本知识和技术，而且培养学生独立分析问题和解决问题的能力和严谨的科学作风，为从事新药研究开发、合理制药、保证安全用药等工作，更好地为卫生保健事业服务打下良好的基础。
第九章 双室模型-3血管外给药
i 1
0.2428<0.4196 故属二室模型
3.
2 用1
r
(拟合度)作进一步判断
ˆ C12 (Ci Ci ) 2
i 1 n n
r12
C12
i 1
i 1 n
2 二室模型处理得到 r 0.998554 2 而按三室模型处理得到 r 0.997501
因为 0.998554>0.997501 故系二室模型.2 与 3 判断结果是一致的。
中国药理学会数学专业委员会受国家卫生部 药品审评办公室的委托组织了五个单位六位 专家集体编制的,在国内应用很广。
药代动力学和生物药剂学程序包PKBP-N 4. PKBP-N1由南京军区总医院于1985年编制
第三节、血管外给药
如图所示地高辛 地高辛
吸收相
分布相
静脉注射
分布相
消除相
消除相
1.
在分布达到平衡之前（在多数病人，该
药分布平衡时间保守估计为6h），其血药 浓度与作用之间并不存在合理的相关性。 2. 效应随着心脏内浓度的增加而增加，即
使此时血药浓度正在下降，这就使得对血
药浓度作出解释极其困难。
第三节 房室模型的划分
举例介绍五种判断方法： 例： 某药静脉注射血药浓度与时间的数据如下：
(hr)
T 0.033 0.25 0.5 1.0 1.5 2 3 4 6 12 C 7.10 5.80 5.40 4.00 3.40 2.95 2.75 2.2 1.9 1.56
(ug/ቤተ መጻሕፍቲ ባይዱl )
此药物属几室模型。
一、模型
t=0时，Xa=FX0 Xc=0 X =0
二、血药浓度公式(9-42、43、44）
0.2428<0.4196 故属二室模型
3.
2 用1
r
(拟合度)作进一步判断
ˆ C12 (Ci Ci ) 2
i 1 n n
r12
C12
i 1
i 1 n
2 二室模型处理得到 r 0.998554 2 而按三室模型处理得到 r 0.997501
因为 0.998554>0.997501 故系二室模型.2 与 3 判断结果是一致的。
中国药理学会数学专业委员会受国家卫生部 药品审评办公室的委托组织了五个单位六位 专家集体编制的,在国内应用很广。
药代动力学和生物药剂学程序包PKBP-N 4. PKBP-N1由南京军区总医院于1985年编制
第三节、血管外给药
如图所示地高辛 地高辛
吸收相
分布相
静脉注射
分布相
消除相
消除相
1.
在分布达到平衡之前（在多数病人，该
药分布平衡时间保守估计为6h），其血药 浓度与作用之间并不存在合理的相关性。 2. 效应随着心脏内浓度的增加而增加，即
使此时血药浓度正在下降，这就使得对血
药浓度作出解释极其困难。
第三节 房室模型的划分
举例介绍五种判断方法： 例： 某药静脉注射血药浓度与时间的数据如下：
(hr)
T 0.033 0.25 0.5 1.0 1.5 2 3 4 6 12 C 7.10 5.80 5.40 4.00 3.40 2.95 2.75 2.2 1.9 1.56
(ug/ቤተ መጻሕፍቲ ባይዱl )
此药物属几室模型。
一、模型
t=0时，Xa=FX0 Xc=0 X =0
二、血药浓度公式(9-42、43、44）
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第九章多室模型用单室模型模拟体内过程，处理方法虽简单，但应用上有局限。
既然把整个机体看作一个隔室，严格来说，进入体内的药物就必须迅速完成向可分布组织、器官与体液的分布，使药物在血浆与这些组织器官、体液间立即达到动态平衡的分布状态。
实际上，由于体内各部分的血流速度不同，达到动态平衡是需要一定时间的。
也就是说，绝对符合单室模型的药物是不存在的，只是为了简化数学处理，将分布速度相差不大的组织或体液合并成了一个隔室。
对某些药物而言，其达到分布动态平衡的时间较短，以至可以忽略不计，这类药物可用单室模型近似处理分析它的体内过程。
也有不少的药物，体内各部位分布速度差异比较显著，分布速度较快的组织、器官和体液连同血浆构成一个隔室属于，称为“中央室”，分布速度较慢的组织、器官和体液等部分，称为“周边室”（外周室），从而构成“双室模型”。
一般而言，血流丰富的组织器官如心、肝、脾、肺、肾等归属于“中央室”，而血流贫乏的如肌肉、骨骼、皮下脂肪等“周边室”。
由于肝肾这两个主要的消除器官都归属于“中央室”，多室模型药物的消除仅发生在中央室。
有些药物还需要用三室或更多的模型来表征，它们都是由一个“中央室”和若干个“周边室”组成。
理论上，药物动力学可以建立任何多室模型，但从实用角度看，四室以上的模型很少见。
同一药物随着实验条件和处理方法的不同，可分成不同的隔室。
分得合理与否，主要看它是否于实际情况相符，也要考虑数据处理是否简单易行。
第一节二室模型静脉注射一、模型建立静注后，药物首先进入中央室，再逐渐向周边室转运，在中央室按一级过程消除，可用下面的模型图表示：X 0为给药剂量；Xc为中央室药量；Xp为周边室药量；k12为药物从中央室向周边室转运的一级速度常数；k21为药物从中央室向周边室转运的一级速度常数；k10X0X p k12k21为药物从中央室消除的一级速度常数。
若药物的转运均服从一级速度过程，即药物的转运速度与该室的药物量成正比，则可用下列微分方程组来描述其转运速度：二、血药浓度与时间的关系上述微分方程采用拉氏变换可求得：式中α称为分布速度常数或快配置速度常数；β称为消除速度常数或慢配置速度常数。
它们分别代表两个指数项即分布相和消除相的特征，由模型参数k 12、k 21、k 10构成，α和β又称为混杂参数，由下式计算：α和β和模型参数间有如下关系：∵ Xc ＝V c ·C设p c pc c p cX k X k dtdX X k X k X k dt dX 2112101221-=--=)()()(120210210t t p tt c e e kX X ek X e k X X αββαβαβαββαα------=--+--=24)()(24)()(1021210211210211210212102112102112k k k k k k k k k k k k k k k k -++-++=-+++++=βα1021102112k k k k k =++=+αββαtc t c eV k X e V k X C βαβαββαα----+--=)()()()(210210c c V k X B V k X A βαββαα--=--=)()()()(210210三、参数的计算 1、基本参数的估算要掌握药物的变化规律，首先应了解中央室内药物的量变关系，由C －t 关系式可知，只要确定了A 、B 、α和β这四个基本参数，就可以确定药物在中央室的转运规律。
根据 ，以lnC －t 可以得到一条二项指数曲线，用残数法进行分析就可求出有关的参数，即A 、B 、α和β。
∵ α >>β，当t 充分大时，趋于零，两边去对数，得就是说末端数据以lnC －t 回归得一直线， 即直线a ，其斜率为－β，外推线与纵轴的交 点得截距为lnB 。
据β可求出消除相的生物半衰期为：对 整理，得式中C 为实测浓度， 为外推浓度， 为残数浓度，用C r 表示，以lnC r －t 回归，得到残数线（直线a ），其斜率为－α，截距为lnA ，分布相的半衰期为：这样我们就把A 、B 、α和β这四个基本参数都求出来了，需要注意的是，在分布相时间内，若取样太迟太少，可能会看不到分布相而把双室模型当成单室模型处理，这在实验设计时必须慎重考虑，以避之。
2、模型参数的求算t t Be Ae C βα--+=t Ae α-tBe C β-=Bt C ln ln +-=βtl n Cbaββ693.0)(2/1=t t t Be Ae C βα--+=tt Ae Be C αβ--=-t Be β-)(t Be C β--αα693.0)(2/1=t当时间t ＝0时，e －αt ＝1，e －βt ＝1，C=C 0 C 0=A+B∵ C 0＝X 0/V c ∴ 把上式变形得，并代入 可以得到：将上式分别代入可得到：模型参数V c 、k 12、k 21、k 10求出后，该药物在体内的药物动力学特征基本就被我们掌握了。
下面我们就通过p209的例题，看一下具体的求解过程。
第二节 二室模型静脉滴注一、模型建立静注时，药物在瞬间全部进入中央室。
而静滴时药物是以恒速逐渐进入中央室的，其模型图可表示为：它与静注给药的不同就是，在给药时间T 内，药物以恒速k 0＝X 0/T 进入中央室，而不是瞬间全部进入。
可用下列微分方程组来描述其转运速度：BA X V c +=0cV X B A 0=+)()(210βαβ--=c V k X B BA B A k ++=αβ211021121021k k k k k ++=+=βααβ1021122110k k k k k --+==βααβk 0X pk 12 k 21k 10p c pc c p cX k X k dtdX X k X k X k k dt dX 21121012210-=--+=二、血药浓度与时间的关系上述微分方程采用拉氏变换可求得：这就是中央室药物经时变化过程的公式，静滴进行时，T ＝t ，当滴注停止后，T 成为常数，就是滴注时间。
1、滴注期间的C －t 过程静滴进行时，T ＝t ，上式写成：将该式展开并通分整理可得：此式反映了滴注开始后血药浓度随时间的推移而逐渐增高，接近于一个恒定的水平即稳态血药浓度。
这与单室模型药物是一样的。
当t →∞时，e －αt 和e －βt 趋于零，上式变成：这就是双室模型药物静滴给药的稳态血药浓度求算公式。
机体总表观分布容积V β与中央室表观分布容积V c 有如下关系：V β·β＝V c k 10 ∴该式重排得：tT t T c ee k K e e k k X ββααβαβββααα-----+---=)(1)(()()1)((210210tc T t c T eV e k K e V e k k C ββααβαβββααα-----+---=)()1)(()()1)((210210)1()()()1()()(210210t c tc e V k K e V k k C βαβαβββααα-----+---=)1(1010100t t c e K e k k V k C βαβααβαβ--------=10k V k C c ss =ββV k C ss 0=ββββss ss C k V V C k 00==2、滴注停止后的C －t 过程滴注停止时，T 就变成定值。
如t ′表示滴注结束时起算的时间，t ＝t ′+T 代入C-t 关系式则有： 设：式中R 、S 与静注时的零时间截距A 和B 的关系为：第三节 二室模型血管外给药一、模型建立血管外给药时，药物要通过胃肠道或肌肉吸收后，才能进入中央室，其模型图为：X 0为给药剂量；F 为吸收率；X a 为吸收部位的药量；其它符号的意义与静注相同。
体内过程为一级动力学过程时，可用下列微分方程组来描述其转运速度：'210'210)()1)(()()1)((t c t t c T eV e k K e V e k k C ββααβαβββααα-------+---=)()1)((210βαααα---=-c T V e k k R )()1)((210βαβββ---=-c t V e k K S ''Re t t Se C βα--+=S e TB Re TA TT)1()1(βαβα---=-=X pk 12k 21X p c pc c p a a ca a aX k X k dtdX X k X k X k X k dt dX X k dt dX 2112101221-=--+=-=二、血药浓度与时间的关系上述微分方程采用拉氏变换可求得：上式两边同除以V c 得：令这就是双室模型药物血管外给药后，中央室药物浓度随时间变化的关系式，其C －t 曲线如图：从图中可看出，药物浓度先升后降，最后平衡的减少，可将曲线分为三部分：a ：吸收相 药物浓度持续上升，此时药物吸收为主要过程；b ：分布相 药物浓度下降，此时药物分布为主要过程；c ：消除相 药物浓度逐渐衰减，体内过程主要是消除。
ta a t a a t k a a a a c ek k FX k e k k FX k e k k k k FX k X a βαβαββαβααβα------+---+---=))(()())(()())(()(210210210ta c a t a c a t k a a c a a e k V k FX k e k V k FX k e k k V k k FX k C a βαβαββαβααβα------+---+---=))(()())(()())(()(210210210))(()())(()())(()(210210210βαββαβααβα---=---=---=a c a a c a a a c a a k V k FX k M k V k FX k L k k V k k FX k N tt t k Me Le Ne C a βα---++=Ctabc三、基本参数的估算C －t 关系式是一个三项指数函数的曲线，可以残数法求出参数。
∵ k a >>β，α >>β，当t 充分大时，e -kat 和e -αt 均趋于零，C －t 关系式可简化为：该式代表C －t 曲线的尾端，就是说通过尾端直线求出参数M 和β。
上式取对数得：尾端数据，以lnC －t 回归得一直线，由其斜率可求出β，截距可求出M 。
我们将 变形得， 令 故C r1的含义就是实测的血药浓度值减去尾端直线外推线上相应的浓度值即残数浓度值，连起来可得到一条残数线，上述关系式就是其方程。