柱面坐标系下的三重积分计算
- 格式：pdf
- 大小：1.09 MB
- 文档页数：8
下载文档原格式
合集下载
三重积分在柱面及球坐标系下的计算
= ∫ dθ ∫
0
2π
R
0
1 2 1 4 2 ( R − ρ ) ρdρ = πR . 2 4
思考： 思考：是否可考虑用切片法来求解？
例2 计算三重积分I = ∫∫∫ ( x + y )dv,
2 2 (V )
z
其中(V )由z = x 2 + y 2 , z = h所围.
解 (V )在xoy面投影域(σ )为圆 : 0 ≤ ρ ≤ h , xy
π
4
θ
y
,0 ≤ ρ ≤ R.
x
∴ I = ∫ dθ
0
2π
∫
π /4
0
dϕ
∫
R
0
ρ 2 ⋅ ρ 2sinϕ dρ
2− 2 5 = πR . 5
练习 试用三种坐标系分别计算三重积分
z
2
σz
I = ∫∫∫ zdv, 其中(V ) : x 2 + y 2 + z 2 ≤ 2 z.
(V )
解法1 解法 直角坐标系(切片法)
1
= 2π ∫ ρ ⋅ 2 1 − ρ 2 dρ
1
4π = . 3
0
解法3 解法 球面坐标系计算
∫∫∫ zdv
(V )
z
2
x2 + y2 + z2 = 2z
球面为 : ρ = 2 cos ϕ , 其中
0 ≤ θ ≤ 2π ,0 ≤ ϕ ≤
ϕ
o
π
2
,0 ≤ ρ ≤ 2 cos ϕ .
θ
ρ cos ϕ ⋅ ρ 2 sin ϕdρ
z
• •
其中(V )由z = R 2 − x 2 − y 2 与 z = 0所围.
柱面坐标系和球面坐标系求三重积分
z x2 y2所围 .
分析 (V )为由半球面与锥面所围,
故可用球面坐标,
y
此 ,0 时 2 ,0 ,0R . x
4
2
I d
/4
d
R22sind
0
0
0
2 2 R5.
5
练习 试用三种坐标系算 分三 别重 计积分
I zdv,其中(V): x2 y2 z2 2z. (V)
解法1 直角坐标(切 系片法 )
x
则 (V )f(c o,s si,n z)d d dz ,
]d d
[ z2(,)f(co ,ssin,z)dz
( ) z1(,)
例1 计算三重积I分 (Vz)dv,
其中(V)由z R2 x2 y2与 z 0所围.
解 (V )向 xo 面 y 投 (x)y 为 影 :0 圆 R , 02 x
I d d
zdz
0
0 1 1 2
x
2012 12d
4 . 3
•1
xy
解法3 球面坐标系计算zdv (V) x2y2z22z
z
2
球面 : 为 2co,s其中
02 ,0,02co .s
2
o
y
I 2d /2d 2coscos2sxind
0
0
0
2/24co5ssind 4 .
0
3
z
h•
此,时 2zh.
I [ h 2dz ]dd ( xy ) 2
•
o•
x
y
( xy )
2d h(3h5)d
0
0
1 h3.
6
思考：本题是否也可考虑用切片法来求解？
4-2-2 球面坐标系下三重积分的计算
在柱面坐标系下三重积分计算的一种新方法
柱面坐标(如图1所示)。
图1柱面坐标系
一般假定r,θ,z的变化范围分别为:
柱面坐标系中的三个坐标面分别
投影法
图2点M在圆柱面r=r0上的投影点M'示意图
,
空间立体Ω(r,θ,z)
点并且和z轴垂直的
图3及图4所示),从而空间区域表示
此时,区域Ω的边界面上有两个曲面r=r
和图4所示的两种情形。
图3区域Ω的边界面(情形1)
图4区域Ω的边界面(情形2)
空间立体Ω的质量可以看作密度不均匀的片D(θ,z)的质量,求出面密度ρ(θ,z)后就
. All Rights Reserved.
),从而
这样,将柱面坐标下的三重积分转
积分:
进一步,可将外层的二重积分转化
投影区域D(θ,z)的形式为,
则
从而,把三重积分转化为先对r,再对z,最后对积分。
如果投影区域D(θ,z)的形式为
则
从而,把三重积分转化为先对r,再对θ,
则三重积分可转化为:
或者:
综上所述,柱面坐标下三重积分为一句口诀,即“一投二交三积分在上面的讨论中,假定了从z轴
. All Rights Reserved.。
柱面坐标和球面坐标计算定积分
一、利用柱面坐标计算三重积分
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
设 M ( x, y, z) 为空间内一点，并设点M 在
xoy 面上的投影 P 的极坐标为r,，则这样的三 个数 r, , z 就叫点 M 的柱面坐标．
z
规定： 0 r ,
0 2,
z .
• M(x, y,z)
or
•
y
P(r, )
x
如图，三坐标面分别为
r 为常数
三个有次序的数r，， 来确定，其中r 为原 点 O 与点 M 间的距离， 为有向线段 OM与 z 轴正向所夹的角， 为从正 z 轴来看自 x 轴按
逆时针方向转到有向线段 OP 的角，这里 P 为
点 M 在 xoy 面上的投影，这样的三个数 r，， 就叫做点 M 的球面坐标．
规定： 0 r , 0 , 0 2.
y
r
sin
sin
,
z r cos .
如图，
z
球面坐标系中的体积元素为
dv r2 sindrdd ,
f ( x, y, z)dxdydz
dr
d r sin
r
o
d
x
r sind rd
d
y
f (r sin cos ,r sin sin ,r cos )r2 sindrdd .
例 3 计算 I ( x2 y2 )dxdydz，其中 是锥面
1 8
I1 rdrd r2 fdz
D1
2
2
d
0
2
4
dr
0
8
r2
r
r
2dz
2
45 3
,
2
I2 rdrd r2 fdz
D2
2
利用柱面坐标计算三重积分
`z
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
z
j r
zdv
dvΒιβλιοθήκη zdvO
dv
a 2 0 2
．
q
x
a y
dv 2 dj dq
2
0
0
2a 3 , r sin jdr 3
a
1 a4 , zdv 2 dj dq r cos j r 2 sin jdr 2 0 0 0 2 4 3a 3a 因此`z ．重心为(0，0， )． 8 8
§9．5 利用柱面坐标和球面坐标计算三重积分
一、利用柱面坐标计算三重积分
柱面坐标、 柱面坐标系的坐标面 直角坐标与柱面坐标的关系、柱面坐标系中的体积元素
柱面坐标系中的三重积分
二、利用球面坐标计算三重积分
球面坐标、球面坐标系的坐标面 直角坐标与球面坐标的关系、球面坐标系中的体积元素 球面坐标系中的三重积分
，r sin q ，z) rdrdqdz．
例1 例1 利用柱面坐标计算三重积分 zdxdydz，其中是由曲
面 zx2y2 与平面 z4 所围成的闭区域．
z 4 zx2y2 或 zr2
解 闭区域可表示为：
r 2z4，0r2，0q2． 于是
zdxdydz zrdrdqdz
2 r sin jdrdjdq dq sin j dj r 4 dr a 2 M , 0 0 0 5
4 3
2
3
a
4 3 其中 M a 为球体的质量． 3
一、利用柱面坐标计算三重积分
设M(x, y, z)为空间内一点，则点M与数 r、q 、z相对应， 其中P(r, q )为点M在xOy面上的投影的极坐标． 三个数 r、q 、z 叫做点M 的柱面坐标． z 这里规定r、q 、z的变化范围为： 0 r<， 0 q 2 ， < z<． O x r y P(r, q ) y z
圆柱坐标系三重积分公式
圆柱坐标系三重积分公式引言三重积分是数学中的一个重要概念，用于求解空间区域内的体积、质量等物理量。
在坐标系中，我们通常使用直角坐标系，也就是以直角为基础的三维坐标系。
然而，在某些情况下，直角坐标系并不是最为方便的选择，而更适合使用圆柱坐标系。
圆柱坐标系是三维空间中的一种常见坐标系，它以柱面的极坐标和高度作为三个坐标轴。
在圆柱坐标系中，三重积分的计算也有相应的公式。
本文将介绍圆柱坐标系下的三重积分公式，以帮助读者更好地理解和应用这一概念。
圆柱坐标系简介圆柱坐标系是由径向、极角和高度三个坐标轴组成的。
其中，径向表示从原点到点的距离，极角表示点在柱面上的位置，高度表示点在垂直于柱面的直线上的位置。
在圆柱坐标系中，点的位置可以用一个三元组 $(r, \\theta, z)$ 来表示，其中r是径向的长度，$\\theta$ 是极角的度数，z是高度。
这种坐标系在某些问题中更方便，特别是具有柱对称性的问题。
圆柱坐标系三重积分公式的推导在圆柱坐标系中，我们需要推导出三重积分的微元体积和积分限的变化关系，以得到三重积分的公式。
首先，考虑微元体积dV，它可以表示为一个微小圆柱体的体积。
微小圆柱体的底面积可以表示为 $dA = r \\, dr \\, d\\theta$，高度为dz，因此微元体积为 $dV = dA \\, dz = r \\, dr \\, d\\theta \\, dz$。
接下来，考虑积分限的变化关系。
在圆柱坐标系中，积分变量的范围可以表示为 $r_1 \\leq r \\leq r_2$，$0 \\leq \\theta \\leq 2\\pi$，$z_1 \\leq z \\leq z_2$，其中r1和r2是径向的最小值和最大值，z1和z2是高度的最小值和最大值。
最后，将微元体积和积分限的变化关系代入三重积分的定义中，即可得到圆柱坐标系下的三重积分公式：$$ \\iiint_V f(r, \\theta, z) \\, dV = \\int_{z_1}^{z_2} \\int_{0}^{2\\pi}\\int_{r_1}^{r_2} f(r, \\theta, z) \\, r \\, dr \\, d\\theta \\, dz $$其中，$f(r, \\theta, z)$ 是被积函数，V是空间区域。
三重积分 柱坐标与极坐标
则二重积分应当考虑用极坐标计算.
这就等于用柱面坐标计算三重积分.
2. 利用柱坐标计算三重积分
设 M (x, y, z) R3,将x, y用极坐标, 代替, 则（, , z)
就称为点M 的柱坐标. 直角坐标与柱面坐标的关系:
x cos y sin
zz
坐标面分别为
例5. 计算三重积分
其中
与球面
所围立体.
解: 在球面坐标系下
0rR
z rR
:
0
π 4
0 2π
π 4
( x2 y2 z2 )dxdydz
2π
d
π
4 sin d
Rr4 dr
Oy x
0
0
0
1 π R5(2 2)
d v r2 sin drd d
圆锥面
球面 r+d r
半径为r及r + dr的球面；
圆锥面及+d rsind
r
圆锥面 + d
0
d
y
x
球面坐标下的体积元素
z
元素区域由六个坐标面围成：
半平面 及+d ；
半径为r及r+dr的球面；
rsind
圆锥面及 + d
d v r 2 sind rd d
常见曲面的柱面坐标方程
曲面 半球面
直角坐标方程 z a2 x2 y2
柱面坐标方程 z a2 r2
圆锥面 旋转抛物面
z x2 y2 z x2 y2
zr z r2
圆柱面 圆柱面 圆柱面
三重积分的几种计算方法
*
例5. 计算 zdxdydz,
其中 ={(x, y, z) | x2+y2+z2≤1, z≥0}.
解：x2+y2+z2=1 r=1
z
用 = 截 得 D()
而 0≤ ≤2 故
0
x
y
原积分
r cos r 2sindrdd
*
2
0 d
r 3cos sin drd
D ( )
z x 0
2
0 d
z
z=z2(x, y)
f (x, y, z)dxdydz
y
[ z2 (x,y) f (x, y, z)dz]dxdy
z=z1(x, y)
D z1 ( x, y)
D
y=y2(x)
0
a y=y1(x) b
x
设 D 为 在 xy 平面上投影区域.
dxdy z2 (x,y) f (x, y, z)dz
z
x2 y2
.
4
y 原积分
a
r 2 r 2 sin drdd *
2
0 d
r 4sindrd
D( )
z
y
a
x
2
0 d
r 4sindrd
D( )
2
0
d
4
0
sin d
0ar
4dr
z
1a5 (2 2)
r=a
5
4
例7. 计算 f (x, y, z)dxdydz,表为球坐标系中的三 次积分，其中 为x2+y2+(z1)2≤1.
0
y= OPsin = rsin sin
yy
z= r cos
例5. 计算 zdxdydz,
其中 ={(x, y, z) | x2+y2+z2≤1, z≥0}.
解：x2+y2+z2=1 r=1
z
用 = 截 得 D()
而 0≤ ≤2 故
0
x
y
原积分
r cos r 2sindrdd
*
2
0 d
r 3cos sin drd
D ( )
z x 0
2
0 d
z
z=z2(x, y)
f (x, y, z)dxdydz
y
[ z2 (x,y) f (x, y, z)dz]dxdy
z=z1(x, y)
D z1 ( x, y)
D
y=y2(x)
0
a y=y1(x) b
x
设 D 为 在 xy 平面上投影区域.
dxdy z2 (x,y) f (x, y, z)dz
z
x2 y2
.
4
y 原积分
a
r 2 r 2 sin drdd *
2
0 d
r 4sindrd
D( )
z
y
a
x
2
0 d
r 4sindrd
D( )
2
0
d
4
0
sin d
0ar
4dr
z
1a5 (2 2)
r=a
5
4
例7. 计算 f (x, y, z)dxdydz,表为球坐标系中的三 次积分，其中 为x2+y2+(z1)2≤1.
0
y= OPsin = rsin sin
yy
z= r cos
三重积分的计算(2)
o
x
y
小柱体的底： 其面积可取为平面极坐标 系中的面积元素rdrd
小柱体的高： dz， 于是柱坐标系中的体积元素为
dV rdrd dz
f ( x, y , z )dxdydz
V
f (r cos , r sin , z)rdrddz
V
rdrd
2、三重积分在柱坐标下的计算：
例2: 计算由x2 + y2=az (a>0), x2 + y2 =2ax 与z=0 所围成的立体的体积。
x2 + y2=az
z
分析：用二重积分计算 曲顶柱体的体积
y
o
z
x2 + y2 =2ax
V
D xy
x y dxdy a
2 2
x
x2 y2 z a y
用三重积分计算： V
dv
下面求柱面坐标系中的体积元素:
x r cos , y r sin , z z.
dV
求柱坐标系中体积元素dV 的表达式
用柱坐标系中的三组坐标面来分割闭区域V， 取一典型小块 如右图，是由半径为r及r+dr的圆柱面； 与xz平面夹角为及+d的半平面； 两个高为z及z+dz的平面； 所围成的小块 ——小柱体 z
计算曲面 解
( x2 y 2 z 2 )2 az3 ,(a 0) 所求体积V dV
V
所围成的立体的体积
在球面坐标系下曲面的方程为：
π 又由ρ 0,即a cos 0, 知 0 φ 2
3
a cos 则 V： a cos3 ( , , ) V , 0 θ 2π
17重积分—— 三重积分的变量代换
13
2
3
z4 4
2 1
5
2
z
• z Dz
o
y
x
: x2 y2 z2，1 z 2
y
Dz
o
zx
Dz : x2 y2 z2 16
z r cos
y
(2) e ydv
令
x
r
sin
2
y y
2 1
e ydv e ydv e ydv
a4
2 2
a
a
4
)
(
a
4
a4 )
o
zx
44 2
4
4 44
a4。
8
10
解法三 投影法
z
zdv
a2 x2 y2
dxdy
zdz
x2 y2
Dxy
x
1 2
(a2
2x2
2
y2
)dxdy
Dxy
再用极坐标变换
1
2
d
a
2 (a2 2r 2 )rdr
21
z
①球面坐标的变化范围
0 r ,
0 ,
M(r,,)
r • M(x,y,z)
0 2 ②三组坐标面
o
z
x
y
x
y
P(x,y,0)
r =常数，即以原点为心的球面。
=常数，即以原点为顶点、z轴为轴的圆锥面。
=常数，即过z轴的半平面。
22
2
3
z4 4
2 1
5
2
z
• z Dz
o
y
x
: x2 y2 z2，1 z 2
y
Dz
o
zx
Dz : x2 y2 z2 16
z r cos
y
(2) e ydv
令
x
r
sin
2
y y
2 1
e ydv e ydv e ydv
a4
2 2
a
a
4
)
(
a
4
a4 )
o
zx
44 2
4
4 44
a4。
8
10
解法三 投影法
z
zdv
a2 x2 y2
dxdy
zdz
x2 y2
Dxy
x
1 2
(a2
2x2
2
y2
)dxdy
Dxy
再用极坐标变换
1
2
d
a
2 (a2 2r 2 )rdr
21
z
①球面坐标的变化范围
0 r ,
0 ,
M(r,,)
r • M(x,y,z)
0 2 ②三组坐标面
o
z
x
y
x
y
P(x,y,0)
r =常数，即以原点为心的球面。
=常数，即以原点为顶点、z轴为轴的圆锥面。
=常数，即过z轴的半平面。
22
利用柱面坐标和球面坐标求积分
: r z a,
2 2
0 r a,
0 2 ,
2 a a
I ( x y )dxdydz d rdr r 2dz
0
0
r
5 a4 a5 3 2 r (a r )dr 2[a ] a . 0 4 5 10
_______________________；其值为__________.
二、计算下列三重积分: 2 2 1、 ( x 2 y 2 )dv ,其中 是由曲面4z 2 25( x y ) 及平面 z 5 所围成的闭区域.
2、 ( x 2 y 2 )dv ,其中 由不等
dxdydz ,
V d d
0 0
2
4
2a
0
r 2 sin dr
2
4 0
4 ( 2a )3 3 sin d ( 2 1)a . 3 3
补充：利用对称性化简三重积分计算
使用对称性时应注意： １、积分区域关于坐标面的对称性； ２、被积函数在积分区域上的关于三个坐标轴 的 奇偶性．
d d
0
2
4 0
a cos 0
r sin dr
4 3
2
4 0
1 a5 sin 3 ( 5 0)d 5 cos
5 a . 10
解2
采用柱面坐标
D : x2 y2 a2 ,
x2 y2 z2 z r ,
0 a x 2 y 2 z 2 A, z 0 所确定. x2 y2 z2 3、 ( 2 2 2 )dxdydz , a b c x2 y2 z2 其中 ( x , y , z ) 2 2 2 1 . a b c 2 2 三、求曲面 z 5 x 2 y 2 及 x y 4 z 所围成的立 体的体积. 2 x 2 y az 4a 2 将球体 x 2 y 2 z 2 4az 分 四、曲面 成两部分,试求两部分的体积之比. 五、求由曲面 z x 2 y 2 , x y a , x 0, y 0, z 0 所围成立体的重心(设密度 1 ).
2 2
0 r a,
0 2 ,
2 a a
I ( x y )dxdydz d rdr r 2dz
0
0
r
5 a4 a5 3 2 r (a r )dr 2[a ] a . 0 4 5 10
_______________________；其值为__________.
二、计算下列三重积分: 2 2 1、 ( x 2 y 2 )dv ,其中 是由曲面4z 2 25( x y ) 及平面 z 5 所围成的闭区域.
2、 ( x 2 y 2 )dv ,其中 由不等
dxdydz ,
V d d
0 0
2
4
2a
0
r 2 sin dr
2
4 0
4 ( 2a )3 3 sin d ( 2 1)a . 3 3
补充：利用对称性化简三重积分计算
使用对称性时应注意： １、积分区域关于坐标面的对称性； ２、被积函数在积分区域上的关于三个坐标轴 的 奇偶性．
d d
0
2
4 0
a cos 0
r sin dr
4 3
2
4 0
1 a5 sin 3 ( 5 0)d 5 cos
5 a . 10
解2
采用柱面坐标
D : x2 y2 a2 ,
x2 y2 z2 z r ,
0 a x 2 y 2 z 2 A, z 0 所确定. x2 y2 z2 3、 ( 2 2 2 )dxdydz , a b c x2 y2 z2 其中 ( x , y , z ) 2 2 2 1 . a b c 2 2 三、求曲面 z 5 x 2 y 2 及 x y 4 z 所围成的立 体的体积. 2 x 2 y az 4a 2 将球体 x 2 y 2 z 2 4az 分 四、曲面 成两部分,试求两部分的体积之比. 五、求由曲面 z x 2 y 2 , x y a , x 0, y 0, z 0 所围成立体的重心(设密度 1 ).
齐民友高数下册上课第10章05柱面坐标与求面坐标系中三重积分的计算(1)
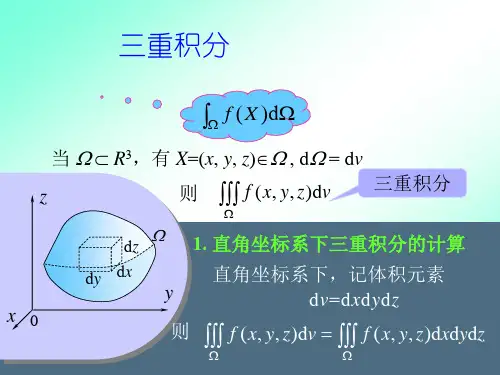
第5节 柱面坐标与球面坐标系下三重积分的计算5.1 利用柱面坐标计算三重积分我们不按课本上的讲法，换一种讲法。
用柱面坐标计算三重积分的步骤： （1）把三重积分写成二套一：将往xOy 平面投影得xy D，设的小z 边界1(,)zz x y 大z 边界2(,)zz x y ，则21(,)(,)(,,)d (,,)xyz x y z x y D f x y z vdxdyf xy z dz（2）用极坐标计算外层的二重积分： 设12(,)|()(),xyD则212211(,)(,)()(cos ,sin )()(cos ,sin )(,,)d (,,) (cos ,sin ,)xyz x y z x y D z z f x y z vdxdyf x y z dzd df zdz注意：用极坐标计算外层二重积分时，总是先对后对积分；用坐标关系cos x ，sin y 代入被积函数和里层定积分的上下限，z不动，并且外层面积元素多一个因子，即dxdyd d ，或说体积元素dxdydzd d dz ．当然，当投影区域xy D 的边界有圆弧或被积函数有22x y 时用柱面坐标计算简单。
离 散数 学【例5.1】 计算三重积分22()d xy v ，其中是由曲线220y z x绕z轴旋转一周而成的曲面与平面2z所围成的区域．解 旋转面的方程为：222x yz ．如图5.1所示，将积分区域投影到xOy 面，得投影区域为：22(,)|4xyD x y x y ．的小z 边界222x y z 大z 边界2z 。
积分区域为：222212(,,)|()2,4x y z x y zx y ，所以2222222222222100222220246()d () 1 d(2)d 211162()2123xy x y D xy vdxdy x y dz d ddz图5.1我们看到，上面计算方法中，用,,z 作坐标（变量）。
设空间有一点(,,)M x y z ．并设M 在xOy 面上的投影点P 的极坐标为,，则这样三个数,,z 就叫做点M 的柱面坐标．一般地,,z 的取值范围为： 0，02，z ．容易看出，所谓柱面坐标，就是：z 不变还是z ，而,x y 换成极坐标。
高等数学随堂讲解三重积分在柱坐标与球坐标系下计算
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
➢柱坐标系 平面极坐标系添加oz轴得到的空间坐标系
➢柱坐标 设 M (x, y, z) R3,
➢直角坐标与柱坐标的关系
x cos
点M的柱坐标
z
y sin
zz
z M (x, y, z)
规定
在柱坐标系下
常数 常数
圆柱面 半平面
o
y
x (x, y,0)
z 常数
平面
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
➢球坐标系下三重积分计算公式
f (x, y, z)dv f (r sin cos , r sin sin , r cos )r 2 sin drdd
二、三重积分在球坐标系下的计算
（一）球坐标系 （二）球坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
三重积分在柱坐标和球坐标系下的计算
一、三重积分在柱坐标系下的计算 二、三重积分在球坐标系下的计算
一、三重积分在柱坐标系下的计算
（一）柱坐标系 （二）柱坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
（一）球坐标系 （二）球坐标系的适用条件 （三）三重积分计算公式 （四）化为累次积分的方法
利用柱面坐标计算三重积分
Ω 2
解
∵ ( x + y + z)
2 2 2
2
= x + y + z + 2( xy + yz + zx )
其中 xy + yz 是关于 y 的奇函数 ,
且 Ω 关于 zox 面对称, ∴
2008年5月12日10时3 分
∫∫∫ ( xy + yz )dv = 0 ,
Ω
21
利用柱面坐标和球面坐标计算三重 积分(33)
一般地， 当积分区域 Ω 关于 xoy 平面对称， 且被 积函数 f ( x , y , z ) 是关于 z 的奇函数，则三重积分为 则三重 零， 若被积函数 f ( x , y , z ) 是关于 z 的偶函数， 积分为 Ω 在 xoy 平面上方的半个闭区域的三重积分 的两倍.
2008年5月12日10时3 分 利用柱面坐标和球面坐标计算三重 积分(33) 19
a ∵ z=a ⇒r= , cosϕ
π x + y =z ⇒ϕ= , 4
2 2 2
a π ∴Ω : 0 ≤ r ≤ , 0 ≤ ϕ ≤ , 0 ≤ θ ≤ 2π , cos ϕ 4
2008年5月12日10时3 分 利用柱面坐标和球面坐标计算三重 积分(33) 14
I = ∫∫∫ ( x 2 + y 2 )dxdydz
2 2 2
8
2π
I1 = ∫∫ rdrdθ ∫r 2 fdz = ∫
D1 2
0
210 π, dθ ∫ dr ∫r 2 r ⋅ r 2dz = 0 3 2
4 8
Ω2
I 2 = ∫∫ rdrdθ ∫r 2 fdz = ∫
D2 2
9-3三重积分的计算
y
2º定顶
下顶：zx22y2z1(x,y)
上顶： z2x2z2(x,y)
–1
( z 2 ( 0 , 0 ) 2 z 1 ( 0 , 0 ) 0 )
2x2
I d xd yx22y2f(x,y,z)d z D
D
O
1xLeabharlann x2y2 111x2
2x2
dx
1
1x2dy
x22y2f(x,y,z)dz.
y
Dxy (x, y)
z 轴的直线， 这直线通过曲面S1穿入 内，
通过曲面S2穿出 外，则 可以表示为
{ ( x , y , z ) z 1 ( x , y ) z z 2 ( x , y ) ( x , y , ) D x }y
“先一后二”法描述: 先将 x, y 看作定值，
z z2 S2
(3) 定限
过Dxy中任意一点(x, y)，作平行于z 轴的直线，
由下至上穿，穿入点所对应的 (出)
竖坐标为最内层积分的下限.
zz z2
SS22
(上)
z1 SS11
f(x,y,z)dv
OO
b xa
DDxxyy
yy
D abxd d yx xyd1y(2yx(d x)z)y 1z(2x(z1fxz,(2y,(x()yxx,)fy,,()yy)x ,,zy )d ,zz)dz.xx
其中 F ( ,, z ) f ( c o s ,s i n , z )
例6 计算三重积分1x12y2dv,其中由抛物面
x2y24z与平面 zh(h0)所围成 .
解 为求出 在xOy面上的投影区域， z
由方程组
zh
x2y24z
利用柱面坐标与球面坐标计算三重积分
f ( r cos , r sin , z )rdrddz.
rdrd
Dr
z2 ( r , ) z1 ( r , )
f ( r cos , r sin , z )dz .
通常化为先对 z、再对 r、后对θ 的三次积分.
先将Ω在xOy面上的投影域用极坐标不等式表示
设M(x, y, z)为空间内一点,记向量OM来自长为r , OM与z轴z
r
M ( x, y, z )
z
正方向间的夹角为 , 再将OM
A x
x
O
y
y
P
向xOy平面投影, 记投影向量与x轴正方向的 夹角为 , 称 ( r , , ) 为点M的球面坐标. 规定 0 r , 0 , 0 2 .
=常数: 半平面P
0
y
x
直角坐标与柱面坐标的关系为
x r cos , y r sin , z z.
在柱面坐标下 1. 若被积函数形如
x y r . 因此
2 2 2
f (x y ) ;
2 2
2. 积分区域Ω是由柱面、锥面、旋转抛物面、平 面或球面所围成.
y
球面坐标下的体积元素
z
元素区域由六个坐标面围成：
圆锥面
球面r+d r
半平面 及+d ； 圆锥面及+d
rsind
半径为r及r+dr的球面；
r
圆锥面+d
1
1
2 1dr 2 0 1 r
1
1 r
Dxy
0
1
y
(整理)在柱坐标系下三重积分计算法的探讨.
在柱坐标系下三重积分计算法的探讨‘计算三重积分的基本方法是将三重积分转化隽三次单积分进行计算，{l{；转诧过程在妻熊坐标系、柱坐标系和球坐标系下均可进行。
对在直角坐标系下如何转化的问题，笔者已在文¨几珏1中进行过讨论，而在柱坐标系和球坐标系下且易画出积分区域草网的情形，一般教材中都有。
因此，本文着重讨论在柱坐标系下且不易画趱积分区域草图的情形嚣量，如傅将三重积分转化为柱坐标系下三次单积分的阕题。
由于在转化过程中最关键的地方是如何确定单积分的上下限，即如何用柱坐标将积分区域用不等式组表出。
所以，为能较好地理解在柱坐标系下化三熏积分为三(累)次积分的公式，下面先介绍“卜型区域”、“足一墅区域”穰“歇移一型区域”、“Z醐_型区域”的概念。
1 0--型区域和JR一型区域(1)Ell不等式组fa置、口囊p ，、给出的平面区域(图1)Lrl(秽，燕r S r2‘一)D={(r，参)l^(参)黑r≤r2(移)，g≤0蕊零}称为护型区域，其中1(0)、r2(0)是(伐，卢]上的单值连续踊数。
卜型区域D的几何特征：1)逸域D壶连续趣线r=^(拶)(称为里边界线)，，=r2(拶)(称隽外边界线)及射线拶=痿与拶；届所围成；．2)从极点出发经过D内部的射线与D的边界曲线的交点不多于两点(图1)。
(a)(一般情形))0=伐圈1 0一型区域Fig．I Region of 0·-type(b)(特殊情形)·收稿日期：2008—04—22终毒簦会：薹艳梅《1963一)，女，云篱省昆羁泰入，捌教授，主要从事基础数学教学王佟。
0=伐万方数据第1期董艳梅．等：程柱坐标系下三重积分计算法的探讨·73·(2)由不等式组l口(7)≤o爆05(7’给出的平面区域(图2)埝≤rl S r g砭D={(r，一)1 0蠛rt s r蝶如，01(r)蠖秽s 02(r)}称为置一型隧域，其中0，(，．)、眈(r)是[r，，r2]上的单值连续函数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
z z
知交线为
r2 z2 4
r2 3z
z 1, r 3,
把闭区域 投影到 xoy 面上，如图，
: r2 z 4 r2， 3 0 r 3, 0 2.
I
2
3
4r2
0
d 0
dr r2
3
r zdz
13 . 4
柱面坐标下三重积分的计算
类似于极坐标下计算二重积分，有 些三重积分采用柱面坐标会更简便。
1、柱面坐标介绍
设 M ( x, y, z) 为空间内一点，并设点 M 在
xoy 面上的投影 P 的极坐标为 ,，则这样的三
个数 , , z 就叫点 M 的柱面坐标．
z
规定： 0 ,
0 2 ,
M(x, y,z)
z .
o
yLeabharlann P(, )x如图，三组坐标面分别为
为常数 为常数
z 为常数
圆柱面； 半平面； 平 面．
柱面坐标与直角坐标的 关系为
x cos ,
y
sin
,
x
z z.
z
M (x, y, z)
z
o P(, )
y
2、柱面坐标下的计算公式
如图，柱面坐标系中的 体积元素为
dv dddz,
z
d
d
dz
o
f ( x, y, z)dxdydz
y
d
x
f ( cos , sin , z)dddz.
3、例题
例1 计算 I zdxdydz，其中是球面
x2 y2 z2 4与抛物面 x2 y2 3z
所围的立体.
3、例题
x r cos
解
由
y
r
sin
,