2020年第十八届“无悔金杯”少年数学邀请赛决赛试卷(小中组a卷)

第十八届华罗庚金杯少年数学邀请赛决赛试题 A一、填空题（每小题10 份，共80 分）1.计算：1190.12528112.5____82.2. 农谚“逢冬数九”讲的是，从冬至之日起，每九天分为一段，依次称之为一九，二九，……，九九，冬至那天是一九的第一天．2012 年12 月21 日是冬至，那么2013 年的元旦是________九的第________天．3.某些整数分别被357957911、、、除后，所得的商化作带分数时，分数部分分别是22223579、、、则满足条件大于 1 的最小整数是________．4. 如下图，在边长为12 厘米的正方形ABCD 中，以AB 为底边作腰长为10 厘米的等腰三角形P AB ，则三角形P AC 的面积是________5. 有一筐苹果，甲班分，每人 3 个还剩11 个；乙班分，每人 4 个还剩10 个；丙班分，每人 5 个还剩12 个．那么这筐苹果至少________个．6. 两个大小不同的正方体粘在一起，构成下图所示的立体图形，其中，小积木的粘贴面的四个顶点分别是大积木的粘贴面各边的一个三等分点．如果大积木的棱长为3，则这个立体图形的表面积为________．7. 设n 是小于50 的自然数，那么使得 4 n 和7n 有大于 1 的公约数的所有n 的可能值之和为________8. 由四个完全相同的正方体堆积成如下图所示的立体，则立体的表面上（包括底面）所有黑点的总数至少是________．二、解答下列各题（每题10 分，共40 分，要求写出简要过程）9. 用四个数字 4 和一些加、减、乘、除号和括号，写出四个分别等于3、4、5 和 6 的算式．10. 小明与小华同在小六（一）班，该班学生人数介于20 和30 之间，且每个人的出生日期均不相同．小明说：“本班比我大的人数是比我小的人数的两倍”，小华说：“本班比我大的人数是比我小的人数的三倍”．问这个班有多少名学生？11. 小虎周末到公园划船，九点从租船出处发，计划不超过十一点回到租船处．已知，租船处在河的中游，河道笔直，河水速度是 1.5 千米/小时；划船时，船在静水中的速度是3千米/小时，每划船半小时，小虎就要休息十分钟让船顺水漂流，问：小虎的船最远可以离租船处多少千米？12. 由四个相同的小正方形拼成下图．能否将连续的24 个自然数分别放在图中所示24黑点处（每处放一个，每个数只使用一次），使得图中所有正方形边上所放的数之和都相等？若能，请给出一个例子；若不能，请说明理由．三、解答下列各题（每题15 分，共30 分，要求写出详细过程）13. 用八个下图所示的2的小长方形可以拼成一个4的正方形．若一个拼成正方形图形经过旋转与另一个拼成的正方形图形相同，则认为两个拼成的正方形相同．问：在所有可能拼成的正方形图形中，上下对称、第一行有两个空白小方格且空白小方格相邻的图形有多少种？14. 不为零的自然数n 既是2010 个数字和相同的自然数之和，也是2012 个数字和相同的自然数之和，还是2013 个数字和相同的自然数之和，那么n最小是多少。

总分第十八届华罗庚金杯少年邀请赛决赛试题A（小学高年级组）（时间2013年4月20日10：00～11：30）一、填空题（每小题10分,共80分）1．计算:19×0.125+281×81-12.5=________.解析：原式=（19+281-100）×0.125=200×0.125=252．农谚‘逢冬数九’讲的是,从冬至之日起,每九天分为一段,依次称之为一九,二九,……,九九,冬至那天是一九的第一天.2012年12月21日是冬至,那么2013年的元旦是________九的第________天.解析：31-21+1+1=12,12÷9=1…3，2013年的元旦是二九的第3天.3．某些整数分别被119977553，，，除后,所得的商化作带分数时,分数部分分别是92725232，，，,则满足条件且大于1的最小整数是________.解析：设整数为A,分别被119977553，，，除后,所得的商分别为A A A A 911795735，，，;)1(911921911)1(7972179)1(5752157)1(3532135-++=-++=-++=-++=A A A A A A A A ，，，显然，当A-1是[3，5，7，9]的时候满足题意。

所以A-1=315，A=316。

4．如右图,在边长为12厘米的正方形ABCD 中,以AB 为底边作腰长为10厘米的等腰三角形PAB .则三角形PAC 的面积等于________平方厘米.解析:过P点做PE⊥AB,由于三角形PAB为等腰三角形，所以AE=EB=6cm。

根据勾股定理：PE 2=102-62=64=82，所以PE=8cm。

S△PAB=12×8÷2=48cm 2，S△PCB=12×6÷2=36cm 2，S△PAC=48+36-12×12÷2=12cm 2。

第十八届华罗庚金杯少年数学邀请赛决赛试题 A 参考答案（小学高年级组）一、填空题（每题 10 分, 共 80 分）题号 1 2 3 4 5 6 7 8答案25 2, 3 316 12 62 74 94 54二、解答下列各题（每题 10 分, 共 40 分, 要求写出简要过程）9.解答.例如(4 + 4 + 4) ÷ 4 = 3 ,4 - (4 - 4) ⨯ 4 = 4 ,(4 ⨯ 4 + 4) ÷ 4 = 5 ,(4 + 4) ÷ 4 + 4 = 6 .10.答案：25解答. 设比小明小的学生为x人,比小华小的学生为y人.因为比小明大的学生为2x人,所以全班学生共 N =3x +1人;又因为比小华大的学生为3y人,所以全班学生共N=4y+1人. 这样, N-1既是 3 的倍数, 又是 4 的倍数, 因此N-1是3⨯4=12的倍数. 这个班学生人数大于 20 而小于 30, 所以N-1只可能是 24. 因此这个班共有学生N=24+1=25人.11.答案：1.375解答.小虎划船的全部时间为120分钟,他每划行30分钟,休息10分钟,周期为40分钟, “华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解所以一共可分为 3 个 30 分钟划行时间段, 有 3 个 10 分钟休息划船时, 顺水的船速与逆水的船速之比为 4.5:1.5=3:1. 因为小虎要把船划到离租船处尽可能远, 他在划船的过程中只能换一次划船的方向, 而且是在尽可能远处. 分两种情况讨论.1)开始向下游划船, 设最远离租船处x千米. 因为回到租船处是逆水, 所以小虎只有 110 分钟可用. 由于划船时顺流速度是逆流速度的 3 倍, 所以用在向下游划船的时间不能超过半小时. 另外两次休息时间只能用在返程, 在休息期间内船向下游漂流了13⨯1.5 , 所以⎛ 1 ⎫x ÷4.5+  x + ⨯1.5⎪ ÷1.5 = 1.5 .3⎝ ⎭整理上式得x +3x +1.5=6.75,4x= 5.25,x =1.3125(千米).2)开始向上游划, 设最远离租船处y千米. 小虎可用 120 分钟, 有两次休息时间用在向上游. 所以⎛ 1 ⎫ ⎛ 1 ⎫y + ⨯1.5⎪ ÷1.5 +  y - ⨯1.5⎪ ÷ 4.5 = 1.5 .3 6⎝ ⎭ ⎝ ⎭整理上式得4 y+5 ⨯1.5 = 6.75 , 4 y= 5.5 , y =1.375(千米).6综合 1) 和 2) 的讨论, 小虎的船最多离租船处 1.375 千米.12.答案：不能解答. 设放的最小自然数为a,则放的最大自然数为a+23.于是这24个数的和为A= 12(2a+ 23).假设可能, 设每个正方形边上的数之和为S . 因为共有5个正方形, 这些和的和为5S . 因为每个数在这些和中出现两次, 所以有5S= 2A.“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解记最小的 16 个数的和为B , 则B=8(2a+15) . 下面分两种情形讨论:(1)若 B ≤ S ,则S = 2 A = 24 (2a+ 23) ≥ 8(2a+15) , 9.8a+110.4 ≥16a+120 ,5 5不存在自然数 a 使得不等式成立.(2)情形 B > S 也是不可能的,因为此时不可能选择最大正方形边上的16个数使得这16 个数的和等于S .三、解答下列各题（每题 15 分, 共 30 分, 要求写出详细过程）13.答案：5解答. 用右图代替题目中的2⨯1小长方形.因为题目所给的小长方形上下不对称,所以同一个小长方形在拼成的上下对称的正方形中, 不会既在上半部分也在下半部分. 这样, 就可以只考虑上半部分的不同情形.1)相邻的空白格在第一行最左边或最右边. 因为要排除旋转相同的, 所以只考虑相邻空白格在最右边的情况, 有下图所示的 2 种图形,2)相邻的空白格在第一行中间. 去掉旋转重合的, 有下图所示的 3 种图形,所有不同的图形为 5 种.14.答案：6036“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解解答. 令n = a1+ a2++ a2010 = b1 + b2 + + b2012 = c1 + c2 ++ c2013 ,其中, 所有的a i数字和相同, 所有的b j数字和相同, 所有的c k数字和相同. 两个自然数数字的和相同, 则它们除以 9 的余数相同, 即a i = 9u i + r, i =1, 2, , 2010,bj = 9v j + s, j =1, 2, , 2012,c k = 9w k + t, k =1, 2, , 2013.则n= 9 ⨯ (u1+u2+ +u2010 ) + 2010⨯r= 9 ⨯ (v1+v2+ +v2012 ) + 2012⨯s (1)= 9 ⨯ (w1+w2+ +w2013 ) + 2013⨯t,由上面的等式可得,9 ⨯ (u1+u2++ u2010 + 223 ⨯ r) + 3r = 9 ⨯ (v1 + v2 ++ v2012 + 223 ⨯ s) + 5 ⨯ s ,(2)9 ⨯ (w1+w2++ w2013 + 223 ⨯ t) + 6 ⨯ t = 9 ⨯ (v1 + v2 ++ v2012 + 223 ⨯ s) + 5 ⨯ s ,(3) 由 (2) 可以得出s是 3 的倍数, 只能是 0, 3 或 6. 下面三种情况讨论:1)s =0.此时,对j=1, 2,, 2012 ,因为b j=9v j的数字和不为零,所以v j≥1. 则n =9⨯(v1+ v2++ v2012 ) ≥ 9 ⨯ 2012 = 18108 .2)s =6.此时“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解客服电话：400 650 0888 n =9(v1+ v2++ v2012 ) + 2012 ⨯ 6 ≥ 12072 .3)s =3,此时n= 9(v1+v2+ +v2012 ) + 2012 ⨯ 3 ≥ 6036 .可以取 r =2, t =1.而6036 = 3 + 3 + + 3 = 2 + 2 + + 2 +11 +11 + +112012 个x 个y 个=10 +10 + +10 +1 +1 + +1.=m 个n 个下面计算 x, y 与 m, n,⎧x + y =2010, ⎨ ⎧m + n =2013,⎨⎩10m+n= 6 0 3,6即6036 = 2⨯1786 +11⨯224 =10⨯447 +1566 = 3⨯2012.最终, 满足条件的最小自然数是 6036.“华杯赛”官网四大类网络课程√专题讲座√赛前串讲√真题详解√月月练讲解第 5 页共5页。

2013年第十八届“华罗庚金杯”少年数学邀请赛（武汉赛区）决赛试卷（小学高年级组）一、填空题（共8小题，每小题10分，满分80分）1．（10分）计算：＝．2．（10分）自动扶梯停止运行时，一个小孩要用90秒钟才能走完60米长的自动扶梯．自动扶梯运行时则可用60秒钟将乘客从底端送到顶端．若小孩在运行的自动扶梯上行走，问小孩从扶梯底端到达顶端需要秒．3．（10分）两个骑车人在不同的赛道上训练．骑车人A用圆形赛道，其直径是1千米；骑车人B用直线赛道，其长度为5千米．骑车人A用10分钟完成3圈，而骑车人B用5分钟行进了2个来回．那么骑车人A与骑车人B的速度比是（）A．1：1.6πB．π：10C．3：4D．3π：40 4．（10分）山洞里有一堆桃子，是三只猴子的共同财产．猴老大来到山洞后将桃子按5：4的比例分成两部分，并取走较多的一部分；猴老二来到后，将剩下的桃子又按5：4的比例分成两部分，并取走较多的一部分；剩余的桃子归猴老三．已知猴老大比猴老三多拿了29个桃子，则猴老二拿了个桃子．5．（10分）如图排列的前五个三角形都是直角三角形，则构成这100个三角形的所有线段中有条线段长度为整数．6．（10分）从1、2、3、…、7中选择若干个数，使得其中偶数之和等于奇数之和．则符合条件的取法（）种．A．6B．7C．8D．97．（10分）若一个四位数5ab4是一个数的平方，则a+b＝．8．（10分）从小明家到游泳池的路上有200棵树．在往返的路途中，小明用红丝带系在一些树上做标记，去游泳池的时候，他在第1棵树、第6棵树、第11棵树、…上做了标记，每次都隔4棵树标记一棵；返回时，他在遇到的第1棵树、第9棵树、第17棵树、…上做了标记，每次都隔7棵树标记一棵．则他回到家时，没有被标记的树共有棵．二、解答下列各题（每题10分，满分40分）9．（10分）如图，沿正方体XYTZ﹣ABCD的两个平面BCTX和BDTY切割，将此正方体切成4块．请问含有顶点A的那一块占正方体体积的几分之几？10．（10分）如图，ABCD是一个长方形，从G、F、E引出的小横线都平行于AB．若AD ＝12，则AG等于多少？11．（10分）影院正在放映《玩具总动员》、《冰河世纪》、《怪物史莱克》、《齐天大圣》四部动漫电影，票价分别为50元、55元、60元、65元．来影院的观众至少看一场，至多看两场．因时间关系《冰河世纪》与《怪物史莱克》不能都观看，若今天必有200人看电影所花的钱一样多，则影院今天至少接待观众多少人？12．（10分）现有四种颜色的灯泡（每种颜色的灯泡足够多），要在三棱柱ABC﹣A1B1C1各顶点上装一个灯泡，要求同一条棱两端点的灯泡颜色不相同，且每种颜色的灯泡都至少有一个，安装方法共有多少种？三、解答下列题（共2小题，每题15分，满分30分.要求写出详细过程）13．（15分）将从1到30的自然数分成两组，使得第一组中所有数的乘积A能被第二组中所有数的乘积B整除．则的最小值是多少？14．（15分）如图，在边长大于20cm的正方形PQRS中，有一个最大的圆O，若圆周上一点T到PS的距离为8cm，到PQ的距离为9cm．则圆O的半径是多少厘米？2013年第十八届“华罗庚金杯”少年数学邀请赛（武汉赛区）决赛试卷（小学高年级组）参考答案与试题解析一、填空题（共8小题，每小题10分，满分80分）1．（10分）计算：＝2013．【分析】首先根据平方差公式分别对繁分数的分子和分母进行化简，然后再求解即可．【解答】解：＝＝＝2013故答案为：2013．2．（10分）自动扶梯停止运行时，一个小孩要用90秒钟才能走完60米长的自动扶梯．自动扶梯运行时则可用60秒钟将乘客从底端送到顶端．若小孩在运行的自动扶梯上行走，问小孩从扶梯底端到达顶端需要36秒．【分析】把自动扶梯的长度看作单位“1”，则这个小孩走完60米长的自动扶梯所用时间为，自动扶梯将乘客从底端送到顶端用的时间为，那么小孩从扶梯底端到达顶端需要的时间为1÷（+），解决问题．【解答】解：1÷（+）＝1÷＝36（秒）答：小孩从扶梯底端到达顶端需要36秒．故答案为：36．3．（10分）两个骑车人在不同的赛道上训练．骑车人A用圆形赛道，其直径是1千米；骑车人B用直线赛道，其长度为5千米．骑车人A用10分钟完成3圈，而骑车人B用5分钟行进了2个来回．那么骑车人A与骑车人B的速度比是（）A．1：1.6πB．π：10C．3：4D．3π：40【分析】通过分析可知；A的速度为：πD×3÷10＝π×1000×3÷10＝300π（米/分）B的速度为：5000×2×2÷5＝4000（米/分）其速度比为：A：B＝π×1000×3÷10：5000×2×2÷5，据此解答即可．【解答】解：由题目中的数据，求得A的速度为：πD×3÷10＝π×1000×3÷10＝300π（米/分）B的速度为：5000×2×2÷5＝4000（米/分）其速度比为：A：B＝300π：4000＝3π：40故选：D．4．（10分）山洞里有一堆桃子，是三只猴子的共同财产．猴老大来到山洞后将桃子按5：4的比例分成两部分，并取走较多的一部分；猴老二来到后，将剩下的桃子又按5：4的比例分成两部分，并取走较多的一部分；剩余的桃子归猴老三．已知猴老大比猴老三多拿了29个桃子，则猴老二拿了20个桃子．【分析】首先根据题意，设这堆桃子的总量为单位“1”，分别求出三只猴子各拿走的比例，然后根据猴老大比猴老三多拿了29个桃子，求出桃子的总量，进而求出猴老二拿了多少个桃子即可．【解答】解：根据题意，设这堆桃子为单位“1”，则猴老大拿走了，则猴老二拿走了：×，猴老三拿走了：×，则桃子的总数：＝81（个），候老二拿走的个数：81××＝20（个）答：猴老二拿了20个桃子．故答案为：20．5．（10分）如图排列的前五个三角形都是直角三角形，则构成这100个三角形的所有线段中有110条线段长度为整数．【分析】观察图形可知：第一个三角形2条直角边长度为整数，从第二个三角形开始，每个三角形都有一个边长为1的直角边；则边长为1的线段有：2+99＝101（条）；前一个三角形的斜边是后一个三角形的一个直角边，根据勾股定理分别求出每个三角形斜边的长，找出开方后为整数的边，再加上101即可求出答案．【解答】解：观察图形可知：边长为1的线段有：2+99＝101（条）；根据勾股定理分别求出每个三角形斜边的长为：、、、…、；根据：12＝1，22＝4，32＝9，…102＝100；可知三角形斜边的长中有9个开方后为整数，即三角形斜边的长中有9条边的长度为整数．则：101+9＝110（条）答：构成这100个三角形的所有线段中有110条线段长度为整数．故答案为：110．6．（10分）从1、2、3、…、7中选择若干个数，使得其中偶数之和等于奇数之和．则符合条件的取法（）种．A．6B．7C．8D．9【分析】找出1，2，3，…，7这7个自然数那些是奇数，哪些是偶数，列出符合条件偶数之和等于奇数之和的算式，据此解答即可．【解答】解：1，2，3，4，5，6，7中1，3，5，7是奇数，2，4，6是偶数，1+3＝41+5＝63+7＝4+63+5＝2+61+7＝2+61+5＝2+45+7＝2+4+6共7种故选：B．7．（10分）若一个四位数5ab4是一个数的平方，则a+b＝9．【分析】702＝4900，802＝6400，5000多的一个四位数，应该是70到80之间的一个两位数的平方．又它的末位数是4，所以这个两位数的个位只能是2或8．722＝5184，符合题意．再检验一下782是否符合题意即可．【解答】解：722＝72×72＝5184符合题意．782＝78×78＝6084，不符合题意．舍去．所以a＝1，b＝8．a+b＝1+8＝9．故答案为：9．8．（10分）从小明家到游泳池的路上有200棵树．在往返的路途中，小明用红丝带系在一些树上做标记，去游泳池的时候，他在第1棵树、第6棵树、第11棵树、…上做了标记，每次都隔4棵树标记一棵；返回时，他在遇到的第1棵树、第9棵树、第17棵树、…上做了标记，每次都隔7棵树标记一棵．则他回到家时，没有被标记的树共有140棵．【分析】根据题意，可得去游泳池的时候，每5棵树标记一棵，一共标记了200÷5＝40棵；返回时，每8棵树标记一棵，一共标记了200÷8＝25棵；重复标记的棵数是200÷（5×8）＝5棵，用40加上25，减去5，求出一共标记了多少棵树，最后用200减去标记的棵树，求出没有被标记的树共有多少棵即可．【解答】解：去游泳池的时候，每5棵树标记一棵，一共标记了200÷5＝40（棵）；返回时，每8棵树标记一棵，一共标记了200÷8＝25（棵）；重复标记的棵数是200÷（5×8）＝5（棵），200﹣（40+25﹣5）＝200﹣60＝140（棵）答：没有被标记的树共有140棵．故答案为：140．二、解答下列各题（每题10分，满分40分）9．（10分）如图，沿正方体XYTZ﹣ABCD的两个平面BCTX和BDTY切割，将此正方体切成4块．请问含有顶点A的那一块占正方体体积的几分之几？【分析】沿面BCTX切割，此时含有顶点A的那一块占正方体体积的，再沿BDTY切割，含有顶点A的那一块占沿面BCTX切割后的，由乘法原理可得含有顶点A的那一块占正方体体积为：×＝．【解答】解：沿面BCTX切割，此时含有顶点A的那一块占正方体体积的，再沿BDTY切割，含有顶点A的那一块占沿面BCTX切割后的，所以含有顶点A的那一块占正方体体积为：×＝．答：含有顶点A的那一块占正方体体积的．10．（10分）如图，ABCD是一个长方形，从G、F、E引出的小横线都平行于AB．若AD ＝12，则AG等于多少？【分析】因为四边形ABCD是一个长方形，黑豆网https://黑豆网涵盖电影，电视剧，综艺，动漫等在线观看资源！金马医药招商网:金马医药招商网是专业提供医药代理招商的资讯信息发布平台，科技新闻网:科技新闻网每天更新最新科技新闻,这里有最权威的科技新闻资料。

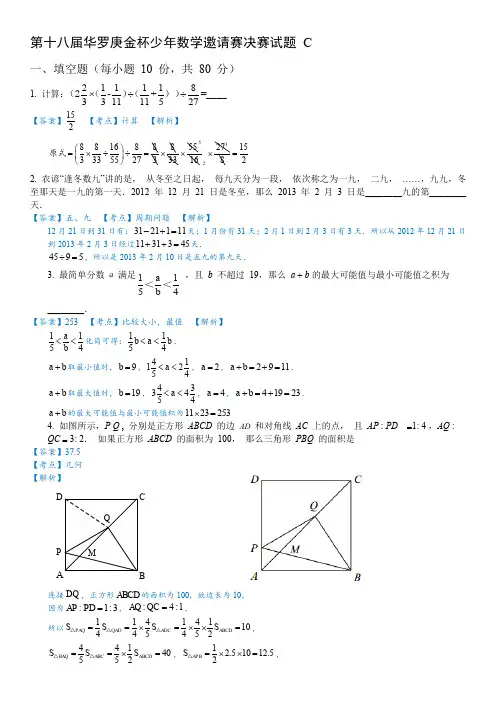
第十八届华罗庚金杯少年数学邀请赛决赛试题 C一、填空题（每小题 10 份，共 80 分）1. 计算：211118-+=____331111527⨯÷÷（2（）（）） 【答案】152【考点】计算 【解析】 8816883335527⎛⎫=⨯÷÷= ⎪⎝⎭原式38⨯3355⨯5163227⨯8152=2. 农谚“逢冬数九”讲的是， 从冬至之日起， 每九天分为一段， 依次称之为一九， 二九， ……，九九，冬至那天是一九的第一天．2012 年 12 月 21 日是冬至，那么 2013 年 2 月 3 日是________九的第________天．【答案】五、九 【考点】周期问题 【解析】12月21日到31日有：3121111-+=天；1月份有31天；2月1日到2月3日有3天．所以从2012年12月21日到2013年2月3日经过1131345++=天．4595÷=，所以是2013年2月10日是五九的第九天．3. 最简单分数 a 满足1a 15b 4＜＜ ，且 b 不超过 19，那么 a + b 的最大可能值与最小可能值之积为________．【答案】253 【考点】比较大小，最值 【解析】1154a b <<化简可得：1154b a b <<． a b +取最小值时，9b =，411254a <<，2a =，2911a b +=+=．a b +取最大值时，19b =，433454a <<，4a =，41923ab +=+=．a b +的最大可能值与最小可能值积为1123253⨯=4. 如图所示，P Q , 分别是正方形 ABCD 的边 AD 和对角线 AC 上的点， 且 AP : PD =1: 4 ，AQ : QC = 3: 2． 如果正方形 ABCD 的面积为 100， 那么三角形 PBQ 的面积是 【答案】37.5 【考点】几何 【解析】ABCDPMQ连接DQ ，正方形ABCD 的面积为100，故边长为10， 因为:1:3AP PD =，:4:1AQ QC =， 所以11414110445452PAQ QAD ADC ABCD S S S S ==⨯=⨯⨯=△△△， 44140552BAQ ABC ABCD S S S ==⨯=△△，12.51012.52APB S =⨯⨯=△，所以10412.537.5PBQ QAP QAB PAB S S S S =+-=+-=△△△△．5. 四位数 abcd 与 cdab 的和为 3333，差为 693，那么四位数abcd 为________．【答案】2013或1320 【考点】和差问题 【解析】大数等于()333369322013+÷=，小数等于()333369321320-÷=．20131320abcd =或6. 两个较小的正方体积木分别粘在一个大正方体积木的两个面上，构成下图所示的立体图形，其中，每个小积木粘贴面的四个顶点分别是大积木粘贴面各边的一个五等分点．如果三个积木的棱长互不相同且最大的棱长为 5， 那么这个立体图形的表面积是________． 【答案】270【考点】立体几何表面积 【解析】三视图法：表面积在原来棱长为5的正方体表面积的基础上增加了4个棱长为a 的正方形的一面的面积和4个棱长为b 的正方形的一面的面积；（题中三个积木的棱长互不相同）b 3241a2221417a =+=，2223213b =+=，所以表面积为：655417413270⨯⨯+⨯+⨯=．7. 设 a ，b ，c 分别是 0 ~9 的数字，它们不同时都是 0 也不同时都是 9．将循环小数0.a bc∙∙化成分数最简分数后，分子有________种不同情况． 【答案】660 【考点】计数：容斥原理 【解析】0.999abcabc =，根据题意1998abc =~，但是结果要化为最简分数，所以化简后会有重复．由3999337=⨯，可得： 1、 1）1998~中3的倍数有9983323⎡⎤=⎢⎥⎣⎦个； 2）1998~中4381=的倍数有9981281⎡⎤=⎢⎥⎣⎦个； 说明abc 是3的倍数但不是81的倍数的有33212320-=个，这些数的分子全部可以化简成不是3的倍数的数．2、1998~中37的倍数有9982637⎡⎤=⎢⎥⎣⎦个； 说明abc 是37的倍数有26个，这些数的分子全部可以化简成不是37的倍数的数．3、1998~中3和37的倍数有9988111⎡⎤=⎢⎥⎣⎦个； 说明abc 是111的倍数有8个，这些数的分子全部可以化简成不是111的倍数的数．根据容斥原理，约分后会有重复的数有320268338+-=个，则分子有998338660-=种不同情况．8. 由四个完全相同的正方体堆积成如下图所示的立体图形，则立体的表面上（包括底面） 所有黑点的总数至少是【答案】55 【考点】立体几何：空间想象、最值问题 【解析】如图所示，与3点相邻的面分别有2点、1点、4点和6点，所以3的对面为5；与4点不相对的面分别有1点、3点、6点、5点，所以2的对面为4；则1的对面为6．如下图，分别为这个立体图形的六个方向的视图：右视图左视图后视图正视图124114324526，5？5仰视图俯视图333本题的难点在于左视图中绿色的确定，通过原图可以看出，当3上面，2在左面时1在后面；所以当2在上面2在前面时，1应该在左面．唯一不能确定的是底视图的中间红色部分，为了让表面的数字和最小，则可以取1．故最大值为()()()()()()62541423214133351555+++++++++++++++++=．二、解答下列各题（每题 10 分，共 40 分，要求写出简要过程）9. 下图中，大正方形的周长比小正方形的周长多 80 厘米，阴影部分的面积为 880 平方厘米．那么，大正方形的面积是多少平方厘米？ 【答案】1024 【考点】几何面积【解析】将图中空白的正方形摆正，放在大正方形的角上，如下图：两正方形的周长相差80厘米， 则右上角的小正方形C 的边长为80420÷=厘米．则长方形A 和B 的面积都是()2880202240-÷=平方厘米，则空白正方形的边长为2402012÷=厘米，小正方形的面积是1212144⨯=平方厘米． 大正方形的面积是1448801024+=平方厘米．10. 某高中根据入学考试成绩确定了录取分数线，录取了四分之一的考生．所有被录取者的成绩平均分比录取分数线高 10 分，所有没有被录取的平均分比录取分数线低 26 分，所有考生的平均成绩是 70 分．那么录取分数线是多少？【答案】87 【考点】平均数问题 【解析】假设一共有4人参加考试，则有1人录取，3人没有录取． 设录取分数线为x 分，则有()()110326470x x ⨯++⨯-=⨯ 解得87x =，录取分数线，是87分．11. 设 n 是小于 50 的自然数，求使得 3n +5 和 5n +4 有大于 1 的公约数的所有 n ． 【答案】7，20，33，46 【考点】数论：因数倍数 【解析】假设()35,54n n m ++=，35n am +=，54n bm +=．()()()3555431525151253135313n n n n am bm m a b +⨯-+⨯=+--⨯-⨯=⨯-=所以m 是13的因数，且m 大于1，m =13． 则3513n a +=，5413n b +=．()()()543513132113n n b an b a +-+=--=⨯-21n -是13的倍数且n 小于50，所以2113,39,65,91n -=时，n 分别等于7，20，33，46．12. 一次数学竞赛中，参赛各队每题的得分只有 0 分，3 分和 5 分三种可能．比赛结束时，有三个队的总得分之和为 32 分．若任何一个队的总得分都可能达到32 分，那么这三个队的总得分共有多少种不同的情况？【答案】255 【考点】不定方程，计数 【解析】设三队得3分的题共x 道，得5分的题共y 道，则有3532x y +=．解得：1）91x y =⎧⎨=⎩；2）44x y =⎧⎨=⎩．当三队得3分的题共9道，得5分的题共1道．三队的3分的题共9道，三队分配共有3129311155C C -+-==种；三队得5分的题共1道，三队分配共有3种． 则这种情况共有553165⨯=种．当三队得3分的题共4道，得5分的题共4道．三队得3分的题共4道，三队分配共有312431615C C -+-==种；三队得5分的题共4道，三队分配共有312431615C C -+-==种，但是当一队得5分题数大于等于3个时，由于3个5分与5个3分的总分都是15分，所以会与1）中情况重复．比如一队的得分为15分，可以为5个3分得来，也可以由3个5分得来，这种情况重复．而一队得5分题数大于等于3个的情况分两类：①一队得5分题数等于4个，共3种情况；②一队得5分题数等于3个，共有326⨯=种．则与1）不重复的排法有15366--=种． 则这种情况共有15690⨯=种． 综上所述，共有16590255+=种．三、解答下列各题（每小题 15 分，共 30 分，要求写出详细过程）13. 在等腰直角三角形 ABC 中，∠ A = 90 ， AB = AC =1，矩形 EHGF 在三角形 ABC 内，且 G ， H 在边 BC 上．求矩形 EHGF 的最大面积．【答案】14【考点】平面几何：直线型 【解析】KD A BCEFGH过A 做BC 的垂线，垂足为D ，交EF 于K 令BH GC EH a ===此时2EH HG BC +=（和一定）当22EH HG a ==时，2EH HG ⨯最大，EH HG ⨯最大此时24BC a a a a =++=，422AD a a =÷=，24224ABC S a a a =⨯÷=△此时四边形EFGH 的面积最大，21111222224EFGH ABC S EH HG a a a S =⨯=⨯===⨯=△ 14. 用八个下图所示的 2 ⨯1 的长方形可以拼成一个 4⨯ 4的正方形， 若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同，则认为两个拼成的正方形相同．问：有几种【答案】10 【考点】构造与论证 【解析】首先构造一个44⨯的正方形（如下图）根据一条对角线是其对称轴可知：图中同样的字母小正方形代表它们是同类型的．以中叉的数量分类讨论：中有1个叉：，只有1种．中有2个叉：为时，有3种：为时，有2种：为时，有4种：为时，有4种：中有3个叉时无法构造，不存在．但是上述的1324414++++=种图形中以下四个是两个对角线都是对称轴，不符合题意．综上所述符合题意共有14410-=种．。

- 1 -第二十届华罗庚金杯少年数学邀请赛决赛试题A 组试卷解析（小学中年级组A 卷）一、填空题（每小题 10分, 共80分）1. 计算: 3752(392)5030(3910)÷⨯+÷⨯=________.【考点】整数计算【难度】☆☆【答案】61【分析】原式3752(392)1006(392)=÷⨯+÷⨯(37521006)7847587861=+÷=÷=2. 右图中, G F D C B A ∠+∠+∠+∠+∠+∠ 等于________度.【考点】几何、角度计算【难度】☆☆【答案】360【分析】连接CD ，有G F EDC ECD ∠+∠=∠+∠，这样就转化成四边形的内角和了，四边形的内角和是360度.3. 商店以每张2角1分的价格进了一批贺年卡, 共卖14.57元. 若每张的售价相同, 且不超过买入价格的两倍, 则商店赚了________元.【考点】数论、分解质因数【难度】☆☆【答案】4.7元【分析】14.57元=1457分，14573147=⨯每张的售价不超过买入价格的两倍，47是张数，31分是售价； 商店赚了(3121)47470-⨯=（分）=4.7元.4. 两个班植树, 一班每人植3棵, 二班每人植5棵, 共植树115棵. 两班人数之和最多为________.【考点】组合、最值问题【难度】☆☆【答案】37人.【分析】设一班a 人，二班b 人，则有35115a b +=， 求两班人数最多，算式转化成： 3()2115a b b ++=，a b +最大，b 尽可能的小，2b =时，37a b +=。

两班人数之和最多的是37人.5. 某商店第一天卖出一些笔, 第二天每支笔降价1元后多卖出100支, 第三天每支笔比前一天涨价3元后比前一天少卖出200支. 如果这三天每天卖得的钱相同, 那么第一天每支笔售价是________元.【考点】应用题【难度】☆☆☆【答案】4元【分析】设第一天每支笔售价x 元，卖出n 支，有(1)(100)(1)(100)nx x n nx x n =-+⎧⎨=+-⎩可得到1001001002200x n x n =+⎧⎨=-⎩，解得3004n x =⎧⎨=⎩6. 一条河上有A, B 两个码头, A 在上游, B 在下游. 甲、乙两人分别从A, B同时出发, 划船相向而行, 4小时后相遇. 如果甲、乙两人分别从A, B 同时出发, 划船同向而行, 乙16小时后追上甲. 已知甲在静水中划船的速度为每小时6千米, 则乙在静水中划船每小时行驶________千米.【考点】行程、流水行船【难度】☆☆☆【答案】10【分析】在流水行船问题中，两船相遇的速度和即两船船速和，两船追及速度差即两船船速差。

第十八届华罗庚金杯少年邀请赛初赛试题A（小学高年级组）（时间2013年3月23日10：00～11：00）一、选择题（每题10分，满分60分，以下每题的四个选项中，仅有一个是正确的，请将表示正确答案的英文字母写在每题的圆括号内。

）1．2012.25×2013.75－2010.25×2015.75＝（）。

A．5 B．6 C．7 D．8解析：巧算问题原式=（2010.25+2）×（2015.75-2）－2010.25×2015.75=2015.75×2－2010.25×2－4=7所以选C。

2．2013年的钟声敲响了, 小明哥哥感慨地说: 这是我有生以来第一次将要渡过一个没有重复数字的年份。

已知小明哥哥出生的年份是19的倍数, 那么2013年小明哥哥的年龄是（）岁。

A．16 B．18 C．20 D．22解析：简单数论。

从1990年～2012年，年份中都有重复数字，其中是19的倍数的数只有1900+95=1995，2012—1995=18（岁），所以选B。

3．一只青蛙8点从深为12米的井底向上爬, 它每向上爬3米, 因为井壁打滑, 就会下滑1米, 下滑1米的时间是向上爬3米所用时间的三分之一。

8点17分时, 青蛙第二次爬至离井口3米之处, 那么青蛙从井底爬到井口时所花的时间为（）分钟。

A．22 B．20 C．17 D．16解析：周期问题。

下滑1米的时间是向上爬3米所用时间的三；爬一米和滑一米的时间相同，以爬三米，滑一米为一个周期；（3-1）×3+3=9m,青蛙第一次爬至离井口3米之处，（3-1）×4+1=9m，青蛙第二次爬至离井口3米之处，此时，青蛙爬了4个周期加1米，用时17分钟，所以青蛙每爬1m或滑1m所用时间为1分钟。

（12—3）÷（3-1）=4…1，青蛙从井底爬到井口经过5个周期，再爬2m，用时5×（3+1）+2=22分钟，选A。

第十八届华罗庚金杯少年数学邀请赛决赛（A）卷【小中组】一、填空题（每小题10分,共80分）1.计算:(2014×2014+2012)-2013×2013=________.2.将长方形的纸片ABCD按右图的方式折叠后压平,使三角形DCF落在三角形DEF的位置,顶点E恰落在边AB上.已知∠1＝20°,那么∠2是________度.3.鸡兔同笼,共有40个头,兔脚的数目比鸡脚的数目的10倍少8只,那么兔有________只.4.第一次操作将图a左下角的正方形分为四个小正方形,见图b;第二次操作再将图b左下角的小正方形分为四个更小的正方形,见图c;这样继续下去,当完成第六次操作时,得到的图形中共有________个正方形.图a图b图c5.右面的加法竖式中,相同的汉字代表1至9中的相同数字,而不同的汉字代表不同的数字.则竖式中的“数学”所表示的两位数共有________个.6.大小两个正方体积木粘在一起,构成右图所示的立体图形,其中小积木的下底面的四个顶点,恰好是大积木的上底面各边的中点．如果大积木的棱长为2,那么这个立体图形的表面积是________.7.某班学生人数大于20而小于30,其中女同学的人数是男同学的2倍.全班报名参加“华杯赛”的人数是未报名人数的3倍少1人.这个班有学生________名.8.见右图,图形内的数字分别表示所在的矩形或三角形的面积,那么阴影三角形的面积为________.二、简答题（每小题15分,共60分,要求写出简要过程）9.用4个数码4和一些加、减、乘、除号和小括号,写出值分别等于2、3、4、5、6的五个算式.10.右图是U,V,W,X四辆不同类型的汽车每百千米的耗油量.如果每辆车都有50升油,那么这四辆车最多可行驶的路程总计是多少千米?11.某商店卖出一支钢笔的利润是9元,一个小熊玩具的进价为2元.一次,商家采取“买4支钢笔赠送一个小熊玩具”的打包促销,共获利润1922元.问这次促销最多卖出了多少支钢笔?12.编号从1到10的10个白球排成一行,现按照如下方法涂红色:1）涂2个球;2）被涂色的2个球的编号之差大于2，求不同的涂色方法有多少种?第十八届华罗庚金杯少年数学邀请赛决赛（A ）卷参考答案【小中组】一、填空题（每小题10分,共80分）1.解析：【知识点】运算律，平方差公式原式6039201240272012)20132014()20132014(20122013201422=+=+-⨯+=+-=2.解析：【知识点】平面几何o 201=∠=∠CDF ，DCF ∠与CDF ∠互余，则o o o 702090=-=∠DFC ，o 70=∠=∠DFC DFE ，o o o o 4070701802=--=∠。

2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷（小中组A卷）一、填空题（每小题10分，共80分）1．（10分）计算：（2014×2014+2012）﹣2013×2013 ．2．（10分）将长方形的纸片ABCD按右图的方式折叠后压平，使三角形DCF 落在三角形DEF的位置，顶点E恰落在边AB上．已知∠1＝22°，那么∠2是度．3．（10分）鸡兔同笼，共有40个头，兔脚的数目比鸡脚的数目的10倍少8只，那么兔有只．4．（10分）第一次操作将图a左下角的正方形分为四个小正方形，见图b；第二次操作再将图b左下角的小正方形分为四个更小的正方形，见图c；这样继续下去，当完成第六次操作时，得到的图形中共有个正方形．5．（10分）如图加法竖式中，相同的汉字代表1至 9中的相同数字，而不同的汉字代表不同的数字．则竖式中的“数学”所表示的两位数共有个．6．（10分）大小两个正方体积木粘在一起，构成如图所示的立体图形，其中小积木的下底面的四个顶点，恰好是大积木的上底面各边的中点．如果大积木的棱长为2，那么这个立体图形的表面积是．7．（10分）某班学生人数大于20而小于30，其中女同学的人数是男同学的2倍．全班报名参加“华杯赛”的人数是未报名人数的3倍少1人．这个班有学生名．8．（10分）如图，图形内的数字分别表示所在的矩形或三角形的面积，那么阴影三角形的面积为．二、简答题（每小题15分，共60分，要求写出简要过程）9．（15分）用四个数字4和一些加、减、乘、除号和括号，写出四个分别等于3、4、5和6的算式．10．（15分）如图是U，V，W，X四辆不同类型的汽车每百千米的耗油量．如果每辆车都有50升油，那么这四辆车最多可行驶的路程总计是多少千米？11．（15分）某商店卖出一支钢笔的利润是9元，一个小熊玩具的进价为2元．一次商家采取“买4支钢笔赠送一个小熊玩具”的打包促销，共获利润1922元．问这次促销最多卖出了多少支钢笔？12．（15分）编号从1到10的10个白球排成一行，现按照如下方法涂红色：（1）涂2个球；（2）被涂色的2个球的编号之差大于2．那么不同的涂色方法有多少种？2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷（小中组A卷）参考答案与试题解析一、填空题（每小题10分，共80分）1．（10分）计算：（2014×2014+2012）﹣2013×2013 6039 ．【分析】把2014看作2013+1，把2012看作2013﹣1，进行简算即可．【解答】解：（2014×2014+2012）﹣2013×2013＝[（2013+1）×（2013+1）+（2013﹣1）]﹣2013×2013＝（2013+1）×（2013+1）+2013﹣1﹣2013×2013＝2013×2013+2013+2013+1+2013﹣1﹣2013×2013＝（2013×2013﹣2013×2013）+（1﹣1）+（2013+2013+1+2013）＝6039．故答案为：6039．2．（10分）将长方形的纸片ABCD按右图的方式折叠后压平，使三角形DCF 落在三角形DEF的位置，顶点E恰落在边AB上．已知∠1＝22°，那么∠2是44 度．【分析】由题意可知：因为是翻折，∠CFD应该和∠EFD相等，又因∠DEF 等于90°，∠1＝22°，于是利用三角形的内角和定理即可求出∠DFE的度数，又因∠CFD和∠EFD和∠2构成了一个平角，平角是180°，据此即可求出∠2的度数．【解答】解：因为翻折，∠CFD＝∠EFD＝90°﹣22°＝68°，∠2＝180°﹣68°﹣68°＝44°．故答案为：44．3．（10分）鸡兔同笼，共有40个头，兔脚的数目比鸡脚的数目的10倍少8只，那么兔有33 只．【分析】设兔有x只，则鸡有（40﹣x）只，根据脚的倍数关系：兔脚的数＝鸡脚的数×10倍+8只，可列方程解答即可．【解答】解：设兔有x只，则鸡有（40﹣x）只，根据脚的倍数关系可列方程：4x+8＝10×2×（40﹣x）4x+8＝800﹣20xx＝33答：兔子有33只．故答案为：33．4．（10分）第一次操作将图a左下角的正方形分为四个小正方形，见图b；第二次操作再将图b左下角的小正方形分为四个更小的正方形，见图c；这样继续下去，当完成第六次操作时，得到的图形中共有29 个正方形．【分析】图a有5个正方形，以后每次操作将一个正方形数目变成四个小正方形，每次增加4个正方形．所以答案为5+6×4＝29．【解答】解：5+6×4＝29．故答案为：29．5．（10分）如图加法竖式中，相同的汉字代表1至 9中的相同数字，而不同的汉字代表不同的数字．则竖式中的“数学”所表示的两位数共有 3 个．【分析】根据“学+学+学”没有进位，可知“学”只有3种可能．“学”＝1，“学习”＝17，“数学”＝51；“学”＝2，“学习”＝24，“数学”＝72；“学”＝3，“学习”＝31，“数学”＝93．竖式中的“数学”所表示的两位数共有3个．【解答】解：根据题干分析可得：所以数学表示的两位数是51或72或93，一共有3个．答：竖式中的“数学”所表示的两位数共有 3个．故答案为：3．6．（10分）大小两个正方体积木粘在一起，构成如图所示的立体图形，其中小积木的下底面的四个顶点，恰好是大积木的上底面各边的中点．如果大积木的棱长为2，那么这个立体图形的表面积是32 ．【分析】如图，因为小积木的下底面的四个顶点，恰好是大积木的上底面各边的中点，所以大正方体一个面的面积是小正方体一个面的面积的2倍．因此，这个立体图形的表面积是大正方体的表面积加上小正方体四个面的面积．据此解答．【解答】解：6×2×2+4×（2×2÷2）＝24+4×2＝24+8＝32．答：这个立体图形的表面积是32．故答案为：32．7．（10分）某班学生人数大于20而小于30，其中女同学的人数是男同学的2倍．全班报名参加“华杯赛”的人数是未报名人数的3倍少1人．这个班有学生27 名．【分析】女同学的人数是男同学的2倍，所以全班人数是3的倍数，全班人数只能是21，24，27；全班报名参加“华杯赛”的人数是未报名人数的3倍少1人，所以全班人数加1人，是4的倍数；检验的全班人数为27人．【解答】解：根据分析知：全班人数是3的倍数，全班人数只能是21，24，27；全班报名参加“华杯赛”的人数是未报名人数的3倍少1人，所以全班人数加1人，是4的倍数；检验的全班人数为27人．故答案为：27．8．（10分）如图，图形内的数字分别表示所在的矩形或三角形的面积，那么阴影三角形的面积为9 ．【分析】如下图所示：OA×OC＝30，OD×OF＝12，将两个式子的等号的两边分别相乘，得出OA×OC×OD×OF＝30×12，而OC×OD＝10×2＝20，由此得出OA×OF，进而求出阴影三角形的面积．【解答】解：因为OA×OC＝30，OD×OF＝12，所以OA×OC×OD×OF＝30×12＝360．又因为OC×OD＝10×2＝20，所以OA×OF＝360÷20＝18．所以S△AGF＝GF•AG＝OA•OF＝×18＝9；答：阴影三角形的面积为9．故答案为：9．二、简答题（每小题15分，共60分，要求写出简要过程）9．（15分）用四个数字4和一些加、减、乘、除号和括号，写出四个分别等于3、4、5和6的算式．【分析】因为12÷4＝3，4+4+4＝12，所以可以写成（4+4+4）÷4＝3；因为4×（4﹣4）＝0，4﹣0＝4，所以可以写成4﹣（4﹣4）×4＝4；因为4×5＝20，20÷4＝5，所以可以写成（4×4+4）÷4＝5；因为2+4＝6，（4+4）÷4＝2，所以可以写成（4+4）÷4+4＝6．【解答】解：（4+4+4）÷4＝3；4﹣（4﹣4）×4＝4；（4×4+4）÷4＝5；（4+4）÷4+4＝6；10．（15分）如图是U，V，W，X四辆不同类型的汽车每百千米的耗油量．如果每辆车都有50升油，那么这四辆车最多可行驶的路程总计是多少千米？【分析】根据统计图所提供的信息，可以看出每种车每百千米的耗油量，用50（升）除以每种车的百千米耗油量（升），就是每种车行驶的路程，把四辆车行驶的路程相加即可．【解答】解：（50÷20+50÷25+50÷5+50÷10）×100＝（2.5+2+10+5）×100＝19.5×100＝1950（千米）答：这四辆车最多可行驶的路程总计是1950千米．11．（15分）某商店卖出一支钢笔的利润是9元，一个小熊玩具的进价为2元．一次商家采取“买4支钢笔赠送一个小熊玩具”的打包促销，共获利润1922元．问这次促销最多卖出了多少支钢笔？【分析】根据题意，“买4支钢笔赠送一个小熊玩具”这样卖4支钢笔实得利润9×4﹣2＝34元，要这次促销钢笔卖出最多，则要求尽量打包销售．由此可以求出1922是34的多少倍就是打包卖出多少个4支，进而求出最多卖出多少支钢笔．据此解答．【解答】解析：要这次促销钢笔卖出最多，则要求尽量打包销售．1922÷（4×9﹣2）＝1922÷34＝56（倍）…18（元）；18÷9＝2（支）；56×4+2＝224+2＝226（支）．答：这次促销最多卖出了226支钢笔．12．（15分）编号从1到10的10个白球排成一行，现按照如下方法涂红色：（1）涂2个球；（2）被涂色的2个球的编号之差大于2．那么不同的涂色方法有多少种？【分析】本题采用枚举法，令被涂色的第一个球的编号小于第二个球的编号，由于8+2＝10，要使编号之差大于2，所以第二个球编号最大是7，那么第一个球可以是1～7号中的任意一个，由此进行逐个情况讨论，最后再把各种情况的种数相加即可．【解答】解：第一个球涂1号，则另一个球可涂4～10；有7种不同的情况；第一个球涂2号，则另一个球可涂5～10；有6种不同的情况；第一个球涂3号，则另一个球可涂6～10；有5种不同的情况；第一个球涂4号，则另一个球可涂7～10；有4种不同的情况；第一个球涂5号，则另一个球可涂8～10；有3种不同的情况；第一个球涂6号，则另一个球可涂9～10；有2种不同的情况；第一个球涂7号，则另一个球可涂10；有1种不同的情况；所以，不同的涂色方法有：7+6+5+4+3+2+1＝28（种）．答：不同的涂色方法有28种．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:52:49；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800第11页（共11页）。

2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷（小高组B卷）一、填空题（每空3分，第8小题6分，共30分）1．（3分）计算：19×0.125+281×+12.5＝．2．（6分）农谚‘逢冬数九’讲的是，从冬至之日起，每九天分为一段，依次称之为一九，二九，…，九九，冬至那天是一九的第一天．2012年12月21日是冬至，那么2013年的2月10日是九的第天．3．（3分）某些整数分别被，，，除后，所得的商化作带分数时，分数部分分别是，，，，则满足条件且大于1的最小整数是．4．（3分）如图，P，Q分别是正方形ABCD的边AD和对角线 AC上的点，且PD：AP＝4：1，QC：AQ＝2：3，如果正方形ABCD的面积为25，那么三角形PBQ的面积是．5．（3分）有一筐苹果，甲班分，每人3个还剩10个；乙班分，每人4个还剩11个；丙班分，每人5个还剩12个．那么这筐苹果至少有个．6．（3分）两个大小不同的正方体积木粘在一起，构成图所示的立体图形，其中，小积木的粘贴面的四个顶点分别是大积木的粘贴面各边不是中点的一个四等分点．如果大积木的棱长为4，则这个立体图形的表面积为．7．（6分）甲、乙两车分别从A，B两地同时出发相向而行，甲车每小时行40千米，乙车每小时行60千米．两车分别到达B地和A地后，立即返回．返回时，甲车的速度增加二分之一，乙车的速度不变．已知两车两次相遇处的距离是50千米，则A，B两地的距离为千米．8．（3分）用“学”和“习”代表两个不同的数字，四位数“”与“”的积是一个七位数，且它的个位和百万位数字与“学”所代表的数字相同，那么“”所能代表的两位数共有个．二、解答下列各题（每题10分，共40分，要求写出简要过程）9．（10分）如图中，不含“*”的长方形有多少个？10．（10分）如图，三角形ABC中，AD＝2BD，AD＝EC，BC＝18，三角形AFC 的面积和四边形DBEF的面积相等，那么AB的长度是多少？11．（10分）若干人完成了植树2013棵的任务，每人植树的棵数相同．如果有5人不参加植树，其余的人每人多植2棵不能完成任务，而每人多植3棵可以超额完成任务．问：共有多少人参加了植树？12．（10分）由四个完全相同的正方体堆积成如图所示的立体，则立体的表面上（包括底面）所有黑点的总数至多是．三、解答下列各题（每小题15分，共30分，要求写出详细过程）13．（15分）用八个如图所示的2×1的小长方形可以拼成一个4×4的正方形．若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同，则认为两个拼成的正方形相同．问：可以拼成几种两条对角线都是其对称轴的正方形图形？14．（15分）对于155个装有红、黄、蓝三种颜色球的盒子，有三种分类方法：对于每种颜色，将该颜色的球数目相同的盒子归为一类．若从1到30之间所有的自然数都是某种分类中一类的盒子数，那么，（ 1）三种分类的类数之和是多少？（ 2）说明，可以找到三个盒子，其中至少有两种颜色的球，它们的数目分别相同．2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷（小高组B卷）参考答案与试题解析一、填空题（每空3分，第8小题6分，共30分）1．（3分）计算：19×0.125+281×+12.5＝50 ．【分析】根据乘法分配律进行简算．【解答】解：19×0.125+281×+12.5＝19×0.125+281×0.125+100×0.125＝（19+281+100）×0.125＝400×0.125＝50．故答案为：50．2．（6分）农谚‘逢冬数九’讲的是，从冬至之日起，每九天分为一段，依次称之为一九，二九，…，九九，冬至那天是一九的第一天．2012年12月21日是冬至，那么2013年的2月10日是六九的第7 天．【分析】先求出2012年12月21日到2013年的2月10日经过了多少天，再求这些天里有几个9天，还余几天，再根据余数推算是几九第几天即可．【解答】解：2012年12月21日到2013年的2月10日的元旦共有11+31+10＝52天，52÷9＝5…7，说明已经经过了5个9天，还余7天，这一天就是六九的第7天．答：2013年的2月10日是六九的第7天．故答案为：六，7．3．（3分）某些整数分别被，，，除后，所得的商化作带分数时，分数部分分别是，，，，则满足条件且大于1的最小整数是3466 ．【分析】设这个数为x，则：x÷＝x，x÷＝x，x÷＝x，x÷＝x，因此这个数应是分母的最小公倍数+1，据此解答．【解答】解：设这个数为x，则：x÷＝x，x÷＝x，x÷＝xx÷＝x因此这个数应是分母的最小公倍数+1，即5×7×9×11+1＝3465+1＝3466答：满足条件且大于1的最小整数是3466．故答案为：3466．4．（3分）如图，P，Q分别是正方形ABCD的边AD和对角线 AC上的点，且PD：AP＝4：1，QC：AQ＝2：3，如果正方形ABCD的面积为25，那么三角形PBQ的面积是 6.5 ．【分析】过Q点作，EF∥AB，交AD于F，交BC于E，QG⊥DC于G，根据相似比可以求出各线段的长度，再用正方形的面积分别减去其余的部分，可得最后结果．【解答】解：连结QD，作EF∥AB，交AD于F，交BC于E，QG⊥DC于G，因为正方形ABCD的面积为25，所以AD＝EF＝5；因为QC：AQ＝2：3，根据正方形的对称性，所以QE＝QG＝2，QF＝3．因为PD：AP＝4：1，所以AP＝1，PD＝4．S△PQD＝S正方形ABCD﹣S△CQB﹣S△DQC﹣S△PQD﹣S△PAB＝25﹣2×5÷2﹣2×5÷2﹣4×3÷2﹣1×5÷2＝25﹣5﹣5﹣6﹣2.5＝6.5．答：三角形PBQ的面积是6.5．故答案为：6.5．5．（3分）有一筐苹果，甲班分，每人3个还剩10个；乙班分，每人4个还剩11个；丙班分，每人5个还剩12个．那么这筐苹果至少有67 个．【分析】因为10÷3＝3…1，11÷4＝2…3，12÷5＝2…2，苹果个数除以3余1，除以4少1，除以5余2，满足除以3余1，除以4少1的数最少是7，7除以5余数刚好是2，又因为苹果个数大于12，3、4、5的最小公倍数是60，所以这筐苹果至少有：60+7＝67；由此解答即可．【解答】解：10÷3＝3…1，11÷4＝2…3，12÷5＝2…2，满足除以3余1，除以4少1的数最少是7，7除以5余数刚好是2，又因为苹果个数大于12，所以苹果至少：3×4×5+7＝60+7＝67（个）；答：这筐苹果至少有67个．故答案为：67．6．（3分）两个大小不同的正方体积木粘在一起，构成图所示的立体图形，其中，小积木的粘贴面的四个顶点分别是大积木的粘贴面各边不是中点的一个四等分点．如果大积木的棱长为4，则这个立体图形的表面积为136 ．【分析】观察图形可知，大正方体与小正方体的相连的两个面如图所示：因为大正方体的棱长是4，则四周的小直角三角形的直角边分别是3、1；如果把四周的四个直角三角形剪下来，正好拼成一个一个面的面积是4×4﹣3×1÷2×4＝10的正方形，根据正方形的面积公式可得：大正方体的一个面的面积是4×4＝16；则这个立方体的表面积就是大正方体的表面积与小正方体的四个面的面积之和，据此即可解答．【解答】解：根据题干分析可得：大正方体的一个面的面积是：4×4＝16，小正方体一个面的面积是：4×4﹣3×1÷2×4＝16﹣6＝10，所以这个立体图形的表面积是：16×6+10×4＝96+40＝136，答：这个立体图形的表面积为136．故答案为：136．7．（6分）甲、乙两车分别从A，B两地同时出发相向而行，甲车每小时行40千米，乙车每小时行60千米．两车分别到达B地和A地后，立即返回．返回时，甲车的速度增加二分之一，乙车的速度不变．已知两车两次相遇处的距离是50千米，则A，B两地的距离为千米．【分析】已知原来甲车每小时行40千米，乙车每小时行60千米，则此时两车的速度比是40：60＝2：3，则第一次相遇时，甲行了全程的＝，乙行了全程的＝；甲车加速后，速度是每小时60×（1+）＝60千米，即两车返回时的速度相同．当甲到达B地时，乙速度快，在此之前就返回了，由于此时甲行完全程，则乙所行路程是甲的，即此时乙从A地返回又行了全程的﹣1＝，剩下路程两人速度一样，则各行一半，即在距B地处相遇，所以50千米占全程的﹣＝，则全程是50÷千米．【解答】解：甲乙两车的速度比是：40：60＝2：3，甲车加速后是每小时行：60×（1+）＝60千米，（﹣1）÷2＝50÷（﹣）＝50÷（﹣）＝50＝（千米）答：两地相距千米．故答案为：．8．（3分）用“学”和“习”代表两个不同的数字，四位数“”与“”的积是一个七位数，且它的个位和百万位数字与“学”所代表的数字相同，那么“”所能代表的两位数共有 3 个．【分析】因为四位数“”与“”的积是一个七位数，且它的个位和百万位数字与“学”所代表的数字相同，那么习＝1，若习取大于1的数字，则不满足题意，又因为1111×2222＝2468642，1111×3333＝3702963，1111×4444＝4937284，1111×5555＝6171605，不符合题意，据此即可解答问题．【解答】解：根据题干分析可得：1111×2222＝2468642，1111×3333＝3702963，1111×4444＝4937284，它们的积的个位和百万位数字与“学”所代表的数字相同，那么习＝1，所以“”所能代表的两位数有21、31、41，一共有3个．答：“”所能代表的两位数共有 3个．故答案为：3．二、解答下列各题（每题10分，共40分，要求写出简要过程）9．（10分）如图中，不含“*”的长方形有多少个？【分析】如下图：含有A的标记*的长方形有4×15＝60个，含有B的标记*的长方形有4×15＝60个，含有标记A和标记B的长方形有4×4＝16个，所以含有*的三角形有60+60﹣16＝104个，再算出图中一共长方形的个数，据此解答．【解答】解：图中共有长方形：×＝21×10＝210（个），含有A的标记*的长方形：4×15＝60（个），含有B的标记*的长方形：4×15＝60（个），含有标记A和标记B的长方形：4×4＝16（个），所以含有*的长方形：60+60﹣16＝104（个），不含“*”的长方形：210﹣104＝106．答：不含“*”的长方形有106个．10．（10分）如图，三角形ABC中，AD＝2BD，AD＝EC，BC＝18，三角形AFC 的面积和四边形DBEF的面积相等，那么AB的长度是多少？【分析】此题可以设想通过求得AD、BD的长度，来求AB的长度．因为AD ＝EC，只要求出EC的长度，就可知AD的长度．根据三角形AFC的面积和四边形DBEF的面积相等，求得＝，即可求出EC＝BC＝×18＝6；再根据AD＝2BD，求得2BD＝6，则BD＝3，因此求出AB的长度，解决问题．【解答】解：设S△AFC＝S四边形DBEF＝1，S△CEF＝x，S△ADF＝y，因为AD＝2BD，所以＝＝，即＝＝，解得y＝2x+1则＝＝＝，所以＝．所以EC＝×BC＝×18＝6，则AD＝EC＝6．又因为AD＝2BD，BD＝AD÷2＝6÷2＝3．综上，AB＝AD+BD＝6+3＝9．答：AB的长度是9．11．（10分）若干人完成了植树2013棵的任务，每人植树的棵数相同．如果有5人不参加植树，其余的人每人多植2棵不能完成任务，而每人多植3棵可以超额完成任务．问：共有多少人参加了植树？【分析】根据时间知“若干人完成了植树2013棵的任务，每人植树的棵数相同”，则人数与棵数是2013的因数，可设原来有a人，每人植树b棵，则ab＝2013，因有5人不参加植树，所以，a＞5．“如果有5人不参加植树，其余的人每人多植2棵不能完成任务，而每人多植3棵可以超额完成任务”．则2（a﹣5）＜5b＜3（a﹣5）．据此解答．【解答】解：设原来a人，每人b棵ab＝2013，a＞52（a﹣5）＜5b＜3（a﹣5）2（a﹣5）÷5＜b＜3（a﹣5）÷5b在0.5（a﹣5）附近2013＝33×61符合a＝61，b＝33共有61人参加植树．答：共有61人参加了植树．12．（10分）由四个完全相同的正方体堆积成如图所示的立体，则立体的表面上（包括底面）所有黑点的总数至多是59 ．【分析】每个正方体总点数为1+2+3+4+5+6＝21，4个正方体共84个黑点，因为要求黑点的总数至多是多少，因此，遮住的部分的点数应尽量少．然后根据相邻边的点数推出个正方体被遮住的面上的点数，解决问题．【解答】解：每个正方体总点数为1+2+3+4+5+6＝21，4个正方体共84个黑点，因为要求黑点的总数至多是多少，因此，遮住的部分的点数应尽量少．根据相邻边的点数推出：最上面正方体底面点数为5；右面正方体的左面的点数为6；中间正方体5的对面是2，因此被遮住部分的总点数为21﹣5﹣2﹣6＝8；左边正方体右面的点数为6．因此立体的表面上（包括底面）所有黑点的总数至多是84﹣（5+6+8+6）＝84﹣25＝59．故答案为：59．三、解答下列各题（每小题15分，共30分，要求写出详细过程）13．（15分）用八个如图所示的2×1的小长方形可以拼成一个4×4的正方形．若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同，则认为两个拼成的正方形相同．问：可以拼成几种两条对角线都是其对称轴的正方形图形？【分析】用右图代替题目中的2×1小长方形，因为题目所给的小长方形的上下不对称，所以同一个小长方形在拼成的两条对角线都是其对称轴的正方形图形中，这样，就可以只考虑上半部分的不同情形，据此画图分析解解答．【解答】解：如图：答：以拼成4种两条对角线都是其对称轴的正方形图形．14．（15分）对于155个装有红、黄、蓝三种颜色球的盒子，有三种分类方法：对于每种颜色，将该颜色的球数目相同的盒子归为一类．若从1到30之间所有的自然数都是某种分类中一类的盒子数，那么，（ 1）三种分类的类数之和是多少？（ 2）说明，可以找到三个盒子，其中至少有两种颜色的球，它们的数目分别相同．【分析】根据题意，可得a1，a2，a3，…，a i；b1，b2，b3，…，b j；c1，c2，c3，…，c k，包含了1到30的所有整数，所以n≥30，另一方面，3×155＝a1+a2+a3+…+a i+b1+b2+b3+…+b j+c1+c2+c3+…+c k≥1+2+3+…+30＝＝465＝3×155．故三种分类的类数之和是30．进而论证得出答案．【解答】解：（1）因为 a1，a2，a3，…，a i；b1，b2，b3，…，b j；c1，c2，c3，…，c k包含了1到30的所有整数，所以n≥30，另一方面，3×155＝a1+a2+a3+...+a i+b1+b2+b3+...+b j+c1+c2+c3+...+c k≥1+2+3+ (30)＝465＝3×155．所以n＝i+j+k＝30，三种分类的类数之和是30．（2）不妨设a1＝30，记这30个盒子的类为A类．因为i+j+k＝30，必有j≤14或k≤14，不妨设j≤14．A类的30个盒子分到这不超过14个类中去，必有一类至少有三个盒子，这三个盒子里的红球数相同并且黄球数也相同．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:52:54；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800。

2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷（小中组B卷）一、填空题（每小题10分，共80分）1．（10分）计算：（2014×2014+2012）﹣2013×2013 ．2．（10分）将长方形的纸片ABCD按右图的方式折叠后压平，使三角形DCF 落在三角形DEF的位置，顶点E恰落在边AB上．已知∠1＝22°，那么∠2是度．3．（10分）亮亮上学，若每分钟行40米，则8：00准时到校；若每分钟行50米，则7：55到校．亮亮的家与学校的距离是米．4．（10分）第一次操作将图a左下角的正方形分为四个小正方形，见图b；第二次操作再将图b左下角的小正方形分为四个更小的正方形，见图c；这样继续下去，当完成第五次操作时，得到的图形中共有个正方形．5．（10分）“熊大”ד熊二”＝“熊兄弟”．若相同的汉字代表 0至9中的相同数字，不同的汉字代表不同的数字，且“大”＞“二”，则所有满足条件的“熊兄弟”代表的三位数之和是．6．（10分）鸡兔同笼，共有40个头，兔脚的数目比鸡脚的数目的10倍少8只，那么兔有只．7．（10分）如图所示的手串中，从挂坠的珠子开始逆时针将珠子1至22依次编号．小明玩数珠子游戏，规则是：从1号珠子开始顺时针逐个珠子连续地数自然数，但每当数到含数字7或7的倍数的数时就跳过它，直接数下一个数．例如：数到6时下一个数8，数到13时下一个数15，…．那么数到100时应落在第号珠子上．8．（10分）布袋中有60个彩球，每种颜色的球都有6个．蒙眼取球，要保证取出的球中有三个同色的球，至少要取出个球．二、简答题（每小题15分，共60分，要求写出简要过程）9．（15分）一块长方形的地ABCD分成如图所示的两个长方形，分别承包给甲、乙两户．甲户的蔬菜大棚与乙户的鸡场面积相等，剩下的部分甲户比乙户的面积多96亩．已知BF＝3CF，那么长方形ABCD的总面积是多少亩？10．（15分）如图是U，V，W，X四辆不同类型的汽车每百千米的耗油量．如果每辆车都有50升油，那么这四辆车最多可行驶的路程总计是多少千米？11．（15分）甲、乙、丙、丁四人分2013块糖果，甲分得的糖果比乙的2倍多10块，比丙的3倍多18块，比丁的5倍少55块．那么甲分得糖果多少块？12．（15分）编号从1到10的10个白球排成一行，现按照如下方法涂红色：（1）涂2个球；（2）被涂色的2个球的编号之差大于2．那么不同的涂色方法有多少种？2013年第十八届“华罗庚金杯”少年数学邀请赛决赛试卷（小中组B卷）参考答案与试题解析一、填空题（每小题10分，共80分）1．（10分）计算：（2014×2014+2012）﹣2013×2013 6039 ．【分析】把2014看作2013+1，把2012看作2013﹣1，进行简算即可．【解答】解：（2014×2014+2012）﹣2013×2013＝[（2013+1）×（2013+1）+（2013﹣1）]﹣2013×2013＝（2013+1）×（2013+1）+2013﹣1﹣2013×2013＝2013×2013+2013+2013+1+2013﹣1﹣2013×2013＝（2013×2013﹣2013×2013）+（1﹣1）+（2013+2013+1+2013）＝6039．故答案为：6039．2．（10分）将长方形的纸片ABCD按右图的方式折叠后压平，使三角形DCF 落在三角形DEF的位置，顶点E恰落在边AB上．已知∠1＝22°，那么∠2是44 度．【分析】由题意可知：因为是翻折，∠CFD应该和∠EFD相等，又因∠DEF 等于90°，∠1＝22°，于是利用三角形的内角和定理即可求出∠DFE的度数，又因∠CFD和∠EFD和∠2构成了一个平角，平角是180°，据此即可求出∠2的度数．【解答】解：因为翻折，∠CFD＝∠EFD＝90°﹣22°＝68°，∠2＝180°﹣68°﹣68°＝44°．故答案为：44．3．（10分）亮亮上学，若每分钟行40米，则8：00准时到校；若每分钟行50米，则7：55到校．亮亮的家与学校的距离是1000 米．【分析】由题意，每分钟行40米，刚好够分；若每分钟行50米，则少5×50＝250米，所以250÷（50﹣40）＝25分钟，亮亮的家与学校的距离是25×40＝1000米；据此解答．【解答】解：每分钟行40米，刚好够分；若每分钟行50米，则少5×50＝250米，所以250÷（50﹣40）＝25分钟，亮亮的家与学校的距离是25×40＝1000米；答：亮亮的家与学校的距离是1000米．故答案为：1000．4．（10分）第一次操作将图a左下角的正方形分为四个小正方形，见图b；第二次操作再将图b左下角的小正方形分为四个更小的正方形，见图c；这样继续下去，当完成第五次操作时，得到的图形中共有25 个正方形．【分析】图a有5个正方形，以后每次操作将一个正方形数目变成四个小正方形，每次增加4个正方形，所以可得计算公式：5+n（n﹣1）．【解答】解：当完成第五次操作时，得到的图形中共有：5+4n＝5+4×5＝25（个）答：当完成第五次操作时，得到的图形中共有25个正方形．故答案为：255．（10分）“熊大”ד熊二”＝“熊兄弟”．若相同的汉字代表 0至9中的相同数字，不同的汉字代表不同的数字，且“大”＞“二”，则所有满足条件的“熊兄弟”代表的三位数之和是686 ．【分析】根据题意，“熊”＝1，若“大”ד二”＜10，则“大”+“二”＜10；若“大”ד二”＞9，则“大”+“二”＜9；然后运用枚举法，解决问题．【解答】解：根据题意，“熊”＝1，若“大”ד二”＜10，则“大”+“二”＜10；若“大”ד二”＞9，则“大”+“二”＜9；枚举：“熊二”＝10，弟为0，“熊大”没有可以取的值．因为不同的汉字代表不同的数字；“熊二”＝12，“熊大”可以为13，14，15，16（舍去，数字重复）；“熊二”＝13，“熊大”可以为14，15（舍去，数字重复）；“熊二”＝14，“熊大”没有可以取的值．所以“熊兄弟”代表的三位数之和是：12×（13+14+15）+13×14＝686．故答案为：686．6．（10分）鸡兔同笼，共有40个头，兔脚的数目比鸡脚的数目的10倍少8只，那么兔有33 只．【分析】设兔有x只，则鸡有（40﹣x）只，根据脚的倍数关系：兔脚的数＝鸡脚的数×10倍+8只，可列方程解答即可．【解答】解：设兔有x只，则鸡有（40﹣x）只，根据脚的倍数关系可列方程：4x+8＝10×2×（40﹣x）4x+8＝800﹣20xx＝33答：兔子有33只．故答案为：33．7．（10分）如图所示的手串中，从挂坠的珠子开始逆时针将珠子1至22依次编号．小明玩数珠子游戏，规则是：从1号珠子开始顺时针逐个珠子连续地数自然数，但每当数到含数字7或7的倍数的数时就跳过它，直接数下一个数．例如：数到6时下一个数8，数到13时下一个数15，…．那么数到100时应落在第 4 号珠子上．【分析】含数字7或7的倍数的数有：个位是：7，17，27，…，97，十位：70，71，72，…，79，7的倍数：100÷7＝14…2，其中7、70、77既是7的倍数又含有7，据此解答即可．【解答】解：含数字7或7的倍数的数有：个位是：7，17，27， (97)十位：70，71，72，…，79，7的倍数：100÷7＝14…2，其中7、70、77既是7的倍数又含有7，因此共有10+10+14﹣4＝30，100﹣30＝70，70÷22＝3 (4)答：数到100时应落在第4号珠子上．故答案为：4．8．（10分）布袋中有60个彩球，每种颜色的球都有6个．蒙眼取球，要保证取出的球中有三个同色的球，至少要取出21 个球．【分析】60÷6＝10，有10种彩球，考虑最不利情况，每种彩球都拿了2个，再拿一个就能保证取出的球中有三个同色的球，所以答案为2×10+1＝21．【解答】解：60÷6＝10（个），2×10+1＝21（个）；答：至少要取出21个球；故答案为：21．二、简答题（每小题15分，共60分，要求写出简要过程）9．（15分）一块长方形的地ABCD分成如图所示的两个长方形，分别承包给甲、乙两户．甲户的蔬菜大棚与乙户的鸡场面积相等，剩下的部分甲户比乙户的面积多96亩．已知BF＝3CF，那么长方形ABCD的总面积是多少亩？【分析】根据题意，可知BF＝3CF，所以甲户的长方形面积是乙户的长方形面积的3倍，甲户的蔬菜大棚与乙户的鸡场面积相等，剩下的部分甲户比乙户的面积多96亩．则说明甲户的长方形面积比乙户的长方形面积多96亩，根据差倍问题，乙户的长方形面积为96÷（3﹣1）＝48亩，所以长方形ABCD的总面积是48×（1+3）＝192亩．【解答】解：因为BF＝3CF，所以长方形ABEF的面积＝长方形EFCD面积×3，甲户的蔬菜大棚与乙户的鸡场面积相等，剩下的部分甲户比乙户的面积多96亩．乙户的长方形面积为：96÷（3﹣1）＝48（亩），所以长方形ABCD的总面积是：48×（1+3）＝192（亩）．10．（15分）如图是U，V，W，X四辆不同类型的汽车每百千米的耗油量．如果每辆车都有50升油，那么这四辆车最多可行驶的路程总计是多少千米？【分析】U类型：100千米耗油20升，先用50升除以20升，求出50升能跑多少个100千米，再乘上100千米，就是U型车可以行驶的路程；同理求出V，W，X各可以跑多少千米，然后相加即可．【解答】解：（50÷20）×100+（50÷25）×100+（50÷5）×100+（50÷10）×100＝250+200+1000+500＝1950（千米）答：这四辆车最多可行驶的路程总计是1950千米．11．（15分）甲、乙、丙、丁四人分2013块糖果，甲分得的糖果比乙的2倍多10块，比丙的3倍多18块，比丁的5倍少55块．那么甲分得糖果多少块？【分析】设甲分得糖果x块，依据题意可得：乙分得糖×（x﹣10）块，丙分得×（x﹣18）块，丁分得糖×（x+55）块，再根据四人共分得2013块可列方程：x+×（x﹣10）+×（x﹣18）+×（x+55）＝2013，依据等式的性质即可求解．【解答】解：设甲分得糖果x块x+×（x﹣10）+×（x﹣18）+×（x+55）＝20132x＝20132x÷2＝2013x＝990答：甲分得糖果990块．12．（15分）编号从1到10的10个白球排成一行，现按照如下方法涂红色：（1）涂2个球；（2）被涂色的2个球的编号之差大于2．那么不同的涂色方法有多少种？【分析】本题采用枚举法，令被涂色的第一个球的编号小于第二个球的编号，由于8+2＝10，要使编号之差大于2，所以第二个球编号最大是7，那么第一个球可以是1～7号中的任意一个，由此进行逐个情况讨论，最后再把各种情况的种数相加即可．【解答】解：第一个球涂1号，则另一个球可涂4～10；有7种不同的情况；第一个球涂2号，则另一个球可涂5～10；有6种不同的情况；第一个球涂3号，则另一个球可涂6～10；有5种不同的情况；第一个球涂4号，则另一个球可涂7～10；有4种不同的情况；第一个球涂5号，则另一个球可涂8～10；有3种不同的情况；第一个球涂6号，则另一个球可涂9～10；有2种不同的情况；第一个球涂7号，则另一个球可涂10；有1种不同的情况；所以，不同的涂色方法有：7+6+5+4+3+2+1＝28（种）．答：不同的涂色方法有28种．声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布日期：2019/5/7 10:51:35；用户：小学奥数；邮箱：pfpxxx02@；学号：20913800第11页（共11页）。

总分第十八届华罗庚金杯少年邀请赛决赛试题A(小学中年级组)(时间2013年4月20日10:00-11:30)一、填空题《每小跑10分.共80分)1.计算：(2014×20l∙H2012)-20l3×20l3.解析：(20MX20M+2Q12)-2013X2013=(2013+1)×(2013+1)*2013—1-2013×2013-2013×2013*2013^2013H∙201312013X2013=6039或用平方差公式，(2014×2014+2012)-2013×2013=201Γ-2013^2012=2012+2013÷2011=6039考试中展比接的方法,死算也。

K.2.超长方形的纸片A8C/)按右图的方式折：3后；1」'.使形。

“*在三角形。

EF的位置.JS点E恰落在边AB上.己知N1=20°,加么N2是------- 度.解析：因为翎折,∕CFD=∕EFD=9(V-22"=68°λ-------------- S iZ2=i80o-68o-68o=44°3.亮亮上学，若株分钟行∙10米，则8:00准时到校：若年分钟行50米，则7:55到校.亮亮的家与学校的距国是米.解析：行程里盈亏何虺.每分钟行4。

代刚好膨分：苦行分钟行50米,则少5X50=250米所以25。

+(50-40)=25分钟,亮亮的家与学校的距离是25X40=1000米.法二：六年级可以用.走同样路程.速度比与时间成反比,速度比为4:5,则时间比为5:4.8:007:55=5分钟,则若每分伸行40米.亮亮用时5÷(5-4)X5=25分钟，所以亮亮的家3学校的距点是25X10=1000米.1.第一次操作将图a左下角的正方形分为四个小正方形.见图b;笫二次操作再将图b左下角的小正方形分为四个更小的正方形.见图c：这样缚续卜2.当完成第八.次操作时.得到的图形中共有个正方形.解析:找规律，图a有S个正方形,以后短次悚作将•个正方形数日变成四个小正方形,鲜次Je加4个正方形。

第十八届华罗庚金杯少年数学邀请赛初赛试卷A（小学中年级组）第十八届华罗庚金杯少年数学邀请赛初赛试卷A（小学中年级组）装（时间: 2013 年 3 月23 日10:00 ~ 11:00）一、选择题(每小题10 分, 满分60 分. 以下每题的四个选项中, 仅有一个是正确的, 请将表示正确答案的英文字母写在每题的圆括号内.)1. 45 与40 的积的数字和是（）.（A）9 （B）11 （C）13 （D）152. 在下面的阴影三角形中, 不能由右图中的阴影三角形经过旋转、订平移得到的是图（）中的三角形.（A）（B）（C）（D）3. 小东、小西、小南、小北四个小朋友在一起做游戏时, 捡到了一条红领巾, 交给了老师. 老师问是谁捡到的？小东说不是小西；小西说是小南；小南说小东说的不对；小北说小南说的也不对. 他们之中只有一个人说对了, 这个人是（）.线（A）小东（B）小西（C）小南（D）小北4. 2013 年的钟声敲响了, 小明哥哥感慨地说：这是我有生以来遇到的第一个没有重复数字的年份. 已知小明哥哥出生的年份是19 的倍数, 那么2013 年小明哥哥的年龄是（）岁.（A）16 （B）18 （C）20 （D）22总分第十八届华罗庚金杯少年数学邀请赛初赛试卷A（小学中年级组）5. 如右图, 一张长方形的纸片, 长20 厘米, 宽16 厘米. 如果从这张纸上剪下一个长10 厘米, 宽5 厘米的小长方形, 而且至少有一条边在原长方形的边上, 那么剩下纸片的周长最大是（）厘米.（A）72 （B）82 （C）92 （D）1026. 张老师每周的周一、周六和周日都跑步锻炼20 分钟, 而其余日期每日都跳绳20 分钟. 某月他总共跑步5 小时, 那么这个月的第10 天是（）.（A）周日（B）周六（C）周二（D）周一二、填空题(每小题10 分, 满分40 分)7. 如右图, 一个正方形被分成了4 个相同的长方形, 每个长方形的周长都是20 厘米. 则这个正方形的面积是平方厘米.8. 九个同样的直角三角形卡片, 拼成了如右图所示的平面图形.这种三角形卡片中的两个锐角较大的一个是度.9. 幼儿园的老师给班里的小朋友送来55 个苹果, 114 块饼干, 83 块巧克力. 每样都平均分发完毕后, 还剩3 个苹果, 10 块饼干, 5 块巧克力. 这个班最多有位小朋友.10. 如下图, 将长度为9 的线段AB 九等分, 那么图中所有线段的长度的总和是.第十八届华罗庚金杯少儿数学邀请赛初赛试卷A(小中年级组)试题解析一、选择题1. 45 与 40 的积的数字和是（）.（A）9 （B）11 （C）13 （D）15【答案】A【解析】45×40=1800,1+8=9【难度】☆【知识点】两位数乘法计算2. 在下面的阴影三角形中, 不能由右图中的阴影三角形经过旋转、平移得到的是图（）中的三角形.（A）（B）（C）（D）【答案】B 【解析】由观察可得：A、C、D 都可通过旋转得到，而 B 是通过原图翻转得到。

2021年7月30日星期五多云文档名称：《(完整word版)第十八届华罗庚金杯少年数学邀请赛决赛试题B》文档作者：凯帆创作时间：2021.07.30第十八届华罗庚金杯少年数学邀请赛决赛试题 B一、填空题（每小题 10 份，共 80 分）1. 计算：1190.12528112.5____8⨯+⨯-=【答案】50【考点】计算：提公因数 【解析】()1111928110088811928110081400850=⨯+⨯+⨯=⨯++=⨯=原式2. 农谚“逢冬数九”讲的是，从冬至之日起，每九天分为一段，依次称之为一九，二九…… 九九，冬至那天是一九的第一天．2012 年 12 月 21 日是冬至，那么 2013 年 2 月 10 日是________九的第________天．【答案】六、七 【考点】周期问题 【解析】12月21日到31日有：3121111-+=天；1月份有31天；2月1日到2月10日有10天．所以从2012年12月21日到2013年2月10日经过11311052++=天．52÷9=57，所以是2013年2月10日是六九的第七天．3. 某些整数分别被57911791113、、、 除后，所得的商化作带分数时，分数部分分别是222257911、、、 则满足条件大于 1 的最小整数是________．【答案】3466 【考点】余数问题 【解析】法一：设这个整数为n ，则有5775n n ÷=的分数部分是25，说明75n ÷余2． 同理：97n 余2；119n ÷余2；1311n ÷余2．()()()()225075225222709722721192292229013112211222110n n n n n n n n n n n n ⎧-÷÷÷⎧⎧⎪⎪⎪-÷÷÷⎪⎪⎪⇒⇒⎨⎨⎨÷÷-÷⎪⎪⎪⎪⎪⎪÷÷-÷⎩⎩⎩余余余余余余余余余余余余 所以22n -是[]5,7,9,113465=的倍数；若223465n -=，则1733.5n =，不符合；则22n -最小是23465⨯．所以2223465n -=⨯，解得346513466n =+=，所以n 最小是3466． 法二：设这个整数为n ，则有()72mod5n ≡，()92mod7n ≡，()112mod9n ≡，()132mod11n ≡，由余数的可乘性可以看出，因为()72mod5≡，所以()1mod5n ≡；同理，()1mod7n ≡，()1mod9n ≡，()1mod11n ≡，故1n -是7，8，9，10的公倍数，且n 不等于1，故n 最小为[]5,7,9,1113466+=4. 如图所示，P ， Q , 分别是正方形 ABCD 的边 AD 和对角线 AC 上的点， 且 AP ： PD = 1: 4 ，AQ ：QC :=3: 2 ．如果正方形 ABCD 的面积为 25，那么三角形 PBQ 的面积是______ 【答案】6.5 【考点】几何 【解析】连接DQ ，正方形ABCD 的面积为25，故边长为5，因为:1:4AP PD =，:3:2AQ QC =， 所以1131311.5555552PAQ QAD ADC ABCD S S S S ==⨯=⨯⨯=△△△正方形，3317.5552BAQ ABC ABCD S S S ==⨯=△△正方形，12APB S =⨯1⨯5=2.5△，所以1.57.52.5 6.5PBQ PAQ BAQ PAB S S S S =+-=+-=△△△△．5. 有一箱苹果，甲班分，每人 3 个还剩 10 个；乙班分，每人 4 个还剩 11 个；丙班分，每人 5 个还剩 12 个，那么这箱苹果至少有________个．A BCDPMQ【答案】67【考点】余数问题【解析】设甲班有x 人，乙班有y 人，丙班有z 人，共有A 个苹果，可得310411512A x y z =+=+=+，可以看出()101mod3A ≡≡，()113mod 4A ≡≡，()122mod5A ≡≡，利用逐级满足法，如下：[]16073423,450A =++=的倍数且除以余的倍数且除以余但是A 显然要大于12，故最小的A 应该为[]73,4,567+=．注：本题并没有说明一定要尽可能地多分，故在每人分5个的情况下，丙班虽然只有11人，依然可以剩12个不分．6. 两个大小不同的正方体积木粘在一起，构成下图所示的立体图形，其中，小积木的粘贴面的四个顶点分别是大积木的粘贴面各边不是中点的一个四等分点． 如果大积木的棱长为 4，则这个立体图形的表面积为________．【答案】136【考点】三视图；弦图 【解析】3这个立体图形的表面积就是大正方体的表面积加上小正方体四个面的面积．大正方体的表面积为44696⨯⨯=，而如图所示，利用弦图小正方体的一个面的面积为2221310S AB ==+=，故整个表面积为96410136+⨯=．7. 甲、乙两车分别从 A ，B 两地同时出发相向而行，甲车每小时行 40 千米，乙车每小时60 千米．两车分别到达 B 地和 A 地后，立即返回．返回时甲车的速度增加二分之一，乙车的速度不变．已知两次相遇处的距离是 50 千米，则 A 、B 两地的距离为________千米．【答案】10007【考点】行程问题 【解析】B A乙甲01234567根据题意，:=2:3v v 甲乙，变速后:=1:1v v 甲加乙，故可以得到::2:3:3v v v =甲乙甲加，由于路程一定，所以时间 比为::3:2:2t t t =甲乙甲加，作柳卡图，如图所示，假设第一次相遇在C 地，第二次相遇在D 地，可以看出C 地距离A 地为全程的25，D 地距离A 地位全程的34， 故CD 间的距离为全程的3274520-=，故此时全程为7100050207÷=千米．8. 用“学”和“习”代表两个不同的数字，四位数“ 学学学学 ”与“习习习习 ”的积是七位数，且它的个位和百万位数字与“学”所代表的数字相同，那么“ 学 习 ”【答案】3【考点】数字谜 【解析】111111111234321⨯=⨯⨯⨯=⨯⨯学学学学习习习习学习学习由“学学学学”与“习习习习”的积是七位数可知，⨯学习等于1,2,3,,8．但是当⨯学习等于5、6、7、8时，所得的乘积的个位和百万位数字不同，舍去．当⨯学习等于1时，积的个位就是1，则1=学，1=学，但是“学”和“习”代表两个不同的数字，不符合题意．当⨯学习等于2时，积的个位就是2，则2=学，1=习． 当⨯学习等于3时，积的个位就是3，则3=学，1=习． 当⨯学习等于4时，积的个位就是4，则4=学，1=习．综上，“学习”所能代表21，31，41共3个．二、解答下列各题（每题 10 分，共 40 分，要求写出简要过程）9. 下图中，不含“★”的长方形有多少个？【答案】106【考点】几何计数 【解析】A含有标记A 的“*”的长方形有：41560⨯=个；B含有标记B 的“*”的长方形有：41560⨯=个；AB含有标记A 和B 的“*”的长方形有：4416⨯=个； 则有“*”的长方形有606016104+-=个．图中共有22752110210C C ⨯=⨯=个长方形． 不含“*”的长方形有210104106-=个长方形．10. 如下图，三角形 ABC 中， AD 2 BD ， AD EC ， BC 18 ，三角形 AFC的面积和四边形 DBEF 的面积相等，那么 AB 的长度是多少？【答案】9【考点】几何：等积变形 【解析】设1AFC DBEF S S ∆==四边形，CEF S x ∆=，ADF S y ∆=．因为2AD BD =，所以21ADC CBD S AD S BD ∆∆==，即1211ADF AFC EFC DBEF S S y S S x ∆∆∆++==++四边形． 解得21y x =+． 则()211211ADF DBEF ABE AEC AFC EFC S S x S S S S x ∆∆∆∆∆+++===++四边形，所以21BE EC =． 所以11186123EC BC =⨯=⨯=+，则6AD EC ==. 又因为2AD BD =，2623BD AD =÷=÷=. 综上639AB AD BD =+=+=．11. 若干人完成了植树 2013 棵的任务，每人植树的棵树相同．如果有 5 人不参加植树，其余的人每人多植 2 棵不能完成任务，而每人多植 3 棵可以超额完成任务．问：共有多少人参加了植树？【答案】61【考点】因数倍数 【解析】设共有a 人参加植树，每人植b 棵树． 2013a b ⨯=，说明a 是2013的因数．201331161=⨯⨯，2013的因数有1，3，11，33，61，183，671，2013共8个． 由题意可知，a 是大于5，所以a 可以取值11，33，61，183，671，2013． 1）11a =时，每人种183棵树，5人离开后有1156-=人，每人多种2棵：()618321110⨯+=小于2013，符合题意； 每人多种3棵：()618331116⨯+=小于2013，不符合题意． 2）33a =时，每人种61棵树，5人离开后有33528-=人， 每人多种2棵：()286121764⨯+=小于2013，符合题意； 每人多种3棵：()286131792⨯+=小于2013，不符合题意． 3）时，每人种33棵树，5人离开后有61556-=人， 每人多种2棵：()563321960⨯+=小于2013，符合题意； 每人多种3棵：()563332016⨯+=大于2013，符合题意． 4）183a =时，每人种11棵树，5人离开后有1835178-=人， 每人多种2棵：()1781122314⨯+=大于2013，不符合题意； 5）671a =时，每人种3棵树，5人离开后有6715666-=人， 每人多种2棵：()666323330⨯+=大于2013，不符合题意；6）2013a =时，每人种1棵树，5人离开后有201352008-=人， 每人多种2棵：()2008126024⨯+=大于2013，不符合题意； 综上，共有61人参加了植树．12. 由四个完全相同的正方体推积成如下图所示的立体图形，则立体图形的表面上（包括底【答案】59【考点】最值；逻辑推理 【解析】如图所示，与2点相邻的面分别有1点、3点、4点和6点，所以2的对面为5；与4点不相对的面分别有1点、2点、5点、6点，所以4的对面为3；则1的对面为6．如下图，分别为这个立体图形的六个方向的视图：本题的难点在于左视图中黄色的确定，通过原图可以看出，当2在上面，1在右面时4在前面；所以当2在上面3在前面时，1应该在左面．唯一不能确定的是底视图的中间蓝色部分，为了让表面的数字和最大，则可以取6．故最大值为63541423222565314159+++++++++++++++++=三、解答下列各题（每题 15 分，共 30 分，要求写出详细过程）13. 用八个下图所示的 2 1的长方形可以拼成一个 4 4 的正方形，若一个拼成的正方形图形经过旋转与另一个拼成的正方形图形相同，则认为两个拼成的正方形相同．问：可以拼成几种两条对角线都是其对称轴的正方形图形？45361423正视图背视图俯视图底视图左视图右视图2225？53141【答案】4【考点】构造与论证【解析】法一：首先构造一个44⨯的正方形（如下图）根据两条对角线都是其对称轴可知：图中同样的颜色小正方形代表它们是同类型的，即图中四个标为A小正方形同类型，四个标为B小正方形同类型．分类讨论：1）当A类型和B类型的小正方形都是时，44⨯的正方形如下（拼法不唯一）：2）当A类型和B类型的小正方形都是时，44⨯的正方形如下（拼法不唯一）：3）当A类型小正方形为，B类型小正方形为时，44的正方形有两种（拼法不唯一）：法二：首先，我们可以看到它是关于两条对角线都对称的图形，所以在对角线上的带标记的方格必为偶数个，于是我们可以利用在对角线上的标记正方形的个数进行分类．同时我们注意到两条对角线将16方格的大正方形分成了4个大的等腰直角三角形，这4个等腰直角三角形都应该是一样的，它们都是由两个正方形和四个小的等腰直角三角形组成，同时每个等腰直角三角形要承担2个带标记的小方格，；第一类：两条对角线上有被标记的小方格均为0个时，记为（0，0）时，则每个等腰直角三角形中若要承担2个小方格，则必须是两个完整的正方形，有如下1种，第二类：两条对角线上有被标记的小方格为（0，2）时，则每个等腰直角三角形只需承担1.5个标记的小方格，则至少有一个为小等腰直角三角形为标记的小方格的一部分，这时对角线上将不止2个，故不存在；第三类：两条对角线上有被标记的小方格为（0，4）时，则每个等腰直角三角形只需承担1个标记的小方格，这个小方格必为等腰直角三角形中的一个小正方形承担，有如下1种，第四类：两条对角线上有被标记的小方格为（2，2）时，则每个等腰直角三角形只需承担1个标记的小方格，与第三类类似，有如下1种，第五类：两条对角线上有被标记的小方格为（2，4）时，则每个等腰直角三角形只需承担0.5个标记的小方格，与第二类类似，不存在，第六类：两条对角线上有被标记的小方格为（4，4）时，只有一种，如下：综上，共计4种．14. 对于 155 个装有红、黄、蓝三种颜色球的盒子，有三种分类方法：对于每种颜色，将该颜色的球数目相同的盒子归为一类．若从 1 到 30 之间所有的自然数都是某种分类中的一类的盒子数，那么，1）三种分类的类数之和是多少？2）说明，可以找到三个盒子，其中至少有两种颜色的球，它们的数目分别相同．【答案】1）30；2）见详解【考点】构造与论证；抽屉原理【解析】（1）1~30每个自然数均对应某种分类中一类的盒子数，则三种分类中各类盒子的总个数最少：()12330130302465++++=+⨯÷=个．每种分类中各类盒子的总个数最多155个，三种分类中各类盒子的总个数最多：1553465⨯=个．综上所述，三种分类中各类盒子的总个数为465个，且三种分类中每类的盒子数为1~30中的自然数且各不相同，按每种颜色分类均包含所有155个盒子．则三种分类的类数之和为30．（2）假设盒子数为30的这一类是按红色分类的，则这30个盒子在按蓝色和黄色分类时均对应其中的一个类别．（假设是别的颜色不影响分析结果）按蓝色和黄色分类时类别的个数总和最多29个，其中必有一类颜色对应的类别个数小于等于14个，假定按蓝色分类时类别数小于等于14个．那么红色个数相同的这30个盒子按蓝色分类时分配在最多14个类别中，301422÷=，至少有3个盒子在一个类别中，同一个类别的盒子蓝色球数量相同，即红色球数相同的盒子中至少有3个盒子蓝色相同．综上所述，必存在至少3个盒子其中至少有两种颜色的球数分别相同。

《18届华罗庚金杯少年数学邀请赛小学高年级教程》P155：初赛模拟测试题（1）6：一副扑克牌54张，将大小王视为0点，A视为1点，J视为11点，Q视为12点，K视为13点，任意抽出若干张，不计花色，如果要求每次抽出的牌中必定有2张牌的点数之和等于14，那么至少要取（）牌。

教程答案：29。

我的答案:28因为：54张牌用最坏情况，2张大小王,4组A—6，4×6，再抽一张7，这时最坏情况抽完，然后再抽一张，就可以这些最坏情况的某一张，加起来和等于14点。

所以总共要抽：2+4×6+1+1=28张。

所以最低要取出28张牌。

P159：决赛模拟测试题（1）5：7098能表示成----种若干个（至少两个）连续非零自然数之和。

教程里的答案是12，这个答案和P19页，例1的答案是矛盾的。

而且教程中说这类题要穷举。

我的答案:11【7098=2×3×7×132，共有（1+1）×（1+1）×（1+1）×（2+1）=12个奇因数，12-1=11】原因，例：把18、27分成两个或两个以上连续正整数之和，共有多少种不同的拆法。

18=2×32即18=3×6，那么以6为中心，分别向两边扩1个数，和6总共是3个数：5、6、7 又18=9×2，那么以2为中心，分别向两边扩4个数，和6总共是9个数：-2、-1、0、1、2、3、4、5、6，其中在相加过程中-2、-1、0、1、2相抵消，剩余3、4、5、6又18=1×18，这里不能以1为中心，把18-1=17两边平均分，以18为中心的1个数没意义。

所以18=5+6+7=3+4+5+6，有两种不同的拆法在18=2×32中奇数的个数是2+1=3个，（1,3,6）其中是3个以6为中心的连续数，和6个以3为中心的连续数。

但是1不可以拆分，所以要3-1=2，即只要两种拆法。