工科数学分析教程(上册)(杨小远 主编)思维导图
- 格式:xmin
- 大小:6.86 KB
- 文档页数:1

工科数学分析(2)写在前➢停课不停学, 停课不停教;•虽没有传统课堂面对面的教与学•但有录课视频在网络平台随时学习➢祸兮福所倚, 福兮祸所伏;➢上课所需✓有网、PC或手机、下载app(学生)✓电子教材、课件、录课视频(老师)➢课程要求:时间、完整观看、完成作业、每周至少一次在线互动(检查+答疑)•存在问题:网络?观看成效?提交作业?1. 数项级数2. 函数列与函数项级数3. Fourier级数4. 多元函数的极限与连续目录5. 多元函数的微分学6. 多元函数的积分学➢数项级数研究内容:数项级数的敛散性判别法1112n++++12n a a a ++++221112n ++++无穷多个数相加有限个数相加第十一章数项级数第一节数项级数的基本概念与性质一、问题的提出二、数项级数的概念三、数项级数的基本性质重点:数项级数收敛的概念、性质难点:性质的应用一、问题的提出引例1. 计算圆的面积AR正六边形的面积正十二边形的面积1a2 1a a+正形的面积n23⨯na a a +++ 21na a a A +++≈ 21即()12lim n n A a a a →∞=+++即任何有限项求和都达不到预期的值, 必须进行无穷项求和.12n a a a =++++割之弥细, 所失弥少. 割之又割, 以至于不可割, 则与圆合体而无所失.引例2. 芝诺悖论——阿基里斯(Achilles)悖论内容:若乌龟在前, 则Achilles永远追不上乌龟!10 m1 m0.1m为什么v 2=10m/sv 1=1m/st 1=1st 2=0.1st 3=0.01s1. 路程上看:++++01.01.0110=10.11110 m1 m0.1m为什么v 2=10m/sv 1=1m/st 1=1st 2=0.1st 3=0.01s2. 时间上看:+++01.01.01=1.111引例3.)1664(年莱布尼茨.71513114π +−+−=,103103103103333.032 +++++=n ,23846 89793 26535 14159.3π =,1091051011041013π5432 ++++++=问题1:不加辨别地认定无穷多个数相加就是一个确定的数?+−+−=1111s (11)(11)000.s =−+−+=++=1(11)(11)100 1.s =−−−−−=−−−=s s −=−+−−=1)111(1 法一:法二:法三:.21=⇒s 问题2:有限个数相加的运算性质能简单地推广到无穷多个数的加法吗?(11)(11)0s =++−++=法四:错错错错1=definednn a ∞=∑12n a a a ++++结论:在没有给出无穷多个数相加的收敛性之前,不能随意结合(即加括号)、交换等.1nn kk s a ==∑研究问题的数学工具:数列极限理论()12lim n n a a a →∞=+++lim nn s →∞=第十一章数项级数第一节数项级数的基本概念与性质一、问题的提出二、数项级数的概念三、数项级数的基本性质重点:数项级数收敛的概念、性质难点:性质的应用二、数项级数的概念1. 数项级数的定义或简称(无穷)级数一般项(或通项)级数的第n 个部分和121nn n aa a a ∞==++++∑121nn n kk s a a a a ==+++=∑级数的部分和数列{}n s2. 级数的收敛与发散若,lim s s n n =∞→ 则称级数1nn a ∞=∑收敛, 且收敛到和,s 记作 121n n n s a a a a ∞==++++=∑否则, 称级数1nn a∞=∑发散.1nn a∞=∑收敛(发散)⇔n n s ∞→lim 存在(不存在){}()n s ⇔数列收敛发散例1 讨论等比级数(几何级数)+++++=∑∞=nn naq aq aq a aq20)0(≠a的敛散性.解1,q ≠如果时211n n ns a aq aq aqa aq q−=++++−=−3. 典型例题1, q <当时0lim =∞→nn q qa s n n −=∴∞→1lim 1,q >当时∞=∞→nn q lim ∞=∴∞→n n s lim 级数收敛级数发散1,q =如果时1,,n q s na ==→∞当时1,q a a a a =−−+−+当时级数变为级数发散级数发散为什么?综上01,1,n n q aq q ∞=⎧<⎪⎨≥⎪⎩∑当时收敛当时发散..1)1(2q S q q S −=+++= 注1. 在引例2中,.1 21<=v v q 二者之比记为Achilles 追赶乌龟的过程中跑过的路程为快者必能追上慢者!注2. 应用实例: 分形几何中的Koch 雪花给定一个正三角形, 将每条边三等分, 然后以中间三分之一段为边向外作小正三角形, 在每条新得到的边上重复类似的操作.求Koch 雪花的周长与面积(设正三角形的边长为1)43,311==A P 面积周长初始状态第一次操作11212913,34A A A P P ⋅⋅+==第二次操作1223123)91(43,)34(A A A P P ⋅⋅⋅+==,2,1)34(11==−n P P n n 2111134()9n n n n A A A −−−⎧⎫⎡⎤=+⎨⎬⎢⎥⎣⎦⎩⎭1121211)91(43)91(43913A A A A n n −−⋅⋅++⋅⋅+⋅+=,3,2=n 周长为面积为22111414141()()()3393939n A −⎧⎫⎡⎤=+++++⎨⎬⎢⎥⎣⎦⎩⎭第次分叉:n于是雪花的面积有∞=∞→n n P lim 11132331(1).45519A A ⎛⎫ ⎪=+=+= ⎪ ⎪−⎝⎭结论:Koch 雪花的面积有限.22111414141()()()3393939n A −⎧⎫⎡⎤++++++⎨⎬⎢⎥⎣⎦⎩⎭但周长无限.例2 判别无穷级数++⋅−++⋅+⋅)12()12(1531311n n 的收敛性. 解1111335(21)(21)n s n n =+++⋅⋅−⋅+)121121(21)5131(21)311(21+−−++−+−=n n ),1211(21+−=n )1211(21lim lim +−=∴∞→∞→n s n n n ,21=.21,和为级数收敛∴例3 判别无穷级数)11(ln 1n n +∑∞=的收敛性. 解341ln 2ln ln ln 23 ln 2(ln 3ln 2)(ln 4ln 3)(ln(1)ln )n n s n n n +∴=++++=+−+−+++−ln(1)()n n =+→∞→∞.级数发散∴1ln ln(1)ln ,n n a n n n+==+−第十一章数项级数第一节数项级数的基本概念与性质一、问题的提出二、数项级数的概念三、数项级数的基本性质重点:数项级数收敛的概念、性质难点:性质的应用证明1,lim 0.n n n n a a ∞→∞==∑若收敛则定理1(级数收敛的必要条件)011(1), sin .n n n n n ∞∞==−∑∑例如发散1lim , ,n n n n n s s a s s −→∞==−设存在lim 0.n n a s s →∞=−=故等价叙述为:1lim 0, .n n n n a a ∞→∞=≠∑若则发散三、数项级数的基本性质注(1) 提供了判别级数发散的一种方法(2) 定理的逆命题为真吗?+++++n131211例如调和级数lim 0,n n a →∞=即便有1.1n n ∞=∑但级数发散这是因为121111111111(1)()()(23456789101111 )()1621222m m m m s ++=++++++++++++++++++8项4项2项2项项m2,21加括号后的每项均大于121.2m m s ++>→∞定理2()111,,.n n n n n n n a b λa μb ∞∞∞===+∑∑∑设都收敛则也收敛()111.n n n n n n n λa μb λa μb ∞∞∞===+=+∑∑∑且证明11,{},{}n n n n n n a b s σ∞∞==∑∑设的部分和数列分别为()1{}n n n n n a b s λμλμσ∞=++∑则的部分和数列为lim()lim lim n n n nn n n s s λμσλμσ→∞→∞→∞∴+=+特别的 设级数1nn a ∞=∑与1nn b ∞=∑分别收敛于和s 与,σ则级数1()nn n ab ∞=±∑收敛,且和为 σ±s , 即111()n n nn n n n a b ab ∞∞∞===±=±∑∑∑逐项相加(相减)性1212()()n n a a a b b b ++++±++++1122()()()n n a b a b a b =±+±++±+两个级数都收敛的条件下!11(1)1[],.23nn n n ∞+=−+∑判断的敛散性若收敛则求其和例4解111(1)11[()]222nnn n n ∞∞+==−=⋅−∑∑,收敛.311收敛同理∑∞=n n 11111111134[()],,11226321()123nnn n ∞∞==−⋅−==−==−−−∑∑又.312161]312)1([11=+−=+−∑∞=+n n n n 故1“.,”,n n a ∞=∑加括号后组成的新级数也收 敛且若收敛和不变则定理3(收敛级数有结合律)设原来级数的部分和数列记为证明设加括号的新级数为11211211()() ()k k n n n n n n a a a a a a a a −+++++++++++++++{}n s11,n s σ=lim lim lim ,.k k n n k k n s s s σ→∞→∞→∞===收敛22,n s σ=,,,k k n s σ=11211211()() ()k k n n n n n n a a a a a a a a −+++++++++++++++{},k σ其部分和数列记为满足{}{},k n s σ故是的一个子列从而由子列极限一致性知+−+−)11()11(例如+−+−1111收敛,发散.扩展2如果加括号后所成的级数发散,则原级数发散.扩展1反之呢?不一定!(定理3的逆否命题)定理4如果括号中各项符号相同, 且加括号后收敛,则原级数必收敛, 且和不变.证明新级数的部分和数列:原级数的部分和数列:11211211()() ()k k n n n n n n a a a a a a a a −+++++++++++++++12,,,,,k σσσ12,,,,,n s s s lim ,k k σσ→∞=1σ↓112121,,,,,,,,n n n s s s s s +1,k n k s σσ−≤≤或者1k n k s σσ−≤≤11,k k n n n −+≤<要么此时成立利用夹逼性可知, n s 收敛.,{}{},k k n k n s s σσ=且从而是的一个子列111,,,,,,,k k k n n n n s s s s −−+2σ↓1k σ−↓kσ↓,,k k n n k n n s s σ===故要么从而1.n pkk n a ε+=+<∑恒有证明{}1lim n nnn n a s s ∞→∞=⇔⇔∑收敛存在是基本列**0,,,,N N n N p N ε⇔∀>∃∈>∈当时对一切.n p n s s ε+−<1nn a ∞=∑收敛**0,,,,N N n N p Nε⇔∀>∃∈>∀∈使时1.n p k k n a ε+=+<∑即定理5 (柯西收敛准则)定理6 添加、去掉、改变级数的有限项, 不改变级数的收敛性..112收敛性级数利用柯西审敛原理证明∑∞=n n例5211111(1)n pn pn pk k n k n k n a k k k +++=+=+=+=<−∑∑∑证1210,[]10,,0,||.n n n p N n N p a a a εεε+++∴∀>∃=+>>∀>+++<使得当时都有成立111111,1n pk n k k n n p n +=+⎛⎫=−=−< ⎪−+⎝⎭∑证111122n n n =+++++,212=>n n .级数发散∴.131211发散证明调和级数 +++++n例622111n nk k n k n a k=+=+=∑∑定理7证明都有对一切时当,*,,*,0N p N n N N ∈>∈∃>∀ε 若1n n a ∞=∑收敛, 则1n n a ∞=∑收敛. 设1nn a∞=∑收敛, 则由柯西收敛定理可知1.n pk k n a ε+=+<∑11.n pn pkk k n k n aa ε++=+=+∴≤<∑∑再由柯西收敛定理可知1nn a∞=∑收敛.绝对值的三角不等式四、小结1.由定义,若s s n →,则级数收敛;2.按基本性质.数项级数的基本概念基本判别法,,0,.n n a →∞→例如当则级数发散思考题.lim ,ln 131211存在证明设n n n x n nx ∞→−++++= 收敛存在的充要条件是提示:∑∞=−∞→−11)(lim n n n n n x x x教程上作业:习题9.1.1 1(1, 3), 2习题9.1.2 1(2), 2(2), 4, 6, 8(1, 3)黄本上作业:习题11.1 1(偶数), 2 (偶数), 4, 5第3节一般项级数的收敛性一、绝对收敛与条件收敛二、交错级数及其审敛法三、Dirichlet和Abel判别法重点:非正项级数的判敛法难点:条件收敛第3节一般项级数的收敛性一、绝对收敛与条件收敛二、交错级数及其审敛法三、Dirichlet和Abel判别法1. 柯西收敛准则一、绝对收敛与条件收敛定义1正项和负项任意出现的级数称为一般项级数.1.n pkk n a ε+=+<∑恒有1nn a ∞=∑收敛**0,,,,N N n N p Nε⇔∀>∃∈>∀∈使时例1{},0,n n a a >设数列单调递减且证明120,0,,.2n n N n N a a εε+∀>∃>>++<当时有2120, 22().n n n n a na a a ε+>∴≤++<2lim 20.n n na →∞∴=21220(21)20, ()n n n n a na a n +≤+≤+→→∞lim 0.n n na →∞∴=1,lim 0.n n n n a na ∞→∞==∑证明:若级数收敛则。


八年级上数学思维导图完整版1. 数与式数与式是数学的基础,掌握好数与式的概念对于学习更高级的数学知识非常重要。
•整数:正整数、负整数、零•分数:分子、分母、带分数•实数:有理数、无理数•表达式:算式中的字母代表未知数,可以是常数、代数式和函数•列式:把一类东西用类似的形式列出来的式子2. 一元一次方程与不等式一元一次方程与不等式是数学中常见的问题求解方法,通过变量的求解来获得解的集合。
2.1 一元一次方程•方程:等号连接的代数式,具有相等关系•等式:两个代数式相等•等式的性质:等式两边可以同时加(减)、乘(除)同一个数,等式仍然成立•一元一次方程:未知数的最高次数是1的方程,常用形式为ax + b = 0•解方程原则:对等式两边进行相同运算,保持等式成立2.2 一元一次不等式•不等式:不等号连接的代数式,具有不等关系•不等式的性质:不等式两边可以同时加(减)、乘(除)同一个正数,不等关系不变;两边乘(除)同一个负数,不等关系颠倒•一元一次不等式:未知数的最高次数是1的不等式,常用形式为ax + b > 03. 图形的认识图形的认识是数学几何中的基础知识,通过对图形特性的认识,可以进行几何推理和问题解决。
3.1 点、线、面•点:几何中最基本的概念,没有大小和方向•线:由无数个点组成,没有宽度和厚度,有无数个方向•线段:具有起点和终点的线•射线:具有起点但无终点的线•面:由无数个点和线组成,有无数个方向•平面图形:封闭的有限个线段构成的图形,例如矩形、正方形、三角形等3.2 图形的基本性质•线段的长度:用长度单位表示,如cm、m等•线段的相等:线段的长度相等•角的概念:由两条射线的公共端点所确定的图形•角的度量:用角度表示,以度为单位•垂直:两条线段、射线、直线相交且互相垂直•平行:两条线段、射线、直线永远不相交,且在同一个平面中•三角形的内角和:任意一角的两个邻角之和为180°•矩形的特性:4条边两两相等且相邻两条边互相垂直4. 面积与体积面积和体积是研究图形大小的重要概念,通过计算可以得到准确的数值。



六年级上册数学知识结构图六年级上册的数学知识结构图是一个复杂的网络,它涵盖了许多不同的概念和公式。
本文将详细介绍这个结构图,帮助大家更好地理解六年级上册的数学知识。
一、分数分数是六年级上册数学知识结构图的核心之一。
它包括分数的概念、分数的性质、分数的加减法、分数的乘除法以及分数的混合运算等。
在学习分数的过程中,学生需要掌握分数的表示方法,理解分数的意义,并能够进行分数的四则运算。
二、小数小数也是六年级上册数学知识结构图的重要部分。
它包括小数的概念、小数的性质、小数的加减法、小数的乘除法以及小数的混合运算等。
在学习小数的过程中,学生需要掌握小数的表示方法,理解小数的意义,并能够进行小数的四则运算。
三、百分数百分数是六年级上册数学知识结构图的另一个重要部分。
它包括百分数的概念、百分数的性质、百分数的加减法、百分数的乘除法以及百分数的混合运算等。
在学习百分数的过程中,学生需要掌握百分数的表示方法,理解百分数的意义,并能够进行百分数的四则运算。
四、比例比例是六年级上册数学知识结构图中用来描述两个量之间关系的一个重要概念。
它包括比例的概念、比例的性质、比例的加减法、比例的乘除法以及比例的混合运算等。
在学习比例的过程中,学生需要掌握比例的表示方法,理解比例的意义,并能够进行比例的四则运算。
五、面积与体积面积与体积是六年级上册数学知识结构图中两个重要的几何概念。
面积指的是一个平面图形所占的区域大小,而体积则是指一个立体图形所占的空间大小。
在学习面积与体积的过程中,学生需要掌握各种平面图形和立体图形的面积和体积计算方法。
六、统计与概率统计与概率是六年级上册数学知识结构图中两个重要的概率统计概念。
统计主要研究如何收集、整理和分析数据,而概率则主要研究随机事件发生的可能性大小。
在学习统计与概率的过程中,学生需要掌握如何使用表格和图形来表示数据、如何计算平均数和标准差等统计指标以及如何计算事件发生的概率。
七、综合应用综合应用是六年级上册数学知识结构图中最高级的一部分,它要求学生能够将所学到的数学知识应用到实际问题中。
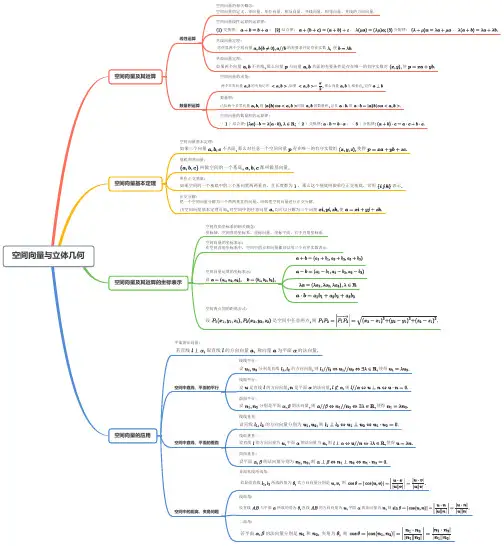
空间向量与立体几何空间向量及其运算空间向量基本定理空间向量的应用空间向量及其运算的坐标表示线性运算数量积运算空间向量的相关概念:空间向量的定义、零向量、单位向量、相反向量、共线向量、相等向量、直线的方向向量.共面向量定理:如果两个向量不共线那么向量与向量共面的充要条件是存在唯一的有序实数对使共线向量定理:对任意两个空间向量的充要条件是存在实数使空间向量的夹角:两个非零向量的夹角记作如果那么向量互相垂直记作数量积:已知两个非零向量则叫做的数量积记作即空间向量的数量积的运算律:()结合律()交换律;()分配律空间向量线性运算的运算律:交换律:;结合律:,分配律:,空间向量基本定理:如果三个向量不共面那么对任意一个空间向量存在唯一的有序实数组使得基底和基向量:叫做空间的一个基底都叫做基向量单位正交基底:如果空间的一个基底中的三个基向量两两垂直,且长度都为,那么这个基底叫做单位正交基底,常用表示正交分解:把一个空间向量分解为三个两两垂直的向量,叫做把空间向量进行正交分解.由空间向量基本定理可知对空间中的任意向量均可以分解为三个向量使空间直角坐标系的相关概念:坐标轴、空间直角坐标系、坐标向量、坐标平面、右手直角坐标系.空间向量的坐标表示:在空间直角坐标系中,空间中的点和向量都可以用三个有序实数表示.空间向量运算的坐标表示:设空间两点间的距离公式:设是空间中任意两点则平面的法向量:若直线取直线的方向向量称向量为平面的法向量空间中直线、平面的平行空间中直线、平面的垂直空间中的距离、夹角问题线线平行:设分别是直线的方向向量则使得线面平行:设是直线的方向向量是平面的法向量则面面平行:设分别是平面的法向量则使得线线垂直:设直线的方向向量分别为则线面垂直:设直线的方向向量为平面的法向量为则使得面面垂直:设平面的法向量分别为则异面直线所成角:若异面直线所成的角为其方向向量分别是则线面角:设直线与平面所成的角为直线的方向向量为平面的法向量为则二面角:若平面的法向量分别是和夹角为则直线和圆的方程直线的倾斜角与斜率直线的方程倾斜角与斜率:已知直线的倾斜角为则直线的斜率为直线的斜率:经过两点的直线的斜率公式为两直线平行和垂直的判定:设两条直线的斜率分别为();()点斜式方程:斜截式方程:两点式方程:一般式方程:不同时为直线的交点坐标与距离公式圆的方程直线与圆、圆与圆的位置关系两直线的交点坐标:方程组的解就是两直线交点的坐标两点间的距离公式:间的距离公式为点到直线的距离公式:点到直线的距离两条平行直线间的距离:若直线的方程分别为则两平行线的距离标准方程:圆心为半径为的圆的标准方程一般方程:直线与圆的位置关系圆与圆的位置关系相交,有两个公共点相切,只有一个公共点相离,没有公共点判断直线与圆的位置关系的方法代数方法(判断直线与圆方程联立所得方程组的解的情况)几何方法(比较圆心到直线的距离与半径r的大小)相交,有两个公共点相切,包括外切和内切,只有一个公共点相离,包括外离和内含,没有公共点圆锥曲线的方程椭圆椭圆的定义:一般地,把平面内与两个定点,的距离的和等于常数(大于的点的轨迹叫做椭圆椭圆的几何性质抛物线抛物线的定义:平面内与一个定点和一条定直线不经过点的距离相等的点的轨迹叫做拋物线点叫做抛物线的焦点,直线叫做抛物线的准线焦点在轴上,,范围:,顶点坐标,,,两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距,焦距的一半称为半焦距.焦点在轴上,,范围,顶点坐标,,,双曲线双曲线的定义:一般地,把平面内与两个定点,的距离的差的绝对值等于非零常数小于的点的轨迹叫做双曲线双曲线的几何性质共同性质:;关于轴、轴、原点对称;焦距,长轴长,短轴长;离心率两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.共同性质:;关于轴、轴、原点对称;焦距,实轴长,虚轴长;离心率焦点在轴上,,范围:,顶点坐标:,焦点在轴上,,范围,顶点坐标:,渐近线:渐近线:抛物线的几何性质顶点:;离心率:焦点:准线:开口方向:向右关于轴对称焦点:准线:开口方向:向左关于轴对称范围:,焦点:准线:开口方向:向上关于轴对称范围:,焦点:准线:开口方向:向下关于轴对称范围:,范围:,一元函数的导数及其应用导数的概念及其意义导数的运算导数在研究函数中的应用瞬时速度的概念:物体在某一时刻的速度称为瞬时速度.平均变化率:比值,即叫做函数从到的平均变化率导数(瞬时变化率):在处可导并把这个确定的值叫做在处的导数(也称为瞬时变化率记作或即基本初等函数的导数导数的四则运算法则简单复合函数的导数函数的单调性函数的极值函数的最大(小)值导数的几何意义:函数在处的导数就是切线的斜率,即这就是导数的几何意义导函数的概念:当时,是一个唯一确定的数,当变化时,就是的函数,称为的导函数简称导数的导函数有时也记作,即若为常数,则;若,且,则;若,则;若,则;若,且,则;特别地,若,则;若,且,则;特别地,若,则;函数和、差的求导法则:函数积、商的求导法则:;;复合函数的概念:一般地,对于两个函数和,如果通过中间变量,可以表示成的函数,那么称这个函数为函数和的复合函数,记作复合函数的导数求法:一般地,对于复合函数,导数为,即对的导数等于对的导数与对的导数的乘积函数的单调性与导函数的正负之间的关系:在某个区间上,如果,那么函数在区间上单调递增;在某个区间上,如果,那么函数在区间上单调递减判断函数的单调性的步骤:第步,确定函数的定义域;第步,求出导数的零点;第步,用的零点将的定义域划分为若干个区间列表给出在各区间上的正负,由此得出函数在定义域内的单调性导数与函数图象的关系:一般地,如果一个函数在某一范围内导数的绝对值较大,那么函数在这个范围内变化得较快,这时函数的图象就比较“陡峭”(向上或向下);反之,函数在这个范围内变化得较慢,函数的图象就比较“平缓”.极值的定义:函数在点的函数值比它在点附近其他点的函数值都小,;而且在点附近的左侧,右侧类似地,函数在点的函数值比它在点附近其他点的函数值都大,;而且在点附近的左侧,右侧叫做函数的极小值点,叫做函数的极小值;叫做函数的极大值点,叫做函数的极大值极小值点、极大值点统称为极值点,极小值和极大值统称为极值求函数极值的步骤:解方程,当时:如果在附近的左侧,右侧,那么是极大值;如果在附近的左侧,右侧,那么是极小值最值的定义:如果是某个区间上函数的最大(小)值点,那么不小(大)于函数在此区间上的所有函数值求函数最值的步骤:求函数在区间上的极值将函数的各极值与端点处的函数值,比较,其中最大的一个是最大值,最小的一个是最小值画函数图象的步骤:求出函数的定义域;求导数及函数的零点;用的零点将的定义域划分为若干个区间,列表给出在各区间上的正负,并得出的单调性与极值;确定的图象所经过的一些特殊点,以及图象的变化趋势;画出的大致图象。