高一物理常见临界问题资料

牛顿运动定律运用中的临界问题在应用牛顿定律解题时常遇到临界问题，它包括：平衡物体（a=0）的平衡状态即将被打破而还没有被打破的瞬间；动态物体（a≠0）的状态即将发生突变而还没有变化的瞬间。

临界状态也可归纳为加速度即将发生突变的状态。

加速度发生突变的本质原因是物体的外力发生了突变，物体处于临界状态，必然隐含着某些力（如弹力、摩擦力等）的突变。

抓住这些力突变的条件，是我们解题的关键。

一、和绳子拉力相联系的临界情况例1. 小车在水平路面上加速向右运动，一质量为m的小球用一条水平线和一条斜线（与竖直方向成30°角）把小球系于车上，求下列情况下，两绳的拉力：（1）加速度；（2）加速度。

解析：小车处于平衡态（a=0）对小球受力分析如下图所示。

当加速度a由0逐渐增大的过程中，开始阶段，因m在竖直方向的加速度为0，角不变，不变，那么，加速度增大（即合外力增大），OA绳承受的拉力必减小。

当时，m存在一个加速度，物体所受的合外力是的水平分力。

当时，a增大，（OA绳处于松弛状态），在竖直方向的分量不变，而其水平方向的分量必增加（因合外力增大），角一定增大，设为a。

当时，。

当，有：（1）（2）解得当，有：。

点评：1. 通过受力分析和对运动过程的分析找到本题中弹力发生突变的临界状态是绳子OA拉力恰好为零；2. 弹力是被动力，其大小和方向应由物体的状态和物体所受的其他力来确定。

二、和静摩擦力相联系的临界情况例2. 质量为m=1kg的物体，放在=37°的斜面上如下图所示，物体与斜面的动摩擦因数，要是物体与斜面体一起沿水平方向向左加速运动，则其加速度多大？解析：当物体恰不向下滑时，受力分析如下图所示，解得当物体恰不向上滑时，受力分析如下图所示，解得因此加速度的取值范围为：。

点评：本题讨论涉及静摩擦力的临界问题的一般方法是：1. 抓住静摩擦力方向的可能性。

2. 最大静摩擦力是物体即将由相对静止变为相对滑动的临界条件。

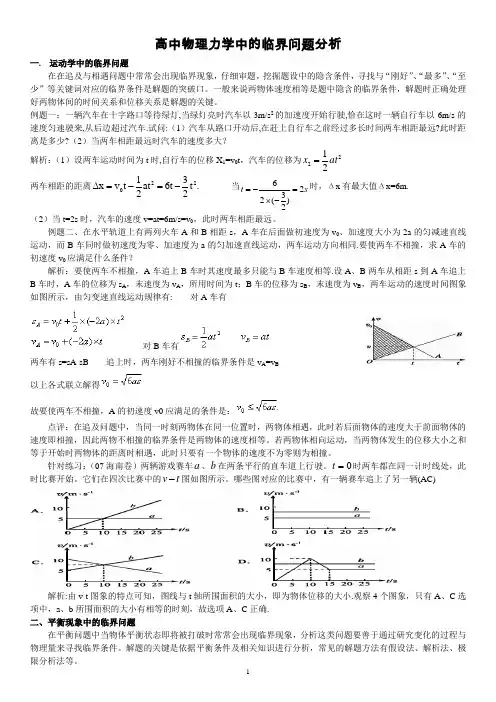
高中物理力学中的临界问题分析一. 运动学中的临界问题在在追及与相遇问题中常常会出现临界现象，仔细审题，挖掘题设中的隐含条件，寻找与“刚好”、“最多”、“至少”等关键词对应的临界条件是解题的突破口。

一般来说两物体速度相等是题中隐含的临界条件，解题时正确处理好两物体间的时间关系和位移关系是解题的关键。

例题一：一辆汽车在十字路口等待绿灯,当绿灯亮时汽车以3m/s 2的加速度开始行驶,恰在这时一辆自行车以6m/s 的速度匀速驶来,从后边超过汽车.试问:（1）汽车从路口开动后,在赶上自行车之前经过多长时间两车相距最远?此时距离是多少?（2）当两车相距最远时汽车的速度多大？解析：（1）设两车运动时间为t 时,自行车的位移X 1=v 0t ，汽车的位移为2221at x = 两车相距的距离22013x v t at 6t t .22∆=-=- 当s t 2)23(26=-⨯-=时，Δx 有最大值Δx=6m.（2）当t=2s 时，汽车的速度v=at=6m/s=v 0，此时两车相距最远。

例题二、在水平轨道上有两列火车A 和B 相距s ，A 车在后面做初速度为v 0、加速度大小为2a 的匀减速直线运动，而B 车同时做初速度为零、加速度为a 的匀加速直线运动，两车运动方向相同.要使两车不相撞，求A 车的初速度v 0应满足什么条件？解析：要使两车不相撞，A 车追上B 车时其速度最多只能与B 车速度相等.设A 、B 两车从相距s 到A 车追上B 车时，A 车的位移为s A ，末速度为v A ，所用时间为t ；B 车的位移为s B ，末速度为v B ，两车运动的速度时间图象如图所示，由匀变速直线运动规律有: 对A 车有 对B 车有两车有s=sA-sB 追上时，两车刚好不相撞的临界条件是v A =v B以上各式联立解得故要使两车不相撞，A 的初速度v0应满足的条件是：点评：在追及问题中，当同一时刻两物体在同一位置时，两物体相遇，此时若后面物体的速度大于前面物体的速度即相撞，因此两物不相撞的临界条件是两物体的速度相等。

动力学连接体问题和临界问题1、动力学中的连接体模型，学会使用整体法与隔离法分析。

2、掌握动力学的临界分析。

一、动力学的连接体问题1．连接体：两个或两个以上相互作用的物体组成的具有相同加速度的整体叫连接体．如几个物体叠放在一起，或并排挤放在一起，或用绳子、细杆等连在一起，在求解连接体问题时常用的方法为整体法与隔离法．2．整体法：把整个连接体系统看做一个研究对象，分析整体所受的外力，运用牛顿第二定律列方程求解．其优点在于它不涉及系统内各物体之间的相互作用力．3．隔离法：把系统中某一物体(或一部分)隔离出来作为一个单独的研究对象，进行受力分析，列方程求解．其优点在于将系统内物体间相互作用的内力转化为研究对象所受的外力，容易看清单个物体(或一部分)的受力情况或单个过程的运动情形．4．整体法与隔离法的选用求解各部分加速度都相同的连接体问题时，要优先考虑整体法；如果还需要求物体之间的作用力，再用隔离法．求解连接体问题时，随着研究对象的转移，往往两种方法交替运用．一般的思路是先用其中一种方法求加速度，再用另一种方法求物体间的作用力或系统所受合力．无论运用整体法还是隔离法，解题的关键还是在于对研究对象进行正确的受力分析．二、动力学的临界问题1．临界问题：某种物理现象(或物理状态)刚好要发生或刚好不发生的转折状态．2．关键词语：在动力学问题中出现的“最大”“最小”“刚好”“恰能”等词语，一般都暗示了临界状态的出现，隐含了相应的临界条件．3．临界问题的常见类型及临界条件：(1)接触与脱离的临界条件：两物体相接触(或脱离)的临界条件是弹力为零．(2)相对静止或相对滑动的临界条件：静摩擦力达到最大静摩擦力．(3)绳子断裂与松弛的临界条件：绳子所能承受的张力是有限的，绳子断与不断的临界条件是实际张力等于它所能承受的最大张力，绳子松弛的临界条件是绳上的张力为零．(4)加速度最大与速度最大的临界条件：当所受合力最大时，具有最大加速度；当所受合力最小时，具有最小加速度．当出现加速度为零时，物体处于临界状态，对应的速度达到最大值或最小值．4．解答临界问题的三种方法(1)极限法：把问题推向极端，分析在极端情况下可能出现的状态，从而找出临界条件．(2)假设法：有些物理过程没有出现明显的临界线索，一般用假设法，即假设出现某种临界状态，分析物体的受力情况与题设是否相同，然后再根据实际情况处理．(3)数学法：将物理方程转化为数学表达式，如二次函数、不等式、三角函数等，然后根据数学中求极值的方法，求出临界条件．题型1动力学的连接体问题[例题1]（2023秋•密云区期末）如图是采用动力学方法测量空间站质量的原理图。

高中物理几种临界问题的分析与探讨高中物理中的临界问题是一类重要且复杂的问题，它们涉及物体在特定条件下从一种状态转变为另一种状态的瞬间。

这类问题通常要求学生具备深厚的物理基础、敏锐的问题分析能力和准确的计算技巧。

以下是对高中物理中几种常见临界问题的分析与探讨：一、平衡物体的临界问题定义：平衡物体的临界问题主要关注物体在即将失去平衡（或达到新的平衡）的瞬间所满足的条件。

特点：物体处于静止或匀速直线运动状态（加速度a=0）。

临界状态通常表现为某些力的突然变化（如弹力、摩擦力等）。

分析方法：受力分析：对物体进行详细的受力分析，找出所有作用在物体上的力。

状态分析：确定物体当前的状态（静止、匀速直线运动）以及即将转变的状态。

寻找临界条件：根据牛顿第二定律（F=ma），当a=0时，合力F 也为零。

因此，需要找出使合力为零的临界条件。

二、动态物体的临界问题定义：动态物体的临界问题涉及物体在加速度即将发生突变的瞬间所满足的条件。

特点：物体具有非零加速度（a≠0）。

临界状态通常表现为加速度的突然变化。

分析方法：运动过程分析：对物体的运动过程进行详细分析，找出加速度即将发生突变的瞬间。

受力分析：在临界状态下对物体进行受力分析，特别是关注那些即将发生变化的力（如弹力、摩擦力等）。

应用牛顿第二定律：根据牛顿第二定律建立方程，并求解出临界条件下的加速度或相关物理量。

三、连接体中的临界问题定义：连接体中的临界问题涉及两个或多个相互连接的物体在特定条件下所表现出的临界现象。

特点：物体间存在相互作用力（如弹力、摩擦力等）。

临界状态通常表现为相互作用力的突然变化或物体间相对运动的开始。

分析方法：整体法与隔离法结合：首先采用整体法分析连接体的整体运动情况；然后采用隔离法分析单个物体的受力情况和运动情况。

寻找临界条件：根据连接体的运动特点和受力情况找出临界条件（如相互作用力达到最大值、物体间相对运动的开始等）。

建立方程求解：根据牛顿第二定律或动量定理等物理规律建立方程并求解出临界条件下的相关物理量。

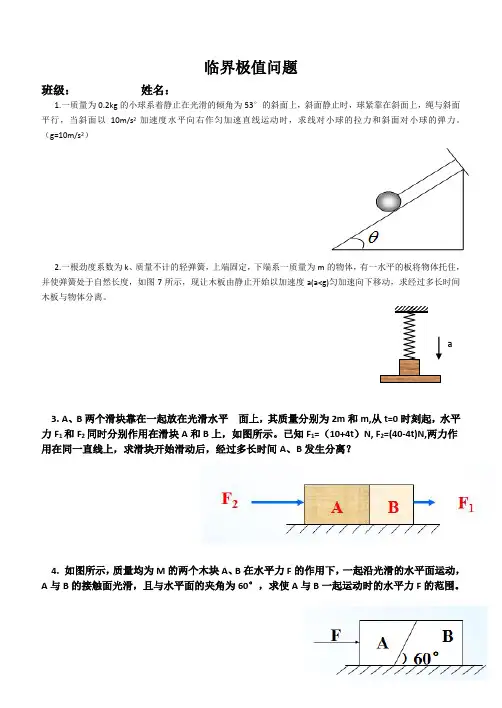
临界极值问题班级： 姓名：1.一质量为0.2kg 的小球系着静止在光滑的倾角为53°的斜面上，斜面静止时，球紧靠在斜面上，绳与斜面平行，当斜面以10m/s 2加速度水平向右作匀加速直线运动时，求线对小球的拉力和斜面对小球的弹力。

（g=10m/s 2） 2.一根劲度系数为k 、质量不计的轻弹簧，上端固定，下端系一质量为m 的物体，有一水平的板将物体托住，并使弹簧处于自然长度，如图7所示，现让木板由静止开始以加速度a(a<g)匀加速向下移动，求经过多长时间木板与物体分离。

3. A 、B 两个滑块靠在一起放在光滑水平 面上，其质量分别为2m 和m,从t=0时刻起，水平力F 1和F 2同时分别作用在滑块A 和B 上，如图所示。

已知F 1=（10+4t ）N, F 2=(40-4t)N,两力作用在同一直线上，求滑块开始滑动后，经过多长时间A 、B 发生分离？4. 如图所示，质量均为M 的两个木块A 、B 在水平力F 的作用下，一起沿光滑的水平面运动，A 与B 的接触面光滑，且与水平面的夹角为60°，求使A 与B 一起运动时的水平力F 的范围。

a5. 如图示，质量为M=2Kg 的木块与水平地面的动摩擦因数μ=0.4，木块用轻绳绕过光滑的定滑轮，轻绳另一端施一大小为20N 的恒力F ，使木块沿地面向右做直线运动，定滑轮离地面的高度h=10cm ，木块M 可视为质点，问木块从较远处向右运动到离定滑轮多远时加速度最大？最大加速度为多少？6.如图所示，两个完全相同的球，重力大小为G ，两球与水平地面间的动摩擦因数都为µ，一根轻绳两端固定在两个球上，在绳的中点施加一个竖起向上的接力F ，当绳被拉直后，两段绳间的夹角为α。

问当F 至少多大时，两球将会发生滑动。

7.如图所示，一块质量为M 、长为l 的匀质板放在很长的水平桌面上，板的左端有一质量为m 的物块，物块上连接一根很长的细绳跨过位于桌面边缘的定滑轮，某人以恒定速度v 向下拉绳，若桌面光滑，物块最多只能到达板的中点，而且此时板的右端沿未触碰定滑轮。

物理临界问题总结
物理临界问题是指在某些物理现象或过程中，某些因素在达到一定条件时发生突变，导致物理状态发生质的变化。

解决临界问题需要找到临界状态，即物理现象或过程发生质变的转折点。

以下是一些常见的物理临界问题：
1. 速度最大或最小问题：在运动学中，物体在某些力的作用下做变速运动，当速度达到最大或最小值时，物体的加速度为零，此时是临界状态。

2. 角度问题：在分析力的合成与分解时，当两个力的夹角为90度时，合力的大小达到最大值或最小值，这是临界状态。

3. 追及问题：在运动学中，当两物体速度相等时，距离最小或最大，这是追及问题的临界状态。

4. 平衡问题：在分析受力平衡时，当某个力为零时，物体处于平衡状态，这是临界状态。

5. 折射和反射问题：在光学中，当光线经过介质交界处时，会发生折射和反射现象。

当光线垂直入射或反射角等于入射角时，折射和反射达到最大或最小值，这是临界状态。

6. 弹簧问题：在分析弹簧的弹力时，当弹簧处于原长或处于最大限度压缩或拉伸时，弹力为零或达到最大值，这是临界状态。

7. 电场和磁场问题：在电场和磁场中，当电荷或电流垂直进入电场或磁场时，电场力或洛伦兹力达到最大值或最小值，这是临界状态。

解决临界问题的关键是找到临界状态，通过分析物理现象或过程的转折点来解决问题。

在解题过程中，需要注意物理量的变化趋势和转折点，以及如何利用这些信息来解决问题。

牛顿运动定律运用中的临界问题在应用牛顿定律解题时常遇到临界问题，它包括：平衡物体（a=0）的平衡状态即将被打破而还没有被打破的瞬间；动态物体（a≠0）的状态即将发生突变而还没有变化的瞬间。

临界状态也可归纳为加速度即将发生突变的状态。

加速度发生突变的本质原因是物体的外力发生了突变，物体处于临界状态，必然隐含着某些力（如弹力、摩擦力等）的突变。

抓住这些力突变的条件，是我们解题的关键。

一、和绳子拉力相联系的临界情况例1. 小车在水平路面上加速向右运动，一质量为m的小球用一条水平线和一条斜线（与竖直方向成30°角）把小球系于车上，求下列情况下，两绳的拉力：（1）加速度；（2）加速度。

解析：小车处于平衡态（a=0）对小球受力分析如下图所示。

当加速度a由0逐渐增大的过程中，开始阶段，因m在竖直方向的加速度为0，角不变，不变，那么，加速度增大（即合外力增大），OA绳承受的拉力必减小。

当时，m存在一个加速度，物体所受的合外力是的水平分力。

当时，a增大，（OA绳处于松弛状态），在竖直方向的分量不变，而其水平方向的分量必增加（因合外力增大），角一定增大，设为a。

当时，。

当，有：（1）（2）解得当，有：点评：1. 通过受力分析和对运动过程的分析找到本题中弹力发生突变的临界状态是绳子OA拉力恰好为零；2. 弹力是被动力，其大小和方向应由物体的状态和物体所受的其他力来确定。

二、和静摩擦力相联系的临界情况例2. 质量为m=1kg的物体，放在=37°的斜面上如下图所示，物体与斜面的动摩擦因数，要是物体与斜面体一起沿水平方向向左加速运动，则其加速度多大？解析：当物体恰不向下滑时，受力分析如下图所示，解得当物体恰不向上滑时，受力分析如下图所示，解得因此加速度的取值范围为：点评：本题讨论涉及静摩擦力的临界问题的一般方法是：1. 抓住静摩擦力方向的可能性。

2. 最大静摩擦力是物体即将由相对静止变为相对滑动的临界条件。