季节指数法例题

气候预测
分析气温、降雨量等气候因素的季节性变化， 预测未来气候趋势。
02
季节指数计算模型的种类
简单季节指数计算模型
优点
简单易懂，计算过程相对简单。
缺点
未考虑时间序列数据的趋势和循环因素，可能存在误差。
乘法季节指数计算模型
优点
能够较好地反映季节因素对时间序列数据的影响，适用于季节因素对数据影响较大的情况。
05
季节指数计算模型的局限 性
数据质量的影响
数据来源
数据来源的可靠性、准确性和完整性对季节指数计算结果的准确性有直接影响。如果数 据存在误差或偏差，将导致计算结果失真。
数据处理
数据预处理和清洗过程对消除异常值、缺失值和重复值至关重要，否则会影响计算结果 的准确性。
模型选择的主观性
模型选择
不同的季节指数计算模型可能产生不同的结 果，因为每种模型都有其特定的假设和理论 依据。在选择模型时，主观判断和经验可能 影响最终结果。
VS
分析市场变化规律可以帮助企业了解 市场动态，把握市场机遇，制定更加 科学合理的经营策略。
制定营销策略和计划
季节指数计算模型可以用来制定营销策略和计划，通过对历史销售数据的分析，找出产品的销售旺季 和淡季，制定更加精准的营销策略和计划。
制定营销策略和计划可以帮助企业提高营销效果，增加销售额和市场份额，提升品牌知名度和美誉度 。
适用范围
适用于数据量大、特征复杂的情况，如电商、金融等领域。
动态季节指数计算模型
动态季节指数计算模型
根据时间变化和数据更新，动态调整季节指数的计算方法和参数，以提高季节指数的实时性和准确性。
模型构建
首先建立动态调整机制，根据时间序列数据的变化情况，实时调整模型的参数和计算方法。然后采用动态时间规整等 方法，将不同时间点的数据归一化处理，以便进行比较和分析。最后根据归一化后的数据计算季节指数。

ˆ (2)抛物线方程：yt a bt ct 2
若时间序列的二级增长量大体相同， 可配合抛物线方程。
ˆ (3)指数曲线方程： yt ab
t
若时间序列的环比发展速度大体相同， 可配合指数曲线方程。
1.直线趋势
最小二乘法
满足Q ( y y) min ˆ
2
ˆ yt a bt
加权移动平均法是对各期指标值进 行加权后计算移动平均数。在中心化移 动平均中，移动平均数代表移动平均中 项时期的长期趋势值。
（二）数学模型法
选择合适的模型
ˆ (1)线性方程： yt a bt
若时间序列的逐期增长量相对稳定近似 一个常量，可配合直线方程。
逐期 增长量
二级 环比发 增长量 展速度 Nhomakorabea第一季度为 175 89.31% 156.29 （万人） 第二季度为 175 105.87% 185.27 （万人） 第三季度为 175 142.02% 248.54 （万人） 第四季度为 175 62.80% 109.90 （万人）
2.若已知第一季度人数为160万人，则以后各季度为：
3．移动平均法
移动平均法是测定时间序列趋势变动 的基本方法。它在时间序列中按一定项 数逐项移动计算平均数，达到对原始序 列进行修匀的目的。
（1）简单移动平均法
1）奇数项移动平均 （例如取3项）
1. 2. 3. 4. 5. 6. 7. 8. 9. n. yn y1 y2 y3 y4 y5 y6 y7 y8 y9
t 0
年份 1990 1991 1992 1993 1994 1995 1996
t
1 2 3 4 5 6 7
t

统计学计算题复习（学生版）统计学复习提纲一、期末考卷题型1. 单项选择题；2. 多项选择题；3. 简答题4. 计算题二、知识点复习1. 统计学分类、指标、变量、参数、统计量等概念，以及各种统计图形；2．统计数据的相关内容，以及测量数据分布的测度的描述；平均数、中位数和众数的计算公式。

3. 调查的各种方式； 4. 组距数列的相关概念。

5. 置信区间的相关概念，以及单个总体均值、比例、方差的区间估计；6. 估计单个总体均值、比例时的样本容量的计算公式；7. 单个总体均值、比例、方差的假设检验；8. 相关系数和回归系数的相关知识；9. 一元、二元回归模型的EXCEL操作结果的解释以及模型的建立和检验；10. 时间序列的各种分类；平均速度等指标、移动平均法的概念等；平均发展水平的计算和季节指数的计算； 11.统计指数的相关概念，制作综合指数要点和原则，综合指数、平均指数的计算。

1统计学计算题复习一．平均数、中位数和众数的计算和三者之间的关系1．算术平均数。

也叫均值，是全部数据的算术平均，是集中趋势的最主要测度值。

主要适用于定距数据和定比数据，但不适用于定类数据和定序数据。

2．众数。

众数是一组数据中出现次数最多的变量值，用Mo表示。

主要用于测度定类数据的集中趋势。

组距式数列确定众数，是先根据出现次数确定众数所在组，然后利用下列公式计算众数的近似值：M?L?0f?f?1?i (f?f?1)?(f?f?1) 3．中位数。

中位数是一组数据按从小到大排序后，处于中间位置上的变量值，用Me表示。

主要用于测度定序数据的集中趋势。

分组数据计算中位数时，先根据公式N确定中位数所在的组，然后用下列公式计算2N?Sm?1中位数的近似值： M?L?2?i efm4.众数、中位数和算术平均数的关系 x?Me?Mo，数据是对称分布； x＜Me＜Mo，数据是左偏分布； x＞Me＞Mo，数据是右偏分布。

例题1：某地区有下列资料：人均月收入400以下400~500 500~600 600~700 700~800 800~900 900以上合计要求计算算术平均数、众数、中位数。

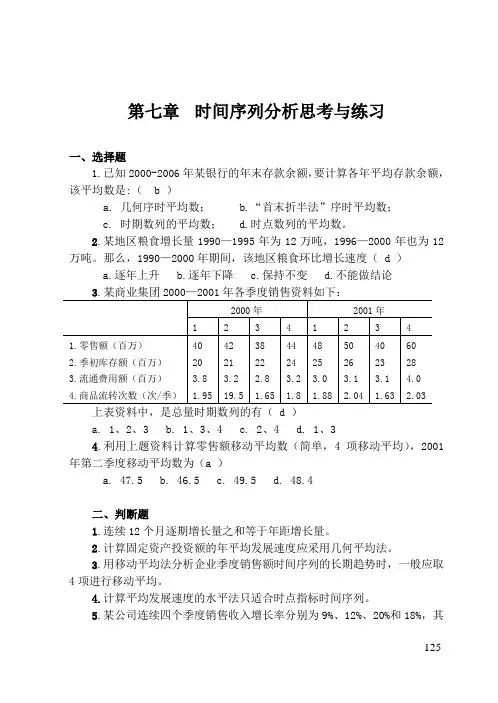
第七章时间序列分析思考与练习一、选择题1.已知2000-2006年某银行的年末存款余额，要计算各年平均存款余额，该平均数是:（ b ）a. 几何序时平均数；b.“首末折半法”序时平均数；c. 时期数列的平均数；d.时点数列的平均数。

2.某地区粮食增长量1990—1995年为12万吨，1996—2000年也为12万吨。

那么，1990—2000年期间，该地区粮食环比增长速度（ d ）a.逐年上升b.逐年下降c.保持不变d.不能做结论上表资料中，是总量时期数列的有（ d ）a. 1、2、3b. 1、3、4c. 2、4d. 1、34.利用上题资料计算零售额移动平均数（简单，4项移动平均），2001年第二季度移动平均数为（a ）a. 47.5b. 46.5c. 49.5d. 48.4二、判断题1.连续12个月逐期增长量之和等于年距增长量。

2.计算固定资产投资额的年平均发展速度应采用几何平均法。

3.用移动平均法分析企业季度销售额时间序列的长期趋势时，一般应取4项进行移动平均。

4.计算平均发展速度的水平法只适合时点指标时间序列。

5.某公司连续四个季度销售收入增长率分别为9%、12%、20%和18%，其125126环比增长速度为0.14%。

正确答案：（1）错；（2）错；（3）对；（4）错；（5）错。

三、计算题：1．某企业2000年8月几次员工数变动登记如下表：试计算该企业8月份平均员工数。

解：该题是现象发生变动时登记一次的时点序列求序时平均数，假设员工人数用y 来表示，则： 1122n 12y y ...y y=...nnf f f f f f ++++++121010124051300151270311260()⨯+⨯+⨯+=≈人 该企业8月份平均员工数为1260人。

2. 某地区“十五”期间年末居民存款余额如下表：试计算该地区“十五”期间居民年平均存款余额。

解：居民存款余额为时点序列，本题是间隔相等的时点序列，运用“首末折半法”计算序时平均数。

21.6 21.2 107.1% 21.4%
21.5 21.9 108.6 21.7%
25.5
100
25.04
100
127.8
25.6%
21
二、实际预测 1、情形一：已知年度预测值，预测其它各季度值。
计算公式：某季度预测值＝年度预测值×该季的季节比重 例题：已知2006年度预测值为7385吨，要求利用季节变差预测各值。
一、数据模式的分析法
1、叠加法
y
H
k
t 水平型： Y=H+S 或
y
k t
Y=H+S+C+I T
S +0
S
s>0 t
s<0
t1
t
+
t1
t
t1
趋势型： Y=T+S
Y=T+S+C+I
t
2
第一节 季节变动数据模式分析法及预测步骤
2、乘积法
y
H
S
k
k
t
t
水平季节型： Y=H×S 或 Y=H×S×C×I
y
T
S
85.8 87.3 86.3 84.7 428.3 85.7%
86.3 87.8 86.0 87.6 434.5 86.9%
102.6 103.0 102.0 100.2 511.0 102.2%
表中第一个数据来源：2150/1710.75=1.257=125.7% 其它数据同上。
12
第二节 季节指数预测法
年份
第一季度
2001
2150
2002
2192
2003
2089

7
270 271 290
8
122 193 153
9
70 62 77
10
33 27 17
11
23 17 37
12
16 13 46
解：
• 1.采用最小平方法建立直线趋势模型： • 建立趋势模型：参考平均趋势法EXCEL
• Tt=126.972+0.048 t
• Y=a+bt（其中 t 0 ）
ay n
Yˆ t Yˆ N SIi
SIi——第i季度的季节指数； t ——时间序列的项数，t = 4（N1）+i。
• 若利用一次指数平滑法进行估计，取=0.5， S0=Y1=11。各年的季平均预测值的计算结 果见表 2：
表 2 季平均预测值计算表 单位：万件
年份 年次
1996 1 1997 2 1998 3 1999 4 2000 5 2001 6
一季度季节指数：SI1=1012.5=0.8=80%； 二季度季节指数：SI2=1412.5=1.12=112%； 三季度季节指数：SI3=1812.5=1.44=144%； 四季度季节指数：SI4=812.5=0.64=64%。
6.建立季节变动预测模型。
水平型季节变动预测模型为（以季度为 单位）：
1997
11 14 17 10 52 13.00
1998
8 16 21 6 51 12.75
1999
10 12 20 8 50 12.50
2000
12 15 16 10 53 13.25
合计 50 70 90 40 250
同季平均数 10 14 18 8
12.50
季节指数(%) 80 112 144 64 400 100.00

季节指数法的原理及应用1. 什么是季节指数法？季节指数法是一种时间序列分析方法，主要用于确定季节性因素对于时间序列数据的影响程度，以及进行季节性趋势的预测和调整。

它基于一种假设，即历史上的季节性变化趋势会在未来重复出现，因此可以利用历史数据来分析和预测未来的季节性变化。

2. 季节指数法的原理季节指数法的原理基于以下步骤： 1. 数据收集和整理：收集时间序列数据，以季度为单位进行整理，例如每个季度的销售额或生产数量。

2. 季节性因素的计算：计算每个季度的平均值，即该季度的数据在历史上的平均水平。

将每个季度的平均值除以整个时间序列的平均值，得到季节指数。

季节指数反映了该季度相对于整体平均的季节性因素。

3. 趋势性分析：对除去季节性因素后的数据进行趋势性分析，例如利用移动平均线或指数平滑法进行趋势性预测。

4. 季节性调整：将趋势性分析得出的预测结果乘以对应季度的季节指数，得到最终的季节性调整结果。

3. 季节指数法的应用季节指数法在实际应用中具有广泛的应用价值，以下是一些常见的应用场景：3.1 销售预测•对于某些产品或行业，销售额可能呈现明显的季节性变化。

通过季节指数法，可以分析每个季度的销售水平相对于整体销售水平的影响程度，从而预测未来季度的销售趋势，并作出相应的调整和决策。

3.2 生产计划•季节指数法可以帮助生产企业优化生产计划，根据季节性因素调整生产数量和时间，以适应季节性需求的变化。

例如，对于农产品，不同季节的需求量可能会有显著差异，通过季节指数法可以预测出不同季节的需求量，从而合理安排生产计划。

3.3 股票市场分析•季节指数法可以用于股票市场的分析，特别是对于某些行业或股票具有明显季节性特征的情况下。

通过分析季节指数，可以了解该股票或行业在不同季度的涨跌情况，从而制定更具针对性的投资策略。

3.4 旅游业规划•季节指数法在旅游业规划中也具有应用价值。

通过分析每个季度的季节指数，可以了解不同季度的旅游需求量以及旅游价格的波动情况，从而制定合理的旅游行程和价格策略，更好地满足游客的需求。

第十章
时间序列 预测法
四、 季节指数预测法
❖ 本法适用于有季节变动特征的经济现象数量预测
销量
200
150
销售量(万元)
100
销量
季度
50
1998年 1999年 2000年 2001年
0
0
4
8
12
16
20
第一季度 148 138 150 145 第二季度 62 64 58 66
第三季度 76 80 72 78
年份 一季度 二季度 三季度 四季度
1995 120 1996 124 1997 138 1998 142
165 182 197 218
282 312 354 370
114 123 140 148
年份
一季度
1995
120
1996
124
1997
138
1998
142
各年同季平 均数
131
季节指数度 四季度
165
282
114
182
312
123
197
354
140
218
370
148
190.5 329.5 131.25
97.41% 168.49% 67.11% 213.82 369.83 147.32
同年各季 平均数 170.25 185.25 207.25 219.50
2 、季节指数预测法的步骤
第1步 第2步
n
计算各年同季（或同月）的平均值
yi
yi
i 1
n
n
计算所有年所有季（或月）的总平均值
y
yi
i 1
n
第3步 计算各季（或月）的季节比率（即季节指数）

利用季节指数预测法进行预测时,时间序列的时间单位或是 季,或是月,变动循环周期为4季或是12个月. 运用季节指数进行预测,首先,要利用统计方法计算出预测 目标的季节指数,以测定季节变动的规律性;然后, 在已 知季度的平均值的条件下, 预测未来某个月(季)的预测值.
二,简单季节指数法
简单季节指数法是根据呈现季节变动的时间序列 资料,用求算术平均值方法直接计算各月或各季 的季节指数,据此达到预测目的的一种方法.
预测过程如下
1.六年各相同季节的平均销售量(Ai) A1=1970÷6≈262(单位) 同理 A2=180,A3≈138.3,A4=180(单位) 2.六年所有季度的平均销售量(B) M—6年销售量总和
B=M/ (4*6)=4560/24=190 (单位) 3.各季节销售指数(Ci = Ai /B) C1=262÷19≈1.38 同理 C2≈0.95,C3≈0.73,C4≈0.95 4.修正2010年各季度预测值 Y t = (a + b *T )Ci
四,简单季节指数法实例分析
技能核算题: 技能核算题:某公司从1996年到2001年,每一年各季度的
纺织品销售量见下表.预测2010年各季度纺织品的销售量. (单位:件) 年度 2004 2005 2006 2007 2008 2009 年度销售量 600 660 700 750 850 1000 第一季 度 180 210 230 250 300 400 第二季度 150 160 170 180 200 220 第三季 度 120 130 130 140 150 160 第四季度 150 160 170 180 200 220
练习: 练习:根据某市2007-2009年销售资料预测2010年各
个季节的销售量(单位:件)

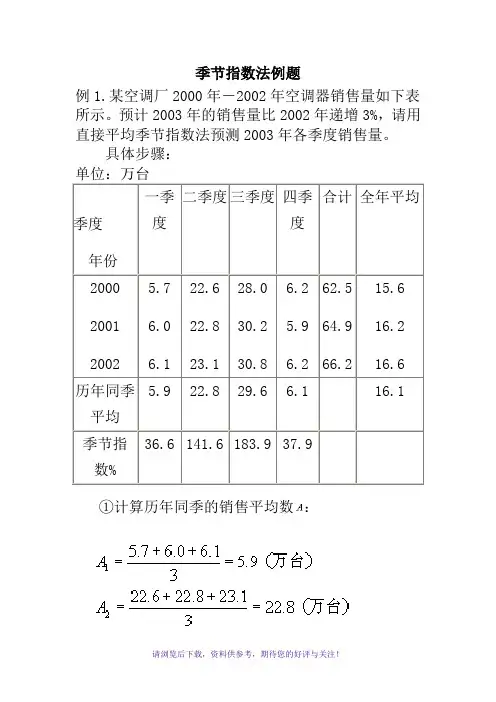
季节指数法例题
例1.某空调厂2000年－2002年空调器销售量如下表所示。

预计2003年的销售量比2002年递增3%，请用直接平均季节指数法预测2003年各季度销售量。

具体步骤：
季度
年份
一季
度
二季度三季度四季
度
合计全年平均
2000
2001
2002
5.7
6.0
6.1
22.6
22.8
23.1
28.0
30.2
30.8
6.2
5.9
6.2
62.5
64.9
66.2
15.6
16.2
16.6 历年同季
平均
5.9 22.8 29.6
6.1 16.1
季节指
数%
36.6 141.6 183.9 37.9
①计算历年同季的销售平均数：
同理，
②计算历年季度总平均数：
③计算季节指数：
同理有：
④计算2003年各季度预测值：
依据题意：
2003年销售预测值=（万台）
2003年第一季度预测值=（万台）
2003年第二季度预测值=（万台）
2003年第三季度预测值=（万台）
2003年第四季度预测值=（万台）。

bˆ1 0.2(aˆ1 aˆ0) (1 0.2)bˆ0 0.2(40.61 39.25) 0.81 1.072
Cˆ1 0.1X1 / aˆ1 (1 0.1)Cˆ01 0.138/ 40.61 0.9 0.917 0.91149
同理： aˆ2 0.3 41/ 0.968 0.7(40.6 1.027) 41.884
Cˆ T 是对季节指数的估计。利用前T-1期的数据对 CˆT 的
估计值是 CˆT L ，利用本期数据对 Cˆ T 所作的估计应是 X T / aˆT
因此，对季节指数的最终估计值 CˆT 应为 XT / aˆT
和
Cˆ T
的加
L
权平均。同样的道理，第一项 X T / aˆT 是为了从观测值中消
除长期趋势，其结果只包含季节变动和随机变动.对 X T / aˆT 和 CˆT进L 行加权平均，以消除随机干扰以反映季节变动 11
运用一次指数平滑公式时，每个时期对模型中的参数重
新估计．在时期T,当获得新的观测值XT后，下列指数平滑
公式用来计算新的参数估计值：
每个方程式能修匀一个与数 据样式的三种成分：随机性， 线性，季节性之一有关的参数
aˆT XT / CˆTL (1)(aˆT1 bˆT1) bˆT (aˆT aˆT1) (1 )bˆT1 CˆT X T / aˆT (1 )CˆT L
式中: at、bt、Ct 是模型的参数； Ct 是积性季节因子
定义符号L为季节波动的周期长度，则
L
Ct L
t 1
积性季节模型同时考虑了线
性趋势和季节因素的影响.右图
描述了经济变量的这种变化过
程或行为
8
为了建立预测模型，定义 bˆT、CˆT 分别是模型中斜率和季 节因素在时间T的估计值，aˆT是以T为原点的常数项估计值

第4章 季节变动分析预测法季节变动是指现象随着季节转换而呈现周期性的变动。

它具有以下基本特征：⑴波动性；⑵重复性；⑶周期长度固定；⑷可预见性。

反映季节变动的指标主要有两个：⑴季节指数，反映各种季节变动因素对现象影响的相对程度，它在相乘型季节变动分析预测模型中使用；⑵季节变差，反映各种季节变动因素对现象变化影响的绝对程度，它在相加型季节变动分析预测模型中使用。

运用季节变动分析预测法进行分析预测，要求所研究的现象时间序列必须是三年或三年以上的季节（分月、分季等）资料，且序列中必须包含有明显的季节变动。

第一节 平均季节变动分析预测法一、 平均季节指数法 分析预测模型 tt fY Y ∙=∧∧预测步骤：首先测定出各月（季）的季节指数；其次估计确定现象预测月（季）所在年的全年月（季）平均数；最后利用分析预测模型进行预测 。

㈠ 季节指数的测定 1、 直接月(季)平均法就是直接计算历年相同月（季）的平均数和历年所有月（季）的平均数，将两者的比率作为各月（季）的季节指数。

具体步骤为；第一步，计算历年相同月(季)的简单算术平均数。

计算公式第二步，计算历年所有月(季)的总平均数。

计算公式LYY Li i∑==1第三步，用各月(季)的平均数除以总的月(季)平均数，即为各月(季)的季节指数。

),,2,1(L i YY f i i ==在预测中，假定预测年份各对应月(季)的季节指数与之相同。

【例1】)4,3,2,1;12,,2,1(1==∑==i i Y KY i Kj ji或2、 全年比率平均法第一步：计算每年全年的月(季)平均数。

),,2,1(k i LY Y ji j ==第二步：将每年各月（季）数值除以该年全年月(季)平均数，求得每年各月(季)的比率。

),,2,1;,,2,1(k j L i Y Y f jji ji ===第三步：将历年相同月(季)的比率进行简单计算平均，得到各月(季)的季节指数。

),,2,1(1L i Kf f kj jii ==∑=㈡ 预测月(季)所在年的全年月(季)平均数的确定 第一种方法：若所研究的现象在预测月(季)所在年的环境与预测月(季)上一年的环境大体相同，可将上一年的全年月(季)平均值作为预测月(季)所在年全年月(季)平均值的估计数。

对带有季节变动的时间序列数据的预测分析例题一：现有某地区某产品产量近三年的分月资料。

试测试该种产品2012年10月的产量解：（1）首先观察时间序列数据，具有哪些变动，进而确定选用哪种预测方法在给出的时间序列数据中我们可以明显判断出来，6月-8月销量比其他月份高出很多，而且每年都是这样，说明这列时间序列数据含有季节变动。

则应该用季节变动模型进行预测。

其次，判断整个时间序列数据是否具有趋势变动，是否是每年的平均销量均比上一年要多或者是少，第一年的均值为1y =11 第二年的均值为 2y =16 第三年的均值为3y =23 ，那么这列时间序列数据带有趋势变动。

则判断不能选用周期平均法。

最后判断是否随着年份的增加，时间序列数据的季节变动幅度在逐渐增大。

判断方法为：用每年的峰值减去均值，得到一个离差，如果每年的离差带有趋势变动，呈逐年增加或者减少，那么说明时间序列的季节变动幅度有变化。

第一年峰值为22，均值为11，离差为11.第二年峰值为29，均值为16，离差为13；第三年峰值为42，均值为23，离差为19。

判断离差在逐年增加。

说明季节变动的幅度在逐年增加。

则选择季节交乘预测模型。

也可画出散点图判断。

（2） 季节交乘预测模型为：()ˆt ya bt fi =+⨯ 其中fi 为季节指数；()a bt +为趋势值根据预测模型，知道预测值为预测期趋势值与预测期季节指数的乘积。

我们要预测的是2012年10月份的销售量，因此需要2012年10月份季节指数，和10月份的趋势值就可以知道10月份的销量。

而2012年10月份的季节指数是根据2011年2010年和2009年，前三年10月份的季节指数得出的。

所以首先需要求出前三年10月份的季节指数。

季节指数Ytfi Ft=; 其中Yt 代表的是观察值，Ft 代表的是趋势值。

因此首先求出，前三年10月份的趋势值。

趋势值即为，如果这列时间序列数据只有直线趋势变动，没有季节变动的时候的值。

第四章 时季节性指数平滑法法
含有季节变动的时序，用数学方法拟合其演变规 律并进行预测是相当复杂的. 但, 如果我们能够设法 从时序中分离出长期趋势, 并找出季节变动的规律, 将二者结合起来预测.就可以使问题得到简化, 也能 够达到预测精度的要求。 基于这种设想，季节变动预测法方的基本思路是 首先找到描述整个时序总体发展趋势的数学模型即 分离趋势的趋势方程；其次找出季节变动对预测对 象的影响，即分离季节影响；最后将趋势方程与季 节影响因素合并，得到能够描述时间序列总体发展 1 规律的预测模型，并用于预测。
T r T T
T Lr
在没有趋势变化的情况下预测方程为
9 ˆ ˆ ˆT CT Lr X T r a
对预测方程
ˆ ) ˆ (1 )(a ˆT X T / C ˆ a b T L T 1 T 1
ˆT a
ˆ X / C 是对趋势值的估计．第一项 T T L 是为从XT中消
去除XT ，将得到小于原值XT的值.其减的百分数恰好等于
T-L 期间的值高于平均值的百分比.相反的调整发生在季
节调整因子小于１或100％的情况下。
3
为了建立预测模型和使用平滑式ST的平滑过程连续进行 需要用一次指数平滑法计算数据IT-L的值，因此我们用下
列公式: I T X T / ST (1 ) I T L
ˆ 取该时序每期变化量的平均数 取该时间序列的平均数， b 0
例如，有时序的季节数据X１，X２，X3，X4，则:
ˆ0 ( X1 X 2 X 3 X 4 ) / 4 X a
ˆ [(X X ) ( X X ) ( X X )]/ 3 b 0 2 1 3 2 4 3
XT ST (1 ) ST 1 I T L

移动平均趋势剔除法计算季节指数例题1. 引言在统计学和经济学中，移动平均趋势剔除法是一种常用的方法，用于计算和调整时间序列数据中的季节性因素。

通过该方法，我们可以分析并剔除数据中的季节性波动，从而更准确地判断趋势和周期性变化。

本文将以季节指数的计算为例，介绍移动平均趋势剔除法的具体应用过程。

2. 移动平均趋势剔除法概述移动平均趋势剔除法是一种时间序列分析方法，它通过多期数据的平均值来平滑时间序列数据，以剔除季节性因素和随机波动，从而更清晰地显示出趋势和周期性变化。

在计算季节指数时，移动平均趋势剔除法可以帮助我们准确地预测季节性变动，并据此做出有效的决策和规划。

3. 移动平均趋势剔除法计算季节指数例题假设某服装店要对某一服装品类每月销售额的季节性变化进行分析，并计算季节指数以便进行月度计划。

现有一年的销售数据如下：（这里请填入实际的数据）接下来，我们将按照移动平均趋势剔除法的步骤来计算季节指数。

第一步：计算季节调整因子我们需要确定移动平均的期数，通常选择12个月。

然后按照以下公式计算季节调整因子：\[季节调整因子 = \frac{实际销售额}{移动平均值}\]根据这个公式，我们可以得到每个月的季节调整因子。

第二步：计算季节指数接下来，我们将每个月的季节调整因子求平均值，作为对应月份的季节指数。

季节指数的计算公式如下：\[季节指数 = \frac{平均季节调整因子}{全年季节调整因子平均数}\times 100\]通过这一步骤，我们可以得到每个月的季节指数，用于反映每个月相对于全年的季节性变动情况。

4. 分析和结论借助移动平均趋势剔除法的计算过程，我们得到了某服装品类每月销售额的季节指数。

通过对季节指数的分析，我们发现（这里请填入你对季节指数数据的分析和结论）。

5. 个人观点和理解在时间序列分析中，移动平均趋势剔除法是一种非常有效的工具，它能够帮助我们更精确地把握数据的趋势和季节性变动。

而通过计算季节指数，我们可以更深入地了解时间序列数据中的季节性变化规律，从而为实际决策提供可靠的依据。

简单季节指数法的步骤[1]简单季节预测法的具体步骤如下：1.收集历年按季度记录的历史统计资料；2.计算出n年各相同季度的平均值(A)；3.计算出n年每一个季度的平均值(月)；4.计算季节指数，即用各季度的平均值除以所有季度的平均值：式中C=A/BC——季节指数。

5.利用季节指数(C),对预测值进行修正：Yt = (a + bT)C i式中Ci——第i季度的季节指数(i=1,2,3,4)；Yt——第t季度的销售量；a——待定系数；b——待定系数；T——预测期季度数，[编辑]简单季节指数法实例分析[1]例如，某公司从1996年到2001年，每一年各季度的纺织品销售量见下表。

预测2001年各季度纺织品的销售量。

1996 600 180 150 120 150 1997 660 210 160 130 160 1998 700 230 170 130 170 1999 750 250 180 140 180 2000 850 300 200 150 200 2001 1000 400 220 160 220 合计4560 1570 1080 830 1080 季节指数 1.38 0.95 0.73 0.95预测过程如下：1.六年各相同季节的平均销售量(Ai)A1=1970÷6≈262(单位)同理A_2=180，A_3≈138.3，A_4=180(单位)2.六年所有季度的平均销售量(B)(单位) M——6年销售量总和3.各季节销售指数(Ci)Ci=262÷19≈1.38同理C2≈0.95，C3≈0.73，C4≈0.954.修正2002年各季度预测值(1)建立时间序列线性回归预测模型由上表可得知各有关数据，利用公式(1)(2)y_t=190+1.90T式中T=-23,-21,…,-1,1,3,…,23(2)修正2002年各季度预测值第一季度预测值=(190+1.90×25)×1.38≈328(单位) 第二季度预测值=(190+1.90×27)×0.95≈229(单位) 第三季度预测值=(190+1.90×29)×0.73≈179(单位) 第三季度预测值=(190+1.90×31)×0.95≈236(单位)注意：如果n为奇数，例如n=9，则T=-4，-3，-2，1，0，1，2，3，4.季节销售指数也可以按月计算。

季节指数是用来评估某项指标在不同季节或时间段的变化程度，常用于经济、气候等领域。

下面是一个季节指数计算公式的例题：
例题：某公司的销售额在四个季度分别为：第一季度200 万元，第二季度180 万元，第三季度240 万元，第四季度220 万元。

计算该公司的季节指数。

解答：
季节指数的计算步骤如下：
计算每个季度的平均销售额。

平均销售额= （第一季度销售额+ 第二季度销售额+ 第三季度销售额+ 第四季度销售额）/ 4
平均销售额= （200 + 180 + 240 + 220）/ 4
= 840 / 4
= 210 万元
计算每个季度的季节指数。

季节指数= 季度销售额/ 平均销售额
第一季度季节指数= 200 / 210 ≈0.952
第二季度季节指数= 180 / 210 ≈0.857
第三季度季节指数= 240 / 210 ≈1.143
第四季度季节指数= 220 / 210 ≈1.048
所以，该公司的季节指数为：
第一季度：0.952
第二季度：0.857
第三季度：1.143
第四季度：1.048
季节指数可以用来衡量销售额在不同季度间的波动情况，数值大于1表示销售额高于平均水平，数值小于1表示销售额低于平均水平。