《高等数学》函数的单调性与曲线的凹凸性
- 格式：pdf
- 大小：545.63 KB
- 文档页数：13
下载文档原格式
合集下载
3.4 函数的单调性与曲线的凹凸性
从几何上看，曲线的凹凸性反映的是曲线弧上两点，连接这两点间的弦与 这两点间的弧段的位置关系。
第三章 微分中值定理与导 数的应用
9
定理 2
设 f (x ) 在 a ,b 上连续，在 (a ,b ) 内具有一阶和二阶导数，那么
> 0 ，则 f ( x ) 在 a ,b 上的图形是凹的； < 0 ，则 f ( x ) 在 a ,b 上的图形是凸的。 ∈ a ,b ，且 x 1 < x 2 ，记 x 0 =
= 0 处，曲线 y = x 3 有水平切线，即 x 轴。
一般地，如果 f ′ (x ) 在某区间内的有限个点处为零，在其余各点处保持固定 符号时，函数 f (x ) 在该区间上是单调的。 结论在 f ′ (x )
= 0 有无限个解时未必成立。
第三章 微分中值定理与导 数的应用
7
例6 证
证明：当 x 令 f (x )
=0
< a < 1,b = 2k + 1 k ∈ Z + ,ab > 1 +
(
)
3π 2
，
Van Der Waerden 构造并证明： f (x )
=
n =0
∑
∞
ϕ 10n x
10n
(
) ，其中
x − x , ϕ (x ) = x + 1 − x ,
> 1 时， 2 x > 3 −
1
x
。
1 = 2 x − 3 − ，则 x
f ′ (x ) =
1
x
−
1
x
2
=
1
x2
高数第三章第四次函数单调性凹凸性
b
o a
x
o a
f ( x ) 0
b x
定理 设y f ( x )在 [a , b] 上连续，在(a , b)内可导.
（1） 若在(a , b)内f ( x ) 0， f ( x ) 在 [a , b] 上单调增加； ( 2)若在 (a , b)内 f ( x ) 0， f ( x ) 在 [a , b] 上单调减少 .
三、曲线凹凸的判定
y
y f (x )
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
f ( x ) 递增
y 0
f ( x ) 递减
b x y 0
定理2 如果 f ( x ) 在 [a , b] 上连续, 在 (a , b) 内具有
一阶和二阶导数, 若在 (a , b) 内 (1) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凹的; ( 2) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凸的.
1 (x ) x4 x4 4 (x ) 4! 8 12 x4 1 lim lim x 0 x 0 x4 1 ( x2 ) 6 2 2 x (x ) 2 2 x2
4
一、单调性的判别法
y
y f ( x)
A
B
y
A y f ( x)
B
）
f ( x ) 0
三、曲线凹凸的判定
例5 判断曲线 y x 3 的凹凸性. 解： y 3 x 2 , y 6x , 当x 0时， y 0,
曲线 在(,0]为凸的；
o a
x
o a
f ( x ) 0
b x
定理 设y f ( x )在 [a , b] 上连续，在(a , b)内可导.
（1） 若在(a , b)内f ( x ) 0， f ( x ) 在 [a , b] 上单调增加； ( 2)若在 (a , b)内 f ( x ) 0， f ( x ) 在 [a , b] 上单调减少 .
三、曲线凹凸的判定
y
y f (x )
A
B
y
y f ( x)
B
A
o
a
b
x
o
a
f ( x ) 递增
y 0
f ( x ) 递减
b x y 0
定理2 如果 f ( x ) 在 [a , b] 上连续, 在 (a , b) 内具有
一阶和二阶导数, 若在 (a , b) 内 (1) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凹的; ( 2) f ( x ) 0, 则 f ( x ) 在 [a , b] 上的图形是凸的.
1 (x ) x4 x4 4 (x ) 4! 8 12 x4 1 lim lim x 0 x 0 x4 1 ( x2 ) 6 2 2 x (x ) 2 2 x2
4
一、单调性的判别法
y
y f ( x)
A
B
y
A y f ( x)
B
）
f ( x ) 0
三、曲线凹凸的判定
例5 判断曲线 y x 3 的凹凸性. 解： y 3 x 2 , y 6x , 当x 0时， y 0,
曲线 在(,0]为凸的；
高等数学方明亮34函数的单调性与曲线的凹凸性
y f (x) B
A
yA y f (x) B
oa
bx
f ( x) 0
oa
bx
f ( x) 0
定理 1 (函数单调性的判定法） 设函数 y f (x) 在 [a,b] 上 连 续 , 在 (a,b) 内 可 导 ．（ 1 ） 如 果 在 (a,b) 内 ， f (x) 0 ，则 y f (x) 在 [a,b] 上单调增加；（2）如果在 (a,b) 内， f (x) 0 ，则 y f (x) 在[a,b] 上单调减少．
2019年9月14日星期六
9
目录
上页
下页
返回
定义 设函数 f (x) 在区间 I 上连续，如果对 I 上任意
两点 x1, x2 （不妨设 x1 x2 ）及任意正数 (0 1) ，恒
有
f [x1 (1 ))x2 ] f (x1) (1 ) f (x2 ),
解：已知 f (x0 ) 0 ，不妨设 f (x0 ) 0 ， 由于 f (x0 ) 在 x x0 的某邻域内连续，
因此必存在 0 ，当 x (x0 , x0 ) 时 f (x) 0
又已知 f (x0 ) 0
从而当 x (x0 , x0 ) 时 f (x) f (x0 ) 0 ，函数凸
则称曲线 y f (x) 在 I 上是凹的．
类似地，可给出曲线是凸的定义，若上式中不等 号反向，则称曲线 y f (x) 在 I 上是凸的．
直接利用定义来判别曲线的凹凸性是比较困难的，
下面利用二阶导数来判别曲线的凹凸性．
2019年9月14日星期六
10
目录
上页
下页
返回
函数的单调性与曲线的凹凸性PPT课件
6.4 函数的单调性与曲线的凹凸性
函数的单调性与曲线的凹凸性
第1页，共42页。
6.4 函数的单调性与曲线的凹凸性
一、函数单调性的判别法
y
y f (x) B
f ( x) 0
A
y
A y f (x) f ( x) 0
B
Oa
bx
Oa
bx
定理6.8 设函数y = f (x)在[a, b]上连续, 在
f ( x) cos x 2 , f ( x) sin x 0,
f ( x)的图形是凸的.
又f
(0)
0,
f
(
)
0,
因此f
(x)
0, 即
2
sin x 2 x.
第23页，共42页。
6.4 函数的单调性与曲线的凹凸性
二、曲线的拐点及其求法
1.定义
连续曲线上凹凸的分界点称为曲线的
几何上
y y x3
方法：须确定单调区间 、区间端点值（或单侧极限） ，从而判定根的个数以及根所在的区间。
解
令f (x) ex| x
f
'(x)
e x e x
1， 1,
2| x2 x2
e x
e
x
x2， x2,
x2 x2
x 0是导数为零的点，x 2是导数不存在的点，
第14页，共42页。
6.4 函数的单调性与曲线的凹凸性
注 (1)驻点和导数不存在的点不一定是单调区间的分
界点。
y
y x3
如, y x3 , y x0 0,
但在(,)上 单调增加.
O
x
(2):区间内有限个点（或无穷多个离散点）导数为零, 不影响区间的单调性.
函数的单调性与曲线的凹凸性
第1页，共42页。
6.4 函数的单调性与曲线的凹凸性
一、函数单调性的判别法
y
y f (x) B
f ( x) 0
A
y
A y f (x) f ( x) 0
B
Oa
bx
Oa
bx
定理6.8 设函数y = f (x)在[a, b]上连续, 在
f ( x) cos x 2 , f ( x) sin x 0,
f ( x)的图形是凸的.
又f
(0)
0,
f
(
)
0,
因此f
(x)
0, 即
2
sin x 2 x.
第23页，共42页。
6.4 函数的单调性与曲线的凹凸性
二、曲线的拐点及其求法
1.定义
连续曲线上凹凸的分界点称为曲线的
几何上
y y x3
方法：须确定单调区间 、区间端点值（或单侧极限） ，从而判定根的个数以及根所在的区间。
解
令f (x) ex| x
f
'(x)
e x e x
1， 1,
2| x2 x2
e x
e
x
x2， x2,
x2 x2
x 0是导数为零的点，x 2是导数不存在的点，
第14页，共42页。
6.4 函数的单调性与曲线的凹凸性
注 (1)驻点和导数不存在的点不一定是单调区间的分
界点。
y
y x3
如, y x3 , y x0 0,
但在(,)上 单调增加.
O
x
(2):区间内有限个点（或无穷多个离散点）导数为零, 不影响区间的单调性.
高等数学3.4函数的单调性与曲线的凹凸性
ln(1 x ).
三、曲线的凹凸性 问题: 如何研究曲线的弯曲方向?
y
y
C
B
A
y f ( x)
y
y f ( x)
o
x
o
x1
x2 x
o
x1
x2
x
图形上任意弧段 位于所张弦的下方
图形上任意弧段 位于所张弦的上方
三、曲线的凹凸性
y
y f ( x)
y
y f ( x)
o
x1
x2
x
o
解方程f ( x ) 0 得，x1 1, x2 2.
x 1 时 f ( x ) 0, 在( ,1]上 单调增加 1 x 2 时 f ( x ) 0, 在[1, 2]上 单调减少
2 x 时 f ( x ) 0, 在[2, )上 单调增加
设函数 y f ( x )在[a, b]上连续，在(a, b)内可导. （1） 如果在(a, b)内f ( x ) 0，那末函数 y f ( x ) 在[a, b] 上单调增加； (2) 如果在(a, b)内 f ( x ) 0，那末函数 y f ( x ) 在[a, b] 上单调减少.
四、曲线凹凸的判定
y
y f (x)
A
B
y
y f ( x)
B
A
y 0 f ( x ) 递增 y 0 f ( x ) 递减 定理1 在( a , b ) 内 有一阶和二阶导数， 如果 f ( x ) 在 [a , b] 上 连续；
若在 ( a , b ) 内 (1) f ( x ) 0, 则函数 f ( x ) 在 [a , b] 上的图形 是凹的 (2) f ( x ) 0,则函数 f ( x ) 在 [a , b] 上的图形 是凸的
函数的单调性和曲线的凹凸性
故在(0, +)上 f (x)单增.
例4. 证明不等式 ex – (1+x) > 1– cosx, (x > 0)
证明思路: 用两次单调性
证: 设 F(x) = ex – (1+x) – (1– cosx)
= ex –x +cosx –2
则 F(0)=0. 要证F(x) > 0 (x > 0)
故曲线在(0, +)上是凹的.
即有 f (tx +(1– t) y) < t f (x) + (1– t) f (y) 即
定义2. 设f (x)C(U(x0)), 若曲线 y = f (x)在点 (x0, f (x0))的左右两侧凹凸性相反, 则称点(x0, f (x0))为该曲线的拐点.
= t f (x1)+(1– t) f (x2)
= t x1+(1– t) x2 x = x2+(x1– x2)t
弦上对应点的纵坐标B: y2+(y1– y2)t = t y1+(1– t)y2
STEP1
STEP2
STEP3
STEP4
故得如下定义.
定义1. 设 f (x)在[a, b]上有定义,x1, x2[a, b](x1x2) 和t(0, 1), 若有
凹凸性标志着图形弯曲的方向.
如图(a), (b)
y=f (x)
o
y
x
x1
x2
A
B
(x1, y1)
(x2, y2)
x
x
o
y
x1
x2
A
B
y=f (x)
(x2, y2)
(x1, y1)
函数的单调性与曲线的凹凸性
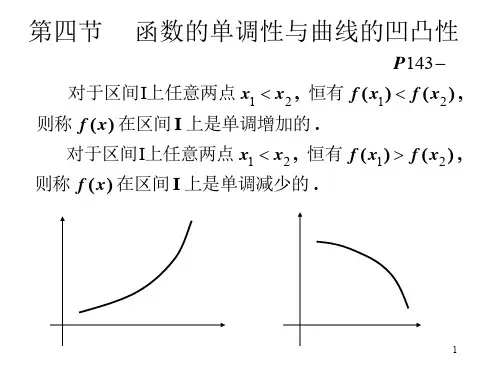
§3.4 函数的单调性与曲线的凹凸性一、函数单调性的判别法 定理1 设)(x f 在区间I 上可导，则)(x f 在I 上递增（减）的充要条件是)()('00≤≥x f .证 若f为增函数，则对每一I x ∈0，当0x x ≠时，有()()000≥--x x x f x f 。
令0x x →，即得00≥)('x f 。
反之，若)(x f 在区间I 上恒有0≥)('x f ，则对任意I x x ∈21,（设21x x <），应用拉格朗日定理，存在，使得()()()01212≥-=-x x f x f x f ξ')(。
由此证得f 在I 上为增函数。
定理2 若函数f 在),(b a 内可导,则f 在),(b a 内严格递增(递减)的充要条件是:(1)),(b a x ∈∀有)()('00≤≥x f ;(2) 在),(b a 内的任何子区间上0≠)('x f .推论 设函数在区间I 上可微,若))('()('00<>x f x f , 则f 在I 上(严格)递增(递减).注1 若函数f 在),(b a 内(严格)递增(递减),且在点a 右连续,则f在),[b a 上亦为(严格)递增(递减), 对右端点b 可类似讨论.注2 如果函数)(x f 在定义区间上连续，除去有限个导数不存在的点外，导数存在且连续，那么只要用方程0=)('x f 的根及)('x f 不存在的点来划分函数)(x f 的定义区间就能保证)('x f 在各个部分区间保持固定符号，因而函数)(x f 在每个部分区间上单调。
注意：如果函数)(x f 在区间],[b a 上连续，在),(b a 内除个别点处一阶导数为零或不存在外，在其余点上都有0>)('x f （或0<)('x f ），那么由于连续性，)(x f 在区间],[b a 上仍然是单调增加（或单调减少）的。
第四节函数的单调性与曲线的凹凸性共36页
x2
x
=
3
是极值点
y 2 7 6ab0
x 3
( 3)
联立(1)-(3),得 a = －6, b = 9, c = 2.
例15. 利用函数的凹凸性证明不等式:
ex
ey
xy
e 2 (xy).
2
证明: 令f(x)ex,
f(x)ex0, (x (, ) )
f(x)在( , )上是凹的
同理可证明(2).
例1．讨 论 函 f(x) 数 exx1的 单.调 性
解： 定 义 D:( 域 , ) . f(x)ex 1.
x
f (x) f (x)
(, 0)
0 (0, )
0
f(x)在( ,0]单调减 ;在少 [0,)上单调增. 加
说明:导数等于零的点(即驻点)划分函数的定义 区间为两个具有单调性的区间.
令f(x)0, x10,x2 2 ;x3 1是不可导.
(3) 列表判断:
x (,2) 2 (2,1) 1 (1, 0) 0 (0,)
f (x) 0 不存在 0
f (x)
单调增加区间: ( ,2][0, ) 单调减少区间: [2, 0].
1x 因f为 (x)在 [0,) 上连 , 续 且 (0 , 在 )内 ,可 f(x ) 0 导 ,
所以 f(x)在 [0, )上单调 ;由 增 f(0) 加 0, 知x当 0时 , f(x)f(0), 即 xln 1(x).
3. 曲线
y1ex2 的凹区间是 ( 1 , 2
( D )f ( 1 ) f ( 0 ) f ( 1 ) f ( 0 )
提示: 利用 f (x)单调增加 , 及
f( 1 ) f( 0 ) f()( 0 1 )
x
=
3
是极值点
y 2 7 6ab0
x 3
( 3)
联立(1)-(3),得 a = －6, b = 9, c = 2.
例15. 利用函数的凹凸性证明不等式:
ex
ey
xy
e 2 (xy).
2
证明: 令f(x)ex,
f(x)ex0, (x (, ) )
f(x)在( , )上是凹的
同理可证明(2).
例1．讨 论 函 f(x) 数 exx1的 单.调 性
解： 定 义 D:( 域 , ) . f(x)ex 1.
x
f (x) f (x)
(, 0)
0 (0, )
0
f(x)在( ,0]单调减 ;在少 [0,)上单调增. 加
说明:导数等于零的点(即驻点)划分函数的定义 区间为两个具有单调性的区间.
令f(x)0, x10,x2 2 ;x3 1是不可导.
(3) 列表判断:
x (,2) 2 (2,1) 1 (1, 0) 0 (0,)
f (x) 0 不存在 0
f (x)
单调增加区间: ( ,2][0, ) 单调减少区间: [2, 0].
1x 因f为 (x)在 [0,) 上连 , 续 且 (0 , 在 )内 ,可 f(x ) 0 导 ,
所以 f(x)在 [0, )上单调 ;由 增 f(0) 加 0, 知x当 0时 , f(x)f(0), 即 xln 1(x).
3. 曲线
y1ex2 的凹区间是 ( 1 , 2
( D )f ( 1 ) f ( 0 ) f ( 1 ) f ( 0 )
提示: 利用 f (x)单调增加 , 及
f( 1 ) f( 0 ) f()( 0 1 )
函数单调性与曲线凹凸性
二阶可导,
则 定理3.
（由定理3保证）
且点( x0 , f ( x0 )) 是曲线的拐点. 则 证明： f ( x ) 二阶可导,
f ( x ) 存在且连续 ,
定理3. 且点( x0 , f ( x0 )) 是曲线的拐点. 则 证明： f ( x ) 二阶可导,
f ( x ) 存在且连续,
f ( x )在x0 取得极值,
由费马引理
f ( x ) 0.
拐点的求法：
设函数f ( x )在x0的邻域内二阶可导, 且f ( x0 ) 0,
(1) x0两侧f ( x )变号, 点( x0 , f ( x0 ))即为拐点;
( 2) x0两侧f ( x )不变号, 点( x0 , f ( x0 ))不是拐点.
若 f ( x ) 0, 则函数f ( x )在[a , b]上单调递增, 若 f ( x ) 0 , 则函数f ( x )在[a , b]上单调递减, 推论 如果f ( x )连续, 且除有限个(或可数个)点外,
f ( x ) 0或( f ( x ) 0), 则函数f ( x )单调递增(递减),
第四节 函数的单调性与曲线的凸凹性
一、函数单调性的判定法 二、曲线的凹凸与拐点
一、 函数单调性的判定法
定理 1. 设函数f ( x )在[a , b]上连续, 在(a , b)内可导
若 f ( x ) 0, 则函数f ( x )在[a , b]上单调递增, 若 f ( x ) 0 , 则函数f ( x )在[a , b]上单调递减, 证: 不妨设 f ( x ) 0 , x I ,任取 x1 , x2 I ( x1 x2 ) 由拉格朗日中值定理得
3 x 2 , y 6 x , 令 f ( x ) 0 , 得 x 0 y
高等数学第四节函数的单调性与曲线的凹凸性
f ( x) 0的点都是孤立点 , 所以 f ( x) 在 ( , ) 单调增加 . #
分区间讨论:
在 (0, 2 )内, f ( x) 0 , f ( x) 在 [0, 2 ] 单调增加 ; 在 (2 , 4 )内, f ( x) 0 , f ( x) 在[2 , 4 ] 单调增加 ,
1
一 . 单调性的判别法 .
y
y f (x) B
A
yA y f (x) B
oa
bx
f ( x) 0
oa
bx
f ( x) 0
定理1 . 设函数 y f ( x) 在[a , b] 上连续 , 在 (a , b)内可导 .
(1) 如果在 (a , b)内 f ( x) 0 ,
则 f ( x2 ) f ( x1) 0 , y f ( x) 在[a , b] 上单调减少.
3
例1 . 讨论函数 y e x x 1的单调性. 解 . 函数的定义域 : D (,)
y e x 1. 在 ( , 0)内, y 0 ,
在 ( , 0]内, 函数单调减少 .
f ( x) 在 [ 0, ) 连续 , 在 ( 0 , )内 f ( x) 0 , 所以 f ( x) 在[ 0 , ) 单调增加 . 当 x 0 时 , f ( x) f (0) 0 , 即 x ln(1 x) 0 , x ln(1 x) .
第四节 函数的单调性与曲线的凹凸性
P143 对于区间I上任意两点 x1 x2 , 恒有 f ( x1) f ( x2 ) , 则称 f ( x) 在区间 I 上是单调增加的 . 对于区间I上任意两点 x1 x2 , 恒有 f ( x1) f ( x2 ) , 则称 f ( x) 在区间 I 上是单调减少的 .
3-4 函数的单调性与曲线的凹凸性(高等数学)
§3.4 函数的单调性与曲线的凹凸性教学内容：一．函数的单调性1.定理：设函数()f x 在区间I 上可导，对一切x I ∈有（1）()0f x '>，则函数()f x 在I 上单调增加；（2）()0f x '<，则函数()f x 在I 上单调减少．2．讨论函数单调性的步骤如下：(1) 确定()f x 的定义域；(2) 求f x '()，并求出()f x 单调区间所有可能的分界点(包括()0'=f x 的驻点、()'f x 不存在的点、()f x 的间断点)，并根据分界点把定义域分成相应的区间；(3) 判断一阶导数()'f x 在各区间内的符号，从而判断函数在各区间中的单调性.二．曲线的凹凸性与拐点1.定义：设函数()f x 在区间I 上连续，如果对I 上任意两点1x 和2x ，总有1212()()22++⎛⎫< ⎪⎝⎭x x f x f x f ，则称在区间I 上的图形是凹的（或下凸的）；如果总有1212()()22++⎛⎫> ⎪⎝⎭x x f x f x f ，则称在区间I 上的图形是凸的（或下凸的）.2.定义：设函数()f x 在开区间(,)a b 内可导, 如果在该区间内()f x 的曲线位于其上任何一点切线的上方，则称该曲线在(,)a b 内是凹的，区间(,)a b 称为凹区间；反之，如果()f x 的曲线位于其上任一点切线的下方，则称该曲线在(,)a b 内是凸的，区间(,)a b 称为凸区间．曲线上凹凸区间的分界点称为曲线的拐点．注：拐点是位于曲线上而不是坐标轴上的点，因此应表示为00(,())x f x ，而0x x =仅是拐点的横坐标，若要表示拐点，必须算出相应的纵坐标0()f x ．3.定理：设函数()f x 在[,]a b 上连续，在(,)a b 内二阶可导，那么（1）若对(,)x a b ∀∈，()0f x ''>，则()f x 在[,]a b 上的图形是凹的；（2）若对(,)x a b ∀∈，()0f x ''<，则()f x 在[,]a b 上的图形是凸的．4．求函数的凹凸区间和拐点的步骤：（1）确定函数的连续区间（初等函数即为定义域）；（2）求出函数二阶导数，并解出二阶导数为零的点和二阶导数不存在的点，划分连续区间；（3）依次判断每个区间上二阶导数的符号，确定每个区间的凹凸性，并进一步求出拐点坐标．。
3.4 函数的单调性与曲线的凹凸性
解方程 ′ () = 0 得, 1 = 1, 2 = 2.
(−∞, 1) (1,2)
(2, +∞)
′ ()
+
−
+
()
单增
单减
单增
单调增区间为
(−∞, 1], [2, +∞).
单调减区间为
[1,2].
第四节 函数的单调性与曲线的凹凸性
第三章 微分中值定理与导数的应用
例4 确定函数 () =
注意:
区间内个别点导数为零,不影响区间的单调性.
例如:
= 3, ′ቚ
=0
= 0, 但在(−∞, +∞)上单调增加.
一般地, 有如下定理：
定理2
设函数 = ()在[, ]上连续, 在(, )内可导.
(1) 如果在(, )内 ′ ()≥0, 且等号仅在有限多个点处成立,
例8
求曲线 = 3 4 − 4 3 + 1 #43;∞).
2
= 36( − ).
=
−
3
2
″
令 = 0, 得 1 = 0, 2 = .
3
′
12 3
″ ()
()
12 2 ,
″
(−∞, 0)
0
(0, 2ൗ3)
2ൗ
3
+
0
−
0
+
拐点(0,1)
凸的
拐点(2ൗ3 , 11ൗ27)
3. 利用单调性证明不等式
π
sin 2
例5 证明: 当0 < ≤ 时,
≥ .
2
π
证
π
sin 2
(−∞, 1) (1,2)
(2, +∞)
′ ()
+
−
+
()
单增
单减
单增
单调增区间为
(−∞, 1], [2, +∞).
单调减区间为
[1,2].
第四节 函数的单调性与曲线的凹凸性
第三章 微分中值定理与导数的应用
例4 确定函数 () =
注意:
区间内个别点导数为零,不影响区间的单调性.
例如:
= 3, ′ቚ
=0
= 0, 但在(−∞, +∞)上单调增加.
一般地, 有如下定理：
定理2
设函数 = ()在[, ]上连续, 在(, )内可导.
(1) 如果在(, )内 ′ ()≥0, 且等号仅在有限多个点处成立,
例8
求曲线 = 3 4 − 4 3 + 1 #43;∞).
2
= 36( − ).
=
−
3
2
″
令 = 0, 得 1 = 0, 2 = .
3
′
12 3
″ ()
()
12 2 ,
″
(−∞, 0)
0
(0, 2ൗ3)
2ൗ
3
+
0
−
0
+
拐点(0,1)
凸的
拐点(2ൗ3 , 11ൗ27)
3. 利用单调性证明不等式
π
sin 2
例5 证明: 当0 < ≤ 时,
≥ .
2
π
证
π
sin 2
高数讲义第四节函数的单调性与凹凸性
2、曲线凹凸的判定
特点：（1）曲线弧总位于 切线的下方。
（2）切线的斜率随 x 的增大 而减少。
y y f (x)
B
A oa
bx
即 f ( x)在[a, b]上单调减少.
由单调性判断可知：
若 f ( x) 0 f ( x)单调减少 曲线 y f ( x)是凸的.
2、曲线凹凸的判定
定理2 如果 f ( x) 在 [a, b] 上连续, 在 (a, b) 内具有
o
x
当 x 0时， y 0, 在(,0]上单调增加；
当0 x 时， y 0, 在[0,)上单调增加；
在(,)上函数单调增加.
一般地:若 f (x) 在区间内除有限个点处的导数为零, 在其余点处导数恒为正（或恒为负），则 f (x) 在该 区间上仍旧是单调增加的（或单调减少的 ） .
注意:单调性也常用来证明不等式或方程的根的个数.
一阶和二阶导数 , 若在 (a, b) 内 (1) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凹的; (2) f ( x) 0,则 f ( x) 在 [a, b] 上的图形是凸的.
说明： （1）证明的思路与单调性的情形完全一样。
（2）若将区间 [ a , b ] 换为其它形式的区间（包括 无穷区间），定理2的结论仍然成立。
解 D : (,).
f ( x) 6x2 18x 12 6( x 1)( x 2) 解方程f ( x) 0 得，x1 1, x2 2. 将 D划分为: (, 1], [1, 2] , [2, ) 当 x 1时， f ( x) 0, 在(,1]上单调增加； 当1 x 2时， f ( x) 0, 在[1,2]上单调减少；
f (1) 1 0, f (0) 1 0,
高等数学课件——函数的单调性与曲线的凹凸性
1.讨论曲线y ln x的凹凸性.
2.讨论曲线y x3的凹凸性.
3.讨论曲线y 3 x的凹凸性.
注：y f ( x)凹凸区间的分界点可能是 使f ''( x) 0的点； 或者f ''( x)不存在的点.
def :曲线上有一点( x0 , f ( x0 )),曲线在该点一边是上凸的， 在另一边是上凹的.称该点为曲线的拐点.
证： 不妨设 0 x1 x2
f ( x1 x2 ) f ( x2 ) f ( x1 ) f ( x1 x2 ) f ( x2 ) f ( x1 ) f (0) f ( 2 ) x1 f (1 ) x1 ( x2 2 x1 x2 , 0 1 x1 ) x1 f ( )( 2 1 ) 0 (1 2 )
4.讨论函数f ( x) 2x3 9x2 12x 3的单调性.
解：D f R. f '( x) 6 x 2 18 x 12. 令f '( x) 0得：x1 1, x2 2. x1 1, x2 2将D f 划分为(-,1],[1, 2],[2, ). 在(-,1)内，f '( x) 0. f ( x)在(-,1]上单调递增； 在(1，内， 2) f '( x) 0. f ( x)在[1, 2]上单调递减； 在(2, )内，f '( x) 0. f ( x)在[2, )上单调递增.
§3-4函数的单调性与曲线的凹凸性
函数的单调性 曲线的凹凸性
一、函数的单调性
已观察：f ( x)单调增加，则f '( x) 0; f ( x)单调减少，则f '( x) 0.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章
第八节 函数的单调性与 曲线的凹凸性
一、函数单调性的判定法 二、曲线的凹凸与拐点
机动 目录 上页 下页 返回 结束
一、 函数单调性的判定法
定理 1. 设函数 f (x) 在开区间 I 内可导, 若 f (x) 0 ( f (x) 0), 则 f (x) 在 I 内单调递增(递减) .
证: 无妨设 f (x) 0, x I , 任取 x1 , x2 I (x1 x2 )
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号, 则曲线的凹凸性不变 .
2) 根据拐点的定义及上述定理, 可得拐点的判别法如下:
若曲线 y f (x) 在点 x0 连续, f (x0 ) 0 或不存在, 但 f (x) 在 x0 两侧异号, 则点(x0 , f (x0 )) 是曲线 y f (x) 的一个拐点.
若恒有 f ( x1 x2 ) 2
f (x1) f (x2 ) , 则称 2
f (x)的
图形A 是凸的 .
yyy
连续曲线上有切线的凹凸分界点
称为拐点 .
ooo
xx11
xx11xx22 22
xx22
xxx
机动 目录 上页 下页 返回 结束
定理2.(凹凸判定法) 设函数 f (x)在区间I 上有二阶导数
f (x) 在 I 上单调递增 f (x) 在 I 上单调递减
2.曲线凹凸与拐点的判别
f (x) 0, x I
曲线 y f (x) 在 I 上向上凹
+
f (x) 0, x I
曲线 y f (x) 在 I 上向上凸
–
拐点 — 连续曲线上有切线的凹凸分界点
机动 目录 上页 下页 返回 结束
f
( x2
)
f (x1 x2 ),
2
说明 (1) 成立; (2) 证毕
机动 目录 上页 下页 返回 结束
例4. 判断曲线 y x4的凹凸性.
y
解: y 4x3, y 12x2
当x 0时，y 0; x 0时, y 0, 故曲线 y x4在 ( , ) 上是向上凹的. o x
说明:
(1) 在 I 内f (x) 0 , 则 f (x) 在 I 内图形是凹的 ;
(2) 在 I 内 f (x) 0 , 则 f (x) 在 I 内图形是凸的 .
证: x1 , x2 I , 利用一阶泰勒公式可得
f (x1)
f ( x1 x2)
2
f
(
x1
2
x2)( x1
x1 x2 2
)
解: 1) 求 y
y 12x3 12x2,
y
36x2
24x
36 x( x
2 3
)
2) 3)
求拐点可疑点坐标 令 y 0 得 x1 0 , 列表判别
x2
2 3
,
对应
y1
(0,1)
1,
y(2322, 1212171)7
3
x ( ,0)
0
(0, 32)
2 3
(
2 3
,
)
y 0 0
y
凹
1
凸
11 27
凹
故该曲线在
( ,0)
及
(
2 3
,
)
上向上凹, 在(0,
2 3
)
上
向上凸
,
点
(
0
,
1
)
及(
2 3
,
1217)
均为拐点.
机动 目录 上页 下页 返回 结束
内容小结
作业：P150：1，3单，5双，6，9（3） （4），10（1）（2），11（2），14
1. 可导函数单调性判别 f (x) 0, x I f (x) 0, x I
令 f (x) 0 , 得 x 1, x 2
x (, 1) f (x)
1 (1 , 2) 0
2 (2, ) 0
f (x)
2
1
y
故 f (x) 的单调增区间为 (, 1), (2, );
2 1
f (x)的单调减区间为(1, 2).
o
12 x
机动 目录 上页 下页 返回 结束
说明: 1) 单调区间的分界点除驻点外,也可是导数不存在的点.
机动 目录 上页 下页 返回 结束
例5. 求曲线 y 3 x 的拐点.
解:
y
1 3
2
x3
,
y
2 9
x
5 3
x ( ,0) 0
(0, )
y y凹
不存在
0
凸
因此点 ( 0 , 0 ) 为曲线 y 3 x 的拐点 . y
o
x
机动 目录 上页 下页 返回 结束
例6. 求曲线 y 3x4 4x3 1的凹凸区间及拐点.
f
(1 )
2!
( x1
x1
2
x2)2
f (x2 )
f ( x1 x2)
2
f
(
x1
2
x2)
( x2
x1
2
x2)
f
(2
2!
)
(
x2
x1
2
x2)2
两式相加
f (x1)
f
(
x2
)
2
f
(
x1
2
x2)
1 2!
(
x2 x1 2
)2
[
f
(1)
f (2 )]
当 f (x) 0时,
f
( x1) 2
例:3.
证明0
x
2
时,
成立不等式
sin x
x
2
.
证明 目录 上页 下页 返回 结束
二、曲线的凹凸与拐点
定义 . 设函数 f (x) 在区间 I 上连续 ,x1 , x2 I ,
(1)
若恒有 f ( x1 x2 ) 2
f (x1) B
图形是凹的;
(2)
例如, y 3 x2 , x ( , )
y
3
2
3
x
y x0
2) 如果函数在某驻点两边导数同号,
y y 3 x2
o
x
y
y x3
则不改变函数的单调性 .
例如, y x3 , x ( , )
o
x
y 3x2
y x0 0
机动 目录 上页 下页 返回 结束
例2： 证明 x tan x 0
由拉格朗日中值定理得
f (x2 ) f ( x1) f ( )(x2 x1) 0 (x1 , x2 ) I
故 f (x1) f ( x2 ). 这说明 f (x) 在 I 内单调递增.
证毕
机动 目录 上页 下页 返回 结束
例1. 确定函数 f (x) 2x3 9x2 12x 3的单调区间. 解: f (x) 6x2 18x 12 6(x 1)(x 2)
第八节 函数的单调性与 曲线的凹凸性
一、函数单调性的判定法 二、曲线的凹凸与拐点
机动 目录 上页 下页 返回 结束
一、 函数单调性的判定法
定理 1. 设函数 f (x) 在开区间 I 内可导, 若 f (x) 0 ( f (x) 0), 则 f (x) 在 I 内单调递增(递减) .
证: 无妨设 f (x) 0, x I , 任取 x1 , x2 I (x1 x2 )
1) 若在某点二阶导数为 0 , 在其两侧二阶导数不变号, 则曲线的凹凸性不变 .
2) 根据拐点的定义及上述定理, 可得拐点的判别法如下:
若曲线 y f (x) 在点 x0 连续, f (x0 ) 0 或不存在, 但 f (x) 在 x0 两侧异号, 则点(x0 , f (x0 )) 是曲线 y f (x) 的一个拐点.
若恒有 f ( x1 x2 ) 2
f (x1) f (x2 ) , 则称 2
f (x)的
图形A 是凸的 .
yyy
连续曲线上有切线的凹凸分界点
称为拐点 .
ooo
xx11
xx11xx22 22
xx22
xxx
机动 目录 上页 下页 返回 结束
定理2.(凹凸判定法) 设函数 f (x)在区间I 上有二阶导数
f (x) 在 I 上单调递增 f (x) 在 I 上单调递减
2.曲线凹凸与拐点的判别
f (x) 0, x I
曲线 y f (x) 在 I 上向上凹
+
f (x) 0, x I
曲线 y f (x) 在 I 上向上凸
–
拐点 — 连续曲线上有切线的凹凸分界点
机动 目录 上页 下页 返回 结束
f
( x2
)
f (x1 x2 ),
2
说明 (1) 成立; (2) 证毕
机动 目录 上页 下页 返回 结束
例4. 判断曲线 y x4的凹凸性.
y
解: y 4x3, y 12x2
当x 0时，y 0; x 0时, y 0, 故曲线 y x4在 ( , ) 上是向上凹的. o x
说明:
(1) 在 I 内f (x) 0 , 则 f (x) 在 I 内图形是凹的 ;
(2) 在 I 内 f (x) 0 , 则 f (x) 在 I 内图形是凸的 .
证: x1 , x2 I , 利用一阶泰勒公式可得
f (x1)
f ( x1 x2)
2
f
(
x1
2
x2)( x1
x1 x2 2
)
解: 1) 求 y
y 12x3 12x2,
y
36x2
24x
36 x( x
2 3
)
2) 3)
求拐点可疑点坐标 令 y 0 得 x1 0 , 列表判别
x2
2 3
,
对应
y1
(0,1)
1,
y(2322, 1212171)7
3
x ( ,0)
0
(0, 32)
2 3
(
2 3
,
)
y 0 0
y
凹
1
凸
11 27
凹
故该曲线在
( ,0)
及
(
2 3
,
)
上向上凹, 在(0,
2 3
)
上
向上凸
,
点
(
0
,
1
)
及(
2 3
,
1217)
均为拐点.
机动 目录 上页 下页 返回 结束
内容小结
作业：P150：1，3单，5双，6，9（3） （4），10（1）（2），11（2），14
1. 可导函数单调性判别 f (x) 0, x I f (x) 0, x I
令 f (x) 0 , 得 x 1, x 2
x (, 1) f (x)
1 (1 , 2) 0
2 (2, ) 0
f (x)
2
1
y
故 f (x) 的单调增区间为 (, 1), (2, );
2 1
f (x)的单调减区间为(1, 2).
o
12 x
机动 目录 上页 下页 返回 结束
说明: 1) 单调区间的分界点除驻点外,也可是导数不存在的点.
机动 目录 上页 下页 返回 结束
例5. 求曲线 y 3 x 的拐点.
解:
y
1 3
2
x3
,
y
2 9
x
5 3
x ( ,0) 0
(0, )
y y凹
不存在
0
凸
因此点 ( 0 , 0 ) 为曲线 y 3 x 的拐点 . y
o
x
机动 目录 上页 下页 返回 结束
例6. 求曲线 y 3x4 4x3 1的凹凸区间及拐点.
f
(1 )
2!
( x1
x1
2
x2)2
f (x2 )
f ( x1 x2)
2
f
(
x1
2
x2)
( x2
x1
2
x2)
f
(2
2!
)
(
x2
x1
2
x2)2
两式相加
f (x1)
f
(
x2
)
2
f
(
x1
2
x2)
1 2!
(
x2 x1 2
)2
[
f
(1)
f (2 )]
当 f (x) 0时,
f
( x1) 2
例:3.
证明0
x
2
时,
成立不等式
sin x
x
2
.
证明 目录 上页 下页 返回 结束
二、曲线的凹凸与拐点
定义 . 设函数 f (x) 在区间 I 上连续 ,x1 , x2 I ,
(1)
若恒有 f ( x1 x2 ) 2
f (x1) B
图形是凹的;
(2)
例如, y 3 x2 , x ( , )
y
3
2
3
x
y x0
2) 如果函数在某驻点两边导数同号,
y y 3 x2
o
x
y
y x3
则不改变函数的单调性 .
例如, y x3 , x ( , )
o
x
y 3x2
y x0 0
机动 目录 上页 下页 返回 结束
例2： 证明 x tan x 0
由拉格朗日中值定理得
f (x2 ) f ( x1) f ( )(x2 x1) 0 (x1 , x2 ) I
故 f (x1) f ( x2 ). 这说明 f (x) 在 I 内单调递增.
证毕
机动 目录 上页 下页 返回 结束
例1. 确定函数 f (x) 2x3 9x2 12x 3的单调区间. 解: f (x) 6x2 18x 12 6(x 1)(x 2)