回归直线方程课堂习题

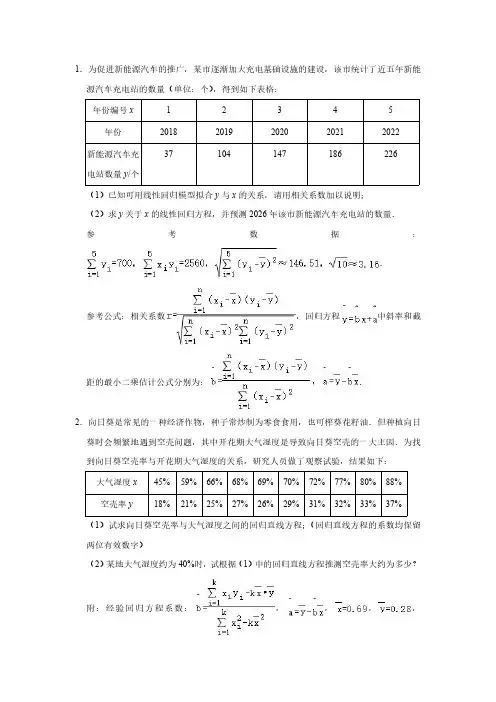
1．为促进新能源汽车的推广，某市逐渐加大充电基础设施的建设，该市统计了近五年新能源汽车充电站的数量（单位：个），得到如下表格：年份编号x 12345年份20182019202020212022新能源汽车充电站数量y /个37104147186226（1）已知可用线性回归模型拟合y 与x 的关系，请用相关系数加以说明；（2）求y 关于x 的线性回归方程，并预测2026年该市新能源汽车充电站的数量．参考数据：．参考公式：相关系数，回归方程中斜率和截距的最小二乘估计公式分别为：．2．向日葵是常见的一种经济作物，种子常炒制为零食食用，也可榨葵花籽油．但种植向日葵时会频繁地遇到空壳问题，其中开花期大气湿度是导致向日葵空壳的一大主因．为找到向日葵空壳率与开花期大气湿度的关系，研究人员做了观察试验，结果如下：大气湿度x 45%59%66%68%69%70%72%77%80%88%空壳率y18%21%25%27%26%29%31%32%33%37%（1）试求向日葵空壳率与大气湿度之间的回归直线方程；（回归直线方程的系数均保留两位有效数字）（2）某地大气湿度约为40%时，试根据（1）中的回归直线方程推测空壳率大约为多少？附：经验回归方程系数：，，，，，．3．随着时代的不断发展，社会对高素质人才的需求不断扩大，我国本科毕业生中考研人数也不断攀升，2020年的考研人数是341万人，2021年考研人数是377万人．某中学数学兴趣小组统计了本省5所大学2022年的毕业生人数及考研人数（单位：千人），收集数据如下表所示．A 大学B 大学C 大学D 大学E 大学2022年毕业人数x （千人）765432022年考研人数y （千人）2.52.31.81.91.5（1）利用最小二乘估计建立y 关于x 的线性回归方程；（2）该小组又利用上表数据建立了x 关于y 的线性回归方程，并把这两条拟合直线画在同一坐标系xOy 下，横坐标x ，纵坐标y 的意义与毕业人数x 和考研人数y 一致．请比较前者与后者的斜率k 1与k 2的大小．4．为助力乡村振兴，某电商平台为某地的农副特色产品开设直播带货专场，得到天数与直播间人数的数据如下表所示：日期第一天第二天第三天第四天第五天第六天第七天日期代码x 1234567直播间人数y （万人）4122123252728（1）求直播间人数y 和日期代码x 的样本相关系数（精确到0.01）；（2）若使用y ＝c +dlnx 作为y 关于x 的回归方程模型，计算该回归方程（结果保留1位小数），并预测至少要到哪一天直播间人数可以超过30万人．参考公式和数据：相关系数其中，回归直线方程中，e 266614032681.2206.413.22.6510.87.39参考答案与试题解析一．解答题（共4小题）1．为促进新能源汽车的推广，某市逐渐加大充电基础设施的建设，该市统计了近五年新能源汽车充电站的数量（单位：个），得到如下表格：年份编号x 12345年份20182019202020212022新能源汽车充电站数量y /个37104147186226（1）已知可用线性回归模型拟合y与x 的关系，请用相关系数加以说明；（2）求y 关于x的线性回归方程，并预测2026年该市新能源汽车充电站的数量．参考数据：．参考公式：相关系数，回归方程中斜率和截距的最小二乘估计公式分别为：．【解答】解：（1），＝＝≈3.16，＝2560﹣5×3×140＝460，则r ＝≈0.99，因为0.99＞0.75，所以可用线性回归模型拟合y与x的关系；（2）＝4＝1+0+1+4＝10，b＝＝＝46，a＝﹣b＝140﹣46×3＝2，所以，当x＝9时，，即预测2026年该市新能源汽车充电站的数量为416个．2．向日葵是常见的一种经济作物，种子常炒制为零食食用，也可榨葵花籽油．但种植向日葵时会频繁地遇到空壳问题，其中开花期大气湿度是导致向日葵空壳的一大主因．为找到向日葵空壳率与开花期大气湿度的关系，研究人员做了观察试验，结果如下：大气湿度x45%59%66%68%69%70%72%77%80%88%空壳率y18%21%25%27%26%29%31%32%33%37%（1）试求向日葵空壳率与大气湿度之间的回归直线方程；（回归直线方程的系数均保留两位有效数字）（2）某地大气湿度约为40%时，试根据（1）中的回归直线方程推测空壳率大约为多少？附：经验回归方程系数：，，，，，．【解答】解：（1）由已知得．所以．所以回归直线方程为y ＝0.35x +0.04．（2）由（1）知当大气湿度为40%时，空壳率约为0.35×0.4+0.04＝0.18＝18%．3．随着时代的不断发展，社会对高素质人才的需求不断扩大，我国本科毕业生中考研人数也不断攀升，2020年的考研人数是341万人，2021年考研人数是377万人．某中学数学兴趣小组统计了本省5所大学2022年的毕业生人数及考研人数（单位：千人），收集数据如下表所示．A 大学B 大学C 大学D 大学E 大学2022年毕业人数x （千人）765432022年考研人数y （千人）2.52.31.81.91.5（1）利用最小二乘估计建立y 关于x 的线性回归方程；（2）该小组又利用上表数据建立了x 关于y 的线性回归方程，并把这两条拟合直线画在同一坐标系xOy 下，横坐标x ，纵坐标y 的意义与毕业人数x 和考研人数y 一致．请比较前者与后者的斜率k 1与k 2的大小．【解答】解：（1）由表可知＝×（7+6+5+4+3）＝5，＝×（2.5+2.3+1.8+1.9+1.5）＝2，x i yi ＝7×2.5+6×2.3+5×1.8+4×1.9+3×1.5＝52.4，＝72+62+52+42+32＝135，所以＝＝＝0.24，＝2﹣0.24×5＝0.8，故y 关于x 的线性回归方程为＝0.24x +0.8．（2）由题意知，k1＝，k2＝，其中＝，所以＝＝r2≤1（其中r为相关系数），即k1≤k2，下面证明k1≠k2，若k1＝k2，则y i＝0.24x i+0.8（i＝1，2，3，4，5）恒成立，而2.5≠0.24×7+0.8，所以k1≠k2，故k1＜k2．4．为助力乡村振兴，某电商平台为某地的农副特色产品开设直播带货专场，得到天数与直播间人数的数据如下表所示：日期第一天第二天第三天第四天第五天第六天第七天日期代码x1234567直播间人数y（万人）4122123252728（1）求直播间人数y和日期代码x的样本相关系数（精确到0.01）；（2）若使用y＝c+dlnx作为y关于x的回归方程模型，计算该回归方程（结果保留1位小数），并预测至少要到哪一天直播间人数可以超过30万人．参考公式和数据：相关系数其中，回归直线方程中，e2 6661403268 1.2206.413.2 2.6510.87.39【解答】解：（1）由表可知，＝×（1+2+3+4+5+6+7）＝4，＝×（4+12+21+23+25+27+28）＝20，所以相关系数＝＝≈0.93．（2）令u＝lnx，则y＝c+du，所以＝＝＝≈12.3，＝﹣＝20﹣×1.2≈5.2，所以＝5.2+12.3u，即＝5.2+12.3lnx，当y＞30时，5.2+12.3lnx＞30，解得x＞7.5，故预测至少要到第8天直播间人数可以超过30万人．。

4.3.1 一元线性回归模型第1课时 相关关系、回归直线方程、回归直线方程的性质 课后训练巩固提升1.(多选题)四名同学根据各自的样本数据研究变量x,y 之间的相关关系,并求得回归直线方程,分别得到以下四个结论,其中一定不正确的是( )A.y 与x 负相关,且y ^=2.347x-6.423 B.y 与x 负相关,且y ^=-3.476x+5.648 C.y 与x 正相关,且y ^=5.437x+8.493 D.y 与x 正相关,且y ^=-4.326x-4.578解析:当y 与x 线性相关时,y 与x 正相关的充要条件是b ^>0,y 与x 负相关的充要条件是b ^<0,故AD 一定不正确. 答案:AD2.已知x 与y 之间的一组数据如下表.若已求得y 关于x 的回归直线方程为y ^=2.2的值为( ) A.1 B.0.85C.0.7D.0.5 解析:=m+15.54,则m+15.54=2.2×1.5+0.7,解得m=0.5.故选D.答案:D3.已知根据如下样本数据得到的回归直线方程为y ^=b ^x+a ^,则( ) A.a ^>0,b ^>0 B.a ^>0,b ^<0 C.a ^<0,b ^>0D.a ^<0,b ^<0解析:作出散点图(图略),可知a ^>0,b ^<0. 答案:B4.已知变量x 与y 正相关,且由观测数据算得x =3,y =3.5,则由该观测数据求得的回归直线方程可能是( ) A.y ^=0.4x+2.3 B.y ^=2x-2.4 C.y ^=-2x+9.5 D.y ^=-0.3x+4.4解析:由变量x 与y 正相关,可知C,D 均错.又回归直线经过样本点的中心(3,3.5),经验证,可知A 正确,B 错误.故选A. 答案:A5.过(3,10),(7,20),(11,24)三点的回归直线方程是( ) A.y ^=1.75+5.75xB.y ^=-1.75+5.75xC.y ^=5.75+1.75xD.y ^=5.75-1.75x解析:由题意易得,b ^=1.75,a ^=5.75,故所求的回归直线方程为y ^=5.75+1.75x.故选C. 答案:C6.为了均衡教育资源,调查了某地若干户家庭的年收入x(单位:万元)和年教育支出y(单位:万元).调查显示,年收入x 与年教育支出y 具有线性相关关系,并由调查数据得到y 关于x 的回归直线方程为y ^=0.15x+0.2.由回归直线方程可知,家庭年收入每增加1万元,年教育支出平均增加 万元. 答案:0.157.期中考试后,某校高三(9)班对全班50名学生的成绩进行分析,得到数学成绩y 关于总成绩x 的回归直线方程为y ^=6+0.4x.由此可以估计,若2名同学的总成绩相差50分,则他们的数学成绩大约相差 分. 解析:由回归系数b ^=0.4可知,x 每增大1个单位,y ^增大0.4个单位,故两名同学的总成绩相差50分,他们的数学成绩大约相差50×0.4=20(分). 答案:208.在一项关于16艘轮船的研究中,船的吨位区间为[192,3 246](单位:吨),船员的人数为5~32,船员人数y 关于吨位x 的回归直线方程为y ^=9.5+0.006 2x,(1)若两艘船的吨位相差1 000,估计这两艘船的船员人数相差多少; (2)估计吨位最大的船和最小的船的船员人数.解:(1)由题意可知,这两艘船的船员人数大约相差0.0062×1000≈6. (2)当x=192时,y ^=9.5+0.006 2×192≈11, 当x=3 246时,y ^=9.5+0.006 2×3 246≈30.故估计吨位最大的船和最小的船的船员人数分别为30和11.9.从某居民区随机抽取10个家庭,获得第i 个家庭的月收入x i (单位:千元)与月储蓄y i (单位:千元)的数据资料,算得∑i=110x i =80,∑i=110y i =20,∑i=110x i y i =184,∑i=110x i 2=720.(1)求家庭的月储蓄y 关于月收入x 的回归直线方程y ^=b ^x+a ^; (2)判断变量x 与y 之间是正相关还是负相关;(3)若该居民区某家庭月收入为7千元,估计该家庭的月储蓄. 解:(1)由题意知,n=10, x =110∑i=110x i =8,y =110∑i=110y i =2,则b ^=184-10×8×2720-10×82=0.3,a ^=2-0.3×8=-0.4.故所求回归直线方程为y ^=0.3x-0.4. (2)因为b ^=0.3>0,所以x 与y 之间是正相关. (3)当x=7时,y ^=0.3×7-0.4=1.7. 故该家庭的月储蓄约为1.7千元.10.某同学家开了一家饮品店,他为了研究气温对热饮销售的影响,经过统计,得到卖出的热饮杯数y 与当天气温x 的对比表如下.(1)作出散点图;(2)y与x是正相关还是负相关;(3)求y关于x的回归直线方程;(4)若某天的气温为2 ℃,估计这天卖出的热饮杯数. 解:(1)作出散点图如图所示.(2)由散点图可知,y与x负相关.(3)根据数据可知,x=16911,y=122811,b^≈-2.352,a^=y−b^x≈147.767.故所求的回归直线方程为y^=-2.352x+147.767.(4)当x=2时,y^=143.063.因此,当某天的气温为2 ℃时,这天大约可以卖出143杯热饮.。

回归分析练习题（有答案）作者:日期:1.1回归分析的基本思想及其初步应用一、选择题1.某同学由x 与y 之间的一组数据求得两个变量间的线性回归方程为均值为2，数据y 的平均值为3，则（）A .回归直线必过点（2,3）C 点（2,3）在回归直线上方B.回归直线一定不过点（2,3）D 点（2,3）在回归直线下方y bx a ，已知：数据x 的平2.在一次试验中，测得（x, y）的四组值分别是A （1,2）,B（2,3）,C（3,4）,D（4,5），则丫与X 之间的回归直线方程为（）A.$x1B .$ x 2C$2x1D.$ x 13.在对两个变量x ，y 进行线性回归分析时，有下列步骤：①对所求出的回归直线方程作出解释；③求线性回归方程；④求未知参数；②收集数据（X j 、y i ），i 1,2，…，n ；⑤根据所搜集的数据绘制散点图）如果根据可行性要求能够作岀变量A.①②⑤③④Bx, y 具有线性相关结论，则在下列操作中正确的是（C.②④③①⑤D .②⑤④③①.③②④⑤①4.下列说法中正确的是（）B人的知识与其年龄具有相关关系D 根据散点图求得的回归直线方程都是有意义的A.任何两个变量都具有相关关系C.散点图中的各点是分散的没有规律5.给出下列结论：2 2（1）在回归分析中，可用指数系数R 的值判断模型的拟合效果，R 越大，模型的拟合效果越好；（2）在回归分析中，可用残差平方和判断模型的拟合效果，残差平方和越大，模型的拟合效果越好；（3）在回归分析中，可用相关系数r 的值判断模型的拟合效果，较合适带状区域的宽度越窄，说明模型的拟合精度越高.A.y 平均增加1.5个单位B.A. 1B )个..2r 越小，模型的拟合效果越好；（4）在回归分析中，可用残差图判断模型的拟合效果，残差点比较均匀地落在水平的带状区域中，说明这样的模型比y 平均增加2个单位C.y 平均减少1.5个单位C.3DD.y 平均减少2个单位.4以上结论中，正确的有（6.已知直线回归方程为y7.2 1.5x ，则变量x 增加一个单位时（)下面的各图中，散点图与相关系数r 不符合的是（）\ 1V ||一1,— 1 < r<(>■r?■* ■■■■* ■..* .**打4X（7UV1）D.'8.一位母亲记录了儿子39岁的身高，由此建立的身高与年龄的回归直线方程为据此可以预测这个孩子10岁时的身高，则正确的叙述是（A.身高一定是145.83cm C.身高低于145.00cm BD）7.19x 73.93,.身高超过146.00cm身高在145.83cm左右9.（A）预报变量在x轴上，解释变量在y轴上（B）解释变量在x轴上，预报变量在y轴上（C）（D）在画两个变量的散点图时，下面哪个叙述是正确的（）可以选择两个变量中任意一个变量在x轴上可以选择两个变量中任意一个变量在y轴上10.两个变量y与x的回归模型中，通常用R2来刻画回归的效果，则正确的叙述是（22）A.R越小，残差平方和小2B.R越大，残差平方和大2c.R于残差平方和无关D.R越小，残差平方和大211.两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟合效果最好的模型是（）A.模型1的相关指数R2为0.98 B.模型2的相关指数R2为0.802 2C.模型3的相关指数R为0.50 D.模型4的相关指数R为0.2512.回归直线上相应位置的差异的是A.总偏差平方和B.C.回归平方和13.回归直线方程为残差平方和D.相关指数R2在回归分析中，代表了数据点和它在（）工人月工资（元）依劳动生产率（千元）变化的60 90x，下列判断正确的是（）A.劳动生产率为1000元时，工资为50元B.劳动生产率提高1000元时，工资提高150元C.劳动生产率提高1000元时，工资提高90元D.劳动生产率为1000元时，工资为90元14.下列结论正确的是（）①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.A.①② E.①②③ C.①②④ D.①②③④15.已知回归直线的斜率的估计值为中心为（4,5），则回归直线方程为（）1.23，样本点的A.$ 1.23x 4B.$ 1.23x 5C.$ 1.23x 0.08D.y 0.08x 1.2316.在比较两个模型的拟合效果时，甲、乙两个模型的相关指数果好的模型是 __________.17.在回归分析中残差的计算公式为 ____________.18.线性回归模型y bx a e（a和b为模型的未知参数）中，e称为_________________.19.若一组观测值（X1,yJ（X2,y2）…（Xn,y“）之间满足yi=bXi+a+e（i=1、2.…n）若恒为0,则氏为______________R2的值分别约为0.96和0.85，则拟合效20.调查某市出租车使用年限x 和该年支出维修费用y (万元)，得到数据如下:使用年限x 维修费用y(求线性回归方程;n22.233.845.556. 567.0(2)由(1)中结论预测第10年所支出的维修费用.i 1(X i x) (y iy).n(X ii 1x)2bx21.以下是某地搜集到的新房屋的销售价格闵屋面积Ey 和房屋的面积x 的数据:11524.Q1102 1. CIB-413G29.21口丘22t 肖年愉梧(1)画岀数据对应的散点图；(2)求线性回归方程，并在散点图中加上回归直线；(3)据(2)的结果估计当房屋面积为150m2时的销售价格(4)求第2个点的残差。

（新课标）2018-2019学年苏教版高中数学必修三2.4 线性回归方程课时目标 1.理解两个变量的相关关系的概念.2.会作散点图，并利用散点图判断两个变量之间是否具有相关关系.3.会求线性回归方程．1．与函数关系不同，相关关系是一种有关系，但不是确定性的关系．2．能用直线方程________近似表示的相关关系叫做线性相关关系，该方程叫______，给出一组数据(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )，线性回归方程中的系数a ，b 满足⎩⎪⎨⎪⎧b ＝ a ＝.上式还可以表示为⎩⎪⎨⎪⎧b ＝ ，a ＝ .一、填空题1．下列两个变量之间的关系，不是函数关系的为______．(填序号) ①匀速行驶车辆的行驶距离与时间； ②圆半径与圆的面积；③正n 边形的边数与内角度数之和； ④人的年龄与身高．2．下列有关线性回归的说法，不正确的是________．①变量取值一定时，因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系；②在平面直角坐标系中用描点的方法得到表示具有相关关系的两个变量的一组数据的图形叫做散点图；③线性回归方程最能代表观测值x 、y 之间的关系； ④任何一组观测值都能得到具有代表意义的线性回归方程．3．工人月工资(元)依劳动生产率(千元)变化的线性回归方程为 ＝60＋90x ，下列判断正确的是________．①劳动生产率为1千元时，工资为50元； ②劳动生产率提高1千元时，工资提高150元；③劳动生产率提高1千元时，工资约提高90元；④劳动生产率为1千元时，工资90元．4．某商品销售量y(件)与销售价格x(元/件)在实际生活中的回归方程可能是________．①＝－10x＋200；②＝10x＋200；③＝－10x－200；④＝10x－200.5．给出两组数据x、y的对应值如下表，若已知x、y是线性相关的，且线性回归方程：y＝a＋bx，经计算知：b＝－1.4，则a＝________.x 45678y 121098 66.线性回归方程表示的直线＝a＋bx必经过点____________．7．若对某个地区人均工资x与该地区人均消费y进行调查统计得y与x具有相关关系，且线性回归方程＝0.7x＋2.1(单位：千元)，若该地区人均消费水平为10.5，则估计该地区人均消费额占人均工资收入的百分比约为________．8．设有一个回归方程＝3－2.5x，当变量x增加一个单位时，变量y________个单位．9．期中考试后，某校高三(9)班对全班65名学生的成绩进行分析，得到数学成绩y对总成绩x的线性回归方程为＝6＋0.4x.由此可以估计：若两个同学的总成绩相差50分，则他们的数学成绩大约相差______分．二、解答题10．下表是某旅游区游客数量与平均气温的对比表：平均气温(℃)－1410131826数量(百个)202434385064若已知游客数量与平均气温是线性相关的，求回归方程．11．5个学生的数学和物理成绩(单位：分)如下表：学生A B C D E学科数学8075706560物理7066686462画出散点图，判断它们是否具有相关关系，若相关，求出回归方程．能力提升12．在研究硝酸钠的可溶性程度时，观测它在不同温度的水中的溶解度，得观测结果如下：温度x(℃)010205070溶解度y 66.776.085.0112.3128.0则由此得到回归直线的斜率约为________．13．炼钢是一个氧化降碳的过程，钢水含碳量的多少直接影响冶炼时间的长短，必须掌握钢水含碳量和冶炼时间的关系．如果已测得炉料熔化完毕时，钢水的含碳量x与冶炼时间y(从炉料熔化完毕到出钢的时间)的一列数据，如下表所示：x(0.01% )104181917714713415191204121y(min)10202118515513517205235125若由数据知y对x呈线性相关关系．(1)求线性回归方程．(2)预测当钢水含碳量为160时，应冶炼多少分钟？1．线性回归方程＝bx＋a中的系数a，b的计算公式为：⎩⎪⎨⎪⎧b ＝∑ni ＝1(x i －x )(y i －y )∑n i ＝1 (x i －x )2＝∑ni ＝1x i y i －n x y ∑ni ＝1x 2i －n x 2a ＝y －b x其中：b 是回归方程的斜率，a 是截距． 2．回归方程的求解过程 计算x ，y ，∑ni ＝1x 2i ，∑ni ＝1x i y i ⇓计算b ＝∑ni ＝1x i y i －n x y ∑n i ＝1x 2i －n x 2，a ＝y －b x⇓3．在回归方程 ＝bx ＋a 中，当回归系数b >0时，说明两个变量呈正相关关系，它的意义是：当x 每增加一个单位时y 就增加b 个单位；当b <0时，说明两个变量呈负相关关系，它的意义是：当x 每增加一个单位时，y 就减少b 个单位．2．4 线性回归方程知识梳理2. ＝bx ＋a 线性回归方程 n ∑ni ＝1x i y i －(∑ni ＝1x i )(∑ni ＝1y i )n ∑ni ＝1x 2i －(∑ni ＝1x i )2y －b x∑ni ＝1x i y i －n x y ∑ni ＝1x 2i －n x2＝∑ni ＝1(x i －x )(y i －y )∑ni ＝1(x i －x )2y －b x作业设计 1．④解析 人的年龄与身高具有相关关系． 2．④解析 只有所有的数据点都分布在一条直线附近时，才能得到回归直线． 3．③解析 因工人月工资与劳动生产率变化的线性回归方程为 ＝60＋90x ，当x 由a 提高到a ＋1时， 2－ 1＝60＋90(a ＋1)－60－90a ＝90. 4．①解析 ∵在实际生活中，当销售价格提高时，商品销售量一般要降低，∴排除②、④，又∵③中x>0时 <0不合题意，∴③错． 5．17.4 解析x ＝15(4＋5＋6＋7＋8)＝6，y ＝15(12＋10＋9＋8＋6)＝9.a ＝y －b x ＝9＋1.4×6＝9＋8.4＝17.4. 6．(x ，y )解析 由a ＝y －b x 得y ＝b x ＋a ， 即点(x ，y )适合方程 ＝a ＋bx. 7．87.5%解析 设该地区人均工资收入为y ， 则y ＝0.7x ＋2.1，当y ＝10.5时，x ＝10.5－2.10.7＝12.10.512×100%＝87.5%. 8．减少2.5解析′＝3－2.5(x＋1)＝3－2.5x－2.5＝－2.5，因此，y的值平均减少2.5个单位．9．20解析令两人的总成绩分别为x1，x2.则对应的数学成绩估计为＝6＋0.4x1，2＝6＋0.4x2，所以| 1－2|＝|0.4(x1－x2)|＝0.4×50＝20.10．解x＝706＝353，y＝2306＝1153，∑6i＝1x2i＝1＋16＋100＋169＋324＋676＝1 286，∑6i＝1x i y i＝－20＋96＋340＋13×38＋18×50＋26×64＝3 474.b＝∑6i＝1x i y i－6x y∑6 i＝1x2i－6x2＝3 474－6×353×11531 286－6×(353)2≈1.68，a＝y－b x≈18.73，即所求的回归方程为＝1.68x＋18.73.11．解以x轴表示数学成绩，y轴表示物理成绩，可得到相应的散点图如图所示：由散点图可知，两者之间具有相关关系，且为线性相关．列表，计算i 1 2 3 4 5x i80 75 70 65 60y i70 66 68 64 62x i y i 56004950476041603720x2i 64005625490042253600x＝70，y＝66，∑5i＝1x2i＝24 750，∑5i＝1x i y i＝23 190设所求回归方程为＝bx＋a，则由上表可得b＝∑5i＝1x i y i－5x y∑5 i＝1x2i－5x2＝90250＝0.36，a ＝y －b x ＝40.8.∴所求回归方程为 ＝0.36x ＋40.8. 12．0.880 9 解析x ＝30，y ＝93.6，∑5i ＝1x 2i ＝7 900，∑5i ＝1x i y i ＝17 035，所以回归直线的斜率b ＝∑5i ＝1x i y i －5x y ∑5i ＝1x 2i －5x 2＝17 035－5×30×93.67 900－4 500≈0.880 9.13．解 (1)列出下表，并用科学计算器进行计算： i 1 2 3 4 5 6 7 8 9 10 x i 104 180 190 177 147 134 150 191 204 121 y i 100 200 210 185 155 135 170 205 235 125 x i y i10400360003990032745227851809025500391554794015 125x ＝159.8，y ＝172，∑10i ＝1x 2i ＝265 448，∑10i ＝1y 2i ＝312 350，∑10i ＝1x i y i ＝287 640 设所求线性回归方程为 ＝bx ＋a ，b ＝∑10i ＝1x i y i －10x y∑10i ＝1x 2i －10x2≈1.27，a ＝y －b x ≈－30.95.即所求的线性回归方程为 ＝1.27x －30.95.(2)当x ＝160时， ＝1.27×160－30.95≈172(min )，即大约冶炼172 min .。

回归直线方程公式详解及例题回归直线方程，听起来是不是有点严肃？这玩意儿就像是数学里的“小白兔”，看起来很复杂，但其实乍一看也不过是个简单的小家伙。

让咱们聊聊这个直线方程的由来，还有怎么用它解决问题。

说白了，就是用一条直线把一堆数据给“牵”起来，让我们看清楚它们之间的关系。

就像在赶集一样，把各种水果摆成一排，想要了解哪个最受欢迎。

这里，最常见的回归直线方程是y = mx + b。

听起来不算复杂吧？不过咱们慢慢来，不急。

y代表咱们要预测的东西，比如说，你想知道你的成绩和学习时间的关系，那y就可以是你的成绩；x就是你花在学习上的时间。

m，这个家伙叫做斜率，表示的是y和x之间的关系，简单来说就是学习时间每增加一个小时，成绩大概能提高多少分。

b则是当你啥都不做时，你的成绩是多少，这个也很重要，没错，人生不就是这么回事吗？想象一下，拿出一根铅笔和一张纸，把这些点点画出来。

每个点就代表了一次测量，比如说你在不同时间学习的成绩。

画得可真像一幅抽象画，虽然一开始没法看出什么，但如果仔细一看，就能发现某种趋势。

这就是回归分析的魔力，它能帮你找到这些点之间的规律。

慢慢地，这些点就会聚成一条线，给你展示出学习时间和成绩之间的关系。

再来聊聊如何计算这些参数。

有很多软件和工具可以帮你做这些。

但如果你想亲自尝试，手动计算也是个不错的选择。

先得算出这些数据的平均值，接着用这些平均值来计算m和b。

想象一下，m的计算就像是在算你朋友圈里哪个小伙伴总是抢着买单。

搞定这些，y = mx + b就能顺利出炉了。

说到这里，有些小伙伴可能会想，回归直线到底有什么用呢？这玩意儿其实是个超有用的工具。

比如说，商家可以用它预测销量，学校可以分析成绩趋势，甚至天气预报也会用到。

想想看，如果你知道晴天和下雨天的概率，你是不是就能提前决定穿哪双鞋？这不就是让生活更简单吗？回归直线也有它的局限性。

毕竟，生活可不是总那么简单。

数据点就像是小孩子一样顽皮，根本不愿意听话，完全不按常理出牌。

高二数学回归直线方程的练习题1. 已知直线L1过点A(2,3)，斜率为3，求直线L1的方程。

我们可以使用直线的点斜式来求解直线L1的方程，点斜式的一般形式为：y - y1 = m(x - x1)，其中m为直线的斜率，(x1, y1)为直线上的一点。

代入已知条件，可以得到直线L1的方程为：y - 3 = 3(x - 2)化简得：y - 3 = 3x - 6进一步整理得：y = 3x - 3所以，直线L1的方程为 y = 3x - 3。

2. 已知直线L2过点B(4,5)，斜率为-2，求直线L2的方程。

同样地，我们使用直线的点斜式来求解直线L2的方程。

代入已知条件，可以得到直线L2的方程为：y - 5 = -2(x - 4)化简得：y - 5 = -2x + 8进一步整理得：y = -2x + 13所以，直线L2的方程为 y = -2x + 13。

3. 直线L1和直线L2的交点坐标是多少？为了找到直线L1和直线L2的交点坐标，我们可以将两个方程联立起来，求解其解。

将直线L1和L2的方程联立得到：3x - 3 = -2x + 13整理得：5x = 16解得：x = 16/5将x的值代入其中一个方程，例如直线L1的方程，可以解出y的值：y = 3(16/5) - 3= 48/5 - 3= 48/5 - 15/5= 33/5所以，直线L1和直线L2的交点坐标为 (16/5, 33/5)。

总结：通过解题，我们找到了直线L1和直线L2的方程，并求得它们的交点坐标 (16/5, 33/5)。

这些练习题帮助我们熟悉了直线的方程和求解交点的方法，提高了我们对回归直线方程的理解和运用能力。

第十二章简单回归分析习题一、是非题1．直线回归反映两变量间的依存关系，而直线相关反映两变量间的相互线性伴随变化关系.2．对同一组资料，如相关分析算出的r越大，则回归分析算出的b值也越大. 3．对同一组资料，对r与b分别作假设检验，可得t r=t b4．利用直线回归估计X值所对应的Y值的均数置信区间时，增大残差标准差可以减小区间长度.5．如果直线相关系数r=0，则直线回归的SS残差必等于0.二、选择题1. 用最小二乘法确定直线回归方程的原则是各观察点距直线的( )．A．纵向距离之和最小 B. 纵向距离的平方和最小C. 垂直距离之和最小D．垂直距离的平方和最小E．纵向距离的平方和最大2．Y＝14十4X是1~7岁儿童以年龄(岁)估计体质量(市斤)的回归方程，若体质量换成位kg，则此方程( )A 截距改变B 回归系数改变C 两者都改变D 两者都不改变E．相关系数改变4．直线回归系数假设检验，其自由度为( )A．n B. n-1C．n-2 D. 2n-1E．2(n-1)5．当r＝0时，Y＝a+b X回归方程中( )A a必大于零B a必大于XC a必等于零D a必大于YE a必等于b6．在多元线性回归分析中，反应变量总离均差平方和可以分解为两部分，残差是指( )．A．观察值与估计值之差B．观察值与平均值之差C．估计值与平均值的平方和之差D．观察值与平均值之差的平方和E．观察值与估计值之差的平方和三、筒答题1．用什么方法考察回归直线是否正确?2．简述回归系数方差分析Y的平方和与自由度的分解.3. 举例说明如何用直线回归方程进行预测和控制？4. 直线回归分析时怎样确定自变量和因变量？5. 简述曲线回归常用的几种曲线形式.。

13．(09·江苏理)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投10次，投中的次数如下表：学生 1号 2号 3号 4号 5号 甲组 6 7 7 8 7 乙组 6 7 6 7 9则以上两组数据的方差中较小的一个为s 2＝______.21．(本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据x 3 4 5 6 y 2.5 3 4 4.5(1)请画出上表数据的散点图；(2)请根据上表提供的数据，求出y 关于x 的回归直线方程； (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？13．(09·江苏理)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习，每人投10学生 1号 2号 3号 4号 5号 甲组 6 7 7 8 7 乙组 6 7 6 7 9[答案] 25[解析] x甲＝6＋7＋7＋8＋75＝7，x 乙＝6＋7＋6＋7＋95＝7，∴s 2甲＝(6－7)2＋(7－7)2＋(7－7)2＋(8－7)2＋(7－7)25 ＝25， s 2乙＝(7－6)2＋(7－7)2＋(7－6)2＋(7－7)2＋(7－9)25 ＝65， 21．(本题满分12分)下表提供了某厂节能降耗技术改造后，生产甲产品过程中记录的产量x (吨)与相应的生产能耗y 3 4 5 6 y 2.5 3 4 4.5(1)(2)请根据上表提供的数据，求出y 关于x 的回归直线方程； (3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的回归直线方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？[解析] (1)散点图如图．(2)x －＝4.5，y －＝3.5，b ^＝∑x i y i －4x － y －∑x 2i －4x －2＝66.5－6386－81＝0.7，a ^＝3.5－0.7×4.5＝0.35，∴回归直线方程为y ^＝0.7x ＋0.35. (3)90－(0.7×100＋0.35)＝19.65(t) ∴降低了19.65吨．分组频数频率[122,126)50.04[126,130)80.07[130,134)100.08[134,138)220.18[138,142)330.28[142,146)200.17[146,150)110.09[150,154)60.05[154,158)50.04合计1201122 126 130 134 138 142 146 150 158 154 身高（cm ）o0.01 0.02 0.03 0.04 0.05 0.06 0.07 频率/组距。

线性回归方程一、考点、热点回顾一、相关关系：1、⎩⎨⎧<=1||1||r r 不确定关系：相关关系确定关系：函数关系2、相关系数：∑∑∑===-⋅---=ni ini ini iiy y x x y y x x r 12121)()())((，其中：（1）⎩⎨⎧<>负相关正相关00r r ；（2）相关性很弱；相关性很强；3.0||75.0||<>r r3、散点图：初步判断两个变量的相关关系。

二、线性回归方程：1、回归方程：a x b yˆˆˆ+= 其中2121121)())((ˆxn x yx n yx x x y yx x bn i i ni ii n i i ni ii--=---=∑∑∑∑====，x b y aˆˆ-=（代入样本点的中心） 2、残差：（1）残差图：横坐标为样本编号，纵坐标为每个编号样本对应的残差。

（2）残差图呈带状分布在横轴附近，越窄模型拟合精度越高。

（3）残差平方和∑=-ni i iyy12)ˆ(越小，模型拟合精度越高。

3、相关指数：∑∑==---=n i ini i iy yyyR 12122)()ˆ(1（1）其中：∑=-ni i iyy12)ˆ(为残差平方和；∑=-ni i y y 12)(为总偏差平方和。

（2）)1,0(2∈R ，越大模型拟合精度越高。

二、典型例题+拓展训练典型例题1：在一组样本数据),,,2)(,(),,(),,(212211不全相等n n n x x x n y x y x y x ≥的散点图中，若所有样本点),2,1)(,(n i y x i i =都在直线121+-=x y 上，则样本相关系数为（ ） 21.21.1.1.--D C B A典型例题2：设某大学的女生体重)(kg y 与身高)(cm x 具有线性相关关系，根据一组样本数据)2,1)(,(n i y x i i =，用最小二乘法建立的回归方程为71.8585.0ˆ-=x y ，则不正确的是（ ）A.y 与x 具有正的线性相关关系；B.回归直线过样本点的中心),(y xC.若该大学某女生身高增加1cm,则其体重约增加0.85kgD.若该大学某女生身高为170cm,则可断定其体重必为58.79kg扩展2.一台机器使用时间较长，但还可以使用.它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器运转的速度而变化，下表为抽样试（1）对变量y 与x 进行相关性检验；（2）如果y 与x 有线性相关关系，求回归直线方程；（3）若实际生产中，允许每小时的产品中有缺点的零件最多为10个，那么，机器的运转速度应控制在什么范围内？典型例题3.为了对x 、Y 两个变量进行统计分析，现有以下两种线性模型： 6.517.5y x =+，717y x =+，试比较哪一个模型拟合的效果更好.52211521()155110.8451000()i i i ii y y R yy ==-=-=-=-∑∑，221R =-521521()18010.821000()ii i ii yy y y ==-=-=-∑∑，84.5%＞82%，所以甲选用的模型拟合效果较好.扩展1.下列说法正确的是（ ）（1）残差平方和越小，相关指数2R 越小，模型拟合效果越差； （2）残差平方和越大，相关指数2R 越大，模型拟合效果越好； （3）残差平方和越小，相关指数2R 越大，模型拟合效果越好； （4）残差平方和越大，相关指数2R 越小，模型拟合效果越差；A.（1）（2）B.（3）（4）C.（1）（4）D.（2）（3）扩展2.关于某设备的使用年限x （年）和所支出的维修费用y （万元）有下表所示的资料：若由资料知，y 对x 呈线性相关关系，求：（1）线性回归方程a x b yˆˆˆ+=中的回归系数b a ˆ,ˆ； （2）残差平方和与相关指数2R ，作出残差图，并对该回归模型的拟合精度作出适当判断； （3）使用年限为10年时，维修费用大约是多少？三、典型例题4.非线性回归模型：某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x （单位：千元）对年销售量y （单位：t ）和年利润z （单位：千元）的影响，对近8年的年宣传费和年销售量（i=1,2，···，8）数据作了初步处理，得到下面的散点图及一些统计量的值。

高二第二学期第一章线性回归方程同步练习题（文科）（1）一、选择题1 . 下列两个变量之间的关系哪个不是函数关系（ D ） A ．角度和它的余弦值 B.正方形边长和面积 C ．正ｎ边形的边数和它的内角和 D.人的年龄和身高2．某市纺织工人的月工资（元）依劳动生产率（千元）变化的回归方程为y=50+80x ，则下列说法中正确的是（ C ）A ．劳动生产率为1000元时，月工资为130元B ．劳动生产率提高1000元时，月工资提高约为130元C ．劳动生产率提高1000元时，月工资提高约为80元D ．月工资为210元时，劳动生产率为2000元 3．设有一个回归方程为y=2-1.5x ，则变量x 每增加一个单位时，y 平均 （ C ） A ．增加1.5单位 B ．增加2单位 C ．减少1.5单位 D ．减少2单位4．实验测得四组(x ，y )的值为(1,2)，(2,3)，(3,4)，(4,5)，则y 与x 之间的回归直线方程为( A )A.y ^＝x ＋1 B.y ^＝x ＋2 C.y ^＝2x ＋1 D.y ^＝x －15．由一组样本(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )得到的回归直线方程y ^＝a ＋bx ，下面有四种关于回归直线方程的论述：(1)直线y ^＝a ＋bx 至少经过点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )中的一个点；(2)直线y ^＝a ＋bx 的斜率是∑ni ＝1x i y i －n x y ∑ni ＝1x 2i －n x 2；(3)直线y ^＝a ＋bx 必过(x ，y )点； (4)直线y ^＝a ＋bx 和各点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )的偏差∑ni ＝1 (y i －a －bx i )2是该坐标平面上所有的直线与这些点的偏差中最小的直线．其中正确的论述有( D )A ．0个 B ．1个C ．2个 D ．3个解析 线性回归直线不一定过点(x 1，y 1)，(x 2，y 2)，…，(x n ，y n )中的任何一点；b ＝∑ni ＝1x i y i －n x y∑ni ＝1x 2i －n x 2就是线性回归直线的斜率，也就是回归系数；线性回归直线过点(x ，y )；线性回归直线是平面上所有直线中偏差∑ni ＝1(y i －a －bx i )2取得最小的那一条．故有三种论述是正确的，选D. 6．某化工厂为预测产品的回收率y ，需要研究它和原料有效成分含量x 之间的相关关系，现取8对观测值，计算，得∑8i ＝1x i ＝52，∑8i ＝1y i ＝228，∑8i ＝1x 2i ＝478，∑8i ＝1x i y i ＝1849，则其线性回归方程为( A ) A.y ^＝11.47＋2.62x B.y ^＝－11.47＋2.62x C.y ^＝2.62＋11.47x D.y ^＝11.47－2.62x解析 利用回归系数公式计算可得a ＝11.47，b ＝2.62，故y ^＝11.47＋2.62x . 7. 下列变量之间的关系是函数关系的是（ A ）A ．已知二次函数c bx ax y ++=2，其中a ，b 是已知常数，取b 为自变量，因变量是这个函数的判别式ac b Δ42-=B ．光照时间和果树的亩产量C ．降雪量和交通事故发生率D ．每亩用肥料量和粮食亩产量 8. 列有关线性回归的说法，不正确是（ D ）A.变量取值一定时，因变量的取值带有一定的随机性的两个变量之间的关系叫做相关关系B.在平面直角坐标系中用描点的方法得到表示具有相关关系的两个变量的一组数据的图形叫做散点图C.线性回归直线方程最能代表观测值x ，y 之间的关系D.任何一组观测值都能得到具有代表意义的回归直线方程 9.已知x 与y 之间的一组数据：则y 对x 的线性回归方程y ＝bx ＋A. (2,2) B. (1.5,3.5) C. (1,2) D. (1.5,4)10. 设回归直线方程为y ＝2－1.5x ，若变量x 增加1个单位，则( C )． A. y 平均增加1.5个单位 B. y 平均增加2个单位 C. y 平均减少1.5个单位 D. y 平均减少2个单位二、填空题11.下列关系中，是相关关系的为 （填序号）.①学生的学习态度与学习成绩之间的关系；②教师的执教水平与学生的学习成绩之间的关系； ③学生的身高与学生的学习成绩之间的关系；④家庭的经济条件与学生的学习成绩之间的关系. 答案 ①②12.下列有关线性回归的说法，正确的是 （填序号）.①相关关系的两个变量不一定是因果关系②散点图能直观地反映数据的相关程度 ③回归直线最能代表线性相关的两个变量之间的关系④任一组数据都有回归直线方程 答案 ①②③13.下列命题：①线性回归方法就是由样本点去寻找一条贴近这些样本点的直线的数学方法； ②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归直线yˆ=b ˆx +a ˆ及回归系数b ˆ,可以估计和预测变量的取值和变化趋势. 其中正确命题的序号是 .答案 ①②③14．下列关系：①人的年龄与其拥有的财富之间的关系；②曲线上的点与该点的坐标之间的关系；③苹果的产量与气候之间的关系；④森林中的同一树木，其截面直径与高度之间的关系；⑤学生的身高与其学号之间的关系，其中有相关关系的是___①③④_____(填序号)．15.已知回归方程为yˆ=0.50x-0.81,则x=25时，y ˆ的估计值为 .答案 11.69 16．下表是某厂1～4由散点图可知，用水量y 与月份x 之间有较好的线性相关关系，其线性回归直线方程是y ^＝－0.7x ＋a ，则a 等于______．解析 x ＝2.5，y ＝3.5，∵回归直线方程过定点(x ，y )，∴3.5＝－0.7×2.5＋a .∴a ＝5.25. 17．某服装商场为了了解毛衣的月销售量y (件)与月平均气温x (℃)之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：由表中数据算出线性回归方程y ＝bx ＋a 中的b ≈－2，气象部门预测下个月的平均气温约为6℃，据此估计，该商场下个月毛衣的销售量约为________件．答案 46解析 由所提供数据可计算得出x ＝10，y ＝38，又b ≈－2代入公式a ＝y －b x 可得a ＝58，即线性回归方程y ^＝－2x ＋58，将x ＝6代入可得．18．正常情况下，年龄在18岁到38岁的人们，体重y （kg ）依身高x （cm ）的回归方程为y=0.72x-58.5。

第42讲 回归直线方程一、单选题1．（2021·陕西王益·高一期中）下表是某厂1～4月份用水量（单位：百吨）的一组数据：用水量与月份之间有较好的线性相关关系，其线性回归方程是ˆ525ybx =+.，则b 等于（ ） A ．1- B ．0.9- C ．0.8- D ．0.7-【答案】D 【详解】由于回归直线必经过点(),x y ，而 2.5x =， 3.5y =，∴3.5 2.5 5.5ˆ2b=⨯+，∴0.7b =-. 故选:D .2．（2021·河南许昌·（文））下表是某产品1~4月份销量（单位：百件）的一组数据，分析后可知，销量y 与月份)(17x x <<之间有较好的线性相关关系，其线性回归方程是0.6ˆˆ=-+yx a ，则预测5月份的销量是（ ）A ．2B ．1.5C ．2.5D ．1.6【答案】A 【详解】 由数表得1234 4.543 2.52.5,3.544x y ++++++====， 由此得样本点的中心(2.5,3.5)，并且该点在回归直线0.6ˆˆ=-+yx a 上， 则有ˆ3.50.6 2.5a=-⨯+，解得ˆ5a =，即回归直线方程为0.65ˆy x =-+， 当5x =时，0.6552ˆy=-⨯+=， 所以预测5月份的销量是2. 故选：A3．（2021·安徽黄山·高二期末（文））如果某地的财政收入x 与支出y 满足线性回归方程ˆˆybx a e =++（单位：亿元），其中，ˆ0.8b=，2a =，0.5e ≤．若今年该地区财政收入为10亿元，则年支出预计不会超过（ ）A ．9亿元B ．9.5亿元C ．10亿元D ．10.5亿元【答案】D 【详解】因为ˆˆ0.82ybx a e x e =++=++，所以当10x =时， 8210100.510.5y e e =++=+≤+=．故选：D ．4．（2021·云南保山·（文））某种产品的投入x （单位：万元）与收入y （单位：万元）之间的关系如表：若已知与的线性回归方程为 6.517.5y x =+，那么当投入为4万元时，收入的随机误差为（ ）万元．（随机误差＝真实值－预测值） A ．-4.5 B ．4.5 C ．3.5 D ．-3.5【答案】D 【详解】取4x =，得 6.517.543.5y x =+=，∴当投入为4万元时，随机误差4043.5 3.5=-=-， 故选：D ．5．（2021·河北运河·沧州市一中）下表记录了某产品的广告支出费用x （万元）与销售额y （万元）的几组数据：） A ．30 B ．26 C ．23 D ．20【答案】D 【详解】解：由已知可得：1(2356)44x =+++=，代入ˆ72yx =+，得30y =， 154045304t ∴+++=⨯，解得：20t =，故选：D ．6．（2021·江苏盐城·高二期中）已知某品牌的新能源汽车的使用年限x （单位：年）与维护费用y (单位：千元)之间有如下数据：7年时，维护费用约为（ ）千元．附：线性回归方程y bx a =+中的系数，()()()121,niii nii x x y y b a y bx x x ==--==--∑∑A ．4B ．5C ．8.2D ．8.3【答案】C 【详解】解：由题意得1(24568)55x =++++=，1(3 4.5 6.57.59) 6.15y =++++=，因为y 关于x 的线性回归方程为 1.05y x a =+， 所以6.1 1.055a =⨯+，解得0.85a =，所以y 关于x 的线性回归方程为 1.050.85y x =+， 所以当7x =时， 1.0570.858.2y =⨯+=，所以当使用年限为7年时，维护费用约为8.2千元， 故选：C7．（2021·安徽谯城·亳州二中高二期末（理））某商店对每天进店人数x 与某种商品成交量y （单位：件）进行了统计，得到如下对应数据：由表中数据，得线性回归方程为.253ˆybx =-．如果某天进店人数是人，预测这一天该商品销售的件数为（ ） A ．48 B ．52C ．57D ．59【答案】D 【详解】因为10152025303540257x ++++++==，561214202325157y ++++++==所以样本中心点为()25,15，代入.25ˆ3ˆybx =-可得1525.ˆ325b =-解得：0.73b =， 回归方程为0.7335ˆ.2yx =- 将85x =代入可得0.7385 3.2558.859ˆy=⨯-=≈， 故选：D.8．（2021·全国高三专题练习（文））恩格尔系数(Engel ’sCoefficien )是食品支出总额占个人消费支出总额的比重.居民可支配收入是居民可用于最终消费支出和储蓄的总和，即居民可用于自由支配的收入.如图为我国2013年至2019年全国恩格尔系数和居民人均可支配收入的折线图.给出三个结论：①恩格尔系数与居民人均可支配收入之间存在负相关关系； ②一个国家的恩格尔系数越小，说明这个国家越富裕；③一个家庭收入越少，则家庭收入中用来购买食品的支出所占的比重就越小. 其中正确的是（ ） A ．① B ．②C ．①②D ．②③【答案】C 【详解】由折线图可知，恩格尔系数在逐年下降，居民人均可支配收入在逐年增加， 故两者之间存在负相关关系，结论①正确；恩格尔系数越小，居民人均可支配收入越多，经济越富裕，结论②正确； 家庭收入越少，人们为解决温饱问题，收入的大部分用来购买食品，结论③错误. 故选：C 二、多选题9．（2021·渝中·重庆巴蜀中学高三月考）中国茶文化博大精深，茶水的口感与茶叶类型和水的温度有关为了建立茶水温度y 随时间x 变化的函数模型，小明每隔1分钟测量一次茶水温度，得到若干组数据()11,x y ，()22,x y ，⋅⋅⋅，(),n n x y ，绘制了如图所示的散点图.小明选择了如下2个函数模型来拟合茶水温度y 随时间x 的变化情况，函数模型一：()0,0y kx b k x =+<≥；函数模型二：()0,01,0x y ka b k a x =+><<≥，下列说法正确的是（ ）A ．变量y 与x 具有负的相关关系B ．由于水温开始降得快，后面降得慢，最后趋于平缓，因此模型二能更好的拟合茶水温度随时间的变化情况C ．若选择函数模型二，利用最小二乘法求得到x y ka b =+的图象一定经过点(),x yD ．当5x =时，通过函数模型二计算得65.1y =，用温度计测得实际茶水温度为65.2，则残差为0.1 【答案】ABD 【详解】观察散点图，变量x 与y 具有负的相关关系，A 正确；由于函数模型二中的函数()0,01,0xy ka b k a x =+><<≥，在0x ≥时，函数单调递减，可得B 正确；若选择函数模型二，利用最小二乘法求出的回归方程一定经过(),xa y ，C 错误；由于残差=真实值-预测值，因此残差为65.265.10.1-=，故D 正确. 故选: ABD.10．（2021·全国）由一组样本数据()11,x y ，()22,x y ，…，(),n n x y 得到的经验回归方程为y b x a ∧∧∧=+，那么下面说法正确的是（ ） A ．直线y b x a ∧∧∧=+必经过点(),x yB ．直线y b x a ∧∧∧=+至少经过点()11,x y ，()22,x y ，…，(),n n x y 中的一个C ．直线y b x a ∧∧∧=+的斜率为1221ni ii nii x ynx y xnx==--∑∑D ．经验回归方程y b x a ∧∧∧=+最能代表样本数据中x ，y 之间的线性关系，b ∧大于0时x 与y 正相关，b ∧小于0时x 与y 负相关 【答案】ACD 【详解】回归直线一定过样本点的中心，故A 正确； 回归直线可以不经过所有的样本点，故B 不正确； 通过最小二乘法知，C 是正确的；回归方程是一次函数，由一次函数的性质可知，D 是正确的． 故选：ACD ．11．（2021·珠海市第二中学高二期中）下列说法正确的是（ ）A ．从匀速传递的产品生产流水线上，质检员每10分钟抽取一件产品进行某项指标检测，这样的抽样方法是系统抽样．B ．在回归分析模型中，残差平方和越小，说明模型的拟合效果越好．C ．若两个随机变量的线性相关性越强，则相关系数r 的值越接近于±1．D ．在回归直线方程0.110y x =-+中，当解释变量x 每增加1个单位时，预报变量就增加0.1个单位． 【答案】ABC 【详解】解：对于A ，从匀速传递的产品生产流水线上，质检员每10分钟抽取一件产品进行某项指标检测，这样的抽样方法是系统抽样，所以A 正确；对于B ，在回归分析模型中，残差平方和越小，说明模型的拟合效果越好，所以B 正确； 对于C ，因为r 越接近1，说明线性相关性越强，所以C 正确；对于D ，因为回归方程是用来估计取值，所以当解释变量x 每增加1个单位时，预报变量估计增加0.1个单位，所以D 错误， 故选：ABC12．（2021·重庆市秀山高级中学校高三月考）已知变量x ，y 之间的线性回归方程为0.710.3y x =-+，且变量x ，y 之间的一组相关数据如表所示，则下列说法正确的是（ ）A ．变量x ，y 之间呈负相关关系B ．可以预测，当20x 时， 3.7y =-C ．4m =D ．该回归直线必过点()9,4 【答案】ABD 【详解】对于A ：由线性回归方程为0.710.3y x =-+可知：0.70-<，所以变量x ，y 之间呈负相关关系，故选项A 正确； 对于B ：当20x 时，0.72010.3 3.7y =-⨯+=-，故选项B 正确；对于C ：68101294x +++==，6321144m m y ++++==，因为回归直线过样本中心点，所以110.7910.34m+=-⨯+，解得：5m =，故选项C 不正确； 对于D ：由C 可知5m =，所以11544y +==，所以该回归直线必过样本中心点()9,4，故选项D 正确； 故选：ABD. 三、填空题13．（2021·全国）如图是一组数据(),x y 的散点图，经最小二乘法计算，y 与x 之间的经验回归方程为1y b x ∧∧=+，则b ∧=______．【答案】0.8 【详解】013424x +++==，0.9 1.9 3.2 4.42.64y +++==， 将（2，6）的坐标代入1y b x ∧∧=+，解得0.8b ∧=． 故答案为：0.814．（2021·衡水市第十四中学）已知x 与y 之间的一组数据如下，且它们之间存在较好的线性关系.则y与x 的回归直线方程y bx a =+必过定点___________.【答案】73,4⎛⎫⎪⎝⎭【详解】根据表格中的数据，可得024634x +++==，12123744m m m y +++-+-==， 即样本中心为73,4⎛⎫ ⎪⎝⎭，所以y 与x 的回归直线方程y bx a =+必过定点73,4⎛⎫⎪⎝⎭.故答案为：73,4⎛⎫⎪⎝⎭.15．（2021·湖北高三开学考试）海水稻的灌溉是将海水稀释后进行灌溉.某试验基地为了研究海水浓度x （‰）对亩产量y （吨）的影响，测得了某种海水稻的亩产量与海水浓度的数据如下表.绘制散点图发现，可用线性回归模型拟合亩产量y 与海水浓度x 之间的相关关系，最小二乘法计算得y 与x 之间的线性回归方程为.88ˆ0ˆybx =+，则ˆb =___________【答案】ˆ0.1b =- 【详解】由表格中的数据，可得3456755x ++++==，0.520.480.390.30.210.385y ++++==，把点(5,0.38)代入回归方程.88ˆ0ˆybx =+，可得50.880.38b +=，解得0.1b =-. 故答案为：ˆ0.1b=-. 16．（2021·浙江丽水·高二课时练习）某市农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温度与实验室每天每100颗种子中的发芽数，得到如下数据：由表中根据12月2日至12月4的数据，求的线性回归方程ybx a =+中的3b =，则a 为______，若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过1颗，则认为得到的线性回归方程是可靠的，则求得的线性回归方程____.(填“可靠”或“不可幕”)【答案】ˆ8a=- 可靠 【详解】 （1）由题得11121326263212,2833x y ++++====， 所以样本中心点为（12,28），所以ˆ28=312+a⨯， 所以ˆ8a=-. 所以ˆ38y x =-. （2）由题得ˆ38yx =-. 12月1日的估计值为：ˆ310822y=⨯-=,23-22=1,没有超过1. 12月5日的估计值为：ˆ38816y=⨯-=，16-16=0，没有超过1. 所以求得的线性回归方程可靠.故答案为(1). ˆ8a=- (2). 可靠 四、解答题17．（2021·全国高二课时练习）有一位同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计，得到一个卖出热饮杯数与当天气温的对比表：（2）你能从散点图中发现气温与热饮销售杯数之间关系的一般规律吗？ 【答案】（1）图见解析；（2）答案见解析. 【详解】(1)以x 轴表示温度，以y 轴表示热饮杯数，可作散点图如图.(2)从图中可以看出，各点散布在从左上角到右下角的区域里， 因此，气温与热饮销售杯数之间是具有相关关系， 即气温越高，卖出去的热饮杯数越少.18．（2021·全国高三月考（文））某科技公司研发了一项新产品A ，经过市场调研，对公司1月份至6月份销售量及销售单价进行统计，销售单价x （千元）和销售量y （千件）之间的一组数据如下表所示： 月份i 12 3 4 5 6 销售单价i x 9 9.51010.5 118 销售量i y1110 86515y x （2）若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过065．千元，则认为所得到的回归直线方程是理想的，试问（1）中所得到的回归直线方程是否理想？参考公式：回归直线方程ˆˆˆybx a =+，其中i ii 122ii 1ˆnnx y n x yb xnx==-⋅⋅=-∑∑.参考数据：5i i i 1392x y ==∑，52i i 1502.5x ==∑.【答案】（1）ˆ3240yx =-+．；（2）是. 【详解】 （1）因为()199.51010.511105x =++++=，()1111086585y =++++=， 所以23925108ˆ 3.2502.5510b-⨯⨯==--⨯，得()ˆ8 3.21040a=--⨯=， 于是y 关于x 的回归直线方程为 3.240ˆyx =-+； （2）当8x =时，ˆ 3.284014.4y=-⨯+=， 则ˆ14.4150.60.65yy -=-=<， 故可以认为所得到的回归直线方程是理想的.19．（2021·全国高一期末）农民脱贫致富，已经成为当下中国社会的大政方针，如何精准脱贫，已经成为各政府部门最关注的事情．某县因地制宜，选择了有机蔬菜种植项目进行发展经济．在有机蔬菜的种植过程中，有机肥料使用是必不可少的，根据统计某种有机蔬菜0.5亩的产量増加量y （百斤）与有机肥料x （千克）的使用量之间有如下关系表：（1）依据表中的数据，求出关于的线性回归方程ˆˆybx a =+； （2）根据所求线性回归方程，估计如果有机蔬菜使用有机肥料12千克，则有机蔬菜0.5亩产量增加量y 是多少百斤？附：回归方程系数公式1122211()(),()in niii ii i nnii i x x y y x y nx yy bx a b x x xnx====---=+==--∑∑∑∑．【答案】（1）6ˆ.ˆ0.6807yx =+；（2）8.92百斤． 【详解】 解：（1）1234535x ++++==，1.42.1 2.93.54.12.85y ++++==，∴51()()iii x x y y =--∑(13)(1.4 2.8)=--(23)(2.1 2.8)+--(33)(2.9 2.8)+--(43)(3.5 2.8)+--(53)(4.1 2.8)+--6.8=；521()ii x x =-∑411410=+++=，则 6.80.681ˆ0b==，则知6ˆˆ0.7a y bx =-=， 所以y 关于x 的线性回归方程为：6ˆ.ˆ0.6807yx =+； （2）当x ＝12时，y ＝0.68×12＋0.76＝8.92（百斤）， ∴如果有机蔬菜使用有机肥料12千克，估计有机蔬菜0.5亩产量的增加量y 是8.92百斤．20．（2021·崇仁县第二中学（文））某厂家营销人员收集了日平均气温x （单位：C ︒）与某款取暖器的日销售额y （单位：万元）的有关数据如下表：已知日销售额y 与日平均气温x 之间具有线性相关关系．（1）根据上表数据，用最小二乘法求出y 关于x 的线性回归方程；（2）根据（1）求出的线性回归方程，预测日平均气温为7C -时该取暖器的日销售额为多少万元．参考公式：在线性回归方程ˆˆˆybx a =+中，1221ˆni ii nii x y nxyb xnx ==-=-∑∑，ˆˆay bx =-． 参考依据：51524i i i x y ==-∑．【答案】（1）ˆ 2.415.4yx =-+；（2）32.2万元. 【详解】解：（1）由已知条件可得2345645x -----==-，2023252730255y ++++==，51524i ii x y==-∑，52190i i x ==∑，则152215ˆ 2.45ni ii ii x y xybxx==-==--∑∑．再由25( 2.4)(4)ˆa=--⨯-，可得ˆ15.4a =． 所以回归直线方程为ˆ 2.415.4yx =-+． （2）由回归直线方程为ˆ 2.415.4yx =-+可得， 当7x =-时，ˆ32.2y =，即预测日平均气温为 7C -时，该取暖器的日销售额为32.2万元．。

1．相关关系的分类从散点图上看，点散布在从左下角到右上角的区域内，对于两个变量的这种相关关系，我们将它称为正相关；点散布在从左上角到右下角的区域内，两个变量的这种相关关系称为负相关．2．线性相关从散点图上看，如果这些点从整体上看大致分布在一条直线附近，则称这两个变量之间具有线性相关关系，这条直线叫回归直线．3．回归方程(1)最小二乘法：使得样本数据的点到回归直线的距离平方和最小的方法叫最小二乘法．(2)回归方程：两个具有线性相关关系的变量的一组数据：(x1，y1)，(x2，y2)，…，(x n，y n)，其回归方程为y^＝b^x＋a^，则b^，a^其中，b是回归方程的斜率，a是在y轴上的截距．4．样本相关系数r＝∑i＝1n(x i－x)(y i－y)∑i＝1n(x i－x)2∑i＝1n(y i－y)2，用它来衡量两个变量间的线性相关关系．(1)当r＞0时，表明两个变量正相关；(2)当r＜0时，表明两个变量负相关；(3)r的绝对值越接近1，表明两个变量的线性相关性越强；r的绝对值越接近于0，表明两个变量之间几乎不存在线性相关关系．通常当|r|＞0.75时，认为两个变量有很强的线性相关关系．5．线性回归模型(1)y＝bx＋a＋e中，a、b称为模型的未知参数；e称为随机误差．(2)相关指数用相关指数R2来刻画回归的效果，其计算公式是：R2＝，R2的值越大，说明残差平方和越小，也就是说模型的拟合效果越好．在线性回归模型中，R2表示解释变量对预报变量变化的贡献率，R2越接近于1，表示回归效果越好．规律(1)函数关系是一种确定的关系，相关关系是一种非确定的关系．事实上，函数关系是两个非随机变量的关系，而相关关系是非随机变量与随机变量的关系．注意(1)回归分析是对具有相关关系的两个变量进行统计分析的方法，只有在散点图大致呈线性时，求出的回归直线方程才有实际意义，否则，求出的回归直线方程毫无意义．(2)线性回归方程中的截距和斜率都是通过样本数据估计而来的，存在误差，这种误差会导致预报结果的偏差；而且回归方程只适用于我们所研究的样本总体．考向一相关关系的判断例1．下列选项中，两个变量具有相关关系的是( )A．正方形的面积与周长B．匀速行驶车辆的行驶路程与时间C．人的身高与体重D．人的身高与视力答案：C例2．对变量x、y有观测数据(x i，y i)(i ＝1,2，…，10)，得散点图1；对变量u，v 有观测数据(u i，v i)(i＝1,2，…，10)，得散点图2.由这两个散点图可以判断( )A．变量x与y正相关，u与v正相关B．变量x与y正相关，u与v负相关C.变量x与y负相关，u与v正相关D．变量x与y负相关，u与v负相关解析：选C.由题图1可知，各点整体呈递减趋势，x与y负相关，由题图2可知，各点整体呈递增趋势，u与v正相关．例3．下面哪些变量是相关关系()．A．出租车车费与行驶的里程B．房屋面积与房屋价格C．身高与体重D．铁块的大小与质量解析A，B，D都是函数关系，其中A一般是分段函数，只有C是相关关系．答案 C例4.如图所示，有5组(x，y)数据，去掉________组数据后，剩下的4组数据的线性相关性最大．解析：因为A、B、C、E四点分布在一条直线附近且贴近某一直线，D点离得远．答案：D例5．对变量x，y有观测数据(x i，y i)(i＝1,2，…，10)，得散点图(1)；对变量u，v 有观测数据(u i、v i)(i＝1,2，…，10)，得散点图(2)．由这两个散点图可以判断()．A．变量x与y正相关，u与v正相关B．变量x与y正相关，u与v负相关C．变量x与y负相关，u与v正相关D．变量x与y负相关，u与v负相关解析由题图(1)可知，各点整体呈递减趋势，x与y负相关；由题图(2)可知，各点整体呈递增趋势，u与v正相关．答案 C例6．下列关系属于线性负相关的是( )A．父母的身高与子女身高的关系B．球的体积与半径之间的关系C．汽车的重量与汽车每消耗1 L汽油所行驶的平均路程D．一个家庭的收入与支出解析：选C.A、D中的两个变量属于线性正相关，B中两个变量是函数关系．例7.山东鲁洁棉业公司的科研人员在7块并排、形状大小相同的试验田上对某棉花新品种进行施化肥量x对产量y影响的试验，得到如下表所示的一组数据(单位：kg)：(1)画出散点图；(2)判断是否具有相关关系．[审题视点] (1)用x 轴表示化肥施用量，y 轴表示棉花产量，逐一画点．(2)根据散点图，分析两个变量是否存在相关关系．解 (1)散点图如图所示(2)由散点图知，各组数据对应点大致都在一条直线附近，所以施化肥量x与产量y具有线性相关关系．利用散点图判断两个变量是否有相关关系是比较简便的方法．在散点图中如果所有的样本点都落在某一函数的曲线上，就用该函数来描述变量之间的关系．即变量之间具有函数关系．如果所有的样本点落在某一函数的曲线附近，变量之间就有相关关系；如果所有的样本点都落在某一直线附近，变量之间就有线性相关关系．例8. 根据两个变量x，y之间的观测数据画成散点图如图所示，这两个变量是否具有线性相关关系________(填“是”与“否”)．解析从散点图看，散点图的分布成团状，无任何规律，所以两个变量不具有线性相关关系．答案否考向二线性回归方程例9．对有线性相关关系的两个变量建立的回归直线方程y^＝a＋bx中，回归系数b( )A．不能小于0 B．不能大于0C．不能等于0 D．只能小于0解析：选C.∵b＝0时，r＝0，这时不具有线性相关关系，但b能大于0也能小于0.例10．已知回归方程y^＝4.4x＋838.19，则可估计x与y的增长速度之比约为________．解析：x与y的增长速度之比即为回归方程的斜率的倒数14.4＝1044＝522.答案：5 22例11．某商品销售量y(件)与销售价格x(元/件)负相关，则其回归方程可能是()．A.y^＝－10x＋200 B.y^＝10x＋200 C.y^＝－10x－200 D.y^＝10x－200 解析因为销量与价格负相关，由函数关系考虑为减函数，又因为x，y不能为负数，再排除C，故选A.答案 A例12.下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.(1)请画出上表数据的散点图；(2)请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程y^＝b^x＋a^；(3)已知该厂技改前生产100吨甲产品的生产能耗为90吨标准煤．试根据(2)求出的线性回归方程．预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？(参考数值：3×2.5＋4×3＋5×4＋6×4.5＝66.5)[审题视点] (2)问利用公式求a ^、b ^，即可求出线性回归方程．(3)问将x ＝100代入回归直线方程即可． 解 (1)由题设所给数据，可得散点图如图所示．(2)由对照数据，计算得：i ＝14x 2i ＝86，x ＝3＋4＋5＋64＝ 4.5(吨)，y ＝2.5＋3＋4＋4.54＝3.5(吨)． 已知∑i ＝14x i y i ＝66.5，所以，由最小二乘法确定的回归方程的系数为：b ^＝∑i ＝14x i y i －4x ·y ∑i ＝14x 2i －4x 2＝66.5－4×4.5×3.586－4×4.52＝0.7，a ^＝y －b ^x ＝3.5－0.7×4.5＝0.35.因此，所求的线性回归方程为y ^＝0.7x ＋0.35.(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗，得降低的生产能耗为：90－(0.7×100＋0.35)＝19.65(吨标准煤)．在解决具体问题时，要先进行相关性检验，通过检验确认两个变量是否具有线性相关关系，若它们之间有线性相关关系，再求回归直线方程．例13.为了解儿子身高与其父亲身高的关系，随机抽取5对父子的身高数据如下：则y对x的线性回归方程为()．A．y＝x－1 B．y＝x＋1C．y＝88＋12x D．y＝176解析由题意得x＝174＋176＋176＋176＋1785＝176(cm)，y＝175＋175＋176＋177＋1775＝176(cm)，由于(x，y)一定满足线性回归方程，经验证知选C.答案 C例14.某地最近十年粮食需求量逐年上升，下表是部分统计数据：(1)利用所给数据求年需求量与年份之间的回归直线方程y^＝bx＋a；(2)利用(1)中所求出的直线方程预测该地2012年的粮食需求量．解(1)由所给数据看出，年需求量与年份之间是近似直线上升，下面来配回归直线方程，为此对数据预处理如下：对预处理后的数据，容易算得，x＝0，y＝3.2，b＝26040＝6.5，a＝y－b x＝3.2.由上述计算结果，知所求回归直线方程为y －257＝b(x－2 006)＋a＝6.5(x－2 006)＋3.2，即y^＝6.5(x－2 006)＋260.2.①(2)利用直线方程①，可预测2012年的粮食需求量为6．5(2 012－2 006)＋260.2＝6.5×6＋260.2＝299.2(万吨)．例15．下列有关回归直线方程y^＝bx＋a 的叙述正确的是( )①反映y^与x之间的函数关系；②反映y与x之间的函数关系；③表示y^与x之间的不确定关系；④表示最接近y与x之间真实关系的一条直线．A．①② B．②③C．③④ D．①④解析：选D.y^＝bx＋a表示y^与x之间的函数关系，而不是y与x之间的函数关系；但它反映的关系最接近y与x之间的真实关系，故选D.例16．设有一个回归方程y^＝3－5x，变量x增加一个单位时( )A．y平均增加3个单位B．y平均减少5个单位C．y平均增加5个单位D．y平均减少3个单位解析：选B.∵－5是斜率的估计值，说明x每增加一个单位，y平均减少5个单位．例17．对两个变量y和x进行回归分析，得到一组样本数据：(x1，y1)，(x2，y2)，…，(x n，y n)，则下列说法中不．正确的是( ) A．由样本数据得到的回归方程y^＝b^x＋a^必过样本中心(x，y)B．残差平方和越小的模型，拟合的效果越好C．用相关指数R2来刻画回归效果，R2越小，说明模型的拟合效果越好D．若变量y和x之间的相关系数为r ＝－0.9362，则变量y和x之间具有线性相关关系解析：选C.C中应为R2越大拟合效果越好．例18．已知回归方程y^＝2x＋1，而试验得到一组数据是(2,4.9)，(3,7.1)，(4,9.1)，则残差平方和是( )A ．0.01B ．0.02C ．0.03D ．0.04解析：选C.当x ＝2时，y ^＝5， 当x ＝3时，y ^＝7，当x ＝4时，y ^＝9.∴e ^1＝4.9－5＝－0.1，e ^2＝7.1－7＝0.1， e ^3＝9.1－9＝0.1.∴ i ＝13e ^i 2＝(－0.1)2＋(0.1)2＋(0.1)2＝0.03.例19．下列说法：①将一组数据中的每个数据都加上或减去同一个常数后，方差恒不变；②回归方程y ^＝bx ＋a 必过点(x ，y )； ③曲线上的点与该点的坐标之间具有相关关系；④在一个2×2列联表中，由计算得K2＝13.079，则其两个变量间有关系的可能性是 90%.其中错误的是________．解析：①正确．由回归方程的定义及最小二乘法思想，知②正确．③④不正确．答案：③④例20．在2009年十一国庆8天黄金周期间，某市物价部门，对本市五个商场销售的某商品的一天销售量及其价格进行调查，五个商场的售价x元和销售量y件之间的一组数据如下表所示：9通过分析，发现销售量对商品的价格x具有线性相关关系，则销售量y对商品的价格x的回归直线方程为________．解析：由数据表可得x＝10，y＝8，离差x－x：－1，－0.5,0，0.5,1；离差y－y：3,2,0，－2，－3.∴b^＝－1×3－0.5×2－0.5×2－1×3 1＋0.25＋0＋0.25＋1＝－3.2，a ^＝y －b ^x ＝40，∴回归直线方程为y ^＝－3.2x ＋40. 答案：y ^＝－3.2x ＋40例21．在某地区的12～30岁居民中随机抽取了10个人的身高和体重的统计资料如表：根据上述数据，画出散点图并判断居民的身高和体重之间是否有相关关系．解：以x 轴表示身高，y 轴表示体重，可得到相应的散点图如图所示：由散点图可知，两者之间具有相关关系，且为正相关．12.某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数，得到如下资料：该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求线性回归方程，再对被选取的2组数据进行检验．(1)求选取的2组数据恰好是不相邻2天数据的概率；(2)若选取的是12月1日与12月5日的2组数据，请根据12月2日至12月4日的数据，求出y关于x的线性回归方程y^＝b^ x＋a^；(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗，则认为得到的线性回归方程是可靠的，试问(2)中所得的线性回归方程是否可靠？解：(1)设抽到不相邻2组数据为事件A，因为从5组数据中选取2组数据共有10种情况，每种情况都是等可能出现的，其中抽到相邻2组数据的情况有4种，所以P(A)＝1－410＝35.(2)由数据求得，x＝12，y＝27，由公式求得．b^＝52，a^＝y－b^x＝－3.所以y关于x的线性回归方程为y^＝5 2 x－3.(3)当x＝10时，y^＝52×10－3＝22，|22－23|<2；当x＝8时，y^＝52×8－3＝17，|17－16|<2.所以该研究所得到的线性回归方程是可靠的．。

选修1-2 1.2回归分析一、选择题1．已知回归直线方程y ^＝2－2.5x ，若变量x 每增加1个单位，则( ) A ．y 平均增加2.5个单位 B ．y 平均增加1个单位 C ．y 平均减少2.5个单位 D ．y 平均减少2个单位 [答案] C2．已知x ，y 的一组数据如下表所示：则y 与x 之间的线性回归方程y ＝β0x ＋β1必过定点( ) A ．(0,0) B ．(x ，0) C ．(0，y ) D ．(x ，y ) [答案] D[解析] 回归直线过样本点的中心(x ，y )．3．一位母亲记录了儿子3～9岁的身高，数据如下表所示，由此建立了身高对年龄的回归模型y ＝7.1x ＋79.93.用这个模型预测这个孩子10岁时的身高，则下列叙述中正确的是( )B ．身高在145.83 cm 以上C ．身高在145.83 cm 左右D ．身高在145.83 cm 以下 [答案] C[解析] 由回归直线方程所得的预报变量y 的值，并不是预报变量的精确值，而是预报变量可能取值的平均值．4．三点(3,10)，(7,20)，(11,24)的回归方程是( ) A.y ^＝5－17x B.y ^＝－17＋5x C.y ^＝17＋5xD.y ^＝17－5x[答案] B5．对于线性相关系数r ，以下说法正确的是( ) A ．r 只能为正值，不能为负值B ．|r |≤1，且|r |越接近于1，相关程度越大；相反则越小C ．|r |≤1，且|r |越接近于1，相关程度越小；相反则越大D ．不能单纯地以r 来确定线性相关程度 [答案] B6．(2010·湖南文，3)某商品销售量y (件)与销售价格x (元/件)负相关，则其回归方程可能是( )A.y ^＝－10x ＋200 B.y ^＝10x ＋200 C.y ^＝－10x －200D.y ^＝10x －200[答案] A[解析] 本题主要考查变量的相关性． 由负相关的定义知，A 正确． 7．有下列说法：①在残差图中，若残差点比较均匀地落在水平的带状区域内，说明选用的模型比较合适； ②用相关指数R 2来刻画回归的效果，R 2越大，说明模型的拟合效果越好；③比较两个模型的拟合效果，可以比较残差平方和的大小，残差平方和越小的模型，拟合效果越好．其中正确命题的个数是( ) A ．0个 B ．1个 C ．2个 D ．3个 [答案] D8．在建立两个变量y 与x 的回归模型中，分别选择了4个不同的模型，它们的相关指数R 2的值如下，其中拟合效果最好的模型是( )A ．模型1的相关指数R 2为0.98 B ．模型2的相关指数R 2为0.80 C ．模型3的相关指数R 2为0.50 D ．模型4的相关指数R 2为0.25 [答案] A[解析] R 2的值越大，模型的拟合效果越好．故选A. 9．下列关于残差图的描述中错误的是( ) A ．残差图的横坐标可以是样本编号B ．残差图的模坐标可以是解释变量或预报变量C ．残差点分布的带状区域的宽度越窄，相关指数越小D ．残差点分布的带状区域的宽度越窄，回归平方和越大 [答案] C[解析] 残差图和相关指数都可以刻画回归模型的拟合效果．残差点分布的带状区域越窄，相关指数R 2越大，说明回归模型的拟合效果越好．故选C.10．三点(3,10)，(7,20)，(11,24)的回归方程是( ) A.y ^＝5－17x B.y ^＝－17＋5x C.y ^＝17＋5xD.y ^＝17－5x[答案] B 二、填空题11．回归分析是处理变量之间________关系的一种数量统计方法． [答案] 相关12．已知回归直线方程为y ^＝0.50x －0.81，则x ＝25时，y 的估计值为________． [答案] 11.6913．对于同一资料，如果将x 作自变量，y 作因变量，得回归系数b ；将y 作自变量，x 作因变量，得回归系数b ′.则相关系数r 与b 、b ′的关系是________．[答案] bb ′＝r 2三、解答题14．假设关于某种设备的使用年限x (年)与所支出的维修费用y (万元)有如下统计资料：已知∑x 2i ＝90，∑y 2i i i 79≈8.9，2≈1.4，n －2＝3时，r 0.05＝0.878. (1)求x ，y ；(2)对x ，y 进行线性相关性检验；(3)如果x 与y 具有线性相关关系，求出回归直线方程； (4)估计使用年限为10年时，维修费用约是多少？ [解析] (1)x ＝2＋3＋4＋5＋65＝4，y ＝2.2＋3.8＋5.5＋6.5＋7.05＝5.0.(2)步骤如下：①作统计假设：x 与y 不具有线性相关关系． ②n －2＝3时，r 0.05＝0.878.③∑x i y i －5x ·y ＝112.3－5×4×5＝12.3， ∑x 2i －5x 2＝90－5×42＝10， ∑y 2i －5y 2＝140.8－125＝15.8， ∴r ＝12.310×15.8＝12.32·79＝12.31.4×8.9≈0.987.④|r |＝0.987>0.878，即|r |>r 0.05，所以有95%的把握认为“x 与y 之间具有线性相关关系”，再求回归直线方程是有意义的．(3)由于b ^＝∑x i y i －5x ·y ∑x 2i －5x2＝112.3－5×4×590－5×42＝1.23， a ^＝y －b x ＝5－1.23×4＝0.08，所以回归直线方程为y ^＝1.23x ＋0.08.(4)当x ＝10时，y ^＝1.23×10＋0.08＝12.38(万元)，即估计用10年时间，维修费用约为12.38万元．15．一台机器由于使用时间较长，按不同的转速生产出来的某机械零件有一些会有疵点，每小时生产有疵点零件的多少随机器运转的速度而变化，下表为抽样试验结果：(1)对变量(2)如果y 与x 有线性相关关系，求回归直线方程；(3)若实际生产中，允许每小时的产品中有疵点的零件最多为10个，那么机器运转速度应控制在什么范围内？[解析] (1)y 与x 有线性相关关系； (2)y ＝0.7286x －0.8571；(3)机器的转速应控制在14.9013转/秒以下．16．已知某地每单位面积菜地年平均使用氮肥量x (kg)与每单位面积蔬菜年平均产量y (t)之间的关系有如下数据：(1)求x 与y 之间的相关系数，并检验是否线性相关；(2)若线性相关，求蔬菜产量y 与使用氮肥量x 之间的回归直线方程，并估计每单位面积施氮肥150kg 时，每单位面积蔬菜的年平均产量．[解析](1)列出下表，并用科学计算器进行相关计算：x ＝15＝101，y ＝15≈10.11， ∑i ＝115x 2i ＝161125，∑i ＝115y 2i ＝1628.55，∑i ＝115x i y i ＝16076.8.故蔬菜产量与施用氮肥量的相关系数r ＝16076.8－15×101×10.11(161125－15×1012)(1628.55－15×10.112)≈0.8643.由小概率0.05与n －2在附表中查得相关系数临界值r 0.05＝0.514，则r >r 0.05，说明有95%的把握认为蔬菜产量与施用氮肥量之间存在着线性相关关系．(2)设所求的回归直线方程为y ^＝b ^x ＋a ^，则b ^＝∑i ＝115x i y i －15x y∑i ＝115x 2i －15x 2＝16076.8－15×101×10.11161125－15×1012≈0.0937， a ^＝y －b x ≈10.11－0.0937×101＝0.6463，∴回归直线方程为y ^＝0.0937x ＋0.6463.∴当每单位面积施氮肥150kg 时，每单位面积蔬菜年平均产量为0.0937×150＋0.6463≈14.701(t)．[说明] 本题主要考查对两个变量的相关性检验和回归分析．(1)使用样本相关系数计算公式来完成；(2)先作统计假设，由小概率0.05与n－2在附表中查得相关系数临界值r0.05，若r>r0.05则线性相关，否则不线性相关．。

2.4线性回归方程（一）【新知导读】1.下列两个变量之间的关系中，哪个不是函数关系 ( ) A ．角度和它的余弦值 B ．正方形边长和面积 C ．正n 边形的边数和其内角和 D ．人的年龄和身高2．回归直线方程y bx a ∧=+中的y ∧是预测值，与实际中的y 关系为 ( ) A ．y y ∧-越小，说明回归偏差越小 B ．y y ∧-越大，说明回归偏差越小 C ．y y ∧-越小，说明回归偏差越小D ．y y ∧-越小，说明回归偏差越小3．回归直线方程的系数a ，b 的最小二乘法估计中，使函数(,)Q a b 最小，Q 函数指( )A ．21()niii y a bx =--∑ B ．1niii y a bx=--∑C ．2()i i y a bx -- D ．i i y a bx --【范例点睛】例1．以下是收集到的新房屋销售价格y 与房屋的大小x 的数据：(3)计算此时(,)Q a b 和(2,0.2)Q 的值，并作比较． 【课外链接】1．假设学生在初一和初二数学成绩是线性相关的．若10个学生初一()x 和初二()y 数学分数如下：【随堂演练】1．下列说法错误的是（ ）A ．如果变量η和ξ之间存在线性相关关系，那么根据它们的一组数据得到一列点(,)i i x y (1,2,3,...,i n =)将散步在某一直线的附近B ．如果变量η和ξ之间不存在线性相关关系，那么根据它们的一组数据(,)i i x y (1,2,3,...,i n =)不能写出一个线性方程C ．设x ，y 是具有线性相关关系的两个变量，且x 关于y 的线性回归方程为y bx a ∧=+，其中,a b 叫做回归系数D ．在回归分析中，变量间的关系若是非确定性的关系，则因变量不能由自变量唯一确定 2．三点(3,10)，（7,20），（11,24）的线性回归方程是 ( ) A ． 5.75 1.75y x ∧=- B ． 1.75 5.75y x ∧=+ C ． 1.75 5.75y x ∧=- D ． 5.75 1.75y x ∧=+ 3．已知x ，y 之间的一组数据：则y 与x 的线性回归方程y bx a =+必过 ( )A ．(2,2)点B ．(1.5,0)点C ．(1,2)点D ．(1.5,4)点4．设有一个回归方程为32y x ∧=+，变量x 增加一个单位时，则y 平均增加______个单位．5．已知线性回归方程为0.500.81y x ∧=-，则25x =时，y 的估计值为_____________． 6．某地区某种病的发病人数呈上升趋势，统计近四年这种病的新发病人数的线性回归分析如下表表示：如不加控制，仍按这个趋势发展下去，请预测从2006年初到2009年底的四年时间里，该地区这种病的新发病总人数为_______________．7．我们考虑两个表示变量x 与y 之间的关系的模型，δ为误差项，模型如下： 模型1：64y x =+；模型2：64y x δ=++． (1) 如果3x =，1δ=，分别求两个模型中的y 值； (2) 分别说明以上两个模型是确定性模型还是随机性模型．8．在10年期间，某城市居民的年收入与某种商品的销售额之间的关系如下表所示：(1)画出散点图；(2)如果散点图中的各点大致分布在一条直线附近，求y与x间的线性回归方程．9．已知关于某设备的使用年限x 与所支出的维修费用y (万元)，有如下统计资料：设y 对x 呈线性相关关系．试求：(1)线性回归方程y bx a ∧=+的回归系数a ，b ； (2)估计使用年限为10年，维修费用是多少？10．在钢线含量对于电阻的效应的研究中，得到以下的数据：(1)画出散点图(2)求线性回归方程．2.4线性回归方程（一） 【新知导读】 1．D 2．C 3．A 【范例点睛】 例1．(1)(2)5n =，51545ii x==∑，109x =，51116i i y ==∑，23.2y =，55160952i i x ==∑，5112592i i i x y ==∑，25129525451160.1962560952545b ⨯-⨯=≈⨯-，23.20.1962109 1.8166a =-⨯≈， ∴线性回归方程为0.1962 1.8166y x =+；(3)(1.8166,0.1962) 5.1771Q ≈，(2,0.2)7.0Q ≈，由此可知，求得的 1.8166a =，0.1962b =是使函数(,)Q a b 取最小值的a ，b 值． 【课外链接】 解：71x =Q ,52150520ii x==∑,72.3y =,10151467i ii x y==∑,所以210514677107231.21821050520710b ⨯-⨯=≈⨯-，72.3 1.21827114.912a =-⨯=-，所以回归直线方程为1.218214.192y x ∧=-．【随堂演练】1. B2. D3.B4. 35. 11.696.139497.解：(1)模型1：6464318y x =+=+⨯=；模型2：64643119y x δ=++=+⨯+=． (2)模型1中相同的x 值一定得到相同的y 值，所以是确定性模型；模型2中相同的x 值，因δ的不同，所得y 值不一定相同，且δ为误差项是随机的，所以模型2是随机性模型． 8. 解：(1)(2)由题意：37.97x =，39.1y =；102114633.67ii x==∑，10115202.9i ii x y==∑，于是1011022211015202.91037.9739.11.44714663.671037.9710i ii i i x y x yb x x==--⨯⨯==≈-⨯-∑∑，39.1 1.447a y bx =-=-⨯37.9715.843≈-．所以所求线性回归方程为 1.44715.843y bx a x ∧=+=-．9．解：(1)4x =,5y =，52190i i x ==∑，51112.3i i i x y ==∑，于是回归系数2112.35459054b -⨯⨯=-⨯ 1.23=，5 1.2340.08a y bx =-=-⨯=；(2)线性回归方程是 1.230.08y x ∧=+，当10x =年时，1.23100.0812.38y ∧=⨯+=(万)，即估计使用10年时，维修费用是12.38万元．10．解：(1)(2)可求得13.958412.5503y x ∧=+。

高中数学例题：回归直线方程的求解例3．在钢铁中碳含量对于电阻的效应的研究中，得到如下表所示的一组数据：（1）画出散点图； （2）求回归方程．【解析】由散点图知能用回归直线拟合样本数据，然后，利用表中的数据，可以得到b ，a 计算公式中所需的数据，代入易得b ，a ． （1）作出散点图如下图所示．（2）由散点图可以看出，这些点大致分布在一条直线的附近，可求回归方程．由表中的数据可求得711 3.800.54377i i x x ===≈∑，711145.420.7777i i y y ===≈∑，7212.595ii x==∑，7185.61i ii x y==∑．则7172221785.6170.54320.7712.552.59570.5437i ii i i x y x yb x x==--⨯⨯==≈-⨯-∑∑， 20.7712.550.54313.96a y bx =-=-⨯≈．所以回归方程为12.5513.96y x =+．【总结升华】 求线性回归直线方程的步骤为： 第一步：列表i i i i x y x y ，，；第二步：计算211nni i i i i x y xx y ==∑∑，，　，　　；第三步：代入公式计算b a ，的值； 第四步：写出直线方程. 举一反三：【变式1】 某产品的广告费用x 与销售额y 的统计数据如下表：根据上表可得回归方程中的为9．4，据此模型预报广告费用为6万元时销售额为A ．63．6万元B ．65．5万元C ．67．7万元D ．72．0万元【答案】选B 【解析】4235492639543.5,4244x y ++++++==== 429.4 3.59.1a y bx ∴=-=-⨯=，∴回归方程为9.49.1y x =+，∴当6x =时，9.469.1y =⨯+=65.5，故选B .【变式2】 观察两相关变量得如下数据：求两变量间的回归方程．ˆˆy bx a =+b【答案】y x = 【解析】列表：计算得：0x =，0y =。

确定回归直线方程有三法一、利用回归直线过定点确定回归直线方程 例1观察两个相关变量的如下数据：则两个变量间的回归直线为（ ）A ．0.51y x =-B ．y x =C ．20.3y x =+D ．1y x =+解析：本题主要考查直线方程经过样本点的中心()x y ，，因此只需求出，点评：回归直线方程y a bx =+经过样本点的中心()x y ，二、利用公式确定回归直线方程例2．某5名学生的数学和化学成绩如下表：（1）画出散点图；（2）求化学成绩()y 对数学成绩（x ）的回归直线方程 解析：（1）散点图（略）；（2）73.2x =，67.8y =，5125054i i i x y ==∑，52127174i i x ==∑，所以5152221525054573.267.80.62527174573.25i ii ii x yxy b xx==--⨯⨯==≈-⨯-∑∑．67.80.62573.222.05a y bx =-=-⨯=．所以y 对x 的回归直线方程为0.62522.05y x =+．点评：利用公式求解时应注意以下几点：①求b 时应先求出211nni i i i i x y x y x ==∑∑，，，，由a y bx =-求a 的值，并写出回归直线方程②线性回归方程中的截距a 和斜率b 都是通过样本估计而来，存在着误差，这种误差可能导致预报结果的偏差③回归直线方程y a bx =+中的b 表示x 增加1个单位时y 的变化量为b ，而a 是不随x 的变化而变化的量．④可以利用回归直线方程y a bx =+预报在取某一个值时，y 的估计值三、先判定相关性再确定回归直线方程例3．10名同学在高一和高二的数学成绩如下表：77 其中为高一数学成绩，y 为高二数学成绩 （1）y 与是否具有相关关系；（2）如果y 与具有相关关系，求回归直线方程 解析：（1）由已知表格中的数据，利用计算器进行计算得71x =，72.3y =，10151467i i i x y ==∑．102150520ii x ==∑，102152541i i y ==∑，1010i ix yx yr -=∑0.780297=≈由0.7802970.75>知，有很大的把握认为与y 之间具有线性相关关系（2）y 与具有线性相关关系，设回归直线方程y a bx =+， 则1011022211051467107172.31.2250520107110i ii ii x yxy b xx==--⨯⨯===-⨯-∑∑，72.3 1.227114.32a y bx =-=-⨯=-，所以y 关于x 的回归直线方程为 1.2214.32y x =-．点评：利用样本相关系数r 来判断两个变量之间是否具有线性相关关系时，可以依据|r|>时，我们认为有很强的线性相关关系，可以求回归直线方程，并可用求得的回归直线方程来预报变量的取值，若|r|<，则认为两个变量之间没有线性相关关系，这时求回归直线方程没有实际价值。

回归直线练习题回归直线是一种统计学中常用的回归分析方法，用于确定自变量和因变量之间的线性关系。

通过该方法，我们可以通过自变量的取值来预测因变量的值。

在本练习题中，我们将通过给定数据，建立回归直线模型，并进行相关统计分析。

1. 数据收集与准备在开始回归直线练习题之前，我们首先需要收集相关数据，并对其进行处理和准备。

假设我们要研究某地区的年降雨量与农作物产量之间的关系，我们收集了过去十年的数据，并将其整理如下：年份（自变量）：2009、2010、2011、2012、2013、2014、2015、2016、2017、2018降雨量（mm）（因变量）：600、550、700、650、680、720、750、690、610、6302. 绘制散点图在建立回归直线模型之前，我们可以先绘制散点图来观察数据的分布情况。

散点图可以直观地展示自变量和因变量之间的关系，有助于我们判断是否适合使用回归直线进行建模。

根据给定数据，我们绘制了如下散点图：（在这里插入绘制的散点图）从散点图中可以看出，年降雨量与农作物产量呈现一定的正相关关系，即年降雨量较高时，农作物产量也相对较高。

3. 建立回归直线模型接下来，我们将利用最小二乘法来建立回归直线模型。

最小二乘法是一种常用的回归分析方法，通过最小化数据点到回归直线的垂直距离之和，确定最佳拟合直线。

通过对给定数据进行回归分析，我们得到回归直线的方程为：农作物产量 = 0.3 * 年降雨量 - 35根据该方程，我们可以通过已知的年降雨量来预测相应的农作物产量。

4. 模型评估为了评估回归直线模型的拟合效果，我们可以计算回归直线的相关系数（R）和平方误差（SSE）。

相关系数描述了自变量和因变量之间的线性关系程度，取值范围为-1到1，值越接近1或-1，表明拟合效果越好。

平方误差表示回归直线对实际数据的预测误差程度，平方误差越小表明模型拟合效果越好。

通过计算，我们得到回归直线的相关系数为0.85，并且平方误差为250。