第八周作业答案

课计划语文八年级上册人教版答案一、学情分析。

八年级学生经过七年级的语文学习，已经具备了一定的基础知识和基本技能。

在阅读方面，他们能够理解一些简单的记叙文、说明文，但对于文言文的理解和古诗词的赏析能力还有待提高。

在写作方面，能够写出结构较为完整的记叙文，但在立意深刻、语言优美等方面仍需加强训练。

二、教材分析。

1. 单元结构。

- 八年级上册人教版语文教材共有六个单元，每个单元围绕一个主题进行编排。

- 第一单元以“战争记忆”为主题，通过不同体裁的文学作品，让学生感受战争的残酷，体会正义与和平的珍贵。

- 第二单元以“爱的旋律”为主题，包含描写亲情、友情等多种情感的文章，有助于培养学生丰富的情感世界。

- 第三单元是说明文单元，学生将学习不同类型的说明文，掌握说明方法、顺序和语言特点等知识。

- 第四单元以“科学精神”为主题，文章展现了科学家们的探索精神和伟大贡献，激励学生崇尚科学。

- 第六单元是古代诗歌单元，让学生领略中国古代诗歌的优美意境和丰富内涵。

2. 重点知识与技能。

- 重点培养学生的阅读理解能力，包括对不同体裁文章的理解、分析和评价能力。

- 提高学生的文言文阅读水平，掌握常见的文言实词、虚词和句式。

- 加强写作训练，特别是在记叙文的细节描写、议论文的论证思路等方面。

三、教学目标。

1. 知识与技能目标。

- 学生能够正确、流利、有感情地朗读课文，积累文中的生字词、优美语句等。

- 掌握各种文学体裁（记叙文、说明文、文言文、诗歌）的基本特点和阅读方法。

- 提高文言文的翻译能力，能准确地解释常见的文言实词、虚词。

- 学会运用多种写作手法进行不同类型的写作，如记叙文的倒叙、插叙，说明文的打比方、列数字等说明方法。

2. 过程与方法目标。

- 通过小组合作学习，培养学生的合作探究能力和交流表达能力。

- 引导学生在阅读中进行批注、赏析，提高自主学习能力。

- 在写作训练中，通过教师的指导和同学之间的互评，不断提高写作水平。

如皋高新区实验初中八年级英语第八周周末作业命题人；顾慧香审核：八年级英语组如皋高新区实验初中第八周周末作业八年级英语（共100分，答题时间45分钟）姓名：________ 学号：________ 得分：________ 家长签字：________一、选择题。

（20分）( )1.All of us will become_______ old, so we should be kind to _____ old.A. / ; theB. the ; /C. an ; theD. the ; an( )2. -----What is the ______ of the sign on the bottle ?----- It _____ “this side up”.A. means; meanB. meaningful; meaning Ｃ.means; meaning Ｄ.meaning; means( )3.Could you ______ these boys? They are going to take part in football match next month.A. train asB. train forC. train toD. train( )4.All of us think ________ dangerous to play with fire.A. that isB. this isC. what isD. it is( )5.As a stranger, he didn’t know _______ in this new place.A. when to expectB. how to expectC. what to expectD. who to expect( )6.It is sad that his daughter was born ______ a weak heart.A. atB. withC. fromD. in( )7.The car is _______ expensive ________ he can’t afford it.A. too; toB. so; thatC. such; thatD. enough; that( )8.In our country , the disabled ________taken good care of.A. beB. isC. areD. being( )9. The colour of this book is similar to ________ of mine.A itB oneC thatD this( )10.You’re not good at English, but you can’t __________.A. give it toB. give to itC. give it upD. give up it( )11.We are _____friends , if we work ____with each other, we can finish the hard work..A. close; closelyB. closely; closeC. close; closeD. closely; closely( )12 I like using WeChat. WeChat makes ______ easier for friends to contact with each other.A itB thatC thisD them( )13.----Has she had ________ for the job?-----Yes, she has taught English for more than 10 year.A. many experiencesB. any experiencesC. enough experiencesD. much experience( )14.If we can give a _______ hand, the people in need will get better soon.A. helpfulB. helpingC. helplessD. help( )15.----It’s a fine day. Shall we go camping?----- But we need to be home before six.A. Not at all.B. Good idea !C. You are right.D. Have a nice time!( ) 16. --- Tom, it’s time to go to bed.--- Oh, I won’t do that __________ I finish my homework.A. ifB. tillC. afterD. when( ) 17. It is __________ of young man to donate his pocket money to Project Hope.A. possibleB. kindC. easyD. difficult( ) 18. --- ________ is the theme park?--- It’s about half an hour’s bus ride.A. How longB. How soonC. How farD. How often( ) 19. Project Hope provides poor children ______ chances to go to school.A. withB. forC. byD. to( )20. --- It's easy for five workers to push the broken van away.--- Yes, _______.A. When the cat's away, the mice will playB. Every dog has its dayC. Many hands make light workD. Don't put all your eggs in one basket二、完形填空。

2024-2025学年上学期七年级北师大版数学周末练习（第八周）一、选择题（共36分）1、1.用一个平面去截一个四棱柱，截面形状不可能是()A.三角形B.五边形C.六边形D .七边形2.下列代数式是整式的有()①-23mn ；②y 3-5y +3y ；③29；④a b +c ；⑤5x yπ++；⑥2x y xy -；⑦m ；⑧x 2+2x +23A .3个B .4个C .5个D .6个3.已知a 是有理数，下列各式：(-a )2=a 2；(-a )3=a 3，-a 2=|-a 2|，|-a 3|=a 3，-a 2=(-a )2，其中一定成立的有()A.1个 B.2个 C.3个 D.4个4.从市场融资情况看，2017年上半年内，共享单车以22起融资成为分享经济领域内融资事件数最多的细分领域，融资额达到104.33亿元，将104.33亿用科学记数法可表示为()A 1.04×1010B 1.04×1011C 1.0433×1010D 1.0433×10115.已知5x m +2y 3与14x 6y n +1是同类项，则(-m )3+n 2等于()A.-64 B.-60C .68 D.626、若代数式3x 2－4x ＋6的值为9，则x 2－43x ＋8的值为()A ．17B ．15C ．11D ．97、若a 是一位数，b 是两位数，把a 放在b 的左边，所得的三位数可以表示为（）A．10,.10,.100,.a b B b a C a b D ab+++8、三个连续奇数排成一行，第一个数为x，最后一个数为y，且x＜y．用下列整式表示中间的奇数时，不正确的一个是（）A．x+2B．y﹣2C．x﹣y+4D．（x+y）9.一个多项式加上2325y y --得到多项式3546y y --，则原来的多项式为（）A．35321y y y ++-B．325326y y y --- C.325321y y y +--D．325321y y y ---10.如图所示，图①中的多边形(边数为12)是由等边三角形“扩展”而来的，图②中的多边形是由正方形“扩展”而来的，…，依此类推，则由正n 边形“扩展”而来的多边形的边数为()．A．n (n －1)B．n (n ＋1)C．(n ＋1)(n －1)D．n 2＋211、如图，把半径为0.5的圆放到数轴上，圆上一点A 与表示1的点重合，圆沿着数轴正方向滚动一周，此时点A 表示的数是（）A．πB．π+1C．2πD．π﹣112、填在下面各正方形中的四个数之间都有一定的规律，按此规律得出a 、b 的值分别为（）A ．10、91B ．12、91C ．10、95D ．12、95二、填空题（共24分）1、35xy π-的系数是.次数是__________.2、若23x y -+的值为3则425x y -+的值为__________．3、已知2|2m +1|+13(n -5)2=0，则m n 的值是.4.如果有理数x 、y 满足条件：|x -2|=5，|y |=3，|x -y |=y -x ，则x +2y =.5.对于任意非零实数a 、b ，定义运算“⊕”，使下列式子成立：1⊕2=-32，2⊕1=32，(-2)⊕5=2110，7⊕(-2)=-2110，…，则a ⊕b =.6、按照如图所示的操作步骤，若输入的值为2，则输出的值为_______。

第八周课文8彩色的梦-9枫树上的喜鹊一、看拼音，写词语。

cǎi sè mènɡ xiǎnɡ lā shǒu cǎo pínɡ（）（）（）（）fānɡ biàn jiāo shū yóu xì mǔ qīn（）（）（）（）二、比一比，再组词。

菜（）拉（）般（）精（）彩（）垃（）船（）晴（）戏（）第（）教（）每（）找（）弟（）哮（）母（）三、查字典。

“森”共___画，第5画是___，组词___。

“结”共___画，第5画是___，组词___。

“灵”共___画，第3画是___，组词___。

“母”共____画，第5画是____，组词____。

“游”共____画，第3画是____，组词____。

“便”共____ 画，最后1画是____，组词____ 。

四、在括号内填上合适的量词。

一（）房子一（）森林一（）画笔一（）梦想一（）小船一（）太阳伞一（）绿荫一（）诗歌五、写出下列词语的近义词和反义词，并填空。

近义词：似乎——（）遮蔽——（）发觉——（）反义词：喜欢——（）上升——（）伤心——（）从上面的反义词中选择合适的词语填空。

1、孩子的成绩有所（ ），家长不要一味指责，要帮孩子分析原因，一起努力，这样孩子的成绩才会（ ）。

2、她在放学的路上帮助了别人，心里很（ ）。

可是因为回家晚了，妈妈训斥了她，她很（ ）。

六、按样子写词语。

叽叽喳喳（AABB ）___________ ___________ ____________又大又圆（ABAC ）___________ ___________ ____________红彤彤（ABB ）___________ ___________ ____________东张西望（含反义词）___________ ___________ ____________一、按要求写句子。

1、我有一大把彩色的梦，有的．．长，有的．．圆，有的．．硬。

班级学号姓名第八章生物氧化作业及参考答案一. 填空1．生物氧化有3种方式：____ _____、______ _____和______ ____ 。

2．生物氧化是氧化还原过程，在此过程中有______ ___、_____ ____和____ ____ 参与。

3．原核生物的呼吸链位于__ _______。

4．G0＇为负值是_________反应，该反应可以_________进行。

5．△G0＇与平衡常数的关系式为_________，当Keq＝1时，△G0＇为_________。

6．生物分子的E0＇值小，则电负性_________，供出电子的倾向_________。

7．生物体内高能化合物有_________、_________、_________、_________、_________、_________等类。

8．细胞色素c的辅基是____ _____与蛋白质以_________键结合。

9．在无氧条件下，呼吸链各传递体都处于_________状态。

10．NADH呼吸链中氧化磷酸化的偶联部位是_________、_________、_________。

11．磷酸甘油与苹果酸经穿梭后进人呼吸链氧化，其P/O比分别为_____和_____。

12．举出三种氧化磷酸化解偶联剂_________、_________、_________。

13．举出4种生物体内的天然抗氧化剂_________、_________、_________、_________。

15．生物氧化是_________在细胞中_________，同时产生_________的过程。

16．反应的自由能变化用_________表示，标准自由能变化用_________表示，生物化学中pH 7.0时的标准自由能变化则表示为_________。

17．高能磷酸化合物通常指水解时______ ___的化合物，其中最重要的是___ ____，被称为能量代谢的__ _______。

人教部编版二年级下语文双休日作业第八周课文8彩色的梦-9枫树上的喜鹊一、看拼音，写词语。

cǎi sè mènɡ xiǎnɡ lā shǒu cǎo pínɡ（）（）（）（）fānɡ biàn jiāo shū yóu xì mǔ qīn （）（）（）（）二、比一比，再组词。

菜（）拉（）般（）精（）彩（）垃（）船（）晴（）戏（）第（）教（）每（）找（）弟（）哮（）母（）三、查字典。

“森”共画，第5画是，组词。

“结”共画，第5画是，组词。

“灵”共画，第3画是，组词。

“母”共____画，第5画是____，组词。

“游”共____画，第3画是____，组词 _。

“便”共____ 画，最后1画是____，组词____ 。

四、在括号内填上合适的量词。

一（）房子一（）森林一（）画笔一（）梦想一（）小船一（）太阳伞一（）绿荫一（）诗歌五、写出下列词语的近义词和反义词，并填空。

近义词：似乎——（）遮蔽——（）发觉——（）反义词：喜欢——（）上升——（）伤心——（）从上面的反义词中选择合适的词语填空。

1、孩子的成绩有所（），家长不要一味指责，要帮孩子分析原因，一起努力，这样孩子的成绩才会（）。

2、她在放学的路上帮助了别人，心里很（）。

可是因为回家晚了，妈妈训斥了她，她很（）。

六、按样子写词语。

叽叽喳喳（AABB）___________ ___________ ____________又大又圆（ABAC）___________ ___________ ____________红彤彤（ABB）___________ ___________ ____________东张西望（含反义词）___________ ___________ ____________一、按要求写句子。

1、我有一大把彩色的梦，有的．．圆，有的．．硬。

．．长，有的（用加点的字造句）___________________，有的________，有的________，有的________。

小学语文五年级上册第八单元回顾25 古人谈读书一、圈出加点字的正确读音。

（原练习册第一题）敏儿好．学（hǎo hào）漫．浪诵读（màn wàn）默而识．之（shí zhì）心既到矣．（yī yǐ）二、阅读课文，选择正确的答案。

（填序号）（原练习册第二题，题干有改动）1.对“三到之中，心到最急”一句的解释，正确的一项是（）A．“三到”之中，“心到”是最难懂的。

B．“三到”之中，“心到”是最让人着急的。

C．“三到”之中，“心到”是最关键、最重要的。

2.下列说法正确的是（）A.“敏而好学”与“敏以求之者也”中两个“敏”字的意思是一样的。

B.“吾尝终日不食”与“余尝谓读书有三到”中两个“尝”字的意思是一样的。

C.“学如不及，犹恐失之”的意思是：学习如果不及格，就非常担心、害怕。

3.把“心既到矣，眼口岂不到乎？”这句话改写成陈述句，最恰当的一项是（）A.心既到矣，眼口均可到。

B.心既到矣，眼口岂能到。

C.心既到矣，眼口可不到。

三、根据课文内容填空。

（原练习册第三题）1._______________，_______________，是知也。

（《论语》）2.吾尝终日不食，__________不寝，__________，__________，不如学也。

（《论语》）3.宋朝的朱熹说过，“读书有三到”。

这“三到”指__________、__________、__________。

四、根据要求填空。

（根据练习册第四题改编）1.“学而不厌，诲人不倦”这幅书法作品最适合挂在（①火车站的大厅②学校的礼堂③家里的客厅）（填序号）。

2.看到《好古敏求》的这本书，我想到《论语》中的这句“，好古，。

”“好古敏求”也是一个成语，意思是：____________________________。

3.很多人用“书山有路勤为径，学海无涯苦作舟”来激励自己刻苦学习。

《古人谈读书（一）》中，有一句话与它意思相近，这句话是五、课文中的哪些内容对你有启发？请联系自己的读书体会，写一写。

七年级下第八周数学周末作业班级： 姓名： 座号： 一、精心选一选：（本题共12小题，每小题3分，共36分）1. 下列计算中，正确的是【 】A ．32x x x ÷=B ．623a a a ÷=C ． 33x x x =⋅D ．336x x x += 2. 下列运算正确的是【 】A ．1055a a a =+B ．2446a a a =⨯C ．a a a =÷-10D ．044a a a =- 3. 下列三条线段，能组成三角形的是【 】A ．3，3，3B ．3，3，6C ．3 ，2 ，5D ．3，2，64. 若规定一种新的运算“※”：a ※b = a －b ，如3※2=3－2=91，则21※2的值为【 】．A ．41 B ．－ 41C ．4D ．－45. 如图，OA ⊥AB 于点A ，点O 到直线AB 的距离是【 】 A ．线段OA B ．线段OA 的长度 C ．线段OB 的长度D ．线段AB 的长度6. 已知△ABC 中，∠A 、∠B 、∠C 三个角的比例如下，其中能说明△ABC 是直角三角形的是【 】A ．2：3：4B ．1：2：3C ．4：3：5D ．1：2：27.下面的说法中，①若∠α=∠β，则∠α和∠β是一对对顶角；②若∠α与∠β互为补角，则∠α+∠β=180o ；③一个角的补角比这个角的余角大90o ；④同旁内角相等，两直线平行．正确的个数为【 】A ．1B ．2C ．3D ．48.一个正方形的边长增加cm 3，面积相应增加239cm ，则这个正方形的边长为【 】A ．6cmB ．5cmC ．8cmD ．7cm9. 适合条件∠A=12∠B=13∠C 的△ABC 是【 】 A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等边三角形 10.若4x 2＋2ax ＋1是一个完全平方式，则a 的值为【 】 A ．1 B ．2 C ． ±1 D ．±2 11.如图，下列判断中错误的是【 】A 、∠A+∠ADC=180°—→AB∥CDB 、AB ∥CD —→∠ABC+∠C=180°C 、∠1=∠2—→AD∥BCD 、AD ∥BC —→∠3=∠412. 水池中原有3升水，现每分钟向池内注1升，则水池内水量Q （升）与注水时间t （分）之间关系的图象大致为（ ）二、认真填一填（每小题3分，共12分）13.如果一个三角形两边为2cm ，7cm ，且第三边为奇数，则三角形的周长是_____. 14．在△ABC 中，∠A =60°，∠C =2∠B ，则∠C =_____. 15. 如图，已知∠1=20°，∠2=25°，∠A=55°， 则∠BOC 的度数是_____．16. 设a （a －1）－（a 2－b ）=2，则222a b －ab=三．解答题17．计算（每小题4分，共8分）（1）2（m ＋1）2－(2m ＋1)(2m －1) （2）(－a 2) 3 ²(a 4) 2÷(－a 3) 4 解：原式= 解：原式=ABDC 1 23 418．（本小题满分5分）先化简，再求值[]x y y x y x y x 25)3)(()2(22÷--+-+，其中21,2=-=y x解：原式=19. （本小题满分6分）已知：如图，AD ∥BE ，∠1=∠2．求证：∠A=∠E ． 证明：20. （本小题满分8分）如图是甲、乙两人同一地点出发后，路程随时间变化的图象．（1）此变化过程中，__________是自变量，_________是因变量． （2）甲的速度________乙的速度.（大于、等于、小于） （3）6时表示____ ____（4）路程为150km ，甲行驶了____小时， 乙行驶了_____小时．（5）9时甲在乙的________（前面、后面、相同位置） （6）乙比甲先走了3小时，对吗？__________21. （本小题满分8分）如图，某市有一块长为（3a+b ）米，宽为（2a+b ）米的长方形地块，•规划部门计划将阴影部分进行绿化，中间将修建一座雕像，则绿化的面积是多少平方米？•并求出当a=3，b=2时的绿化面积． 解：22. （本小题满分8分）如图，若AB ∥CD ，EF 与AB 、CD 分别相交于E 、F ，EP ⊥EF ，∠EFD 的平分线与EP 相交于点P ，且∠BEP =40°，求∠P 的度数. 解：23. （本小题满分9分）探究题（1）探究发现：如图，已知AB ∥CD ，∠A =36º，∠C =120º，求∠F －∠E 的大小.解：（2）拓展延伸：如图，已知AB ∥CD ，猜想∠F ，∠E ，∠A ，∠C 的关系是 .（直接写出结论）A B CDEPFABEDCF。

2020-2021学年江苏省徐州市新沂市棋盘中学高二（下）第八周作业数学试卷（3）一、单选题（本大题共2小题，共10.0分）1.甲、乙、丙、丁、戊五名同学参加某种技术竞赛，决出了第一名到第五名的五个名次，甲、乙去询问成绩，组织者对甲说：“很遗憾，你和乙都未拿到冠军”；对乙说：“你当然不会是最差的”.从组织者的回答分析，这五个人的名次排列的不同情形种数共有()A. 30B. 36C. 48D. 542.记者要为4名志愿者和他们帮助的2位老人照相，要求排成一排，2位老人不相邻，不同的排法共有()种．A. 240B. 360C. 480D. 720二、单空题（本大题共1小题，共5.0分）(i为虚数单位)的实部等于______．3.复数3+ii2三、解答题（本大题共2小题，共24.0分）4.实数k为何值时，复数z=(k2−3k−4)+(k2−5k−6)i是：(1)实数；(2)虚数；(3)纯虚数；(4)0．5.函数f(x)=xe x−lnx−ax．(1)若函数y=f(x)在点(1,f(1))处的切线与直线y=2(e−1)(x−1)平行，求实数a的值；(2)若函数f(x)在[1,+∞)上单调递增，求实数a的取值范围；(3)在(1)的条件下，求f(x)的最小值．答案和解析1.【答案】D【解析】【分析】本题考查排列、组合的应用和分步计数原理，关键是根据题意的叙述，确定甲乙的名次情况，进而进行分类讨论，是简单题．根据题意，分析可得，甲乙都没有得到冠军，而乙不是最后一名，分2种情况讨论：①甲是最后一名，则乙可以为第二、三、四名，剩下的三人安排在其他三个名次，②甲不是最后一名，甲乙需要排在第二、三、四名，剩下的三人安排在其他三个名次，由加法原理计算可得答案．【解答】解：根据题意，甲乙都没有得到冠军，而乙不是最后一名，分2种情况讨论：①甲是最后一名，则乙可以为第二、三、四名，即乙有3种情况，剩下的三人安排在其他三个名次，有A33=6种情况，此时有3×6=18种名次排列情况；②甲不是最后一名，甲乙需要排在第二、三、四名，有A32=6种情况，剩下的三人安排在其他三个名次，有A33=6种情况，此时有6×6=36种名次排列情况；则一共有36+18=54种不同的名次排列情况，故选：D．2.【答案】C【解析】【分析】本题考查分步计数原理，是一个基础题，正确运用插空法是关键．本题是一个分步问题，采用插空法，先将4名志愿者排成一列，再将2位老人插到4名志愿者形成的5个空中，根据分步计数原理得到结果．【解答】解：由题意知本题是一个分步问题，采用插空法，先将4名志愿者排成一列，再将2位老人插到4名志愿者形成的5个空中，则不同的排法有A44A52=480种，故选：C．3.【答案】−3【解析】【分析】直接由虚数单位i的运算性质化简，则复数的实部可求．本题考查复数代数形式的乘法运算，考查了虚数单位i的运算性质，是基础题．【解答】解：∵3+ii2=3+i−1=−3−i．∴复数3+ii2(i为虚数单位)的实部等于−3．故答案为：−3．4.【答案】解：(1)当k2−5k−6=0，即k=6或k=−1时，z是实数．(2)当k2−5k−6≠0，即k≠6且k≠−1时，z是虚数；(3)当k2−5k−6≠0，且k2−3k−4=0，z是纯虚数，即k=4时为纯虚数；(4)当k2−5k−6=0，且k2−3k−4=0，即k=−1时，z是0．【解析】利用复数z=a+bi中，b=0为实数；b≠0为虚数；a=0且b≠0为纯虚数；a=b=0，z=0分别得到关于k的方程解之．本题考查了复数的基本概念；属于基础题．5.【答案】解：(1)f′(x)=e x+xe x−1x−a(x>0)，则f′(1)=2e−1−a=2(e−1)，解得a=1；(2)依题意，f′(x)=(x+1)e x−1x −a≥0在[1,+∞)上恒成立，即a≤(x+1)e x−1x在[1,+∞)上恒成立，令g(x)=(x+1)e x−1x (x≥1)，则g′(x)=(x+2)e x+1x2，易知g′(x)>0在[1,+∞)上恒成立，∴函数g(x)在[1,+∞)上单增，∴g(x)min=g(1)=2e−1，故a≤2e−1；(3)当a=1时，f(x)=xe x−lnx−x(x>0)，f′(x)=(x+1)e x−1x−1，f″(x)=(x+2)e x+1x2>0，∴f′(x)在[0,+∞)上单增，又f′(1e)<0,f′(1)>0，∴存在x0∈(1e ,1)，使得f′(x0)=0，此时e x0=1x0，∴x∈(0,x0)时，f′(x)<0，f(x)单减，x∈(x0,+∞)时，f′(x)>0，f(x)单增，∴f(x)min=f(x0)=x0e x0−lnx0−x0=x0⋅1x0−ln1e x0−x0=1．【解析】(1)求导后，利用导数的几何意义可得f′(1)=2e−1−a=2(e−1)，由此求得实数a的值；(2)依题意，a≤(x+1)e x−1x在[1,+∞)上恒成立，由此容易求解；(3)将a=1代入，求导后，得出单调性情况，进而求得最下值．本题考查导数的几何意义及利用导数研究函数的单调性，极值及最值，考查逻辑推理能力，运算求解能力，属于中档题．。

软件工程吴迪第八章课后答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】软件工程课后答案《软件工程》作业及答案1-1什么是软件危机?它有哪些典型表现?为什么会出现软件危机?答:软件危机是指在计算机软件的开发和维护过程中所遇到的一系列严重问题。

概括地说，软件危机包含下述两方面的问题：如何开发软件，以满足对软件日益增长的需求；如何维护数量不断膨胀的已有软件。

软件危机典型表现：对软件开发成本和进度的估计常常很不准确。

用户对“已完成的”软件系统不满意的现象经常发生。

软件产品的质量往往靠不住。

软件常常是不可维护的。

软件通常没有适当的文档资料。

软件成本在计算机系统总成本中所占的比例逐年上升。

软件开发生产率提高的速度，远远跟不上计算机应用迅速普及深入的趋势。

产生软件危机的原因：一方面与软件本身的特点有关，另一方面也和软件开发与维护的方法不正确有关。

软件不同于硬件，它是计算机系统中的逻辑部件而不是物理部件。

管理和控制软件开发过程相当困难。

软件是规模庞大，而且程序复杂性将随着程序规模的增加而呈指数上升。

目前相当多的软件专业人员对软件开发和维护还有不省糊涂观念，在实践过程中或多或少地采用了错误的方法和技术，这是使软件问题发展成软件危机的主要原因。

1-2假设你是一家软件公司的总工程师，当你把图给手下的软件工程师们观看，告诉他们及早发现并改正错误的重要性时，有人不同意你的观点，认为要求在错误进入软件之前就清除它们是不现实的，并举例说：“如果一个故障是编码错误造成的，那么，一个人怎么能在设计阶段清除它呢?”你怎么反驳他?1-3什么是软件工程?它有哪些本质特性?怎样用软件工程消除软件危机?答:软件工程是指导计算机软件开发和维护的一门工程学科。

采用工程的概念、原理、技术和方法来开发与维护软件，把经过时间考验而证明正确的管理技术和当前能够得到的最好的技术方法结合起来，以经济地开发出高质量的软件并有效地维护它。

阜宁县陈集中学七年级数学周末作业(第八周)一、选择题：（每题2分，计20分）1、31-的绝对值是 A 、3- B 、31-C 、3D 、312、在式子21,32,1,0,,2---+x xy n m b a 中单项式的个数为 A 、2 B 、3 C 、4 D 、53、下列说法中正确的是A 、0是最小的整数B 、最大的负有理数是1-C 、两个负数绝对值大的负数小D 、有理数a 的倒数是a1 4、下列去括号过程中错误的是A 、y x y x 3)3(+-=--B 、c b a c b a --=+-)(C 、c b a c b a +-=--2)(2D 、c b a c b a -+=-+)( 5、下列计算中正确的是A 、b a b a b a 22232-=- B 、xy y x 523=+ C 、235=-xy xy D 、32a a a =+6、在20,1.0,5.2,1,3-----与这五个数中：最大的数与绝对值最大的那个数的乘积是 A 、3 B 、2 C 、60 D 、1.07、两个互为相反数的有理数相乘，积为A 、正数B 、负数8、有理数b a 和在数轴上的位置如图，则b a -是 A 、正数 B 、负数 C 、零 D 、非正数 9、已知代数式b a 2-的值为3-，则代数式342+-b a 的值为A 、6B 、3-C 、9D 、010、计算2的正整数次幂：2562,1282,642,322,162,82,42,2287654321========…，观察归纳各种计算结果中个位数字的规律，可得20062的个位数字是A 、2B 、4C 、6D 、8二、填空题：（每空2分，计22分）11、如果m 3-表示一个物体向北运动m 3，那么m 4+表示____________，物体原地不动记为______. 12、212-的相反数是________，倒数是________。

13、单项式2343y x y x nm-与是同类项，则n m -=________，这两个单项式的和是________。

第八章楼地面(59)+3一．判断题1.在排板布置中，当楼面板板宽的方向与墙间出现的缝隙为50mm时，应增加局部现浇板来解决。

（）2.房间内设吊顶就是为了使顶棚平整、美观。

（）3.钢筋砖过梁，可以不受跨度的限制。

（）4.一般要求钢筋混凝土预制板，在墙上的搁置长度不小于100mm。

（）5.楼地面层采用蓄热系数较大的材料时，会让人在四季都感到舒适。

（）6.吊顶有隔声的作用。

（）7.一般楼板的建造费用占建筑物总造价的40%。

（）8.楼层的构造层次主要有面层、结构层、顶棚层、附加层。

（）9.如果房间平面形状为方形，板下两个方向的梁呈等距离布置无主次之分，且间距较小。

这种楼板称为井字梁式楼板。

（）10.无梁楼板的柱网以方形较为经济，跨度一般不超6m，板厚通常不小于120mm。

（）11．预制空心板安装时只能两端受力。

（）12．地坪层一般由面层、垫层和基层三个基本构造层次组成。

（）13．地面要求较高以及薄而脆的面层须采用刚性垫层。

（）14．人们居住或人们长时间停留的房间，楼地面材料应有较好的蓄热性和弹性。

（）15. 强化木地板和复合木地板，都有三氧化二铝的耐磨层。

（）16.地毯的安装固定，要借助于钉条和粘胶带。

（）17.素土夯实层是地面的结构层。

（）18．洁净度要求较高的场所，适宜做自流平材料的楼地面。

（）19．水泥矿渣是做楼地面垫层的好材料。

（）20．用水房间的楼地面，应低于其他房间100mm。

（）二．选择题1. 现浇水磨石地面常嵌固分格条(玻璃条、铜条等)，其目的是（）。

A. 防止面层开裂B. 便于磨光C. 面层不起灰D. 增添美观2．楼板层的隔声构造措施不正确的是（）。

A.楼面上铺设地毯B.设置矿棉毡垫层C.做楼板吊顶处理D.设置混凝土垫层3. 现浇钢筋混凝土楼板的优点是（）。

A.造价低B.施工快C.强度高D.省模板4.水磨石地面一般适用于（）等房间。

A.居住建筑中的卧室、起居室B.公共建筑中的门厅、休息厅C. 宿舍D.宾馆客房5. 在钢筋混凝土装配式楼板的平面布置中，为提高房间净空高度，可采用（）。

第八周作业答案7-1填空题（1）有一瓶质量为M 的氢气，温度为T ，视为刚性分子理想气体，则氢分子的平均平动动能为____________，氢分子的平均动能为______________，该瓶氢气的内能为____________________．[答案：32w kT =， 2i kT ε==25k T ，2mol M iE RT M =52mol M RT M =] （2）容积为 3.0×102m 3的容器内贮有某种理想气体20 g ，设气体的压强为0.5 atm ．则气体分子的最概然速率 ，平均速率 和方均根速率 ．[答案：由理想气体状态方程 molM RTM pV =可得p υ===3.86×104m/sυ===4.38×104m/s===MpV73.1 4.74×104m/s ]（3）题7-1图所示的两条f (υ)~υ曲线分别表示氢气和氧气在同一温度下的麦克斯韦速率分布曲线．由此可得氢气分子的最概然速率为___________；氧气分子的最概然速率为___________．[答案：由p υ=，及M M <mol 氢mol 氧可知，υp 氢=2000 m·s -1 ;又p p υυ=氧氢p p υυ=氧-1 ] (4) 一定量的某种理想气体，当体积不变，温度升高时，则其平均自由程λ ，平均碰撞频率Z 。

（减少、增大、不变）[答案：体积不变，n不变，由λ=可知， λ不变体积不变，n 不变，但T 升高，υ增大，由2Z d n υ=可知，Z 增大．]7-2选择题(1) 容器中贮有一定量的理想气体，气体分子的质量为m ，当温度为T 时，根据理想气体的分子模型和统计假设，分子速度在x 方向的分量平方的平均值是：题7-1图-1)［ ］(A) 2xυ=．(B) 2x υ=(C) 23xkT m υ= ． (D) 2x kT m υ= ．[答案：D 。

税务会计题库第一周作业：会计总论一、单选题（共5题，55.6分）1、下列选项中符合会计管理活动论观点的是A、会计是一种经济信息活动B、会计是一个经济信息系统C、会计是一种管理经济系统的工具D、会计是以提供经济信息、提高经济效益为目的的一种管理活动正确答案： D2、会计的基本职能是（）A、反映与分析B、核算与监督C、反映与核算D、控制与监督正确答案： B3、会计分期是指A、将持续正常的生产经营活动人为的划分成一个个间断、相等的期间B、将持续正常的生产经营活动人为的划分成一个个间断、不等的期间C、将持续正常的生产经营活动人为的划分为一个个连续、相等的期间D、将持续正常的生产经营活动人为的划分成一个个连续、不等的期间正确答案： C4、会计信息的内部使用者有( )。

A、股东B、首席执行官C、供应商D、政府机关正确答案： B5、明确会计反映的特定对象，界定会计核算范围的基本假设是( )。

A、会计主体B、持续经营C、会计分期D、货币计量正确答案： A二、多选题（共2题，22.2分）1、会计信息的外部使用者包括( )。

A、债权人B、顾客C、信用代理人D、工商业协会E、竞争者正确答案： ABCDE2、会计的特点包括（）A、以货币为主要计量单位B、核算具有连续性、系统性、全面性和综合性C、有一套专门的核算方法D、以实物为主要计量单位正确答案： ABC三、判断题（共2题，22.2分）1、会计可反映过去已经发生的经济活动，也可反映未来可能发生的经济活动正确答案：错误2、一般认为，在会计学说史上，将帕乔利复式簿记著作的出版和会计职业的出现视为近代会计史中的两个里程碑正确答案：正确第二周作业：会计要素1一、单选题（共4题，40分）1、会计对象是指会计工作的（）A、单位B、企业C、公司D、客体正确答案： D2、企业的原材料属于会计要素中的A、资产B、负债C、所有者权益D、权益正确答案： A3、属于非流动资产的是A、存货B、应收账款C、应付账款D、固定资产正确答案： D4、属于负债项目的有A、应收账款B、预收账款C、预付账款D、资本公积正确答案： B二、多选题（共3题，30分）1、关于负债，下列各项表述中正确的有A、负债按其流动性不同，分为流动负债和非流动负债B、负债通常是在未来某一时日通过交付资产和提供劳务来清偿C、负债是企业由于过去的交易或事项而承担的现时义务D、长期负债的偿还期均在一年以上（含一年）。

第八章 空间解析几何与向量代数第一节 向量及其线性运算一、填空题1.点(1,2,3)-在第Ⅴ卦限，点(2,3,1)--在第Ⅲ卦限．2.点(,,)x y z 到xoy 面、yoz 面、xoz 面的距离分别为z ，x ，y ；到x 轴、y 轴、z.3.点(,,)a b c 关于yoz 面的对称点是(,,)a b c -；与(,,)a b c -关于xoz 面对称；关于原点的 对称点是(,,)a b c ---．4.点M 的向径与x 轴成45角，与y 轴成60角，长度为6，若在z 轴上的坐标是负值，则点M的坐标为3)-．提示：设(,,)OM x y z =，cos 6x xr α===，x =1cos 26y y r β===，3y =；由222coscos cos 1αβγ++=，有1cos 2γ=-，3z =-.5.与向量(16,15,12)a =-平行，方向相反且长度为75的向量为(48,45,36)--．6．设()()11112222,,,,,M x y z M x y z ,则12M M=7.与向量(6,7,6)a =- 平行的单位向量为676,,111111⎛⎫±- ⎪⎝⎭．8.向量AB在x 轴、y 轴、z 轴上的投影依次为44-，，7，它的终点坐标为(2,1,7)B -， 则起点坐标(2,3,0)-．提示：若(,,)A x y z ，则AB(4,4,7)(2,1,7)x y z =-=----.9. 若()(),,,,,,x y z x y z a a a a b b b b ==则a b ± =(,,)x x y y z z a b a b a b ±±±． b a ⇔ ∥y x z x y za a ab b b ==．10．在xoy 面上，与三点(3,1,2),(4,2,2),(0,5,1)A B C --等距离的点为3821,,055⎛⎫-- ⎪⎝⎭．提示：设点(,,0)D x y ，由222AD BD CD ==得26108142x y x y -=⎧⎨-+=⎩.二、单项选择题1.设向量,a b互相平行，但方向相反，当0a b >> 时，必有 A ．Ａ．a b a b +=- Ｂ．a b a b +>- Ｃ．a b a b +<- Ｄ．a b a b +>+2.下列各组角可以作为某向量的方向角的是 A ．A ．90,150,60αβγ===B ．45,135,60αβγ===C ．60αβγ===D ．60,120,150αβγ===三、计算题1.已知两点()1M 和()23,0,2M ．计算向量12M M的模、方向余弦和方向角．解：()1M ，()23,0,2M ，∴()121,M M =-，122M M = ．∴1212M M M M11,222⎛⎫-=- ⎪ ⎪⎝⎭，方向余弦为12-，，12，方向角为0120，0135，060． 2.设()()()3,5,8,2,4,7,5,1,4m n p ==--=- ，求向量43a m n p =+-在x 轴上的投影及在y 轴上的分向量．解：()()()3,5,8,2,4,7,5,1,4m n p ==--=-，∴ 43(13,7,15)a m n p =+-= ， 故在x 轴上的投影为13，在y 轴上的分向量为7j ． 3.向量a 与三坐标轴的正向构成相等的锐角，其模长为3，求a ．解：设 (,,)a x x x = ，且0x >，由3a = ，有239x =，得x =∴a =．第二节 数量积 向量积一、填空题1．a ⇔ ⊥b 0b a ⋅= ；a b ⇔ ∥0a b ⨯=．2．向量()(),,,,,x y z x y z a a a a b b b b ==,若两向量夹角为θ，则 cos θa b a b a b ++3．向量()()3,1,2,1,2,1a b =--=- ,则()23a b -⋅= 18-,2a b ⨯= 10214i j k ++．4．已知点()()()2,4,,3,7,5,,10,9A n B C m 三点共线，则m = 4 ，n = 1 ．5．已知点()()()1231,1,2,3,3,1,3,1,3M M M -,与,M M M M 1223同时垂直的单位向量为2,2)--． 提示：与,M M M M 1223 同时垂直的单位向量为M M M M M M M M ⨯±⨯12231223.6．设()()2,5,1,1,3,2a b ==- ,a b λμ+与z 轴垂直，则λ与μ的关系2λμ=． 提示：()0a b k λμ+⋅=.7．,,a b c 为三个非零向量，a b ⊥,a 与c 的夹角为π3，b 与c 的夹角为π6，且a =1,2,3bc == ，则a b c ++=提示：2()()a b c a b c a b c ++=++⋅++ . 二、单项选择题1. 已知()()0,3,4,2,1,2a b ==- ，则ab =Pr j C ． A ．３ Ｂ．13-Ｃ．－１ Ｄ．１提示：515a a b b a⋅-===-Prj . 2.已知向量,a b的模分别为4,2a b ==，且a b ⋅= ，则a b ⨯= C ．A．2B．．．2 提示： cos(,)a b a b a b ⋅= ，cos(,)2a b = ， sin(,)a b a b a b ⨯==三、计算题1．()()()2,3,1,1,1,3,1,2,0a b c =-=-=-,求()a b c ⨯⋅ ．解：23185113i j ka b i j k ⨯=-=--+-，所以()(8,5,1)(1,2,0)2a b c ⨯⋅=--⋅-= ．2．求向量()4,3,4a =- 在向量()2,2,1b =上的投影．解：6Pr j 23b a b a b ⋅====． 3．已知3,26,72a b a b ==⨯=，求a b ⋅ ．解：∵sin 72a b a b θ⨯== ∴7212sin 32613θ==⨯，5cos 13θ==±，从而5cos 3263013a b a b θ⎛⎫⋅==⨯⨯±=± ⎪⎝⎭．4．化简：()()()a b c c a b c b b c a ++⨯+++⨯--⨯．解：()()()a b c c a b c b b c a ++⨯+++⨯--⨯a cbc a b c b b a c a =⨯+⨯+⨯+⨯-⨯+⨯ a c b c a b b c a b c a =⨯+⨯+⨯-⨯+⨯-⨯2()a b =⨯ ．第三节 曲面及其方程一、填空题1．xoy 面上双曲线224936x y -=分别绕x 轴、y 轴旋转一周所得旋转曲面的方程依次 为36)(94222=+-z y x 和369)(4222=-+y z x .2．曲面2221x y z --=是由xoy 面上的曲线221x y -=绕x 轴旋转一周所得或由xoz 面上 曲线122=-z x 绕x 轴旋转一周所得.3．2221484x y z ++=表示的曲面为 旋转椭球面 ． 4．2235x y z +=表示的曲面为 椭圆抛物面 ．5．z =表示的曲面为 圆锥面的上半部分 ．6.22y x =表示的曲面为 母线平行于z 轴的抛物柱面 ．二、计算题1．一动点与两定点()2,3,1A 和()4,5,6B 等距离，求这动点的轨迹方程． 解：设动点为),,(z y x P ，则由题意知：22||||PB PA =,从而222222)6()5()4()1()3()2(-+-+-=-+-+-z y x z y x即 0631044=-++z y x ∴动点的轨迹方程为：0631044=-++z y x ． 2.将xoz 坐标面上的曲线z x a =+分别绕x 轴及z 轴旋转一周，求所生成的旋转曲面的方程. 解：在xoz 面上的a x z +=绕x 轴旋转一周，所得旋转曲面为：a x z y +=+±22即222)(z y a x +=+，同理，绕z 轴旋转一周后，得旋转曲面方程为：a y x z ++±=22， 即222)(y x a z +=-．3.说明下列旋转曲面是怎样形成的：⑴2221499x y z ++= ⑵22214yx z -+= 解：(1) xoy 面上的曲线19422=+y x (或xoz 面上的曲线19422=+z x )绕x 轴旋转一周所得；(2) xoy 面上的曲线1422=-y x (或yoz 面上的曲线1422=-y z )绕y 轴旋转一周所得． 4.画出由曲面4z =22z x y =+及221x y +=所围立体(含z 轴部分).解：4z =)4,0,0(的下半圆锥面，22z x y =+表示旋转抛物面，221x y +=表示圆柱面，从而三者所围立体即可得到，如图所示．第四节 空间曲线及其方程一、填空题1.母线平行于y 轴且经过曲线2222222160x y z x z y ⎧++=⎨+-=⎩的柱面方程为223216x z +=. 2.球面z =z =xoy 面上的投影方程为221x y z ⎧+=⎨=⎩. z 22z x y =+ 221x y +=4z =图8-1x yO3.旋转抛物面()2204z x y z =+≤≤在xoy 面上的投影为224x y z ⎧+≤⎨=⎩，在yo z 面上的投 影为240y z x ⎧≤≤⎨=⎩.4.圆锥面z =22z x =所围立体在xoy 面上的投影为2220x y xz ⎧+≤⎨=⎩，在xoz面上的投影为0x z y ⎧≤≤⎪⎨=⎪⎩ 二、单项选择题1.曲线2221:1645230x y z x z Γ⎧+-=⎪⎨⎪-+=⎩关于xoy 面的投影柱面的方程是 A . A .2220241160x y x +--= B .22441270y z z +--=C .22202411600x y x z ⎧+--=⎨=⎩D .224412700y z z x ⎧+--=⎨=⎩2.曲线22203y z x z ⎧+-=⎨=⎩在面xoy 上的投影曲线的方程是 B .A .220y x z ⎧=⎨=⎩B .2290y x z ⎧=-⎨=⎩C .2293y x z ⎧=-⎨=⎩D .223y xz ⎧=⎨=⎩三、将曲线方程22222443812y z x zy z x z ⎧++=⎨+-=⎩化成母线分别平行于x 轴及z 轴的柱面的交线方程. 解：将22222443812y z x z y z x z ⎧++=⎨+-=⎩分别消去,x z ，得 224y z z += ① 240y x += ②再将①②联立得交线方程：222440y z zy x ⎧+=⎨+=⎩．第五节 平面及其方程一、填空题1.设一平面经过点()000,,x y z,且垂直于向量(),,A B C ，则该平面方程为000()()()0A x x B y y C z z -+-+-=. 2.平面260x y z -+-=与平面250x y z ++-=的夹角为π3.3.平行于xoz 面且经过点()2,5,3-的平面方程为50y +=.4.经过x 轴和点()3,1,2--的平面方程为20y z +=. 提示：过x 轴的平面方程设为0By CZ +=.5.点()1,2,1到平面22100x y z ++-=的距离为 1 .提示：d =.二、求平行于x 轴且经过两点()4,0,2-和()5,1,7的平面方程.解：设所求平面方程为0By Cz D ++=， 又平面过()4,0,2-()5,1,7两点2070C D B C D -+=⎧∴⎨++=⎩, 29D CB C=⎧∴⎨=-⎩， ∴所求平面方程为：920y z --=． 三、一平面过点()1,0,1-且平行于向量()2,1,1a = 和()1,1,0b =-,试求该平面方程.解：设平面的法向量为n ，则n a b =⨯ ，2113110i j kn i j k ∴==+--，从而(1,1,3)n =-． 又 平面过点(1,0,1)-，∴所求平面方程为(1)3(1)0x y z -+-+=，即340x y z +--=.四、求平面2250x y z -++=与各坐标面夹角的余弦.解：平面2250x y z -++=的法向量(2,2,1)n =-，设平面与,,yoz xoz xoy 面的夹角分别为,,αβγ， 又yoz 面的法向量(1,0,0)i =2c o s .3n i n i α⋅∴== 同理．21cos ,cos .33βγ== 第六节 空间直线及其方程一、填空题1．设直线经过点()000,,x y z ，且平行于向量(),,m n p ,则该直线的对称式方程为00o x x y y z z m n p ---==,参数方程为000x x mty y nt z z pt=+⎧⎪=+⎨⎪=+⎩. 2．直线124x y z x y z -+=⎧⎨++=⎩的对称式方程为302213x y z --+==-. 3．过点()0,2,4且与两平面21x z +=和32y z -=平行的直线方程为024231x y z ---==-. 4．直线30x y z x y z ++=⎧⎨--=⎩与平面10x y z --+=的夹角为 0 .5．点()3,1,2-到直线10240x y z x y z +-+=⎧⎨-+-=⎩的距离为. 提示：过(3,1,2)A -与10:240x y z L x y z +-+=⎧⎨-+-=⎩垂直的平面为1y z +=，该平面与直线L 的交点131,,22B ⎛⎫-⎪⎝⎭，则A 到直线L 的距离即为AB .6．过直线1:L 4020x z y +-=⎧⎨-=⎩且平行于直线221:211x y zL +-==的平面方程为 320x y z -++=.提示：过1L 的平面束:(4)(2)0x z y λ∏+-+-=， 2∥L ∏20n s ∴⋅= ,2(1,,1),(2,1,1)n s λ==210λ∴++=,得3λ=-．∴平面为43(2)0x z y +---=，即320x y z -++=..7．直线326040x y z x y z D -+-=⎧⎨+-+=⎩与z 轴相交，则D = 3 .二、单项选择题1．两直线1158:121x y z L --+==-与26:23x y L y z -=⎧⎨+=⎩的夹角为 C . A ．π6 B ．π4 C ．π3 D ．π22．直线111x x y y z z m n p---==与平面0Ax By Cz D +++=的夹角θ满足 C . A ．sin θ=B ．cos θ=C ．sin θ=D ．cos θ=3．过点()2,0,3-且与直线247035210x y z x y z -+-=⎧⎨+-+=⎩垂直的平面方程是 A .A ．16(2)14(0)11(3)0x y z --+-++=B .(2)2(0)4(3)0x y z ---++=C ．3(2)5(0)2(3)0x y z -+--+=D .16(2)14(0)11(3)0x y z -++++-= 4．设直线3210:21030x y z L x y z +++=⎧⎨--+=⎩及平面:4220x y z ∏-+-=，则直线L C .A ．平行于∏B ．在∏上C ．垂直于∏D ．与∏斜交提示：判断直线的方向向量与平面的法向量的关系.三、计算题1．求过点()4,1,3-且与直线230:510x y L y z --=⎧⎨-+=⎩平行的直线方程．解：设直线L 的方向向量12025051i j ks i j k =-=++-，∴所求直线的方向向量(2,1,5)s '=，从而直线方程为：413215x y z -+-==． 2．求直线2403290x y z x y z -+=⎧⎨---=⎩在平面41x y z -+=上的投影直线的方程．解：过已知直线的平面束方程为：329(24)0x y z x y z λ---+-+=，即(32)(14)(2)90x y z λλλ+-++--=．要使其与平面41x y z -+=垂直，则满足4(32)1420,λλλ++++-= 11.13λ=-1731371170.x y z ∴+--= ∴投影直线方程为 41.1731371170x y z x y z -+=⎧⎨+--=⎩ 3．求过直线20:4236x y L x y z +=⎧⎨++=⎩且切于球面2224x y z ++=的平面方程．解：设所求平面方程为：4236(2)0x y z x y λ++-++=即(42)(2)360x y z λλ++++-= 由题意知：(0,0,0)到平面的距离为22=即2440λλ++=2λ∴=-∴所求平面方程为：2z =．第八章 自测题一、填空题（每小题3分，共24分）1．设a =()2,5,1-，b =()1,3,2,问λ与μ有怎样的关系2λμ=，λa +μb 与z 轴垂直． 2．若已知向量a =()3,4,0,b =()1,2,2,则a ,b夹角平分线上的单位向量为．提示： a ，b 夹角平分线上的单位向量为a b a b a ba b+±+.3．若两个非零向量a ,b的方向余弦分别为111cos ,cos ,cos αβγ和222cos ,cos ,cos αβγ， 设a ,b夹角为ϕ，则cos ϕ=122112cos cos cos cos cos cos ααββγγ++．4．过直线122232x y z -+-==-且与平面3250x y z +--=垂直的平面方程为 81390x y z -++-=．提示：L ：122232x y z -+-==-，化为一般方程12232232x y y z -+⎧=⎪⎪-⎨+-⎪=⎪-⎩， 即32102320x y y z ++=⎧⎨+-=⎩，过L 的平面束为：321(232)0x y y z λ++++-= ① (3,22,3)n λλ=+ ，(3,2,1)s =-，由0n s ⋅= 得13λ=-，代入①，可得平面方程.5．直线1l :158121x y z --+==-与直线2l :623x y y z -=⎧⎨-=⎩的夹角θ=1arccos 6． 6．点()3,-4,4到直线452221x y z ---==-的距离为 提示：过()A 3,-4,4与L ：452221x y z ---==-垂直的平面为：2(3)2(4)(4)0x y z --++-=，与L 的交点为(8,1,4)B ，A 到L 的距离即为AB . 7．曲线22210x y z x y z ⎧++=⎨++=⎩在xoy 面上的投影曲线为2222210x y xy z ⎧++=⎨=⎩．8．与两直线112x y t z t=⎧⎪=-+⎨⎪=+⎩及121121x y z ++-==都平行，且过原点的平面方程为 0x y z -+=．二、单项选择题（每小题3分，共12分）1．点()3,2,2P -在平面32210x y z -+-=上的投影点是 B ． A ．()3,1,2- B ．301720,,777⎛⎫-⎪⎝⎭ C ．()7,2,1 D ．()2,21,3--提示：过()3,2,2P -与平面 垂直的直线为322312x y z -+-==-，其与平面∏的交点即为投影点. 2．直线224213x y z -+-==-与平面4x y z ++=的关系是 A ． A ．直线在平面上 B ．平行 C ．垂直 D ．三者都不是 3．两平行平面23490x y z -++=与234150x y z -+-=的距离为 C ．A ．629 B ．2429 CD提示：两平行平面的距离为平面上任一点到另一平面的距离 4．xoz 平面上曲线e xz =绕x 轴旋转所得旋转曲面方程为 A ．Ae x = B ．22e x y z += C ．22e xy z += D．z =三、计算题（共64分）1．求与坐标原点O 及点()2,3,4A 距离之比为1:2的点的全体所组成的曲面方程，它表示 怎样的曲面？（本题6分）解：设所求曲面上的点为(,,)x y z ，则由题意知：2222221(2)(3)(4)4x y z x y z ++=-+-+-， ∴ 曲面方程为：222333468290x y z x y z +++++-=，表示一球面．2．将空间曲线方程222160x y z x z ⎧++=⎨+=⎩化为参数方程．（本题5分）解：把z x =-代入22216x y z ++=，得22216x y +=，令x t =，4sin y t =，则z t =-，∴空间曲线方程的参数方程为：4sin x ty t z t⎧=⎪=⎨⎪=-⎩．3．求中心点在直线247045140x y z x y z +--=⎧⎨++-=⎩上且过点A ()0,3,3和点B ()1,3,4-的球面方程．（本题6分）解：把247045140x y z x y z +--=⎧⎨++-=⎩化为对称式方程：7002322x y z ---==-，设球心坐标为 73,2,22O t t t ⎛⎫- ⎪⎝⎭，则OA OB =，从而 ()()()222227932233423222t t t t t ⎛⎫⎛⎫-+-=-+-+- ⎪ ⎪⎝⎭⎝⎭，∴32t =， ∴(1,3,3)O -，1OA =，所以球面方程为222(1)(3)(3)1x y z ++-+-=．4．求通过直线0230x y z x y z ++=⎧⎨-+=⎩且平行于直线23x y z ==的平面方程．（本题7分）解：设所求平面的方程为：(23)0x y z x y z λ+++-+=，即(12)(1)(13)0x y z λλλ++-++=，(12,1,13)n λλλ=+-+ ，又∵直线11123x y z==平行于平面， ∴1112(1)(13)023λλλ++-++=， ∴1115λ=-， ∴所求平面方程为：726180x y z -+=．5．点()2,1,1P --关于平面∏的对称点为1P ()-2,3,11，求∏的方程．（本题7分）解：设1PP 的中点为0P ，则0(0,1,5)P ，1(4,4,12)PP =- ，∵1//PP n ，取(1,1,3)n =-，由题意知所求∏的方程为：(0)(1)3(5)0x y z --+-+-=，即3160x y z -++-=．6．直线10:10x y z L x y z +--=⎧⎨-++=⎩在平面:0x y z ∏++=上投影直线L 0的方程．（本题7分）解：设所求平面方程为：1(1)0x y z x y z λ+--+-++=，即(1)(1)(1)10x y z λλλλ++-+-+-=，1(1,1,1)n λλλ=+--， 又∵2(1,1,1)n = ，22n n ⊥， ∴1110λλλ++-+-= ∴1λ=-，∴ 10y z --=， ∴ 投影直线L 0的方程为：10y z x y z -=⎧⎨++=⎩．7．求过直线5040x y z x z ++=⎧⎨-+=⎩且与平面48120x y z --+=成π4角的平面方程．（本题7分）解：设所求平面的方程为：5(4)0x y z x z λ+++-+=，即(1)5(1)40x y z λλλ+++-+=，1(1,5,1)n λλ=+- ，又∵2(1,4,8)n =--，1212πcos 4n n n n ⋅==，=即，解得34λ=-， 又平面40x z -+=与平面48120x y z --+=的夹角余弦cos ==θ π.4∴=θ ∴所求平面方程为：207120x y z ++-=及40x z -+=.8．求过点()P 2,1,3且与直线l :11321x y z+-==-垂直相交的直线方程．（本题7分） 解：由题意知，过点P ()2,1,3且垂直与l 的平面方程为：3(2)2(1)(3)0x y z -+---=即3250x y z +--=，令3121x t y t z t=-⎧⎪=+⎨⎪=-⎩，代入上述平面方程，解得37t =．所以平面与l 的交点为02133,,777P ⎛⎫- ⎪⎝⎭，由于所求直线的方向向量0//s P P ，所以取(2,1,4)s =- ， 所以直线方程为213214x y z ---==-． 9．直线过点()3,5,9A --且和直线1l :3523y x z x =+⎧⎨=-⎩,2l :47510y x z x =-⎧⎨=+⎩相交，求此直线方程．（本题7分）解：设所求直线为l ，则l 与1l ，2l 分别相交，1l ：5332y z x -+==，2l ：71045y z x +-==， 所以取11(0,5,3)P l -∈，1(1,3,2)s = ，1(3,0,6)AP = ；22(0,7,10)Pl -∈，2(1,4,5)s =， 2(3,12,19)AP =- ，令111(18,0,9)n s A P =⨯=-，222(136,4,24)n s AP =⨯=--，过l 与1l 的平面方程为：2(3)(9)0x z +-+=，即230x z --=；过l 与2l 的平面方程为：34(3)(5)6(9)0x y z +---+=，即346530x y z --+=；所以直线l 的方程为：230346530x z x y z --=⎧⎨--+=⎩．。

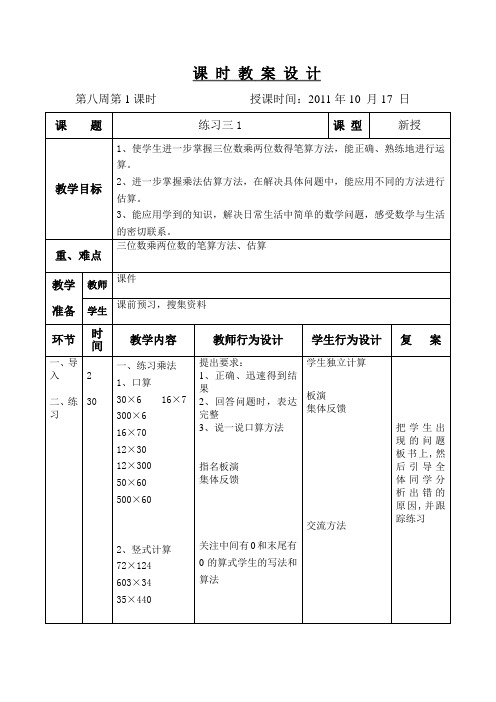
课时教案设计第八周第1课时授课时间：2011年10 月17 日课题练习三1 课型新授教学目标1、使学生进一步掌握三位数乘两位数得笔算方法，能正确、熟练地进行运算。

2、进一步掌握乘法估算方法，在解决具体问题中，能应用不同的方法进行估算。

3、能应用学到的知识，解决日常生活中简单的数学问题，感受数学与生活的密切联系。

重、难点三位数乘两位数的笔算方法、估算教学准备教师课件学生课前预习，搜集资料环节时间教学内容教师行为设计学生行为设计复案一、导入二、练习230一、练习乘法1、口算30×6 16×7300×616×7012×3012×30050×60500×602、竖式计算72×124603×3435×440提出要求：1、正确、迅速得到结果2、回答问题时，表达完整3、说一说口算方法指名板演集体反馈关注中间有0和末尾有0的算式学生的写法和算法学生独立计算板演集体反馈交流方法把学生出现的问题板书上,然后引导全体同学分析出错的原因,并跟踪练习三、小结3二、估算练习1、不用计算，判断对错5818=4534 （）150×40=600 （）88×34=318 （）350×70=2450（）2、小明从10点开始打字，打到10点25分，每分约打110个字，共打了多少字？如果打到10时35分，它能完成4000字的打字任务吗？3、P38-5师：有哪几种判断方法？请学生归纳判断方法：1、用估算2、抓积的个位数特点3、积的末尾0的个数让学生认真观察课文情景图和土上的信息再让学生独立解答指名板演集体反馈引导学生总结本节课的收获以及提出疑问。

学生独立判断学生说一说自己是如何判断的通过此题使学生感受数学与生活的密切联系。

让学生独立估算判断题要找出错误的原因并改正给优等生预备几个题目,让不同层次的学生都有发展板书设计练习三72×124 603×3435×440作业预习神奇的计算工具必做38页第2题选做练习册第1、2题课后反思在指导学生说解题思路时。

旅游文学与写作作业八1、普通话为什么以北京地区的语音为标准音，而不以四川话话为标准音呢？【答案】这是历史发展的必然。

从两个方面来看：第一，从文献资料提供的依据来看，北京语音的标准音的地位，早在元代时期就已经得到了公认。

元代的周德清所编写的《中原音韵》（大约在1324年期间成书）的语音依据是在北京取样的。

第二，从北京这个地方的历史发展来看，北京这个地方的城市的历史发展，把中原之音的代表话——北京语音，推到了“标准音”的地位。

元代定都北京，北京成为中国的政治、经济、文化的中心，在十四世纪期间，一种以北方话为基础的共同语的口语形式开始形成，后来称之为“官话”。

明、清时期，“官话”广及全国。

“五四”时期把“官话”改为“国语”，当时的教育部还颁布了《注音字母》来拼注国语。

国语运动和白话文运动使得中华民族的共同语，在口头上和书面上有了迅猛的发展，趋向于成熟。

新中国成立后，将“国语”改为“普通话”。

所以说普通话以北京语音为标准音是历史的必然。

2、为什么北方方言会成为现代汉民族共同语的基础方言？【答案】北方方言成为现代汉民族共同语的基础方言是历史发展的结果。

（1）北方反演的代表城市北京，长期以来是我国的国度所在地，是政治文化中心。

（2）北方方言分布区域随历史发展不断扩大，成为汉语诸方言中通行最广、使用人数最多的方言。

（3）从晚唐五代以来直至明清，有许多重要的白话文著作是用北方方言或以北方方言为基础写成的。

3、官话方言的共同特点和主要差异表现在哪些方面？【答案】官话方言的共同特点是：（1）古全浊声母今读塞音、塞擦音时，平声为送气清音、仄声为不送气清音。

（2）复印的韵尾只有两个鼻辅音。

（3）声调多数为阴平、阳平、上声、去声四类。

官话方言的内部差异主要表现在声调方面。

4、蚊子的翅膀每秒振动500~600次，苍蝇的翅膀每秒振动352次，能说蚊子发出的声音比苍蝇的大吗？【答案】BD虽然蚊子的翅膀每秒振动500~600次，苍蝇的翅膀每秒振动352次，但是不能说蚊子发出的声音比苍蝇的大，只是蚊子发出的声音比苍蝇的高。

八年级下学期第八周双休作业02阅读《五柳先生传》回答1—6题先生不知何许．．( )人也，亦不详．( )其姓字，宅边有五柳树，因以为号焉。

闲静少言，不慕荣利。

好读书，不求甚解．．．．( )；每有会意．．( )，便欣然忘食。

性嗜（）酒，家贫不能常得。

亲旧．．( )知其如此，或．( )置酒而招之；造饮辄．( )尽，期．( )在必醉。

既醉而退，曾不吝情．．．．( )去留。

环堵萧然( )，不蔽风日；短褐穿结，箪瓢屡．( )空，晏如．．( )也。

常著文章自娱，颇（）示己志。

忘怀得失，以此自终．．( )。

赞曰：黔娄之妻有言：“不戚戚．．．．( )于贫贱，不汲汲( )于富贵。

”其言兹若人之俦．( )乎？衔觞．( )赋诗，以乐其志。

无怀氏之民欤？葛天氏之民欤？1、解释文中加点的词。

2、翻下列句子。

好读书，不求甚解；每有会意，便欣然忘食。

常著文章自娱，颇示己志。

忘怀得失，以此自终。

不戚戚于贫贱，不汲汲于富贵。

3、文中哪句话说明五柳先生是一位真正的隐士？4、五柳先生的三大志趣是：5、赞中的哪句话与传文中的“不慕荣利”相照应？6、结合课文内容和自己的课外阅读所知，说说五柳先生是一个怎样的人。

阅读《雪》，答题（一）江南的雪，可是滋润美艳之至了；那是还在隐约着的青春的消息，是极壮健的处子的皮肤。

雪野中有血红的宝珠山茶，白中隐青的单瓣梅花，深黄的磬口的蜡梅花；雪下面还有冷绿的杂草。

胡蝶确乎没有；蜜蜂是否来采山茶花和梅花的蜜，我可记不真切了。

但我的眼前仿佛看见冬花开在雪野中，有许多蜜蜂们忙碌地飞着，也听得他们嗡嗡地闹着。

（二）但是，朔方的雪花在纷飞之后，却永远如粉，如沙，他们决不粘连，撒在屋上，地上，枯草上，就是这样。

屋上的雪是早已就有消化了的，因为屋里居人的火的温热。

别的，在晴天之下，旋风忽来，便蓬勃地奋飞，在日光中灿灿地生光，如包藏火焰的大雾，旋转而且升腾，弥漫太空，使太空旋转而且升腾地闪烁。

在无边的旷野上，在凛冽的天宇下，闪闪地旋转升腾着的是雨的精魂……是的，那是孤独的雪，是死掉的雨，是雨的精魂。