Lecture No12_Equivalence Calculations with Continuous Payment
- 格式:pptx
- 大小:273.92 KB
- 文档页数:7

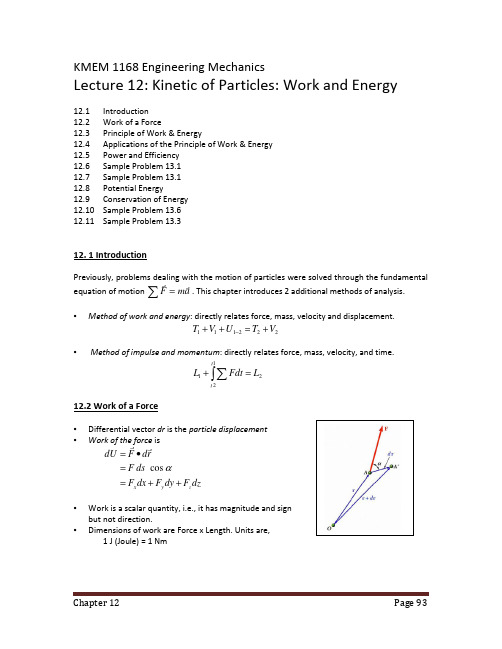
KMEM 1168 Engineering MechanicsLecture 12: Kinetic of Particles: Work and Energy12.1 Introduction 12.2 Work of a Force12.3 Principle of Work & Energy12.4 Applications of the Principle of Work & Energy 12.5 Power and Efficiency 12.6 Sample Problem 13.1 12.7 Sample Problem 13.1 12.8 Potential Energy12.9 Conservation of Energy 12.10 Sample Problem 13.6 12.11 Sample Problem 13.312. 1 IntroductionPreviously, problems dealing with the motion of particles were solved through the fundamentalequation of motion a m F rr =∑. This chapter introduces 2 additional methods of analysis.•Method of work and energy : directly relates force, mass, velocity and displacement. 222111V T U V T +=++−•Method of impulse and momentum : directly relates force, mass, velocity, and time.2121L Fdt L t t =+∫∑12.2 Work of a Force• Differential vector dr is the particle displacement •Work of the force isdzF dy F dx F ds F rd F dU z y x ++==•=αcos r r• Work is a scalar quantity, i.e., it has magnitude and sign but not direction.• Dimensions of work are Force x Length. Units are,1 J (Joule) = 1 Nm• Work of a force during a finite displacement,• Work is represented by the area under the curve of F t plotted against s .• Work of a constant force in rectilinear motion,•Forces which do not do work (ds = 0 or cos a = 0):a) reaction at frictionless pin supporting rotating bodyb) reaction at frictionless surface when body in contact moves along surface c) weight of a body when its center of gravity moves horizontally12.3 Principle of Work & Energy•Consider a particle of mass m acted upon by a force•Integrating from A 1to A 2,•The work of the force is equal to the change in kinetic energy of the particle.• Units of work and kinetic energy are the same:12.4 Applications of the Principle of Work & Energy•The bob is held at point 1 and if we wish to find the velocity of pendulum bob at point 2, we have to consider the method of work and energy. Force P acts normal to path and does no work.•In this method, unlike the method of Newton 2nd Law, we can find velocity without having to determine expression for acceleration and integrating.•All quantities are scalars and can be added directly. Forces which do no work (eg. In this case is the tension in the cord P)are eliminated from the problem. Principle of work and energy cannot be applied to directly determine the acceleration of the pendulum bob.•The tension in the cord is required to supplement the method of work and energy with an application of Newton’s second law.•As the bob passes through A 2,12.5 Power and Efficiency•Power = rate at which work is done.vF dt r d F dt dU r r r r •=•==•Dimensions of power are work/time or force x velocity. Units for power are• Efficiency is the ratio of the power output to the power input,12.6 Sample Problem 13.1An automobile weighing 4000 N is driven down a 5oincline at a speed of 88 m /s when the brakes are applied causing a constant total breaking force of 1500 N.Determine the distance traveled by the automobile as it comes to a stop.• Evaluate the change in kinetic energy.()()m N 15488008810/4000sm 88221212111⋅====mv T v0022==T v•Determine the distance required for the work to equal the kinetic energy change.()()()()x x x U 11515sin 4000150021−=°+−=→()0115115488002211=−=+→x T U Tm 6.1345=x12.7 Sample Problem 13.2Two blocks are joined by an inextensible cable as shown. If the system is released from rest, determine the velocity of block A after it has moved 2 m.Assume that the coefficient of friction between block A and the plane is μk= 0.25 and that the pulley isweightless and frictionless.• Apply the principle of work and energy separately to blocks A and B .Block A:()()()()()()()()()221221221120024902220:N490196225.0N 196281.9200v F vm F F T U T W N F W C A A C A k A k A A =−=−+=+======→µµBlock B:()()()()()()()()2212212211300229402220:N 294081.9300v F vm W F T U T W c B B c B =+−=+−=+==→•When the two relations are combined, the work of the cable forces cancel. Solve for the velocity.()()()()22120024902v F C =−()()()()221300229402v F c =+−()()()()()()2212215004900300200249022940vv=+=− s m 43.4=v12.8 Potential EnergyThere are 2 kinds of potential energyi) Gravitational Potential Energy, V g ii) Elastic Potential Energy, V eGravitational Potential Energy (V g )• Work of the force of gravity W ,2121y W y W U −=→• Work is independent of path followed, it depends only on the initial and final values of W(dy).()()2121g g V V U −=→•Choice of datum from which the elevation y is measured is arbitrary. But always choose the lower position as the datum to avoid negative potential energy. Units of work and potential energy are the same:J m N )(=⋅==dy W V gElastic Potential Energy, V e• Work of the force exerted by a spring dependsonly on the initial and final deflections of the spring,2221212121kx kx U −=→• The potential energy of the body with respect tothe elastic force,()()2121221e e e V V U kxV −==→•Note that the preceding expression for V e is valid only if the deflection of the spring is measured from its undeformed position.=→21U 221kx12.9 Conservation of Energy•Conservation of energy equation,constant2211=+=+=+V T E V T V T• When a particle moves under the action of conservative forces, the total mechanical energy (E) is constant.•Friction forces are not conservative. Total mechanical energy of a system involving friction decreases. Mechanical energy is dissipated by friction into thermal energy or heat.ll W V T W V T =+==11110()ll l W V T V W g g Wmv T =+====22222212022112.10 Sample Problem 13.6A 20-N collar slides without friction along a vertical rod as shown. The spring attached to the collar has an undeflected length of 4 cm and a constant of 3 N/cm. If the collar is released from rest at position 1, determine its velocity after it has moved 6 cm to position 2.• Apply the principle of conservation of energy betweenpositions 1 and 2.Position 1:()()0024cmN 24483112212121=+=+=⋅=−==T V V V kx V g e ePosition 2:()()()()222221222212221102021cm N 6612054cmN 120620cmN 544013v mv T V V V Wy V kx V g e g e ==⋅−=−=+=⋅−=−==⋅=−==•Conservation of Energy:cmN 66cm N 240222211⋅−=⋅++=+v V T V T↓=s m 5.92v12.11 Sample Problem 13.3A spring is used to stop a 60 kg package which is sliding on a horizontal surface. The spring has a constant k = 20 kN/m and is held by cables so that it is initially compressed 120 mm. The package has a velocity of 2.5 m/s in the position shown and the maximum deflection of the spring is 40 mm. Determine(a) the coefficient of kinetic friction between the package and surface(b) the velocity of the package as it passes again through the position shown.(a) Use principle of work and energy equation,NF g N µ==60222111V T U V T +=++→021)(212122212+∆=−∆+x k s N x k mu µ()()222)04.012.0)(20000(2)04.06.0)(60()12.0)(20000(215.26021+=+−+g µ 20.0=µ(b) Apply the principle of work and energy for the rebound of the package.333222V T U V T +=++→ 2323222121)(210x k mv s N x k ∆+=−∆+µ2232)12.0)(20000(21)60(21)64.0)(60)(2.0()16.0)(20000(21+=−v g s m v /11.13=NB: Part B demonstrates that the final velocity at 3 is less than the initial velocity at 1. This is due to the loss of energy due to friction. The total mechanical energy is not conserved.。

一、概述Equivalence classes是数学中一个重要的概念,它在各个数学分支中都有着广泛的应用。
由于其重要性,我们有必要对equivalence classes进行深入的研究和分析,以便更好地理解和应用它们。
二、equivalence classes的定义Equivalence classes是集合论和抽象代数中的一个重要概念。
在集合论中,equivalence classes是一种关于等价关系的划分,其中所有与给定元素相关的元素都被划分到同一个等价类中。
equivalence classes将集合中的元素划分成若干个不相交的子集,这些子集中的元素被认为是相等的。
在抽象代数中,equivalence classes也广泛应用于裙、环、域等代数结构的研究中。
三、equivalence classes的性质1. 自反性:对于任意元素a,a与自身是等价的。
2. 对称性:如果a与b等价,那么b也与a等价。
3. 传递性:如果a与b等价,b与c等价,则a与c也等价。
四、equivalence classes的应用1. 在集合论中,equivalence classes广泛应用于商集的构造和研究中。
商集是指通过等价关系来划分原集合得到的集合,equivalence classes刚好可以用来表示商集中的每一个等价类。
2. 在抽象代数中,equivalence classes被广泛应用于裙、环、域等代数结构的研究中。
在裙的理论中,equivalence classes可以用来表示同余关系,从而得到模运算的概念。
五、equivalence classes的扩展除了在集合论和抽象代数中的应用外,equivalence classes的概念还可以被扩展到其他领域中。
在计算机科学中,equivalence classes被广泛应用于等价类划分算法中,用于优化程序性能和数据处理效率。
在经济学和社会科学中,equivalence classes也可以被用来划分不同的经济或社会裙体,以便更好地进行分析和研究。

2.4 整数、有理数与实数4-A Integers and rational numbersThere exist certain subsets of R which are distinguished because they have special properties not shared by all real numbers. In this section we shall discuss such subsets, the integers and the rational numbers.有一些R的子集很著名,因为他们具有实数所不具备的特殊性质。
在本节我们将讨论这样的子集,整数集和有理数集。
To introduce the positive integers we begin with the number 1, whose existence is guaranteed by Axiom 4. The number 1+1 is denoted by 2, the number 2+1 by 3, and so on. The numbers 1,2,3,…, obtained in this way by repeated addition of 1 are all positive, and they are called the positive integers.我们从数字1开始介绍正整数,公理4保证了1的存在性。
1+1用2表示,2+1用3表示,以此类推,由1重复累加的方式得到的数字1,2,3,…都是正的,它们被叫做正整数。
Strictly speaking, this description of the positive integers is not entirely complete because we have not explained in detail what we mean by the expressions “and so on”, or “repeated addition of 1”.严格地说,这种关于正整数的描述是不完整的,因为我们没有详细解释“等等”或者“1的重复累加”的含义。

笔译测试一、解释术语1、Translation consists in?________________________________________________________________________ 2Translation as a science or an art?________________________________________________________________________ 3 Criteria of Translation________________________________________________________________________ 4What is dynamic equivalence?________________________________________________________________________ 5The methods of Translation?________________________________________________________________________ ________________________________________________________________________ 6What is method?________________________________________________________________________ 7What is diction?________________________________________________________________________ 8What is Amplification?________________________________________________________________________ 9What are purposes and obligatory?________________________________________________________________________ 10Note to omission?________________________________________________________________________二、句子翻译(2做3没做 )My holiday afternoons were spent in ramble about thesurrounding country.2)The sight of his native town called back his childhood.、I love my love with an E, because she's enticing; I hate her with anE, because she's engaged. I took her to the sign of the exquisite,and treated her with an elopement, her name's Emily, and she livesin the East.一朝春尽红颜老,花落人忘两不知。

常用离散数学名词中英文对照集合:set元素:element严格定义:well defined成员:member外延原理:principle of extension泛集(全集):universal set空集:empty set(null set)子集:subset文氏图:venn diagram并:union交:intersection相对补集:relative complement绝对补集:absolute complement补集:complement对偶性:duality幂等律:idempotent laws组合律:associative laws交换律:commutative laws分配律:distributive laws同一律:identity laws对合律:involution laws求补律:complement laws对偶原理:principle of duality有限集:finite set计算原理:counting principle类:class幂集:power set子类:subclass子集合:subcollection命题:proposition命题计算:proposition calculus语句:statement复合:compound子语句:substatement合取:conjunction析取:disjuction否定:negation真值表:truth table重言式:tautology矛盾:contradiction逻辑等价:logical equivalence命题代数:algebra of propositions 逻辑蕴涵:logicalimplication关系:relation有序对:ordered pair划分:parti-on偏序:partial order整除性:divisibility常规序:usual order上确界:supremum下确界:infimum上(下)界:upper(lower) bound乘积集:product set笛卡儿积:cartesian product笛卡儿平面:cartesian plane二元关系:binary relation定义域:domain值域:range相等:equality恒等关系:identity relation全关系:universal ralation空关系:empty ralation图解:graph坐标图:coordinate diagram关系矩阵:matrix of the relation 连矢图:arrow diagram有向图:directed graph逆关系:inverse relation转置:transpose复合:composition自反:reflexive对称的:symmetric反对称的:anti-symmetric可递的:transitive等价关系:equivalence relation半序关系:partial ordering relation 函数:function映射:mapping变换:transformation像点:image象:image自变量:independent variable因变量:dependent variable函数图象:graph of a function合成函数:composition function可逆函数:invertible function一一对应:one to one correspondence 内射:injective满射:surjective双射:bijective基数度:cardinality基数:cardinal number图论:graph theory多重图:multigraphy顶点:vertix(point,node)无序对:unordered pair边:edge相邻的adjacent端点:endpoint多重边:multiple edge环:loop子图:subgraph生成子图:generated subgraph平凡图:trivial graph入射:incident孤立点:isolated vertex连通性:connectivity通路:walk长度:length简单通路:chain(trail)圈:path回路:cycle连通的:connected连通分支:connected component距离:distance欧拉图:eulerian graph欧拉链路:eulerian trail哈密顿图:hamilton graph哈密顿回路:hamilton cycle货郎行程问题:traveling salesman完全图:complete graph正则图:regular graph偶图:bipartive graph树图:tree graph加权图:labeled graph同构图:isomorphic graph同构:isomorphism同胚的:homeomorphic平面图:planar graph着色问题:colortion区域:region地图:map非平面图:nonplanargraph着色图:colored graphs顶点着色:vertex coloring色散:chromatic number四色原理:four color theorem对偶地图:dual map退化树:degenerate tree生成树:spanning tree有根树:rooted tree根:root水平(深度):level(depth)叶子:leaf分支:branch有序有根树:ordered rooted tree二元运算符:binary operational symbol半群:semigroup单位元素:identity element右(左)单位元素:right(left) identity左(右)消去律:left(right) cancellation law) 逆:inverse并列:juxtaposition有限群:finite group正规子群:normal subgroup非平凡子群:nontrivial subgroup循环群:cyclic group环:ring整环:integral domain域:field交换环:commutative ring加性环:additive group汇合:meet格:lattice有界格:bounded lattice分配格:distributeve lattice补格:complemented lattice表示定理:representation theorem。