下载文档原格式
2023人教版八年级数学下册知识点汇总
本文档汇总了2023人教版八年级数学下册的重要知识点。
以下是各个章节的知识点概述：
第一章：实数
- 实数的分类与性质
- 实数的运算法则
- 实数的比较与排序
- 实数的绝对值和相反数
第二章：一元二次方程
- 一元二次方程的定义和性质
- 一元二次方程的解法
- 一元二次方程的图象和根的关系
第三章：统计与概率
- 统计调查与数据分析
- 概率的基本概念与计算
第四章：平面图形
- 平面图形的分类与性质
- 平面图形的周长和面积计算- 平行线与平面图形的关系
第五章：三维图形
- 空间几何体的分类与性质- 空间几何体的体积计算
第六章：函数
- 函数的概念和性质
- 函数的表示与运算
- 解函数方程和不等式
第七章：线性方程组
- 线性方程组的概念和解法
- 线性方程组的应用
第八章：平均数
- 算术平均数的概念和计算
第九章：数列
- 等差数列的定义和计算
- 等差数列的通项公式和求和公式
以上是2023人教版八年级数学下册的重要知识点概述，希望对你的研究有所帮助。
总字数：{word_count}。
新人教版八年级数学下册复习资料(2023
年)汇总
新人教版八年级数学下册复资料完整版(2023年)汇总
本文档旨在为八年级学生提供2023年数学下册的复资料完整版汇总。
以下是各个章节的内容概述：
第一章：实数
本章主要介绍实数的概念和性质，包括有理数和无理数的认识以及实数的比较和运算方法。
第二章：代数式及其运算
该章节介绍代数式的概念，包括多项式和一元一次方程的运算方法和应用。
第三章：函数
此章节重点讲解函数的概念、性质以及函数与方程的关系。
第四章：图形的变换
本章主要介绍二维图形的平移、旋转和翻转变换，以及对应的图形性质和判定方法。
第五章：圆的性质和构造
该章节将深入讲解圆的性质和构造方法，包括圆的周长、面积计算，以及与圆相关的问题求解。
第六章：统计
此章节将介绍统计学的基本概念和应用，包括数据的收集和整理，以及统计图表的绘制和分析。
第七章：概率
本章主要介绍概率的基本概念和计算方法，包括事件的概率、概率的性质和概率实验的设计。
第八章：三角形
该章节将深入讲解三角形的性质和定理，包括三角形内角和外角的关系，以及三角形的面积计算方法。
第九章：相似
此章节将介绍相似的概念和判定方法，以及相似三角形的性质和应用。
第十章：二次根式
本章主要介绍二次根式的性质和运算方法，包括二次根式的化简、化简结果的判定和应用。
本文档收集了以上各章的重点知识点和相关题，旨在帮助同学们全面复数学下册内容，提高解题准确率和思维能力。
注意：本文档中的内容仅供参考，具体的教学和复习建议还请以教材为准。
人教版八下数学知识点归纳
人教版八年级下册数学知识点主要包括以下内容：
1.平面图形：
•多边形的性质、相似三角形、三角形的面积、平行四边形、梯形、圆的性质等。
2.立体图形：
•空间图形的性质、棱柱、棱锥、棱台、球体等。
3.运算与方程：
•整式的加减乘除、分式的加减乘除、一元一次方程、一元一次方程组、二次根式的化简等。
4.数学实践：
•统计图表、平均数、方差、分布律、样本调查等。
5.函数：
•函数的概念、函数的图像、函数的性质、一次函数、反比例函数、指数函数、二次函数等。
6.几何变换：
•平移、旋转、对称、放缩等几何变换的性质和应用。
7.统计与概率：
•简单事件的概率、概率的性质、互斥事件、独立事件、排列组合等。
8.解决问题：
•利用所学知识解决实际问题的能力培养。
以上是人教版八年级下册数学主要的知识点归纳，具体内容可能因不同的教材版本和教学要求有所不同。
如果需要更详细的内容，建议查阅对应的教材或教学大纲。
人教版八年级下册数学基础知识归纳
本文档旨在对人教版八年级下册数学基础知识进行归纳总结。
下面将以模块的形式介绍各个知识点。
1. 几何基本概念
- 点：没有长度、宽度和高度，只有位置的概念
- 直线：由无限多个点连成的线，没有弯曲
- 射线：一个端点和无限多个点组成的线段
- 线段：有两个端点的线，有固定长度
2. 图形与运算
- 平面图形：点、线、面构成的图形
- 三角形：有三条边的图形
- 四边形：有四条边的图形
- 圆：由一个点到另一个点的距离相等的所有点组成的图形
3. 相似与全等
- 相似：形状相同但大小不同的图形
- 全等：形状和大小都相同的图形
4. 等腰三角形和等边三角形
- 等腰三角形：有两条边相等的三角形
- 等腰直角三角形：有两边相等且其中一个角为直角的三角形- 等边三角形：三边都相等的三角形
5. 直角三角形和勾股定理
- 直角三角形：其中一个角为直角的三角形
- 勾股定理：c² = a² + b²，其中c为斜边，a和b为直角边
6. 海伦公式
- 海伦公式：S = √[p(p-a)(p-b)(p-c)]，其中S为三角形的面积，p为半周长，a、b、c为三边的长度。
7. 三角形面积的计算
- 高度定理：三角形的面积等于底边乘以高的一半：S = 1/2 ×底边 ×高
- 三角形面积公式：S = 1/2 × a × b × sinC，其中a、b为两边的长度，C为夹角的度数。
以上为人教版八年级下册数学基础知识的归纳总结。
希望对您的学习有所帮助！。
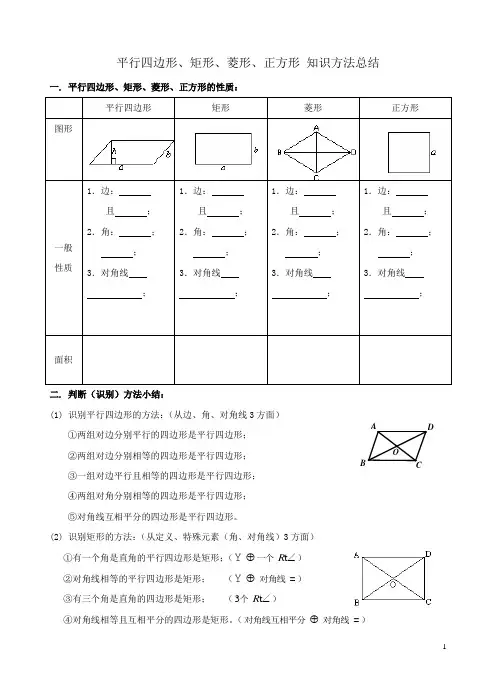
OA平行四边形、矩形、菱形、正方形 知识方法总结一. 平行四边形、矩形、菱形、正方形的性质：平行四边形矩形菱形正方形图形一般 性质1．边：且 ； 2．角： ；； 3．对角线 ；1．边：且 ； 2．角： ；； 3．对角线 ；1．边：且 ； 2．角： ； ； 3．对角线 ；1．边：且 ； 2．角： ；； 3．对角线 ；面积二. 判断（识别）方法小结：(1) 识别平行四边形的方法：（从边、角、对角线3方面）①两组对边分别平行的四边形是平行四边形； ②两组对边分别相等的四边形是平行四边形； ③一组对边平行且相等的四边形是平行四边形； ④两组对角分别相等的四边形是平行四边形； ⑤对角线互相平分的四边形是平行四边形。
(2) 识别矩形的方法：（从定义、特殊元素（角、对角线）3方面） ①有一个角是直角的平行四边形是矩形；（ t R ⊕∠Y 一个 ） ②对角线相等的平行四边形是矩形； （ ⊕Y 对角线 =） ③有三个角是直角的四边形是矩形； （3t R ∠个 ）④对角线相等且互相平分的四边形是矩形。
（ ⊕对角线互相平分对角线 =）(3) 识别菱形的方法：（从定义、特殊元素（边、对角线）3方面） ①有一组邻边相等的平行四边形是菱形； （ =⊕Y 一组邻边 ） ②对角线互相垂直的平行四边形是菱形； （ ⊕⊥Y 对角线 ） ③四边都相等的四边形是菱形； （4= 边）④对角线互相垂直平分的四边形是菱形。
（ ⊕⊥对角线互相平分对角线 ） (4) 识别正方形的方法：（从边、角、对角线3方面） 抓本质：矩形+菱形①有一组邻边相等且有一个角是直角的平行四边形是正方形；（ = Rt ∠⊕⊕Y 一组邻边一个 ） ②对角线互相垂直且相等的平行四边形是正方形； （ ⊕⊕⊥=Y 对角线 对角线） ③有一组邻边相等的矩形是正方形； （ =⊕ 矩形一组邻边 ） ④对角线互相垂直的矩形是正方形； （ ⊕⊥矩形对角线 ） ⑤有一个角是直角的菱形是正方形； （ Rt ∠⊕菱形一个 ） ⑥对角线相等的菱形是正方形； （⊕=菱形 对角线）⑦对角线互相垂直平分且相等的四边形是正方形。
八年级(人教版)平面几何知识点总结本文档将总结八年级(人教版)平面几何的知识点，帮助学生复和巩固所学内容。
1. 几何基础概念- 点：具有位置但无大小的几何对象。
- 线段：由两个点确定的线段。
- 直线：由多个点无限延伸而成的线。
- 射线：以一个点为起点，通过另一个点无限延伸而成的线。
- 角：由两条射线共享一个起点组成的图形。
- 三角形：具有三条边和三个内角的多边形。
2. 三角形的性质- 三角形内角和为180度。
- 等边三角形的三边相等，三个角均为60度。
- 等腰三角形的两边相等，两个角相等。
- 直角三角形的一个角为90度。
3. 四边形的性质- 矩形：四条边都相等的四边形，四个内角都为90度。
- 正方形：既是矩形又是菱形的四边形，四边相等，四个内角都为90度。
- 菱形：对边平行且边长相等的四边形，相邻两个角是对角的倾斜角的一半。
- 平行四边形：对边平行的四边形，对边分别相等，对角分别相等。
4. 圆的性质- 圆：平面上到一个固定点距离相等的所有点的集合。
- 圆心：固定点。
- 半径：连接圆心和圆上任意一点的线段。
- 圆的直径是半径的两倍。
- 圆的周长等于直径乘以π。
5. 相似形- 相似：两个图形的形状相似，但大小不同。
- 对应角相等：两个相似图形的对应角都相等。
- 对应边成比例：两个相似图形的对应边的比例相等。
6. 平行线与交叉线- 平行线：永远不会相交的两条直线。
- 交叉线：相交于同一点的两条直线。
- 同位角：两条平行线和交叉线之间的内角或外角。
以上是本文档的简要总结，涵盖了八年级平面几何的基础知识点。
希望对学生们的学习有所帮助！。
八年级下册几何知识点总结在初中阶段的数学学习中，几何作为其中一门重要的学科，涉及到了平面几何、立体几何、解析几何等方面。
本文将从几何的基础概念入手，列举八年级下册的重点知识点，供同学们复习参考。
一、基本概念1.点、线、面：几何学的三个最基本的概念。
2.平行线：在同一个平面内，两条直线没有交点，且在无限延伸的过程中仍然保持这种位置关系，我们可以称它们为平行线。
3.垂线：与一条直线相交，且互相成直角的直线为垂线。
4.角度：由两条射线、一个端点共同确定的平面角叫做角度。
5.相似图形：两个图形形状相同，但大小不一，我们称这两个图形为相似图形。
二、几何图形的性质1.三角形（1）直角三角形：有一个角为90度的三角形。
（2）等腰三角形：两边长度相等的三角形。
（3）等边三角形：三边长度均相等的三角形。
2.四边形（1）矩形：对角线相等，且每对对边平行的四边形。
（2）正方形：四边长度相等，并且每个角都是直角的四边形。
（3）菱形：对角线相等，且每个角都是锐角或钝角的四边形。
3.圆形（1）圆心角：以圆心为顶点的角。
（2）弧度：圆心角所对的弧长与圆的半径之比称为该圆心角的弧度。
（3）正弦、余弦、正切：利用三角函数求解圆的相关性质。
三、平面图形的计算1.三角形（1）勾股定理：直角三角形中，直角边的平方和等于斜边的平方。
（2）正弦定理：在任意一个三角形ABC中，角A的对边为a，角B的对边为b，角C的对边为c，则有a/sinA = b/sinB = c/sinC。
（3）余弦定理：在任意一个三角形ABC中，角A的对边为a，角B的对边为b，角C的对边为c，则有a² = b² + c² - 2bc*cosA。
2.四边形（1）矩形的面积公式：面积=长x宽。
（2）正方形的面积公式：面积=边长²。
（3）菱形的面积公式：面积=对角线之积的一半。
3.圆形（1）周长公式：圆的周长=2πr。
（2）面积公式：圆的面积=πr²。
新人教版数学八年级下册知识点汇总本文档汇总了新人教版数学八年级下册的知识点。
第一章函数与线性方程1. 函数的概念与性质2. 线性方程与函数3. 一次函数4. 函数图像与线性方程的解5. 函数关系与线性方程的解6. 函数的运算第二章四边形1. 任意四边形2. 平行四边形3. 矩形4. 正方形5. 菱形6. 梯形7. 三角形的面积第三章几何变换1. 平移与错切2. 原点对称与轴对称3. 尺规作图第四章图形的相似与尺寸1. 相似的概念与性质2. 相似三角形的判定3. 相似三角形与相似比例4. 对应边成比例与对应角相等第五章数据及其概率1. 数列的概念与表示2. 等差数列3. 概率的概念与计算第六章方程1. 方程的解2. 一元一次方程3. 一元一次方程的应用4. 两个变量的线性方程组5. 二次方程的概念与解法第七章平面直角坐标系中的图形1. 直角坐标系2. 线段的中点3. 相交线与平分线4. 解析几何中的实线和虚线5. 圆第八章有理数和实数1. 有理数2. 实数的简介第九章三角形1. 三角形的元素及其关系2. 三角形的相似判定3. 中线、垂线与高线4. 全等三角形及其判定5. 合同三角形的性质第十章配方法等式1. 用配方法解方程2. 一元二次方程第十一章平面图形的性质1. 线段的垂直平分线2. 过点作圆3. 正多边形4. 螺旋线第十二章多边形的面积1. 平行四边形的面积2. 三角形的面积3. 高度与四边形的面积第十三章浓度和密度1. 浓度与密度的计算第十四章投影与视图1. 平行投影2. 视图第十五章集合1. 集合的概念与表示2. 集合间的关系以上是数学八年级下册的知识点汇总。
请根据具体需求查阅相关章节，以帮助研究和复。
（此文档内容仅适用于新人教版数学八年级下册，不包含其他版本的内容）。
新人教版八年级数学(下册)第四单元知识
点总结
本单元主要内容为几何初步，以下为知识点总结：
1. 平行线及其性质
- 定义：在同一个平面内，若两条直线没有交点，则这两条直线互相平行。
- 判定方法：
- 充分条件一：同一直线上的两个锐角或两个钝角相等，则所在直线平行。
- 充分条件二：以直线为一边的内角和小于180度，则与这条直线不交的另一条直线与这条直线平行。
- 充分条件三：过点做平行于已知直线，所得直线与已知直线平行。
- 平行线性质：两个平行线夹角相等，平行线上的任意一条直线与另一平行线的交线上的对应角相等，同侧内角互补，异侧角互补。
2. 三角形
- 定义：由三条边和三个内角组成的图形叫做三角形。
- 分类：
- 按边分类：等边三角形、等腰三角形、一般三角形。
- 按角分类：锐角三角形、直角三角形、钝角三角形。
- 三角形性质：
- 半周角定理：三角形的一个角的度数等于所对的边的半周角度数。
即∠B=1/2∠ACB。
- 三角形内角和定理：三角形三个内角的度数和为180°。
- 三边关系定理：任意一边小于另外两边之和，任意一边大于另一边之差。
- 直角三角形定理：勾股定理和一般勾股定理。
- 三角形面积公式：S=1/2×a×b×sinC
以上为本单元主要知识点总结，应理解并掌握。
平面几何综合复习【典型例题】：例3、已知：如图在∆ABC 中，AB =AC 。
延长AB 到D ，使BD =AB ，取AB 的中点E ，连结CD 和CE 求证：CD =2CE分析：（1）要证长线段CD 是某小量的2倍，可在长线段上截取一半，这种方法，叫“截取法”或（折半法），要证CD =2CE ，可考虑在CD 上截取一半，再证明CE 等于CD 的一半即可。
证明： 过B 点作BF //AC 交CD 于F ， AB =BD∴=DF CF ,且BF AC =12AB AC ACB //,∴∠=∠2BF AC ACB //,,∴∠=∠∴∠=∠112又 BE AB BF AC BE BF ==∴=1212.,在∆∆CEB CFB 和中BE BF BC BC =∠=∠=⎧⎨⎪⎩⎪12 ∴≅∴==∆∆CEB CFB EC CF CD ,12即CE =2EC分析：（2）这类题目还可以将短线延长，或说加倍法，证它等于长线段的方法，也称“拼加法”。
提示： 将CE 延长到G ，使EG =CE ， 连结AG ，BG ，可证明∆ACG ≅∆BDC ，从而得到CG =CD ，因而有CD =2CE 。
例4、已知：如图，在∆ABC 中，D 、E 分别在AB 、AC 上，BD=CE ，BE 、CD 的中点分别是M ，N ，直线MN 分别交AB ，AC 于点P 、Q求证：AP=AQ分析：这是一道已知中点求证线段相等的问题，往往可以通过中位线，将条件、结论分别转移到可以建立直接联系的图形上，此题要证AP =AQ ，就要证∠=∠APQ AQP M N ， ,分别是BE 、CD 中点，且BD =CE ，又BC 是∆BDC 和∆BCE 的公共边，∴取BC 的中点F ，再连MF 、NF ，就可以通过三角形中位线定理将已知条件以及要证明的∠=∠APQ AQP 等量代换到∆FMN 中，从而可证得AP =AQ 。
证明： 取BC 的中点F ，连结FM ，FN ∵M ，N 分别是 BE CD ,的中点∴==FM CE FN BD 1212，并且MF //CE ，FN //BD ，∵CE =BD ，∴FM =FN∴∠FMQ =∠FNP∠FMQ=∠AQM （两直线平行，内错角相等） ∴∠FNP =∠APN ，∴∠APN =∠AQM ∴AP =AQ例5、已知：∆ ABC 中，AB =AC ，D 是AB 上一点，E 是AC 延长线上一点，BD =CE ，DE 交BC 于F 求证：DE =EF分析：DF 和EF 分别在∆DBF 和∆ECF 中，但这两个三角形并不全等，如何构造全等形呢？只需作DG //AC 交BC 于G 点，易证∆DGF ≅∆ECF ，所以DF =EF ，这种添加辅助线的方法属于中心对称型。
例6、已知Rt ∆ACB 中，∠ACB =90︒，CD ⊥AB ，BE 平分 ∠ABC ，交CD 于E ，EF //AB 交AC 于F 求证：CE =AF分析：要证线段CE =AF ，我们可以将它们转化到两个三角形中，过E 点作EG ⊥BC 于G ，所以EG =DE ，这种填加辅助线的方法属于转对称型，再作FH ⊥AB 于H ，利用平行线间距离相等，可易证得∆HAF ≅∆GCE ，从而证得CE =AF ，另解还可以过E 点作KM //AC 交AB 于K ，交BC 于M ，证∆MCE ≅∆DKE 即可例7、已知：∆ABC 中，∠ACB =90︒，AD 为BC 边上的中线，E 为AD 的中点，CE 的延长线交AB 于F ，FG /AC 交AD 于G 求证：FB =2CG分析：要证FB =2CG ，只要证CG =12BF ，由于CG 和BF 分别在两个三角形中没有直接的关系，所以寻求另解一条线段作为中介量，建立起CG 和FB 之间的联系，分析题目条件可知∆CEG ≅∆AEF ，所以AF =CG ，只要证AF =12FB 即可证明： 作DH //CF 交AB 于H ，Rt ∆ADC 中，ACD =90︒， E 是斜边AD 中点，∴CE =AE ，∴∠1=∠2 ∵AC //FG ，∴∠1=∠3，∠2=∠4，∴∠3=∠4 ∴EG =EF 在∆AEF 中和∆CEG 中，有 CE AEEG EF ==∠=∠⎧⎨⎪⎩⎪56∴∆AEF ≅∆ CEG 中，∴AF =CGDH //CF ，E 为AD 中点，∴AF =FHDH //CF ，D 为BC 中点，∴FH =HB∴AF =FH =HB ，∴AF=12FBCG =AF ，∴CG =12FB ，即FB =2CG例8、设∆ABC 是等腰直角三角形，AB =AC ，D 是斜边BC 的中点，E ，F 分别是AB 、AC 边上的点，且DE ⊥DF ，若BE =12，CF =5，求：线段EF 的长？分析：这是一道几何中的计算题要求EF 的长，首先发现它在Rt 它在Rt ∆EAF 中，这时利用勾股定理可求出，连结AD 后可证∆ADE ≅∆CDF 解； 连结AD ，则在∆ADE 和∆CDF 中， ∠+∠=︒∠+∠=︒∴∠=∠∠=∠=︒ADE ADF CDF ADF ADE CDF DAE DCF 909045，，又AD =CD ，∴≅∴==∆∆ADE CDF AE CF 5又AF +FC =AC =AB =AE +BE =5+12=17∴=-=-==+=AF AC FC EAF EF AE AF 175121322在中Rt ∆,即EF 的长为13例9、已知：如图，过正方形ABCD 的顶点A 作直线交BD 于E ，交CD 于F ，交BC 的延长线于G ，若H 是FG 的中点 求证：EC ⊥CH分析：这道题主要是利用正方形的性质，证明两条线段互相垂直，只要能证明∠ECH 是90︒即可，此题可先间接证出∠4+∠5=90︒，从而推出∠ECH =90︒，通过∆∠ABE ≅∆CBE ，及Rt ∆FCG 的斜边中线CH 可证得证明： 简述：在正方形ABCD 中，∠=∠=︒1245 ∵AB =BC ，BE =BE ∴∆ABE ≅∆CBE ∴∠3=∠4，又H 是Rt FCG 斜边上的中点∴=∴∠=∠∴∠+∠=∠+∠=︒∴⊥CH HG GG EC CH534690 例10、已知：如图在平行四边形ABCD 中，AE =CF ，BM =DN 求证：四边形EMFN 是平行四边形分析：本题主要是考查平行四边形的判定方法，下面简述两种证法。
证法一： ABCD 是平行四边形 ∴AD //BC ，AD =BC∴∠=∠==12,, AE FC DN BM ∴ DE =BF ,DM =BN ∴≅∆∆DEM BFN∠=∠=34,MB NF ∴ME //NF∴EMFN 是平行四边形证法二： 证∴≅∆∆DEM BFN （同证法一） ∴ME =NF 同理可证 ∆∆DEN BFM ≅ ∴EN =FM ∴EMFN 是平行四边形。
例11、如图：等腰梯形ABCD 中，AD //BC ，对角线AC 和BD 相交于E ，已知，∠ABD =60︒，BD =12，且BE ∶ED =5∶1，S 梯形ABCD=363，求这个梯形的周长？分析：由BD =12，且BE ∶ED =5∶1，可得BE =10，ED =2，易证，∆∆ABD DCA ≅故∠=∠=︒∴∠=︒ADB DAC AED AED 6060,,∆为等边三角，AD =DE =2，同理BC =10，作AF ⊥BC 于F ，DG ⊥BC 于G ，则四边形AFGD 是矩形，由梯形面积公式可求出AF DG BF GC ===63,而()=-12BC AD =()121024-=，再由勾股定理求出AB =CD =231 故梯形周长为12+431 解：BD BE ED BE DE ==∴==1251102,,,;且∶∶ 梯形ABCD 为等腰梯形，∴==AB CD AC BD ,AD =AD∴≅∴∠=∠=︒∆∆ABD DCA DAC ADB ,60∴∠=︒∴AED AED 60,∆为等边三角形 ∴==AD DE 2 同理可求： BC =10 作AF ⊥BC 于F ，DG ⊥BC 于G ， 则四边形AFGD 为矩形∴===∠=∠FG AD AB AC ABC DCB 2,, ∠=∠=︒AFB DGC 90 ∴≅∆∆ABF DCG()()∴==-=-=BF GC BC FG 12121024 S ABCD梯形=363()()∴+⨯=+⨯=1236312102363BC AD AF AF ,即 ∴AF ABF =63，中Rt ∆()AB AF BF =+=+==2222634124231同理：DC =231∴梯形周长=AD +BC +AB +CD =2+10+231+231=12+431 此题综合性较强，涉及到的知识点很多，但证明的关键是证出∆ABC 是等边三角形，从而求出上、下两底的长度，并且要正确添加辅助线。
【综合练习】： 一、填空题：（1）∆ABC 中，AB =AC ，DE 是AB 的中垂线，∆BCE 的周长为14厘米，BC =5厘米，那么AB 的长为 厘米。
（2）若∆ABC 的三个外角的度数之比为3∶4∶5，则最大边AB 与最小边BC 关系是 ；而三条边之间的关系是 ；（3）等腰三角形的周长为23+，腰长为1，则底角等 度。
（4）如图在Rt ∆ABC 中，∠=︒C 90 BD 平分∠ABC 交AC 于D ，DE 是斜边AB 的垂直平分线，且DE =1厘米，则AC = 厘米。
（5）把长为8cm 的长方形纸片对折，按图中的虚线剪出一个梯形并打开，则找开后的梯形中位线长为 cm 。
（6）若等腰三角形的底角为15︒，腰长为2，则腰上的高为 。
（7）若等腰梯形的周长80cm ，中位线与腰长相等，则它的中位线等于 cm 。
（8）已知平行四边形ABCD 的对角线AC 和BD 相交于点O ，如果∆AOB 的面积是3，那么平行四边形ABCD 的面积是 。
（9）已知菱形的两条对角线的长分别是6和8，那么它的边长是 。
（10）菱形中有一个内角是60︒，菱形的边长为6，则菱形两条对角线的长为 。
三、选择题：（1）如果等边三角形的边长为3，那么连结各边中点所成的三角形的周长为（ ）A ．9B ．6C ．3D ．92（2）在∆ABC 中，已知b =4，c =5, A =30︒,则∆ABC 的面积是（ ）A ．10B ．103C ．5D ．53（3）如果一个多边形的内角和等于720︒，那么这个多边形是（ ） A ．四边形 B ．五边形 C ．六边形 D ．七边形（4）下列多边形中，是轴对称图形，但不是中心对称图形的是（ ） A ．平行四边形 B ．正方形 C ．等边三角形 D ．直角梯形（5）已知：平行四边形ABCD 的周长为24，AB ∶AD =1∶2，那么AB 的长是（ ） A ．4B ．6C ．8D ．16（6）设F 为正方形ABCD 的边AC 上一点，CE ⊥CF 交AB 的延长线于E ，若正方形ABCD 的面积为64，∆ CEF 面积为50，则∆CBE 的面积为（ ） A ．20 B ．24 C ．25 D ．26（7）在 ∆ABC 中，若∠=︒A 60，AB =23, AC =3，则S ∆ABCD =（ ）A ．9B ．92C ． 33D ．332（8）如图在四边形ABCD 中，AD =BC ，E 、F 、G 分别是AB 、CD 、AC 的中点，若∠DAC =20︒，∠ACB =66︒，∠则FEG =（ ） A ．47︒ B ．46︒ C ． 41︒ D ．23︒（9）已知一个等腰梯形的高是2m ，它的中位线长是5m,一个底角为45︒，这个梯形的周长是（ ） A ．14B ．()522+cmC ．()1022+mD ．()1042+m（10）已知正方形的面积为8cm 2,则正方形的对角线长为（ ） A ．22cm B ．42cmC ．4cmD ．2cm【答案】：一、 （1）9 （2）AB =2BC ，132∶∶ （3）30︒ （4）3 （5）5（6）1（7）20 （8）12 （9）5 （10）6，63二、 （1）D （2）C （3）C （4）C （5）A （6）B （7）B （8）D （9）D （10）C【综合练习二】： 证明与计算： 1、已知：等腰三角形ABC 的顶角A 为120︒，底边长为20cm ，求：腰长2、已知；如图，∆ABC 中，AB =AC ，D ，E ，F 分别为AB 、BC 、CA 上的点，且BD =CE ， ∠=∠DEF B ,求证：∆DEF 是等腰三角形3、已知：如图，四边形ABCD 为矩形四边形ABDE 为等腰梯形，AE //BD ， 求证：∆∆BED BCD ≅4、如图：平行四边形ABCD 中，BE ⊥CD ，BF ⊥AD ，垂足分别为E 、F ，CE =2，DF =1，∠=︒EBF 60，求平行四边形ABCD 的面积。
