有关BJH孔径分布计算模型

bjh孔径分布曲线
孔径分布曲线是用来描述一组孔径数据的分布情况的统计图形。

在材料科学、粉末冶金、颗粒物理等领域中经常会涉及到对孔径进行分析和研究。

常见的孔径分布曲线有以下几种：
1. 频率分布曲线：频率分布曲线是将不同孔径范围的孔径数量与孔径范围进行对应，以展示各个孔径范围内孔径的分布情况。

可以使用直方图或者柱状图表示。

2. 累积分布曲线：累积分布曲线是将孔径按照从小到大的顺序排列，并绘制出其累积百分比随孔径变化的曲线。

通常使用曲线图表示。

3. 概率密度分布曲线：概率密度分布曲线是通过对孔径数据进行统计分析，得到孔径的概率密度函数，并将其画成曲线。

常见的概率密度分布曲线有正态分布曲线、韦伯分布曲线等。

4. 等效直径分布曲线：等效直径分布曲线是将不同孔径的颗粒按照其等效直径进行分类，并记录各个等效直径范围内的颗粒数量。

可以使用直方图或柱状图表示。

这些孔径分布曲线可以帮助我们了解材料中孔径的分布情况，从而有助于进一步分析和研究材料的性质和特点。

关于氮气等温吸脱附计算比表面积、孔径分布的若干说明目的：是让大家对氮气等温吸脱附有一个基本的理解和概念，不会讲太多源头理论，内容不多，力求简明实用。

本人有幸接触吸脱附知识的理论和实践，做个总结一是长久以来的心愿，二则更希望能和大家共同学习、探讨和提高。

由于内容是自己的总结和认识，很可能会有部分错误，希望大家能给予建议、批评和指导，好对内容做进一步的完善。

我们拿到的数据，只有吸脱附曲线是真实的，比表面积、孔径分布、孔容之类的都是带有主观人为色彩的数据。

经常听到有同学说去做个BET，其实做的不是BET，是氮气等温吸脱附曲线，BET （Brunauer-Emmet-Teller）只是对N2-Sorption isotherm中p/p0=0.05~0.35之间的一小段用传说中的BET公式处理了一下，得到单层吸附量数据Vm，然后据此算出比表面积，如此而已。

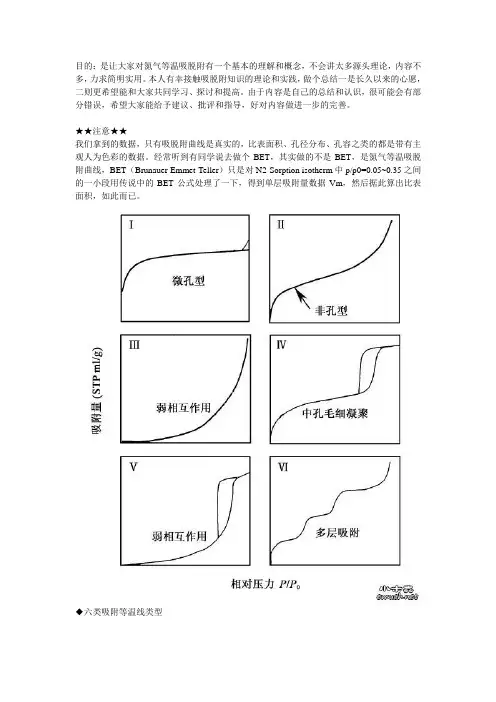
◆六类吸附等温线类型screen.width*0.7) {this.resized=true; this.width=screen.width*0.7; this.alt='Click here to open new window';}" border=0>几乎每本类似参考书都会提到，前五种是BDDT(Brunauer-Deming-Deming-Teller)分类，先由此四人将大量等温线归为五类，阶梯状的第六类为Sing增加。

每一种类型都会有一套说法，其实可以这么理解，以相对压力为X轴，氮气吸附量为Y轴，再将X 轴相对压力粗略地分为低压（0.0-0.1）、中压(0.3-0.8)、高压（0.90-1.0）三段。

那么吸附曲线在：低压端偏Y轴则说明材料与氮有较强作用力(?型，??型，Ⅳ型)，较多微孔存在时由于微孔内强吸附势，吸附曲线起始时呈?型；低压端偏X 轴说明与材料作用力弱(???型，Ⅴ型)。

中压端多为氮气在材料孔道内的冷凝积聚，介孔分析就来源于这段数据，包括样品粒子堆积产生的孔，有序或梯度的介孔范围内孔道。

bjh吸附平均孔径吸附平均孔径（Bjh Average Pore Diameter）是反映吸附材料孔隙结构特征的一个重要参数。

它指的是吸附材料在一定条件下，吸附剂分子在孔隙内的平均自由路径长度。

吸附平均孔径的大小直接决定了吸附材料对分子的吸附能力和选择性。

吸附平均孔径的计算通常基于BJH（Barret-Joyner-Halenda）理论模型。

该理论是由Barrett等人在1951年提出的，被广泛应用于多孔材料的孔隙结构表征。

根据BJH理论，通过测量吸附物在吸附剂表面的浸润度，绘制等温线，然后对吸附等温线进行分析，可以得到吸附材料的孔隙分布曲线。

吸附平均孔径的大小与吸附材料的储存能力、传质性能和反应速率密切相关。

较大的吸附平均孔径表明吸附材料具有较大的孔隙空间，有利于分子的扩散和传质，同时也可以提高反应速率。

而较小的吸附平均孔径则可以增加吸附材料与分子之间的接触面积，提高吸附能力和选择性。

为了准确测量吸附平均孔径，常见的方法包括氮气吸附法（BET 法）、水蒸汽吸附法（DFT法）和压汞法等。

其中，氮气吸附法是最常用的方法之一。

通过测量氮气在吸附表面和孔隙内的吸附量，利用BJH 理论模型进行计算，可以得到吸附平均孔径和吸附材料的孔隙分布。

吸附平均孔径的研究在很多领域都具有重要意义。

在环境科学中，研究吸附材料的孔隙结构和吸附平均孔径有助于理解吸附过程和提高废水处理效率。

在石油工业中，对吸附剂的孔隙结构和吸附平均孔径的研究可以优化催化剂的性能，提高油品的裂化效率。

在材料科学中，研究吸附材料的孔隙结构和吸附平均孔径可以指导新材料的设计和合成，提高吸附材料的性能。

总之，吸附平均孔径作为吸附材料的重要参数，在吸附过程和材料研究中具有重要的指导意义。

通过了解和控制吸附平均孔径的大小，可以提高吸附材料的吸附能力和选择性，优化反应过程，提高催化效率和材料的性能。

因此，深入研究吸附平均孔径的测量方法和孔隙结构分析对于促进吸附材料的应用和开发具有重要意义。

bjh法孔径分布
BJH法（Barrett-Joyner-Halenda）是一种常用的多孔介质孔径分布分析方法。

该方法通过对多孔介质中各孔的渗流性质进行测定，推算出孔径的分布情况。

BJH法的基本原理是，多孔介质在一定的温度和压力条件下，孔径大于一定大小的孔隙只能通过压力差来流动。

因此，可以通过测量不同压力下的孔隙流量来推算出孔隙的大小分布。

BJH法的具体步骤如下：
1. 将样品经过表面积测定和骨架密度测定后，进行真空处理，以去除内外部的吸附水和气体。

2. 用低温液氮对试样进行提取，使孔隙内的液体迅速蒸发，形成干燥状态的样品。

3. 将样品放入装有压力计的孔隙容器中，在各个压力下测量孔隙的渗流性质。

4. 根据试验结果，通过对孔隙渗流性质与孔径大小的关系进行分析，得出孔径分布曲线。

通过BJH法可以得到多孔介质的孔径分布信息，包括孔隙体积、孔隙直径、孔隙形状等。

这些信息对于了解多孔材料的渗透性、吸附性能和传质性能等具有重要意义。

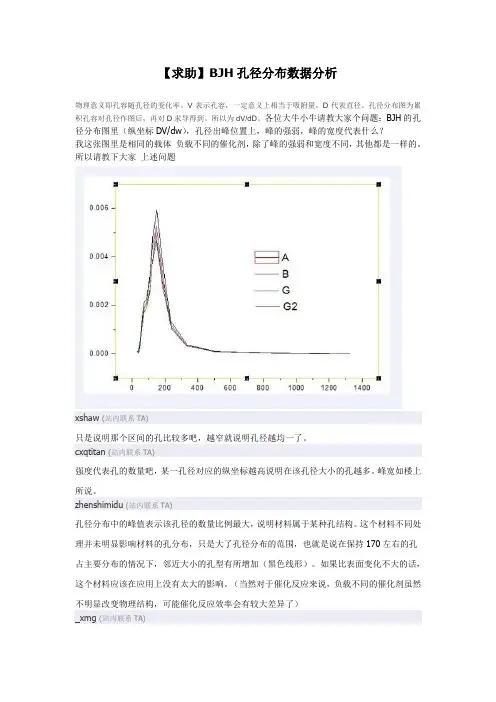
【求助】BJH孔径分布数据分析物理意义即孔容随孔径的变化率。

V表示孔容，一定意义上相当于吸附量，D代表直径。

孔径分布图为累积孔容对孔径作图后，再对D求导得到。

所以为dV/dD。

各位大牛小牛请教大家个问题：BJH的孔径分布图里（纵坐标DV/dw），孔径出峰位置上，峰的强弱，峰的宽度代表什么？我这张图里是相同的载体负载不同的催化剂，除了峰的强弱和宽度不同，其他都是一样的。

所以请教下大家上述问题xshaw(站内联系TA)只是说明那个区间的孔比较多吧，越窄就说明孔径越均一了。

cxqtitan(站内联系TA)强度代表孔的数量吧，某一孔径对应的纵坐标越高说明在该孔径大小的孔越多。

峰宽如楼上所说。

zhenshimidu(站内联系TA)孔径分布中的峰值表示该孔径的数量比例最大，说明材料属于某种孔结构。

这个材料不同处理并未明显影响材料的孔分布，只是大了孔径分布的范围，也就是说在保持170左右的孔占主要分布的情况下，邻近大小的孔型有所增加（黑色线形）。

如果比表面变化不大的话，这个材料应该在应用上没有太大的影响。

（当然对于催化反应来说，负载不同的催化剂虽然不明显改变物理结构，可能催化反应效率会有较大差异了）_xmg(站内联系TA)峰高代表孔的数量的多少，峰宽代表孔的粒径的均一程度:hand::hand:yanqing0122(站内联系TA)表示孔径的分布情况，可以计算出孔径的平均值和孔径的大小dong314(站内联系TA)你的实验做得很好。

负载之后峰位置没有变化，说明没有堵住孔，负载之后继续是很好的介孔材料，峰高低说明负载的多少，负载的强度不同，缝宽的问题，所有的峰都有一定的宽度，除非质谱是一条垂线，你这个宽度算是很窄的了。

光电帝国(站内联系TA)均一程度，越窄越均一。

出现几个孔容是由于机器根据不同的方法算出的孔容，比如BET法和BJH法，这个你可以根据自己需要选择，我们一般用BJH的 dV/dD是BJH数据里有的，应该是给你的，应该是用BJH数据里的第1组和第4组数据作出孔径分布图【求助】BJH孔径分布数据分析作者: 风轻云淡278(站内联系TA)发布: 2010-03-27做了BET，拷回来的数据很奇怪，做不了文献里那样的孔径分布图（Pore Volume(cm³/g.nm) 对pore diameter(nm) ）,刚才看了下，这里似乎缺了一组数据，dV/dD，单位是(cm³/g.nm)请问根据现有数据，如何计算得到呢？我用Incremental Pore Volume除以pore diameter，作图，好像与给的图不一样。

98Univ. Chem. 2020, 35 (2), 98−106收稿：2019-06-11；录用：2019-10-08；网络发表：2019-10-24 *通讯作者，Email: ceszjh@•师生笔谈• doi: 10.3866/PKU.DXHX201906022对BJH 方法计算孔径分布过程的解读张伟庆，黄滨，余小岚，张建辉*中山大学化学学院， 广州 510275摘要：介绍了用BJH 方法计算介孔孔径分布时对孔隙做了哪些几何假设和忽略、为简化计算做了哪些算术近似，以及各个参数的推导过程、孔径分布计算步骤和要点；还介绍了在目前仪器水平下BJH 方法的适用范围, 如何对数据进一步整理以便得到所需要的分析测试报告。

文章为后续调整测试参数、改进测试方法也有一定的参考作用，还讨论了在阅读实验报告时经常遇到的一些问题。

关键词：介孔；孔径分布；Kelvin 方程中图分类号：G64；O6Interpretation of BJH Method for Calculating Aperture Distribution ProcessWeiqing Zhang, Bin Huang, Xiaolan Yu, Jianhui Zhang *School of Chemistry, Sun Yat-Sen University, Guangzhou 510275, P. R. China.Abstract: This paper introduces the geometric assumptions and neglects of the pore size distribution calculated by BJH method, the arithmetic approximation for simplified calculation, the derivation process of each parameter, the calculation steps and key points of the pore size distribution. This paper also introduces the application scope of BJH method at the current instrument level, and how to further integrate the data. In order to get the required analysis and test report, references are provided for the subsequent adjustment of test parameters and improvement of test methods. Some problems often encountered in reading experimental reports are also discussed.Key Words: Mesoporous; Distribution of pore size; Kelvin equation现在大多数分析仪器的测试都采用计算机控制、采集信息及用配套软件处理数据，这为分析和测试提供了很大方便，不过，这同时也带来一些风险，如若不考虑样品及测试的具体情况、贸然用软件默认的模板生成的测试报告其可信度就要特别注意。

孔径分布的若干说明zz fromemuch我们拿到的数据，只有吸脱附曲线是真实的，比表面积、孔径分布、孔容之类的都是带有主观人为色彩的数据。

经常听到有同学说去做个BET，其实做的不是BET，是氮气等温吸脱附曲线，BET(Brunauer-Emmet-Teller)只是对N2-Sorptionisotherm中p/p0=0.05~0.35之间的一小段用传说中的BET公式处理了一下，得到单层吸附量数据Vm，然后据此算出比表面积，如此而已。

◆六类吸附等温线类型screen.width*0.7){this.resized=true;this.width=screen.width*0.7;t his.alt='Clickheretoopennewwindow';}"border=0几乎每本类似参考书都会提到，前五种是BDDT(Brunauer-Deming-Deming-Teller)分类，先由此四人将大量等温线归为五类，阶梯状的第六类为Sing增加。

每一种类型都会有一套说法，其实可以这么理解，以相对压力为X轴，氮气吸附量为Y轴，再将X轴相对压力粗略地分为低压(0.0-0.1)、中压(0.3-0.8)、高压(0.90-1.0)三段。

那么吸附曲线在:低压端偏Y轴则说明材料与氮有较强作用力(型，型，Ⅳ型)，较多微孔存在时由于微孔内强吸附势，吸附曲线起始时呈型;低压端偏X轴说明与材料作用力弱(型，Ⅴ型)。

中压端多为氮气在材料孔道内的冷凝积聚，介孔分析就来源于这段数据，包括样品粒子堆积产生的孔，有序或梯度的介孔范围内孔道。

BJH方法就是基于这一段得出的孔径数据;高压段可粗略地看出粒子堆积程度，如型中如最后上扬，则粒子未必均匀。

平常得到的总孔容通常是取相对压力为0.99左右时氮气吸附量的冷凝值。

◆几个常数※液氮温度77K时液氮六方密堆积氮分子横截面积0.162平方纳米，形成单分子层铺展时认为单分子层厚度为0.354nm※标况(STP)下1mL氮气凝聚后(假定凝聚密度不变)体积为0.001547mL例:如下面吸脱附图中吸附曲线p/p0最大时氮气吸附量约为400mL，则可知总孔容=400*0.001547=400/654=约0.61mL※STP每mL氮气分子铺成单分子层占用面积4.354平方米例:BET方法得到的比表面积则是S/(平方米每克)=4.354*Vm，其中Vm由BET方法处理可知Vm=1/(斜率+截距)◆以SBA-15分子筛的吸附等温线为例加以说明screen.width*0.7){this.resized=true;this.width=screen.width*0.7;t his.alt='Clickheretoopennewwindow';}"border=0此等温线属IUPAC分类中的IV型，H1滞后环。

BJH标准是指Barrett-Joyner-Halenda（BJH）方法，这是一种用于测定介孔固体孔径分布的标准方法。

该方法基于氮气吸附法，通过测量吸附和解吸曲线来确定孔径分布。

BJH标准的具体原理是，在液氮温度下，氮气在介孔固体中吸附和解吸，根据吸附和解吸曲线可以计算出孔径分布。

吸附曲线显示了不同压力下氮气的吸附量，而解吸曲线显示了不同压力下氮气的解吸量。

通过这些曲线，可以推断出孔径分布。

BJH标准通常被用于研究和开发多孔材料，如催化剂、吸附剂和分离剂等。

该标准提供了一种通用的方法来比较不同材料之间的孔径分布，从而有助于评估材料的性能和优化其应用。

需要注意的是，BJH标准是一种实验方法，其结果受到实验条件和样品质量的影响。

因此，在使用BJH标准时，需要遵循标准的操作规程，并注意实验条件的控制和样品的处理。

目的：是让大家对氮气等温吸脱附有一个基本的理解和概念，不会讲太多源头理论，内容不多，力求简明实用。

本人有幸接触吸脱附知识的理论和实践，做个总结一是长久以来的心愿，二则更希望能和大家共同学习、探讨和提高。

由于内容是自己的总结和认识，很可能会有部分错误，希望大家能给予建议、批评和指导，好对内容做进一步的完善。

★★注意★★我们拿到的数据，只有吸脱附曲线是真实的，比表面积、孔径分布、孔容之类的都是带有主观人为色彩的数据。

经常听到有同学说去做个BET，其实做的不是BET，是氮气等温吸脱附曲线，BET（Brunauer-Emmet-Teller）只是对N2-Sorption isotherm中p/p0=0.05~0.35之间的一小段用传说中的BET公式处理了一下，得到单层吸附量数据Vm，然后据此算出比表面积，如此而已。

◆六类吸附等温线类型几乎每本类似参考书都会提到，前五种是BDDT(Brunauer-Deming-Deming-Teller)分类，先由此四人将大量等温线归为五类，阶梯状的第六类为Sing增加。

每一种类型都会有一套说法，其实可以这么理解，以相对压力为X轴，氮气吸附量为Y轴，再将X轴相对压力粗略地分为低压（0.0-0.1）、中压(0.3-0.8)、高压（0.90-1.0）三段。

那么吸附曲线在：低压端偏Y轴则说明材料与氮有较强作用力(І型，ІІ型，Ⅳ型)，较多微孔存在时由于微孔内强吸附势，吸附曲线起始时呈І型；低压端偏X轴说明与材料作用力弱(ІІІ型，Ⅴ型)。

中压端多为氮气在材料孔道内的冷凝积聚，介孔分析就来源于这段数据，包括样品粒子堆积产生的孔，有序或梯度的介孔范围内孔道。

BJH方法就是基于这一段得出的孔径数据；高压段可粗略地看出粒子堆积程度，如І型中如最后上扬，则粒子未必均匀。

平常得到的总孔容通常是取相对压力为0.99左右时氮气吸附量的冷凝值。

◆几个常数※液氮温度77K时液氮六方密堆积氮分子横截面积0.162平方纳米，形成单分子层铺展时认为单分子层厚度为0.354nm※标况（STP）下1mL氮气凝聚后（假定凝聚密度不变）体积为0.001547mL例：如下面吸脱附图中吸附曲线p/p0最大时氮气吸附量约为400 mL，则可知总孔容＝400*0.001547＝400/654＝约0.61mL※STP每mL氮气分子铺成单分子层占用面积4.354平方米例：BET方法得到的比表面积则是S/(平方米每克)＝4.354*Vm，其中Vm由BET方法处理可知Vm=1/(斜率＋截距)◆以SBA-15分子筛的吸附等温线为例加以说明此等温线属IUPAC 分类中的IV型，H1滞后环。

bjh吸附平均孔径
BJH吸附平均孔径是一种测量孔隙大小的方法，通常用于表征多孔材料的孔隙分布。

BJH是Barrer, Joyner和Halenda的缩写，他们是该方法的提出者。

BJH吸附平均孔径是通过吸附-脱附等温线数据计算得出的。

在实验中，样品会暴露在特定压力下的压力下，通过记录吸附和脱附吸附剂量，得到等温线数据。

然后，根据BJH方法的
计算公式，可以得到孔径分布曲线和孔径分布数据。

BJH方法假设样品中的孔隙为圆柱形，并且具有一定的孔径大小范围。

它基于孔隙大小与吸附剂量之间的关系，从而推导出孔径分布。

BJH吸附平均孔径是通过求解上述方程得出的结果，它代表了样品中孔隙大小的平均值。

这个平均孔径可以作为评估多孔材料孔隙大小和分布的重要指标之一。

总之，BJH吸附平均孔径是通过BJH方法计算得出的多孔材
料的孔径分布中的平均值。

它在研究和评估多孔材料的孔隙性质和催化性能方面具有重要的应用价值。