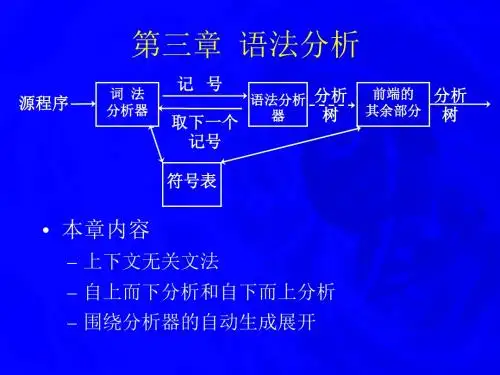
编译原理-语法分析器

编译原理实验实验二语法分析器实验二：语法分析实验一、实验目的根据给出的文法编制LR（1）分析程序，以便对任意输入的符号串进行分析。

本次实验的目的主要是加深对LR（1）分析法的理解。

二、实验预习提示1、LR（1）分析法的功能LR（1）分析法的功能是利用LR（1）分析表，对输入符号串自下而上的分析过程。

2、LR（1）分析表的构造及分析过程。

三、实验内容对已给语言文法，构造LR(1)分析表，编制语法分析程序，要求将错误信息输出到语法错误文件中，并输出分析句子的过程（显示栈的内容）；实验报告必须包括设计的思路，以及测试报告（输入测试例子，输出结果）。

语法分析器一、功能描述：语法分析器，顾名思义是用来分析语法的。

程序对给定源代码先进行词法分析，再根据给定文法，判断正确性。

此次所写程序是以词法分析器为基础编写的，由于代码量的关系，我们只考虑以下输入为合法：数字自定义变量+ * （）$作为句尾结束符。

其它符号都判定为非法。

二、程序结构描述：词法分析器：class wordtree；类，内容为字典树的创建，插入和搜索。

char gettype(char ch)：类型处理代入字串首字母ch，分析字串类型后完整读入字串，输出分析结果。

因读取过程会多读入一个字母，所以函数返回该字母进行下一次分析。

bool isnumber(char str[])：判断是否数字代入完整“数字串”str,判断是否合法数字，若为真返回1，否则返回0。

bool isoperator(char str[])：判断是否关键字代入完整“关键字串”str,搜索字典树判断是否存在，若为存在返回1，否则返回0。

语法分析器：int action(int a,char b)：代入当前状态和待插入字符，查找转移状态或归约。

node2 go(int a)：代入当前状态，返回归约结果和长度。

void printstack()：打印栈。

int push(char b)：将符号b插入栈中，并进行归约。

青岛理工大学课程实验报告
（2）.递归下降分析程序示意图（左）语法串分析程序示意图（右）
（4）statement 语法分析程序流程图（左）expression表达式分析函数示意图（右）
（3）term分析函数示意图（左）factor分析过程示意图（右）
调试过程及实验1.测试一
输入begin x:=9; x:=2*3; b:=a+x;end ;# 后经语法分析输出如图所示：
结
果
2.测试二
输入x:=a+b*c end # 后经语法分析输出如图所示：
3.测试三
输入 begin q:=6; d：=4； end #,经语法分析输出如图所示：
4.测试四
输入 begin a:=4;b:=5;c:=a*b+a #,经语法分析输出如图所示：
总结
通过本次试验，我们设计出了一个比较符合要求的语法分析器，同时了解了语法分析的过程，其主程序大致流程为：“置初值”→调用wordScanAnalyse函数读下一个单词符号→调用IrParse→结束。

分析程序的各个判断条件可以知道，需要调用函数factor();expression();yucu();term();statement();lrparser();其中嵌套了条件语句
使得拥有较为全面的处理机制，当程序不以“begin”开头，或不以“end #”。

《编译原理词法分析器语法分析课程设计-《编译原理》课程设计院系信息科学与技术学院专业软件工程年级级学号 2723姓名林苾湲西南交通大学信息科学与技术学院12月目录课程设计1 词法分析器 (2)设计题目 (2)设计内容 (2)设计目的 (2)设计环境 (2)需求分析 (2)概要设计 (2)详细设计 (4)编程调试 (5)测试 (11)结束语 (13)课程设计2 赋值语句的解释程序设计 (14)设计题目 (14)设计内容 (14)设计目的 (14)设计环境 (14)需求分析 (15)概要设计 (16)详细设计 (16)编程调试 (24)测试 (24)结束语 (25)课程设计一词法分析器设计一、设计题目手工设计c语言的词法分析器（能够是c语言的子集）。

二、设计内容处理c语言源程序，过滤掉无用符号，判断源程序中单词的合法性，并分解出正确的单词，以二元组形式存放在文件中。

三、设计目的了解高级语言单词的分类，了解状态图以及如何表示并识别单词规则，掌握状态图到识别程序的编程。

四、设计环境该课程设计包括的硬件和软件条件如下：.硬件（1）Intel Core Duo CPU P8700（2）内存4G.软件（1）Window 7 32位操作系统（2）Microsoft Visual Studio c#开发平台.编程语言C#语言五、需求分析.源程序的预处理：源程序中，存在许多编辑用的符号，她们对程序逻辑功能无任何影响。

例如：回车，换行，多余空白符，注释行等。

在词法分析之前，首先要先剔除掉这些符号，使得词法分析更为简单。

.单词符号的识别并判断单词的合法性：将每个单词符号进行不同类别的划分。

单词符号能够划分成5中。

(1)标识符：用户自己定义的名字，常量名，变量名和过程名。

(2)常数：各种类型的常数。

(3) 保留字（关键字）：如if、else、while、int、float 等。

(4) 运算符：如+、-、*、<、>、=等。

《LL（1）分析器的构造》实验报告一、实验名称LL(1)分析器的构造二、实验目的设计、编制、调试一个LL(1)语法分析器，利用语法分析器对符号串的识别，加深对语法分析原理的理解。

三、实验内容和要求设计并实现一个LL(1)语法分析器，实现对算术文法:G[E]:E->E+T|TT->T*F|FF->(E)|i所定义的符号串进行识别，例如符号串i+i*i为文法所定义的句子，符号串ii+++*i+不是文法所定义的句子。

实验要求:1、检测左递归，如果有则进行消除；2、求解FIRST集和FOLLOW集；3、构建LL(1)分析表；4、构建LL分析程序，对于用户输入的句子，能够利用所构造的分析程序进行分析，并显示出分析过程。

四、主要仪器设备硬件：微型计算机。

软件： Code blocks（也可以是其它集成开发环境）。

五、实验过程描述1、程序主要框架程序中编写了以下函数，各个函数实现的作用如下：void input_grammer(string *G);//输入文法Gvoid preprocess(string *G,string *P,string &U,string &u,int &n,int &t,int &k);//将文法G预处理得到产生式集合P，非终结符、终结符集合U、u，int eliminate_1(string *G,string *P,string U,string *GG);//消除文法G中所有直接左递归得到文法GGint* ifempty(string* P,string U,int k,int n);//判断各非终结符是否能推导为空string* FIRST_X(string* P,string U,string u,int* empty,int k,int n)；求所有非终结符的FIRST集string FIRST(string U,string u,string* first,string s)；//求符号串s=X1X2...Xn的FIRST集string** create_table(string *P,string U,string u,int n,int t,int k,string* first)；//构造分析表void analyse(string **table,string U,string u,int t,string s)；//分析符号串s2、编写的源程序#include<cstdio>#include<cstring>#include<iostream>using namespace std;void input_grammer(string *G)//输入文法G,n个非终结符{int i=0;//计数char ch='y';while(ch=='y'){cin>>G[i++];cout<<"继续输入?(y/n)\n";cin>>ch;}}void preprocess(string *G,string *P,string &U,string &u,int &n,int &t,int &k)//将文法G预处理产生式集合P，非终结符、终结符集合U、u，{int i,j,r,temp;//计数char C;//记录规则中（）后的符号int flag;//检测到（）n=t=k=0;for( i=0;i<50;i++) P[i]=" ";//字符串如果不初始化，在使用P[i][j]=a时将不能改变，可以用P[i].append(1,a)U=u=" ";//字符串如果不初始化，无法使用U[i]=a赋值，可以用U.append(1,a) for(n=0;!G[n].empty();n++){ U[n]=G[n][0];}//非终结符集合，n为非终结符个数for(i=0;i<n;i++){for(j=4;j<G[i].length();j++){if(U.find(G[i][j])==string::npos&&u.find(G[i][j])==string::npos)if(G[i][j]!='|'&&G[i][j]!='^')//if(G[i][j]!='('&&G[i][j]!=')'&&G[i][j]!='|'&&G[i][j]!='^')u[t++]=G[i][j];}}//终结符集合，t为终结符个数for(i=0;i<n;i++){flag=0;r=4;for(j=4;j<G[i].length();j++){P[k][0]=U[i];P[k][1]=':';P[k][2]=':';P[k][3]='=';/* if(G[i][j]=='('){ j++;flag=1;for(temp=j;G[i][temp]!=')';temp++);C=G[i][temp+1];//C记录（）后跟的字符，将C添加到（）中所有字符串后面}if(G[i][j]==')') {j++;flag=0;}*/if(G[i][j]=='|'){//if(flag==1) P[k][r++]=C;k++;j++;P[k][0]=U[i];P[k][1]=':';P[k][2]=':';P[k][3]='=';r=4;P[k][r++]=G[i][j];}else{P[k][r++]=G[i][j];}}k++;}//获得产生式集合P，k为产生式个数}int eliminate_1(string *G,string *P,string U,string *GG)//消除文法G1中所有直接左递归得到文法G2，要能够消除含有多个左递归的情况）{string arfa,beta;//所有形如A::=Aα|β中的α、β连接起来形成的字符串arfa、betaint i,j,temp,m=0;//计数int flag=0;//flag=1表示文法有左递归int flagg=0;//flagg=1表示某条规则有左递归char C='A';//由于消除左递归新增的非终结符，从A开始增加，只要不在原来问法的非终结符中即可加入for(i=0;i<20&&U[i]!=' ';i++){ flagg=0;arfa=beta="";for(j=0;j<100&&P[j][0]!=' ';j++){if(P[j][0]==U[i]){if(P[j][4]==U[i])//产生式j有左递归{flagg=1;for(temp=5;P[j][temp]!=' ';temp++) arfa.append(1,P[j][temp]);if(P[j+1][4]==U[i]) arfa.append("|");//不止一个产生式含有左递归}else{for(temp=4;P[j][temp]!=' ';temp++) beta.append(1,P[j][temp]);if(P[j+1][0]==U[i]&&P[j+1][4]!=U[i]) beta.append("|");}}}if(flagg==0)//对于不含左递归的文法规则不重写{GG[m]=G[i]; m++;}else{flag=1;//文法存在左递归GG[m].append(1,U[i]);GG[m].append("::=");if(beta.find('|')!=string::npos) GG[m].append("("+beta+")");else GG[m].append(beta);while(U.find(C)!=string::npos){C++;}GG[m].append(1,C);m++;GG[m].append(1,C);GG[m].append("::=");if(arfa.find('|')!=string::npos) GG[m].append("("+arfa+")");else GG[m].append(arfa);GG[m].append(1,C);GG[m].append("|^");m++;C++;}//A::=Aα|β改写成A::=βA‘，A’=αA'|β，}return flag;}int* ifempty(string* P,string U,int k,int n){int* empty=new int [n];//指示非终结符能否推导到空串int i,j,r;for(r=0;r<n;r++) empty[r]=0;//默认所有非终结符都不能推导到空int flag=1;//1表示empty数组有修改int step=100;//假设一条规则最大推导步数为100步while(step--){for(i=0;i<k;i++){r=U.find(P[i][0]);if(P[i][4]=='^') empty[r]=1;//直接推导到空else{for(j=4;P[i][j]!=' ';j++){if(U.find(P[i][j])!=string::npos){if(empty[U.find(P[i][j])]==0) break;}else break;}if(P[i][j]==' ') empty[r]=1;//多步推导到空else flag=0;}}}return empty;}string* FIRST_X(string* P,string U,string u,int* empty,int k,int n){int i,j,r,s,tmp;string* first=new string[n];char a;int step=100;//最大推导步数while(step--){// cout<<"step"<<100-step<<endl;for(i=0;i<k;i++){//cout<<P[i]<<endl;r=U.find(P[i][0]);if(P[i][4]=='^'&&first[r].find('^')==string::npos) first[r].append(1,'^');//规则右部首符号为空else{for(j=4;P[i][j]!=' ';j++){a=P[i][j];if(u.find(a)!=string::npos&&first[r].find(a)==string::npos)//规则右部首符号是终结符{first[r].append(1,a);break;//添加并结束}if(U.find(P[i][j])!=string::npos)//规则右部首符号是非终结符,形如X：：=Y1Y2...Yk{s=U.find(P[i][j]);//cout<<P[i][j]<<":\n";for(tmp=0;first[s][tmp]!='\0';tmp++){a=first[s][tmp];if(a!='^'&&first[r].find(a)==string::npos)//将FIRST[Y1]中的非空符加入first[r].append(1,a);}}if(!empty[s]) break;//若Y1不能推导到空，结束}if(P[i][j]==' ')if(first[r].find('^')==string::npos)first[r].append(1,'^');//若Y1、Y2...Yk都能推导到空，则加入空符号}}}return first;}string FIRST(string U,string u,string* first,string s)//求符号串s=X1X2...Xn的FIRST集{int i,j,r;char a;string fir;for(i=0;i<s.length();i++){if(s[i]=='^') fir.append(1,'^');if(u.find(s[i])!=string::npos&&fir.find(s[i])==string::npos){ fir.append(1,s[i]);break;}//X1是终结符，添加并结束循环if(U.find(s[i])!=string::npos)//X1是非终结符{r=U.find(s[i]);for(j=0;first[r][j]!='\0';j++){a=first[r][j];if(a!='^'&&fir.find(a)==string::npos)//将FIRST(X1)中的非空符号加入fir.append(1,a);}if(first[r].find('^')==string::npos) break;//若X1不可推导到空，循环停止}if(i==s.length())//若X1-Xk都可推导到空if(fir.find(s[i])==string::npos) //fir中还未加入空符号fir.append(1,'^');}return fir;}string** create_table(string *P,string U,string u,int n,int t,int k,string* first)//构造分析表，P为文法G的产生式构成的集合{int i,j,p,q;string arfa;//记录规则右部string fir,follow;string FOLLOW[5]={")#",")#","+)#","+)#","+*)#"};string **table=new string*[n];for(i=0;i<n;i++) table[i]=new string[t+1];for(i=0;i<n;i++)for(j=0;j<t+1;j++)table[i][j]=" ";//table存储分析表的元素，“ ”表示error for(i=0;i<k;i++){arfa=P[i];arfa.erase(0,4);//删除前4个字符，如：E::=E+T,则arfa="E+T"fir=FIRST(U,u,first,arfa);for(j=0;j<t;j++){p=U.find(P[i][0]);if(fir.find(u[j])!=string::npos){q=j;table[p][q]=P[i];}//对first（）中的每一终结符置相应的规则}if(fir.find('^')!=string::npos){follow=FOLLOW[p];//对规则左部求follow()for(j=0;j<t;j++){if((q=follow.find(u[j]))!=string::npos){q=j;table[p][q]=P[i];}//对follow（）中的每一终结符置相应的规则}table[p][t]=P[i];//对#所在元素置相应规则}}return table;}void analyse(string **table,string U,string u,int t,string s)//分析符号串s{string stack;//分析栈string ss=s;//记录原符号串char x;//栈顶符号char a;//下一个要输入的字符int flag=0;//匹配成功标志int i=0,j=0,step=1;//符号栈计数、输入串计数、步骤数int p,q,r;string temp;for(i=0;!s[i];i++){if(u.find(s[i])==string::npos)//出现非法的符号cout<<s<<"不是该文法的句子\n";return;}s.append(1,'#');stack.append(1,'#');//’#’进入分析栈stack.append(1,U[0]);i++;//文法开始符进入分析栈a=s[0];//cout<<stack<<endl;cout<<"步骤分析栈余留输入串所用产生式\n";while(!flag){// cout<<"步骤分析栈余留输入串所用产生式\n"cout<<step<<" "<<stack<<" "<<s<<" ";x=stack[i];stack.erase(i,1);i--;//取栈顶符号x,并从栈顶退出//cout<<x<<endl;if(u.find(x)!=string::npos)//x是终结符的情况{if(x==a){s.erase(0,1);a=s[0];//栈顶符号与当前输入符号匹配，则输入下一个符号cout<<" \n";//未使用产生式，输出空}else{cout<<"error\n";cout<<ss<<"不是该文法的句子\n";break;}}if(x=='#'){if(a=='#') {flag=1;cout<<"成功\n";}//栈顶和余留输入串都为#，匹配成功else{cout<<"error\n";cout<<ss<<"不是该文法的句子\n";break;}}if(U.find(x)!=string::npos)//x是非终结符的情况{p=U.find(x);q=u.find(a);if(a=='#') q=t;temp=table[p][q];cout<<temp<<endl;//输出使用的产生式if(temp[0]!=' ')//分析表中对应项不为error{r=9;while(temp[r]==' ') r--;while(r>3){if(temp[r]!='^'){stack.append(1,temp[r]);//将X::=x1x2...的规则右部各符号压栈i++;}r--;}}else{cout<<"error\n";cout<<ss<<"不是该文法的句子\n";break;}}step++;}if(flag) cout<<endl<<ss<<"是该文法的句子\n";}int main(){int i,j;string *G=new string[50];//文法Gstring *P=new string[50];//产生式集合Pstring U,u;//文法G非终结符集合U，终结符集合uint n,t,k;//非终结符、终结符个数,产生式数string *GG=new string[50];//消除左递归后的文法GGstring *PP=new string[50];//文法GG的产生式集合PPstring UU,uu;//文法GG非终结符集合U，终结符集合uint nn,tt,kk;//消除左递归后的非终结符、终结符个数,产生式数string** table;//分析表cout<<" 欢迎使用LL(1)语法分析器!\n\n\n";cout<<"请输入文法（同一左部的规则在同一行输入，例如：E::=E+T|T；用^表示空串）\n";input_grammer(G);preprocess(G,P,U,u,n,t,k);cout<<"\n该文法有"<<n<<"个非终结符：\n";for(i=0;i<n;i++) cout<<U[i];cout<<endl;cout<<"该文法有"<<t<<"个终结符：\n";for(i=0;i<t;i++) cout<<u[i];cout<<"\n\n 左递归检测与消除\n\n";if(eliminate_1(G,P,U,GG)){preprocess(GG,PP,UU,uu,nn,tt,kk);cout<<"该文法存在左递归！\n\n消除左递归后的文法:\n\n"; for(i=0;i<nn;i++) cout<<GG[i]<<endl;cout<<endl;cout<<"新文法有"<<nn<<"个非终结符：\n";for(i=0;i<nn;i++) cout<<UU[i];cout<<endl;cout<<"新文法有"<<tt<<"个终结符：\n";for(i=0;i<tt;i++) cout<<uu[i];cout<<endl;//cout<<"新文法有"<<kk<<"个产生式：\n";//for(i=0;i<kk;i++) cout<<PP[i]<<endl;}else{cout<<"该文法不存在左递归\n";GG=G;PP=P;UU=U;uu=u;nn=n;tt=t;kk=k;}cout<<" 求解FIRST集\n\n";int *empty=ifempty(PP,UU,kk,nn);string* first=FIRST_X(PP,UU,uu,empty,kk,nn);for(i=0;i<nn;i++)cout<<"FIRST("<<UU[i]<<"): "<<first[i]<<endl;cout<<" 求解FOLLOW集\n\n";for(i=0;i<nn;i++)cout<<"FOLLOW("<<UU[i]<<"): "<<FOLLOW[i]<<endl; cout<<"\n\n 构造文法分析表\n\n"; table=create_table(PP,UU,uu,nn,tt,kk,first);cout<<" ";for(i=0;i<tt;i++) cout<<" "<<uu[i]<<" ";cout<<"# "<<endl;for( i=0;i<nn;i++){cout<<UU[i]<<" ";for(j=0;j<t+1;j++)cout<<table[i][j];cout<<endl;}cout<<"\n\n 分析符号串\n\n";cout<<"请输入要分析的符号串\n";cin>>s;analyse(table,UU,uu,tt,s);return 0;}3、程序演示结果（1）输入文法（2）消除左递归（3）求解FIRST和FOLLOW集（4）构造分析表（5）分析符号串匹配成功的情况：匹配失败的情况五、思考和体会1、编写的LL(1)语法分析器应该具有智能性，可以由用户输入任意文法，不需要指定终结符个数和非终结符个数。

编译原理语法分析器实验报告西安邮电大学编译原理实验报告学院名称：计算机学院****：***实验名称：语法分析器的设计与实现班级：计科1405班学号：04141152时间：2017年5月12日把SELECT (i)存放到temp中结果返回1；1.构建好的预测分析表2.语法分析流程图一．实验结果正确运行结果：错误运行结果：二．设计技巧和心得体会这次实验编写了一个语法分析方法的程序，但是在LL（1）分析器的编写中我只达到了最低要求，就是自己手动输入的select集，first集，follow集然后通过程序将预测分析表构造出来，然后自己编写总控程序根据分析表进行分析。

通过本次试验，我能够设计一个简单的语法分析程序，实现对词法分析程序所提供的单词序列进行语法检查和结构分析，进一步掌握常用的语法分析方法。

还能选择最有代表性的语法分析方法，如LL(1) 语法分析程序、算符优先分析程序和LR分析分析程序。

三．源代码package com.LL1;import java.util.ArrayDeque;import java.util.Deque;/*** LL1文法分析器，已经构建好预测分析表,采用Deque实现* Created by HongWeiPC on 2017/5/12.*/public class LL1_Deque {//预测分析表private String[][] analysisTable = new String[][]{{"TE'", "", "", "TE'", "", ""},{"", "+TE'", "", "", "ε", "ε"},{"FT'", "", "", "FT'", "", ""},{"", "ε", "*FT'", "", "ε", "ε"},{"i", "", "", "(E)", "", ""}};//终结符private String[] VT = new String[]{"i", "+", "*", "(", ")", "#"};//非终结符private String[] VN = new String[]{"E", "E'", "T", "T'", "F"};//输入串strTokenprivate StringBuilder strToken = new StringBuilder("i*i+i");//分析栈stackprivate Deque<String> stack = new ArrayDeque<>();//shuru1保存从输入串中读取的一个输入符号，当前符号private String shuru1 = null;//X中保存stack栈顶符号private String X = null;//flag标志预测分析是否成功private boolean flag = true;//记录输入串中当前字符的位置private int cur = 0;//记录步数private int count = 0;public static void main(String[] args) {LL1_Deque ll1 = new LL1_Deque();ll1.init();ll1.totalControlProgram();ll1.printf();}//初始化private void init() {strToken.append("#");stack.push("#");System.out.printf("%-8s %-18s %-17s %s\n", "步骤", "符号栈", "输入串", "所用产生式");stack.push("E");curCharacter();System.out.printf("%-10d %-20s %-20s\n", count, stack.toString(), strToken.substring(cur, strToken.length()));}//读取当前栈顶符号private void stackPeek() {X = stack.peekFirst();}//返回输入串中当前位置的字母private String curCharacter() {shuru1 = String.valueOf(strToken.charAt(cur));return shuru1;}//判断X是否是终结符private boolean XisVT() {for (int i = 0; i < (VT.length - 1); i++) {if (VT[i].equals(X)) {return true;}}return false;}//查找X在非终结符中分析表中的横坐标private String VNTI() {int Ni = 0, Tj = 0;for (int i = 0; i < VN.length; i++) {if (VN[i].equals(X)) {Ni = i;}}for (int j = 0; j < VT.length; j++) {if (VT[j].equals(shuru1)) {Tj = j;}}return analysisTable[Ni][Tj];}//判断M[A,a]={X->X1X2...Xk}//把X1X2...Xk推进栈//X1X2...Xk=ε，不推什么进栈private boolean productionType() {return VNTI() != "";}//推进stack栈private void pushStack() {stack.pop();String M = VNTI();String ch;//处理TE' FT' *FT'特殊情况switch (M) {case "TE'":stack.push("E'");stack.push("T");break;case "FT'":stack.push("T'");stack.push("F");break;case "*FT'":stack.push("T'");stack.push("F");stack.push("*");break;case "+TE'":stack.push("E'");stack.push("T");stack.push("+");break;default:for (int i = (M.length() - 1); i >= 0; i--) {ch = String.valueOf(M.charAt(i));stack.push(ch);}break;}System.out.printf("%-10d %-20s %-20s %s->%s\n", (++count), stack.toString(), strToken.substring(cur, strToken.length()), X, M);}//总控程序private void totalControlProgram() {while (flag) {stackPeek(); //读取当前栈顶符号令X=栈顶符号if (XisVT()) {if (X.equals(shuru1)) {cur++;shuru1 = curCharacter();stack.pop();System.out.printf("%-10d %-20s %-20s \n", (++count), stack.toString(), strToken.substring(cur, strToken.length()));} else {ERROR();}} else if (X.equals("#")) {if (X.equals(shuru1)) {flag = false;} else {ERROR();}} else if (productionType()) {if (VNTI().equals("")) {ERROR();} else if (VNTI().equals("ε")) {stack.pop();System.out.printf("%-10d %-20s %-20s %s->%s\n", (++count), stack.toString(), strToken.substring(cur, strToken.length()), X, VNTI());} else {pushStack();}} else {ERROR();}}}//出现错误private void ERROR() {System.out.println("输入串出现错误，无法进行分析");System.exit(0);}//打印存储分析表private void printf() {if (!flag) {System.out.println("****分析成功啦！****");} else {System.out.println("****分析失败了****");}}}。

编译原理语法分析器编译原理语法分析器是编译器中的重要组成部分，它负责将源代码解析成抽象语法树，为后续的语义分析和代码生成做准备。

本文将介绍语法分析器的原理、分类和常用算法。

一、语法分析器的原理语法分析器的主要任务是根据给定的文法定义，将源代码解析成一个个语法单元，并构建出一棵抽象语法树。

它通过递归下降、预测分析和LR分析等算法来实现。

1. 递归下降法递归下降法是一种基于产生式的自顶向下分析方法。

它从文法的开始符号出发，通过不断地推导和回溯，逐步地构建抽象语法树。

递归下降法易于理解和实现，但对左递归和回溯有一定的局限性。

2. 预测分析法预测分析法也是自顶向下的分析方法，它通过预测下一个输入符号来选择适当的产生式进行推导。

为了提高效率，预测分析法使用预测分析表来存储各个非终结符和终结符的关系。

3. LR分析法LR分析法是一种自底向上的分析方法，它使用LR自动机和LR分析表来进行分析。

LR自动机是一个有限状态控制器，通过状态转移和规约动作来解析源代码。

LR分析表存储了状态转移和规约的规则。

二、语法分析器的分类根据语法分析器的特性和实现方式，可以将其分为LL分析器和LR 分析器。

1. LL分析器LL分析器是基于递归下降法和预测分析法的一类分析器。

它从左到右、从左到右地扫描源代码，并根据预测分析表进行推导。

常见的LL分析器有LL(1)分析器和LL(k)分析器。

2. LR分析器LR分析器是基于LR分析法的一类分析器。

它先通过移进-归约的方式建立一棵语法树，然后再进行规约操作。

LR分析器具有强大的语法处理能力，常见的LR分析器有LR(0)、SLR(1)、LR(1)和LALR(1)分析器。

三、常用的语法分析算法除了递归下降法、预测分析法和LR分析法，还有一些其他的语法分析算法。

1. LL算法LL算法是一种递归下降法的改进算法，它通过构造LL表和预测分析表实现分析过程。

LL算法具有很好的可读性和易于理解的特点。

2. LR算法LR算法是一种自底向上的分析方法，它通过建立LR自动机和构造LR分析表来进行分析。

编译原理实验⼆：LL（1）语法分析器⼀、实验要求 1. 提取左公因⼦或消除左递归（实现了消除左递归） 2. 递归求First集和Follow集 其它的只要按照课本上的步骤顺序写下来就好（但是代码量超多...），下⾯我贴出实验的⼀些关键代码和算法思想。

⼆、基于预测分析表法的语法分析 2.1 代码结构 2.1.1 Grammar类 功能：主要⽤来处理输⼊的⽂法，包括将⽂法中的终结符和⾮终结符分别存储，检测直接左递归和左公因⼦，消除直接左递归，获得所有⾮终结符的First集，Follow集以及产⽣式的Select集。

#ifndef GRAMMAR_H#define GRAMMAR_H#include <string>#include <cstring>#include <iostream>#include <vector>#include <set>#include <iomanip>#include <algorithm>using namespace std;const int maxn = 110;//产⽣式结构体struct EXP{char left; //左部string right; //右部};class Grammar{public:Grammar(); //构造函数bool isNotTer(char x); //判断是否是终结符int getTer(char x); //获取终结符下标int getNonTer(char x); //获取⾮终结符下标void getFirst(char x); //获取某个⾮终结符的First集void getFollow(char x); //获取某个⾮终结符的Follow集void getSelect(char x); //获取产⽣式的Select集void input(); //输⼊⽂法void scanExp(); //扫描输⼊的产⽣式，检测是否有左递归和左公因⼦void remove(); //消除左递归void solve(); //处理⽂法，获得所有First集，Follow集以及Select集void display(); //打印First集,Follow集,Select集void debug(); //⽤于debug的函数~Grammar(); //析构函数protected:int cnt; //产⽣式数⽬EXP exp[maxn]; //产⽣式集合set<char> First[maxn]; //First集set<char> Follow[maxn]; //Follow集set<char> Select[maxn]; //select集vector<char> ter_copy; //去掉$的终结符vector<char> ter; //终结符vector<char> not_ter; //⾮终结符};#endif 2.1.2 AnalyzTable类 功能：得到预测分析表，判断输⼊的⽂法是否是LL(1)⽂法，⽤预测分析表法判断输⼊的符号串是否符合刚才输⼊的⽂法，并打印出分析过程。

编译原理语法分析实验报告一、实验目的本实验主要目的是学习和掌握编译原理中的语法分析方法，通过实验了解和实践LR(1)分析器的实现过程，并对比不同的文法对语法分析的影响。

二、实验内容1.实现一个LR(1)的语法分析器2.使用不同的文法进行语法分析3.对比不同文法对语法分析的影响三、实验原理1.背景知识LR(1)分析器是一种自底向上（bottom-up）的语法分析方法。

它使用一个分析栈（stack）和一个输入缓冲区（input buffer）来处理输入文本，并通过移进（shift）和规约（reduce）操作进行语法分析。

2.实验步骤1）构建文法的LR(1)分析表2）读取输入文本3）初始化分析栈和输入缓冲区4）根据分析表进行移进或规约操作，直至分析过程结束四、实验过程与结果1.实验环境本实验使用Python语言进行实现，使用了语法分析库ply来辅助实验。

2.实验步骤1）构建文法的LR(1)分析表通过给定的文法，根据LR(1)分析表的构造算法，构建出分析表。

2）实现LR(1)分析器使用Python语言实现LR(1)分析器，包括读取输入文本、初始化分析栈和输入缓冲区、根据分析表进行移进或规约操作等功能。

3）使用不同的文法进行语法分析选择不同的文法对编写的LR(1)分析器进行测试，观察语法分析的结果。

3.实验结果通过不同的测试案例，实验结果表明编写的LR(1)分析器能够正确地进行语法分析，能够识别出输入文本是否符合给定文法。

五、实验分析与总结1.实验分析本实验通过实现LR(1)分析器，对不同文法进行语法分析，通过实验结果可以观察到不同文法对语法分析的影响。

2.实验总结本实验主要学习和掌握了编译原理中的语法分析方法，了解了LR(1)分析器的实现过程，并通过实验提高了对语法分析的理解。

六、实验心得通过本次实验，我深入学习了编译原理中的语法分析方法，了解了LR(1)分析器的实现过程。

在实验过程中，我遇到了一些问题，但通过查阅资料和请教老师，最终解决了问题，并完成了实验。