《对称分量法》PPT课件

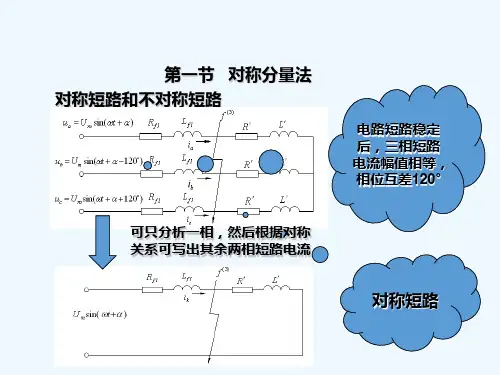
第一节对称分量法图4—1(a)、(b)、(c)表示三组对称的三相相量。

第一组相量Fa(1)、相量F b(1). 相量Fc(1)，幅值相等。

相位为“a 超前b 120度，b超前c 120度，称为正序；第二组相量Fa(2). 相量F b(2)相量.Fc(2)，幅值相等，相序与正序相反，称为负序；第三组相量Fa(0)、相量.F b(0)、相量Fc(0)，幅值和相位均相同，称为零序。

在图4—1(d)中将每一组的带下标a的三个相量合成为Fa,，带下标b的合成为Fb，,带下标c的合成为F是三个小对称的相量，即三组对称的相量合成得相量Fa、Fb、Fc是三个不对称的相量。

写成数学表达式为：由于每一组是对称的，固有下列关系：将式（4-2）代入式（4-1）可得：此式表示上述三个不对称相量和三个对称相量中a相量的关系。

其矩阵形式为：或简写为式（4-4）和式（4-5）说明三相对称相量合成得三个不对称相量。

其逆关系为：或简写为式(4—6)和(4—7)说明由三个不对称的相量可以唯一地分解成三组对称的相量(即对称分量)；正序分量、负序分员和不序分量。

实际上，式(4—4)和(4—6)表示三个对称相量Fa、Fb、Fc和另外三个相量Fa(1)、 Fa(2)、 Fa(0)之间的线性变换关系。

如果电力系统某处发生不对称短路，尽管除短路点外三相系统的元件参数都是对称的，三相电路的电流和电压的基频分量都变成不对称的相量。

将式(4—6)的变换关系应用于基频电流（或电压），则有即将三相不对称电流(以后略去“基频”二字)Ia、Ib、Ic经过线性变换后，可分解成三组对称的电流。

即a相电流Ia分解成Ia(1)、Ia(2)、Ia(0)，b相电流Ib分解成Ib(1)、Ib(2)、Ib(0),c相电流Ic分解成Ic(1)、Ic(2)、Ic(0)。

其中Ia(1)、Ib(1)、Ic(1)一组对称的相量，称为正序分量电流；Ia(2)、Ib(2)、Ic(2)也是一组对称的相量。

对称分量法正序:A相领先B相120度，B相领先C相120度,C相领先A相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序.单相接地故障时候，系统有正序、负序和零序分量。

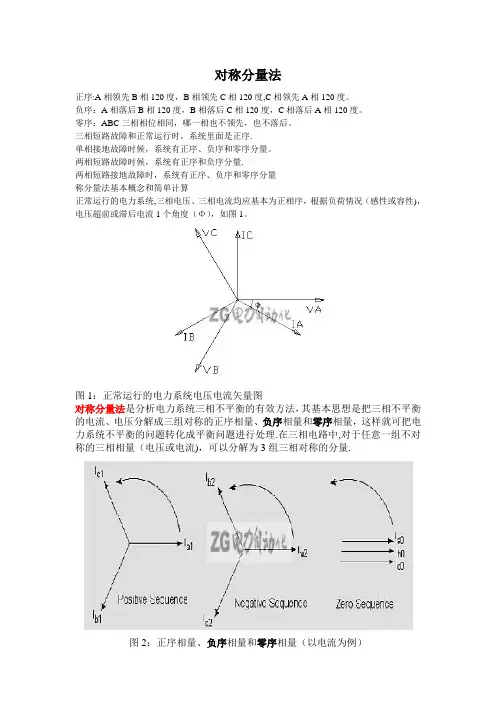
两相短路故障时候，系统有正序和负序分量.两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统,三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性)，电压超前或滞后电流1个角度（Φ），如图1。

图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理.在三相电路中,对于任意一组不对称的三相相量（电压或电流)，可以分解为3组三相对称的分量.图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时,三相相量与其对称分量之间的关系（如电流)为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量：Ib1=α2 Ia1 ，Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0式中，α为运算子，α=1∠120°有α2＝1∠240°, α3＝1，α+α2+1=0由各相电流求电流序分量：I1=Ia1= 1/3（IA +αIB +α2 IC）I2=Ia2= 1/3(IA +α2IB +αIC)I0=Ia0= 1/3(IA +IB +IC）以上3个等式可以通过代数方法或物理意义（方法）求解。

) ---------------- 5 //J PostNS teajsnfce 'biZero Sequence 对称分量法正序：A相领先B相120度，B相领先C相120度，C相领先A相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量。

两相短路故障时候，系统有正序和负序分量。

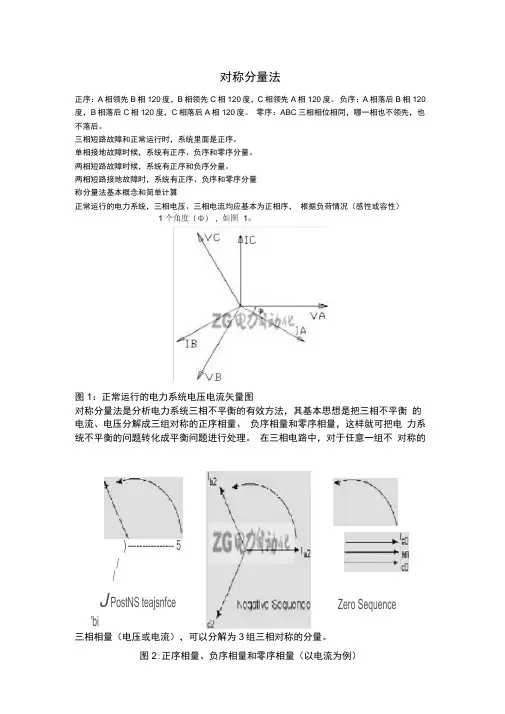
两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性）图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2:正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系（如电流）为：IA=la1+la2+laO ------------------------------------------------------------------------------- O1IB=lb1+lb2+lbO= 2d a1+ a Ia2 + laO ---------------------------------- 02IC=lc1+lc2+lcO= a la1+la2+la0 ------------------------------------- 03对于正序分量：lb仁a 2 lai, Ic1= a Ia1 对于负序分量：Ib2= a Ia2, Ic2= a 2la2 对于零序分量：IaO= IbO = IcO 式中，a为运算子，a =亿12O°有a = 1Z 24O°由各相电流求电流序分量：I1 = la1= 1/3（IA + a lB IC）a I2=la2= 1/3（IA + 2 IBc+ a IC） IO=IaO= 1/3（IA +IB +IC）以上3个等式可以通过代数方法或物理意义（方法）求解。

§第13讲 《对称分量法》
一、教学目标 对称分量法原理，它是分析、计算不对称短路的基础。

相量的旋转因子及由旋转因子组成的变换矩阵，它是具体进行对称量与不对称量之间互换的计算因子。

二、教学重点
对称概念；对称分量法；不对称量；对称分量；正序量概念、负序量概念、零序量概念；旋转因子；不对称量与对称分量之间的变换矩阵；不对称量与对称分量之间α=e j 1200的互换计算；变换矩阵表示了不对称量与对称分量之间的关系。

三、教学难点
对称分量法的数学意义和物理意义
四、教学内容和要点 ⑴ 首先以电压或电流为例搞清什么是正序、负序、零序对称量。

对称是三相量数值相等，相位差相同。

正序量相量的顺序是a 、b 、c 按顺时针方向排序。

负序是a 、b 、c 按逆时针方向排序。

零序，a 、b 、c 相位差是00（或3600）。

旋转因子表示相量按正方向旋转120α=e j 12000，
和其关系 ，10
α31=2++=αα⑵ 三相不对称量可以唯一地用一组对称分量合成，反之，三相不对称量可以唯一地 分解成一组对称分量，合成和分解通过变换矩阵T 及其逆矩阵T −1
来实现。

他们既适用于电压变换也适用于电流变换。

记住变换矩阵
五、采用的教学方法和手段
教学方法（如：讲述法、讨论法、实验法等）：讲述法
教学手段（如：挂图、模型、仪器、投影、幻灯等）：板书。

对称分量法正序：A相领先B相120度，B相领先C相120度，C相领先A相120度。

负序：A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先，也不落后。

三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量。

两相短路故障时候，系统有正序和负序分量。

两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况（感性或容性），电压超前或滞后电流1个角度（Φ），如图1。

图1：正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量，这样就可把电力系统不平衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系（如电流）为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1IB=Ib1+Ib2+Ib0=α2 Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2 Ia2+Ia0―――――――――――○3对于正序分量：Ib1=α2 Ia1 ，Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0式中，α为运算子，α=1∠120°有α2＝1∠240°, α3＝1, α+α2+1=0由各相电流求电流序分量：I1=Ia1= 1/3(IA +αIB +α 2 IC)I2=Ia2= 1/3(IA +α2 IB +αIC)I0=Ia0= 1/3(IA +IB +IC)以上3个等式可以通过代数方法或物理意义（方法）求解。

对称分量法正序：A相领先B相120度，B相领先C相120度，C相领先A相120度。

负序:A相落后B相120度，B相落后C相120度，C相落后A相120度。

零序：ABC三相相位相同，哪一相也不领先,也不落后.三相短路故障和正常运行时，系统里面是正序。

单相接地故障时候，系统有正序、负序和零序分量.两相短路故障时候，系统有正序和负序分量.两相短路接地故障时，系统有正序、负序和零序分量称分量法基本概念和简单计算正常运行的电力系统，三相电压、三相电流均应基本为正相序，根据负荷情况(感性或容性），电压超前或滞后电流1个角度（Φ），如图1.图1:正常运行的电力系统电压电流矢量图对称分量法是分析电力系统三相不平衡的有效方法，其基本思想是把三相不平衡的电流、电压分解成三组对称的正序相量、负序相量和零序相量,这样就可把电力系统不平衡的问题转化成平衡问题进行处理。

在三相电路中，对于任意一组不对称的三相相量（电压或电流），可以分解为3组三相对称的分量。

图2：正序相量、负序相量和零序相量（以电流为例）当选择A相作为基准相时，三相相量与其对称分量之间的关系(如电流）为：IA=Ia1+Ia2+Ia0――――――――――――――――――――――――――○1 IB=Ib1+Ib2+Ib0=α2Ia1+αIa2 + Ia0――――――――――○2IC=Ic1+Ic2+Ic0=α Ia1+α2Ia2+Ia0―――――――――――○3对于正序分量:Ib1=α2 Ia1 ,Ic1=αIa1对于负序分量：Ib2=αIa2 ，Ic2=α2Ia2对于零序分量：Ia0= Ib0 = Ic0式中,α为运算子，α=1∠120°有α2＝1∠240°，α3＝1，α+α2+1=0由各相电流求电流序分量：I1=Ia1= 1/3（IA +αIB +α2 IC)I2=Ia2= 1/3（IA +α2IB +αIC）I0=Ia0= 1/3（IA +IB +IC)以上3个等式可以通过代数方法或物理意义（方法）求解。