控制系统的微分方程传递函数
- 格式：pdf
- 大小：3.92 MB
- 文档页数：40
下载文档原格式
合集下载
机械控制基础
系统线性化过程中，需注意的地方： 系统线性化过程中，需注意的地方：
(1)线性化是相应于某一额定工作点的，工作点不同，则所得 (1)线性化是相应于某一额定工作点的 工作点不同， 线性化是相应于某一额定工作点的， 的方程系数也往往不同。 的方程系数也往往不同。 (2)变量的偏移愈小，则线性化精度愈高。 (2)变量的偏移愈小 则线性化精度愈高。 变量的偏移愈小， (3)增量方程中可认为其初始条件为零， (3)增量方程中可认为其初始条件为零，即广义坐标原点平移 增量方程中可认为其初始条件为零 到额定工作点处。 到额定工作点处。 (4)线性化只适用于没有间断点、折断点的单值函数。 4)线性化只适用于没有间断点 折断点的单值函数。 线性化只适用于没有间断点、 (5)某些典型的本质非线性 如继电器特性、 某些典型的本质非线性， 死区、 (5)某些典型的本质非线性，如继电器特性、间隙、死区、摩 擦等，由于存在不连续点，不能通过泰勒展开进行线性化， 擦等，由于存在不连续点，不能通过泰勒展开进行线性化， 只有当它们对系统影响很小时才能忽略不计， 只有当它们对系统影响很小时才能忽略不计，否则只能作为 非线性问题处理。 非线性问题处理。
2.1 控制系统的微分方程
实际的物理系统往往有死区、饱和、 实际的物理系统往往有死区、饱和、间隙等各类 非线性现象。严格来讲， 非线性现象。严格来讲，几乎所有的实际的物理系统 都是非线性的。 都是非线性的。
尽管线性系统理论已是相当成熟， 尽管线性系统理论已是相当成熟，但非线性系统 理论还不完善。另外， 理论还不完善。另外，由于叠加原理不适用于非线性 系统，这给解非线性系统带来很大不便。 系统，这给解非线性系统带来很大不便。故对非线性 系统进行线性化处理，用线性系统理论进行分析。 系统进行线性化处理，用线性系统理论进行分析。
第二章 控制系统的传递函数
第二章
控制系统的传递函数
2．1 微分方程模型（时间域模型）
一、控制系统微分方程的分类
线性系统：可由线性微分方程描述的系统。线性微分方程是指微分方程 是定常和线性的。线性系统可应用叠加原理，将多输入及多输出的 系统转化为单输入和单输出的系统进行处理分析，最后进行叠加。 另外线性系统还有一个重要的性质，就是齐次性，即当输入量的数 值成比例增加时，输出量的数值也成比例增加，而且输出量的变化 规律只与系统的结构、参数及输入量的变化规律有关，与输入量数 值的大小是无关的。 非线性系统：研究非线性系统的运动规律和分析方法的一个分支学科。 非线性系统最重要的问题之一就是确定模型的结构，如果对系统的 运动有足够的知识，则可以按照系统运动规律给出它的数据模型。 一般来说，这样的模型是由非线性微分方程和非线性差分方程给出 的，对这类模型的辨别可以采用线性化，展开成特殊函数等方法。 非线性系统理论的研究对象是非线性现象，它反映出非线性系统运 动本质的一类现象，不能采用线性系统的理论来解释，主要原因是 非线性现象有频率对振幅的依赖性、多值响应和跳跃谐振、分谐波 振荡、自激振荡、频率插足、异步抑制、分岔和混沌等。
控制系统的传递函数
例 2：RLC 电路（L-R-C 无源四端网络）如图，建立输入输出间的微分方程关
由基尔霍夫定律，回路的压降为 0，即输入电压由电感、电阻、电容上的电压 平衡。 Ur=UL+UR+UC 电流 与 有 即 的关系
第二章
控制系统的传递函数
与 在数值上具有一 ～
注意：该系统也是一个二阶系统 与例 1 相比，它们具有相同的模型形式。当
线性系统满足叠加原理，而非线性系统不满足叠加原理。
第二章
控制系统的传递函数
二、微分方程模型的建立 根据系统物理机理建立系统微分方程模型的基本步骤： （1）确定系统中各元件的输入、输出物理量； （2）根据物理定律或化学定律（机理），列出元件的原始方程，在条 件允许的情况下忽略次要因素，适当简化； （3）列出原始方程中中间变量与其他因素的关系； （4）消去中间变量，按模型要求整理出最后形式。
控制工程基础---第四章传递函数
积分环节
微分环节
惯性环节
一阶微分环节
振荡环节
二阶微分环节
延时环节
第三节传递函数的方块图
一、组成元素
1、方块单元：表示环节或系统的传递函数。
2、叠加点：表示信号的运算及其结果。
3、信号线：带箭头的直线或折线。箭头的方向表示信号的流向。
二、基本运算
1、串联
2、并联
3、反馈
三、等效移动原则
1、引出点的移动：保证引出信号不变
2、对于实际的物理系统，
四、概念
1、零点、极点：
零点：系统传递函数分子s多项式为零的根。
极点：系统传递函数分母s多项式为零的根。
2、传递系数： 。
3、特征方程：传递函数分母s多项式。
4、阶：系统特征方程s的最高指数。
例3、以例1、例2的结果为例。
第二节典型环节及其传递函数
名称
微分方程
传递函数
比例环节
例：系统方块图如图示，简化求传递函数。
将a点后移
五、方块图的建立
1、步骤：
建立系统微分方程组。
对微分方程图连接。
2、举例
例1：建立电路的方块图，并传递函数。
解：
例2、建立图示系统的方块图，求传递函数。
解：设中间变量为x(t)，其力平衡方程为
例3、建立直流电动机的方块图，求传递函数。
第四章传递函数
第一节传递函数
一、定义：系统初始状态为零，系统输出与输入的拉氏变换之比。
二、求法：
1、由微分方程求取。
若系统的微分方程为
对微分方程的两端求拉氏变换
例1：系统微分方程为 ，求系统的传递函数。
解：由给定的微分方程，
例2：求R-C电路的传递函数。
微分环节
惯性环节
一阶微分环节
振荡环节
二阶微分环节
延时环节
第三节传递函数的方块图
一、组成元素
1、方块单元：表示环节或系统的传递函数。
2、叠加点：表示信号的运算及其结果。
3、信号线：带箭头的直线或折线。箭头的方向表示信号的流向。
二、基本运算
1、串联
2、并联
3、反馈
三、等效移动原则
1、引出点的移动：保证引出信号不变
2、对于实际的物理系统，
四、概念
1、零点、极点：
零点：系统传递函数分子s多项式为零的根。
极点：系统传递函数分母s多项式为零的根。
2、传递系数： 。
3、特征方程：传递函数分母s多项式。
4、阶：系统特征方程s的最高指数。
例3、以例1、例2的结果为例。
第二节典型环节及其传递函数
名称
微分方程
传递函数
比例环节
例：系统方块图如图示，简化求传递函数。
将a点后移
五、方块图的建立
1、步骤：
建立系统微分方程组。
对微分方程图连接。
2、举例
例1：建立电路的方块图，并传递函数。
解：
例2、建立图示系统的方块图，求传递函数。
解：设中间变量为x(t)，其力平衡方程为
例3、建立直流电动机的方块图，求传递函数。
第四章传递函数
第一节传递函数
一、定义：系统初始状态为零，系统输出与输入的拉氏变换之比。
二、求法：
1、由微分方程求取。
若系统的微分方程为
对微分方程的两端求拉氏变换
例1：系统微分方程为 ，求系统的传递函数。
解：由给定的微分方程，
例2：求R-C电路的传递函数。
控制工程基础3-第2章 (数学模型1：微分方程,传递函数)
at
sa
2
• 拉氏变换的基本性质 (1) 线性性质
L[af1 (t ) bf 2 (t )] aL[ f1 (t )] bL[ f 2 (t )]
原函数之和的拉氏变换等于各原函数的拉氏变换之和。 (2) 微分性质 L 若[ f (t )] F ( s ) ，则有 L[ f (t )] sF ( s) f (0) f(0)为原函数f(t) 在t=0时的初始值。 (3) 积分性质 则 若 L[ f (t )] F ( s )
该标准型为二阶线性常系数微分方程，系统中存在两个储能元件质 量和弹簧，故方程式左端最高阶次为二。
-
机械旋转系统
• [例2]：设有一个惯性负载和粘性摩擦阻尼器组成的机械 旋转系统，试列出以外力矩M(t)为输入信号，角位移 θ(t)为输出信号的数学模型。
M
J
θ
f
解：
1）确定输入量、输出量
M J θ f
F(t) m f
K x(t)
图 2 2 机 械 系 统
d 2x 3）由牛顿第二定律写原始方程： F F (t ) Fk (t ) F f (t ) m 2 dt dx Fk (t ) kx F f (t ) f 4）写中间变量与输出变量的关系式： dt 2 d x dx 5）将上式代入原始方程消中间变量得： m 2 kx f F (t ) dt dt m d 2 x f dx 1 x F (t ) 6）整理成标准型： 令 T2 m T f 2 k dt k dt k m f 2 k k dx 1 2 d x 则方程化为： Tm dt 2 T f dt x k F (t )
第二章 控制系统的数学模型
导 为什么要介绍本章? 分析、设计控制系统的第一步是建立系统的数学模 型。 读
第2章-1-微分方程
K
eo
eo
ei
e
i1 i2 i3
i1 ui u R1
u u 0
d(u uo ) i2 C dt
i3
u uo R2
有源网络的微分方程为
C
duo uo ui dt R2 R1
自 动 控 制 原 理
2.1.3 机电系统
电枢
1．直流电动机，控制电压
Ce (t ) ua (t )
自 动 控 制 原 理
2.1.3 机电系统
La Ra
磁场控制式直流 电动机微分方程为
Rf
转动惯量 J 摩擦系数 f
激磁电流 负载
d 2 (t ) d (t ) Lf J Lf f Rf J R f f (t ) kmu f (t ) 2 dt dt dM c (t ) Lf R f M c (t ) dt
自 动 控 制 原 理
第2章 自动控制系统的数学模型
2.1 控制系统的微分方程
2.2 控制系统的传递函数
2.3 方块图
2.4 控制系统的信号流图
数学模型：系统的输入/输出时间函数描述
物理模型——任何元件或系统实际上都是很复杂的，难以
对它作出精确、全面的描述，必须进行简化或理想化。简 化后的元件或系统称为该元件或系统的物理模型。简化是
V
H
M
x
P M
自 动 控 制 原 理
2.1.1 机械系统
• 简化物理模型 • 列写控制系统各部分的微分方程 • 在平衡点附近线性化 各部分的微分方程：
I V sin H cos
d2 m 2 ( x sin ) H dt
第四章控制系统的传递函数
其中，
n
1 T
——环节的 固有频率
To 2
1 T
——环节的 阻尼比
如果0≤ξ<1，二阶环节称为振荡环节
例7 图示是由质量m、阻尼c、弹簧k组成的动力系统. 求G(s)
依动力平衡原理有 Xi(t) k m c
Xo(t)
d 2 xo dxo m 2 c kxo kxi dt dt
因此，系统的传递函数就是系统单位脉冲响应 的拉氏变换。
一般地,传递函数的表达式为
X o ( s) ao s n a1s n1 a2 s n2 an G( s ) X i ( s) bo s m b1s m1 b2 s m2 bm
2. 传递函数的性质
k
k为比例环节的增益或称为放大系数
例1
解
ni(t)
z1
求一对齿轮传动的传递函数 no z1 k ∴G(s)=k ni z2
最基本的运算放大器
no(t)
z2
例2
i 1= i 2
ei ea ea eo R1 R2
ei eo R1 R2
ei
R2 R1 e i2 a Ko a i3 i1 +
ZL=Ls
3.电容元件
dUC iC C dt
ZC(s) = 1/sC
例5
下图是一个由运算放大器组成的积分器， 求G(s)。 C R i + uc 取拉氏变换 uo Ui(s) R
Zc
i
+ Uo(s)
ui
解：
1 uc idt c
I ( s) U c ( s) cs
K s
1 Zc cs
ms2 X o ( s) csX o (s) kXo ( s) kXi (sG( s) 2 ms cs k
传递函数
可以看出，若输入R(s)一定时，则系统的输出 C(s)完全由 (s)形式和参数决定。因此，传递 函数(s)反映了系统本身的特性。
传递函数的概念
2）、传递函数表征系统和元件本身的 固有特性，它由系统的结构和参数决定 而与输入信号无关，传递函数不反映系 统的具体物理结构。 3）、传递函数通常是复变量S的有理真分 式，它的分母多项式的最高次数 n ,高于或 等于分子多项式的最高次数 m ，即 n>= m。
Yo ( s) k ( s ) 2 Yi ( s) m s fs k
P201
传递函数的概念 设线性控制系统的输入为r（t），输出 为c（t），则其输入输出微分方程的 一 般表达式为： dnc(t) dn--1c(t) dc(t) a0——— +a1———+…..+a ———+anc(t) n--1 n n--1 dt dt dt dmr(t) dm--1r(t) dr(t) =b0——— +b1——— +…+bm--1———+bmr(t) m m--1 dt dt dt (n ≽ m)
传递函数的概念
假定初始条件为零，上式的拉氏变换为：
[a0sn+a1sn--1+…+a n--1 s+an]C(s) =[b0sm+b1sm--1+…+bm--1s+bm]R(s) 式中：C(s)=L[c(t)] , R(s)=L[r(t)] b0sm+b1sm--1+…+bm--1s+bm 则:C(s)= ———————————— R(s) a0sn+a1sn--1+…an—1s+an b0sm+b1sm--1+…+bm--1s+bm B (s) 令:(s)= ——————————— = —— n n--1 a0s +a1s +…a n—1s+an A (s)
《控制工程》传递函数
1．系统由单变量非线性函数所描述
df 1 d2 f Dx + Dx 2 f ( x) f ( x0 ) + dx x 2! dx 2 0 x0 1 d3 f + 3! dx 3 D x 3 + LL f ( x0 ) +
y= f (x) y(t):输出 x(t):输入 df Dx dx x 0 df Dx dx x 0
1相加点c前移再相加点交换第二章传递函数2内环简化3内环简化1g1g2h1图2321g1g2h1g2g3h2图2334总传递函数1g1g2h1g2g3h2g1g2g3图2341分支点e前移h2g3h1图230第二章传递函数2内环简化3内环简化g2图236第二章传递函数4总传递函数图238含有多个局部反馈的闭环系统中当满足下面条件时1只有一条前向通道2各局部反馈回路间存在公共的传递函数方块递函数之和每一反馈回路的开环传结论
i
式中：a n…a 0, b m…b 0 均为常系数
x 0 (t)为系统输出量，x i(t)为系统输入量
第二章 传递函数 若输入、输出的初始条件为零，即 (K ) x 0 (0 ) 0 K = 0, 1 ,…, n－1
x i(
K)
(0 ) 0
K = 0, 1 ,…, m－1
a n x(0n)( t ) + a n 1 x(0n 1)( t ) + L + a0 x0( t ) 对微分方程两边取拉氏变换得： bm x(i m)( t ) + bm 1 x( m 1)( t ) + L + b0 xi( t )
( ( an X 0n) (t ) + an1 X 0n 1) (t ) + … + a0 X 0 (t )
控制系统的传递函数
表示成零点、极点形式：
m
G(s)
Y (s) X (s)
bm an
Q(s) P(s)
Kg
(s zi )
i 1 n
(s pj )
z 式中： 称为传递函数的零点， i
j 1
称为传递函p数j 的极点。
Kg
bm an
Tuesday, June 16, 2020
—传递系数（零极点形式传递函数增益）
9
传递函数的表现形式
零初始条件下输出量的拉氏变换与输入量拉氏变换之比。也可写成：Y(s)=G(s) X(s)。
通过拉氏反变换可求出时域表达式y(t)。
Tuesday, June 16, 2020
2
传递函数的基本概念
[总结]: 传递函数是由线性微分方程（线性系统）当初始值为零时进行拉氏变化得到
的。
已知传递函数G(s)和输入函数X(s)，可得出输出Y(s)。通过反变换可求出 时域表达式y(t)。
Gm (s)M k f (t), G f
c (s) Gu (s) (s) U f (s)
(s)
Gm kf
(s)
U g (s) Mc (s)
5
传递函数的基本概念||例2-8a8'
求下图系统的传递函数。
R
L
方法1：见例2-1
求L上C式uo的'' (拉t)氏变R换C，uo得' (：t) uo (t) ui (t)
Tuesday, June 16, 2020
4
传递函数的基本概念||例2-8
上式有两个输入量，而传递函数只能处理单输入-单输出系统。对于线性系统， 可以将多个输入分别独立处理，然后叠加起来。下面分别讨论两个输入单独作用时 的传递函数。
控制系统的微分方程
控制系统的微分方程数学模型：描述系统输入、输出变量以及内部各变量之间关系的数学表达式。
描述各变量动态关系的表达式称为动态数学模型，常用的动态模型为微分方程。
建立数学模型的方法分为解析法和实验法。
解析法：依据系统及元件各变量之间所遵循的物理、化学定律列写出变量间的数学表达式，并实验验证。
实验法：对系统或元件输入一定形式的信号（阶跃信号、单位脉冲信号、正弦信号等），根据系统或元件的输出响应，经过数据处理而辨识出系统的数学模型。
建立微分方程的步骤：1、分析各元件的工作原理，明确输入、输出量；2、按照信号的传递顺序，列写各变量的动态关系式；3、化简（线性化、消去中间变量），写出输入、输出变量间的数学表达式。
例：RLC 无源网络如图所示，图中R 、L 、C 分别为电阻（Ω）、电感（H)、电容（F);建立输入电压u r (V)和输出电压u c (V)之间的动态方程。
解由基尔霍夫定律得:()1()()()r di t u t Ri t L i t dt dt C=++⎰1()()c C u t i t dt=⎰消去中间变量i (t ),可得:222()d ()2()()c c c rd u t u t T T u t u t dt dt ζ++=22()()()()c c c rd u t du t LC RC u t u t dt dt ++=令，则微分方程为：2,2LC T RC T ζ==式中：T 称为时间常数，单位为s,称为阻尼比，无量纲。
ζ例设有一弹簧、质量块、阻尼器组成的系统如图所示，当外力F 作用于系统时，系统将产生运动。
建立外力F 与质量块位移y (t )之间的动态方程。
其中弹簧的弹性系数为k ，阻尼器的阻尼系数为f ，质量块的质量为m 。
解对质量块进行受力分析，作用在质量块上的力有：外力: F 弹簧恢复力:Ky(t)阻尼力:()dy t f dt由牛顿第二定律得:22()()()d y t dy t m F f Ky t dt dt =−−22()()()d y t dy t m f Ky t Fdt dt ++=222()()2()d y t dy t T T y t kFdt dt ζ++=令，，/T m K =2/T f K ζ=1/k K =/2f mKζ=则微分方程可以写为该方程描述了由质量块、弹簧和阻尼器组成系统的动态关系，它是一个二阶线性定常微分方程。
第二章 (2.1,2.2)控制系统的微分方程、传递函数
拉氏变换的重要应用——解线性定常微分方程
求微分方程的拉氏变换，注意初值！！
求出 C ( s ) 的表达式 拉氏反变换，求得 c (t )
例1 已知系统的微分方程式，求系统的输出响应。
d 2c(t ) dc(t ) 2 2c(t ) r(t ) 2 dt dt d2 解： 在零初态下应用微分定理： 2 s 2
+
i (t )
R
–
u (t )
+
i (t )
u (t ) i (t ) R
du ( t ) 1 i (t ) dt C
di (t ) u (t ) L dt
电容
C
–
u (t )
+
ቤተ መጻሕፍቲ ባይዱi (t )
电感
u (t )
–
L
机械系统三要素的微分方程
设系统输入量为外力，输出量为位移
d 2 x (t) m f (t) 2 dt
d uc (t ) duc (t ) LC RC uc (t ) ur (t ) 2 dt dt
2
3．机械位移系统
输入量为外力: F (t ) 输出量为位移: y (t )
dy 2 (t ) 依据牛顿定律： F m dt 2
dy (t ) d y (t ) F (t ) ky (t ) f m 2 dt dt
d 2 y (t ) dy (t ) m f ky (t ) F (t ) 2 dt dt
微分方程结构一致 二阶线性定常微分方程
不同形式的物理环节和系统可以建立相同形式的数学模型。
系统微分方程由输出量各阶导数和输 入量各阶导数以及系统的一些参数构成。 n阶线性定常系统的微分方程可描述为：
控制工程基础第三章系统的传递函数
如图所示为机械转动系统，由惯性负载和粘性摩擦阻 尼器构成，以转矩Ti为输入量，以角速度w为输出量
机械转动系统
dw ( t) 其运动方程式为：J + Bw ( t )= Ti ( t) dt W (s ) 1 K 其传递函数为：G ( s)= = = Ti (s ) Js + B Ts + 1 J 1 式中 T= , K = 。 B B
B
i(t)
C
uo (t)
x
机械平移系统
d 2x dx m 2 B k x f t dt dt
RLC电路
X s 1 1 2n Gs ＝ 2 F s ms Bs k k s 2 2n s 2 n
n
k m
B 2 km
C
uo (t )
其微分方程为：Ri( t)+ u0 () t = ui () t du0 () t i( t)= C dt 消去中间变量后，得 du0 () t RC + u0 () t = ui () t dt 通过拉氏变换求得电路的传递函数为： U0 (s) 1 G( s)= = Ui (s) Ts+1 式中 T=RC
4. 微分环节
输出量与输入量的微分成比例的环节，称为微分环节 dxi ( t) 其运动方程式为：x0 ( t )= TD dt 其传递函数为： G ( s)= TD s
式中 TD ─ 微分环节的时 间常数 。
当输入量为单位阶跃信号时，输出量就是脉冲函数，这 在实际中是不可能的。因此，理想的微分环节不能实现，在 实际中用来执行微分作用的都是近似的，称为实际微分环节， 其传递函数具有如下形式：
一阶微分环节和二阶微分环节的微分方程分别为：
自动控制理论传递函数
(is 1)
(
2 k
s2
2
k
k
s
1)
k 1
n2
(Tj s 1) (Tl2s2 2 lTl 1)
j 1
l 1
振荡环节
式中： m1 2m2 m, n1 2n2 n
从上式可以看出：传递函数是一些基本因子的乘积。这些
基本因子就是典型环节所对应的传递函数，是一些最简单、最
基本的一些形式。
2020年4月18日
[解]各环节的微分方程和传递函数分别为：
运放Ⅰ：
u1(t)
k1ue
(t),
G1(s)
U1(s) U e (s)
k1
运放Ⅱ： u2 (t) k2[u1(t) u1(t)], G2 (s)
U 2 (s) U1(s)
k2 (s
1)
功放：
ua
(t)
k3u2 (t),
G3 (s)
Ua (s) U 2 (s)
y (t )
k
(1
e
t T
)
，式中：k为放大系数，T为时间常数。
当k=1时，输入为单位阶跃函数时,时域响应曲线和零极点分
布图如下：y(t) 1
原点处斜率为1/T
0.8
j S平面
0.6
0.632
0.4 0.2
1 T
0
Re
0
t
T
通过原点的 斜率为1/T。只有一个极点（-1/T）。
2020年4月18日
17
R
1 Cs
1 Cs
ui (s) RCs 1
2020年4月18日
19
振荡环节
（四）振荡环节：
时域方程：a2 y'' (t) a1 y' (t) a0 y(t) b0 x(t)
控制系统的传递函数
第二章 控制系统的传递函数
借助表达系统输入、输出之间动态关系的微分方程：
a x (n) no
(t)
...
a x (1) 1o
(t)
a0
xo(t)
b x (m) mi
(t)
...
b x (1) 1i
(t)
b0
xi(t)
可对系统进行描述。
i=0,1…n j=0,1,…m
1、线性定常系统 ai,bj 都不是xo(t)和xi(t)及它们导数的函数，也不 是时间的函数；
第二章 控制系统的传递函数
3、同一控制系统可以有不同的数学模型 同一控制系统具有各种物质运动形式（机械传动、电磁量运动、热
变形等），而不同的物质运动形式又分别受不同的物理规律约束，因而 建立的数学模型可能不同。 因此，建立数学模型时，一定要搞清输入 t
b1s m1 a1s n 1
bm1s bm an1s an
(n>m)
2.3.2 几点说明（性质） （1）传递函数是系统数学模型的又一种形式，也是一种表示输入输出
的模型形式。
它表示了系统本身的特性而与输入信号无关。
它仅能表示输入输出关系，而无法表示出系统的内部结构。
传递函数的分母和分子分别反映系统本身与外界无关的固有特性 和系统同外界之间的联系。
（b）图给出了一种大为简化的悬浮系统，设 p 点的运动 为系统的输入，车体的垂直运
动 为系统的输出，只考虑车体在垂直方向的运动时，求
。
（a）汽车悬浮系统
（b）减化悬浮系统
第二章 控制系统的传递函数
2.3.4 反馈控制系统的传递函数
（解释一下方框图----将系统中各元件的名称或功用写在框图单元中，并标 明它们之间的连接顺序和信号流向。主要用来说明系统的构成和工作原理）
自动控制原理传递函数
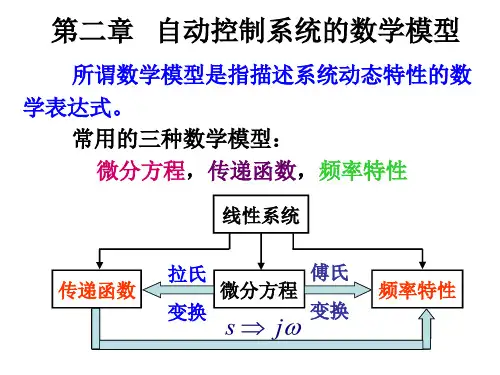
自动控制原理传递函数
自动控制原理传递函数是描述控制系统输入输出关系的数学模型，通常以s域传递函数的形式表示。
在控制系统中，输入信
号经过传递函数的作用，产生输出信号。
传递函数是由系统的微分方程所得到的拉普拉斯变换得到的。
控制系统中的传递函数通常是指示系统的输入与输出之间的关系，称为开环传递函数。
在控制系统中，传递函数是通过将系统的微分方程进行拉普拉斯变换得到的。
传递函数可以用来分析系统的动态性能，并通过调整传递函数的参数来改善系统的稳定性、快速性和准确性。
传递函数通常用以下形式表示：
G(s) = Y(s) / U(s)
其中，G(s)是传递函数，Y(s)是输出信号的拉普拉斯变换，U(s)是输入信号的拉普拉斯变换。
传递函数描述了输入与输出信号之间的关系，以及系统对输入信号的响应速度和稳定性等性能。
控制系统设计中，可以根据给定的性能要求，选择合适的传递函数来实现所需的控制效果。
常见的传递函数包括比例传递函数、积分传递函数、微分传递函数以及它们的组合。
通过对传递函数进行数学分析和计算，可以得到系统的稳定性、频率响应、步跃响应等性能指标。
控制系统设计师可以根据这些指标来优化系统的性能，并进行参数调整和改进。
总之，传递函数是自动控制原理中非常重要的概念，它描述了控制系统输入与输出之间的关系。
通过分析和优化传递函数，可以实现控制系统的稳定性、准确性和快速性等性能要求。
控制系统的传递函数
R
1 Cs
uo
uo (s) 1
ui (s) RCs
② 电动机（忽略惯性和摩擦）
图中，为转角，为' 角速度。
ui
齿轮组
' kui
可见， '
~
ui
t
0 kui (t)dt
为比例环节，
'
~ ui 为积分环节。
Friday, July 19, 2024
16
惯性环节
（三）惯性环节
时域方程：Ty ' (t) y(t) kx(t), t 0
传递函数是由线性微分方程（线性系统）当初始值为零 时进行拉氏变化得到的。
已知传递函数G(s)和输入函数X(s)，可得出输出Y(s)。 通过反变换可求出时域表达式y(t)。
可以由环节的微分方程直接得出传递函数，只要将各阶导
数用各阶s代替即可。即：d
dt
s,...,
dn dt n
sn
Friday, July 19, 2024
Friday, July 19, 2024
9
传递函数的表现形式
[传递函数的几种表现形式]：
表示为有理分式形式：G(s)
Y (s) X (s)
bm s m an s n
bm1sm1 b0 an1sn1 a0
式中：ai , bj —为实常数，一般n≥m
上式称为n阶传递函数，相应的系统为n阶系统。
m
写成时间常数形式：G(s) b0 Q(s) K a0 P(s)
(is 1)
i 1 n
(Tjs 1)
显然： i
1 zi
,
1 Ti p j ,
j 1
i ,Tj 分别称为时间常数，K称为放大系数 m
控制系统的传递函数
(2.6 5)
式中第一项称为零状态响应， 由ur(t)决定的分量； 第二项称为零输入响应， 由初始电压uc (0)决定的 分量。
图2-15表示各分量的变化曲线， 电容电压uc (t)即为两者的合成。
图2-15 RC网络的阶跃响应曲线
RCs + 1 当输入电压ur(t)一定时，电路输出响应的拉氏变换Uc(s)完全由 1/(RCs+1)所确定，式(2.66)亦可写为:
一、传递函数的概念
图2-14所示的RC电路中电 容的端电压uc(t)。根据克希 霍夫定律，可列写如下微分 方程：
i(t)R+uc (t) = ur (t)
(2.60)
1 u c (t ) = ∫ i ( t )d t (2.61) C 消去中间变量i(t)，得到输入ur(t) 与输出uc(t)之间的线性定常微分 方程: d u c (t ) RC + uc (t ) = u r (t ) (2.62) dt
T1 s G (s) = T2 s + 1
(2.75)
它由理想微分环节和惯性环节组成，如图2-21(c)、(d)所示。在 低频时近似为理想微分环节，否则就有式(2.75)的传递函数。
图2-21 微分环节
（五）振荡环节 振荡环节的传递函数为：
2 ωn 1 G (s) = 2 2 = 2 2 T s + 2T ζ s + 1 s + 2ω nζ s + ω n
图2-23 延滞环节
延滞环节的传递函数可求之如下： c(t)= r(t－τ) 其拉氏变换为:
C ( s) = ∫ r (t − τ )e dt = ∫ r (ξ )e − s (ξ +τ ) dξ
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
传递函数的极点就是微分方程的特征根，它们决定了所 描述系统自由运动的模态。
传递函数的零点并不形成自由运动的模态，但它们影响 各模态在响应中所占的比重，因而影响响应曲线的形状。
传递函数 X (s) A sa
零极点分布图
j
-a
0
i
Q: 零点在哪？
时域脉冲响应 x(t) Aeat
0
29
传递函数
X
(s)
比较系数法或特值法 配方法
例1：已知F (s) 10(s 4)
，求 f (t)
(s 1)(s 2)(s 3)
例2：已知 F (s) 10 ，求 f (t)
s(s 2)
例3：已知
F
(s)
10(s s2 (s
2) 1)
，求
f (t)
例4：已知
F (s)
s2
20 4s 13
，求
f (t)
查表法：将 F (s)部分分式展开，变换成能在表中直接查 到原函数的形式。
FF(s()s) BB((ss) AA((ss)
bc00ssmmbc1s1msm11 bmc1ms1sbm cm s(nsa1ps1n)(1 sp2 )an1s( sanpn )
（1） A(s) 0 不同极点
留数法
（2） A(s) 0 有重极点 （3） A(s) 0 有共轭极点
dt 2
dt
微分方程结构一致 二阶线性定常微分方程
不同形式的物理环节和系统可以建立相同形式的数学模型。
系统微分方程由输出量各阶导数和输 入量各阶导数以及系统的一些参数构成。 n阶线性定常系统的微分方程可描述为：
nm
复习拉普拉斯变换
已知原函数为f(t)，
其中：s j
（（（（312）546）））单单序指单正位号位数位弦加阶 斜函脉函原速f跃 坡函(数冲数t度)数函函函se数i数象数nF函a(s1tt数)(12(tt()ta2) 5 0) eat
(s
A1s a)2
B1 b2
零极点分布图
j
b
-a 0
i
时域脉冲响应
x(t) Aeat sin(bt )
0
30
传递函数
X (s)
A1s B1 s2 b2
零极点分布图
j
b
0
i
时域脉冲响应
x(t) Asin(bt )
标准形式： 左端：与输出量有关的项； 右端：与输入量有关的项；
各导数项均按降幂排列！
电气系统三要素的微分方程
电阻
设系统输入量为电流，输出量为电压
+ i(t) R
–
u(t)
u(t) i(t) R
电容 电感
i(t) C
+
–
u(t)
+ i(t)
u(t)
L
–
du(t) 1 i(t) dt C
u(t) L di(t) dt
a0sn a1sn1 an1s an C(s)
b0sm b1sm1 bm1s am R(s)
系统传递函数的一般表达式为：
G(s)
C(s) R(s)
b0 s m a0 s n
b1sm1 a1sn1
bm1s bm an1s an
nm
G(s)
C(s) R(s)
b0 s m a0 s n
b1sm1 a1sn1
bm1s bm an1s an
将分子与分母多项式分别用因式连乘的形式来表示，即
G(s) =
K0 (s –z1 ) (s –z2 ) ··· (s –zm ) (s –p1 ) (s –p2 ) ··· (s –pn )
nm
K0 — 放大系数
s = p1 , p2 ··· , pn — 传递函数的极点
sin
t
零输入 响应
第三节 传递函数
输入
r(t)
c(t)
微微分分方方程程
输出
输入的拉氏变换
R(s)
C(s)
GG((ss))
输出的拉氏变换
一、传递函数的定义
线性定常系统的传递函数，定义为零初始条件下， 系统输出量的拉氏变换与输入量的拉氏变换之比。
传递函数 输出信号的拉氏变换
C(s)
输入信号的拉氏变换 零初始条件 R(s)
+
+
i
u
Cu
r-
-c
微分方程： 信号量小写变大写，下标不变，t变s
LC
d
2uc (t) dt 2
RC
duc (t) dt
uc
(t)
ur
(t)
Uc (s) L[uc (t)]
Ur (s) L[ur (t)] 微分定理
零初始条件 LCs2Uc (s) RCsUc (s) Uc (s) Ur (s)
传递函数
G(s)
Uc (s) Ur (s)
LCs2
1 RCs
1
机机械械位位移移系系统统
微分方程：
m d 2 y(t) f dy(t) ky(t) F (t)
dt 2
dt
零初始条件
微分定理
ms2Y (s) fsY (s) kY (s) F (s)
传递函数
G(s)
Y (s) F (s)
ms2
该方法适用于内部结构清楚的系统。
2、系统辨识法(实验法) 利用系统或元件的输入-输出信号来建立数学模
型。 该方法适用于对系统或元件一无所知的情况下。
第一节 控制系统的微分方程
一、 建立系统微分方程的一般步骤
（1） 确定系统的输入变量和输出变量 。
（2） 建立初始微分方程组。
（3） 消除中间变量，将式子标准化。
s
(s2 4s 5)C(s) (s 4)c(0) c '(0) 1 s
C(s)
s(s2
1 4s
5)
(s
4)c(0) s2 4s
c '(0) 5
零状态 响应
1 5
1 s
4(s 2) (s 2)2 1
(s
13 2)2
1
查表
c(t)
1 5
1(t)
4e2t
cos
t
13e2t
1 sa
数数拉拉拉学学f氏氏氏f(表表变t变(变)ft12达达换)(f换换t(f(式t)式为t为(为))t10s：：)：(：(：i10ettn)()t0ltia)mt0102t1t110st2(1(0tt((ttttttt06700tt))0000000或))t00tcsions
t
t
s2 2
s s2 2
拉氏变换
线性微分方程
代数方程
（时域ｔ）
（复数域ｓ）
微分方程的解
代数方程的解
（时域ｔ） 拉氏反变换 （复数域ｓ）
f (t) L1[F (s)]
拉氏变换的重要应用——解线性定常微分方程
求微分方程的拉氏变换，注意初值！！
求出 C(s) 的表达式
拉氏反变换，求得 c(t)
例1 已知系统的微分方程式，求系统的输出响应。
第二章 自动控制系统的数学模型
所谓数学模型是指描述系统动态特性的数 学表达式。
常用的三种数学模型： 微分方程，传递函数，频率特性
线性系统
传递函数
拉氏
傅氏
微分方程
变换
变换
频率特性
建建立立控控制制系系统统数数学学模模型型的的方方法法
1、理论分析法 根据组成系统的各个元部件所遵循的物理规律或
者化学规律，列写各部件的输入输出关系，然后根据 系统的结构方块图或各信号的传递关系，消除中间变 量，最后找出输入输出关系式。
6. 传函G(s)的反拉氏变换为系统的脉冲响应g(t)，即传函 可定义为
7. 传函是在零初始条件下定义的,只能反映零初始条件 下输入信号引起的输出，不能反映非零初始条件引起 的输出。
思考：设系统传递函数
C(s) R(s)
s2
3 2s
3
，试求初始
条件分别为 c(0) 1 和 c(0) 0 时系统在输入
输出在左，输入在右
按降幂排列
m
d
2 y(t) dt 2
f
dy(t) ky(t) F (t) dt
相似系统
——具有相同结构的数学模型
RL
+
+
i
ur
C uc
-
-
LC
d
2uc (t) dt 2
RC
duc (t) dt
uc
(t)
ur
(t)
m d 2 y(t) f dy(t) ky(t) F (t)
1 fs
k
相似系统
——具有相同结构的数学模型
RL
+
+
i
ur
C uc
-
-
G(s) Uc(s)
1
U (s) LCs2 RCs 1
G(s) Y(s)
1
F (s) ms2 fs k
传递函数 结构一致
设线性定常系统由下述n阶线性定常微分方程描述：
零初始条件——输入、输出及其各阶导数初值为零
s = z1 , z2 ··· , zm — 传递函数的零点
在复平面上表示传递函数的零点和极点的图形，
称为传递函数的零极点分布图。
传递函数分母多项式就是相应微分方程的特征多项 式，传递函数的极点就是微分方程的特征根。
二、传递函数的性质
1. 传递函数是复变量s的有理真分式函数，具有复变函数的 所有性质。 2. 传函与微分方程具有相通性，零初始条件下可通过n阶导 数与n阶s的置换得到传递函数。 3.传递函数表征了系统本身的动态特性。（传递函数只取 决于系统本身的结构参数，而与输入和初始条件等外部因 素无关，可见传递函数有效地描述了系统的固有特性。） 4.只能描述线性定常系统与单输入单输出系统，且内部许 多中间变量的变化情况无法反映，是系统一种外部描述。 5.如果存在零极点对消情况，传递函数就不能正确反映系 统的动态特性。
传递函数的零点并不形成自由运动的模态，但它们影响 各模态在响应中所占的比重，因而影响响应曲线的形状。
传递函数 X (s) A sa
零极点分布图
j
-a
0
i
Q: 零点在哪？
时域脉冲响应 x(t) Aeat
0
29
传递函数
X
(s)
比较系数法或特值法 配方法
例1：已知F (s) 10(s 4)
，求 f (t)
(s 1)(s 2)(s 3)
例2：已知 F (s) 10 ，求 f (t)
s(s 2)
例3：已知
F
(s)
10(s s2 (s
2) 1)
，求
f (t)
例4：已知
F (s)
s2
20 4s 13
，求
f (t)
查表法：将 F (s)部分分式展开，变换成能在表中直接查 到原函数的形式。
FF(s()s) BB((ss) AA((ss)
bc00ssmmbc1s1msm11 bmc1ms1sbm cm s(nsa1ps1n)(1 sp2 )an1s( sanpn )
（1） A(s) 0 不同极点
留数法
（2） A(s) 0 有重极点 （3） A(s) 0 有共轭极点
dt 2
dt
微分方程结构一致 二阶线性定常微分方程
不同形式的物理环节和系统可以建立相同形式的数学模型。
系统微分方程由输出量各阶导数和输 入量各阶导数以及系统的一些参数构成。 n阶线性定常系统的微分方程可描述为：
nm
复习拉普拉斯变换
已知原函数为f(t)，
其中：s j
（（（（312）546）））单单序指单正位号位数位弦加阶 斜函脉函原速f跃 坡函(数冲数t度)数函函函se数i数象数nF函a(s1tt数)(12(tt()ta2) 5 0) eat
(s
A1s a)2
B1 b2
零极点分布图
j
b
-a 0
i
时域脉冲响应
x(t) Aeat sin(bt )
0
30
传递函数
X (s)
A1s B1 s2 b2
零极点分布图
j
b
0
i
时域脉冲响应
x(t) Asin(bt )
标准形式： 左端：与输出量有关的项； 右端：与输入量有关的项；
各导数项均按降幂排列！
电气系统三要素的微分方程
电阻
设系统输入量为电流，输出量为电压
+ i(t) R
–
u(t)
u(t) i(t) R
电容 电感
i(t) C
+
–
u(t)
+ i(t)
u(t)
L
–
du(t) 1 i(t) dt C
u(t) L di(t) dt
a0sn a1sn1 an1s an C(s)
b0sm b1sm1 bm1s am R(s)
系统传递函数的一般表达式为：
G(s)
C(s) R(s)
b0 s m a0 s n
b1sm1 a1sn1
bm1s bm an1s an
nm
G(s)
C(s) R(s)
b0 s m a0 s n
b1sm1 a1sn1
bm1s bm an1s an
将分子与分母多项式分别用因式连乘的形式来表示，即
G(s) =
K0 (s –z1 ) (s –z2 ) ··· (s –zm ) (s –p1 ) (s –p2 ) ··· (s –pn )
nm
K0 — 放大系数
s = p1 , p2 ··· , pn — 传递函数的极点
sin
t
零输入 响应
第三节 传递函数
输入
r(t)
c(t)
微微分分方方程程
输出
输入的拉氏变换
R(s)
C(s)
GG((ss))
输出的拉氏变换
一、传递函数的定义
线性定常系统的传递函数，定义为零初始条件下， 系统输出量的拉氏变换与输入量的拉氏变换之比。
传递函数 输出信号的拉氏变换
C(s)
输入信号的拉氏变换 零初始条件 R(s)
+
+
i
u
Cu
r-
-c
微分方程： 信号量小写变大写，下标不变，t变s
LC
d
2uc (t) dt 2
RC
duc (t) dt
uc
(t)
ur
(t)
Uc (s) L[uc (t)]
Ur (s) L[ur (t)] 微分定理
零初始条件 LCs2Uc (s) RCsUc (s) Uc (s) Ur (s)
传递函数
G(s)
Uc (s) Ur (s)
LCs2
1 RCs
1
机机械械位位移移系系统统
微分方程：
m d 2 y(t) f dy(t) ky(t) F (t)
dt 2
dt
零初始条件
微分定理
ms2Y (s) fsY (s) kY (s) F (s)
传递函数
G(s)
Y (s) F (s)
ms2
该方法适用于内部结构清楚的系统。
2、系统辨识法(实验法) 利用系统或元件的输入-输出信号来建立数学模
型。 该方法适用于对系统或元件一无所知的情况下。
第一节 控制系统的微分方程
一、 建立系统微分方程的一般步骤
（1） 确定系统的输入变量和输出变量 。
（2） 建立初始微分方程组。
（3） 消除中间变量，将式子标准化。
s
(s2 4s 5)C(s) (s 4)c(0) c '(0) 1 s
C(s)
s(s2
1 4s
5)
(s
4)c(0) s2 4s
c '(0) 5
零状态 响应
1 5
1 s
4(s 2) (s 2)2 1
(s
13 2)2
1
查表
c(t)
1 5
1(t)
4e2t
cos
t
13e2t
1 sa
数数拉拉拉学学f氏氏氏f(表表变t变(变)ft12达达换)(f换换t(f(式t)式为t为(为))t10s：：)：(：(：i10ettn)()t0ltia)mt0102t1t110st2(1(0tt((ttttttt06700tt))0000000或))t00tcsions
t
t
s2 2
s s2 2
拉氏变换
线性微分方程
代数方程
（时域ｔ）
（复数域ｓ）
微分方程的解
代数方程的解
（时域ｔ） 拉氏反变换 （复数域ｓ）
f (t) L1[F (s)]
拉氏变换的重要应用——解线性定常微分方程
求微分方程的拉氏变换，注意初值！！
求出 C(s) 的表达式
拉氏反变换，求得 c(t)
例1 已知系统的微分方程式，求系统的输出响应。
第二章 自动控制系统的数学模型
所谓数学模型是指描述系统动态特性的数 学表达式。
常用的三种数学模型： 微分方程，传递函数，频率特性
线性系统
传递函数
拉氏
傅氏
微分方程
变换
变换
频率特性
建建立立控控制制系系统统数数学学模模型型的的方方法法
1、理论分析法 根据组成系统的各个元部件所遵循的物理规律或
者化学规律，列写各部件的输入输出关系，然后根据 系统的结构方块图或各信号的传递关系，消除中间变 量，最后找出输入输出关系式。
6. 传函G(s)的反拉氏变换为系统的脉冲响应g(t)，即传函 可定义为
7. 传函是在零初始条件下定义的,只能反映零初始条件 下输入信号引起的输出，不能反映非零初始条件引起 的输出。
思考：设系统传递函数
C(s) R(s)
s2
3 2s
3
，试求初始
条件分别为 c(0) 1 和 c(0) 0 时系统在输入
输出在左，输入在右
按降幂排列
m
d
2 y(t) dt 2
f
dy(t) ky(t) F (t) dt
相似系统
——具有相同结构的数学模型
RL
+
+
i
ur
C uc
-
-
LC
d
2uc (t) dt 2
RC
duc (t) dt
uc
(t)
ur
(t)
m d 2 y(t) f dy(t) ky(t) F (t)
1 fs
k
相似系统
——具有相同结构的数学模型
RL
+
+
i
ur
C uc
-
-
G(s) Uc(s)
1
U (s) LCs2 RCs 1
G(s) Y(s)
1
F (s) ms2 fs k
传递函数 结构一致
设线性定常系统由下述n阶线性定常微分方程描述：
零初始条件——输入、输出及其各阶导数初值为零
s = z1 , z2 ··· , zm — 传递函数的零点
在复平面上表示传递函数的零点和极点的图形，
称为传递函数的零极点分布图。
传递函数分母多项式就是相应微分方程的特征多项 式，传递函数的极点就是微分方程的特征根。
二、传递函数的性质
1. 传递函数是复变量s的有理真分式函数，具有复变函数的 所有性质。 2. 传函与微分方程具有相通性，零初始条件下可通过n阶导 数与n阶s的置换得到传递函数。 3.传递函数表征了系统本身的动态特性。（传递函数只取 决于系统本身的结构参数，而与输入和初始条件等外部因 素无关，可见传递函数有效地描述了系统的固有特性。） 4.只能描述线性定常系统与单输入单输出系统，且内部许 多中间变量的变化情况无法反映，是系统一种外部描述。 5.如果存在零极点对消情况，传递函数就不能正确反映系 统的动态特性。