八年级期中精选试卷测试卷 (word版,含解析)

2023-2024学年河南省信阳市罗山县八年级（上）期中生物试卷一、选择题（共20小题，每小题1分，共20分。

每小题只有一个选项符合题目要求。

）1．（1分）我国淡水鱼中，被称为四大家鱼的是（ ）A．草鱼．鲫鱼．青鱼．鲤鱼B．鲢鱼．草鱼．鲫鱼．青鱼C．鳙鱼．鲢鱼．草鱼．青鱼D．草鱼．青鱼．鲤鱼．鳙鱼2．（1分）下列各组动物行为，从行为获得的途径看属于同一类的是（ ）A．孔雀开屏、惊弓之鸟B．鼠走迷宫、大雁南飞C．老马识途、小猴学车D．黄牛耕地、蜘蛛结网3．（1分）气温升高，草丛中会有毒蛇出没，应注意安全。

要了解某种毒蛇习性（ ）A．《鱼类学》B．《昆虫学》C．《爬行动物学》D．《哺乳动物学》4．（1分）下列有关生物与人类密切关系的叙述，正确的是（ ）①蚯蚓能疏松土壤，提高作物产量②家畜是食物中动物蛋白的重要来源③有的鸟具有很高的观赏价值④鱼类的侧线用来保持身体的平衡A．①②③B．①②④C．①③④D．②③④5．（1分）中医药材很多来自动物制品，下列对应错误的一项是（ ）A．知了——蝉蜕B．河蚌——珍珠粉C．水蛭——蛭素D．蜗牛——海螵蛸6．（1分）小明找到了四个与动物有关的成语，其中所涉及到的动物都属于恒温动物的成语是（ ）A．虎头蛇尾B．鹬蚌相争C．蛛丝马迹D．鸡犬不宁7．（1分）海马身体侧扁，全身无鳞，躯干被骨板包围，在水中能以身立状前进，有鳍，终生生活在水中，由此可知（ ）A．甲壳动物B．软体动物C．鱼类D．无法判断8．（1分）体壁有黏液，能够进行气体交换的是（ ）A．蟾蜍和蝾螈B．青蛙和蜥蜴C．蚯蚓和鲤鱼D．大鲵和鳄鱼9．（1分）大山雀的食量很大，一天所吃的食物相当于自身重量的10%～30%。

从运动方面分析，其主要原因是（ ）A．为繁殖后代做准备B．为了扩大分布范围C．为了维持较高的体温D．飞行需要消耗大量的能量10．（1分）红火蚁是全球公认的百种最具危险的入侵物种之一。

2021年我国有12个省份遭到了红火蚁的入侵。

2023～2024学年度上学期期中阶段质量检测试题八年级生物2023.11注意事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共8页，满分100分，考试时间60分钟。

答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在答题卡规定的位置。

考试结束后，将本试卷和答题卡一并交回。

2.答题注意事项见答题卡，答在本试卷上不得分。

第Ⅰ卷（共50分）第Ⅰ卷为选择题，共25道题，每题2分，共50分。

在每题所列出的四个选项中，只有一项是最符合题目要求的。

请将选出的答案用2B铅笔涂到答题卡相应位置。

1.桃花水母又称桃花鱼，是一种最原始、最低等的无脊椎腔肠动物，距今已有6.5亿年，出现时间比恐龙早几亿年。

桃花水母对生存环境有极高的要求，水质不能有任何污染，活体罕见，极难制成标本，被列为世界最高级别的“极危生物”。

下列有关桃花水母的叙述错误的是（）A.用刺细胞进行攻击和防御B.身体由内胚层和外胚层两层细胞组成C.身体呈辐射对称D.食物从口摄入，从肛门排出残渣2.在蒙山一条小溪的石块下面，人们发现了一种小动物，它们身体像柳叶，背腹扁平，背面呈褐色，三角形的前端背面有两个黑色眼点。

下列关于这种动物的叙述，错误的是（）A.眼点能够感光B.可以通过管状的咽捕食水中的小动物C.属于线形动物，有口无肛门D.身体呈两侧对称，前端感觉器官集中3.建国初，蛔虫病曾在我国大面积肆虐，是由于蛔虫寄生在人体小肠内所引起的，表现出面部白斑、腹痛、生长迟缓等症状，严重时可导致肠梗阻、肠穿孔等，给人民健康造成了巨大伤害。

下列关于蛔虫及蛔虫病说法错误的是（）A.体表有角质层，具有保护作用B.消化管结构简单，肠仅由一层细胞组成C.生殖器官和运动器官都很发达D.注意个人饮食卫生，有利于预防蛔虫病4.单环刺缢，俗称海肠，其身体呈长圆筒形，腹部有刚毛，末端有横裂形的肛门。

根据这些特征你认为海肠最可能属于（）A.腔肠动物B.线形动物C.环节动物D.软体动物5.在中医学上，蚯蚓被称为地龙。

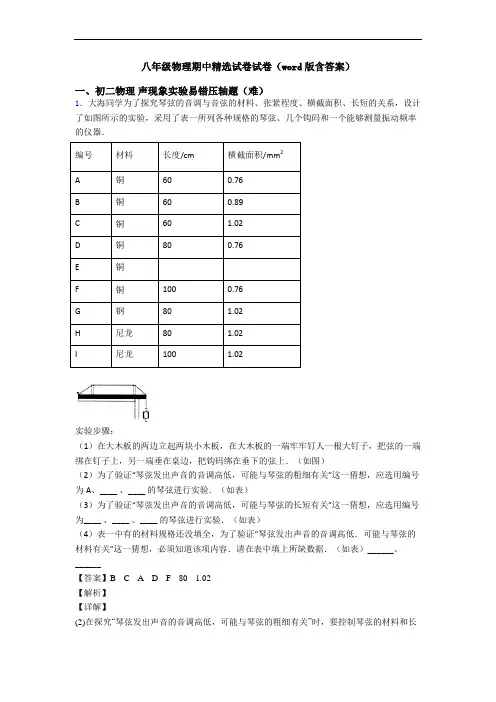
八年级物理期中精选试卷试卷（word版含答案）一、初二物理声现象实验易错压轴题（难）1．大海同学为了探究琴弦的音调与音弦的材料、张紧程度、横截面积、长短的关系，设计了如图所示的实验，采用了表一所列各种规格的琴弦、几个钩码和一个能够测量振动频率的仪器．编号材料长度/cm 横截面积/mm2A 铜60 0.76B 铜60 0.89C 铜60 1.02D 铜80 0.76E 铜F 铜100 0.76G 钢80 1.02H 尼龙80 1.02I 尼龙100 1.02实验步骤：（1）在大木板的两边立起两块小木板，在大木板的一端牢牢钉人一根大钉子，把弦的一端绑在钉子上，另一端垂在桌边，把钩码绑在垂下的弦上．（如图）（2）为了验证“琴弦发出声音的音调高低，可能与琴弦的粗细有关”这一猜想，应选用编号为A、____ 、____ 的琴弦进行实验．（如表）（3）为了验证“琴弦发出声音的音调高低，可能与琴弦的长短有关”这一猜想，应选用编号为____ 、____ 、____ 的琴弦进行实验．（如表）（4）表一中有的材料规格还没填全，为了验证“琴弦发出声音的音调高低．可能与琴弦的材料有关”这一猜想，必须知道该项内容．请在表中填上所缺数据．（如表）______、______【答案】B C A D F80 1.02【解析】【详解】(2)在探究“琴弦发出声音的音调高低，可能与琴弦的粗细有关”时，要控制琴弦的材料和长度相同，故选A. B. C的琴弦进行实验；(3)探究“琴弦发出声音的音调高低，可能与琴弦的长短有关”时，应控制琴弦的材料和横截面积相同，所以选A. D. F的琴弦进行实验；(4)为了验证“琴弦发出声音的音调高低。

可能与琴弦的材料有关”时，应控制琴弦的长度和横截面积相同，材料不同，符合条件的只有G、H，所以D项中应是：80；1.02.2．（1）把正在发声的手机放在玻璃罩内（如图甲所示），逐渐抽出其中的空气听到的声音越来越小，最后几乎听不到铃声，这说明______．（2）图乙是探究“”的实验装置图，把平面镜放在水平桌面上，再把一张可以沿ON 向前或向后折的纸板竖直地立在平面镜上，纸板上的ON垂直于镜面。

八年级数学上册期中精选试卷检测题（WORD版含答案）一、八年级数学全等三角形解答题压轴题（难）1．如图，AB=12cm，AC⊥AB，BD⊥AB ，AC=BD=9cm，点P在线段AB上以3 cm/s的速度，由A向B运动，同时点Q在线段BD上由B向D运动．（1）若点Q的运动速度与点P的运动速度相等，当运动时间t=1（s），△ACP与△BPQ 是否全等？说明理由，并直接判断此时线段PC和线段PQ的位置关系；（2）将“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA”，其他条件不变．若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能使△ACP与△BPQ全等.（3）在图2的基础上延长AC，BD交于点E，使C，D分别是AE，BE中点，若点Q以（2）中的运动速度从点B出发，点P以原来速度从点A同时出发，都逆时针沿△ABE三边运动，求出经过多长时间点P与点Q第一次相遇．【答案】（1）△ACP≌△BPQ，理由见解析；线段PC与线段PQ垂直（2）1或32（3）9s 【解析】【分析】（1）利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP≌△BPQ，分两种情况：①AC=BP，AP=BQ，②AC=BQ，AP=BP，建立方程组求得答案即可．（3）因为V Q＜V P，只能是点P追上点Q，即点P比点Q多走PB+BQ的路程，据此列出方程，解这个方程即可求得．【详解】（1）当t=1时，AP=BQ=3，BP=AC=9，又∵∠A=∠B=90°，在△ACP与△BPQ中，AP BQA BAC BP=⎧⎪∠=∠⎨⎪=⎩，∴△ACP≌△BPQ（SAS），∴∠ACP=∠BPQ，∴∠APC+∠BPQ=∠APC+∠ACP=90°，∠CPQ=90°，则线段PC与线段PQ垂直.（2）设点Q 的运动速度x,①若△ACP ≌△BPQ ，则AC=BP ，AP=BQ ，912t t xt =-⎧⎨=⎩， 解得31t x =⎧⎨=⎩， ②若△ACP ≌△BPQ ，则AC=BQ ，AP=BP ，912xt t t =⎧⎨=-⎩解得632t x =⎧⎪⎨=⎪⎩， 综上所述，存在31t x =⎧⎨=⎩或632t x =⎧⎪⎨=⎪⎩使得△ACP 与△BPQ 全等. （3）因为V Q ＜V P ，只能是点P 追上点Q ，即点P 比点Q 多走PB+BQ 的路程，设经过x 秒后P 与Q 第一次相遇，∵AC=BD=9cm ，C ，D 分别是AE ，BD 的中点；∴EB=EA=18cm.当V Q =1时，依题意得3x=x+2×9，解得x=9；当V Q =32时， 依题意得3x=32x+2×9， 解得x=12.故经过9秒或12秒时P 与Q 第一次相遇.【点睛】本题考查了一元一次方程的应用，解题的关键是熟练的掌握一元一次方程的性质与运算.2．已知4AB cm =，3AC BD cm ==.点P 在AB 上以1/cm s 的速度由点A 向点B 运动，同时点Q 在BD 上由点B 向点D 运动，它们运动的时间为()t s ．（1）如图①，AC AB ⊥，BD AB ⊥，若点Q 的运动速度与点P 的运动速度相等，当1t =时，ACP △与BPQ 是否全等，请说明理由，并判断此时线段PC 和线段PQ 的位置关系；（2）如图②，将图①中的“AC AB ⊥，BD AB ⊥”为改“60CAB DBA ∠=∠=︒”，其他条件不变．设点Q的运动速度为/xcm s，是否存在实数x，使得ACP△与BPQ 全等？若存在，求出相应的x、t的值；若不存在，请说明理由．【答案】（1）全等，PC与PQ垂直；（2）存在，11tx=⎧⎨=⎩或232tx=⎧⎪⎨=⎪⎩【解析】【分析】（1）利用SAS证得△ACP≌△BPQ，得出∠ACP=∠BPQ，进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出结论即可；（2）由△ACP≌△BPQ，分两种情况：①AC=BP，AP=BQ，②AC=BQ，AP=BP，建立方程组求得答案即可．【详解】解：（1）当t=1时，AP=BQ=1，BP=AC=3，又∠A=∠B=90°，在△ACP和△BPQ中，AP BQA BAC BP=⎧⎪∠=∠⎨⎪=⎩，∴△ACP≌△BPQ（SAS）．∴∠ACP=∠BPQ，∴∠APC+∠BPQ=∠APC+∠ACP=90°．∴∠CPQ=90°，即线段PC与线段PQ垂直．（2）①若△ACP≌△BPQ，则AC=BP，AP=BQ，34tt xt=-⎧⎨=⎩，解得11tx=⎧⎨=⎩，②若△ACP≌△BQP，则AC=BQ，AP=BP，34xtt t=⎧⎨=-⎩，解得232tx=⎧⎪⎨=⎪⎩，综上所述，存在11tx=⎧⎨=⎩或232tx=⎧⎪⎨=⎪⎩使得△ACP与△BPQ全等．【点睛】本题考查全等三角形的判定与性质，在解题时注意分类讨论思想的运用．3．如图1，在长方形ABCD中，AB=CD=5 cm， BC=12 cm，点P从点B出发，以2cm/s的速度沿BC向点C运动，设点P的运动时间为ts．（1）PC=___cm；(用含t的式子表示)（2）当t为何值时，△ABP≌△DCP？．（3）如图2，当点P从点B开始运动，此时点Q从点C出发，以vcm/s的速度沿CD向点D运动，是否存在这样的v值，使得某时刻△ABP与以P，Q，C为顶点的直角三角形全等？若存在，请求出v的值；若不存在，请说明理由．【答案】（1）()122t-；（2）3t=；（3）存在，2v=或53v=【解析】【分析】（1）根据P点的运动速度可得BP的长，再利用BC的长减去BP的长即可得到PC的长；（2）先根据三角形全等的条件得出当BP=CP，列方程求解即得；（3）先分两种情况：当BP=CQ，AB=PC时，△ABP≌△PCQ；或当BA=CQ，PB=PC 时，△ABP≌△QCP，然后分别列方程计算出t的值，进而计算出v的值．【详解】解：（1）当点P以2cm/s的速度沿BC向点C运动时间为ts时2BP tcm=∵12BC cm=∴()122PC BC BP t cm=-=-故答案为：()122t-（2）∵ABP DCP∆≅∆∴BP CP=∴2122t t =-解得3t =．（3）存在，理由如下：①当BP=CQ ，AB=PC 时，△ABP ≌△PCQ ，∴PC=AB=5∴BP=BC-PC=12-5=7∵2BP tcm =∴2t=7解得t=3.5∴CQ=BP=7，则3.5v=7解得2v =．②当BA CQ =，PB PC =时，ABP QCP ∆≅∆∵12BC cm = ∴162BP CP BC cm === ∵2BP tcm =∴26t = 解得3t =∴3CQ vcm =∵5AB CQ cm ==∴35v = 解得53v =． 综上所述，当2v =或53v =时，ABP ∆与以P ，Q ，C 为顶点的直角三角形全等． 【点睛】本题考查全等三角形的判定及性质和矩形的性质，解题关键是将动态情况化为某一状态情况，并以这一状态为等量关系建立方程求解．4．如图1，Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D 是BC 边的中点连接AD ，则易证AD ＝BD ＝CD ，即AD ＝12BC ；如图2，若将题中AB ＝AC 这个条件删去，此时AD 仍然等于12BC ． 理由如下：延长AD 到H ，使得AH ＝2AD ，连接CH ，先证得△ABD ≌△CHD ，此时若能证得△ABC ≌△CHA ，即可证得AH ＝BC ，此时AD ＝12BC ，由此可见倍长过中点的线段是我们三角形证明中常用的方法．（1）请你先证明△ABC≌△CHA，并用一句话总结题中的结论；（2）现将图1中△ABC折叠（如图3），点A与点D重合，折痕为EF，此时不难看出△BDE和△CDF都是等腰直角三角形．BE＝DE，CF＝DF．由勾股定理可知DE2+DF2＝EF2，因此BE2+CF2＝EF2，若图2中△ABC也进行这样的折叠（如图4），此时线段BE、CF、EF还有这样的关系式吗？若有，请证明；若没有，请举反例．（3）在（2）的条件下，将图3中的△DEF绕着点D旋转（如图5），射线DE、DF分别交AB、AC于点E、F，此时（2）中结论还成立吗？请说明理由．图4中的△DEF也这样旋转（如图6），直接写出上面的关系式是否成立．【答案】（1）详见解析；（2）有这样分关系式；（3）EF2＝BE2+CF2.【解析】【分析】（1）想办法证明AB∥CH，推出∠BAC＝∠ACH，再利用SAS证明△ABC≌△CHA即可．（2）有这样分关系式．如图4中，延长ED到H山顶DH＝DE．证明△EDB≌△HD （SAS），推出∠B＝∠HCD，BE＝CH，∠FCH＝90°，利用勾股定理，线段的垂直平分线的性质即可解决问题．（3）图5，图6中，上面的关系式仍然成立．【详解】（1）证明：如图2中，∵BD＝DC，∠ADB＝∠HDC，AD＝HD，∴△ADB≌△HDC（SAS），∴∠B＝∠HCD，AB＝CH，∴AB∥CH，∴∠BAC+∠ACH＝180°，∵∠BAC＝90°，∴∠ACH＝∠BAC＝90°，∵AC＝CA，∴△BAC≌△HCA（SAS），∴AH＝BC，∴AD＝DH＝BD＝DC，∴AD＝12 BC．结论：直角三角形斜边上的中线等于斜边的一半．（2）解：有这样分关系式．理由：如图4中，延长ED到H山顶DH＝DE．∵ED＝DH，∠EDB＝∠HDC，DB＝DC，∴△EDB≌△HDC（SAS），∴∠B＝∠HCD，BE＝CH，∵∠B+∠ACB＝90°，∴∠ACB+∠HCD＝90°，∴∠FCH＝90°，∴FH2＝CF2+CH2，∵DF⊥EH，ED＝DH，∴EF＝FH，∴EF2＝BE2+CF2．（3）图5，图6中，上面的关系式仍然成立．结论：EF2＝BE2+CF2．证明方法类似（2）．【点睛】本题属于几何变换综合题，考查了旋转变换，翻折变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．5．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：DE=BD+CE．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m 上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．（3）如图（3），D 、E 是D 、A 、E 三点所在直线m 上的两动点（D 、A 、E 三点互不重合），点F 为∠BAC 平分线上的一点，且△ABF 和△ACF 均为等边三角形，连接BD 、CE ，若∠BDA=∠AEC=∠BAC ，求证:△DEF 是等边三角形．【答案】(1)见解析；（2）成立，理由见解析；(3)见解析【解析】 【分析】（1）因为DE=DA+AE ，故通过证BDA AEC ≅△△，得出DA=EC ，AE=BD ，从而证得DE=BD+CE.（2）成立，仍然通过证明BDA AEC ≅△△，得出BD=AE ，AD=CE ，所以DE=DA+AE=EC+BD.（3）由BDA AEC ≅△△得BD=AE ，=BDA AEC ∠∠，ABF 与ACF 均等边三角形，得==60BA AC ︒∠F ∠F ，FB=FA ，所以=BA BA AC AC ∠F ＋∠D ∠F ＋∠E ，即FBD FAB ≅∠∠，所以BDF AEF ≅△△，所以FD=FE ，BFD AFE ≅∠∠，再根据=60BFD FA BFA =︒∠＋∠D ∠，得=60AF FA =︒∠E ＋∠D ，即=60FE =︒∠D ，故DFE △是等边三角形.【详解】证明：(1)∵BD ⊥直线m ，CE ⊥直线m∴∠BDA ＝∠CEA=90°，∵∠BAC ＝90°∴∠BAD+∠CAE=90°，∵∠BAD+∠ABD=90°∴∠CAE=∠ABD ，又AB=AC ，∴△ADB ≌△CEA∴AE=BD ，AD=CE ，∴DE=AE+AD= BD+CE(2)∵∠BDA =∠BAC=α，∴∠DBA+∠BAD=∠BAD +∠CAE=180°—α∴∠DBA=∠CAE ，∵∠BDA=∠AEC=α，AB=AC∴△ADB ≌△CEA ，∴AE=BD ，AD=CE∴DE=AE+AD=BD+CE（3）由（2）知，△ADB ≌△CEA ， BD=AE ，∠DBA =∠CAE∵△ABF 和△ACF 均为等边三角形，∴∠ABF=∠CAF=60°∴∠DBA+∠ABF=∠CAE+∠CAF ，∴∠DBF=∠FAE∵BF=AF ，∴△DBF ≌△EAF∴DF=EF ，∠BFD=∠AFE∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°∴△DEF 为等边三角形.【点睛】利用全等三角形的性质证线段相等是证两条线段相等的重要方法.二、八年级数学 轴对称解答题压轴题（难）6．在梯形ABCD 中，//AD BC ，90B ∠=︒，45C ∠=︒，8AB =，14BC =，点E 、F 分别在边AB 、CD 上，//EF AD ，点P 与AD 在直线EF 的两侧，90EPF ∠=︒，PE PF =，射线EP 、FP 与边BC 分别相交于点M 、N ，设AE x =，MN y =．（1）求边AD的长；（2）如图，当点P在梯形ABCD内部时，求关于x的函数解析式，并写出定义域；（3）如果MN的长为2，求梯形AEFD的面积．【答案】（1）6；（2）y=－3x+10(1≤x＜103)；（2）1769或32【解析】【分析】（1）如下图，利用等腰直角三角形DHC可得到HC的长度，从而得出HB的长，进而得出AD的长；（2）如下图，利用等腰直角三角形的性质，可得PQ、PR的长，然后利用EB=PQ+PR得去x、y的函数关系，最后根据图形特点得出取值范围；（3）存在2种情况，一种是点P在梯形内，一种是在梯形外，分别根y的值求出x的值，然后根据梯形面积求解即可．【详解】（1）如下图，过点D作BC的垂线，交BC于点H∵∠C=45°，DH⊥BC∴△DHC是等腰直角三角形∵四边形ABCD是梯形，∠B=90°∴四边形ABHD是矩形，∴DH=AB=8∴HC=8∴BH=BC－HC=6∴AD=6（2）如下图，过点P作EF的垂线，交EF于点Q，反向延长交BC于点R，DH与EF交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF ∴PQ=()162x + 同理，PR=12y ∵AB=8，∴EB=8－x∵EB=QR∴8－x=()11622x y ++ 化简得：y=－3x+10 ∵y ＞0，∴x ＜103当点N 与点B 重合时，x 可取得最小值则BC=NM+MC=NM+EF=－3x+10+614x +=，解得x=1∴1≤x ＜103（3）情况一：点P 在梯形ABCD 内，即（2）中的图形 ∵MN=2，即y=2，代入（2）中的关系式可得：x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二：点P 在梯形ABCD 外，图形如下：与（2）相同，可得y=3x －10则当y=2时，x=4，即AE=4∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质，难点在于第（2）问中确定x 的取值范围，需要一定的空间想象能力．7．（1）已知△ABC 中，∠A ＝90°，∠B ＝67.5°，请画一条直线，把这个三角形分割成两个等腰三角形．（请你选用下面给出的备用图，把所有不同的分割方法都画出来．只需画图，不必说明理由，但要在图中标出相等两角的度数）（2）已知△ABC 中，∠C 是其最小的内角，过顶点B 的一条直线把这个三角形分割成了两个等腰三角形，请探求∠ABC 与∠C 之间的关系．【答案】(1)图形见解析(2) ∠ABC 与∠C 之间的关系是∠ABC＝135°－34∠C 或∠ABC＝3∠C 或∠ABC＝180°－3∠C 或∠ABC＝90°，∠C 是小于45°的任意锐角．【解析】试题分析：（1）已知角度，要分割成两个等腰三角形，可以运用直角三角形、等腰三角形性质结合三角形内角和定理，先计算出可能的角度，或者先从草图中确认可能的情况，及角度，然后画上．（2）在（1）的基础上，由“特殊”到“一般”，需要把直角三角形分成两个等腰三角形的各种情形列方程，可得出角与角之间的关系．试题解析：(1)如图①②(共有2种不同的分割法)．(2)设∠ABC＝y，∠C＝x，过点B的直线交边AC于点D.在△DBC中，①若∠C是顶角，如图，则∠CBD＝∠CDB＝90°－12x，∠A＝180°－x－y.故∠ADB＝180°－∠CDB＝90°＋12x＞90°，此时只能有∠A＝∠ABD，即180°－x－y＝y－1902x⎛⎫-⎪⎝⎭，∴3x＋4y＝540°，∴∠ABC＝135°－34∠C.②若∠C是底角，第一种情况：如图，当DB＝DC时，∠DB C＝x.在△ABD中，∠ADB＝2x，∠ABD＝y－x.若AB ＝AD ，则2x ＝y －x ，此时有y ＝3x ，∴∠ABC ＝3∠C.若AB ＝BD ，则180°－x －y ＝2x ，此时有3x ＋y ＝180°，∴∠ABC ＝180°－3∠C. 若AD ＝BD ，则180°－x －y ＝y －x ，此时有y ＝90°，即∠ABC＝90°，∠C 为小于45°的任意锐角．第二种情况：如图，当BD ＝BC 时，∠BDC ＝x ，∠ADB ＝180°－x ＞90°，此时只能有AD ＝BD ，∴∠A ＝∠ABD ＝12∠BDC ＝12∠C ＜∠C ，这与题设∠C 是最小角矛盾． ∴当∠C 是底角时，BD ＝BC 不成立．综上所述，∠ABC 与∠C 之间的关系是∠ABC＝135°－34∠C 或∠ABC＝3∠C 或∠ABC＝180°－3∠C 或∠ABC＝90°，∠C 是小于45°的任意锐角．点睛：本题考查了等腰三角形的性质；第（1）问是计算与作图相结合的探索．本问对学生运用作图工具的能力，以及运用直角三角形、等腰三角形性质等基础知识解决问题的能力都有较高的要求．第（2）问在第（1）问的基础上，由“特殊”到“一般”，“分类讨论”把直角三角形分成两个等腰三角形的各种情形并结合“方程思想”探究角与角之间的关系．本题不仅趣味性强，创造性强，而且渗透了由“特殊”到“一般”、“分类讨论”、“方程思想”、“转化思想”等数学思想，是一道不可多得的好题．8．如图所示，已知ABC ∆中，10AB AC BC ===厘米，M 、N 分别从点A 、点B 同时出发，沿三角形的边运动，已知点M 的速度是1厘米/秒的速度，点N 的速度是2厘米/秒，当点N 第一次到达B 点时，M 、N 同时停止运动.（1）M 、N 同时运动几秒后，M 、N 两点重合？（2）M 、N 同时运动几秒后，可得等边三角形AMN ∆？（3）M 、N 在BC 边上运动时，能否得到以MN 为底边的等腰AMN ∆，如果存在，请求出此时M 、N 运动的时间？【答案】（1）10；（2）点M 、N 运动103秒后，可得到等边三角形AMN ∆；（3）当点M 、N 在BC 边上运动时，能得到以MN 为底边的等腰AMN ∆，此时M 、N 运动的时间为403秒． 【解析】【分析】（1）设点M 、N 运动x 秒后，M 、N 两点重合,1102x x ⨯+=；（2）设点M 、N 运动t 秒后，可得到等边三角形AMN ∆，如图①，1AM t t =⨯=,102AN AB BN t =-=-根据等边三角形性质得102t t =-；（3）如图②，假设AMN ∆是等腰三角形，根据等腰三角形性质证ACB ∆是等边三角形，再证ACM ∆≌ABN ∆（AAS ），得CM BN =，设当点M 、N 在BC 边上运动时，M 、N 运动的时间y 秒时，AMN ∆是等腰三角形，故10CM y =-，302NB y =-，由CM NB =，得10302y y -=-；【详解】解：（1）设点M 、N 运动x 秒后，M 、N 两点重合,1102x x ⨯+=解得：10x =（2）设点M 、N 运动t 秒后，可得到等边三角形AMN ∆，如图①1AM t t =⨯=,102AN AB BN t =-=-∵三角形AMN ∆是等边三角形∴102t t =-解得103t = ∴点M 、N 运动103秒后，可得到等边三角形AMN ∆. （3）当点M 、N 在BC 边上运动时，可以得到以MN 为底边的等腰三角形，由（1）知10秒时M 、N 两点重合，恰好在C 处，如图②，假设AMN ∆是等腰三角形，∴AN AM =，∴AMN ANM ∠=∠，∴AMC ANB∠=∠，∵AB BC AC==，∴ACB∆是等边三角形，∴C B∠=∠，在ACM∆和ABN∆中，∵AC ABC BAMC ANB=⎧⎪∠=∠⎨⎪∠=∠⎩，∴ACM∆≌ABN∆（AAS），∴CM BN=，设当点M、N在BC边上运动时，M、N运动的时间y秒时，AMN∆是等腰三角形，∴10CM y=-，302NB y=-，CM NB=，10302y y-=-解得：403y=，故假设成立.∴当点M、N在BC边上运动时，能得到以MN为底边的等腰AMN∆，此时M、N 运动的时间为403秒．【点睛】考核知识点：等边三角形判定和性质，全等三角形判定和性质.理解等腰三角形的判定和性质,把问题转化为方程问题是关键.9．已知等边△ABC的边长为4cm，点P，Q分别是直线AB，BC上的动点．（1）如图1，当点P从顶点A沿AB向B点运动，点Q同时从顶点B沿BC向C点运动，它们的速度都为lcm/s，到达终点时停止运动．设它们的运动时间为t秒，连接AQ，PQ．①当t＝2时，求∠AQP的度数．②当t为何值时△PBQ是直角三角形？（2）如图2，当点P在BA的延长线上，Q在BC上，若PQ＝PC，请判断AP，CQ和AC之间的数量关系，并说明理由．【答案】（1）①∠AQP＝30°；②当t＝43秒或t＝83秒时，△PBQ为直角三角形；（2）AC＝AP+CQ，理由见解析.【解析】【分析】（1）①由△ABC是等边三角形知AQ⊥BC，∠B＝60°，从而得∠AQB＝90°，△BPQ是等边三角形，据此知∠BQP＝60°，继而得出答案；②由题意知AP＝BQ＝t，PB＝4﹣t，再分∠PQB＝90°和∠BPQ＝90°两种情况分别求解可得．（2）过点Q作QF∥AC，交AB于F，知△BQF是等边三角形，证∠QFP＝∠PAC＝120°、∠BPQ＝∠ACP，从而利用AAS可证△PQF≌△CPA，得AP＝QF，据此知AP＝BQ，根据BQ+CQ＝BC＝AC可得答案．【详解】解:（1）①根据题意得AP＝PB＝BQ＝CQ＝2，∵△ABC是等边三角形，∴AQ⊥BC，∠B＝60°，∴∠AQB＝90°，△BPQ是等边三角形，∴∠BQP＝60°，∴∠AQP＝∠AQB﹣∠BQP＝90°﹣60°＝30°；②由题意知AP＝BQ＝t，PB＝4﹣t，当∠PQB＝90°时，∵∠B＝60°，∴PB＝2BQ，得：4﹣t＝2t，解得t＝43；当∠BPQ＝90°时，∵∠B＝60°，∴BQ＝2BP，得t＝2（4﹣t），解得t＝83；∴当t＝43秒或t＝83秒时，△PBQ为直角三角形；（2）AC＝AP+CQ，理由如下：如图所示，过点Q作QF∥AC，交AB于F，则△BQF 是等边三角形，∴BQ ＝QF ，∠BQF ＝∠BFQ ＝60°，∵△ABC 为等边三角形，∴BC ＝AC ，∠BAC ＝∠BFQ ＝60°，∴∠QFP ＝∠PAC ＝120°，∵PQ ＝PC ，∴∠QCP ＝∠PQC ，∵∠QCP ＝∠B +∠BPQ ，∠PQC ＝∠ACB +∠ACP ，∠B ＝∠ACB ，∴∠BPQ ＝∠ACP ，在△PQF 和△CPA 中，∵BPQ ACP QFP PAC PQ PC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△PQF ≌△CPA （AAS ），∴AP ＝QF ，∴AP ＝BQ ，∴BQ +CQ ＝BC ＝AC ，∴AP +CQ ＝AC ．【点睛】考核知识点:等边三角形的判定和性质.利用全等三角形判定和性质分析问题是关键.10．如果一个三角形能被一条线段割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．（1）如图1，ABC ∆是等腰锐角三角形，()AB AC AB BC =>，若ABC ∠的角平分线BD 交AC 于点D ，且BD 是ABC ∆的一条特异线，则BDC ∠= 度．（2）如图2，ABC ∆中，2B C ∠=∠，线段AC 的垂直平分线交AC 于点D ，交BC 于点E ，求证：AE 是ABC ∆的一条特异线；（3）如图3，若ABC ∆是特异三角形，30A ∠=，B 为钝角，不写过程，直接写出所有可能的B 的度数．【答案】（1）72；（2）证明见解析；（3）∠B度数为：135°、112.5°或140°.【解析】【分析】（1）根据等腰三角形性质得出∠C=∠ABC=∠BDC=2∠A，据此进一步利用三角形内角和定理列出方程求解即可；（2）通过证明△ABE与△AEC为等腰三角形求解即可；（3）根据题意分当BD为特异线、AD为特异线以及CD为特异线三种情况分类讨论即可.【详解】（1）∵AB=AC，∴∠ABC=∠C，∵BD平分∠ABC，∴∠ABD=∠CBD=12∠ABC，∵BD是△ABC的一条特异线，∴△ABD与△BCD为等腰三角形，∴AD=BD=BC，∴∠A=∠ABD，∠C=∠BDC，∴∠ABC=∠C=∠BDC，∵∠BDC=∠A+∠ABD=2∠A，设∠A=x，则∠C=∠ABC=∠BDC=2x，在△ABC中，∠A+∠ABC+∠C=180°，即：x+2x+2x=180°，∴x=36°，∴∠BDC=72°，故答案为：72；（2）∵DE是线段AC的垂直平分线，∴EA=EC，∴△EAC为等腰三角形，∴∠EAC=∠C，∴∠AEB=∠EAC+∠C=2∠C，∵∠B=2∠C，∴∠AEB=∠B，∴△EAB为等腰三角形，∴AE是△ABC的一条特异线；（3）如图3，当BD是特异线时，如果AB=BD=DC，则∠ABC=∠ABD+∠DBC=120°+15°=135°；如果AD=AC，DB=DC，则∠ABC=∠ABD+∠DBC=75°+37.5°=112.5°；如果AD=DB，DC=DB，则∠ABC=∠ABD+∠DBC=30°+60°=90°，不符合题意，舍去；如图4，当AD是特异线时，AB=BD，AD=DC，则：∠ABC=180°−20°−20°=140°；当CD为特异线时，不符合题意；综上所述，∠B度数为：135°、112.5°或140°.【点睛】本题主要考查了等腰三角形性质的综合运用，熟练掌握相关概念是解题关键.三、八年级数学整式的乘法与因式分解解答题压轴题（难）11．数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片边长为a的正方形，B中纸片是边长为b的正方形，C种纸片是长为a、宽为b的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．（1）请问两种不同的方法求图2大正方形的面积．方法1：s =____________________；方法2：s =________________________； （2）观察图2，请你写出下列三个代数式：()222,,a b a b ab ++之间的等量关系． _______________________________________________________；（3）根据（2）题中的等量关系，解决如下问题：①已知：225,11a b a b +=+=，求ab 的值；②已知()()22202020195a a -+-=，则()()20202019a a --的值是____． 【答案】（1）()2a b +，222a ab b ++；（2）()2222a b a ab b +=++；（3）①7ab =，②2-【解析】【分析】（1）依据正方形的面积计算公式即可得到结论；（2）依据（1）中的代数式，即可得出（a+b ）2，a 2+b 2，ab 之间的等量关系；（3）①依据a+b=5，可得（a+b ）2=25，进而得出a 2+b 2+2ab=25，再根据a 2+b 2=11，即可得到ab=7；②设2020-a=x ，a-2019=y ，即可得到x+y=1，x 2+y 2=5，依据（x+y ）2=x 2+2xy+y 2，即可得出xy=()222()2x y x y +-+=2-，进而得到()()20202019a a --=2-． 【详解】 解：（1）图2大正方形的面积=()2a b +，图2大正方形的面积=222a ab b ++故答案为：()2a b +，222a ab b ++；（2）由题可得()2a b +，22a b +，ab 之间的等量关系为：()2222a b a ab b +=++故答案为：()2222a b a ab b +=++；（3）①()()2222a b a b ab +-+=2251114ab ∴=-=7ab ∴=②设2020-a=x ，a-2019=y ，则x+y=1，∵()()22202020195a a -+-=，∴x 2+y 2=5，∵（x+y ）2=x 2+2xy+y 2，∴xy=()222()2x y x y +-+=-2， 即()()202020192a a --=-．【点睛】本题主要考查了完全平方公式的几何背景，熟练掌握完全平方公式是解本题的关键．12．观察下列等式：22()()a b a b a b -=-+3322()()a b a b a ab b -=-++443223()()a b a b a a b ab b -=-+++55432234()()a b a b a a b a b ab b -=-++++完成下列问题：（1）n n a b -=___________（2）636261322222221+++⋯⋯++++= （结果用幂表示）.（3）已知4,1a b ab -==，求33a b -.【答案】（1）（a-b ）（a n-1+a n-2b+…+ab n-2+b n-1）；（2）264-1；（3）76.【解析】【分析】（1）根据规律可得结果（a-b ）（a n-1+a n-2b+…+ab n-2+b n-1）；（2）利用（1）得出的规律先计算（2-1）63626132(2222221+++⋯⋯++++)即可得出结果；（3）利用（1）得出的规律变形，再用完全平方公式进行变形，变成只含a-b 及ab 的形式，整体代入计算即可得到结果．【详解】解：（1）()()22a b a b a b -=-+，()()3322a b a b a ab b -=-++，()()443223a b a b a a b ab b -=-+++， ()()55432234a b a b a a b a b ab b -=-++++， 由此规律可得：a n -b n =（a-b ）（a n-1+a n-2b+…+ab n-2+b n-1），故答案是：（a-b ）（a n-1+a n-2b+…+ab n-2+b n-1）；（2）由（1）的规律可得（2-1）()636261322222221+++⋯⋯++++=264-1，∴636261322222221+++⋯⋯++++=264-1.故答案是：264-1.（3）已知4,1a b ab -==，求33a b -.()()3322a b a b a ab b -=-++=()() [a b a b --2+3 a b ]∴33a b -=24431⨯+⨯（）=76. 故答案是：76.【点睛】此题考查了多项式乘以多项式，弄清题中的规律是解本题的关键．13．阅读以下文字并解决问题：对于形如222x ax a ++这样的二次三项式，我们可以直接用公式法把它分解成()2x a +的形式，但对于二次三项式2627x x +-，就不能直接用公式法分解了。

20232024学年全国初中八年级下数学人教版期中考试试卷(含答案解析)（考试时间：90分钟，满分：100分）一、选择题（每题2分，共20分）1. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=62. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=63. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=64. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8D. 4x2y=65. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=66. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=67. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=68. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=69. 下列哪个选项是正确的？A. 3x+5y=10C. 5x+3y=15D. 4x2y=610. 下列哪个选项是正确的？A. 3x+5y=10B. 2x4y=8C. 5x+3y=15D. 4x2y=6二、填空题（每题2分，共20分）1. 2x+3y=6，求x的值。

2. 3x+5y=10，求y的值。

3. 4x2y=6，求x的值。

4. 5x+3y=15，求y的值。

5. 2x4y=8，求x的值。

6. 3x+5y=10，求y的值。

7. 4x2y=6，求x的值。

8. 5x+3y=15，求y的值。

9. 2x4y=8，求x的值。

10. 3x+5y=10，求y的值。

三、解答题（每题5分，共25分）1. 解方程组：2x+3y=63x+5y=102. 解方程组：5x+3y=153. 解方程组：2x4y=83x+5y=104. 解方程组：3x+5y=104x2y=65. 解方程组：5x+3y=152x4y=8四、计算题（每题10分，共30分）1. 计算：2x+3y=63x+5y=102. 计算：4x2y=65x+3y=153. 计算：2x4y=83x+5y=10五、应用题（每题10分，共20分）1. 应用题：2x+3y=62. 应用题： 4x2y=6 5x+3y=15答案解析：一、选择题1. A2. B3. C4. D5. A6. B7. C8. D9. A10. B二、填空题1. x=12. y=23. x=24. y=35. x=26. y=27. x=28. y=39. x=210. y=2三、解答题1. x=1, y=22. x=2, y=33. x=2, y=24. x=2, y=35. x=2, y=2四、计算题1. x=1, y=22. x=2, y=33. x=2, y=2五、应用题1. x=1, y=22. x=2, y=38. 简答题（每题5分，共25分）1. 简述一元二次方程的一般形式。

2023-2024学年度第二学期期中考试初二数学试卷一、选择题：(本大题共8小题，每小题3分，共24分. 请将答案涂到答题纸上.)1．中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列“立春”、“谷雨”、“白露”、“大雪”，四幅作品是中心对称图形的是 （ ▲ ）A ．B ．C ．D ． 2．分式b a 221与c ab 261的最简公分母是 （ ▲ ） A ．abc B ．a 2b 2c C ．6a 2b 2c D ．12a 2b 2c3．下列计算正确的是 （ ▲ ）A ．39±=B ．1028=+C ．()55-2=D ．326=÷4．如图，在平行四边形ABCD 中，∠A +∠C ＝80°，则∠D ＝ （ ▲ ）A ．80°B ．40°C ．70°D ．140°5．若k 1＜0＜k 2，则在同一平面直角坐标系内，函数y ＝k 1x 和xk y 2=的图象大致是（ ▲ ） A ． B ． C ． D ．6．若点A （﹣2，y 1），B （﹣1，y 2）都在函数xy 6=的图象上，则y 1，y 2的大小关系是（ ▲ ） A ．y 1＞y 2 B ．y 1＝y 2 C ．y 1＜y 2 D ．不能确定7．甲、乙两人每小时一共可做30个电器零件，两人同时开始工作，当甲做了90个零件时乙做了60个零件，设甲每小时能做x 个零件，根据题意可列分式方程为 （ ▲ ）A ．x x -=309060B ．x x -=306090C ．x x +=309060D ．xx +=309090 8．现有一张平行四边形纸片ABCD ，AD ＞AB ，要求用尺规作图的方法在边BC ，AD 上分别找点M ．N ，使得四边形AMCN 为平行四边形，甲、乙两位同学的作法如图所示，下列判断正确的是 （ ▲ ）A ．甲对、乙不对B ．甲不对、乙对C ．甲、乙都对D ．甲、乙都不对第4题 第8题二、填空题：(本大题共8小题，每小题3分，共24分. 请将答案填写在答题纸上.)9．若代数式51-x 有意义，则实数x 的取值范围是 ▲ ． 10．已知最简二次根式1-x 与二次根式22是同类二次根式，则x ＝ ▲ ．11．如图，A ，B 两地被池塘隔开，小明先在AB 外选一点C ，然后测出AC ，BC 的中点M ，N ，并测量出MN 长为12m ，由此可知A ，B 间距离＝ ▲ m ．12．如图，矩形ABCD 的对角线相交于点O ，AB ＝3，AD ＝4，则线段AO 的长度为 ▲ ．13．如图，在正方形网格中，图②是由图①经过变换得到的，其旋转中心可能是点 ▲ ．14．若关于x 的方程xm x x -=--554有增根，则m ＝ ▲ ． 15．a 是方程x 2﹣x ﹣1＝0的一个根，则代数式2024﹣2a 2+2a 的值是 ▲ ．16．如图，在平面直角坐标系中，正方形OABC 的顶点O 与原点重合，顶点A ，C 分别在x 轴，y 轴上，反比例函数()0,0>>=x k xk y 的图象与正方形的两边AB ，BC 分别交于点M ，N ，连接OM ，ON ，MN ，若∠MON ＝45°，MN ＝3，则k 的值为 ▲ ．三. 解答题：(本大题共9小题，共72分. 请将解答过程填写在答题纸上.)17．(6分)计算：（1）3232-2-210⨯+⎪⎭⎫ ⎝⎛ ． 解方程：（2）0542=--x x 18．(6分)先化简44222112+--÷⎪⎭⎫ ⎝⎛-+x x x x ，再从不等式组0≤x ＜3中选择一个适当的整数，代入求值．19．(7分)如图，菱形ABCD 的对角线交于O 点，BE ∥AC ，CE ∥DB ．（1）求证：四边形OBEC 是矩形；（2）若AB ＝5，BD ＝6，则四边形OBEC 的面积为 ．20．(8分)已知关于x 的一元二次方程x 2﹣（m ﹣4）x ﹣m +3＝0．（1）求证：该方程总有两个实数根； 第11题 第12题 第13题 第16题（2）若x 1，x 2是该方程的两个实数根，且（x 1+1）（x 2+1）＝a ，求a 的值．21．(9分)如图1，反比例函数()0≠=m xm y 与一次函数y ＝kx+b （k ≠0）的图象交于点A （1，3），点B （n ，1），一次函数y ＝kx +b （k ≠0）与y 轴相交于点C ．（1）求反比例函数和一次函数的表达式；（2）连接OA ，OB ，求△OAB 的面积；（3）当xm b kx >+时，x 的范围为 ▲ .22．(4分)已知平行四边形ABCD 是中心对称图形，点E 是平面上一点，请仅用无刻度直尺画出点E 关于平行四边形ABCD 对称中心的对称点F ．（1）如图1，点E 是平行四边形ABCD 的AD 上一点；（2）如图2，点E 是平行四边形ABCD 外一点．23．(8分)第十九届亚运会在杭州举行．某网络经销商购进了一批以杭州亚运会为主题的文化衫进行销售，文化衫的进价每件30元．根据市场调查：在一段时间内，销售单价是45元时，每日销售量是550件；销售单价每涨1元，每日文化衫就会少售出10件．设该批文化衫的销售单价为x 元（x ＞55）．（1）请你写出销售量y （件）与销售单价x （元）的函数关系式 ▲ ．（2）若经销商获得了10000元销售利润，则该文化衫单价x 应为多少元？24．(12分)如图，点P 是y 轴正半轴上的一个动点，过点P作y 轴的垂线l ，与反比例函数xy 4-= 的图象交于点A ．把直线l 上方的反比例函数图象沿着直线l 翻折，其它部分保持不变，所形成的新图象称为“x y 4-=的l 镜像”． （1）当OP ＝3时：①点M ⎪⎭⎫ ⎝⎛2-21-， ▲ “x y 4-=的l 镜像”；（填“在”或“不在”） ②“xy 4-=的l 镜像”与x 轴交点坐标是 ▲ ； （2）过y 轴上的点Q （0，﹣1）作y 轴垂线，与“x y 4-=的l 镜像”交于点B 、C ，点B 在点C 左侧。

东湖高新区2022-2023学年八年级上学期期中物理试卷一、选择题（共18题，每题3分，共54分）1．估测是我们在生活中常用的一种方法。

下列是几个同学估测的数值，其中最接近实际的是（）A．武汉市年平均气温约为37℃B．老师正常讲课时声音的响度约为120dBC．普通口罩的长度约为175dmD．成年人正常步行的速度约为1.1m/s2．如图所示，天舟四号货运飞船正在靠近由天和核心舱与天舟三号货运飞船组成的空间站组合体，即将完成自主交会对接。

下列说法正确的是（）A．“天舟三号”相对于“天舟四号”是运动的B．“天舟三号”相对于“天和核心舱”是运动的C．“天舟四号”相对于“天舟三号”是静止的D．“天舟四号”相对于“天和核心舱”是静止的3．诗词中常蕴含着物理知识，根据下列哪句诗能估算出物体运动的速度（）A．天台四万八千丈B．坐地日行八万里C．春风十里扬州路D．桃花潭水深千尺4．2021年8月1日，在东京奥运会百米半决赛中，苏炳添跑出了9秒83的好成绩，成功晋级决赛，成为第一位闯入奥运百米决赛的黄种人：某汽车以36km/h的速度匀速行驶：自行车1min内通过0.48km的路程。

比较他们速度的大小，则（）A．苏炳添的最大B．汽车的最大C．自行车的最大D．三者一样大5．图为某高速公路上区间测速的警示牌，“区间测速”是指在某一段路程中测量平均速度，根据这两块警示牌，下列说法正确的是（）A．小汽车通过这个区间的时间不应长于12minB．小汽车能以90m/s的平均速度在该区间行驶C．小汽车在该区间行驶的平均速度不能超过25m/sD．小汽车在运动过程中相对于路边护栏是静止的6．小芳步行的部分信息如表，根据信息可推断此过程中小芳（）距离：3000m用时：45min步数：4718配速：15min/kmA．步长约为2m B．每分钟步行15kmC．平均速度为4km/h D．步行3km用时15min7．随着5G信号的快速发展，5G无人物品派送车已应用于实际生活中，图甲所示为无人物品派送车沿直线路径前往派送点的情景。

2023年春季八年级教学质量过程监测语文试题注意事项：1. 本试卷分为试题卷和答题卷两部分，其中试题卷由第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分组成，共8页；答题卷共6页。

满分100分。

考试时间：120分钟。

2.第Ⅰ卷和第Ⅱ卷都解答在答题卷上，考试结束后请将答题卷交回。

第Ⅰ卷(选择题，共14分)一、（10分，每小题2分）1.下列词语中加点字的读音，全都正确．．的一组是( )A．撮．合(cuō) 亢．奋(kànɡ) 连翘．（qiào）梦寐．以求(mèi)B．凫．水(fú) 脑畔．(bàn) 劫．难(jié) 草长莺．飞(yīnɡ)C．缥缈．(miǎo) 锵．然(qiānɡ) 褶．皱(zhě) 天衣无缝．(fènɡ)D. 冗．杂(rǒnɡ) 孕．育(yùn) 臀．围（diàn）运筹帷．幄(wéi)2.下列语句中，书写全部正确．．的一句是( )A. 这腰鼓使人想起：晦暗了又明晰，明晰了又晦暗，尔后最终永远明晰了的大砌大悟。

B. 延安曾经是中共中央的所在地，是“延安精神”的发源地，也是无数人魂牵梦萦的地方。

C. 唉，壮，于今灯笼又不够了。

应该数火把，数探海灯，数缭原的一把烈火。

D. 每每想起小时候在村里上灯学，要挑了灯笼走去挑了灯笼走回的事，便深深感到怅罔。

3.下列各句中加点成语的使用，不正确．．．的一句是( )A. 在同学间,我能较好地协调中间关系、恰当地处理人情世故．．．．,跟很多人都成了能够推心置腹的好朋友。

B. 有的父母习惯在饭桌上教育孩子，一边吃饭，一边正襟危坐．．．．地说几句，效果恐怕不大好。

C.秋风中叶子簌簌而落，北雁南飞，活跃在田间草际的昆虫也都销声匿迹．．．．了。

D. 在这领域，他连半个专家都够不上，竟那样目空一切．．．．，真是叫人不可思议。

4.下列各句中，没有语病．．．．的一句是( )A. 由于母亲对我的悉心培育，使我从小就养成了乐于助人的性格。

20232024学年全国初中八年级上数学人教版期中考卷(含答案解析)（考试时间：90分钟，满分：100分）一、选择题（每题3分，共15分）1. 下列选项中，哪个是勾股定理的逆定理？A. 直角三角形两直角边的平方和等于斜边的平方B. 任意三角形两边的平方和等于第三边的平方C. 直角三角形斜边的平方等于两直角边的平方和D. 任意三角形两边的平方和等于第三边的平方2. 在平面直角坐标系中，点P（2，3）关于y轴的对称点是？A. P（2，3）B. P（2，3）C. P（2，3）D. P（2，3）3. 下列哪个是等差数列？A. 2，4，6，8，10B. 3，6，12，24，48C. 1，3，9，27，81D. 5，10，15，20，254. 下列哪个是等比数列？A. 2，4，6，8，10B. 3，6，12，24，48C. 1，3，9，27，81D. 5，10，15，20，255. 在一个等差数列中，首项为5，公差为3，第10项是多少？A. 32B. 35C. 38D. 406. 在一个等比数列中，首项为2，公比为3，第4项是多少？A. 18B. 27C. 36D. 457. 下列哪个是勾股数？A. 3，4，5B. 5，6，7C. 8，9，10D. 12，13，14二、填空题（每题4分，共20分）1. 下列数列中，第n项是__________。

2. 在平面直角坐标系中，点P（2，3）关于x轴的对称点是__________。

3. 在一个等差数列中，首项为5，公差为3，第10项是__________。

4. 在一个等比数列中，首项为2，公比为3，第4项是__________。

5. 下列数列中，第n项是__________。

三、判断题（每题3分，共15分）1. 直角三角形两直角边的平方和等于斜边的平方是勾股定理。

（）2. 任意三角形两边的平方和等于第三边的平方是勾股定理的逆定理。

（）3. 等差数列的任意两项之差是常数。