空心变压器电路的分析
- 格式：ppt
- 大小：591.50 KB
- 文档页数：18
下载文档原格式
合集下载
空心变压器电路分析.
§3 空心变压器电路分析
返回
原边(初级)等效电路：
设：Z11 R1 jL1 Z22 R2 jL2 ZL R22 jX22 XM M
网孔方程： Z11I1 jXM I2 US
I1 jM I2
•
•
US j L1
j L2 ZL
R1
R2
jXM I1 Z22I2 0
即反得映：阻I2抗
•
•
u1
u2
u2 n u1
i2 1 i1 n
i1 1: n i2
•
u1
u2
•
u2 n u1
i2 1 i1 n
7
说明
i1 n :1 i2
•
•
u1
u2
u1 n i1 1
u2
i2 n
i1 N1 : N2 i2
•
u1
u2
•
u1 N1
u2
N2
i1 N2 i2 N1
伏安关系式的几条规律：
• 电压方程的比值取决于匝数比，匝数与电压成正比； • 电压方程的符号取决于同名端，同名端电压极性相同； • 电流方程的比值取决于匝数比，匝数与电流成反比； • 电流方程的符号取决于同名端，同名端流入为负。
j2 1 A
•
j4 j2
•
B
- j4 j2
Z11 j4
US
I1
Z1 f
原边等效电路
Z1 f
X
2 M
Z22
4 4 1
ZAB 4 j4
3
例2
查等效电路
图示电路中, L1=10mH, L2= 4mH, M=6mH, =1000rad/s, 则 ZMN =___C___。
返回
原边(初级)等效电路：
设：Z11 R1 jL1 Z22 R2 jL2 ZL R22 jX22 XM M
网孔方程： Z11I1 jXM I2 US
I1 jM I2
•
•
US j L1
j L2 ZL
R1
R2
jXM I1 Z22I2 0
即反得映：阻I2抗
•
•
u1
u2
u2 n u1
i2 1 i1 n
i1 1: n i2
•
u1
u2
•
u2 n u1
i2 1 i1 n
7
说明
i1 n :1 i2
•
•
u1
u2
u1 n i1 1
u2
i2 n
i1 N1 : N2 i2
•
u1
u2
•
u1 N1
u2
N2
i1 N2 i2 N1
伏安关系式的几条规律：
• 电压方程的比值取决于匝数比，匝数与电压成正比； • 电压方程的符号取决于同名端，同名端电压极性相同； • 电流方程的比值取决于匝数比，匝数与电流成反比； • 电流方程的符号取决于同名端，同名端流入为负。
j2 1 A
•
j4 j2
•
B
- j4 j2
Z11 j4
US
I1
Z1 f
原边等效电路
Z1 f
X
2 M
Z22
4 4 1
ZAB 4 j4
3
例2
查等效电路
图示电路中, L1=10mH, L2= 4mH, M=6mH, =1000rad/s, 则 ZMN =___C___。
电路分析08-2空心变压器
R22 jX 22
X
2 M
R22
R222
X
2 22
j
X
2 M
X
22
R222
X
2 22
R1 f jX1 f
Z1f：二次侧对一次侧的反映阻抗。 R1f：反映电阻。恒为正 , 表示二次回路吸收的功率
是靠一次回路供给的。
X电1f抗：的反性映质电相抗反。。负号反映了引入电抗与二次回路
当线圈的耦合为零，或者二次开路时，反映阻抗 消失
jL2
X
2 M
Z11
U OC
I2
ZL
二次回路反映阻抗
二次侧等效电路
4
电 路 例 8-8
分析
查等效电路
求图示电路的输入阻抗 ZAB 。
j2 1 A
•
j4 j2
•
B
- j4 j2
Z11 j4
U S
I1
Z1 f
一次侧等效电路
Z1 f
X
2 M
Z22
4 4 1
ZAB 4 j4
5
电 路 例 题(自测题8-7)
3
电 路 二次侧等效电路
分析
返回
二次侧等效电路：
I1 j M I2
设：Z11 R1 jL1
•
•
Z22 R2 jL2 ZL R22 jX22 XM M 应用戴维南定理：
U S
j L1
R1
j L2 ZL
R2
U OC
j M I1
jXM
U S
R1 jL1
jXM Z11
U S
Z0
Z0
R2
电路 分析
8.3
空心变压器
空心变压器
Z eq U OC
2 I2 ZL
其中 Y11US 是在副边开路下的原边电流
Z eq
=
(ωM )2 Z11
+
R2
+
jωL2
2′
大小与同名端位置无关（电源置零条件下）
若要求负载获最大功率，应使 ZL = Zeq
3) 副边受控源等效电路：当先求出原电路的 I1 后，可得副边的互感电压。
1
⎧(ωM )2
二、反映阻抗
⎪⎪ ⎨ ⎪
Z 22 (ωM
)2
⎪⎩ Z11
= =
(ωM )2 副边回路的总阻抗
(ωM )2 原边回路的总阻抗
= =
Z2 f Z1 f
副边反映到原边的阻抗 原边反映到副边的阻抗
1）从物理意义讲，虽然原副边没有电的联系，但由于互感作用使闭合的副边产生感应电流，
反过来这个电流又影响原边电流电压。
2）反映阻抗说明了磁耦合对原副边的影响。其性质与原有阻抗相反，说明感应电流产生的
解：1）谐振是第一条件，应先使n2的
Zin = n22 (− j5) = − j20Ω
即发生并联谐振，∴ 4Ω
2） n1 原边可等效为
当 n12 × 4 = 100Ω 时，
n1的 Rin 会获最大功率，∴ n1 = 5 ，
Pm
=
42 4 ×100
=
1W 25
副边反映到原边的阻抗副边回路的总阻抗原边反映到副边的阻抗原边回路的总阻抗1从物理意义讲虽然原副边没有电的联系但由于互感作用使闭合的副边产生感应电流反过来这个电流又影响原边电流电压
§10－3 空心变压器
变压器：具有无电气连接的二回路耦合电路
⎧原边（初级）加电源 ⎨⎩副边（次级）接负载
2019年10.3 空心变压器和理想变压器 电路原理第一版课件.ppt
US
+
–
(ω M )2 Z 22
( R1 jω L1 ) I 1 - jωM I 2 U S
Z11
jω M I 1 ( R2 jω L2 Z ) I 2 0 Z22 2 U ( M ) S 2 jMI1 Z in Z 11 I Z 22 Z 22 I1
1 I N2 I2 N1
i1 N2 i2 N1
u1 nu2
i1
+
n:1
* *
i2
+
i1 1 i 2 n
u1
–
u2
–
电路符号
nU U 1 2
I1
+
n:1
* *
I2
+
1I I 1 n 2
U1
–
U2
–
相量模型
3. 理想变压器的性质： (a) 阻抗变换性质
10.3 空心变压器和理想变压器
一、空心变压器 芯子 铁心变压器
+ 原边 空心变压器的电路模型
I1
负载
副边
空心变压器
R1 j L1
j M * *
R2
US
+ –
I2
j L2 Z=R+jX
I1
R1 j L1
j M * *
R2
I1
I2
Z11
US
+ –
j L2
Z=R+jX
8W
n:1
**
空心变压器去耦等效电路
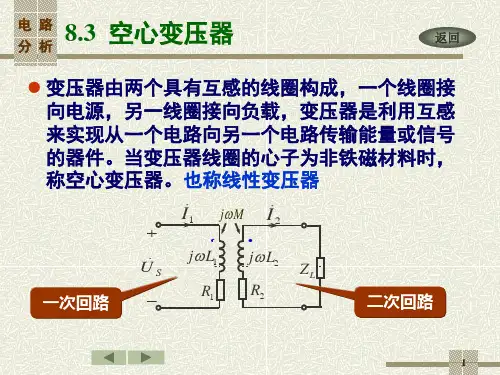
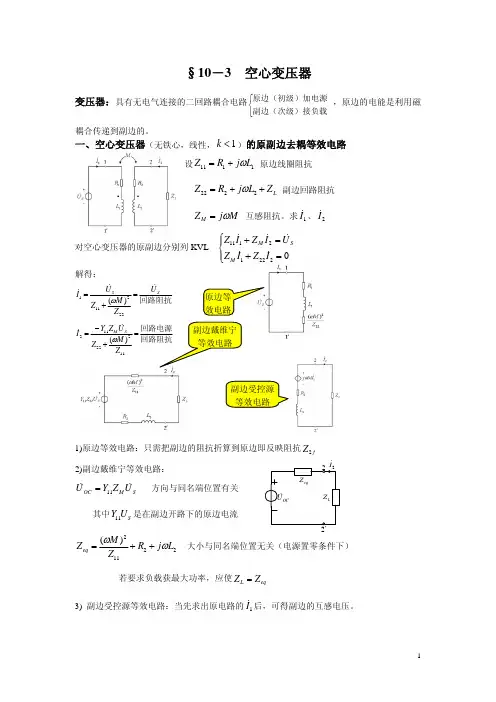
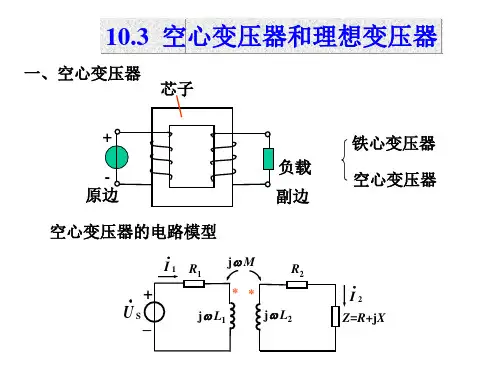
空心变压器去耦等效电路空心变压器去耦等效电路，听起来是不是有点复杂呢？别着急，咱们慢慢来，像喝茶一样细细品味。
想象一下，变压器就像一位魔术师，能把电流从一个地方搬到另一个地方，而且还可以变换电压，简直是电力界的超人。
不过，空心变压器就像是那种不带任何装饰的魔术师，外表简单，但内心却藏着不少秘密。
这空心变压器去耦等效电路，嘿，听起来就是个高大上的名词，其实就是为了让电流在两个不同的电路之间流动时，不互相干扰。
想想看，像两位在舞池中跳舞的小伙伴，如果他们各自的舞步不受对方影响，那岂不是能跳得更好？这去耦的作用，就是为了让电流能在“舞池”里自由自在，不被外界的干扰所打扰。
你瞧，电路中如果有干扰，那就像在大喧嚣的市场中，你想听到朋友的声音却听不清，烦得很。
这个去耦的设计，能让电流各自有各自的节奏，简直就是电路界的“清道夫”。
咱们把复杂的东西简单化，就像用一根绳子把两条鱼绑在一起，鱼能游得更远。
得提一下空心变压器的工作原理。
它没有铁心，像个空心的球，电流在里面来回穿梭。
这就好比你在一个大房间里打乒乓球，没墙壁反弹，球来球去，速度飞快。
而在去耦电路里，这种“空心”的状态就让电流更加灵活，不容易被其他电路的信号影响，像是在无阻碍的空间里自由飞翔。
去耦电路的实现嘛，得用一些电容和电感这些小玩意儿。
想象一下，电容就像个水库，能储存电流，电感就像个弹簧，能储存能量。
二者相互配合，形成了一个稳固的体系。
电流流过时，水库蓄水，弹簧收缩，整个过程就像一场优雅的芭蕾舞，流畅自然。
结果就是，电流在这舞台上大展身手，丝毫不受外界影响。
要是没有去耦电路，电流就会像个调皮的孩子，乱跑乱闹。
比如，一个信号要发送到另一端，却被旁边的信号给搞得七上八下，最后弄得一团糟。
这就好比你在聚会上想和朋友聊天，却总被其他人的喧闹声打断，真是心烦意乱。
所以，空心变压器去耦电路就像是一剂良药，能有效减轻这种“噪音”。
它把信号的“干扰”压到最低，让每一个信号都能独立发展，像是一个个小明星，各自闪耀光芒。
6空心变压器汇总
＋ －
* L1
M
*2 L
Z C
R
uS(t)
I
+
*
M jL1 jL2
*
ZL
U S
–
1/jC
（2）作去耦等效电路 R M jL1 jL2
100
j(L-20)
I
+
*
*
ZL
＋
j100
0
U S
–
1000 －
j20
－j20
1/jC
100 j(L-20) ＋ 10000 －
M L2 1 L1 L1 n
1 i1 ( t ) i2 ( t ) n
1 i1 ( t ) i2 ( t ) n
若i1、i2一个从同名端流入，一个从同名端流出，则有：
（3）变阻抗关系
I1
+
n:1
* *
I2
+
+
I1
Z
U1
–
U2
–
U1
–
n2Z
U n U U 2 2 1 2 2 n ( )n Z I 1 1 / nI 2 I2
Pmax 102 (4 10) 2.5W
解2
应用副边等效电路
U oc
(M ) 2 400 Zl 40 Z11 10
U OC U j 20 10 jM S j 20V Z11 10
(M ) 2 40 Z11
+
–
R2
当
Z l R2 40
40V
i (0 ) i (0 ) 40 1 1A 10 // 10 15 2
5.3空心变压器
I2
Z2
XM Z 11
2
解法二：副边等效电路法
jX M jM j 314 0.465 j146
1
U jX
M
Z11 R1 jL1 20 j1130
U
1
Z 22
Z 22 42.08 j18.84 46.124.1 Z
1
X M 6
R1 R1 '
22
PR2 I 1 R 1 ' 2 . 5 2 12.5W
2 2
PR2 I R 2
2 2
I2
PR2 R2
12 . 5 1 . 2 A 9
练
j1
j1 Zi
( M 2 ) Z 33
( M 1 ) Z 22
2
习
j2
Z 22 U
Z 11 Z 22 Z
Z 11
U
1 2
( M ) Z 22
5.3 空心变压器
二、空心变压器的电压电流方程
M
1
+ -
L1
L2
2
Z 11 I 1 Z M I 2 U 1
RL
U1
I1
1'
I2
2'
R1
R2
XL
Z M I 1 Z 22 I 2 0
j2
试计算图示电路的入端阻抗Z i
j3
j4
解：
Z2'
2 j1 j4
2
Z i2 j3 Z 2 ' j3 j j2
空心变压器
原边等 效电路
副边戴维宁 等效电路
副边受控源 等效电路
1)原边等效电路：只需把副边的阻抗折算到原边即反映阻抗 Z2 f
2)副边戴维宁等效电路：
U OC = Y11Z MU S 方向与同名端位置有关
Z eq U OC
2 I2 ZL
其中 Y11US 是在副边开路下的原边电流
Z eq
=
(ωM )2 Z11
§10－3 空心变压器
变压器：具有无电气连接的二回路耦合电路
⎧原边（初级）加电源 ⎨⎩副边（次级）接负载
，原边的电能是利用磁
耦合传递到副边的。
一、空心变压器（无铁心，线性， k < 1 ）的原副边去耦等效电路
设 Z11 = R1 + jωL1 原边线圈阻抗
Z22 = R2 + jωL2 + ZL 副边回路阻抗
+
R2
+
jωL2
2′
大小与同名端位置无关（电源置零条件下）
若要求负载获最大功率，应使 ZL = Zeq
3) 副边受控源等效电路：当先求出原电路的 I1 后，可得副边的互感电压。
1
⎧(ωM )2
二、反映阻抗
⎪⎪ ⎨ ⎪
Z 22 (ωM
)2
⎪⎩ Z11
= =
(ωM )2 副边回路的总阻抗
(ωM )2 原边回路的总阻抗
而 n1 副边等效为 R2 = 4Ω
2） n1 原边可等效为
当 n12 × 4 = 100Ω 时，
n1的 Rin 会00
=
1W 25
∵ 理想变压器为无源、无耗，∴ Rin 的功率即为 R2 的功率。
收音机上的负载—喇叭的匹配问题和此题类似。
空心变压器
4.
同理，初级在次级中的反映阻抗：
Zref2
( M )2
Z11
【例1】电路如图所示，已知L1=4H，L2=1H，M=0.5H，R1=50Ω，R2=20Ω，
RL=100Ω，正弦电压 uS 100 2 cos 314t V，求初级、次级电流 I1 、 I2 。
解 用反映阻抗的概念求解本题
Z11 R1 jL1 50 j314 4 50 j1256
Z 22 = RL R2 jL2 120 j314 1 336.1569.08
反映阻抗为
(M )2 Y22
314 2
0.52
1 Z 22
24649 336.1569.08
73.33 69.08 26.18 j68.5
I1
Z11
U S
(M ) 2 Y22
50
1000 j1256 26.18
j68.5
84 86.33
mA
I2
jMI1
Z 22
j314 0.5 84 86.33 336.1569.08
39.23 65.41
mA
【例2】ZL 并求负载获得的有功功率。
+
•
US
–
10 j2
**
•
I2
j10
j10
ZL
+
•
US
–
10+j10 Z1r=10–j10
解：Βιβλιοθήκη Z1rω2M 2 Z 22
I1
R1
US
j
L1
R2
( M )2 ZL j
L2
I1
1
......
I2
2
......
变压器空载和负载运行分析ppt课件
4. i1=i0 i2=0 u1≈- e1 u2=u20=e2
变压器空载运行时，主磁场由原边电流产生。当 原边绕组加额定电压时，副边绕组空载电压即为 副边额定电压。
空载电流
主要用来产生主磁场，所以也叫做励磁电流。 同时也会使变压器产生损耗，称为空载损耗。
空载损耗
变压器空载时，原边侧从电源吸收少量的有功 功率，用来供给铁损和原边绕组铜损。由于空 载电流和原边绕组铜损均很小，所以空载损耗 近似等于铁损。
变压器负载运行时，主磁场由原、副边电流共同产生。
负载运行电流
变压器负载运行时，原、副边电流可以分 成两个分量，一个是励磁分量，另一个是 负载分量。
电磁关系将原、副边联系起来,副边电流增 加或减少必然引起原边电流的增加或减少。
1
负载运行功率损耗
铁损pFe空载运行与负载运行时，基本不变。 原、副边绕组铜损：Pcu1=I12R1 Pcu2=I22R2 ；原、
二、变压器负载运行
负载运行指变压器原边绕组接入交流电源，副边绕 组接负载时的运行状态。
5.原副边电路的电 压平衡方程式：
u1 e1 e1s i1R1 u2 e2 e2s i2 R2
电路分析 ：
1. 主磁通Φm由原、副边电流i1 、i2共同产生。 2. 漏磁通Φ1s由原边电流 i1 产生。 3. 漏磁通Φ2s由副边电流 i2产生。 4. e1 、e2：自感+互感；e1s、e2s：自感。
副边绕组铜损与原、副边电流的平方成正比，所 以是可变损耗。
1
1. 变压器空载电流也叫_________电流。 2. 变压器空载损耗主要是_________。 3. 变压器空载运行时主磁场由_____电流产生。 4. 变压器负载运行时主磁场由________电流
空心变压器和理想变压器
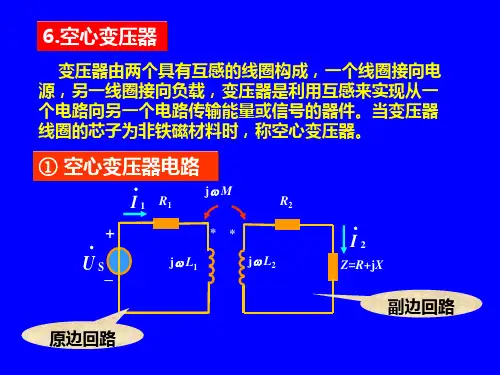
空心变压器和理想变压器1、空心变压器由两组线圈构成的变压器，与电源相连的线圈为原线圈，与负线圈相连的线圈为副线圈，其电路如P239图10-5所示。
对电路用回路法求解可得式中：分别为原边阻抗和副边阻抗。
是副边折算到原边的引入阻抗，它是副边的回路阻抗通过互感反映导原边的等效阻抗。
是原边折算到副边的引入阻抗，是副边的开路电压。
由此可得原边等效电路，如P240图10-6所示。
可直接利用原边等效电路计算，再利用可以求出。
上式中的负号与原边电流参考方向以及耦合电感的同名端均有关。
2、理想变压器1）理想变压器的伏安关系满足以下3个条件的变压器称为理想变压器(如P241图10-7所示)无损耗；全耦合，耦合系数为1；和M均为无限大,但仍保持为匝数比。
理想变压器的伏安关系相量形式的伏安关系2）理想变压器的特点(1) 理想变压器既不能耗能，又不储能，任一时刻的瞬时功率为零。
在电路中起到能量传输作用。
(2) 若在理想变压器次级接一阻抗，由初级看的入端阻抗。
说明理想变压器除能变压、变流作用外还有阻抗变换作用。
(3) 理想变压器是互易二端口。
3、理想变压器电路的分析计算1）含理想变压器电路的分析计算，仍可采用结点法、回路法等，在列写方程时要考虑使用理想变压器的伏安关系。
在初级与次级无耦合支路联系时，也可采用阻抗变换特性，简化为初级等效电路或次级等效电路求解。
2）在应用理想变压器伏安关系时还应注意，电压变换、电流变换时均与同名端及电压、电流的参考方向有关。
3）当理想变压器的第三个条件不被满足时，即和M均不是无穷大，称之为全耦合无损耗变压器，可用含理想变压器电路的模型来描述。
空心变压器电路的分析反映阻抗
jω( L2 jω( L2
M ) M )
例11-3-3 如图所示为自耦变压器电路,其中的两个线圈实际上是
由一个线圈抽头而成。因此，这两个线圈的绕向必然相同，同
例 1
名端必然是图中所示的位置。设这两个线圈的电感分别为L1 及
2
4 -
L2,它们之间的互感为M，试列出求解
•
I
1
和
•
I
2
所需的方程组。
2
Zi Z11 Z1r
反映(射)阻抗 用Z1r表示。
jωL1
•
•
I1
I2
•
•
I1
R1
US jωL1
ω2M 2 Z 22
•
•
I2
jωM I 1
R2 jωL2 RL
例 1
例11-2-1 电路如图(a)所示，已知：L1=5H，L2 =1.2H，M =1H，R=10，
2 3
uS 10 2cos10t V，求稳态电流i2,又若k=1, L1,L2仍为原值,求稳态电流i2。
M前所取符号与Lb中的相反
例11-3-1 求如图所示电路的等效电感Lab。
解：
Lab
14
6 6
(4 ) (4)
2mH
例11-3-2 试求如图所示电路的输入阻抗。
jωM
jω( L1 M ) jω( L2 M )
解：
Zi
jωM
R1 R1
jω( L1 jω( L1
M )R2 M ) R2
4
短路，已知:L1=0.1H,L2=0.4H,
M=0.12H,求ab端的等效电感L。
解：
Zi
Z11 Z1r
jωL1
空心变压器——精选推荐
§8-3 空心变压器一、空心变压器：由于空芯变压器属于一种线性变压器，所以，它可以由图所示电路的虚线方框所围部分作为它的电路模型。
其中与电源相联的一边称为原边(或初级)，其线圈称为原线圈(或原绕组)，R 1、L 1分别为原绕组的电阻和电感；与负载相联的一边称为副边(或次级)，其线圈称为副线圈(或副绕组)，R 2、L 2分别为副线团的电阻和电感。
M 为两线圈之间的互感。
这些都是空芯变压器的参数。
R L 、X L 为负载的电阻和感抗。
二、采用网孔电流法：根据上图所示的电压和电流的参考方向以及同名端，可写出其电路方程为：...1112..1222(j )j .............j (j )0......l s R L I M I U M I R L Z I ωωωω⎧+-=⎪⎨⎪-+++=⎩ ..22121122..221122(j )(j )(j )()j (j )(j )()l l l ss R L Z U I R L R L Z M M U I R L R L Z M ωωωωωωωω⎧++⎪=⎪++++⎨⎪=⎪++++⎩如果令Z 11＝R 1+j ωL 1为原边回路的阻抗，Z 22＝R 2+R L +j ωL 2+j X L 为副边回路的阻抗，Z M＝j ωM 为互感阻抗，由.I 1的表达式可得初级回路输入端的等效阻抗.221111111f 2.22221s()()j j l U M M Z R L Z Z Z R L Z Z I ωωωω==++=++++l Z2f 222()M Z Z ω=----------副边对原边的反射阻抗，故称为次级对初级的反映阻抗。
它表明次级的感性阻抗反映到初级的反映阻抗为容性；反之，次级的容性阻抗反映到初级的反映阻抗为感性。
很显然，当次级回路开路时，反映阻抗R 1f ＝0，则Z 1＝Z 11，次级对初级无影响。
这个结论与.I 2＝0，次级对初级无影响的结论是一致的。
耦合系数123 空心变压器电路分析 反映阻抗124 耦合电
有关。
§12-1 基本概念
2）若不知绕向，用实验方法确定
直流法：如图当开关 S 迅速闭合，若mA表正
向偏转，则1与3为同名端。
当有随时间增大的电
i1 S 1
3
M
+
流从任一端流入一个线圈 时，将会引起另一个线圈 相应同名端电位的升高。
US
L1
2
L2
mA
－
4
例12-1 S打开瞬间， mA表偏转方向？如何 判别同名端？
Ⅱ
a i1 M i2 c
+
u1
L
1 M di2
b
dt
L 2 M di1 dt
+
u2
d
§12-2耦合电感的VCR 耦合系数
课堂练习
写出下面两电路的伏安关系
i1
+
•M
i2 +
u1
L1
L2
u2
•
—
—
（1）
i2
+
•M•
+
u1
L1
L2
u2
i1
—
—
（2）
u1
=
L1
di1 dt
M di2 dt
u2
=
L2
di2 dt
F11
F21
互感电压u21与互感磁
通F21符合右手螺旋关系
L1 i1
－ u1 +
L2
－ u21 + + u21 －
u21
=
d 21
dt
=
M
di1 dt
反之
u21
=
d 21
dt
空心变压器和理想变压器
Z1
ZC
+
••
U_
RL Z2
n:1
答案
n 2, ZC j0.5
PLmax 6.25W
9.4 理想变压器
例 求Zab。 a
I1 0.5:1 I2
+
+•
•+
U
U_1
_U 2
1
j1
_ b
I1 I2
U
答案
Zab I1 0.25(1 j)
9.4 理想变压器
ZL
j MI1
Z 22
式中Z11= R1+jL1是初级回路阻抗，Z22= R2+jL2+ZL是次级回路阻抗。
二、初级等效电路
9.3 空心变压器电路的分析
I1
Z11
U 1
2M2
Z 22
利用所求的初级电流 可得初级等效电路：
输入阻抗：Zi
UI11
R1
j L1
2M 2
或
I1
10o 2000 2000
1 4000
0o
A
I2
nI1
15.8
1 4000
0o
3.95180o mA
Pmax I22RL (3.95103)2 8 125μW
五、理想变压器特点
9.4 理想变压器
既不耗能，也不贮能的二端口元件。
p
u1i1
(0.4 j2 4 ) (0.8 j0.8) 1 j3
*
显然，当ZL Z o (0.8 j0.8) 时获得最大功率
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
图13－11
例13-7 电路如图(a)所示。已知 uS (t ) 10 2 cos103 t V 。 试求电流i1(t),i2(t)和负载可获得的最大功率。
图13－18
解：将耦合电感 b、d两点相连，用去耦等效电路代替耦合 电感，得到图(b)相量模型。
等效电路中三个电感的阻抗为：
Z a j ( L1 M ) ( j4 j1) j3 Z b jM j1 Z c j ( L2 M ) ( j2 j1) j1
图13－16
解：画出相量模型，如图(b)所示。求出反映阻抗
Z ref
2M 2
Z 22
22 (1 j1) 2 j2
求出输入阻抗
Zi Z11 Z ref (1 j3 1 j1) (2 j2)
求出初级电流
U 10 0 S I1 A 2.5 2 45 A Zi 2 j2
(13 25)
图13－17(b)
得到图示戴维宁等效电路。根据最大功率传输
定理，当负载ZL与Zo共轭匹配，即 Z ＝ Z o L 可获得最大功率为 Pmax
2 U oc 4 Ro
*
例13-6 求图13-16电路中1.6负载电阻经调整获得的最大功 率。
图13－16
解：将1.6电阻断开，求含源单口网络的戴维宁等效电路。 求出开路电压
i1 (t ) 2 2 cos(103 t 53.1 )A i2 (t ) 2 2 cos(103 t 3.69 )A
为求负载可获得的最大功率，断开负载ZL=(0.6-j2)
求得
U oc j1 j10(2 j4) US V (2 j1)V 526.6 V 2 j4 20
式中Z11= R1+jL1是初级回路阻抗，Zref是次级回路在 初级回路的反映阻抗
Z ref
2M 2 2M 2 R2 jL2 Z L Z 22
(13 22)
若负载开路，Z22, Zref=0，则Zi=Z11=R1+jL1，不 受次级回路的影响； U U 1 1 I 1 Zi 2M 2 Z11 Z 22
求出次级电流
j M I j 2 2 . 5 2 45 1 I A 2.5A 2 Z 22 2 j2
最后得到：
i1 (t ) 5 cos(10t 45 )A i2 (t ) 2.5 2 cos10tA
1.6负载电阻吸收的平均功率为
P R I 1.6 2.5 W 10W
入阻抗、反映阻抗和等效电路。
2 2 U M Z i 1 R1 jL1 Z11 Z ref Z 22 I1
(13 21)
例13－5 电路如图13-16(a)所示。已知 uS (t ) 10 2 cos10t V
试求：(l) i1(t),i2(t)；
(2) 1.6负载电阻吸收的功率。
求得
j M I j M I 1 1 I 2 R2 jL2 Z L Z 22
(13 20)
2 2 U M Z i 1 R1 jL1 Z11 Z ref Z 22 I 1
(13 21)
图13－15(a)
图13－15(b)
j M U j2 10 S U oc V 6.32518.44 V R1 jL1 1 j3
用与输入阻抗相类似的公式计算输出阻抗
2M 2 Z o R2 jL2 R1 jL1 4 (0.4 j2 ) (0.8 j0.8) 1 j3
当 Z L＝Z o (0.8 j0.8) 时获得最大功率
*
Pmax
2 U oc (6.325) 2 W 12.5W 4Ro 4 0.8
三、用去耦等效电路简化电路分析
含耦合电感的电路，若能将耦合电感用去耦等效电路 代替，可避免使用耦合电感的VCR方程，常可简化电路分 析。现举例说明
(13 23)
再用式(13－20)即可求得次级电流 I 2
j M I j M I 1 1 I 2 R2 jL2 Z L Z 22
(13 20)
若改变图13－15(a)电路中同名端位置，则式(13－18)、
(13－19)和(13－20)中M 前的符号要改变。但不会影响输
2 L 2 2
二、端接电源的空心变压器
现在讨论除负载以外含源单口网络的戴维宁等效电路。 该单口网络的相量模型如图13-17（a）所示。
图13－17
j M U S jMI U oc 1 R1 jL1
(13 24)
2M 2 Z o R2 jL2 Ro jX o R1 jL1
图13－18
用阻抗串并联和分流公式求得：
j1(1 j1) Z i 2 j3 (3 j4) 0.4 0.6 100 U S I A 2 53 . 1 A 1 Z i 3 j4 I 2 j1 236.9 A I 1 j1 1 j1
必作习题：第551~552页
习题十三：13 – 11 、 13 – 13
2002 年春节摄于成都人民公园 13 – 14
j1(2 j3) Z o 0.4 j1 (0.5 j1.8) 2 j4
根据最大功率传输定理，当负载为 Z L Z o (0.5 j1 时 .8) 可获得最大功率
*
Pmax
2 U oc 5 W 2.5W 4Ro 4 0.5
空心变压器电路的分析
不含铁心(或磁芯)的耦合线圈称为空心变压器，它在 电子与通信工程和测量仪器中得到广泛应用。空心变压器 的电路模型如图所示，R1和R2表示初级和次级线圈的电阻。
图13－14
一、端接负载的空心变压器
空心变压器次级接负载的相量模型如图所示。
图13－15(a)
该电路的网孔方程为：
jMI U ( R1 jL1 ) I (13 18) 1 2 1 jMI 1 ( R2 jL2 Z L ) I 2 0 (13 19)