统计物理试题
- 格式:doc
- 大小:57.00 KB
- 文档页数:1

WORD 格式 整理 热力学·统计物理练习题一、填空题 . 本大题 70 个小题,把答案写在横线上。
1. 当热力学系统与外界无相互作用时 , 经过足够长时间 , 其宏观性质时 间改变,其所处的 为热力学平衡态。
2. 系统,经过足够长时间,其不随时间改变,其所处的状态为热力学平衡态。
3.均匀物质系统的热力学平衡态可由力学参量、电磁参量、几何参量、化 学参量等四类参量描述,但有 是独立的。
4.对于非孤立系统, 当其与外界作为一个整体处于热力学平衡态时,此时 的系统所处的状态是 。
5.欲描述非平衡系统的状态,需要将系统分成若干个小部分,使每小部分具有 小,但微观上又包含大量粒子,则每小部分都可视 为。
6.描述热力学系统平衡态的独立参量和 之间关系的方程式叫物态方程,其一般表达式为 。
7.均匀物质系统的独立参量有 个,而过程方程独立参量只有个。
8.定压膨胀系数的意义是在 不变的条件下系统体积随 的相对变化。
9.定容压力系数的意义是在 不变条件下系统的压强随的相 对变化。
10.等温压缩系数的意义是在 不变条件下系统的体积随的 相对变化。
11.循环关系的表达式为。
12.在无摩擦准静态过程中存在着几种不同形式的功,则系统对外界作的功 W Y i dy i ,其中 y i 是, Y i 是与 y i 相应的。
13. U B U A Q W ,其中 是作的功。
W14. dUQW0 ,-W 是作的功,且 -W 等于。
22( 、 均为热力学平衡态1、L2 为15.Q W QW ,L 1L 1 1 2 1L 2准静态过程)。
16.第一类永动机是指的永动机。
17.内能是 函数,内能的改变决定于和。
18.焓是函数,在等压过程中,焓的变化等于的热量。
19.理想气体内能温度有关,而与体积。
学习参考资料分享WORD 格式整理20.理想气体的焓温度的函数与无关。
21.热力学第二定律指明了一切与热现象有关的实际过程进行的。

统计物理期末试题及答案一、选择题(每题3分,共30分)1. 在统计物理中,描述粒子分布的函数是:A. 波函数B. 配分函数C. 统计权重D. 状态方程2. 温度的微观解释是:A. 粒子的平均动能B. 粒子的总动能C. 粒子的势能D. 粒子的动量3. 以下哪个量不是热力学系统的宏观状态量?A. 温度B. 体积C. 粒子数D. 动量4. 理想气体的熵变只与温度变化有关,这是因为:A. 理想气体分子间无相互作用B. 理想气体分子间有相互作用C. 理想气体分子间相互作用可以忽略D. 理想气体分子间相互作用对熵变有影响5. 根据玻尔兹曼统计,一个粒子在能量为E的态上的统计权重是:A. e^(-E/kT)B. e^(E/kT)C. e^(-E/kBT)D. e^(E/kBT)6. 一个系统从状态A到状态B的自由能变化等于:A. ΔF = ΔH - TΔSB. ΔF = ΔU - TΔSC. ΔF = ΔH + TΔSD. ΔF = ΔU + TΔS7. 热力学第二定律表明:A. 能量守恒B. 熵增原理C. 能量转换效率D. 热机效率8. 绝对零度是:A. 温度的下限B. 温度的上限C. 粒子动能的最小值D. 粒子动能的最大值9. 以下哪个过程是不可逆的?A. 理想气体的等温膨胀B. 理想气体的绝热膨胀C. 理想气体的等压膨胀D. 理想气体的等容膨胀10. 根据吉布斯自由能,一个化学反应在恒温恒压下自发进行的条件是:A. ΔG < 0B. ΔG > 0C. ΔG = 0D. ΔG ≠ 0二、填空题(每题2分,共20分)1. 在统计物理中,配分函数Z的定义是:Z = Σ e^(-E_i/kT),其中E_i是第i个能级的_________。
2. 一个系统从状态A到状态B的熵变可以通过公式ΔS = _________来计算。
3. 热力学第三定律指出,当温度趋近于绝对零度时,所有纯物质的完美晶体的_________趋于一个常数。

第21章 统计物理学基础一、作业教材:P193 - P19421-1(能量均分定理);21-2(理想气体内能,理想气体状态方程);21-3(麦克斯韦速率分布);21-4(能量均分定理,三种速率);21-5(统计方法,速率分布函数);21-6(三种速率);21-7(玻尔兹曼分布律);21-9(理想气体状态方程,方均根速率);21-10(平均碰撞频率和平均自由程);二、 典型题1. 一瓶氢气和一瓶氧气温度相同,若氢气分子的平均平动动能为 w = 6.21×10-21 J .试求:(1) 氧气分子的平均平动动能和方均根速率;(2) 氧气的温度。
(阿伏伽德罗常量N A =6.022×1023 mol -1,氧气分子摩尔质量m = 32 g ,玻尔兹曼常量k =1.38×10 -23 J·K -1)涉及知识点:温度概念,平均平动动能解:(1) ∵ T 相等, ∴氧气分子平均平动动能=氢气分子平均平动动能w=6.21×10-21 J .且 ()()483/22/12/12==m w v m/s(2) ()k w T 3/2==300 K .2. 水蒸气分解为同温度T 的氢气和氧气,即222O 21H O H +→,也就是1摩尔的水蒸气可分解成同温度的1摩尔氢气和21摩尔氧气。
当不计振动自由度时,求此过程中内能的增量。
涉及知识点:理想气体内能解: 1 mol H 2O 的内能 32i E RT RT == 分解成 1 mol H 2 522i E RT RT == 0.5 mol O 2 50.524i E RT RT ==5533244E RT RT RT RT ∆=+-= 3. 用绝热材料制成的一个容器,体积为 2V 0 ,被绝热板隔成 A , B 两部分,A 内储有 1 mol 单原子理想气体,B 内储有2 mol 双原子理想气体。
A ,B 两部分压强相等均为p 0 ,两部分体积均为V 0 ,求(1)两种气体各自的内能;(2)抽去绝热板,两种气体混合后处于平衡时的温度。

热力学与统计物理试题一、选择题1. 热力学第一定律表明,一个系统内能的微小改变等于它与周围环境交换的热量与它做的功之和。
若一个气体绝热膨胀,其内能的变化量为:A. 正值B. 负值C. 零D. 无法确定2. 理想气体状态方程为 \( pV = nRT \),其中 \( p \) 代表压力,\( V \) 代表体积,\( n \) 代表物质的量,\( R \) 是气体常数,\( T \) 代表温度。
若温度和物质的量保持不变,而压力增加,则体积的变化为:A. 增加B. 减小C. 不变D. 先增加后减小3. 熵是热力学中用来描述系统无序度的物理量。
在一个孤立系统中,熵的变化趋势是:A. 持续增加B. 持续减少C. 保持不变D. 在特定条件下增加或减少4. 麦克斯韦关系是热力学中描述状态函数之间关系的一组方程。
对于一个理想气体,其等体过程中的温度与熵的关系是:A. 正比B. 反比C. 无关D. 非线性关系5. 统计物理中,微观状态与宏观状态之间的关系是通过什么原理来描述的?A. 能量均分原理B. 等概率原理C. 熵最大原理D. 能量最小原理二、填空题1. 热力学第二定律可以表述为,在一个自发的过程中,熵总是倾向于增加,这个过程是________的。
2. 理想气体的内能只与温度有关,与体积和压力________。
3. 在热力学循环中,卡诺循环的效率是由两个热库的温度决定的,其效率公式为 \( \eta = 1 - \frac{T_{c}}{T_{h}} \),其中 \( T_{c} \) 是________的温度,\( T_{h} \) 是________的温度。
4. 统计物理中,一个系统的宏观状态可以通过多个不同的________来实现。
5. 按照玻尔兹曼熵的定义,一个系统的熵与它的微观状态数目的对数成正比,数学表达式为 \( S = k_B \ln W \),其中 \( k_B \) 是________常数。

第一章 习题10.(a)等温条件下,气体对外作功为22ln 2V VVVdVW pdV RT RT V===⎰⎰ln 2Q W RT =-=- ()0U ∆=(b)等压条件下,由PV RT =,得RTP V =所以 o o o o o o RT V P V V P W ==-=)2( 当体积为2V 时 22P VPV T T R R=== 1252TP P T Q C dT C T RT ===⎰11.(1) ()521 2.110P Q C n T T cal =-=⨯⎪⎭⎫⎝⎛==25041000n (2) 51.510VU nC T cal ∆=∆=⨯ (3)4610W Q U cal =-∆=⨯ (4) 因为0W =,所以51.510Q U cal =∆=⨯12.由热力学第肯定律Q d W d dU += (1)对于准静态过程有PdV W d -=对志向气体V dU C dT =气体在过程中汲取的热量为dTC Q d n =由此()n V C C dT PdV -= (2)由志向气体物态方程RT n PV += (3) 且 P VC C n R +-= 所以 ()()n V P V dT dVC C C C T V-=- (4) 对志向气体物态方程(3)求全微分有dV dP dT V P T+= (5)(4)与(5)联立,消去dTT ,有()()0n V n P dP dVC C C C P V-+-= (6)令n Pn V C C n C C -=-,可将(6)表示为0dV dPn V P += (7)若,,n V P C C C 均为常量,将(7)式积分即得nPV C = (8)式(8)表明,过程是多方过程.14. (a) 以T,P 为电阻器的状态参量,设想过程是在大气压下进行的,假如电阻器的温度也保持为27C 不变,则电阻器的熵作为状态函数也保持不变.(b) 若电阻器被绝热壳包装起来,电流产生的焦耳热Q 将全部被电阻器汲取而使其温度由i T 升为f T ,所以有2()P f imC T T i Rt -= 2600f i Pi RtT T K mC =+= (1卡 = 4.1868焦耳)139.1ln-•===∆⎰K cal T T mC TdT mC S ifT T p p fi15.依据热力学第肯定律得输血表达式Q d W d dU += (1)在绝热过程中,有0=Q d ,并考虑到对于志向气体dT C dU v = (2)外界对气体所作的功为:pdV w d -=,则有0=+pdV dT C v (3)由物态方程nRT pV =,全微分可得nRdT Vdp pdV =+ (4)考虑到对于志向气体有)1(-=-=γv v p C C C nR ,则上式变为dTC Vdp pdV v )1(-=+γ (5)把(5)和(3)式,有0=+pdV Vdp γ (6)所以有 V p V p sγ-=⎪⎭⎫⎝⎛∂∂ (7)若m 是空气的摩尔质量,m +是空气的质量,则有V m +=ρ和m m n +=ss s VV p p ⎪⎪⎭⎫⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ρρ ssV p m V p ⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂+2ρ (8)将式(7)代入(8)式,有+=⎪⎪⎭⎫ ⎝⎛∂∂m pV p sγρ (9) 由此可得+=⎪⎪⎭⎫ ⎝⎛∂∂=m pV p v sγρ有物态方程RT m m nRT pV +==,代入上式,得m RTmpVv γγ==+17.(1) 0C 的水与温度为100C 的恒温热源接触后水温升为100C ,这一过程是不行逆过程.为求水、热源和整个系统的熵变,可以设想一个可逆过程,通过设想的可逆过程来求不行逆过程前后的熵变。

热力学与统计物理期末习题一、简答题1.什么是孤立系?什么是热力学平衡态?2.请写出熵增加原理?并写出熵增加原理的数学表达式?3.说明在S ,V 不变的情形下,平衡态的U 最小。
4.试解释关系式 ∑∑+=l l l l l l da d a dU εε 的物理意义?5.什么是玻色-爱因斯坦凝聚,理想玻色气体出现凝聚体的条件是什么?6.什么是热力学系统的强度量?什么是广延量?7.什么是热动平衡的熵判据?什么是等概率原理?请写出单元复相系的平衡条件。
8.写出吉布斯相律,并判断盐的水溶液的最大自由度数。
9.写出玻耳兹曼关系,并说明熵的统计意义。
10.请分别写出正则分布的量子表达式和经典表达式?11.简述卡诺定理及其推论。
12.什么是特性函数?若自由能F为特性函数,其自然变量是什么?13.说明一般情况下,不考虑电子对气体热容量贡献的原因。
14.写出热力学第二定律的数学表述,并简述其物理意义。
15.试讨论分布与微观状态之间的关系?16.请写出麦克斯韦关系。
17.什么是统计系综?18.利用能量均分定理,写出N个CO分子理想气体的内能与热容量(不考虑振动),并简要说明在常温范围,振动自由度对热容量贡献接近于零的原因。
19.简述经典统计理论在理想气体中遇到的困难。
20.理想玻色气体出现凝聚体的条件是什么?凝聚体有哪些性质?21.试给出热力学第一定律的语言描述和数学描述。
22.试给出热力学第二定律的语言描述和数学描述。
二、填空题1.均匀系统中与系统的质量或物质的量成正比的热力学量,称为 。
2.在等温等容过程中,系统的自由能永不 。
(填增加、减少或不变)3.体在节流过程前后,气体的 不变;理想气体经一节流过程,其焦汤系数=⎪⎪⎭⎫ ⎝⎛∂∂Hp T 。
4.一级相变的特点是 。
5.在满足经典极限条件1>>αe 时,玻色系统、费米系统以及玻耳兹曼系统的微观状态数满足关系 。
6.玻尔兹曼分布的热力学系统的内能U 的统计表达式是 。

一、单选题(每题2分,共10分)
1、F和G是厄密算符,则()
A、FG必为厄密算符;
B、FG−GF必为厄密算符;
C、i(FG+GF)必为厄密算符;
D、i(FG−GF)必为厄密算符
2、氢原子能级的特点是()
A、相邻两能级间距随量子数的增大而增大.
B、能级的绝对值随量子数的增大而增大.
C、相邻两能级间距随量子数的增大而减小.
D、能级随量子数的增大而减小.
3、.一维自由粒子的运动用平面波描写,则其能量的简并度为()
A、1;
B、3
C、2;
D、4
4、下列波函数为定态波函数的是()
A、ψ2
B、ψ1和ψ2
C、ψ3
D、ψ3和ψ4
5、X射线康普顿散射证实了( )
A、电子具有波动性;
B、光具有波动性;
C、光具有粒子性;
D、电子具有粒
二、请给出两套实验方案测量原子的质量;并给出两个不同的实验现象,证实自由原子能级是量子化。
(每个实验方案2.5分,共10分)
三、请用一句话说明在以下每一个实验证实了什么样的量子化特性,(1)光电效应;(2)黑体辐射;(3)夫兰克-赫兹实验;(4)戴维孙-革末实验;(5)、斯特恩-盖拉赫实验;(6)康普顿散射实验。
(每问2分,共12分)
四、一自由原子的总轨道角动量量子数为L=2,总自旋量子数为S=3/2,求自旋轨道耦合项
L S 的可能取值。
(8分)。

《热力学与统计物理》知识30道选择题1. 热力学过程中,系统内能变化的度量是(B )。
A. 压强B. 热量C. 温度D. 熵2. 下列物理量中,与物质的微观粒子状态有关的是(D )。
A. 内能B. 热容C. 压强D. 熵3. 理想气体的内能只与(A )有关。
A. 温度B. 压强C. 体积D. 物质的量4. 在热力学中,熵增加原理适用于(A )。
A. 孤立系统B. 开放系统C. 封闭系统D. 任意系统5. 热力学第二定律表明(C )。
A. 能量可以全部转化为功B. 热可以全部转化为功C. 自发过程总是朝着熵增加的方向进行D. 以上都不对6. 对于一个孤立系统,其熵(A )。
A. 总是增加的B. 总是减少的C. 保持不变D. 无法确定7. 下列哪个过程是不可逆的?(A )A. 热从高温物体流向低温物体B. 气体自由膨胀C. 理想气体等温膨胀D. 以上都不是8. 统计物理中,最基本的概率分布是(B )。
A. 正态分布B. 麦克斯韦-玻尔兹曼分布C. 均匀分布D. 指数分布9. 玻尔兹曼常数的符号是(B )。
A. kB. k B.C. RD. γ10. 在平衡态下,系统的微观状态数最(D )。
A. 多B. 少C. 不确定D. 大11. 热力学温度的单位是(K )。
A. ℃B. FC. JD. K12. 分子的平均动能与(A )成正比。
A. 温度B. 压强C. 体积D. 熵13. 熵的单位是(J/K )。
A. JB. J/KC. KD. 无单位14. 理想气体状态方程的表达式是(pV = nRT )。
A. pV = nRTB. p = nRT/VC. V = nRT/pD. 以上都不是15. 下列哪种物质的热容较大?(A )A. 水B. 铁C. 铜D. 以上都不是16. 统计物理中,粒子的能量是(B )。
A. 连续的B. 分立的C. 以上都不是D. 不确定17. 分子的动能取决于(A )。
A. 温度B. 压强C. 体积D. 以上都不是18. 热力学第一定律可以表示为(ΔU = Q + W )。

一.选择(25分)1.下列不是热学状态参量的是( )A.力学参量B.几何参量C.电流参量 D 。
化学参量2。
下列关于状态函数的定义正确的是( )A.系统的吉布斯函数是:G=U —TS+PVB 。
系统的自由能是:F=U+TSC 。
系统的焓是:H=U —PVD.系统的熵函数是:S=U/T3.彼此处于热平衡的两个物体必存在一个共同的物理量,这个物理量就是( )A.态函数B.内能 C 。
温度 D 。
熵4。
热力学第一定律的数学表达式可写为( )A 。
W Q U U AB +=- B.W Q U U B A +=-C 。
W Q U U A B -=-D 。
W Q U U B A -=-5.熵增加原理只适用于( )A 。
闭合系统 B.孤立系统 C 。
均匀系统 D.开放系统二.填空(25分)1.孤立系统的熵增加原理可用公式表示为( ).2.热力学基本微分方程du=( )。
3.热力学第二定律告诉我们,自然界中与热现象有关的实际过程都是()。
4.在S。
V不变的情况下,平衡态的()最小。
5。
在T。
VB不变的情形下,可以利用( )作为平衡判据。
三.简答(20分)1.什么是平衡态?平衡态具有哪些特点?2.什么是开系,闭系,孤立系?四.证明(10分)证明范氏气体的定容热容量只是温度的函数,与比容无关五.计算(20分)试求理想气体的体胀系数α,压强系数β,等温压缩系数T K参考答案一。
选择 1~5AACAB二。
填空1。
ds≧02。
Tds—pdv3。
不可逆的4。
内能5。
自由能判据三.简答1.一个孤立系统,不论其初态如何复杂,经过足够长的时间后,将会达到这样状态,系统的各种宏观性质在长时间内不发生变化,这样的状态称为热力学平衡态.特点:不限于孤立系统弛豫时间涨落热动平衡2.开系:与外界既有物质交换,又有能量交换的系统闭系:与外界没有物质交换,但有能量交换的系统,孤立系:与其他物体既没有物质交换也没有能量交换的系统四.证明解证:范氏气体()RT b v v a p =-⎪⎭⎫ ⎝⎛+2 T v U ⎪⎭⎫ ⎝⎛∂∂=T V T p ⎪⎭⎫ ⎝⎛∂∂—p =T 2va pb v R =-- T v U ⎪⎭⎫ ⎝⎛∂∂=2va ⇒)(),(0T f v a U v T U +-= =V C V T U ⎪⎭⎫ ⎝⎛∂∂=)(T f ' ;与v 无关。

统计物理学试题(共19页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一 概念公式释义题 概念四个,公式五个,释义一个 (卷面是一百个题) 1.孤立系:与外界既没有物质交换也没有能量交换的系统. 2.闭系:与外界没有物质交换,但有能量交换的系统. 3.开系:与外界既有物质交换,又有能量交换的系统.4.热力学平衡态:一个孤立系统,不论其初态如何复杂,经过足够长的时间后,将会到达这样的状态,系统的各种宏观性质在长时间内不发生任何变化.5.绝热壁:如果器壁具有这样的性质,当两个物体通过器壁相互接触时,两物体的状态可以完全独立的改变,彼此互不影响.6.透热壁: 如果器壁具有这样的性质,当两个物体通过器壁相互接触时,两物体的状态不能完全独立的改变,彼此相互影响.7.热接触:两个物体通过透热壁相互接触.8.热平衡:假设有两个物体,各自处在平衡状体啊.如果令这两个物体进行热接触,经验表明,一般来说两个物体的平衡状态都会受到破坏,他们的状态都将发生改变.但是经过足够长的时间之后,他们的状态便不再发生变化,而达到一个共同的平衡态.9.热平衡定律:如果两个物体各自与第三个物体达到热平衡,它们彼此也必处在热平衡.10.温度:互为热平衡的两个系统,分别存在一个状态函数,而且两个函数的数值相等,该函数就称为系统的温度.11.热力学极限:粒子数∞→N ,体积∞→V 而粒子数密度VN为有限的极限情况.12.准静态过程:进行的非常缓慢的过程,系统在过程中经历的每一个状态都可以看作平衡态.13.内能:系统经绝热过程从初态变到终态,在过程中外界对系统所作的功仅取决于系统的初态和终态而与过程无关.由此可以用绝热过程中外界对系统所作的功定义一个态函数在终态和初态之差,该态函数称作内能.14.热量:如果系统所经历的过程不是绝热过程,则在过程中外界对系统所作的功不等于过程前后其内能的变化,二者之差就是系统在过程中以热量的形式从外界吸收的热量. 15.热容量:一个系统在某一过程中温度升高K 1所吸收的热量. 16.焦耳定律:理想气体的内能只是温度的函数,与体积无关.17.热力学第二定律开氏表述:不可能从单一热源吸热使之完全变为有用的功而不引起其它变化. 18.热力学第二定律克氏表述:不可能把热量从低温物体传到高温物体而不引起其它变化. 19.卡诺定理:所有工作于两个一定温度之间的热机,以可逆机的效率为最高.20.熵(热力学):对于可逆过程,在初态A 和终态B 给定后,积分 TdQBA⎰与可逆过程的路径无关.令 A B BAS S T dQ-=⎰, 称为熵.21.熵增加原理:在绝热条件下,熵减少的过程是不可能实现的.22.节流过程:管子用不导热的材料包着,管子中间有一个多孔塞或节流阀.多孔塞两边各维持着较高的压强1p 和较低的压强2p ,于是气体从高压的一边经多孔塞不断地流到低压的一边,并达到定常状态. 23.绝热去磁制冷:在绝热的条件下减少磁场时,磁介质的温度将降低. 24.态密度:单位能量间隔内的可能状态数.26.能量均分定理:对于处在温度为T 的平衡状态的经典系统,粒子能量中每一个平方项的平均值等于kT 21. 27.刘维尔定理:如果随着一个代表点沿正则方程所确定的轨道在相空间中运动,其领域的代表点密度是不随时间改变的常数.28.微正则系综:具有确定的粒子数N 、体积V 和能量E 的系统的分布函数.29.正则系综:具有确定的粒子数N 、体积V 和温度T 的系统的分布函数称为正则分布. 30.巨正则系综:具有确定的体积V 、温度T 和化学势μ的系统的分布函数.31.系综:设想有大量结构完全相同的系统,处在相同的给定的宏观条件下.我们把这大量系统的集合称为系综.32.Γ空间:以广义坐标和广义动量f 2个变量为直角坐标构成一个f 2空间. 33.最概然分布:微观状态数最多的分布,出现的概率最大,称为最概然分布. 34.熵(统计物理):在统计物理学中有Ωln k S =,是系统混乱度的量度. 1.体胀系数 p T V V ⎪⎭⎫ ⎝⎛∂∂=1α 2.压强系数 VT p p ⎪⎭⎫ ⎝⎛∂∂=1β 3.等温压缩系数 T T p V V ⎪⎪⎭⎫⎝⎛∂∂-=1κ 4.绝热压缩系数 SS p V V ⎪⎪⎭⎫⎝⎛∂∂-=1κ 5.α,β,T κ的关系式 p T βκα= 6.理想气体的物态方程 nRT pV =7.范德瓦耳斯方程 ()nRT nb V V an p =-⎪⎪⎭⎫⎝⎛+228.位力展开 ()()⎥⎥⎦⎤⎢⎢⎣⎡+⎪⎭⎫⎝⎛++⎪⎭⎫ ⎝⎛= T C V n T B V n V nRT p 219.顺磁性固体的物态方程 H TCM =10.热力学第一定律的数学表达式 Q W U U A B +=-系统在终态B 和初态A 的内能之差A B U U -等于在过程中外界对系统所作的功与系统从外界吸收的热量之和.11.等容热容量 VV T U C ⎪⎭⎫⎝⎛∂∂=12.等压热容量 pp T H C ⎪⎭⎫⎝⎛∂∂=13.焓 pV U H +=在等压过程中系统从外界吸收的热量等于态函数焓的增值. 14.理想气体的等压热容量和等容热容量之差 nRT C C V p =-15.简单系统的热力学的基本微分方程 pdV TdS dU -= 在相邻的两个平衡态,状态变量U 、S 、V 的增量之间的关系.16.n 摩尔理想气体的熵(以T 、V 为自变量)0ln ln S V nR T C S V ++= 17. n 摩尔理想气体的熵(以T 、p 为自变量)0ln ln S p nR T C S p +-= 18.简单系统的焓的微分方程 Vdp TdS dH += 19.简单系统的自由能的微分方程 pdV SdT dF --= 20.简单系统的吉布斯函数的微分方程 Vdp SdT dG +-=21.等容热容量的熵表示 VV T S T C ⎪⎭⎫⎝⎛∂∂=22.等压热容量的熵表示 pp T S T C ⎪⎭⎫⎝⎛∂∂=23.温度保持不变时内能随体积的变化率与物态方程的关系 p T p T V U VT -⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂24.温度保持不变时焓随压强变化率与物态方程的关系p T T V T V p H ⎪⎭⎫⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 25.等压热容量、等容热容量之差的一般关系 TV p VT C C κα2=-26.简单系统的开系的热力学基本微分方程 dn pdV TdS dU μ+-= 27.克拉珀龙方程()αβmm V V T LdT dp -=两相平衡曲线的斜率 28.对于玻耳兹曼系统,与分布{}l a 相应的系统的微观状态数 l a l l ll B M a N ∏∏=Ωω!!.. 29.对于玻色系统,与分布{}l a 相应的系统的微观状态数 ()()∏--+=Ωll l l l E B a a !1!!1..ωω 30.对于费米系统,与分布{}l a 相应的系统的微观状态数()∏-=Ωll l l l D F a a !!!..ωω31.玻耳兹曼分布 l e a l l βεαω--= 32.玻色分布 1-=+l e a ll βεαω 33.费米分布 1+=+l e a ll βεαω34.配分函数的表达式 ∑-=ll l e Z βεω135.内能的统计表达式 1ln Z NU β∂∂-= 36.广义作用力的统计表达式 1ln Z yN Y ∂∂-=β 37.熵的统计表达式 ⎪⎪⎭⎫ ⎝⎛∂∂-=11ln ln Z Z Nk S ββ 38.玻耳兹曼关系 Ω=ln k S 某个宏观状态对应的微观状态数愈多,它的混乱度就愈大,熵也愈大. 39.0≥-A B S S 经绝热过程后,系统的熵永不减少 40.克劳修斯等式和不等式02211≤+T Q T Q 41.B A F F W -≤- 系统在等温过程中对外所作的功不大于其自由能的减少. 42.0≤-A B F F 在等温等容条件下系统的自由能永不增加. 43. 0≤-A B G G 在等温等压条件下系统的吉布斯函数永不增加.44. 普朗克公式 323(,)1kT VU T d d ce ωωωωωπ=-45.费米动量和粒子数密度的关系式 ()3123n p F π=二 填空题 (卷面是一百个题) 1.理想气体的压强系数为T 1,理想气体的体胀系数为T1. 2.准静态过程在热力学理论中有着非常重要的地位,一方面在于如果没有摩擦阻力,外界在准静态过程中对系统的作用力可以用描写系统平衡状态的参量表达出来,另一方面在于如果没有摩擦阻力,外界在准静态过程中对系统的作用力可以用描写系统平衡状态的参量表达出来.3.热力学第二定律的克劳修斯表述为不可能把热量从低温物体传到高温物体而不引起其它变化 .4.理想气体的初态为(T , A V ),末态为(T , B V ),其熵变为ABV V nR ln . 5.克拉珀龙方程为()αβmm V V T LdT dp -=. 6.对于费米系统,与分布{}l a 相应的微观状态数为()∏-ll l l l a a !!!ωω.7.根据能量均分定理,在温度T 时,单原子分子气体的定压热容量与定容热容量之比γ为. 8.热源T 吸收热量1Q ,放出热量2Q ,则熵变为TQ Q 21-. 9.磁介质的热力学基本方程为Hdm TdS dU 0μ+=,则有麦氏关系=⎪⎭⎫⎝⎛∂∂m S H S m T ⎪⎭⎫ ⎝⎛∂∂01μ.10.在体积V 内,在d εεε→+的内能范围内,相对论情形下三维自由粒子的的量子态数为()εεπd ch V234. 11.气体分子的速率分布为dv v ekT m n v kTm 222/3224-⎪⎭⎫⎝⎛ππ,则气体的平均速率=v mkTπ8.(计算公式23212αα=⎰∞-dx x e x )12.开系的热力学基本微分方程为dn pdV TdS dU μ+-=. 13.对于玻色系统,与分布{}l a 相应的微观状态数为()()∏--+ll l l l a a !1!!1ωω.14.根据能量均分定理,在温度T 时,双原子分子气体的定压热容量与定容热容量之比γ为.15.热量Q 从高温热源1T 传到低温热源2T ,则熵变为⎪⎪⎭⎫⎝⎛-1211T T Q .16.磁介质的热力学基本方程为Hdm TdS dU 0μ+=,则有麦氏关系=⎪⎭⎫ ⎝⎛∂∂T H S HT m ⎪⎭⎫⎝⎛∂∂0μ .17.气体分子的速率分布为dv v ekT m n v kTm 222/3224-⎪⎭⎫⎝⎛ππ,则气体的方均根速率=s v mkT3.(计算公式2/504832απα=⎰∞-dx x e x ) 18.在等温膨胀过程中,理想气体从热源吸收热量,这热量全部转化为气体对外所作的功;在等温压缩过程中,外界对气体做功,这功通过气体转化为热量传递给热源.19.在绝热压缩过程中,外界对气体做功,这功全部转化为气体的内能而使气体的温度升高.在绝热膨胀过程中,外界对气体所作的功为负值,实际上是气体对外界做功,这功是由气体在过程中所减少的内能转化而来的.20.系统在等温过程中对外所作的功不大于其自由能的减少.换句话说,自由能的减少是在等温过程中从系统所能获得的最大功.21.在等温等容条件下系统的自由能永不增加.在等温等容条件下,系统中发生的不可逆过程总是朝着自由能减少的方向进行的.22.在等温等压条件下,系统的吉布斯函数永不增加,在等温等压条件下系统中发生的不可逆过程总是朝着吉布斯函数减少的方向进行的.23.经绝热过程后,系统的熵永不减少.系统经可逆绝热过程后熵不变,经不可逆绝热过程后熵增加.在绝热条件下熵减少的过程是不可能实现的.24.麦氏关系和雅可比行列式是进行导数变换运算的常用的工具.25.统计物理学从宏观物质系统是由大量微观粒子组成这一事实出发,认为物质的宏观特性是大量微观粒子行为的集体表现,宏观物理量是相应微观物理量的统计平均值.、26.将内能∑=ll l a U ε求全微分有∑∑+=ll l ll l da d a dU εε,第一项是粒子分布不变时由于外参量改变导致的能级改变而引起的内能变换,第二项是粒子能级不变时由于粒子分布改变所引起的内能变化.第一项代表过程中外界对系统所作的功.第二项代表过程中系统从外界吸收的热量.在无穷小的准静态过程中系统从外界吸收的热量等于粒子在各能级重新分布所增加的内能. 27.范德瓦尔斯方程做位力展开的第二位力系数是RTab -,第三位力系数是2b . 28.孤立系统处在稳定平衡状态的必要和充分条件为0<∆S . 29.等温等容系统处在稳定平衡状态的必要和充分条件为0>∆F . 30.等温等压系统处在稳定平衡状态的必要和充分条件为0>∆G . 三 选择题 (这里是三十五个题,卷面是四十个题)1.一定量的理想气体,起始温度为T ,体积为0V .后经历绝热过程,体积变为20V .再经过等压过程,温度回升到起始温度,最后再经过等温过程,回到起始状态.则在此循环过程中( A ) A.气体从外界净吸的热量为负值; B.气体对外界净作的功为正值; C.气体从外界净吸的热量为正值; D.气体内能减少.2.根据热力学第二定律判断下列哪种说法是正确的( D )A.热量能从高温物体传到低温物体,但不能从低温物体传到高温物体;B.功可以全部变为热,但热不能全部变为功;C.有规则运动的能量能够变为无规则运动的能量,但无规则运动的能量不能变为有规则运动的能量;D.气体能够自由膨胀,但不能自动收缩.3.若室内生起炉子后温度从15℃升高到27℃,而室内气压不变,则此时室内的分子数减少了( B ); %; %; %.4.关于热功转换和热量传递过程,有下面一些叙述(1)功可以完全变为热量,而热量不能完全变为功;(2)一切热机的效率都不可能等于l ;(3)热量不能从低温物体向高温物体传递;(4)热量从高温物体向低温物体传递是不可逆的. 以上这些叙述( A )A .只有(2)、(4)是正确的; B.有(2)、(3)、(4)正确; C. 有(1)、(3)、(4)正确; D.全部正确 .5.一瓶氦气和一氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们( C ) A.温度相同,压强相同; B.温度、压强都不相同;C.温度相同,但是氦气的压强大于氮气的压强;D.温度相同,但是氦气的压强小于氮气的压强.6.一绝热密闭的容器,用隔板分成相等的两部分,左边盛有一定量的理想气体,压强为0P ,右边为真空,今将隔板抽去,气体自由膨胀,当气体达到平衡时,气体的压强是( A )A .0P /2; B. 0P ; C.02P γ; D. 0P/γ2 (v p C C /=γ) 7.有一截面均匀的封闭圆筒,中间被一光滑的活塞分隔成两边,如果其中的一边装有某一温度的氢气,为了使活塞停留在圆筒的正中央,则另一边应装入同一温度的氧气的质量为:( C )A .1/6kg ; ; ; 一绝热容器被隔板分成两半,一半是真空,另一半是理想气体.若把隔板抽出,气体将进行自由膨胀,达到平衡后(A ) A.温度不变,熵不变; B.温度升高,熵增加;C.温度降低,熵增加;D.温度不变,熵增加.9.一定量的理想气体,经历某过程后,它的温度升高了.则根据热力学定律可以断定:(1)该理想气体系统在此过程中吸了热,(2)在此过程中外界对该理想气体系统作了正功,(3)该理想气体系统的内能增加了,(4)在此过程中理想气体系统既从外界吸了热,又对外作了正功.以上正确的断言是(A ) A.(3); B.(1)(3); C.(2)(3); D.(3)(4).10.质量一定的理想气体,从同一状态出发,分别经历等温、等压和绝热过程,使其体积增加一倍,那么气体温度的改变(绝对值)在( D )A.绝热过程中最大,等压过程中最小;B.绝热过程中最大,等温过程中最小;C.等压过程中最大,绝热过程中最小;D.等压过程中最大,等温过程中最小.11.一定质量的理想气体的内能E 随体积V 的变化关系为一直线(其延长线过V E -图的原点),则此直线表示的过程为 (B )A.等温过程;B.等压过程;C.等容过程;D.绝热过程.12.所列四图分别表示某人设想的理想气体的四个循环过程.请选出其中一个在物理上可能实现的循环过程的图的标号(D )13. 按2pV =恒量规律膨胀的理想气体,膨胀后的温度为( C )A.升高;B.不变;C.降低;D.无法确定14.一定量理想气体经历的循环过程用V -T 曲线表示如图.在此循环过程中,气体从外界吸热的过程是 ( A )→B ; B. B →C ;→A ; D. B →C 和C →A..15.对于理想气体,下面的系数与p1有关的是( B , D ).A.体胀系数 α;B.等温压缩系数 T κ;C.压强系数 β;D.绝热压缩系数 S κ. 16.下面的热力学量属于强度量的是( A , C ).A.温度T ;B.等压热容量 p C ;C.密度ρ;D.内能U . 17.下面属于二级相变特征的是( C , D ).A.可能出现亚稳态;B.体积存在突变;C.等温压缩系数存在突变;D.磁化率存在突变. 18.对于理想气体,下面的系数为T1的是( A , C ). A.体胀系数 α; B.等温压缩系数 T κ; C.压强系数 β; D.绝热压缩系数 S κ.)(v f 019.下面的热力学量属于广延量的是( B , D ).A.压强 p ;B.等容热容量 V C ;C.磁化强度 M ;D.总磁矩m . 20.下面属于一级相变特征的是( A , B ). A.存在相变潜热; B.体积存在突变; C.热容量存在突变; D.磁化率存在突变.1. 两个容器中分别装有氮气和水蒸气,它们的温度相同,则下列各量中相同的是(C )A .分子平均动能;B .分子平均速率;C .分子平均平动动能;D .最概然速率.2.两容器内分别盛有氢气和氦气,若它们的温度和质量分别相等,则(A ) A.两种气体分子的平均平动动能相等; B.两种气体分子的平均动能相等; C.两种气体分子的平均速率相等;D.两种气体的内能相等.3.已知分子的总数为N ,它们的速率分布函数为()v f ,则速率分布在21v v -区间内的分子的平均速率为(B )A. ⎰21V V dv v vf )(; B.⎰⎰2121v v v v dvv f dvv vf )()(; C. ⎰21V V dv v Nvf )(; D. Ndvv vf v v ⎰21)(.4.麦克斯韦速率分布曲线如图所示,图中A 、B 两部分面积相等,则该图表示(D )A.0v 为最可几速率.B.0v 为平均速率.C.0v 为方均根速率.D.速率大于和小于0v 的分子数各一半.5.容器中储有定量理想气体,温度为T ,分子质量为m ,则分子速度在x 方向的分量的平均值为:(根据理想气体分子模型和统计假设讨论)( D )6.在一容积不变的封闭容器内理想气体分子的平均速率若提高为原来的2倍,则( D ) A.温度和压强都提高为原来的2倍; B.温度为原来的2倍,压强为原来的4倍;C.温度为原来的4倍,压强为原来的2倍;D.温度和压强都为原来的4倍. 7.当气体的温度升高时,麦克斯韦速率分布曲线的变化为(B )A .曲线下的面积增大,最概然速率增大;B .曲线下的面积不变,最概然速率增大;C .曲线下的面积增大,最概然速率减小;D .曲线下的面积不变,最概然速率减小.8.一定量氦气(He)和甲烷(CH 4),都可视为理想气体,温度相同.那么它们分子的平均速率之比4:CH H e υυ为(D ):4; :1; :2; :1.9.一定量氢气和氧气,都可视为理想气体,它们的温度相同,那么它们分子的平均速率之比为(B ) :4; :1; :16. :1 .10.当系统含有两种费米子,其粒子数分别为N 和N ',总能量为E ,体积为V ,l ε和l ε'是两种粒子的能级,两种粒子的分布{}l a 和{}l a '必须满足条件( C )才有可能实现. ①0=∑ll a δ; ②0='∑ll a δ; ③0='+∑∑ll ll a a δδ;④0=∑ll l a δε; ⑤0=''∑ll l a δε; ⑥0=''+∑∑ll l ll l a a δεδε.A.③⑥;B.③④⑤;C.①②⑥;D.①②④⑤.11.设系统含有两种玻色子,其粒子数分别为N 和N '.粒子间的相互作用很弱,可以看作是近独立的.l ε和l ε'是两种粒子的能级,l ω和l ω'是能级的简并度.则在平衡状态下两种玻色子的最概然分布分别为( A , C ). A.1-'=''+'l e a l l εβαω; B.1-'='''+'l e a l l εβαω; [ C[ DC.1-=+lea ll βεαω; D.1-'='''+l ea l l εβαω.12.非简并条件为(A , B , C , D ).A.1>>αe ;B.1<<lla ω;C.2/13/121⎪⎭⎫ ⎝⎛>>⎪⎭⎫ ⎝⎛mkT h N V π; D.13<<λn .13.当系统含有两种玻色子,其粒子数分别为N 和N ',总能量为E ,体积为V 时,两种粒子的分布{}l a 和{}l a '必须满足条件( B )才有可能实现.①N a ll =∑; ②N a ll '='∑; ③N N a a ll ll '+='+∑∑;④E a ll l =∑ε; ⑤E a ll l '=''∑ε; ⑥E a a ll l ll l =''+∑∑εε.A. ①②④⑤;B. ①②⑥;C. ③④⑤;D. ③⑥.14.设系统含有两种费米子,其粒子数分别为N 和N '.粒子间的相互作用很弱,可以看作是近独立的.l ε和l ε'是两种粒子的能级,l ω和l ω'是能级的简并度.则在平衡状态下两种费米子的最概然分布分别为(A , C ). A.1+=+lea ll βεαω; B.1+'='''+'l ea l l εβαω;C.1+'=''+'l ea l l εβαω; D.1+'='''+l ea l l εβαω.15.下列哪些条件容易使得经典极限条件容易得到满足( A , B , C , D ). A.气体愈稀薄; B.温度愈高;C.分子的质量愈大;D.气体中分子的平均距离远大于德布罗意波的平均热波长. 四 简答题(这里是二十七个题,卷面是四十个题) 1.试用熵的概念解释为何盐水的结冰温度比纯水略低.答:结冰减少溶液中盐的有效体积,使盐的熵减少;而体系总沿熵增方向演化,结冰不利于盐的熵增加。
大学统计学专业《大学物理(下册)》期中考试试题附答案姓名:______ 班级:______ 学号:______考试须知:1、考试时间:120分钟,本卷满分为100分。
2、请首先按要求在试卷的指定位置填写您的姓名、班级、学号。
一、填空题(共10小题,每题2分,共20分)1、一圆锥摆摆长为I、摆锤质量为m,在水平面上作匀速圆周运动,摆线与铅直线夹角,则:(1) 摆线的张力T=_____________________;(2) 摆锤的速率v=_____________________。
2、某人站在匀速旋转的圆台中央,两手各握一个哑铃,双臂向两侧平伸与平台一起旋转。
当他把哑铃收到胸前时,人、哑铃和平台组成的系统转动角速度应变_____;转动惯量变_____。
3、将热量Q传给一定量的理想气体:(1)若气体的体积不变,则热量转化为_____________________________。
(2)若气体的温度不变,则热量转化为_____________________________。
(3)若气体的压强不变,则热量转化为_____________________________。
4、图示曲线为处于同一温度T时氦(原子量4)、氖(原子量20)和氩(原子量40)三种气体分子的速率分布曲线。
其中曲线(a)是________气分子的速率分布曲线;曲线(c)是________气分子的速率分布曲线。
5、一根无限长直导线通有电流I,在P点处被弯成了一个半径为R的圆,且P点处无交叉和接触,则圆心O处的磁感强度大小为_______________,方向为_________________。
6、一个半径为、面密度为的均匀带电圆盘,以角速度绕过圆心且垂直盘面的轴线旋转;今将其放入磁感应强度为的均匀外磁场中,的方向垂直于轴线。
在距盘心为处取一宽度为的圆环,则该带电圆环相当的电流为________,该电流所受磁力矩的大小为________ ,圆________盘所受合力矩的大小为________。
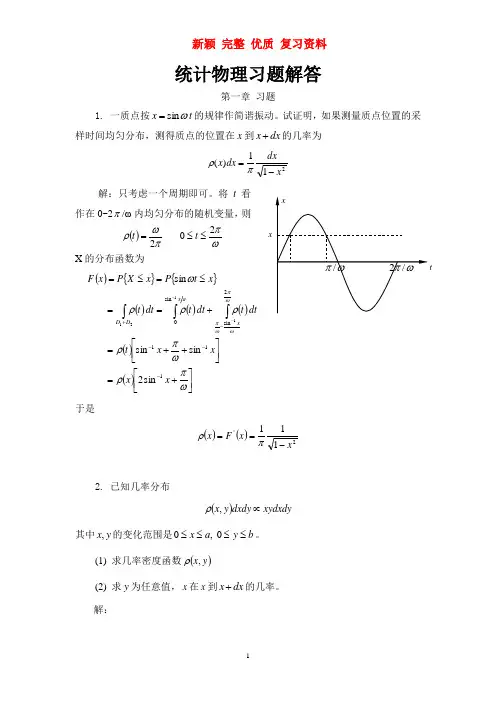
一.简要回答下列问题
a) 等几率原理
b) 能量均分定理
c) 玻色--爱因斯坦凝聚
d) 自发对称破缺
二.设有N 个定域粒子组成的系统,粒子之间相互作用很弱,可以忽略。
设粒子只有三个非简并能级,能量分别为,0,εε-,系统处于平衡态,温度为T 。
求:
(1) 系统的配分函数和熵S 的表达式;
(2) 内能U 及热容C (T ),并求其0T T →→∞与的极限
(3) 0
()/?dT C T T ∞
=⎰
三.N 个二维各向同性简谐振子组成的近独立粒子系统处于平衡态(温度为T ),假设粒子遵
从Boltzmann 分布,其能量表达式是2
22221()()22
x y m p p x y m ωε=+++,量子化的本征能级是(1)n E n ω=+,其中n=0,1,2, 。
(1) 在什么条件下简谐振子能级量子化效应可以忽略?
(2) 分别在高温和低温条件下,计算系统的内能和热容量
提示:高温条件可直接利用能量均分定理; 低温条件首先要计算系统的配分函数
四.考虑二维自由电子气体系统,其能量色散关系为()22/2p x y p p m ε=+,m 为常数,设面积为S ,总的粒子数为N
(1)求零温下系统的化学势(0)μ及内能U
(2)不用计算,从物理分析判断低温下定容热容量与温度的关系是什么? 为什么?
五. 铁磁固体低温下的元激发称为自旋波,它可以看作是一种粒子数不守恒的玻色型元激发,其能谱为r p αε=,其中 ||p p →
=, α 和 r 均为常数。
(1) 求这种元激发的态密度)(εD ;
(2) 实验发现在足够低的温度下,热容2/3~T
C ,试由此确定r 。