2014北京八一中学零模数学(含解析)

海淀区高三年级第二学期期中练习数 学 （文科） 2014.4一、选择题：本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.52i=- A.2i - B.2i + C.12i + D. 12i -解析：55(2)22(2)(2)i i i i i +==+--+2. 已知集合{}{}1,0,1,sin π,,A B y y x x A A B =-==∈=则A.1 B.0 C. 1 D.解析：{0}B =，所以{0}A B ⋂=3. 抛物线28y x =上到其焦点F 距离为5的点有 A.0个B.1个C. 2个D. 4个解析：根据抛物线的定义抛物线上的任意一点到焦点的距离等于到准线的距离，有两个点。

4. 平面向量,a b 满足||2=a ，||1=b ，且,a b 的夹角为60︒，则()⋅+a a b = A.1B. 3C.5D. 7解析：()a a b a a a b +=•+•=4+1=5 5. 函数()2sin f x x x =+的部分图象可能是A B C D解析：由题得函数为奇函数，关于原点对称，x=1时，函数值为正，答案为A 。

6. 已知等比数列{}n a 的前n 项和为n S ，且1S ，22S a +，3S 成等差数列，则数列{}n a 的公比为A ．1B ．2C ．12D ．3 解析：根据题意有22132()S a S S +=+，2111112()a a q a a q a q +=++解得q=3.OyxOyxOyxOyx7. 已知()x f x a 和()x g x b 是指数函数，则“(2)(2)f g ”是“ab ”的A.充分不必要条件B.必要不充分条件C.充分必要条件D. 既不充分也不必要条件解析：根据题意函数式指数函数，a ，b>0,所以22a b >，a b >，反之也成立，所以为充分必要条件。

8. 已知(1,0)A ，点B 在曲线:G ln y x =上，若线段AB 与曲线:M 1y x=相交且交点恰为线段AB 的中点，则称B 为曲线G 关于曲线M 的一个关联点.那么曲线G 关于曲线M 的关联点的个数为A ．0B ．1C ．2D ．4解析：A(1,0),设0,0(ln )B x x 则AB 的中点坐标001ln (,)22x x +，因为中点在1y x =上，所以00(1)ln 4x x +=，利用数形结合，满足条件的点个数1个。

2014年初中毕业学业考试模拟考数学试卷一、选择题（每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求） 1如图，已知⊙O 的两条弦AC ，BD 相交于点E ，∠A =75°，∠C =45°， 那么sin ∠AEB 的值为（ ） A.12 B. 33 C. 22D. 32 2．下列商标是轴对称图形的是 （ ▲ ）（A ） （B ） （C ） （D ）3．下列计算错误．．的是 ( ▲ ) （A ）33--=- （B ）222235x x x += （C ）822= （D ）235()x x =4．如图，是用八块相同的小正方体搭建的一个积木，它的左视图是 ( ▲ )（A ） （B ） （C ） （D ）5. 如图，E 、F 分别是正方形ABCD 的边AB 、BC 上的点，BE =CF ，连结CE 、DF ．将△BCE 绕着正方形的中心O 按逆时针方向旋转到△CDF 的位置，则旋转角可以是 ( ▲ )（A ） ︒45 （B ）︒60 （C ）︒90 （D ）︒1206如图为某班35名学生10次数学考试中获得优秀次数的条形统计图，其中上面部分数据 破损导致数据不完全．已知此班学生优秀次数的中位数是5，则根据图形，无法．．确定的是 下列哪一选项中的数值 ( ▲ ) （A ）3次及以下的人数 （B ）4次及以下的人数 （C ）5次及以下的人数 （D ）6次及以下的人数2 3 4 5 6 78 9 10 个数 (人) BE FC ADO （第7题图）（第6题图）E2D2E1D1EDCAB7．下面给出了一些关于相似的命题，其中真命题有 ( ▲ ) （1）菱形都相似 （2）等腰直角三角形都相似（3）正方形都相似 （4）矩形都相似 （5）正六边形都相似（A ） 1 个 （B ） 2个 （C ） 3个 （D ） 4个 8在平面直角坐标系中，已知两点A （1，2），B （2，0），把线段AB 平移后得线段CD ， 其中A 点对应点是C （3，a ），B 点对应点是D （b ，1），则a －b 的值为 ( ▲ ) （A ）1- （B ）0 （C ）1 （D ）29两个完全相同的矩形如图放置，每个矩形的面积为28，图中阴影部分的面积为20，则每个矩形的周长是 ( ▲ ) （A ）18 （B ）22 （C ）26 （D ）3210．如图，在△ABC 中，AB =AC ，且∠A =108°，点P 为△ABC 所在平面内一点，且点P 与△ABC 的任意两个顶点构成△PAB 、△PBC 、△PAC 均是等腰三角形，则满足上述条件的所有点P 个数为 （ ▲ ）（A ）4 （B ）6 （C ）8 （D ）10二、填空题（每小题4分，共24分）13．分解因式：22x x - = ▲ ．14．若一个正多边形的一个外角是30，则这个正多边形的边数是 ▲ ．15．为了缓解江北区内一些主要路段交通拥挤的现状，交警队在一些主要路口设立了交通路况显示牌（如图）．已知立杆AB 的高度是3m ，从侧面D 点测得显示牌顶端C 点和底端B 点的仰角分别是60和45．则路况显示牌的宽度BC 是 ▲ 米．（结果保留根号） 16如图，在△ABC 中，∠C =90°，以AB 上一点O 为圆心，OA 长为半径的圆与BC 相切于点D ，分别交AC 、AB 于点E 、F ．若AC =6，AB =10，则⊙O 的半径为______________.17．如图，在正方形网格中，点O 、A 、B 均在格点上，则∠AOB 的正弦值是 ▲ ． 18.如图，已知等边ABC △，D 是边BC 的中点，过D 作DE ∥AB 于E ， 连结BE 交AD 于D 1；过D 1作D 1E 1∥AB 于E 1，连结BE 1交AD 于D 2；过D 2作D 2E 2∥AB 于E 2，…，如此继续，若记BDE S △为S 1，记11B D E S △为S 2，记22B D E S △为S 3…，若ABC S △面积为Scm 2，则Sn =_________cm 2. (用含n 与S 的代数式表示)三、解答题（本大题有8小题，共78分）(第15题图)CAB（第12题图）B（第17题图）19．（本题6分）请先化简：xx x ---2111，再选择一个合适的x 值代入求值．20．（本题8分）如图，已知一次函数与反比例函数的图象交于点 A （－3，－1）和B （a ，3）．（1）求反比例函数的解析式和点B 的坐标；（2）连结AO 和BO ，判断△ABO 的形状，请说明理由，并求出它的面积．21.（本题6分）已知：如图，斜坡BQ 坡度为i =1︰2.4（即为QC 与BC 的长度之比），在斜坡BQ 上有一棵香樟树PQ ，柳明在A 处测得树顶点P 的仰角为α，并且测得水平的AB =8米，另外BQ =13米，tanα=0.75．点A 、B 、P 、Q 在同一平面上，PQ ⊥AB 于点C ．求香樟树PQ 的高度．22．（本题10分）如图，在△ABC 中，AB =AC ，以AB为直径的O 分别交AC 、BC 于点D 、E ，点F在AC 的延长线上，且12CBF CAB ∠=∠．（1）求证：直线BF 是O 的切线；（2）若AB =5，5sin 5CBF ∠=，求BC 和BF 的长．（第20题图）OFEDCBA（第22题图）C（第21题）23．（本题10分）如图，△ABC 的边长分别为21、23、1，正六边形网格是由24个边长为1的正三角形组成，每个正三角形的顶点称为网格的格点．在下面三个正六边形网格中各画出一个三角形（画出三角形，并用阴影填充），使其同时满足下面三个条件：（1）三个三角形的顶点都在格点上；（2）三个三角形都与△ABC 相似；（3）三个三角形的面积大小都不同．并直接写出三个三角形与△ABC 的相似比．相似比： 相似比： 相似比：24．（本题12分）如图，在矩形ABCD 中，AB =1，BC =3，F 为线段．．AD 上一点（不与端点A ，D 重合），过F 的直线交矩形的另一边于点E ，且该直线满足21tan =∠DFE ，设AF 长度为x ． （1）记BEF △的面积为S ，求S 与x 的函数关系式；（2）当点E 在线段BC 上时，若矩形ABCD 关于直线EF 的对称图形为矩形A ’B ’C ’D ’，试说明矩形ABCD与矩形A ’B ’C ’D ’理由．CB A25．（本题14分）如图，已知二次函数图象的顶点为P（0，－1），且过点（2，3）．点A是抛物线上一点，过点A作y轴的垂线，交抛物线于另一点B，分别过点B、A作x轴的垂线，垂足分别为C、D，连结PA、PD．（1）求此二次函数的解析式；x轴交点记为E，证明：（2）当点A在第一象限．．．．内时，PA与①PED PDA△∽△；②∠APC＝90°；（3）若∠APD＝45°，当点A在y．轴右侧．．．时，请直接写出点A的坐标．（第26题图）（备用图）参考答案及评分标准一、选择题(每小题4分，共48分，在每小题给出的四个选项中，只有一项符合题目要求) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案DADBDACCCABC二、填空题(每小题4分，共24分) 题号 1314 15 16 17 18答案()2-x x12333-3662++π54 911a b c -++三、解答题(第19题6分，第20、21题各8分，第22－24题各10分，第25题12分，第26题14分，共78分)注： 1. 阅卷时应按步计分，每步只设整分；2. 如有其它解法，只要正确，都可参照评分标准，各步相应给分.19. （本题6分）2111x x x111(1)x x x =--- 1分 1(1)x x x -=-1x= 4分满足1,0x ≠的值代入都可 6分20.（本题8分）：（1）设xky =，将A （﹣3，﹣1）代入，求得k =3， 1分 xy 3=2分 将B （a ，3）代入，求得a =1 3分 B （1,3） 4分（2）AO =BO =10 5分 等腰三角形 6分 S ABC △=4 8分21.（本题8分）（1）列表如下：哥哥 弟弟 3453 3+3=6 4+3=7 5+3=84 3+4=7 4+4=8 5+4=9 53+5=8 4+5=9 5+5=104分总共有9种结果，每种结果出现的可能性相同，而两数和为8的结果有3种，因此P （两数和为8）=135分 （2）答：这个游戏规则对双方不公平．理由：因为P （和为奇数）=49， 6分 P （和为偶数）=59， 7分而4599≠， 所以这个游戏规则对双方是不公平的． 8分 22.（本题10分）相似比：2:1 相似比：1:32 相似比：4:1画对1个给2分，2个4分，3个都对得7分，每个相似比正确得1分，共3分。

2014年北京市高级中等学校招生考试数学试题（含答案全解全析）第Ⅰ卷(选择题,共32分)一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个．．是符合题意的.1.2的相反数是( )A.2B.-2C.-D.2.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )A.0.3× 06B.3× 05C.3× 06D.30× 043.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )D.A. B. C.34.如图是某几何体的三视图,该几何体是( )A.圆锥B.圆柱C.正三棱柱D.正三棱锥5.某篮球队12则这12名队员年龄的众数和平均数分别是( )A.18,19B.19,19C.18,19.5D.19,19.56.园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )A.40平方米B.50平方米C.80平方米D.100平方米7.如图,☉O的直径AB垂直于弦CD,垂足是E,∠A= .5°,OC= ,CD的长为( )A.2B.4C.4D.88.已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )第Ⅱ卷(非选择题,共88分)二、填空题(本题共16分,每小题4分)9.分解因式:ax4-9ay2= .10.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为m.11.如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数y=(k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为.12.在平面直角坐标系xOy中,对于点P(x,y),我们把点P'(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,A n,….若点A1的坐标为(3,1),则点A3的坐标为,点A2 014的坐标为;若点A1的坐标为(a,b),对于任意的正整数n,点A n均在x轴上方,则a,b应满足的条件为.三、解答题(本题共30分,每小题5分)13.如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E.14.计算:(6-π)0+-5--3tan 30°+|-3|.15.解不等式x- ≤x-,并把它的解集在数轴上表示出来.316.已知x-y=3,求代数式(x+1)2-2x+y(y-2x)的值.17.已知关于x的方程mx2-(m+ )x+ =0(m≠0).(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数m的值.18.列方程或方程组解应用题:小马自驾私家车从A地到B地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动汽车所需电费27元.已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.四、解答题(本题共20分,每小题5分)19.如图,在▱ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连结EF,PD.(1)求证:四边形ABEF是菱形;(2)若AB= ,AD= ,∠ABC= 0°,求tan∠ADP的值.20.根据某研究院公布的2009—2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:2013年成年国民倾向的阅读方式人数分布统计图2009—2013年成年国民根据以上信息解答下列问题:(1)直接写出扇形统计图中m的值;(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为本;(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为本.21.如图,AB是☉O的直径,C是的中点,☉O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线DB于点F,AF交☉O于点H,连结BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.22.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC 上,∠BAD=75°,∠CAD=30°,AD= ,BD= DC,求AC的长.小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2) .请回答:∠ACE的度数为,AC的长为.参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.图3五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,-2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.24.在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连结BE,DE,其中DE交直线AP于点F.(1)依题意补全图1;(2)若∠PAB= 0°,求∠ADF的度数;(3)如图2,若 5°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.25.对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数.在所有满足条件的M中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(1)分别判断函数y=(x>0)和y=x+1(- <x≤ )是不是有界函数?若是有界函数,求其边界值;(2)若函数y=-x+ (a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数y=x 2(- ≤x≤m,m≥0)的图象向下平移m 个单位,得到的函数的边界值是t,当m 在什么范围时,满足3≤t≤ ?答案全解全析：一、选择题1.B ∵ +(- )=0,∴ 的相反数为-2.故选B.2.B 300 000=3× 05.故选B.3.D 6张扑克牌中,点数为偶数的有3张,所以抽到点数为偶数的概率是3 =.故选D.4.C 选项A 、B 中的几何体,三视图中一定有一个圆,与所给的三视图不符,排除A,B;选项D 中的几何体的三视图是三个三角形,与所给的三视图也不相符,排除D.只有选项C 中的几何体与所给的三视图相符,故选C.5.A 年龄为18岁的队员最多,故众数为18;12名队员年龄的平均数为5 9 0=19.故选A.6.B 休息的过程中是不进行绿化工作的,即绿化面积S 不变化,由图象可知第1~2小时为园林队休息时间,则休息后园林队的绿化面积为160-60=100(平方米),所用的时间为4-2=2(小时),所以休息后园林队每小时绿化面积为 00÷ =50(平方米).故选B. 7.C∵CO=AO,∴∠COE= ∠A= 5°.∵OC= ,∴CE=OC·sin∠COE= ×=2 .∵AB⊥CD,∴CD= C E=4 故选C.8.A 由图象可知,AP 先由短变长,然后略微变短再变长,最后AP 由长变短.选项A 与题目要求相符;选项B 是先由短变长,然后略微变短再变长,接着再略微变短再变长,最后由长变短,与题目要求不符;选项C 是先由短变长,到达第一个顶点后继续变长,到达第二个顶点后开始变短,到达第三个顶点后继续变短,与题目要求不符;选项D 是先由短变长,在经过点A 的直径与圆的另一个交点处时最长,然后开始变短,与题目要求不符.故选A.评析 解决本题的关键是根据图形特征分析函数图象随自变量变化的趋势,结合图形性质通过定性分析来确定选项.属中档题. 二、填空题9.答案 a(x 2+3y)(x 2-3y)解析 ax 4-9ay 2=a(x 4-9y 2)=a(x 2+3y)(x 2-3y). 10.答案 15解析 设旗杆的高度为x m,则 . 3=5,解得x=15.即旗杆的高度为15 m.11.答案 y=(答案不唯一,满足0<k≤ 即可)解析 要使反比例函数的图象与正方形有交点,则至少要经过点B,且k>0,而点B 的坐标为(2,2),所以k 的最大值为4,即0<k≤ . 12.答案 (-3,1);(0,4);-1<a<1,0<b<2解析 由题意可知,点A 2的坐标为(0,4),点A 3的坐标为(-3,1),点A 4的坐标为(0,-2),点A 5的坐标为(3, ),…,所以每四个点坐标为一个循环.∵ 0 ÷ =503…… ,∴点A 2 014的坐标与点A 2的坐标一致,为(0,4).因为每四个点坐标为一个循环,所以要求a,b 应满足的条件,只需要知道前4个点的坐标即可.∵点A 1的坐标为(a,b),∴点A 2、A 3、A 4的坐标依次为(-b+1,a+1)、(-a,-b+2)、(b-1,-a+ ).∵点A n 均在x 轴上方,∴0,0,-0,-0,∴-1<a<1,0<b<2.评析解决本题的关键是读懂题目要求,并按照题目要求正确操作.尤其是“在x轴上方”即为“纵坐标>0”.属中档题.三、解答题13.证明∵BC∥DE,∴∠ABC=∠D.在△ABC和△EDB中,,∠∠,,∴△ABC≌△EDB.∴∠A=∠E.14.解析原式=1-5-3×33+3=-4.15.解析去分母,得3x- ≤ x-3,移项,得3x- x≤ -3.合并同类项,得-x≤3,系数化为1,得x≥-3.不等式的解集在数轴上表示如下:16.解析(x+1)2-2x+y(y-2x)=x2+2x+1-2x+y2-2xy=x2-2xy+y2+1.∵x-y=∴原式=(x-y)2+1=4.17.解析(1)证明:∵m≠0,∴mx2-(m+2)x+2=0是关于x的一元二次方程.∴Δ=[-(m+2)]2- × m=(m-2)2.∵(m-2)2≥0,∴方程总有两个实数根.(2)由求根公式,得x=( )(- ).∴x1=1,x2=.∵方程的两个实数根都是整数,且m为正整数,∴m= 或2.18.解析设新购买的纯电动汽车每行驶1千米所需的电费为x元.由题意,得 7= 00.5.解得x=0.18.经检验,x=0.18是原方程的解,且符合题意.答:新购买的纯电动汽车每行驶1千米所需的电费为0.18元.四、解答题19.解析(1)证明:∵BF是∠ABC的平分线,∴∠ABF=∠EBF.∴∠AFB=∠EBF.∴∠AFB=∠ABF.∴AB=AF.同理,AB=BE.∴AF=BE.又∵AF∥BE,∴四边形ABEF是平行四边形.∵AB=AF,∴四边形ABEF是菱形.(2)过点P作PG⊥AD于点G,如图.∵四边形ABEF是菱形,∠ABC= 0°,∴△ABE是等边三角形.∵AB= ,∴AE=AB= ,∴AP=AE=2.在Rt△AGP中,可求得∠PAG= 0°.∴AG=AP·cos 0°= ,GP=AP·sin 0°=3.∵AD= ,∴DG=5,.∴tan∠ADP==3520.解析(1)66.0.( )5.00±0.0 .(3)7 500±30.(990÷ .0%×5=7 500) 21.解析(1)证明:连结BC.∵AB是☉O的直径,∴∠ACB=90°.∵C是的中点,∴=.∴AC=BC.∴∠CAB=∠CBA= 5°.∵BD是☉O的切线,∴∠ABD=90°.可得∠CBD=∠D= 5°.∴BC=CD.∴AC=CD.(2)连结OC.∴∠OCA=∠CAB= 5°.∴∠COE=90°.∵E是OB的中点,∴OE=BE.∵∠CEO=∠FEB,∴Rt△COE≌Rt△FBE.∴BF=OC.∵OB= ,∴BF= .由勾股定理,得AF=2.∵∠ABF=∠AHB=90°,∴BH=·=55.22.解析∠ACE的度数为75°,AC的长为3.解决问题:过点D作DF∥AB交AC于点F,如图.∴∠DFE=∠BAC=90°,又∠AEB=∠FED,∴△ABE∽△FDE.∴==.∵BE= ED,AE= ,∴FE= ,∴AF=3.∵∠CAD=30°,∴FD=,AD=2∵= ,∴AB=∵∠ADC=75°,∠CAD=30°,∴∠ACD=75°,∴AC=AD= 3.在Rt△ABC中,由勾股定理可得BC=2.评析本题考查了相似三角形的判定与性质、三角函数等知识.解决本题的关键是读懂题目中给出的操作方法,由平行想到相似三角形.属中档题.五、解答题23.解析( )∵点A,B在抛物线y=2x2+mx+n上,∴-,33m n.解得- ,- .∴抛物线的表达式为y=2x2-4x-2.∴抛物线的对称轴为x=1.(2)由题意可知,点C的坐标为(-3,-4). 设直线BC的表达式为y=kx+b(k≠0).∴3,--3,解得3,0.∴直线BC的表达式为y=3x.∴当x=1时,y=3.结合图象可知,点A在直线BC的下方,且抛物线的顶点坐标为(1,-4),∴- ≤t≤3.24.解析(1)补全图形,如图所示.(2)连结AE,如图.∵点E与点B关于直线AP对称,∴AE=AB,∠EAP=∠BAP= 0°.∵AB=AD,∴AE=AD,∴∠AED=∠ADF.又∠BAD=90°,∴ ∠ADF+ 0°+90°= 0°.∴∠ADF= 5°.(3)AB,FE,FD满足的数量关系为FE2+FD2=2AB2. 证明:连结AE,BF,BD,设BF交AD于点G,如图.∵点E与点B关于直线AP对称,∴AE=AB,FE=FB.可证得∠FEA=∠FBA.∵AB=AD,∴AE=AD.∴∠ADE=∠AED.∴∠ADE=∠ABF.又∵∠DGF=∠AGB,∴∠DFB=∠BAD=90°.∴FB2+FD2=BD2.∵BD2=2AB2,∴FE2+FD2=2AB2.25.解析(1)y=(x>0)不是有界函数;y=x+1(- <x≤ )是有界函数,边界值是3.(2)对于函数y=-x+ (a≤x≤b,b>a),∵y随x的增大而减小,∴y的最大值是-a+1,y的最小值是-b+1.∵函数的最大值是2,∴a=-1.又∵函数的边界值是2,∴-b+ ≥-2,∴b≤3.∴- <b≤3.(3)由题意,函数平移后的表达式为y=x2-m(- ≤x≤m,m≥0).当x=-1时,y=1-m;当x=0时,y=-m;当x=m时,y=m2-m.根据二次函数的对称性,当0≤m≤ 时,1-m≥m2-m;当m>1时,1-m<m2-m.①当0≤m≤时,1-m≥m,由题意,边界值t=1-m.当3≤t≤ 时,0≤m≤.∴0≤m≤.②当<m≤ 时,1-m<m.由题意,边界值t=m.当3≤t≤ 时,3≤m≤ .∴3≤m≤ .③当m>1时,由题意,边界值t≥m.∴不存在满足3≤t≤ 的m值.综上所述,当0≤m≤或3≤m≤ 时,满足3≤t≤ .。

2014年北京市中考数学试卷(含答案和解析)2014年北京市中考数学试卷一、选择题（本题共32分，每小题4分）1.（4分）2的相反数是（）A。

2B。

-2C。

D。

2.（4分）据报道，某小区居民XXX改进用水设备，在十年内帮助他居住小区的居民累计节水300 000吨。

将300 000用科学记数法表示应为（）A。

0.3×10^6B。

3×10^5C。

D。

3×10^43.（4分）如图，有6张扑克牌，从中随机抽取一张，点数为偶数的概率是（）A。

B。

C。

D。

4.（4分）如图是几何体的三视图，该几何体是（）A。

圆锥B。

圆柱C。

正三棱柱D。

正三棱锥5.（4分）某篮球队12名队员的年龄如表：年龄（岁）。

18.19.20.21人数。

5.4.1.2则这12名队员年龄的众数和平均数分别是（）A。

18，19B。

19，19C。

18，19.5D。

19，19.56.（4分）园林队在某公园进行绿化，中间休息了一段时间。

已知绿化面积S（单位：平方米）与工作时间t（单位：小时）的函数关系的图象如图，则休息后园林队每小时绿化面积为（）A。

4平方米B。

5平方米C。

8平方米D。

100平方米7.（4分）如图，圆O的直径AB垂直于弦CD，垂足是E，∠A=22.5°，OC=4，CD的长为（）A。

2B。

4C。

D。

88.（4分）已知点A为某封闭图形边界上一定点，动点P 从点A出发，沿其边界顺时针匀速运动一周。

设点P运动的时间为x，线段AP的长为y。

表示y与x的函数关系的图象大致如图，则该封闭图形可能是（）A。

B。

C。

D。

二、填空题（本题共16分，每小题4分）9.（4分）分解因式：ax^4-9ay^2=_________。

10.（4分）在某一时刻，测得一根高为1.8m的竹竿的影长为3m，同时测得一根旗杆的影长为25m，那么这根旗杆的高度为_________m。

11.（4分）如图，在平面直角坐标系xOy中，正方形OABC的边长为2.写出一个函数y=f(x)（k≠0），使它的图象与正方形OABC有公共点，这个函数的表达式为_________。

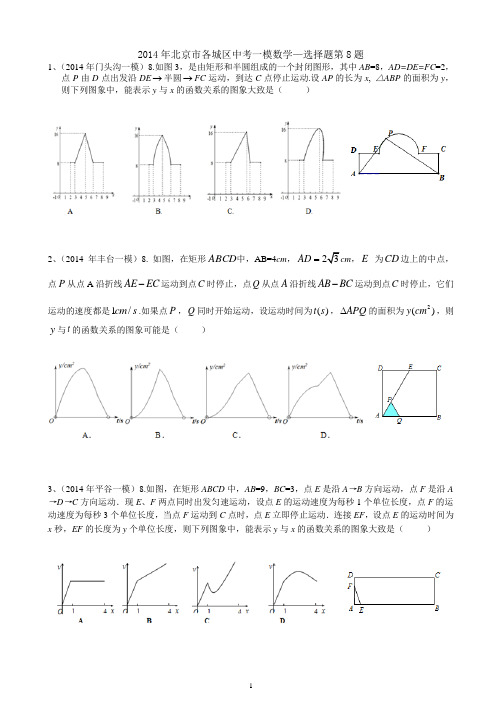
2014年北京市各城区中考一模数学—选择题第8题1、（2014年门头沟一模）8.如图3，是由矩形和半圆组成的一个封闭图形，其中AB =8，AD=DE=FC =2，点P 由D 点出发沿DE →半圆→FC 运动，到达C 点停止运动.设AP 的长为x , △ABP 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）2、（2014年丰台一模）8. 如图，在矩形ABCD 中，AB=4cm ，AD =，E 为CD 边上的中点，点P 从点A 沿折线AE EC -运动到点C 时停止，点Q 从点A 沿折线AB BC -运动到点C 时停止，它们运动的速度都是s cm /1.如果点P ，Q 同时开始运动，设运动时间为)(s t ，APQ ∆的面积为)(2cm y ，则y 与t 的函数关系的图象可能是（ ）3、（2014年平谷一模）8.如图，在矩形ABCD 中，AB =9，BC =3，点E 是沿A →B 方向运动，点F 是沿A →D →C 方向运动．现E 、F 两点同时出发匀速运动，设点E 的运动速度为每秒1个单位长度，点F 的运动速度为每秒3个单位长度，当点F 运动到C 点时，点E 立即停止运动．连接EF ，设点E 的运动时间为x 秒，EF 的长度为y 个单位长度，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）4、（2014年顺义一模）8．如图，点C 为⊙O 的直径AB 上一动点，2AB =，过点C 作DE AB ⊥交⊙O 于点D 、E ，连结AD ，AE ． 当点C 在AB 上运动时，设AC 的长为x ，ADE △的面积为y ，下列图象中，能表示y 与x 的函数关系的图象大致是（ ）5、（2014年石景山一模）8．如图，边长为1的正方形ABCD 中有两个动点P ，Q ,点P 从点B 出发沿BD 作匀速运动，到达点D 后停止；同时点Q 从点B 出发，沿折线BC →CD 作匀速运动，P ，Q 两个点的速度都为每秒1个单位，如果其中一点停止运动，则另一点也停止运动．设P ，Q 两点的运动时间为x 秒，两点之间的距离为y ,下列图 象中，能表示y 与x 的函数关系的图象大致是 （ ）6、（2014年海淀一模）8．如图，点P 是以O 为圆心， AB 为直径的半圆的中点，AB=2，等腰直角三角板45°角的顶点与点P 重合， 当此三角板绕点P 旋转时，它的斜边和直角边所在的直线与直径AB 分别相交于C 、D 两点．设线段AD 的长为x ，线段BC 的长为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）7、（2014年西城一模）8. 如图，在平面直角坐标系xOy 中，以点(23)A ，为顶点任作一直角PAQ ∠，使其两边分别与x 轴、y 轴的正半轴交于点P 、Q ，连接PQ ，过点A 作AH PQ ⊥于点H ，设点P 的横坐标为x ，AH 的长为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）8、（2014年通州一模）8．如图，平行四边形纸片ABCD ，CD ＝5，BC ＝2，∠A ＝60°，将纸片折叠，使点A 落在射线AD 上（记为点A '），折痕与AB 交于点P ，设AP 的长为x ，折叠后纸片重叠部分的面积为y ，可以表示y 与x 之间关系的大致图象是（ ）9、（2014年东城一模）8. 在平面直角坐标系中，四边形OABC 是矩形，点B 的坐标为（4，3）．平行于对角线AC 的直线m 从原点O 出发，沿x 轴正方向以每秒1个单位长度的速度运动，设直线m 与矩形OABC 的两边分别交于点M ，N ，直线m 运动的时间为t （秒）．设△OMN 的面积为S ，则能反映S 与t 之间函数关系的大致图象是（ ）10、（2014年朝阳一模）8．正方形网格中的图形（1）～（4）如图所示，其中图（1）、图（2）中的阴影三角形都是有一个角是60°的直角三角形，图（3）、图（4）中的阴影三角形都是有一个角是60°的锐角三角形．以上图形能围成正三棱柱的图形是（）A．（1）和（2）B．（3）和（4）C．（1）和（4）D．（2）、（3）、（4）11、（2014年密云一模）8．.如右图，MN⊥PQ,垂足为点O，点A、C在直线MN上运动，点B、D在直线PQ上运动.顺次连结点A、B、C、D，围成四边形ABCD。

海淀22、阅读下面材料：在学习小组活动中，小明探究了下面问题：菱形纸片ABCD 的边长为2，折叠菱形纸片，将B 、D 两点重合在对角线BD 上的同一点处，折痕分别为EF 、GH ．当重合点在对角线BD 上移动时，六边形AEFCHG 的周长的变化情况是怎样的？ 小明发现：若60ABC ∠=︒，①如图1，当重合点在菱形的对称中心O 处时，六边形AEFCHG 的周长为_________； ②如图2，当重合点在对角线BD 上移动时，六边形AEFCHG 的周长_________（填“改变”或“不变”）.请帮助小明解决下面问题：如果菱形纸片ABCD 边长仍为2，改变∠ABC 的大小，折痕EF 的长为m ． （1）如图3，若120ABC ∠=︒，则六边形AEFCHG 的周长为_________；（2）如图4，若∠ABC 的大小为2α，则六边形AEFCHG 的周长可表示为________．24、在△ABC 中，AB AC =，将线段AC 绕着点C 逆时针旋转得到线段CD ，旋转角为α，且0180α︒<<︒，连接AD 、BD ．（1）如图1，当100BAC ∠=︒，60α=︒时，∠CBD 的大小为_________； （2）如图2，当100BAC ∠=︒，20α=︒时，求∠CBD 的大小；（3）已知∠BAC 的大小为m （60120m ︒<<︒），若∠CBD 的大小与（2）中的结果相同，请直接写出α的大小．DCBAABCD22．解：①6；..........................................................................................1分 ②不变. (2)分（1）……………………………………………………………………3分 （2）4+4sin α．………………………………………………………………5分24．解：（1）30°；………………………………………………………………………1分 （2）如图作等边△AFC ，连结DF 、BF ．∴AF FC AC ==，60FAC AFC ∠=∠=︒. ∵100BAC ∠=︒，AB AC =， ∴40ABC BCA ∠=∠=︒. ∵20ACD ∠=︒， ∴20DCB ∠=︒.∴20DCB FCB ∠=∠=︒. ① ∵AC CD =，AC FC =， ∴DC FC =．② ∵BC BC =，③∴由①②③，得△DCB ≌△FCB ， ∴DB BF =，DBC FBC ∠=∠.∵100BAC ∠=︒，60FAC ∠=︒，∴40BAF ∠=︒. ∵20ACD ∠=︒，AC CD =， ∴80CAD ∠=︒. ∴20DAF ∠=︒.∴20BAD FAD ∠=∠=︒.④ ∵AB AC =，AC AF =， ∴ AB AF =.⑤ ∵ AD AD =，⑥∴由④⑤⑥，得△DAB ≌△DAF ． ∴FD BD =. ∴FD BD FB == ∴60DBF ∠=︒.∴30CBD ∠=︒. ………………………………………………………………………4分（3）120m α=︒-，60α=︒或240m α=︒-. ……………………………7分 西城22. 阅读下列材料：问题：在平面直角坐标系xOy 中，一张矩形纸片OBCD 按图1所示放置。

北京八一中学分班考试真题一、填空题（每小题5分，共80 分）1. 八百八十万零八十写作。

2. 计算：3.45×6.8+65.5×0.68= 。

3. 方程13x-6=0的解为。

4. 按规律填数：2，5，9，14，20，，35，…5. 甲、乙、丙三个数之和为180，甲数是乙数的3倍，乙数是丙数的2倍，那么甲、乙、丙三个数分别是。

6. 有 13 个自然数，小红计算它们的平均数精确到百分位是 12.56，老师说最后一个数字写错了，那么正确答案应该是。

7. 小明以每分钟50 米的速度从学校步行到家，12 分钟后，小强从学校出发，骑自行车以每分钟125 米的速度去追小明，那么小强分钟可以追上小明。

8. 一个两位数除321，余数是48，那么这个两位数是。

9.把 1 表示成 5 个不同的单位分数的和的形式：11()=+1()+1()+1()+1()10. 平面上 5 条直线最多能把圆的内部分成 部分。

11. 如图，边长为 6 厘米和 8 厘米的两个正方形拼在一起，则图中阴影部分面积是 平方厘米。

12. 规定：5▲2=5+55=60，2▲5=2+22+222+2222+22222=24690，1▲4=1+11+111+1111=1234,那么，4▲3= 。

13. 如图是小伟家到学校的路线，小伟上学沿最短路线走，共有 条不同的路线。

14.甲、乙两人同时从A、B 两地相向而行，第一次在离A地40 千米处相遇，之后两人仍以原速度前进，各自到达目的地后，立即返回，又在离A地20 千米处相遇，则A B两地距离为千米。

15. 如图，是一块在电脑屏幕上出现的长方形色块，由A、B、C、D、E、F 六个正方形组成，已知中间最小的正方形A的边长为1，那么这个长方形色块图的面积是。

16. 设自然数x, y, m, n 满足条件58x y my m n===，则x+y+m+n的最小值是。

二、解答题（每题10 分，共20 分）17. 某人乘船由A地顺流而下到B地，然后又逆流而上到C 地，共乘船 4 小时，已知船在静水中的速度为每小时7.5 千米，水流速度为每小时2.5 千米，若A、C 两地的距离为10 千米，求A、B 两地的距离。