质点运动学典型习题解析2019
- 格式:pdf
- 大小:581.03 KB
- 文档页数:21


质点运动学试题与答案一.选择题:1.一质点在平面上运动,已知质点位置矢量的表示式为 j bt i at r 22+=(其中a 、b 为常量), 则该质点作 (A) 匀速直线运动. (B) 变速直线运动.(C) 抛物线运动. (D)一般曲线运动. [ ] 2.一质点沿x 轴作直线运动,其v -t 曲线如图所示,如t =0时,质点位于坐标原点,则t =4.5 s 时,质点在x 轴上的位置为 (A) 5m . (B) 2m .(C) 0. (D) -2 m .(E) -5 m. [ ] 3.某人骑自行车以速率v 向西行驶,今有风以相同速率从北偏东30°方向吹来,试问人感到风从哪个方向吹来? (A) 北偏东30°. (B) 南偏东30°.(C) 北偏西30°. (D) 西偏南30°. [ ] 4.下列说法中,哪一个是正确的?(A) 一质点在某时刻的瞬时速度是2 m/s ,说明它在此后1 s 内一定要经过2 m 的路程.(B) 斜向上抛的物体,在最高点处的速度最小,加速度最大. (C) 物体作曲线运动时,有可能在某时刻的法向加速度为零.(D) 物体加速度越大,则速度越大. [ ] 二.填空题1.一质点沿x 轴作直线运动,它的运动学方程为 x =3+5t +6t 2-t 3 (SI)则 (1) 质点在t =0时刻的速度=0v__________________;(2) 加速度为零时,该质点的速度=v ____________________.2.一物体作斜抛运动,初速度0v与水平方向夹角为θ,如图所示.物体轨道最高点处的曲率半径ρ为__________________.3.设质点的运动学方程为j t R i t R r sin cos ωω+= (式中R 、ω 皆为常量)则质点的v=___________________,d v /d t =_____________________.4.轮船在水上以相对于水的速度1v 航行,水流速度为2v,一人相对于甲板以速度3v 行走.如人相对于岸静止,则1v 、2v和3v 的关系是___________________.2. -12三.计算:一人自原点出发,25 s 内向东走30 m ,又10 s 内向南走10 m ,再15 s 内向正西北走18 m .求在这50 s 内, (1) 平均速度的大小和方向; (2) 平均速率的大小.有一宽为l 的大江,江水由北向南流去.设江中心流速为u 0,靠两岸的流速为零.江中任一点的流速与江中心流速之差是和江心至该点距离的平方成正比.今有相对于水的速度为0v的汽船由西岸出发,向东偏北45°方向航行,试求其航线的轨迹方程以及到达东岸的地点. 四.证明:一艘船以速率u驶向码头P ,另一艘船以速率v 自码头离去,试证当两船的距离最短时,两船与码头的距离之比为:()()ααcos :cos v v ++u u 设航路均为直线,α为两直线的夹角.答案:一.选择题: BBCC二.填空题:1 5m/s 17m/s2 ρ =v 02cos 2θ /g3 -ωR sin ω t i+ωR cos ω t j4 0321=++v v v三.计算题:1解:(1) BC AB OA OC ++=)45sin )45cos (18)10(30j i j i ︒+︒-+-+=j i73.227.17+=OC ,方向φ =8.98°(东偏北)2分 =∆=∆∆=t OC t r //v 0.35m/s方向东偏北8.98° 1分(2) (路程)()181030++=∆S m=58m, 16.1/=∆∆=t S v m/s 2分2解:以出发点为坐标原点,向东取为x 轴,向北取为y 轴,因流速为-y 方向,B Px y u lαOCAB东y 北φπ/4西 南x由题意可得u x = 0u y = a (x -l /2)2+b令 x = 0, x = l 处 u y = 0, x = l /2处 u y =-u 0,代入上式定出a 、b,而得 ()x x l luu y --=204船相对于岸的速度v(v x ,v y )明显可知是 2/0v v =x y y u +=)2/(0v v , 将上二式的第一式进行积分,有t x 20v=还有,xy t x x y t y y d d 2d d d d d d 0v v ====()x x l l u --20042v 2分 即 ()x x l l u x y--=020241d d v 1分因此,积分之后可求得如下的轨迹(航线)方程:'3020********x l u x l u x y v v +-= 2分到达东岸的地点(x ',y ' )为⎪⎪⎭⎫⎝⎛-=='='=003231v , u l y y l x l x 2分四.证明:证:设任一时刻船与码头的距离为x 、y ,两船的距离为l ,则有αcos 2222xy y x l -+= 2分 对t求导,得()()txyt y x t y y t x x t l l d d cos 2d d cos 2d d 2d d 2d d 2αα--+= 2分 将v , =-=t y u t x d d d d 代入上式,并应用0d d =tl作为求极值的条件, 则得 ααcos cos 0yu x y ux +-+-=v v()()ααcos cos u y u x +++-=v v 3分由此可求得 ααcos cos v v ++=u u y x 1分即当两船的距离最短时,两船与码头的距离之比为y 45 °v 0 u 0xl()()ααcos+uu2分:cos vv+。

第一章质点运动学一选择题1.以下说法中,正确的选项是:()A.一物体若拥有恒定的速率,则没有变化的速度;B.一物体拥有恒定的速度,但仍有变化的速率;C.一物体拥有恒定的加快度,则其速度不行能为零;D. 一物体拥有沿x 轴正方向的加快度而有沿x 轴负方向的速度。
解:答案是 D。
2.长度不变的杆 AB,其端点 A 以 v0匀速沿 y 轴向下滑动, B 点沿 x 轴挪动,则 B 点的速率为:()A . v0 sinB .v0 cos C.v0 tan D.v0 / cos解:答案是 C。
简要提示:设 B 点的坐标为 x, A 点的坐标为 y,杆的长度为l,则x2y2l 2对上式两边关于时间求导:dx dy0,因dxv,dyv0,所以2 x 2 ydtdt dt dt2xv2yv0 = 0即v=v0 y/x =v0tan所以答案是 C。
3.如图示,路灯距地面高为 H,行人身高为 h,若人以匀速 v 背向路灯行走,灯y人头A H vv0hθvx影sB选择题 3图选择题 2图则人头影子挪动的速度u 为()H h Hv h HA.vB.H H h H h 解:答案是 B 。
简要提示:设人头影子到灯杆的距离为 x ,则x s h , x Hs , x H H hdx H ds HvuH h dt Hdt h所以答案是 B 。
4. 某质点作直线运动的运动学方程为x = 3t-5t 3 + 6 (SI),则该质点作A. 匀加快直线运动,加快度沿 x 轴正方向.B. 匀加快直线运动,加快度沿 x 轴负方向.C. 变加快直线运动,加快度沿 x 轴正方向.D. 变加快直线运动,加快度沿x 轴负方向.()解: 答案是 D5. 一物体从某一确立高度以v 0 的初速度水平抛出,已知它落地时的速度为v t ,那么它的运动时间是: ()v t - v 0v t v 0v t2 22v v 0 v t A.B.C.gD.2 gg2 g解:答案是 C 。

第2章《质点运动学》习题解答2.1.1质点的运动学方程为I(1), (3 2t)? 5?,(2).r(2 3t)? (4t 1)j?求质点轨迹并用图表示。
【解】①.x 3 2t,y 5,轨迹方程为y=5x 2 3t②3t消去时间参量t 得:3y 4x 5 0y 4t 12.1.2 质点运动学方程为r e 2t ? e 2t ? 2k?, ( 1).求质点的轨迹;(2)求自t=-1至t=1质点的位移。
【解】2tx e ① y e 2t 消去t 得轨迹:xy=1,z=2z 2② 才 e 2i? e 2? 2!?,才 e 2i? e 2? 20,3 ^1 ^1 (e 2 e 2)? (e 2 e 2) j?2.1.3 质点运动学方程为求自t=0至t=1质点的位移。
【解】4t 2? (2t 3)?,( 1).求质点的轨迹;(2)①.x 4t 2, y 2t 3,消去t 得轨迹方程x (y 3)2②r 0 3?』2.2.1雷达站于某瞬时测得飞机位置为R i 4100m, i 33.70,°.75s 后测得R 2 4240m, 2 29.3°, R,R 2均在铅直平面内。
求飞机瞬时速率的近似值和飞行方向(a 角)。
R i 2 R ; 2RR, cos( i 2)代入数值得: .41002 42402 -2 4100 4240cos 4.4°349.385(m)利用正弦定理可解出34.8902.2.2 一小圆柱体沿抛物线轨道运动,抛物线轨道为y x 2 / 200 (长度mm 。
第一次观察到圆柱体在349.3850.75 465.8(m/s)x=249mn 处,经过时间2ms 后圆柱体移到 x=234mn 处。
求圆柱体瞬时速度的近似4i? 5? r4? 2?t[解]19.6mm/ms152 36.22522112.502.2.3 一人在北京音乐厅内听音乐,离演奏者 17m 另一人在广州听同一 演奏的转播,广州离北京2320km 收听者离收音机2m 问谁先听到声音?声速 为340m/s,电磁波传播的速度为3.0 108m/s 。


第一部分名师综述本专题中难题分为二,一为对运动图像考查,对图像考查范围很广,涉及内容页比较多,几乎涉及了直线运动中所有知识以及应用,特别是利用图像处理追击相遇问题时高考考查重难点,在解题过程中,要注意分析图像轴、点、线、面积、斜率等方面,考查方式多为选择题。
二是对多过程直线运动考查,综合了匀变速直线运动公式、追击相遇问题,考查方式多为计算题, 在做题过程中需要(1)要养成画物体运动示意图,或者x-t 图象与v-t图象习惯,特别是比较复杂运动,画出示意图或者运动图像可使运动过程直观化,物理过程清晰,便于研究,(2)要注意分析研究对象运动过程,搞清楚整个运动过程按运动性质转换可以分为哪几个阶段,各个阶段遵循什么规律,各个阶段又存在哪些联系。
第二部分精选试题1.将甲乙两小球先后以同样速度在距地面不同高度处竖直向上抛出,抛出时间相隔2 s,它们运动图像分别如直线甲乙所示。
则()A.t=2 s时,两球高度相差一定为40 mB.t=4 s时,两球相对于各自抛出点位移相等C.两球从抛出至落到地面所用时间间隔相等D .甲球从抛出至到达最高点时间间隔与乙球相等 【答案】BD2.一火车沿直线轨道从静止发出由A 地驶向B 地,并停止在B 地。
AB 两地相距x ,火车做加速运动时,其加速度最大为a 1,做减速运动时,其加速度绝对值最大为a 2,由此可可以判断出该火车由A 到B 所需最短时间为 。
【答案】t =【解析】:整个过程中火车先做匀加速运动,后做匀减速运动,加速度最大时,所用时间最短,分段运动可用图像法来解。
根据题意作v —t 图,如图所示。
由图可得11v a t =,22va t =, 因为匀变速直线运动速度时间图像与坐标轴围成面积表示位移,所以有:121()2x v t t =+则联立解得t =3.两辆完全相同汽车,沿水平直路一前一后匀速行驶,速度均为0v ,若前车突然以恒定加速度刹车,在它刚停住时,后车以前车刹车时加速度开始刹车,已知前车在刹车过程中所行驶路程为s ,若要保证两辆车上述情况中不相撞,则两车在匀速行驶时保持车距至少应为( )A .sB .2sC .3sD .4s 【答案】B解法一:对前车: 000?t v v v at t a==+→=-① 2220022t v v v as a s-=→= ②对后车:0l v t = ③ 由①②代入③得2l s =,选项B 正确、解法二:作前、后车v-t 图象,如图所示,在前车刹车过程中后车仍以0v 向前做匀速直线运动,在前车刹车时间t 内,后车走路程用矩形面积表示,从图中明显看出2l s =、有同学选C,认为是3s 、错在没有弄清题目要求两车在匀速运动时应保持最小距离并非后车总位移、4.质点由A 向B 做直线运动,A 、B 间距离为L ,已知质点在A 点速度为v 0,加速度为a ,如果将L 分成相等n 段,质点每通过L /n 距离加速度均增加a /n,求质点到达B 时速度。

(2) 一质点沿x 方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度V 0为5m -s '1,则当t 为3s 时,质点的速度 v= ________________________ 。
[答案:23 ms -1]⑶ 轮船在水上以相对于水的速度 V 航行,水流速度为v 2, 一人相对于甲板以速度 V 3行走。
如人相对于岸静止,则V 、V 2和V 3的关系是。
[答案:V 1 V 2 V 30]习题1A /选择题(1) 一运动质点在某瞬时位于矢径r(x, y)的端点处,其速度大小为dr(A) — dtdr (B) —— dtd |r |(C)dt1[答案:D]:,dx 、2,dy 、2(D)W dt )V(2) 一质点作直线运动,某时刻的瞬时速度 v 2m/s ,瞬时加速度a 2m/ s 2,则 一秒钟后质点的速度 (A)等于零 (C)等于 2m/s [答案:D] (B)等于-2m/s (D)不能确定。
(3) 一质点沿半径为 速度大小和平均速率大小分别为 2 R 2 R (A) - t tR 的圆周作匀速率运动,每 t 秒转一圈,在2t 时间间隔中,其平均 (C) 0,0 c 2 R (B) 0,-p 2 R c (D) —,0 [答案:B]/填空题 (1) 一质点,以 m 1 的匀速率作半径为 5m 的圆周运动,则该质点在 5s 内,位移的大小是 _____________________ [答案:10 m ; ;经过的路程是 5 n m]一个物体能否被看作质点,你认为主要由以下三个因素中哪个因素决定:(1) 物体的大小和形状; (2) 物体的内部结构; (3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研 究问题的性质决定。
F 面几个质点运动学方程,哪个是匀变速直线运动(1)x=4t-3; ( 2)x=-4t 3+3t 2+6; ( 3)x=-2t 2+8t+4; ( 4)x=2t 2-4/t 。

第1章 质点运动学 习题及答案1.||与 有无不同?和有无不同? 和有无不同?其不同在哪里?试举例说明.r ∆r ∆t d d r dr dt t d d v dv dt解: ||与 不同. ||表示质点运动位移的大小,而则表示质点运动时其径向长度的r ∆r ∆r ∆r ∆增量;和不同. 表示质点运动速度的大小,而则表示质点运动速度的径向分量;t d d r dr dt t d d r dr dtt d d v 和不同. 表示质点运动加速度的大小, 而则表示质点运动加速度的切向分量.dv dt t d d v dv dt2.质点沿直线运动,其位置矢量是否一定方向不变?质点位置矢量方向不变,质点是否一定做直线运动?解: 质点沿直线运动,其位置矢量方向可以改变;质点位置矢量方向不变,质点一定做直线运动.3.匀速圆周运动的速度和加速度是否都恒定不变?圆周运动的加速度是否总是指向圆心,为什么?解: 由于匀速圆周运动的速度和加速度的方向总是随时间发生变化的,因此,其速度和加速度不是恒定不变的;只有匀速圆周运动的加速度总是指向圆心,故一般来讲,圆周运动的加速度不一定指向圆心.4.一物体做直线运动,运动方程为,式中各量均采用国际单位制,求:(1)第二秒2362x t t =-内的平均速度(2)第三秒末的速度;(3)第一秒末的加速度;(4)物体运动的类型。
解: 由于: 232621261212x(t )t t dx v(t )t t dtdv a(t )t dt=-==-==-所以:(1)第二秒内的平均速度:1(2)(1)4()21x x v ms --==- (2)第三秒末的速度: 21(3)1236318()v ms -=⨯-⨯=- (3)第一秒末的加速度:2(1)121210()a ms -=-⨯= (4)物体运动的类型为变速直线运动。
5.一质点运动方程的表达式为,式中的分别以为单位,试求;(1)质点2105(t t t =+r i j ),t r m,s 的速度和加速度;(2)质点的轨迹方程。

第一章 质点运动学1–1 描写质点运动状态的物理量是。
解:加速度是描写质点状态变化的物理量,速度是描写质点运动状态的物理量,故填“速度”。
1–2 任意时刻a t =0的运动是运动;任意时刻a n =0的运动是运动;任意时刻a =0的运动是运动;任意时刻a t =0,a n =常量的运动是运动。
解:匀速率;直线;匀速直线;匀速圆周。
1–3 一人骑摩托车跳越一条大沟,他能以与水平成30°角,其值为30m/s 的初速从一边起跳,刚好到达另一边,则可知此沟的宽度为()m/s 102=g 。
解:此沟的宽度为m 345m 1060sin 302sin 220=︒⨯==g R θv1–4 一质点在xoy 平面运动,运动方程为t x 2=,229t y -=,位移的单位为m ,试写出s t 1=时质点的位置矢量__________;s t 2=时该质点的瞬时速度为__________,此时的瞬时加速度为__________。
解:将s t 1=代入t x 2=,229t y -=得2=x m ,7=y ms t 1=故时质点的位置矢量为j i r 72+=(m )由质点的运动方程为t x 2=,229t y -=得质点在任意时刻的速度为m/s 2d d ==t x x v ,m/s 4d d t tx y -==v s t 2=时该质点的瞬时速度为j i 82-=v (m/s )质点在任意时刻的加速度为0d d ==ta x x v ,2m/s 4d d -==t a y y v s t 2=时该质点的瞬时加速度为j 4-m/s 2。
1–5 一质点沿x 轴正向运动,其加速度与位置的关系为x a 23+=,若在x =0处,其速度m/s 50=v ,则质点运动到x =3m 处时所具有的速度为__________。
解:由x a 23+=得x xt x x t 23d d d d d d d d +===v v v v 故x x d )23(d +=v v积分得⎰⎰+=305d )23(d x x v v v则质点运动到x =3m 处时所具有的速度大小为 61=v m/s=7.81m/s ;1–6 一质点作半径R =1.0m 的圆周运动,其运动方程为t t 323+=θ,θ以rad 计,t 以s 计。

第一章运动的描述1.1:质点参考系一:知识精讲归纳一、物体和质点1.定义:忽略物体的大小和形状,把物体简化为一个具有质量的点2.物体看作质点的条件:一个物体能否看成质点是由所要研究的问题决定的.当物体的大小和形状对研究问题影响较小,可把物体看作质点3.理想化模型:在物理学中,突出问题的主要因素,忽略次要因素,建立理想化的物理模型,并将其作为研究对象,是经常采用的一种科学研究方法.质点这一理想化模型就是这种方法的具体应用二、参考系1.运动与静止(1)自然界的一切物体都处于永恒的运动中,运动是绝对的(2)描述某个物体的位置随时间的变化,总是相对于其他物体而言的,这便是运动的相对性.2.参考系:要描述一个物体的运动,首先要选定某个其他物体作为参考,这种用来作为参考的物体叫作参考系3.参考系的选择是任意(填“任意”或“唯一”)的4.选择不同的参考系来观察同一个物体的运动,其结果往往会有所不同(填“会有所不同”或“一定相同”)考点技巧归纳:1.对质点的理解(1)质点是用来代替物体的有质量的点,只占有位置而不占有空间,具有被代替物体的全部质量(2)质点是一种“理想化模型”,它是对实际物体的一种科学抽象2.物体能看成质点的条件(1)物体的大小、形状对研究结果没有影响或影响可以忽略时(2)平动的物体(3)当所研究物体的运动涉及的空间远大于物体的尺寸时二:考点题型归纳一:质点的概念与理解1.在以下情况中关于质点的说法正确的是()A.研究“玉兔”号巡视器巡视月球时的运动轨迹时,“玉兔”号巡视器可看作质点B.观察“辽宁舰”航空母舰上的“歼-15”战斗机起飞时,可以把航空母舰看成质点C.研究“玉兔”号从“嫦娥”的怀抱中“走”出来,即两器分离过程中,研究“玉兔”一连串技术含量极高的“慢动作”时,“玉兔”号可看作质点D.研究自行车的运动时,因为车轮在转动,所以无论什么情况下,自行车都不能看成质点2.下列各种情况中,可以把研究对象(加点者)看作质点的是()A.研究在水平推力作用下沿水平面运动的本箱B.研究一列队伍从桥上通过的时间C.研究小木块的翻倒过程D.在研究汽车后轮转动情况3.截至9月18日8时30分,“天问一号”探测器飞行里程已达1.55亿公里,距离地球1800万公里,各系统工作正常,探测器状态良好。
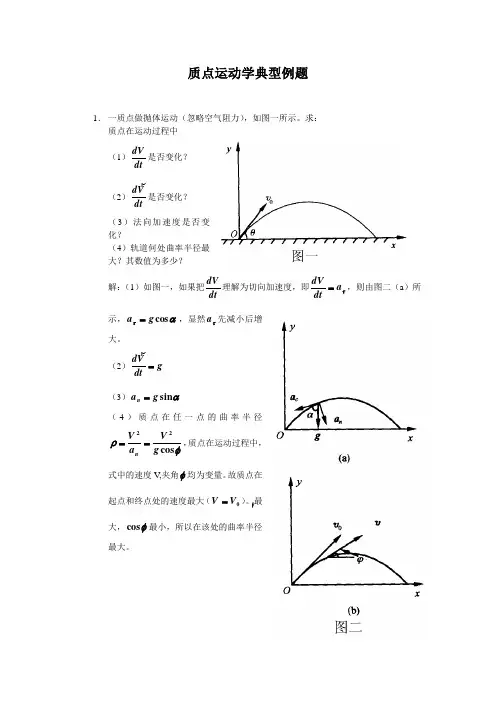
质点运动学典型例题1. 一质点做抛体运动(忽略空气阻力),如图一所示。
求:质点在运动过程中(1)dtdV 是否变化? (2)dtV d 是否变化? (3)法向加速度是否变化?(4)轨道何处曲率半径最大?其数值为多少?解:(1)如图一,如果把dtdV 理解为切向加速度,即τa dt dV =,则由图二(a )所示,ατcos g a =,显然τa 先减小后增大。
(2)g dtV d = (3)αsin g a n =(4)质点在任一点的曲率半径φρcos 22g V a V n ==,质点在运动过程中,式中的速度V,夹角φ均为变量。
故质点在起点和终点处的速度最大(0V V =)。
φ最大,φcos 最小,所以在该处的曲率半径最大。
上抛石块的位移和路程一石块以V=4.9m/s 的初速度向上抛出,经过2S 后,石块的位移y ∆________,路程S______.解:如图一,设定石块上抛的初始点为原点,竖直向上为正方向。
则其运动方程为2021gt t V y -= 2S 内的位移为m y 8.928.92129.42-=⨯⨯-⨯=,负号表明所求位移的方向为竖直向下,即物体在2S 内改变了运动方向。
先求物体到达最高点的时刻,即00=-=gt V dt dy ,S g V t 5.08.99.40=== 则总路程m L L L 25.12)5.1(8.921)5.0(8.9212221=⨯⨯+⨯⨯=+= 求解某一位置的速度质点沿x 轴正向运动,其加速度随位置变化的关系为2331x a +=,如果在x=0处,其速度为s m V /50=,那么,在x=3m 处的速度为多少? 解:因为2331x V dx dV dt dx dx dV dt dV a +====s m V x x V x x V V dx x VdV V V /9)25333(2)23(2322)331(2320332023020=++=++=+=-+=⎰⎰宇宙速度众所周知,人造地球卫星和人造行星是人类认识宇宙的重大发展.但怎样才能把物体抛向天空,使之成为人造卫星或人造行星呢:)这取决于抛体的初速度。
质点的直线运动●运动的描述●1.质点用来取代物体的有质量的点叫做质点,研究一个物体的运动时,假如物体的形状和大小对问题的影响可以忽视,就可以看做质点.2.参照系(1)为了研究物体的运动而假设不动的物体,叫做参照系.(2)对同一物体的运动,所选择的参照系不一样,对它的运动的描述可能会不一样.平常以地球为参照系.3.位移是地址的变化量,是从初地址指向末地址的有向线段.是矢量.(填“矢”或“标”)4.速度物理学顶用位移与发生这个位移所用时间的比值表示物体运动的快慢,即v=x,其是描述物体运动快慢t的物理量.(1)均匀速度:在变速运动中,物体在某段时间内的位移与发生这段位移所用时间的比值叫做这段时间内x的均匀速度,即v=t,其方向与位移的方向同样.(2)瞬时速度:运动物体在某一时辰(或某一地址)的速度,方向沿轨迹上物体所在点的切线方向指向行进的一侧,是矢量.瞬时速度的大小叫速率,是标量.5.加速度定义式:a=v,单位:m/s2,方向与速度变化量的方向同样,是描述物体速度变化快慢的物理量。
t1.关于加速度与速度、速度变化量关系的理解,注意以下三点:(1)速度的大小与加速度的大小没有必然联系.(2)速度变化量与加速度没有必然的联系,速度变化量的大小由加速度和速度变化的时间决定.(3)速度增大或减小是由速度与加速度的方向关系决定的.2.判断直线运动中“加速”或“减速”状况物体做加速运动还是减速运动,要点是看物体的加速度与速度的方向关系,而不是看加速度的变化状况.加速度的大小只反响速度变化(增添或减小)的快慢.a不变,v随时间均匀增添1a和v同向a增大,v增添得愈来愈快a减小,v增添得愈来愈慢a不变,v随时间均匀减小2a和v反向a增大,v减小得愈来愈快a减小,v减小得愈来愈慢1.金丽温高铁开通后,从铁路售票网盘问到G7330次列车缙云西到杭州东的信息如图甲所示,如图乙是用电子地图测距工具测得缙云西站到杭州东站的直线距离约为179.8km,以下说法正确的选项是( ) A.在研究动车过一桥梁所花的时间与动车从缙云西站到杭州东部所花的时间时,动车均可看作质点B.图甲中07∶31表示一段时间C.动车高速行驶时,可以取5m位移的均匀速度近似看做这5m起点地址的瞬时速度D.结合甲、乙,可知G7330列车行驶的最高速度约为128km/h【答案】C2.小李在网络上观看“神州十一号”飞船发射视频,分别截取火箭发射后第6s末和第10s末的图片,如图甲和乙所示,他又上网查到运载“神州十一号”的长征二号FY11运载火箭全长58m,则火箭发射后第6s 末至第10s末的均匀速度最凑近A.22m/sB.14m/sC.10m/sD.5.8m/s【答案】A3.结合图片中交代的情形及数据,以下判断不正确的选项是()A.高速行驶的磁悬浮列车的加速度可能为零B.轿车时速为100km/h,紧急刹车距离为31米(可视为匀减速至静止),由此可得轿车刹车阶段的加速度为a=12.5m/s2C.位于点燃火药的炮膛中的炮弹的速度、加速度可能均为零D.依据图中数据可求出刘翔在110m栏竞赛中经过全程的均匀速率为v=8.42m/s【答案】C【分析】试题分析:高速行驶的磁悬浮列车可能做匀速直线运动,加速度为零,故A对;由v2=2as代入数据可得加速度的大小为12.5m/s2,B对;位于点燃火药的炮膛中的炮弹的速度可能为零,但加速度不为零,C错;由s=vt可得v=8.42m/s,D对。
第1章质点运动学习题解答1-9质点运动学方程为k j e ie r t t ˆ2ˆˆ22++=- .⑴求质点轨迹;⑵求自t=-1到t=1质点的位移。
解:⑴由运动学方程可知:1,2,,22====-xy z e y e x t t ,所以,质点是在z=2平面内的第一像限的一条双曲线上运动。
⑵j e e ie e r r r ˆ)(ˆ)()1()1(2222---+-=--=∆ j i ˆ2537.7ˆ2537.7+-=。
所以,位移大小:︒==∆∆=︒==∆∆=︒=-=∆∆==+-=∆+∆=∆900arccos ||arccos z 45)22arccos(||arccos y 135)22arccos(||arccos x ,22537.72537.7)2537.7()()(||2222r zr y r x y x rγβα轴夹角与轴夹角与轴夹角与1-10⑴k t j t R it R r ˆ2ˆsin ˆcos ++= ,R 为正常数,求t=0,π/2时的速度和加速度。
⑵k t j t i t r ˆ6ˆ5.4ˆ332+-= ,求t=0,1时的速度和加速度(写出正交分解式)。
解:⑴k j t R it R dt r d v ˆ2ˆcos ˆsin /++-== j R a k i R v iR a k j R v j t R i t R dt v d a t t t t ˆ|,ˆ2ˆ|,ˆ|,ˆ2ˆ|.ˆsin ˆcos /2/2/00-=+-=-=+=∴--======ππ ⑵kt j dt v d a k t j t i dt r d v ˆ36ˆ9/,ˆ18ˆ9ˆ3/2+-==+-== ; kj a k j i v j a i v t t t t ˆ36ˆ9|,ˆ18ˆ9ˆ3|,ˆ9|,ˆ3|1100+-=+-=-====== 1-12质点直线运动的运动学方程为x=acost,a 为正常数,求质点速度和加速度,并讨论运动特点(有无周期性,运动范围,速度变化情况等)解:t a dt dv a t a dt dx v t a x x x x cos /,sin /,cos -==-=== 显然,质点随时间按余弦规律作周期性运动,运动范围:a a a a v a a x a x x ≤≤-≤≤-≤≤-,,1-13图中a 、b 和c 表示质点沿直线运动三种不同情况下的x-t 图像,试说明每种运动的特点(即速度,计时起点时质点的位置坐标,质点位于坐标原点的时刻)t(s)解:质点直线运动的速度dt dx v /=,在x-t 图像中为曲线斜率。
《大学物理》质点运动学练习题及答案解析一、选择题:1.以下五种运动中,加速度a 保持不变的运动是 ( D )(A) 单摆的运动。
(B) 匀速率圆周运动。
(C) 行星的椭圆轨道运动。
(D) 抛体运动。
(E) 圆锥摆运动。
2.下面表述正确的是( B )(A)质点作圆周运动,加速度一定与速度垂直; (B) 物体作直线运动,法向加速度必为零;(C)轨道最弯处法向加速度最大; (D)某时刻的速率为零,切向加速度必为零。
3.某质点做匀速率圆周运动,则下列说法正确的是( C )(A)质点的速度不变; (B)质点的加速度不变(C)质点的角速度不变; (D)质点的法向加速度不变4.一运动质点在某瞬时位于矢径()y x r , 的端点处,其速度大小为( D )()()(()22⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx D C dt r d B dt dr A 5. 一质点在平面上运动,运动方程为:j t i t r 222+=,则该质点作( B ) (A)匀速直线运动 (B)匀加速直线运动(C)抛物线运动 (D)一般曲线运动6.一质点做曲线运动,r 表示位置矢量,v 表示速度,a 表示加速度,s 表示路程,a t 表示切向加速度,对下列表达式,正确的是( B ) (A)dt dr v = (B) dt ds v = (C) dtdv a = (D) dt v d a t = 7. 某质点的运动方程为 3723+-=t t X (SI ),则该质点作 [ D ](A)匀加速直线运动,加速度沿 x 轴正方向; (B)匀加速直线运动,加速度沿 x 轴负方向;(C)变加速直线运动.加速度沿 x 轴正方向; (D)变加速直线运动,加速度沿 x 轴负方向8.一质点沿x 轴运动,其运动方程为()SI t t x 3235-=,当t=2s 时,该质点正在( A )(A)加速 (B)减速 (C)匀速 (D)静止1.D2. B3. C4.D5.B ,6B ,7A 8 A二 、填空题1. 一质点的运动方程为x =2t ,y =4t 2-6t ,写出质点的运动方程(位置矢量)j t t i t r )64(22-+=,t =1s 时的速度j i v 22+=,加速度j a 8=,轨迹方程为x x y 32-=。
第1章 质点运动学 习题解答(一). 选择题1.一运动质点在某瞬时位于矢径()y x r , 的端点处, 其速度大小为A. t r d dB. d d t rC. d d t rD.22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x [ ] 【分析与解答】t r d d 表示质点到坐标原点的距离随时间的变化率,d d t r表示速度矢量,d d t r 与t rd d 意义相同,在直角坐标系中,速度大小即速率可由2222d d d d ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛=+=t y t x v v v yx求解,在自然坐标系中,速率可用公式t s v d d =计算。
正确答案是D 。
2. 一质点在平面上运动,已知质点位置矢量的表示式为22at bt =+r i j (其中a 、b 为常量), 则该质点作 A. 匀速直线运动. B. 变速直线运动. C. 抛物线运动. D.一般曲线运动. [ ] 【分析与解答】22at bt =+v i j 是变速运动,22,,ax at y bt x yb ===为直线方程正确答案是B 。
3. 某质点的速度为,已知,时它过点(3,-7),则该质点的运动方程为:A. B.C. D.不能确定 [ ]【分析与解答】22d 24(23)(47)t t t t t ==-+=+-+⎰r v i j c i j正确答案是B 。
4. 以初速将一物体斜向上抛,抛射角为,不计空气阻力,则物体在轨道最高点处的曲率半径为:A. B. C. D.不能确定。
[ ] 【分析与解答】v 0θv 0sin θg g v 02v 02cos 2θg v =2i -8t j t =02t i -4t 2j (2t +3)i -(4t 2+7)j -8j轨道最高点22220,(cos ),x xn v v v v v a g θρ=====v i ,故曲率半径2v g ρ=正确答案是C 。
5. 质点沿半径为R 的圆周作匀速率运动,每T 秒转一圈.在2T 时间间隔中,其平均速度大小与平均速率大小分别为..[ ] 【分析与解答】平均速度为位移除以时间间隔,平均速率为路程除以时间, 质点沿半径为R 的圆周转动一周,位移为零,路程等于。