【中学联盟】山东省实验中学2012届高三5月第二次模拟考试(数学理)

山东省实验中学2012级高三第一次模拟考试数学试题（理）2015.4说明：试题分为第I 卷（选择题）和第II 卷（非选择题）两部分。

试题答案请用2B 铅笔或0.5mm 签字笔填涂到答题卡规定位置上，书写在试题上的答案无效。

考试时间120分钟。

第I 卷（共50分）一、选择题（本题包括10小题，每小题5分，共50分。

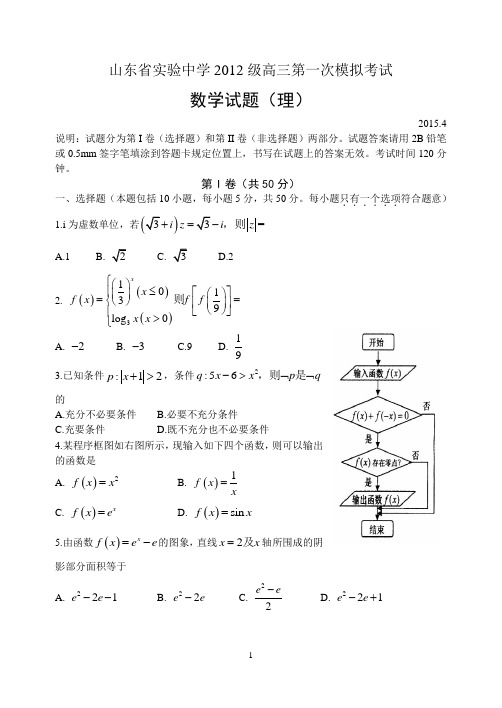
每小题只有一个选项．．．．．．符合题意） 1.i为虚数单位，若)=i z i z =，则 A.1B.C.D.2 2. ()()()310139log 0x x f x f f x x ⎧⎛⎫≤⎡⎤⎪⎛⎫ ⎪==⎝⎭⎨ ⎪⎢⎥⎝⎭⎣⎦⎪>⎩则 A. 2- B. 3- C.9 D. 193.已知条件:12p x +>，条件2:56q x x p q->⌝⌝，则是的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.某程序框图如右图所示，现输入如下四个函数，则可以输出的函数是A. ()2f x x =B. ()1f x x =C. ()x f x e =D. ()sin f x x = 5.由函数()x f x e e =-的图象，直线2x x =及轴所围成的阴影部分面积等于A. 221e e --B. 22e e -C. 22e e -D. 221e e -+6.函数()tan 0442y x x ππ⎛⎫=-<< ⎪⎝⎭的图像如图所示，A 为图像与x 轴的交点，过点A 的直线l 与函数的图像交于B 、C 两点，则()OB OC OA +⋅=uu u r uuu r uu r A. 8- B. 4- C.4 D.87.已知,x y 满足条件5020,33x y x y x y z x x -+≥⎧++⎪+≥=⎨+⎪≤⎩则的最小值 A. 23- B. 13 C. 136 D.48.一个几何体的三视图如图所示，则该几何体的表面积和体积分别是A. 2440+B. 2472+C. 6440+D. 5072+ 9.抛物线()220y px p =>的焦点为F ，准线为l ，A,B是抛物线上的两个动点，且满足23AFB π∠=.设线段AB 的中点M 在l 上的投影为N ，则MNAB 的最大值是A.B.C.D. 10.定义在0,2π⎛⎫ ⎪⎝⎭上的函数()(),f x f x '是它的导函数，且恒有()()tan f x f x x '<⋅成立，则A. 43ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭B. ()12sin16f f π⎛⎫< ⎪⎝⎭C.64f ππ⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭D. 63f ππ⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭第II 卷（非选择题 共100分）二、填空题（本题包括5小题，每小题5分，共25分）11.已知等差数列{}n a 中，532111,2=a a a S ==+，则________.12.一只昆虫在边长分别为5，12，13的三角形区域内爬行，则其到三角形顶点距离小于2的地方的概率为___________.13.双曲线()22102x y m m m -=>+的一条渐近线方程为2=y x m =，则___________. 14.若多项式()()()910310019109111,x x a a x a x a x a +=+++⋅⋅⋅++++=则__________. 15.已知函数()f x 是定义在R 上的奇函数，它的图象关于直线1x =对称，且()()01f x x x =<≤.若函数()1y f x a x=--在区间[]10,10-上有10个零点（互不相同），则实数a 的取值范围是__________.三、解答题（本大题共6小题，共75分.解答应写出文字说明，证明过程或演算步骤）.16. （本小题满分12分）设ABC ∆的内角A,B,C 所对的边分别为a,b,c ，且1cos 2a C cb -=. （I ）求角A 的大小； （II ）若3a =，求ABC ∆的周长l 的取值范围.17. （本小题满分12分）口袋中装有除颜色，编号不同外，其余完全相同的2个红球，4个黑球.现从中同时取出3个球.（I ）求恰有两个黑球的概率；（II ）记取出红球的个数为随机变量X ，求X 的分布列和数学期望E(X).18. （本小题满分12分）如图，在四棱锥P A B C D -中，PC ⊥底面ABCD ，ABCD 是直角梯形，,,22 2.A B A D A B C D A B A D C D⊥===E 是PB 的中点. （I ）求证：平面EAC ⊥平面PBC ；（II ）若二面角P AC E --PA 与平面EAC 所成角的正弦值.19. （本小题满分12分）已知n S 为数列{}n a 的前n 项和，且2231,1,2,3n n S a n n n =+--=…（I ）求证：数列{}2n a n -为等比数列；（II ）设cos n n b a n π=⋅，求数列{}n b 的前n 项和n T ..20. （本小题满分13分）已知椭圆()2222:10x y C a b a b +=>>的离心率为2，过右F 的直线l 与C 相交于A 、B 两点，当l 的斜率为1时，坐标原点O 到l 的距离为1.（I ）求椭圆C 的标准方程；（II ）C 上是否存在点P ，使得当l 绕F 转到某一位置时，有OP OA OB =+u u u r u u r u u u r 成立？若存在，求出所有的P 的坐标与l 的方程；若不存在，说明理由.21. （本小题满分14分）已知函数()(),x k f x e mx m k R =-∈定义域为()0,+∞，（I ）若1k =时，()()1f x +∞在，上有最小值，求m 的取值范围；（II ）若k=2时，()f x 的值域为[)0+∞，，试求m 的值；（III ）试证：对任意实数m,k ，总存在0x ，使得当()0,x x ∈+∞时，恒有()0f x >.。

绝密★启用并使用完毕前山东省实验中学2024届高三5月针对性考试数学试题2024.05注意事项：1.答卷前，先将自己的考生号等信息填写在试卷和答题纸上，并在答题纸规定位置贴条形码.2.本试卷满分150分，分为选择题非选择题.3.选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.4.非选择题的作答：用0.5mm 黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷､草稿纸和答题卡上的非答题区域均无效.一､选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合()(){1},{130}A x x B x x x =>=+-<∣∣，则()A B ⋂=R ð（）A.()3,∞+ B.()1,∞-+ C.(]1,1- D.()1,3-2.已知,a b ∈R ，且0,0a b >>，则“1ab >”是“ln ln 0a b ⋅>”的（）A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件3.等比数列{}n a 的前n 项和为n S ，若121n n S t -=⋅-，则t =（）A.2B.-2C.1D.-14.锂电池在存放过程中会发生自放电现象，其电容量损失量随时间变化规律为pQ kt =，其中Q （单位mAh ）为电池容量损失量，p 是时间t 的指数项，反映了时间趋势由反应级数决定，k 是方程剩余项未知参数的组合，与温度T 和电池初始荷电状态M 等自放电影响因素有关.以某种品牌锂电池为研究对象，经实验采集数据进行拟合后获得0.5p =，相关统计学参数20.995R >，且预测值与实际值误差很小.在研究M 对Q 的影响时，其他参量可通过控制视为常数，电池自放电容量损失量随时间的变化规律为()e A BM p pQ kt t +==，经实验采集数据进行拟合后获得 2.225, 1.3A B ==，相关统计学参数20.999R =，且预测值与实际值误差很小.若该品牌电池初始荷电状态为80%，存放16天后，电容量损失量约为（）（参考数据为：3.22 3.232e 25.08,e 25.33≈≈， 3.265 3.628e 26.26,e 37.64≈≈）A.100.32B.101.32C.105.04D.150.565.在正方体1111ABCD A B C D -中，点,M N 分别是棱1DD 和线段1BC 上的动点，则满足与1AD 垂直的直线MN （）A.有且仅有1条B.有且仅有2条C.有且仅有3条D.有无数条6.已知椭圆2222:1(0)x y C a b a b+=>>的上顶点､左焦点､右顶点分别为,,A F B ，且点A 为AFB 的垂心，则椭圆C 的离心率为（） A.512B.12C.22D.327.已知()7280128(2)1(1)(1)x x a a x a x a x -=+-+-+⋯⋯+-，则56a a +=（）A.-14B.0C.14D.-288.已知()()1122,,,A x y B x y 是圆222x y +=上两点.若12121x x y y +=-，则1212x x y y +++的取值范围是A.22,22⎡-⎢⎣⎦B.[]1,1- C.⎡⎣ D.[]2,2-二､多选题：本题共3小题，每小题6分，共18分.在每个小题给出的选项中，有多项符合题目要求.全部选对的得6分，部分选对的得部分分，有选错的得0分.9.设复数z 在复平面内对应的点为Z ，原点为,i O 为虚数单位，则（）A.若1z =，则1z =±或iz =±B.若点Z 的坐标为()1,1-，则z 对应的点在第三象限C.若2i z =-，则z 的模为7D.若1z ，则点Z 的集合所构成的图形的面积为π10.已知抛物线24y x =的焦点为F ，过F 的直线AB 交抛物线于()()1122,,,A x y B x y 两点，()3,1M ，则（）A.12x x +的最小值为2B.以AF 为直径的圆与y 轴相切C.MA AF +的最小值为4D.22||||AF BF +的最小值为211.数列{}n a 满足()*11*1,41,2,1,4n n m n n a a a n b n a --⎧∈⎪⎪==⎨⎪+∉⎪⎩N N 表示{}n a 落在区间)12,2m m +⎡⎣的项数，其中*m ∈N ，则（）A.310b =B.33344n n n a + C.42163nkk an n==+∑ D.()214413nnkk b==-∑三､填空题：本题共3小题，每小题5分，共15分.12.函数y =__________.13.某班成立了,A B 两个数学兴趣小组，A 组10人，B 组30人，经过一周的补习后进行了一次测试，在该测试中，A 组的平均成绩为130分，方差为115,B 组的平均成绩为110分，方差为215.则在这次测试中全班学生方差为__________.14.在三棱锥中,P ABC AB BC -==，且AB BC ⊥.记直线,,PA PC PB 与平面ABC 所成角分别为,,αβγ，已知260βα== ，当三棱锥P ABC -的体积最小时，tan γ=__________.四､解答题：本题共5小题，共77分.解答应写出文字说明､证明过程或演算步骤.15.（13分）如图，两块直角三角形模具，斜边靠在一起，其中公共斜边10AC =，ππ,34BAC DAC ∠∠==，BD 交AC 于点E .（1）求2BD ；（2）求AE .16.（15分）已知函数()2ln 1,f x x a x a =-+∈R .（1）当1a =-时，求曲线()y f x =在点(1,(1))f 处的切线方程；（2）当0a >时，若函数()f x 有最小值2，求a 的值.17.（15分）如图，在三棱柱111ABC A B C -中，四边形11AA B B 是菱形，AB AC ⊥，平面11AA B B ⊥平面ABC .（1）证明：11A B B C ⊥；（2）已知1π3ABB ∠=，2AB AC ==，平面111A B C 与平面1AB C 的交线为l .在l 上是否存在点P ，使直线1A B 与平面ABP 所成角的正弦值为14？若存在，求线段1B P 的长度；若不存在，试说明理由.18.（17分）已知双曲线2222:1(0,0)x y C a b a b -=>>的离心率e =，1P ，2P 分别为其两条渐近线上的点，若满足12PP PP =的点P 在双曲线上，且12OPP 的面积为8，其中O 为坐标原点.（1）求双曲线C 的方程；（2）过双曲线C 的右焦点2F 的动直线与双曲线相交于A ，B 两点，在x 轴上是否存在定点M ，使MA MB ⋅为常数？若存在，求出点M 的坐标；若不存在，请说明理由.19.（17分）某校数学兴趣小组由水平相当的n 位同学组成，他们的学号依次为1，2，3，…，n .辅导老师安排一个挑战数学填空题的活动，活动中有两个固定的题，同学们对这两个题轮流作答，每位同学在四分钟内答对第一题及四分钟内答对第二题的概率都为12，每个同学的答题过程都是相互独立的挑战的具体规则如下：①挑战的同学先做第一题，第一题做对才有机会做第二题；②挑战按学号由小到大的顺序依次进行，第1号同学开始第1轮挑战；③若第()1,2,3,,1i i n =- 号同学在四分钟内未答对第一题，则认为第i 轮挑战失败，由第1i +号同学继续挑战；④若第()1,2,3,,1i i n =- 号同学在四分钟内答对了第一题，满四分钟后，辅导老师安排该生答第二题，若该生在四分钟内又答对第二题，则认为挑战成功挑战在第i 轮结束；若该生在四分钟内未答对第二题，则也认为第i 轮挑战失败，由第1i +号同学继续挑战；⑤若挑战进行到了第n 轮，则不管第n 号同学答对多少题，下轮不再安排同学挑战.令随机变量n X 表示n 名挑战者在第()1,2,3,,n n X X n =⋅⋅⋅轮结束.（1）求随机变量4X 的分布列；（2）若把挑战规则①去掉，换成规则⑥：挑战的同学先做第一题，若有同学在四分钟内答对了第一题，以后挑战的同学不做第一题，直接从第二题开始作答.令随机变量n Y 表示n 名挑战者在第()1,2,3,,n n Y Y n =⋅⋅⋅轮结束.（i ）求随机变量()*,2n Y n N n ∈≥的分布列；（ii ）证明()()()()()23453n E Y E Y E Y E Y E Y <<<<<<< .山东省实验中学2024届高三5月针对性考试数学试题答案2024.05一､单项选择题1-5CDACD6-8ABD二､多项选择题9.BD 10.ABC 11.BC三､填空题12.52,2,33k k k ππππ⎡⎤++∈⎢⎥⎣⎦Z13.26514.155四､解答题15.【详解】（1）由已知，1cos 1052AB AC BAC ∠=⋅=⨯=，2cos 102AD AC DAC ∠=⋅=⨯=，因为ππ34BAD BAC DAC BAC ∠=∠+∠=∠=+，所以ππππππcos cos cos cos sin 343434BAD ∠⎛⎫=+=-⎪⎝⎭12322622224=⨯-=，所以在ABD △中由余弦定理可得2222cos BD AB AD AB AD BAD=+-⋅⋅∠262550254=+-⨯⨯50=+.（2）因为ππππππ62sin sin sin cos cos sin 3434344BAD ∠⎛⎫=+=+=⎪⎝⎭，又因为ABD ABE ADE S S S =+ ，所以111sin sin sin 222AB AD BAD AB AE BAE AE AD EAD ∠∠∠⋅⋅⋅=⋅⋅⋅+⋅⋅⋅，即162131255242222AE AE ⨯⨯=⨯⨯⨯⨯⨯，解得5AE =.16.【详解】（1）当1a =-时，()2ln 1f x x x =++，()y f x =的定义域为()0,∞+，则1()2f x x x'=+，则1(1)231f =+='，(1)1ln112f =++=，由于函数()f x 在点(1,(1))f 处切线方程为()231y x -=-，即31y x =-.（2）()2ln 1,f x x a x a =-+∈R 的定义域为()0,∞+，()222a x af x x x x-=-='，当0a >时，令()0f x '>，解得：x >()0f x '<，解得：0x <<，所以()f x 在⎛ ⎝上单调递减，在⎫+∞⎪⎪⎭上单调递增，所以，min ()122a f x f a ==-+=，即ln 10222a a a--=则令02at =>，设()ln 1g t t t t =--，()ln g t t '=-，令()0g t '<，解得：1t >；令()0g t '>，解得：01t <<，所以()g t 在()0,1上单调递增，在()1,+∞上单调递减，所以()()11ln110g t g ≤=--=，所以12at ==，解得：2a =.17.【详解】（1）证明：因为平面11AA B B ⊥平面ABC ，平面11AA B B ⋂平面ABC AB =，AC AB ⊥，AC ⊂平面ABC ，所以AC ⊥平面11AA B B ，1A B ⊂ 平面11AA B B ，所以1AC A B ⊥，因为四边形11AA B B 是菱形，所以11AB A B ⊥，又因为1AC AB A ⋂=，AC ､1AB ⊂平面1AB C ，所以1A B ⊥平面1AB C ，因为1B C ⊂平面1AB C ，所以11A B B C ⊥.（2）解：取11A B 中点D ，连接AD ，因为四边形11AA B B 为菱形，则1AB BB =，又因为160ABB ∠=，则1ABB 为等边三角形，由菱形的几何性质可知1160AA B ∠=，111AA A B =，则11AA B 也为等边三角形，因为D 为11A B 的中点，则11AD A B ⊥，11//AB A B ，AB AD ∴⊥，由（1）知，AC ⊥平面11AA B B ，以点A 为坐标原点，AB ､AD ､AC 所在直线分别为x ､y ､z 轴建立如下图所示的空间直角坐标系，则()0,0,0A ､()2,0,0B ､()0,0,2C､()1A -､()1B，()13,A B =，因为11AC AC ∥，AC ⊄平面111A B C ，11AC ⊂平面111A B C ，所以AC ∥平面111A B C ，因为平面111A B C ⋂平面1AB C l =，AC ⊂平面1AB C ，所以AC l ∥，由（1）知l ⊥平面11AA B B ，设()P t，则()AP t = ，()2,0,0AB =.设平面ABP 的法向量(),,n x y z =，则020n AP x tz n AB x ⎧⋅=++=⎪⎨⋅==⎪⎩ ，取z =，可得(0,,n t =，因为直线1A B 与平面ABP 所成角的正弦值为14，则1111cos ,4A B n A B n A B n ⋅<>==⋅，解得1t =±，因此，存在点P ，线段1B P 的长为1.18.【详解】（1）由离心率ce a==，得c ==，所以a b =，则双曲线的渐近线方程为y x =±，因为1P ，2P 分别为其两条渐近线上的点，所以12OP OP ⊥，不妨设()1,P m m ，()2,P n n -，由于12PP PP =，则点P 为12PP 的中点，所以,22m n m n P +-⎛⎫⎪⎝⎭，又点P 在双曲线上，所以()()2222144m n m n a a +--=，整理得：2mn a=因为12OPP 的面积为8，所以121211822OP P S OP OP m mn =⋅=== ，则228a b ==，故双曲线C 的方程为22188x y -=；（2）由（1）可得4c =，所以2F 为()4,0当直线AB 的斜率存在时，设AB 方程为：()4y k x =-，()()1122,,,A x y B x y ，则()224188y k x x y =-⎧⎪⎨-=⎪⎩，所以()2222181680k x k x k -+--=，则21k ≠()()()22222Δ84116832320k k k k =----=+>恒成立，所以221212228168,11k k x x x x k k++=-⋅=---，假设在x 轴上是否存在定点M ，设(),0M t ，则()()()21122121212,,MA MB x t y x t y x x t x x t y y ⋅=-⋅-=-+++()()()212121144x x t x x t k x k x =-+++-⋅-()()()222212121416k x x t k x x k t =+-++++()()()()()2222222222116816184111k k k t k kt k k k k +++-=-+++---()()22228881t t t k k ---+=-要使得MA MB ⋅ 为常数，则2288811t t t --+=，解得2t =，定点()2,0M ，4MA MB ⋅=-；又当直线AB 的斜率不存在时，直线AB 的方程为4x =，代入双曲线22188x y -=可得y =±((,4,A B -，若()2,0M，则((()2,484MA MB ⋅=⋅-=+-=-，符合上述结论；综上，在x 轴上存在定点M ，使MA MB ⋅为常数4-，且()2,0M .19.【详解】（1）()()1411111,2,3224k P X k k -⎛⎫==-⨯⨯= ⎪⎝⎭，()34344P X ⎛⎫== ⎪⎝⎭，因此4X 的分布列为4X 1234P143169642764（2）（i ）()*11,n Y k k n k =≤≤-∈N时，第k 人必答对第二题，若前面1k -人都没有一人答对第一题，其概率为112k kp +'⎛⎫= ⎪⎝⎭，若前面1k -人有一人答对第一题，其概率为()111111122k k k k p C k ++''-⎛⎫⎛⎫=- ⎪⎪⎝⎭⎝⎭=，故()112k n kkP Y k p p k +'''⎛⎫==+= ⎪⎝⎭.当n Y n =时，若前面1n -人都没有一人答对第一题，其概率为112n n p -'⎛⎫= ⎪⎝⎭，若前面1n -人有一人答对第一题，其概率为()112nnp n ''⎛⎫=- ⎪⎝⎭，故()()112nn n n P Y n p p n '''⎛⎫==+=+ ⎪⎝⎭.n Y 的分布列为：nY 123…1n -n P212⎛⎫ ⎪⎝⎭3122⎛⎫⨯ ⎪⎝⎭4132⎛⎫⨯ ⎪⎝⎭…()112nn ⎛⎫- ⎪⎝⎭()112nn ⎛⎫+ ⎪⎝⎭（ii ）()()()112*1111,222k nn n k E Y k n n n n +-=⎛⎫⎛⎫=++∈≥ ⎪⎪⎝⎭⎝⎭∑N .()()()()()()111211111121202222n n n n n n E Y E Y n n n n n n ++++⎛⎫⎛⎫⎛⎫⎛⎫-=+++-+=+> ⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭，故()()()()()2345n E Y E Y E Y E Y E Y <<<<<< ，求得()274E Y =，故()()()()()()()()232431n n n E Y E Y E Y E Y E Y E Y E Y E Y -=+-+-++-⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦ ，∴()()3417111145142222n nn E Y n n -⎛⎫⎛⎫⎛⎫⎛⎫=+⨯+⨯++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，①()()2341711112456122222n n E Y n -⎛⎫⎛⎫⎛⎫⎛⎫=+⨯+⨯+⨯+++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，②②-①，()341171117811314222412n n E Y -⎛⎫⎛⎫⎛⎫<+++++<++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭- .故()()()()()23453n E Y E Y E Y E Y E Y <<<<<<< .。

山东省青岛二中2012届高三下学期阶段性检测数学试题（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页。

全卷满分150分，考试时间120分钟。

注意事项：１.考生在答题前，请务必将自己的姓名、准考证号等信息填在答题卡上．２.选择题每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号，答在试卷上无效。

３.填空题和解答题用0.5毫米黑色墨水签字笔答在答题卡上每题对应的答题区域内。

答在试题卷上无效。

第Ⅰ卷（选择题，共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集U ＝R ，集合{,A x y ==集合{}2,x B y y x R ==∈，则()R C A B =（ ）A.{}2x x > B.{}01x x <≤ C. {}12x x ≤＜ D ．{}0x x < 2.曲线sin ,cos 2y x y x π==和直线x=0,x=所围成的平面区域的面积为（ ）()20.sin cos A x x dx π-⎰ ()4.2sin cos B x x dx π-⎰()20.cos sin C x x dx π-⎰()40.2cos sin D x x dx π-⎰3.对于平面α和共面,m n 的直线，下列命题是真命题的是：（ ）m n m A 所成的角相等，则与若α,.∥n m B 若.∥α,n ∥α，则：m ∥nn m m C ⊥⊥,.α若，则n ∥α ⊂m D 若.α,n ∥α，则：m ∥n4.下列4个命题:（1）命题“若a b <，则22am bm <”；（2）“2a ≤”是“对任意的实数x ，11x x a ++-≥成立”的充要条件； （3）设随机变量ξ服从正态分布N （0，1），若1(1),(10)2P p P p ξξ>=-<<=-则； （4）命题“x R ∃∈，02>-x x ”的否定是：“x R ∀∈，02<-x x ”其中正确的命题个数是（ ）A. 1B. 2C. 3D. 45.为了解某校高三学生的视力情况，随机地抽查了该校100名学生的视力情况，得到频率分布直方图如下左图，由于不慎将部分数据丢失，只知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a ，视力在4.6到5.1之间的学生人数为b,则a 和b 的值分别为（ ）A.0.27 78B.0.27 85C.2.7 78D.2.7 856.如上右图所示的是根据输入的x 值计算y 的值的程序框图，若x 依次取数列216{}()n n N n*+∈中的项，则所得y 值的最小值为（ ）A ．4B ．8C ．16D ．327．已知函数x x f x21log 2)(-=，且实数a >b >c >0满足0)()()(<⋅⋅c f b f a f ，若实数0x 是函数y =)(x f 的一个零点，那么下列不等式中不可能．．．成立的是 （ ） A ．a x <0 B ．a x >0 C ．b x <0 D ．c x <08．三角形的内角平分线定理是这样叙述的：三角形一个内角的平分线分对边所成的两条线段与这个角的两边对应成比例。

高三自评试题数学（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试时间120分钟． 注意事项：1．答卷前，考生务必用2B 铅笔和0.5毫米黑色签字笔（中性笔）将姓名、准考证号、考试科目、试卷类型填涂在答题卡规定的位置上．2．第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试题卷上．3．第Ⅱ卷必须用0.5毫米黑色签字笔（中性笔）作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效． 参考公式：锥体的体积公式为：13V Sh =,其中S 为锥体的底面积，h 为锥体的高.第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题．每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合{},3M m =-,{}22730,N x x x x =++<∈Z ,如果M N ≠∅ ,则m 等于A ．1-B ．2-C ．2-或1-D ．32-2．设复数21z i=+(其中i 为虚数单位)，则23z z +的虚部为A ．2iB ．0C ．10-D ．23．“4a <”是“对任意的实数x ,2123x x a -++≥成立”的 A ．充分必要条件 B ．充分不必要条件 C ．必要不充分条件D ．既非充分也非必要条件4．已知函数2log ,0()91,0x x x f x x ->⎧=⎨+≤⎩，则()31((1))log 2f f f +的值是A ．7B ． 2C ．5D ．35．设m ,n 是两条不同的直线, α,β,γ是三个不同的平面．有下列四个命题： ①若//αβ，m α⊂，n β⊂，则//m n ；②若m α⊥，//m β，则αβ⊥；③ 若n α⊥，n β⊥，m α⊥，则m β⊥； ④ 若αγ⊥，βγ⊥，m α⊥，则m β⊥． 其中错误．．命题的序号是 A ．①③ B ．①④ C ．②③④ D ．②③ 6．执行如图所示的程序框图，若输出的b 的值为31， 则图中判断框内①处应填A ．3B ．4C ．5D ．6 7．函数y =则以下不可能成为该等比数列的公比的数是 A ．34BCD8．以下正确命题的个数为①命题“存在R x ∈，220x x --≥”的否定是：“不存在R x ∈，220x x --<”；②函数131()()2xf x x =-的零点在区间11(,)32内；③已知随机变量ξ服从正态分布2(1,)N σ，(4)0.79P ξ≤=，则(2)0.21P ξ≤-=； ④函数()xxf x ee -=-的图象的切线的斜率的最大值是2-；⑤线性回归直线 y bxa =+ 恒过样本中心(),x y ，且至少过一个样本点. A ．1 B ．2 C ．3 D ．49．设22(13)40a x dx =-+⎰，则二项式26()a x x+展开式中不含．．3x 项的系数和是A ．160-B ．160C ．161D ．161- 10．已知函数1π()cos ,[,]222f x x x x π=+∈-，01sin 2x =，0π[,]22x π∈-，那么下面命题中真命题的序号是①()f x 的最大值为0()f x ② ()f x 的最小值为0()f x③()f x 在0[,]2x π-上是增函数 ④ ()f x 在0π[,]2x 上是增函数A ．①③B ．①④C ．②③D ．②④11．一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的 A.外接球的半径为3B.C.表面积为1 D.外接球的表面积为163π12．已知直线()1y k x =+与抛物线2:4C y x =相交于A 、B 两点，F 为抛物线C 的焦点，若2F A F B =,则k =A．3±B．3±C ．13±D ．23第Ⅱ卷（非选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分． 13．若tan 2,α=则sin cos αα= .14．已知直线y x a =+与圆224x y +=交于A 、B 两点，且0OA OB ⋅=，其中O 为坐标原点，则正实数a 的值为 .15．设x 、y 满足约束条件360200,0x y x y x y --≤⎧⎪-+≥⎨⎪≥≥⎩，则目标函数22z x y =+的最大值为 .16．已知函数()f x 的定义域为[]15,-，部分对应值如下表，()f x 的导函数()y f x '=的图象如图所示. 下列关于()f x 的命题： ①函数()f x 的极大值点为0，4； ②函数()f x 在[]02,上是减函数；③如果当[]1x ,t ∈-时，()f x 的最大值是2，那么t 的最大值为4；④当12a <<时，函数()y f x a =-有4个零点；正视图 侧视图俯视图AC1A 1B 1C ⑤函数()y f x a =-的零点个数可能为0、1、2、3、4个． 其中正确命题的序号是 ．三、解答题：本大题共6小题,共74分,解答时应写出必要的文字说明、证明过程或演算步骤.17．（本小题满分12分）已知向量)c o s ,(s in ),sin 3,(sin x x n x x m -==，设函数n m x f ⋅=)(,若函数)(x g 的图象与)(x f 的图象关于坐标原点对称.（Ⅰ）求函数)(x g 在区间⎥⎦⎤⎢⎣⎡-6,4ππ上的最大值,并求出此时x 的值；（Ⅱ）在ABC ∆中，c b a ,,分别是角C B A ,,的对边，A 为锐角,若23)()(=-A g A f ，7=+c b ，ABC ∆的面积为32，求边a 的长．18．（本小题满分12分）如图，在多面体111ABC A B C -中，四边形11ABB A 是正方形，1A C A B ==，11A C A B BC ==，11//B C BC ，1112B C =B C .（Ⅰ）求证：1//A B 面11A C C ；（Ⅱ）求二面角11C A C B --的余弦值的大小.19．（本小题满分12分）甲居住在城镇的A 处，准备开车到单位B 处上班，若该地各路段发生堵车事件都是相互独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图（例如，A →C →D 算作两个路段：路段A C 发生堵车事件的概率为101，路段C D 发生堵车事件的概率为151，且甲在每个路段只能按箭头指的方向前进）．(Ⅰ）请你为其选择一条由A 到B 的路线，使得途中发生堵车事件的概率最小；101151（Ⅱ）若记路线A →C →F →B 中遇到堵车次数为随机变量ξ，求ξ的分布列及E ξ． 20．（本小题满分12分）已知集合{}21,N A x x n n *==--∈,{}63,N B x x n n *==-+∈，设n S 是等差数列{}n a 的前n 项和,若{}n a 的任一项B A a n ∈,且首项1a 是A B 中的最大数,10750300S -<<-.（Ⅰ）求数列{}n a 的通项公式; （Ⅱ）若数列{}n b满足139(2n a n n b +-=，令n T =246224()n b b b b ++++ ，试比较n T与4821n n +的大小.21．（本小题满分12分）已知函数()()23232f x ln x x =+-.（Ⅰ）求函数()y f x =的极大值； （Ⅱ）令()()()2312g x f x x m x =++-（m 为实常数），试判断函数()g x 的单调性；（Ⅲ）若对任意1163x ,⎡⎤∈⎢⎥⎣⎦，不等式()30a ln x ln f x x '-++>⎡⎤⎣⎦均成立，求实数a 的取值范围.22．（本小题满分14分）已知椭圆1C 、抛物线2C 的焦点均在x 轴上，1C 的中心和2C 的顶点均为坐标原点O ，从每条曲线上各取两个点，将其坐标记录于表中： （Ⅰ）求12C C 、的标准方程；（Ⅱ）请问是否存在直线l 同时满足条件：(ⅰ)过2C 的焦点F ；(ⅱ)与1C 交于不同两点Q 、R ，且满足O Q O R ⊥？若存在，求出直线l 的方程；若不存在，请说明理由．（Ⅲ）已知椭圆1C 的左顶点为A ，过A 作两条互相垂直的弦A M 、A N 分别另交椭圆于M 、N 两点．当直线A M 的斜率变化时，直线M N 是否过x 轴上的一定点，若过定点，请给出证明，并求出该定点坐标;若不过定点，请说明理由．高三自评试题数学（理科）参考答案及评分标准一、选择题：本大题共12小题．每小题5分，共60分． C D B A B B D C C A D A 二、填空题：本大题共4小题，每小题4分，共16分． 13.2514. 2 15. 52 16．①②⑤三、解答题：本大题共6小题，共74分，解答时应写出必要的文字说明、证明过程或演算步骤．17．（本小题满分12分）解：（Ⅰ）由题意得：21cos 2()sin cos 222xf x x x x x -=-=-1sin(2)26x π=-+………………………………………………………2分所以)62sin(21)(π---=x x g ………………………………………………3分因为⎥⎦⎤⎢⎣⎡-∈6,4ππx ，所以⎥⎦⎤⎢⎣⎡-∈-6,3262πππx 所以当262ππ-=-x 即6π-=x 时，函数)(x g 在区间⎥⎦⎤⎢⎣⎡-6,4ππ上的最大值为21.……………………………………………6分 （Ⅱ）由23)()(=-A g A f 得：23)62sin()62sin(1=-++-ππA A化简得：212cos -=A又因为02A π<<，解得：3π=A …………………………………………9分由题意知：32sin 21==∆A bc S ABC ，解得8=bc ，又7=+c b ,所以22222cos ()2(1cos )a b c bc A b c bc A =+-=+-+14928(1)252=-⨯⨯+=故所求边a 的长为5. …………………………………………………………………12分18．（本小题满分12分）解：（Ⅰ）取B C 的中点E ，连结A E ，1C E ，1B E11//B C BC ，11B C =12B C ，1111//,B C EC B C EC ∴=，∴四边形11C EB C 为平行四边形， 从而11//B E C C ， 1C C ⊂面11A C C ，1B E ⊄面11A C C∴1//B E 面11A C C ………………………………………………………………2分 11//B C BC ，11B C =12B C ，1111//,B C BE B C BE ∴=∴四边形11BB C E 为平行四边形 ∴11//B B C E ，且1B B =1C E又 11ABB A 是正方形，∴11//A A C E ，且1A A =1C E 故11AEC A 为平行四边形，∴11//AE A C11A C ⊂面11A C C ，A E ⊄面11A C C∴//A E 面11A C C ………………………………………………………………4分 1AE B E E = ，∴面1//B AE 面11A C C1AB ⊂面1B AE ，∴1//A B 面11A C C ………………………………………6分（Ⅱ） 四边形11ABB A 为正方形, ∴11A A AB AC ===, 1A A AB ⊥∴1A B =11A C A B = ∴1A C =由勾股定理可得：190A AC ∠=，∴1A A AC ⊥AB AC A = ，∴1A A ⊥面ABC ，11A C A B BC ==，BC ∴=由勾股定理可得：90BAC ∠=，∴AB AC ⊥ …………………………………8分故以A 为原点，以A C 为x 轴建立坐标系如图，则1111(1,0,0),(0,0,1),(,,1)22C A C ， (0,1,0)B ，所以1(1,0,1)CA =- ，111(,,1)22C C =- ，1(0,1,1)BA =- ，111(,,1)22B C =- . 设面11A C C 的法向量为1(,,)n x y z = ，由11110,0n CA n CC ⋅=⋅=⇒011022x z x y z -+=⎧⎪⎨-++=⎪⎩，令1z =，则1(1,1,1)n =- 设面11A C B 的法向量为2(,,)n m n k = ，则21210,0n BA n BC ⋅=⋅=则011022n k m n k -+=⎧⎪⎨-+=⎪⎩，令1k =，则2(1,1,1)n =- …………………………10分所以1212121cos ,3n n n n n n ⋅===-设二面角11C A C B --的平面角为α，12,n n θ=所以()1cos cos 3απθ=-= ……………………………………………………12分19．（本小题满分12分）解：（Ⅰ）记路段A C 发生堵车事件为A C ，各路段发生堵车事件的记法与此类同.因为各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，所以路线A →C →D →B 中遇到堵车的概率为()()()()111P P AC C D D B P AC P C D P D B =-⋅⋅=- ()()()1111P AC P CD P DB =----⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦ 9145311015610=-⋅⋅= ……………………………………………………………………2分同理：路线A →C →F →B 中遇到堵车的概率为2P =1－P (AC ·CF ·FB ）=800239（小于310） ………………………………………………………………………4分路线A →E →F →B 中遇到堵车的概率为3P =()911300P A E E F F B -⋅⋅=（大于310）显然要使得由A 到B 的路线途中发生堵车事件的概率最小，只可能在以上三条路线中选择.因此选择路线A →C →F →B ，可使得途中发生堵车事件的概率最小 …………6分（Ⅱ）路线A →C →F →B 中遇到堵车次数ξ可取值为0，1，2，3． ()0P ξ=()561800P A C C F F B =⋅⋅=，()()()()1P P AC C F FB P AC C F FB P AC C F FB ξ==⋅⋅+⋅⋅+⋅⋅=11711931191716371020121020121020122400⋅⋅+⋅⋅+⋅⋅=，()()()()2P P AC C F FB P AC C F FB P AC C F FB ξ==⋅⋅+⋅⋅+⋅⋅ 13111171931771020121020121020122400=⋅⋅+⋅⋅+⋅⋅=，()()13113102012800P P AC C F FB ξ==⋅⋅=⋅⋅=. 所以ξ的分布列为…………………………………………………………9分 ∴E ξ=56163777110123800240024008003⨯+⨯+⨯+⨯= ………………12分20．（本小题满分12分）解: （Ⅰ）根据题设可得: 集合A 中所有的元素可以组成以3-为首项,2-为公差的递减等差数列；集合B 中所有的元素可以组成以3-为首项,6-为公差的递减等差数列.由此可得,对任意的*∈N n ,有B B A =A B 中的最大数为3-,即13a =- …………………………………………2分设等差数列{}n a 的公差为d ,则3(1)n a n d =-+-,1101010()45302a a S d +==-因为10750300S -<<-, ∴7504530300d -<-<-,即616-<<-d 由于B 中所有的元素可以组成以3-为首项,6-为公差的递减等差数列所以)0,(6≠∈-=m Z m m d ,由1666m -<-<-2m ⇒=，所以12-=d …………5分所以数列{}n a 的通项公式为912n a n =-（*∈N n ） ………………………6分（Ⅱ）13922n a n n n b +-==246211[1()]12224()2424(1)1212nn n n T b b b b -=++++=⨯=--………………………7分48244824(221)24212212(21)nn nnn n n T n n n ---=--=+++于是确定n T 与4821n n +的大小关系等价于比较2n 与21n +的大小由2211<⨯+，22221<⨯+，32231>⨯+，42241>⨯+，⋅⋅⋅可猜想当3n ≥时，221n n >+ …………………………………………………………9分 证明如下：证法1：（1）当3n =时，由上验算可知成立. （2）假设n k =时，221k k >+，则12222(21)422(1)1(21)2(1)1k k k k k k k +=⋅>+=+=+++->++ 所以当1n k =+时猜想也成立根据（1）（2）可知 ，对一切3n ≥的正整数，都有221n n >+∴当1,2n =时，4821n n T n <+，当3n ≥时4821n n T n >+ ………………………………12分证法2：当3n ≥时110112(11)2221nnn n n nn n nn n n nn C C C C C C C C n n --=+=++⋅⋅⋅++≥+++=+>+∴当1,2n =时，4821n n T n <+，当3n ≥时4821n n T n >+ ………………………………12分21．（本小题满分12分） 解：（Ⅰ）()()23232f x ln x x =+-, ∴()y f x =的定义域为23,⎛⎫-+∞ ⎪⎝⎭; 由于()()191332x x f x x ⎛⎫+- ⎪⎝⎭'=-+，由()103f x x '=⇒=,当2133x ,⎛⎫∈-⎪⎝⎭时，()0f x '>；当13x ,⎛⎫∈+∞ ⎪⎝⎭时，()0f x '<.∴()y fx =在2133,⎛⎤-⎥⎝⎦上为增函数；在13,⎡⎫+∞⎪⎢⎣⎭上为减函数， 从而()11336f x f ln ⎛⎫==-⎪⎝⎭极大. ………………………………………3分 （Ⅱ）⇒()()()ln 231g x x m x =++-，23x ⎛⎫>-⎪⎝⎭()()3121312323m x m g x m xx-++'⇒=+-=++，………………………………………4分① 当10m -=,即1m =时，()323g x x'=+0>，()g x ∴在23,⎛⎫-+∞ ⎪⎝⎭上为增函数；…………………………………………………………5分②当10m -≠，即1m ≠时，()()()()21313131212323m m x m m x m g x x x⎡⎤+-+⎢⎥--++⎣⎦'==++.由()()21031m g x x m +'=⇒=--,()21213131m m m ⎛⎫+⎛⎫---=- ⎪ ⎪ ⎪--⎝⎭⎝⎭, ∴（ⅰ）若1m >，则()212313m m +-<--，∴ 23x >-时，()0g x '>，()g x ∴在23,⎛⎫-+∞ ⎪⎝⎭上为增函数；…………………………………………………………7分(ⅱ)若1m <，则()212313m m +->--，()221,331m x m ⎛⎫+∈-- ⎪ ⎪-⎝⎭时，()0g x '>；()21,31m x m ⎛⎫+∈-+∞ ⎪ ⎪-⎝⎭时，()0g x '<， ()g x ∴在()221331m ,m ⎛⎤+-- ⎥ -⎝⎦上为增函数,在()2131m ,m ⎡⎫+-+∞⎪⎢⎪-⎣⎭上为减函数. 综上可知：当1m ≥时，()g x 在23,⎛⎫-+∞ ⎪⎝⎭上为增函数；当1m <时，()g x 在()221331m ,m ⎛⎤+-- ⎥ -⎝⎦上为增函数，在()2131m ,m ⎡⎫+-+∞⎪⎢⎪-⎣⎭上为减函数. …………………………9分（Ⅲ）由()30a ln x ln f x x '-++>⎡⎤⎣⎦3023a ln x lnx⇒-+>+,1163x ,⎡⎤∈⎢⎥⎣⎦,360235lnln x ∴≤≤+,而0a ln x -≥， ∴要对任意1163x ,⎡⎤∈⎢⎥⎣⎦，不等式()30a ln x ln f x x '-++>⎡⎤⎣⎦均成立，必须：323lnx+与a ln x -不同时为0. ………………………………………………………11分因当且仅当13x =时，323lnx+=0，所以为满足题意必有103a ln-≠，即13a ln≠. …………………………………………………………………12分22．（本小题满分14分）解：（Ⅰ）设抛物线()22:20C y mx m =≠，则有()220ym x x=≠，据此验证4个点知(3,-、()4,4-在抛物线上，易求xyC4:22= …………………2分设1C ：()222210x y a b ab+=>>，把点（-2，0）（2，22）代入得：⎪⎪⎩⎪⎪⎨⎧=+=121214222b a a⇒ ⎪⎩⎪⎨⎧==1422b a ∴1C 方程为1422=+yx………………………………………………………4分（Ⅱ）容易验证直线l 的斜率不存在时，不满足题意；当直线l 斜率存在时，假设存在直线l 过抛物线焦点(1,0)F ，设其方程为(1)y k x =-，与1C 的交点坐标为()11,Q x y ,()22,R x y由2214(1)x y y k x ⎧⎪+=⎨⎪=-⎩消去y ，得 2222(14)84(1)0k x k x k +-+-=，于是 2122814kx x k+=+，21224(1)14k x x k-=+ …………① ……………………7分212121212(1)(1)[()1]y y k x k x k x x x x =-⨯-=-++即2222122224(1)83(1)141414k kky y k kkk-=-+=-+++……②由O Q O R ⊥ ，即0O Q O R ⋅=，得(*)02121=+y y x x将①、②代入（*）式，得 2222224(1)340141414k kk k kk---==+++，解得2k =±； 所以存在直线l 满足条件，且l 的方程为：22y x =-或22y x =-+…………………9分 （Ⅲ）设直线A M 的斜率为k ()0k ≠，则A M ：(2)y k x =+，A N ：1(2)y x k=-+则22(2),1,4y k x x y =+⎧⎪⎨+=⎪⎩ 化简得：2222(14)161640k x k x k +++-=． ∵此方程有一根为2-，∴222814M k x k-=+⇒2414M k y k=+同理可得22284N k x k -=+⇒244N ky k =-+………………………………………………11分则222222244541428284(1)414M N kkk k k k k k k k k--++==-----++ 所以M N 的直线方程为22224528()144(1)14k k k y x kk k--=--+-+令0y =，则222216(1)2865(14)145k k k x k k k--=+=-++.所以直线M N 过x 轴上的一定点6(,0)5-………………………………………………14分。

山东省实验中学2012级高三第二次模拟考试英语试题2015．6说明：试题分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷为第1页至第9页，第Ⅱ卷为第9页至第10页。

试题答案请用2B铅笔和0.5mm签字笔填涂到答题卡规定位置上，书写在试题上的答案无效。

考试时间120分钟。

第Ⅰ卷（共100分）第一部分听力（共两节，满分30分）该部分分为第一、第二两节。

注意：回答听力部分时，请先将答案标在试卷上。

听力部分结束前，你将有两分钟的时间将你的答案转涂到客观题答题卡上。

第一节（共5小题；每小题1.5分，满分7.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. Where will the woman go first?A. To the beach.B. To the bank.C. To the toilet.2. What does the woman mean?A. The man forgot to do his hair.B. The man should have put on a tie.C. The man isn’t dressed properly.3. How does the woman probably feel?A. Annoyed.B. Hungry.C. Disappointed.4. Why didn’t the man answer the phone?A. He lost his phone.B. He didn’t hear it.C. His phone was power off.5. Who did the woman want to call?A. James.B. Drake.C. Daniel.第二节（共15小题；每小题1.5分，满分22.5分）听下面5段对话或独白。

山东省实验中学2012级第二次模拟考试文综试题（2015.6）本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分，共16页。

满分300分。

考试用时150分钟。

答卷前，考生务必将自己的姓名、座号、准考证号、县区和科类填涂在试卷、答题卡和答题纸规定的位置。

考试结束后，将本试卷、答题卡和答题纸一并交回。

第Ⅰ卷（选择题 140分）注意事项：1．第I卷共35小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是最符合题目要求的。

2、每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不涂在答题卡上，只答在试卷上无效。

右图为南美洲部分区域示意图,据图完成3～4题。

3．图中南赤道暖流越过赤道向北流动的主要影响因素是A．大陆轮廓B．地转偏向力C．东北信风D．赤道低压带4.要监测和预测洋流势力的强弱变化，应用的地理信息技术分别是A.GPS RSB.GIS RSC.RS GISD. GPS GIS下图为欧洲南部沿42°N纬线部分地区剖面示意和①、②两地降水量统计，读图完成7～8题。

7．造成①、②两地年降水量差异显著的主导因素是A.洋流B.大气环流C.地形D.纬度位置8．关于图示地区的叙述，正确的是A．农业地域类型为水稻种植业B．人口自然增长率高C．山麓自然带为温带落叶阔叶林带D．①、②两地气候均为地中海气候右图是地处热带太平洋中的一个岛屿，欲对该岛进行开发。

该岛盛行较强的东南风，有流速较大的河流及森林。

据此完成9～10题。

9．有关该岛的叙述，正确的是A．该岛位于北半球B．该岛的相对高度可能是850米C．该岛的面积可达900平方千米D．图中农场的农业地域类型最有可能是混合农业10．关于该岛屿的开发与发展设想合理的是①在乙地建设小城镇，大力开发森林资源②在丙地建设盐场比甲地更合适③在丁处建设港口和城镇④在戊处建设风能发电站，并营造滨海防护林⑤逐步建设环岛公路和铁路A. ①②③B. ①④⑤C. ③④⑤D.②③④2014年，京津冀一体化发展已经上升为重大国家战略，以疏解首都面临的巨大的人口、资源和环境压力。

2012年普通高考理科数学仿真试题(五) 本试卷分第I卷和第Ⅱ卷两部分，共5页．满分150分．考试用时120分钟．考试结束后，将本试卷和答题卡一并交回． 注意事项： 1．答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上． 2．第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号．答案不能答在试卷上． 3．第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效． 4．填空题请直接填写答案，解答题应写出文字说明、演算步骤或推证过程． 第I卷(共60分) 一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知集合，则下列关系式正确的是 A.B.C.D. 2.设i是虚数单位，则是 A.B.C.1+ID. 3.下列命题中，真命题的个数有 ①；②；③函数是单调递减函数.A.0个B.1个C.2个D.3个 4.如右图，一个简单空间几何体的三视图，其主视图与左视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其体积是 A.B. C.D. 5.已知椭机变量X服从正态分布N（4，1），且，则A.0.0912B.0.3413C.0.3174D.0.1587 6.若则A.112B.28C.D. 7.函数的图象可以是 8.把函数的图象上所有的点向左平移个单位长度，再把所得图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到的图象所表示的函数为 A.B. C.D. 9.如果执行如图所示的程序框图，输入，那么输出等于 A.720 B.120 C.240 D.360 10.已知点F，A分别是椭圆的左焦点、右顶点，B（0,b）满足，则椭圆的离心率等于A.B. C.D. 11. 甲、乙、丙、丁四人参加奥运会射击项目选拔赛，四人的平均成绩和方差如下表所示： 从这四个人中选择一人参加奥运会射击项目比赛，最佳人选是A.甲B.乙C.丙D.丁 12.对于函数，若存在区间（其中a＜b），使得，则称区间M为函数的一个“稳定区间”.给出下列4个函数：①；②；③；④.其中存在“稳定区间”的函数有A.①③B.①②③C.①②③④D. 第II卷（非选择题 共90分） 二、填空题：本大题共4小题，每小题4分，共16分. 13.已知二次函数，点是区域内的随机点，则函数在区间上是增函数的概率为_______. 14.设F1、F2分别为双曲线的左、右焦点，若在双曲线右支上存在点P，满足，且F2到直线PF1的距离等于双曲线的实轴长，则该双曲线的渐近线方程为________. 15.商家通常依据“乐观系数准则”确定商品销售价格，即根据商品的最低销售限价a，最高销售限价b（b＞a）以及实数确定实际销售价格.这里，被称为乐观系数.经验表明，最佳乐观系数恰好使得是和的等比中项，据此可得，最佳乐观系数的值等于_____. 16.给出的下列四个命题中： ①命题“”的否定是“”； ②“”是“直线与直线相互垂直”的充分不必要条件； ③设圆与坐标轴有4个交点，分别为，则； ④关于x的不等式的解集为R，则 其中所有真命题的序号是________. 三、解答题：本大题共6小题，共74分. 17.（本小题满分12分）已知向量，函数 （1）求函数的最小正周期T； （II）已知a、b、c分别为△ABC内角A、B、C的对边，其中A为锐角，且，求A，b和△ABC的面积S. 18.（本小题满分12分）为加强大学生实践、创新能力和团队精神的培养，促进高等教育教学改革，教育部门主办了全国大学生智能汽车竞赛.该竞赛分为预赛和决赛两个阶段，参加决赛的队伍按照抽签方式决定出场顺序，通过预赛，选拔出甲、乙等五支队伍参加决赛. （I）求决赛中甲、乙两支队伍恰好排在前两位的概率； （II）若决赛中甲队和乙队之间间隔的队伍数记为X，求X的分布列和数学期望. 19.（本小题满分12分）在三棱锥P-ABC中，△PAC和△PBC是边长为的等边三角形，AB=2，O是AB中点. （I）在棱PA上求一点M，使得OM//平面PBC； （II）求证：平面PAB⊥平面ABC； （III）求二面角P-BC-A的余弦值. 20.（本小题满分12分）已知数列中，，且 （1）设，求数列成等比数列，求m的值及的前n项和. 21.（本小题满分12分）已知椭圆中心在坐标原点焦点在x轴上，离心率为，它的一个顶点为抛物线的焦点. （I）求椭圆方程； （II）若直线与抛物线相切于点A，求以A为圆心且与抛物线的准线相切的圆的方程； （III）若斜率为1的直线交椭圆于M、N两点，求△OMN面积的最大值（O为坐标原点）. 22.（本小题满分14分）函数 （I）若在处取得极值，求的值； （II）若在其定义域内为单调函数求的取值范围； （III）若在［1,e］上至少存在一点，使得成立，求的取值范围.2012年普通高考理科数学仿真试题(五)答案。

山东省实验中学2012届高考模拟理综试题注意事项：1．本试卷分为第I卷（选择题）和第II卷（非选择题）两部分，满分240分。

考试时间l50分钟。

2．考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

3．答卷前将答题纸和答题卡中的个人信息按要求填写清楚。

可能用到的相对原子质量：Hl C12 N14 O16 Na23 C135.5第I卷（选择题共87分）一、选择题（本题包括13小题，每小题只有一个选项符合题意）1．下列有关实验的说法正确的是A．用标志重捕法调查土壤小动物类群的丰富度B．用醋酸洋红染液使染色体着色C．用纸层析法提取叶绿体中的色素D．用班氏试剂检测葡萄糖的存在2．关于细胞结构、功能及其化合物的说法正确的是A．蓝藻与绿藻都能进行光合作用，但二者在细胞结构上的最主要区别是叶绿体的有无B．同一生物的不同细胞会因细胞分化而导致细胞器在数量上有区别，但种类是相同的C．抗体、酶、载体蛋白发挥相应作用后，不能继续发挥作用的是抗体D．蛋白质的合成不一定要在核糖体上进行，例如哺乳动物的成熟红细胞3．蛇毒的主要成分为蛋白质和多肽。

将眼镜蛇蛇毒处理后注入马体内，可获取抗蛇毒血清，用于治疗被眼镜蛇咬伤的患者。

以下选项与此治疗原理最相似的是A．用免疫抑制剂治疗自身免疫疾病B．骨髓移植治疗慢性粒细胞白血病C．注射干扰素抑制乙肝病毒增殖D．给新生儿注射乙肝抗体阻断病毒的母婴传播4．内质网中的蛋白质运输到高尔基体后，存在着不同的去向，其转运过程如下图。

下列叙述错误的是A．蛋白B通过载体蛋白的协助分泌到细胞外B．受体K的作用使蛋白A被转运回内质网C．高尔基体膜通过囊泡可转化为内质网膜和细胞膜的一部分D．内质网和高尔基体分别形成的囊泡中的蛋白B空间结构不同5．下列有关RNA的叙述中错误的是A．分化后的不同细胞中tRNA种类是相同的B．分化后的不同细胞中mRNA种类是不同的C．mRNA上有多少个决定氨基酸的密码子就有多少个tRNA与之对应D．在所有生物中RNA均转录而来6．下列两组描述分别称为甲和乙，两者符合“甲→乙”关系的是A．遵循基因分离定律：遵循基因自由组合定律B．种群基因频率改变：生物进化C．患有某种遗传病带有致病基因D．原核细胞；细胞中不含有线粒体和叶绿体7．化学与科学、技术、社会、环境密切相关。

高中数学学习材料唐玲出品山东省实验中学2012级高三第二次模拟考试数学试题（理） 2015,6说明：试题分为第I 卷（选择题）和第I 卷（非选择题）两部分．试题答案请用2B 铅笔或0,5mm 签字笔填涂到答题卡规定位置上，书写在试题上的答案无效，考试时间120分钟．一、选择题（本题包括10小题，每小题5分，共50分，每小题只有一个选项符合题意）l-已知全集U=R ，集合 {}{}3|021,|log 0x A x B x x =<<=>，则A. {}|1x x > B ． {}|0x x > C. {}|01x x << D. {}|0x x < 2．若 ,R αβ∈， 则 90αβ+=是sin sin 1αβ+> 的 A ．充分而不必要条件B.必要而不充分条件C ．充耍条件D ．既不充分也不必要条件 3．复数z 满足 (12)7i z i -=+，则复数 z ==( )A. 13i +B.13i -C.3i +D. 3i -4．执行下图所示的程序框图，若要使输入的x 值与输出的y 值相等，则这样的x 值的个数是A. 1B. 2C. 3D.4 5.下列四个命题：①样本方差反映的是所有样本数据与样本平均值的偏离程度； ②某只股票经历了l0个跌停（每次跌停，即下跌l0%）后需再经 过如个涨停(每次涨停，印上涨10%)就酉以回到原来的净值； ③某校高三一级部和二级部的人数分别是m 、n ，本次期末考试 两级部；学平均分分别是a 、b ，则这两个级部的数学平均分为na mb m n+④某中学采伯系统抽样方法，从该校高一年级全体800名学生中抽50名学生做牙齿健康检查，现将800名学生从001到800进行编号，已知从497--512这16个数中取得的学生编号是503，则初始在第1小组00l ～016中随机抽到的学生编号是007. 其中真命题的个数是A.0个B.1个C.2个D.3个6．已知函数 ()sin()f x A x ωϕ=+ (其中A>0, 2πϕ<)的部分图象如图所示，为了得到g(x)=sin 2x 的图象，则只需将f (x)的图象Ａ．向右平移6π个长度单位 Ｂ．向右平移 12π个长度单位C ．向左平移 6π个长度单位 D ．向左平移 12π个长度单位7．已知数列 {}{}n n a b 满足 1111,2,n n a b a a n N *+==-==∈，则数列 {}n a b 的前10项和为 A.()101413- B. ()104413- C. ()91413- D. ()94413- 8．函数 2()(2)xf x x x e =-的图像大致是9．已知A 、B 是圆 22:1O x y +=上的两个点，P 是AB 线段上的动点，当∆AOB 的面积最大时，则 2AO AP AP ⋅-的最大值是 A. -1 B.0 C.18 D. 1210.已知a>0，b>0，c>0，且 2221,4ab a b c =++=，则ab+bc+ac 的最大值为 A. 122+ B.3 C. 3 D. 4第Ⅱ卷（非选择题，共100分）二．填空题（本题包括5小题，每小题5分，共25分）11.已知 ()24f x x x =++-的最小值是n ，则二颈式 1()n x x-展开式中2x 项的系数为__________.12.若双曲线 22:2(0)C x y m m -=>与抛物线 216y x =的准线交于A ，B 两点，且43AB =则m 的值是__________.13.若实数x,y 满足条件 20,0,3,x y x y x +-≥⎧⎪-≤⎨⎪≤⎩， 则z=3x-4y 的最大值是__________.14．一个球的内接圆锥的最大体积与这个球的体积之比为__________.15．用[x]表示不大于实数x 的最大整数， 方程 []2lg lg 20x x --=的实根个数是__________.三．解答题（本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤）． 16.（本小题满分12分）已知函数 ()sin (0)f x x ωω=->在区间 0,3π⎡⎤⎢⎥⎣⎦上单调递减，在区间 2,33ππ⎡⎤⎢⎥⎣⎦上单调递增；如图，四边形OACB 中，a ，b ，c 为△ABC 的内角以B, C 的对边，且 满足 sin sin tan 4cos cos 3B c A BC ω+=-- ．(I)证明：b+c =2a ：(Ⅱ)若b=c ，设 AOB θ∠=．(0),22OB OB θπ<<==，求四边形OACB 面积的最大值．17. （本小题满分12分）如图， 在四棱锥P –ABCD 中，PA ⊥平面ABCD ， ∠DAB 为直角， AB//CD ，AD=CD=2AB=2，E ，F 分别为PC ，CD 的中点． ( I)证明：AB ⊥平面BEF ：(Ⅱ)设PA =h ，若二面角E-BD-C 大于45 ，求h 的取值范围．18.（本小题满分12分）一个袋子装有大小形状完全相同的9个球，其中5个红球编号分别为l ，2，3，4，5：4个白球编号分别为1，2，3，4，从袋中任意取出3个球． (I)求取出的3个球编号都不相同的概率；（II)记X 为取出的3个球中编号的最大值，求X 的分布列与数学期望， 19. （本小题满分12分）数列{}n a 的前n 项和记为 11,2,n n n S a a S n +==+，等差数列 {}n b 的各项为正，其前n 项和为 n T ，且 39T =，又 112233,,a b a b a b +++成等比数列． (I)求 {}n a ，{}n b 的通项公式}( II)求证：当n ≥2时， 2221211145n b b b ++⋅⋅⋅+< 20. （本小题满分13分）如图，椭圆 22122:1(0)x y C a b a b+=>>的离心率为 22，x 轴被曲线 22:C y x b =-截得的线段长等于1C 的短轴长, 2C 与y 轴的交点为M ，过坐标原点O 的直线 l 与2C 相交于点A 、B ，直线MA,MB 分别与 1C 相交于点D 、E. (I)求1C 、 2C 的方程； (Ⅱ)求证：MA ⊥MB ：(Ⅲ)记∆MAB ， ∆MDE 的面积分别为 12,S S ，若 12S S λ=，求 λ的最小值．21．（本小题满分l4分）已知函数 1()(1)ln ,()f x ax a x a R x=+-+∈． (I)当a=0时，求 ()f x 的极值； (Ⅱ)当a<0时，求 ()f x 的单调区间；(Ⅲ)方程 ()0f x =的根的个数能否达到3，若能请求出此时a 的范围，若不能，请说明理由，第二次模拟试题答案（理科数学）一、 选择： DDBDC AABCA二、 填空 11. 15；12. 20；13. -1；14. 8：27；15. 3 三、解答题16解：（Ⅰ）由题意知：243ππω=，解得：32ω=， ……………………2分CB CB B A A cos cos 2sin sin sin sin tan --+==∴ A C A B A A C A B sin cos -sin cos -sin 2cos sin cos sin =+∴ A A C A C A B A B sin 2sin cos cos sin sin cos cos sin =+++∴A C AB A sin 2)(sin )(sin =+++∴……………………………………4分a cb A B C 2sin 2sin sin =+⇒∴=+∴…………………………………………………6分（Ⅱ）因为2b c a b c +==，，所以a b c ==，所以ABC △为等边三角形 …………8分213sin 24OACB OAB ABC S S S OA OB AB θ∆∆=+=⋅+ ……………9分435cos 3-sin +=θθ532sin (-)34πθ=+， ……………………10分 (0)θπ∈，,2--333πππθ∴∈(，)，当且仅当-32ππθ=，即56πθ=时取最大值,OACB S 的最大值为5324+………………12分17.解：（Ⅰ）证：由已知DF ∥AB 且∠DAB 为直角，故ABFD 是矩形，从而AB ⊥BF ． ……(1分)又PA ⊥底面ABCD , ∴平面PAD ⊥平面ABCD ， ……(2分) ∵AB ⊥AD ，故AB ⊥平面PAD ,∴AB ⊥PD ， ……(3分) 在ΔPCD 内，E 、F 分别是PC 、CD 的中点，EF //PD ，……（4分) ∴ AB ⊥EF ． ……(5分)由此得⊥AB 平面BEF ．……(6分)（Ⅱ）以A 为原点，以AB ，AD ，AP 为x 轴,y 轴,z 轴正向建立空间直角坐标系，则)21,0(),0,2,1(hBE BD =-=……(8分)设平面CDB 的法向量为)1,0,0(1=n ，平面EDB 的法向量为),,(2z y x n =，z yxFEPDCBA则 ⎪⎩⎪⎨⎧=⋅=⋅0022BE n BD n⎪⎩⎪⎨⎧=+=+-0202hzy y x 可取⎪⎭⎫ ⎝⎛-=h n 2,1,22 ……(10分) 设二面角E -BD -C 的大小为θ，则|||||||,cos |cos 212121n n n n n n ⋅⋅=><=θ=224522<+h h ， 化简得542>h ，所以552>h …(12分)18解:(I )设“取出的3个球编号都不相同”为事件A ，则“取出的3个球中恰有两个球编号相同”为事件A ，则31)(391714==C C C A P 所以32)(1)(=-=A P A P ………………（4分）(II ) X 的取值为2,3,4,5211)2(3912222212=+==C C C C C X P ，214)3(3914222412=+==C C C C C X P 73)3(3916222612=+==C C C C C X P ，31)5(3928===C C X P…………………（8分） 所以X 的分布列为：X 23 4 5P211 214 73 31的数学期望218531573421432112=⨯+⨯+⨯+⨯=EX ………..12分19解：（Ⅰ）由n S a n n +=+1，得)1(1-+=-n S a n n )2(≥n ，两式相减得1111+=+-=--+n n n n n a S S a a ，所以121+=+n n a a ---------------------------------2分所以)1(211+=++n n a a )2(≥n -------------------------------------3分又,32=a 所以n n n a a 2)1(2122=+=+-，从而12-=nn a )2(≥n ----------------5分而21=a ，不符合上式，所以⎩⎨⎧≥-==2,121,2n n a n n -------------------------------------6分因为}{n b 为等差数列，且前三项的和93=T ，所以32=b ，--------7分可设db d b +=-=3,331，由于7,3,2321===a a a ，于是d b a b a d b a -=+=+-=+10,6,5332211，因为332211,,b a b a b a +++成等比数列，所以36)10)(5(=+-d d ，2=d 或7-=d （舍）所以12)1(21)1(1-=-+=-+=n n d n b b n -----------------------------------9分 （Ⅱ）因为⎪⎭⎫⎝⎛--=-=--<-=k k k k k k b k 11141)22(211)12(1)12(11222 所以，当2≥n 时22222221)12(13111111-++=+++n b b b n⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛--++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+<n n 1113121211411 ⎥⎦⎤⎢⎣⎡-+=n 1141145411=+< -----------------------------------------------------------12分20.解（1）22222c a b a =∴= （1分） 又22b b =，得1b =22221:1,:12x C y x C y ∴=-+= （3分）（2）设直线1122:,(,),(,)AB y kx A x y B x y =则22101y kxx kx y x =⎧⇒--=⎨=-⎩ （4分）211221212(,1)(,1)(1)()1MA MB x y x y k x x k x x ⋅=+⋅+=++++=0MA MB ∴⊥ （6分） （3）设直线1212:1;:1,1MA y k x MB y k x k k =-=-=-1121122110,(,1)111x k y k x x A k k y y k y x ==-⎧⎧=⎧⎪∴-⎨⎨⎨=-=-=-⎪⎩⎩⎩解得或，同理可得222(,1)B k k - 2211212111122S MA MB k k k k ==++ （8分） 1212111222221112141120421,(,)11212211212k x y k x k x k k D x y k k k y y k ⎧==-⎧⎪+=⎧-⎪⎪∴⎨⎨⎨=-++-+=⎩⎪⎪=⎩⎪+⎩解得或 同理可得2222222421(,)1212k k E k k -++1222212221216111122(12)(12)k k S MD ME k k k k ∴==++++ （11分）2122211212152()(12)(12)9161616k S k k k S λ++++===≥所以λ的最小值为169,此时k =1或-1. （13分）21解：（Ⅰ）)(x f 其定义域为),0(+∞. ……………1分当0=a 时，x x x f 1ln )(+= ，22111)(xx x x x f -=-='. 令0)(='x f ，解得1=x ,当10<<x 时，0)(<'x f ；当1>x 时，0)(>'x f .所以)(x f 的单调递减区间是)1,0(，单调递增区间是),1(+∞；所以1=x 时， )(x f 有极小值为1)1(=f ，无极大值 ……………3分(Ⅱ) 222211(1)1(1)(1)()(0)a ax a x ax x f x a x x x x x ----+-'=--==> ………4分令0)(='x f ,得1=x 或ax 1-= 当01<<-a 时，a11-<，令0)(<'x f ，得10<<x 或a x 1->，令0)(>'x f ，得ax 11-<<；当1-=a 时，0)1()(22≤--='x x x f . 当1-<a 时，110<-<a ，令0)(<'x f ，得ax 10-<<或1>x ， 令0)(>'x f ，得11<<-x a；综上所述:当01<<-a 时，)(x f 的单调递减区间是)1,0(，),1(+∞-a， 单调递增区间是)1,1(a-；当1-=a 时，)(x f 的单调递减区间是),0(+∞；当1-<a 时，)(x f 的单调递减区间是)1,0(a-，),1(+∞，单调递增区间是)1,1(a - (10)分（Ⅲ）0≥a 时)0()1)(1()(2>-+='x x x ax x f)0(0)(>='∴x x f 仅有1解,方程0)(=x f 至多有两个不同的解.(注:也可用01)1()(min >+==a f x f 说明.)由(Ⅱ)知01-<<a 时,极小值 01)1(>+=a f , 方程0)(=x f 至多在区间),1(+∞-a 上有1个解.-1a =时)(x f 单调, 方程0)(=x f 至多有1个解.;1-<a 时, 01)1()1(<+=<-a f a f ,方程0)(=x f 仅在区间)1,0(a -内有1个解;故方程0)(=x f 的根的个数不能达到3. …………………14分。

2012年济南市高三5月份模拟考试试题数学（理工类）本卷分第Ⅰ卷和第Ⅱ卷两部分，共4页．满分150分．考试用时120分钟．考试结束后将答题卡交回． 注意事项：1. 答题前，考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号、县区和科类填写在答题卡和试卷规定的位置上.2. 第Ⅰ卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其他答案标号，答案不能答在试卷上.3．第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不能使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．4．填空题直接填写答案，解答题应写出文字说明、证明过程或演算步骤. 参考公式：样本数据n x x x ，，， 21的方差])()()[(1222212x x x x x x ns n -++-+-=，其中x 为样本的平均数；锥体体积公式：Sh V 31=，其中S 为锥体底面的面积，h 为锥体的高； 圆锥的侧面积公式：rl S π=，其中r 是圆锥的底面半径，l 是圆锥的母线长； 圆柱的侧面积公式：rl S π2=，其中r 是圆柱的底面半径，l 是圆柱的母线长.第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、若全集U =R ，集合{235}A x x =+<，B =｛3|log (2)x y x =+｝，则()UC AB =A ．{}14≥-≤x x x 或 B ．{}14>-<x x x 或C ．{}12>-<x x x 或D ．{}12≥-≤x x x 或【解析】}14{}532{<<-=<+=x x x x A ，}2}{02{})2(log {3->>+=+==x x x x x y x B ，所以}12{<<-=⋂x x B A ，所以}21{)(-≤≥=⋂x x x B A C U 或，选D.【答案】D2．已知非零向量a 、b 满足向量+a b 与向量-a b 的夹角为2π，那么下列结论中一定成立的是 A ．=a bB ．||||=a bC ．⊥a bD ．ab【解析】因为向量+a b 与向量-a b 的夹角为2π，所以)()(-⊥+，即0)()(=-∙+0== B.【答案】B３．n S 是数列{}n a 的前n 项和，则“n S 是关于n 的二次函数”是“数列{}n a 为等差数列”的 A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【解析】若n S 是关于n 的二次函数，则设为)0(2≠++=a c bn an S n ，则当2≥n 时，有a b an S S a n n n -+=-=-21，当1=n ,c b a S ++=1,只有当0=c 时，数列才是等差数列，若数列为等差数列，则n ada d n d n n na S n )(22)1(121-+=-+=，当0≠d 为二次函数，当0=d 时，为一次函数，所以“n S 是关于n 的二次函数”是“数列{}n a 为等差数列”的既不充分也不必要条件，选D. 【答案】D４、如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”. 给出下列函数：①()sin cos f x x x =；②()2sin()4f x x π=+；③()sin f x x x =； ④()21f x x =+.其中“同簇函数”的是( ) A ．①② B ．①④ C ．②③ D ．③④【解析】若为“同簇函数”，则振幅相同，将函数进行化简①x x x x f 2sin 21cos sin )(==，③）3sin(2cos 3sin )(π+=+=x x x x f ，所以②③振幅相同，所以选C.【答案】C5．若双曲线22221(0,0)x y a b a b-=>>与直线y =无交点，则离心率e 的取值范围A ．(1,2)B ．(1,2]C ．D ．【解析】因为双曲线的渐近线为x aby ±=，要使直线x y 3=与双曲线无交点，则直线x y 3=，应在两渐近线之间，所以有3≤ab ，即a b 3≤，所以223a b ≤，2223a ac ≤-，即224a c ≤，42≤e ，所以21≤<e ，选B. 【答案】B6．一个几何体的三视图如右图所示，则这个几何体的体积等于( ) A ．4 B ．6 C ．8 D ． 12【解析】由三视图可知这是一个底面是直角梯形，高2=AE ,的四棱锥。

山东省实验中学2012级高三第二次模拟考试数学试题（文）参考答案选择题: 1-5 BDCDC 6-10DBADC填空题：11.100 12.5<n 13.（-7,3）14. 32 15. ①④16.解：(1)由图知A ＝2，T 4＝π3，则2πω＝4×π3，∴ω＝32.……………………………3分又f ⎝⎛⎭⎫－π6＝2sin ⎣⎡⎦⎤32×⎝⎛⎭⎫－π6＋φ＝2sin ⎝⎛⎭⎫－π4＋φ＝0，∴sin ⎝⎛⎭⎫φ－π4＝0， ∵0<φ<π2，－π4<φ－π4<π4，∴φ－π4＝0，即φ＝π4，………………………………………5分∴f (x )的解析式为f (x )＝2sin ⎝⎛⎭⎫32x ＋π4.……………………………6分 (2)由(1)可得f ⎝⎛⎭⎫x －π12＝2sin ⎣⎡⎦⎤32⎝⎛⎭⎫x －π12＋π4 ＝2sin ⎝⎛⎭⎫32x ＋π8，2)12()(⎥⎦⎤⎢⎣⎡-=πx f x g ＝4×1－cos ⎝⎛⎭⎫3x ＋π42 ＝2－2cos ⎝⎛⎭⎫3x ＋π4，…………………………9分 ∵x ∈⎣⎡⎦⎤－π6，π3，∴－π4≤3x ＋π4≤5π4， ∴当3x ＋π4＝π，即x ＝π4时，g (x )max ＝4.……………12分17.(1){}{}{}{}{}{}{}{}{}{}{}3222124232312111413121,,,,,,,,,,,,,,,,,,,,,B A B A B A A A A A B A B A B A A A A A A A{}{}{}{}{}{}{}{}{}{}32312134241433231343,,,,,,,,,,,,,,,,,,,B B B B B B B A B A B A B A B A B A A A …5分(2)以上21个结果对应的射击环数之和依次为14,14,15, 13,12,16,16,17,15,14,18,17,15,14，18,16,15,19,13,17,16． ……………………………………………………………………8分 其中环数之和小于15的结果为{}{}{}{}{}{}{}21232221113121,,,,,,,,,,,,,B B B A B A B A B A A A A A 共7个 ……………………10分所以这2人射击的环数之和小于15的概率为31217= …………………………………12分 18.(Ⅰ)证明：作FM ∥CD 交PC 于M . …………………2分 ∵点F 为PD 中点，∴CD FM 21=. ∵21=k ，∴FM AB AE ==21，…………4分 ∴AEMF 为平行四边形，∴AF ∥EM . ∵AF PEC EM PEC ⊄⊂平面，平面， ∴直线AF//平面PEC . ………………………………………6分 (Ⅱ)存在常数22=k ，使得平面PED ⊥P AB . ………………………………7分 ∵k ABAE=，1AB =，22=k ，∴22AE =. ………………………8分 又∵∠DAB ＝45°，∴AB ⊥DE .又∵PD ⊥平面ABCD ，∴PD ⊥AB . ……………………10分 又∵PD DE D ⋂=，∴AB ⊥平面PDE .∵PAB AB 平面⊂，∴平面PED ⊥平面P AB . …………………………………12分19.(1)证明 由2a n ＋1－2a n ＋a n ＋1a n ＝0得1a n ＋1－1a n ＝12，………………………4分所以数列⎩⎨⎧⎭⎬⎫1a n 是以21为公差的等差数列．………………………5分(2)b 1＝f (0)＝5，所以7(a 1－1)＋5a 1－1＋1＝5，7a 1－2＝5a 1，所以a 1＝1，……………………6分1a n ＝1＋(n －1)12，所以a n ＝2n ＋1.……………7分 b n ＝7a n －2a n＝7－(n ＋1)＝6－n .………………………8分当n ≤6时，T n ＝n2(5＋6－n )＝n (11－n )2；当n ≥7时，T n ＝15＋n －62(1＋n －6)＝n 2－11n ＋602.MFE BDCAP所以，T n＝⎩⎨⎧n (11－n )2，n ≤6，n 2－11n ＋602，n ≥7.………………………12分20解：（Ⅰ）函数)(x f 的定义域为），（∞+0，当1=a 时， x x x x f ln 1)(+-=，22'111)(xx x x x f -=+-=.……………………1分 在)1,0(上，0)('<x f ，)(x f 单调递减；在),1(+∞上，0)('>x f ，)(x f 单调递增. ……………………3分 函数0)1()(min ==f x f .……………………4分（Ⅱ）22'111)(ax ax x ax x f -=+-=，函数)(x f 在),1[+∞上为增函数 等价于0)('≥x f 在),1[+∞上恒成立，……………………5分当0<a 时，0)('≥x f ， )(x f 在),1[+∞上单调递增，满足题设条件.当0>a 时，因为02>ax ，令1)(-=ax x g ，等价于0)(≥x g 在),1[+∞上恒成立，1)(-=ax x g 在),1[+∞上为增函数，所以01)1()(≥-=≥a g x g ，综上所述：所求实数a 的取值范围是0<a 或1≥a .……………………8分（Ⅲ）因为0,011>>⎪⎭⎫⎝⎛++e n n n ，比较11+⎪⎭⎫⎝⎛+n n n 与e 的大小，等价于比较11ln +⎪⎭⎫⎝⎛+n n n 与e ln 的大小，……………………9分 即比较⎪⎭⎫⎝⎛++n n n 1ln )1(与1的大小，即比较⎪⎭⎫⎝⎛+n n 1ln 与11+n 的大小. ……………………10分 由（1）得在),0(+∞上，当1≠x 时， 0)1(ln 1)(=>+-=f x x x x f ，即xx x 1ln ->，------11分 令n n x 1+=，则0>x ，且1≠x ，得>⎪⎭⎫⎝⎛+n n 1ln 11+n ，……………………12分 由此得11+⎪⎭⎫⎝⎛+n n n e >（*N ∈n ）. ……………………13分21解：(I) 22,12==a b b ，解得2=a .……………………………………2分 所求椭圆1C 的方程为1222=+y x .……………………………………3分 （II ）设),,(),,(2211y x N y x M )1,0(),0,1(B F ，根据题意031,132121=++=+y y x x ， 即1,32121-=+=+y y x x .……………………………………4分由122121=+y x ，①, 122222=+y x ,②① - ②得0)(2)(21212121=--+++x x y y y y x x . ,23)(221212121=++=--=y y x x x x y y k MN ……………………………………6分设MN 的中点为（),00y x ），则212,232210210=+==+=y y y x x x ， 直线l 的方程为)23(2321-=-x y ，即0746=--y x .……………………………………8分法二：设)23(21:-=-x k y l .由⎪⎩⎪⎨⎧-=-=+)23(211222x k y y x ， 消去y 得0369)412()42(222=--+-++k k x k k x k ， 设),,(),,(2211y x N y x M则222142412kkk x x +--=+……………………………………4分 )1,0(),0,1(B F ，根据题意031,132121=++=+y y x x ，即1,32121-=+=+y y x x .3424122221=+--=+kkk x x ，解得23=k .……………………………………6分 设MN 的中点为（),00y x ），则212,232210210=+==+=y y y x x x ， 直线l 的方程为)23(2321-=-x y ，即0746=--y x .……………………………………8分 （III ）当直线l 斜率不存在时，MN ，PQ 的中点同为直线l 与x 轴的交点，易知||||NQ PM =.……………………………………9分 当直线l 斜率存在时，设l ：)1(-=x k y .⎪⎩⎪⎨⎧-==+)1(1222x k y y x ，消去y 得，0224)21(2222=-+-+k x k x k ， 2221214kk x x +=+. 设),,(),,(2211y x N y x M MN 的中点),(00y x G ，222102122kk x x x +=+=，20021)1(k k x k y +-=-=.……………………………………11分 ⎪⎩⎪⎨⎧-==+)1(222x k y y x λ，消去y 得，0224)21(2222=-+-+λk x k x k ,2221214k k x x +=+ 设),,(),,(4433y x Q y x P PQ 的中点),('0'0'y x G ，2243'02122k k x x x +=+=，2''021)1(k k x k y +-=-=.……………………………………13分 所以MN 的中点G 与PQ 的中点'G 重合，由此得||||NQ PM =.…………………14分。

山师大附中高三数学（理）第二次模拟试题本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分。

第I 卷1至2页，第II 卷3至4页，答题纸5至7页，共150分。

测试时间120分钟。

第I 卷（共60分）一、选择题：（本大题共12小题。

每小题5分。

共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．设集合}2,1{=A ，则满足}3,2,1{=B A 的集合B 的个数为（ ） A ．1B ．3C ．4D ．82．已知ni im -=+11，其中n m ,是实数，i 是虚数单位，则=+ni m （ ）A ．i 21+B ．i 21-C ．i +2D ．i -23．已知23)2cos(=-ϕπ，且2||πϕ<，则=ϕtan （ ）A ．33-B ．33 C ．3- D ．34．设函数)0(ln 31)(>-=x x x x f ，则)(x f y =（ ）A ．在区间),1(),1,1(e e内均有零点 B ．在区间),1(),1,1(e e内均无零点C ．在区间)1,1(e 内有零点，在区间),1(e 内无零点D ．在区间)1,1(e内无零点，在区间),1(e 内有零点5．实数x 满足θsin 1log 3+=x ，则|9||1|-+-x x 的值为（ ）A ．8B ．8-C ．0D ．106．设函数)(x f 为定义在R 上的奇函数，当0≤x 时，b x x f x-+-=221)(（b 为常数），则=)1(f （ ）A ．3B ．1C ．3-D ．1-7．如果若干个函数的图象经过平移后能够重合，则称这些函数为“互为生成函数”。

给出下列函数①x x f cos sin )(-=；②)co s (s i n 2)(x x x f +=；③2si n 2)(+=x x f ；④.si n )(x x f =其中“互为生成函数”的是（ ）A ．①②B ．①③C ．③④D ．②④8．在ABC ∆内，内角C B A ,,的对边分别是c b a ,,，若bc b a 322=-，B C sin 32sin =，则A=（ ）A ．︒30B ．︒60C ．︒120D ．︒1509．已知a 是实数，则函数ax a x f sin 1)(+=的图象不可能是（ ）10．设命题:p 非零向量||||,,b a b a=是)()(b a b a -⊥+的充要条件；命题:q M 为平面上一动点，C B A ,,三点共线的充要条件是存在角α，使+=MB MA α2sin MC α2cos ，则（ ）A ．q p ∧为真命题B ．q p ∨为假命题C ．q p ∧⌝为假命题D ．q p ∨⌝为真命题11．已知二次函数),,()(2R c b a c bx ax x f ∈++=，满足：对任意实数x ，都有x x f ≥)(，且当)3,1(∈x 时，有2)2(81)(+≤x x f 成立，又0)2(=-f ，则b 为（ ）A ．1B ．21C ．2D ．012．若]2,2[,ππβα-∈，且0sin sin >-ββαα，则下面结论正确的是（ ）A ．βα>B ．0>+βαC ．βα<D ．22βα>第II 卷（非选择题 共90分）二、填空题：本大题共4个小题，每小题4分，共16分。