第三章有理数的运算复习导学案

有理数的加法三级导学案预习导学：预习目标：预习交流与发现1，自学有理数加法法则；预习重点：有理数加法法则。

预习难点：有理数加法法则。

预习流程：1、预习情景设置1，初步了解有理数加法原理；2、自主预习利用数轴探究有理数的加法法则；3、依据有理数的加法法则，自测例1；4、自主合作交流有理数加法法则；5、作自测练习；6、合作交流自学体会。

讲授导学：学习目标：1．经历探索有理数的加法法则的过程，理解有理数的加法法则。

2．能准确地运用有理数的加法法则进行有理数的加法运算。

教学重点：理解与运用有理数的加法法则教学难点：异号两数相加法则的理解。

教学方法：引导、实验、探究导入流程：一、导入新课：1．甲、乙两队进行足球比赛，如果甲队在主场以4：1赢了3球，在客场1：3输了2球，那么2场比赛甲队净胜球累计是多少？如果甲队在主场以1：4输了3球，在客场3：1赢了2球，那么甲队在这两场比赛中的净胜球累计又是多少？2．问：你能把上述过程用算式表示出来吗？规定赢球数记为正，输球数记为负，得算式：3+（—2），（—3）+23．揭示课题：有理数的加法二、预习检测：自学交流与发现1，作课本第35页练习题三，利用数轴探究有理数的加法法则；自主合作交流有理数加法法则，依据有理数的加法法则，自做例1；自测课本第35页练习题一、二。

合作交流结果并释疑。

三、课堂展示反馈自测练习；四、精讲点拨：做有理数的加法，不能总是用数轴或凭经验做啊。

有理数的加法运算有没有什么规律？下面来探索有理数加法法则。

思考：①前面所说，有理数加法中的加数不同，各有多少种形式，能否给它们归归类？三种情况：同号两数相加，异号加数相加，一个数与0相加②观察以上算式，有理数加法运算的结果与小学所学的加法运算的结果有什么不同？③如何确定和的符号？如何确定和的绝对值？以上三个问题层层递进，有序抛出，一个一个地解决，特别是第三个问题的解决，一定要让学生仔细观察算式中的加数与和的关系。

1.4.2 有理数的加减乘除混合运算学习目标：1．能够熟练掌握有理数加减乘除的四则混合运算.2．能解决有理数加减乘除混合运算应用题3．提高分析问题和解决问题的能力．学习重点：正确进行有理数的加、减、乘、除混合运算．学习难点：如何按有理数的加减乘除混合运算顺序正确而合理地进行计算． 学习过程：一、复习引入：1、口算速算．2、填表．（求各数的倒数）二、范例学习例1 （1）982-+÷-（） （2）438020-⨯--÷-（）（）（） （3）()282÷--针对练习：1．有理数的加减乘除混合运算，应先算 ，再算 ，同级运算按从 到 的顺序计算，如果有括号则先算 里的．2．下列计算正确的是（ ）． A.1-34-43⨯÷= B.91-32-65-32-=⨯）（）（ C.41-515-=÷）（ D.2-31-212=÷）（ 3．计算：（1））（）（5-75125-÷； （2））（41-85.52-⨯÷例2某公司去年1～3月平均每月盈利1.3万元，4～6月平均每月亏损3万元，7～10月平均每月盈利3.6万元，11～12月平均每月亏损2.7万元．这个公司去年总的盈亏情况如何？针对练习：4．某公式去年1~3月平均每月2.5万元，4~6月平均每月盈利-1万元，7～10月平均每月盈利4.5万元，11～12月平均每月盈利-1.5万元，那么这家公司去年平均每月盈利多少万元？五、课堂小结六、拓展提升思考：1、边长为a 的正方形的面积是多少？棱长为a 的正方体的体积是多少？2、观察(3)(3)(3)(3)-⨯-⨯-⨯-，22222()()()()()33333-⨯-⨯-⨯-⨯-，a a a a a ⨯⨯⨯⨯这些式子，你能发现他们有什么共同点吗？分别可以记作什么？七、布置作业1、必做题：课本37页习题1.4 1~7题2、选做题：课本38页习题1.4 8、9题。

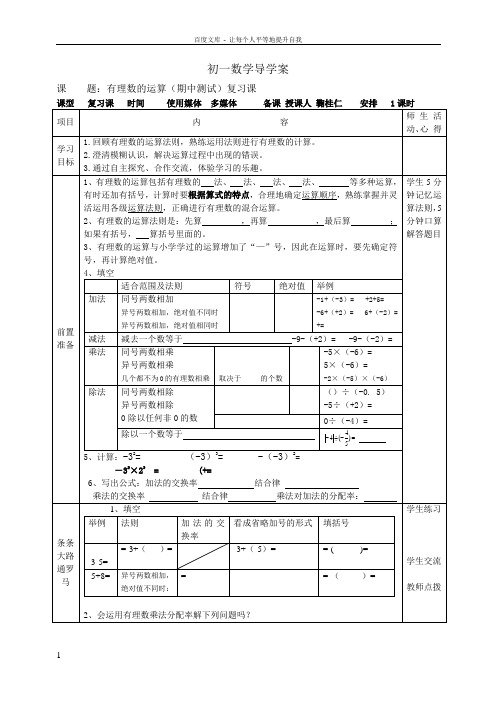
第三章《有理数的运算》复习一、导入激学a,b是两个有理数,完成下面的填空：（1)如果a—b=0，那么a与b的关系是．(2）如果a+b=0，那么a与b的关系是．(3）如果a×b=0,那么a与b的关系是．（4）如果a÷b=0,那么a与b的关系是．二、导标引学【复习目标】1、掌握有理数的有关知识2、学会有理数的基本运算3、巩固复习有理数的运算【复习重点】理解、掌握有理数的相关内容三、复习过程（一）导问互学1、本章我们学习了有理数的哪几种运算？2、根据有理数的加法和乘法的运算法则填写下表：3、利用相反数，有理数的减法可以转化为加法，法则是_______________________．这样，加减法统一成加法．利用倒数，有理数的除法可以转化为乘法，法则是__________________________．这样，乘除法统一成乘法．4、乘方是__________________________________________运算．5、有理数混合运算顺序是________________________________________________．6、有理数加法和乘法的运算律是常见的运算规律．请总结一下你所学过的运算律，并用字母将它们表示出来．7、科学记数法是科学技术上常用的一种记数方法，怎样将一个绝对值大于10的数用科学记数法表示？怎样将科学记数法表示的数写成原来的数？举例说明．解决问题评价：（二)导标达学1、一个有理数与它的相反数之商为，与它的倒数之积为．2、绝对值小于100的所有整数之和，绝对值小于100的所有整数之积．3、一个数是5,另一个数比5的相反数小—1，则这两个数的积为 .4、有一根10米长的绳子，第一次剪去一半,第2次剪去剩余的一半，……剪7次后，剩下的绳子有米．5、吸烟有害健康,全世界每年因吸烟引起的疾病致死的人数大约为600万，数据600万用科学记数法表示为6、两个数的和为正数,则这两个数（ )A 、都为正数B 一个正数,一个负数且正数的绝对值C 、一个为零，一个为正数D 、至少有一个为正数 7、计算（—2)100 +（—2)101所得结果是（ ）A 、210 0B 、-1C 、 —2D 、—210 08、计算：（1）)1279543(+--÷361 (2）|97|-÷2)4(31)5132(-⨯--（3）(－1)3－（1－21)÷3×[3―(―3）2］9、用简便方法计算：（1）)36()436597(-⨯+- (2) 25×(43―21－41)反馈评价： 四、导法慧学1.将所学知识纳入知识体系.2.本节解决问题的具体方法是怎样的？据此请总结此类问题的解题思路。

有理数的运算复习教学设计教学方法和手段1、教学方法基于本节课的特点，在教学中主要采用自主探究合作交流教学法。

师生互动、自主探究、小组合作、类比学习等。

2、教学手段由于本节课主要以复习提升能力为主，信息量很大，因此制作了课件，设计形象具体，增加课堂教学的信息容量，保证学生的活动空间和思维空间，努力提高课堂效率。

课前复习 1、有理数的加法、减法、乘法、除法及乘方法则 2、加法、乘法运算律3、科学记数法，会按要求取一个数的近似数。

教学过程教 学 过 程设计意图教 学 内 容教师导拨与学生活动教学 用具（一）复习巩固1、有理数的加法、减法、乘法、除法及乘方法则2、加法、乘法运算律3、科学记数法，会按要求取一个数的近似数。

老师向学生展示复习的问题，小组合作交流大屏幕展示通过小组合作的学习方式，激发学生的学习兴趣，总结自己的进步，反思不足，及需要改进的地方。

（二）改错探究1．74－4÷2＝70÷2＝352.教师及时发现学生的困惑和不足，大屏幕展通过例题的交流，让学生从观察和探究中发现规律，教师加以引导与启发，并鼓励教 学 过 程设计意图教 学 内 容教师导拨与学生活动 教学 用具3.4.引导学生改正。

学生板演，并指出错误，做好归纳总结。

学生互相交流，教师及时归纳。

示学生用自己的语言表述，让学生归纳与总结错误出现的原因，及时纠正错误，从而提高学生的表达能力与数学语言的组织能力。

（三）尝试初步运用 牛刀小试1.5－2×(－3)让学生在导学案上完成，小组合作交流，分析问题，发现解答中存在的问题，并解决问题。

大屏幕展示通过此题的分析,引导学生在进行有理数混合运算时,遵循观察、思考、动笔、检查的程序进行计算,有助于培养学生严谨的学风和良好的学习习惯.（四）精讲点拨教 学 过 程设计意图教 学 内 容教师导拨与学生活动 教学 用具1.计算(-2)2-(-52)×(-1)5+87÷(-3)×(-1)42.用简便方法计算：3.用科学记数法表示：据估计我国药用牡丹栽培约175500000株（精确到千位）1. 2 3. 4.学生板演，并到板前讲解注意事项，教师对学生没有注意到的关键点加以说明。

2.6《有理数加减混合运算》（三）导学案主备人: 审核人：教师寄语：理论与实践的结合是提升我们的数学应用能力的最佳途径.学习目标：1、知识与技能：经历将一些实际问题抽象成为有理数的加减混合运算的过程,体会数学与现实生活的密切联系。

2、过程与方法：能综合运用有理数及其加法,减法的有关知识解决简单的实际问题。

3、情感态度与价值观：在独立思考的基础上,积极参与对数学问题的讨论,敢于发表自己的观点,并尊重与理解他人的见解,能从交流中获益。

复习旧知：计算⑴8﹢(-3)+ (-5)⑵0.95+(-1.8)+(-0.2)-2.65⑶7.25-2(1\3)-27.75+(-7(2\3)⑷ 3.5-(-(1\2)+(5\2)-0.25学习过程：一、创设情境：课本P47一条河流在枯水期的水位图：年平均水位为0米，现在水位为-3米，小康桥桥面据年平均水位12.5米，此时小康桥面局水面的高度为多少米?小颖：12.5-（-0.3）=12.8（米）小明：12.5+0.3=12.8（米）你知道小颖和小明分别是怎么想的吗？他们的结果为什么相同？二、自主学习自学课本第47页三、自学交流：看书思考p47如何表示水位的高低变化.1水位的高低与“+”“-”的关系是什么?2感受如何把实际问题转化成数学问题水位变化转化为加减混合运算3认识折线统计图的构造及意义------合作交流-----学生发表见解①在水位表示中正数.负数的意义是什么?②求周末的水位的方法是什么?③说说折线统计图的特征,你如何画折线统计图?四、释疑训练1、-(1\3)-(-3(1\2))+(-2(1\4))-(+5(1\6))2、-|-(1\2)+|-(1\3)|-|-0|-(-(1\4))-(-1\9)五、归纳总结1、把实际问题转化为数学问题-----体验数学转化的思想和方法.2、符号的处理方法.3、①你学习了那些知识.②感受了哪些问题类型和方法.课后练习1、若摩托车厂T本周计划能生产４５０辆摩托车．由于工人实行轮休，每次上班人数不一定相等．实行每日生产量与计划量相比情况如下表（增加的辆数为正，减少的辆数为负）星期一二三四五六七增减数－５＋７－３＋４＋１０－９－２５①根据纪录可知，本周三生产了＿＿＿辆．本周总生产量与计划辆数对比增减数为＿＿＿辆．产量最多的一天比产量最少的一天多生产了＿＿＿辆．②用折线统计图表示本周七天的生产情况课后反思。

2012—2013年上期 七年级 数学 导学案 第 课时 编案教师：谢光红 审核：陈勇 审批：殷长贵 授课教师：初一全体数学教师 授课时间： 班级： 姓名： 教师评价：第1页/（共4页） 第2页/（共4页）有理数的概念复习学案学习目标：1、巩固、理解与有理数有关的概念2、运用相关概念解决问题。

学习重点：有理数概念的正确理解与辨析。

学习难点：正确运用相关概念解决问题。

教学方法：归纳与练习相结合 探究点一：知识要点精析： 1、有理数的分类： （1） （2）注意：（1）0既不是正数，也不是负数。

（2）π和无限不循环小数不是有理数 2、数轴：（1）数轴的三要素：（2）数轴上，原点右边表示的数是 ，原点左边表示的数是 ，原点表示的数是 。

（3）在数轴上表示的数，右边的总比左边的 。

注意：所有的有理数都可以用数轴上的一个点表示，但反过并不是数轴上的所有点都表示有理数。

3、相反数：（1）只有 不同的两个数叫做互为相反数。

（2）ɑ的相反数记作 ，ɑ－b 的相反数是 。

（3）正数的相反数是 ，负数的相反数是 ，0的相反数是 。

（4）互为相反数的两个数之和是 。

（5）互为相反数的两个数在数轴上表示的点到原点的距离 。

4、绝对值：（1）几何意义：表示数ɑ的点与原点的距离叫做ɑ的 ，记作|ɑ|。

（2）代数意义：（3）绝对值的非负性：|ɑ| 0；注意：（1）绝对值等于本身的数是 （2）绝对值等于它的相反数是 （3）绝对值相等的两个数的关系是 （4）常见的非负数形式：①|ɑ|≥0→2|ɑ|≥0，21|ɑ|≥0，|ɑ|＋2≥2。

②ɑ2≥0→5ɑ2≥0，57ɑ2≥0，ɑ2＋1≥1。

探究点二：典例精析 1、辨析：（1）带“－”号的数一定是负数（ ） （2）－ɑ一定是负数（ ） （3）零是最小的非负整数（ ） （4）有理数不是整数就是分数（ ）（5）在数轴上离原点越远的点，所表示的有理数越大（ ） （6）表示m 的点在表示一个4m 的点的右边（ ）（7）若一个数的相反数不是负数，那么这个数一定是负数（ ） （8）若ɑ＞0，b ＜0，且|ɑ|＞|b |，则－ɑ＞b （ ） （9）一个有理数的绝对值必为正数（ ） （10）若|ɑ|＝|b |，则ɑ＝b （ ） 2、解答例1：把下列各数填入相应的集合里有理数正有理数正整数整数有理数（统称有限小数和无限循环小数）|ɑ| （ɑ＝0）（ɑ＜0） （ɑ＞0）·第3页/共4页 第4页/共4页导学案装 定线一12，0，2，0.3，一0.5，一（一7），一|一21|，（一1）2，0.45，25，5%，（一2）3，正数集合（ ） 负数集合（ ） 分数集合（ ） 整数集合（ ） 非负数集合（ ） 非负有理数集合（ ） 非负整数集合（ ）例2：已知有理数ɑ，b ，c 在数轴上位置如图所示：用“＜”号把ɑ，一ɑ，一b ，b ，c ，一c ，0连接起来。

有理数复习导学案学习目标:掌握有理数的加、减、乘、除、乘方的运算法则，能进行有理数的加、减、乘、除、乘方的运算和简单的混合运算；教学重难点:绝对值的概念和有理数的运算（包括法则、运算律、运算顺序、混合运算）是本章的重点。

学习过程：一、典型例题例题1：将下列数分别填入相应的集合中：正数集合：{ } 整数集合：{ } 分数集合：{ } 负数集合：{ }例题2：选择（1）.已知x是绝对值最小的有理数，y是最大的负整数，则代数式x3+3x3y+3xy2+y3的值是( )A.0B.1C.-3D.-1（2）.已知三个数在数轴上对应点的位置如图所示，下列几个判断:①；②; ③; ④中，错误的个数是（）个A.1B.2C.3D.4（3）.如果知道a与b互为相反数，且x与y互为倒数，那么代数式|a + b|-2xy的值为（）A.0B.-2C.-1D.无法确定例题3 计算1、2、3 （4）－1+(－)×(－2)二、课堂练习1.计算所得的结果是（）A、0B、32C、D、162. 有理数中倒数等于它本身的数一定是（）A、1B、0C、-1D、±13. 若，则=（）A、– 1B、1C、0D、34. 有理数a，b如图所示位置，则正确的是（）A、a+b>0B、ab>0C、b-a<0D、|a|>|b|5.计算：1、____；=____；____；____ _。

2. _________；（2）三、学生共同总结，调动学生的主动参与意识，再一次突出本节课的学习重点．本节课我们复习了哪些知识？你有什么收获？。

《有理数》导学案一、学习目标1、理解有理数的概念，包括正有理数、零和负有理数。

2、掌握有理数的分类方法，能准确对给定的数进行分类。

3、理解数轴的概念，能用数轴上的点表示有理数，能借助数轴比较有理数的大小。

4、掌握相反数和绝对值的概念及性质，能求一个数的相反数和绝对值。

二、学习重难点1、重点（1）有理数的分类。

（2）数轴的概念及应用。

（3）相反数和绝对值的概念及计算。

2、难点（1）对负数概念的理解。

（2）利用数轴比较有理数的大小。

（3）绝对值的性质及应用。

三、知识梳理1、有理数的概念整数和分数统称为有理数。

整数包括正整数、零和负整数；分数包括正分数和负分数。

例如：5 是正整数，－3 是负整数，0 既不是正数也不是负数；1/2是正分数，－3/4 是负分数。

2、有理数的分类（1）按定义分类：有理数分为整数和分数。

整数分为正整数、零和负整数；分数分为正分数和负分数。

（2）按性质分类：有理数分为正有理数、零和负有理数。

正有理数分为正整数和正分数；负有理数分为负整数和负分数。

3、数轴（1）定义：规定了原点、正方向和单位长度的直线叫做数轴。

（2）数轴的三要素：原点、正方向、单位长度。

（3）数轴上的点与有理数的关系：数轴上的点与有理数一一对应。

例如：在数轴上，原点表示 0，原点右边的点表示正数，原点左边的点表示负数。

4、相反数（1）定义：只有符号不同的两个数叫做互为相反数。

（2）性质：互为相反数的两个数的和为 0。

例如：5 的相反数是－5，－5 的相反数是 5，5 ＋（－5) ＝ 0。

5、绝对值（1）定义：一般地，数轴上表示数 a 的点与原点的距离叫做数 a的绝对值，记作｜a|。

（2）性质：正数的绝对值是它本身；负数的绝对值是它的相反数；0 的绝对值是 0。

例如：｜5| ＝ 5，｜－3| ＝ 3，｜0| ＝ 0。

四、典型例题例 1：把下列各数分别填入相应的集合里。

－5，0，－314，22/7，2021，－13，***********…（每两个 1 之间依次多一个 0）正数集合：｛ 22/7，2021，***********…｝负数集合：｛－5，－314，－13 ｝整数集合：｛－5，0，2021，－13 ｝分数集合：｛－314，22/7 ｝例 2：画出数轴，并用数轴上的点表示下列各数：－3，0，2，－15，5/2解：首先画出数轴，确定原点、正方向和单位长度。