滚动轴承故障诊断(附MATLAB程序)

1．数据导入matlab1.1启动Matlab软件1.2点击载入故障数据中的G2015，Workspace窗口出现：1.3取第一组数据G201，命令窗口输入：G201=G2015(1:1:20000);2. 数据预处理在测试中由数据采集所得的原始信号，在分析前需要进行预处理，以提高数据的可靠性和真实性，并检查信号的随机性，以便正确地选择分析处理方法。

预处理工作主要包括三个方面：一是除去信号中的外界干扰信号和剔除异常数据，如趋势项和异点；二是对原始数据进行适当的平滑或拟合；三是对原始信号的特性进行检验。

当然这些处理工作不是全部必需的，可以选—项或两项容，当认为原始信号获取工作十分可靠或原始数据简单可以直接判断的情况下，也可以不进行这些预处理工作。

以下所做数据预处理，故障轴承以G201为例，正常轴承以Z201为例，观察原始数据经过不同方法做处理前后的变化。

1.1零均值化处理（原理公式见报告P8）命令窗口输入：G201l=G201-sum(G201)/20000;%G201l为零均值处理后的数据。

“20000”为采样点数。

sum为求和语句subplot(2,1,1),plot(G201);subplot(2,1,2),plot(G201l);%显示G201与G201l 得到下面图形：从时域图形上看，是波形整体在Y轴的平移。

再看看频域变化，命令窗口输入：N=20000; %采样点数fs=10000; %采样频率f=(0:N-1)'*fs/N; %进行对应的频率转换G201p=abs(fft(G201)); %进行fft变换，G201p为G201进行fft变换后结果G201lp=abs(fft(G201l)); %进行fft变换，G201lp为G201l进行fft变换后结果subplot(2,1,1),plot(f(1:N/2),G201p(1:N/2));subplot(2,1,2),plot(f(1:N/2),G201lp(1:N/2 )); %显示G201与G201p的频谱图得到下面图形：ω处出现一个由直流分量产生的大谱峰（将从频域图可以明显看出，零均值后消除0=近达到45.4⨯），处理后避免了其对周围小峰值产生的负面影响，便于频域分析。

实用标准课程名称：机械故障诊断设计题目：基于FFT的轴承故障诊断学院：机械工程系班级：学号：姓名：指导老师：李奕璠2017年12月23日摘要滚动轴承是旋转机械中重要的零件，以往的动检工作对滚动轴承强烈振动原因分析不足，不能满足设备维修工作的需要。

所以要定期对旋转机械进行动态监测，根据所测数据做出诊断分析，及时发现滚动轴承强烈震动情况。

傅里叶变换在故障诊断技术中是重要的工具，但傅里叶变换及其逆变换都不适合数字计算机计算，要进行数字计算机处理，必须将连续性信号离散化，无限长数据有限化，再进行采样和截断。

这种算法称为有限离散傅里叶变换（DFT），为了提高效率，在DFT的基础上，运用快速傅里叶变换（FFT）对滚动轴承进行故障诊断。

通过FFT方法分析轴承的信号图，对滚动轴承振动的产生原因进行深入分析，不断总结经验，提高故障分析能力，掌握造成滚动轴承强烈振动的原因，及时消除振动，为设备安全提供可行性措施。

关键词：滚动轴承；故障诊断； FFT23第1章 绪论1.1 滚动轴承概述滚动轴承（rolling bearing ）是将运转的轴与轴座之间的滑动摩擦变为滚动摩擦，从而减少摩擦损失的一种精密的机械元件。

滚动轴承一般由内圈、外圈、滚动体和保持架四部分组成，内圈的作用是与轴相配合并与轴一起旋转；外圈作用是与轴承座相配合，起支撑作用；滚动体是借助于保持架均匀的将滚动体分布在内圈和外圈之间，其形状大小和数量直接影响着滚动轴承的使用性能和寿命；保持架能使滚动体均匀分布，引导滚动体旋转起润滑作用。

图1 滚动轴承结构滚动轴承是各类旋转机械中最常用的通用零件之一，也是旋转机械易损件之一。

据统计，旋转机械的故障越有30%是由轴承故障引起的，它的好坏对机械的工作状况影响很大。

轴承的缺陷会导致机器剧烈振动和产生噪声，甚至会引起设备的损坏。

因此，对重要用途的轴承进行工况检测与故障诊断是非常必要的。

1.2 本次任务本次总共给出了4组通过现场测试得到的滚动轴承运行数据，包括1组正常轴承数据，1组内圈故障数据，1组外圈故障数据，1组滚动体故障数据。

基于支持向量机（SVM）的齿轮箱轴承故障识别一、轴承故障诊断1、概述轴承是旋转设备的一个重要部件，它提供重要的负载承受能力，以支撑转子系统抵抗静态的和动态的外力。

轴承构件，由于它的使用寿命长、负载能力高、能量损失低而被广泛应用于工业和公用设施，是大型机械装备(包括动力机械、机车车辆、泵与风机等)中的关键部件。

高速运转的大型机械装备，其轴承的载荷重且为交变载荷，而且工作环境恶劣，经常发生轴承性能劣化和损坏，影响整个装置的安全可靠性，一旦出现故障将导致严重的损失，有必要对轴承工作状态进行模式识别与诊断。

轴承根据工作的摩擦性质不同可分为滑动摩擦轴承（简称滑动轴承）和滚动摩擦轴承（简称滚动轴承）两大类。

本文所测得的数据来自实验室齿轮箱的滑动轴承，滑动轴承的特点有：(1)在高速重载下能正常工作，寿命长。

(2)精度高。

(3)滑动轴承可做成剖分式的，能满足特殊结构的需要。

(4)液体摩擦轴承具有很好的缓冲和阻尼作用，可以吸收震动，缓和冲击。

(5)滑动轴承的径向尺寸比滚动轴承的小。

(6)起动摩擦阻力较大。

通过对轴承进行故障诊断有以下优势：(1)早期预报、防止事故发生，降低事故发生率;(2)预知性维修，提高设备管理水平，降低维修费用，减少维修时间，增加运行时间;(3)提高设备的设计、制造水平，改进产品质量;(4)确定复杂机器的最佳工作参数，提高效率;(5)降低噪声，泄露等污染，保护环境。

2、滑动轴承失效形式（1）磨粒磨损进入轴承间隙的硬颗粒（如灰尘、砂粒等），在起动、停车或轴颈与轴承发生边缘接触时，都将加剧轴承磨损，导致几何形状改变、精度丧失，轴承间隙加大，使轴承性能在预期寿命前急剧恶化。

（2）刮伤进入轴承间隙中的硬颗粒或轴颈表面粗糙的轮廓峰顶，在轴承上划出线状伤痕，导致轴承因刮伤失效。

（3）咬合（胶合）当轴承温升过高，载荷过大，油膜破裂时，或在润滑油供应不足条件下，轴颈和轴承的相对运动表面材料发生粘附和迁移，从而造成轴承损坏。

滚动轴承故障诊断滚动轴承是应用最为广泛的机械零件质疑，同时，它也是机器中最容易损坏的元件之一。

许多旋转机械的故障都与滚动轴承的状态有关。

据统计，在使用滚动轴承的旋转机械中，大约有30%的机械故障都是由于轴承而引起的。

可见，轴承的好坏对机器工作状态影响极大。

通常，由于轴承的缺陷会导致机器产生振动和噪声，甚至会引起机器的损坏。

而在精密机械中（如精密机床主轴、陀螺等），对轴承的要求就更高，哪怕是在轴承上有微米级的缺陷，都会导致整个机器系统的精度遭到破坏。

最早使用的轴承诊断方法是将听音棒接触轴承部位，依靠听觉来判断轴承有无故障。

这种方法至今仍在使用，不过已经逐步使用电子听诊器来替代听音棒以提高灵敏度。

后来逐步采用各式测振仪器、仪表并利用位移、速度或加速度的均方根值或峰峰值来判断轴承有无故障。

这可以减少对设备检修人员的经验的依赖，但仍然很难发现早期故障。

随着对滚动轴承运动学、动力学的深化研究，对轴承振动信号中频率成分和轴承零件的几何尺寸及缺陷类型的关系有了比较清楚的了解，FFT级数的发展也使得利用频率域分析和检测轴承故障成为一种有效的途径。

也是目前滚动轴承监测诊断的基础。

从发展的历程看，滚动轴承故障检测诊断技术大致经历了以下阶段：1961年，W.F.Stokey完成了轴承圈自由共振频率公式的推导，并发表；1964年，O.G.Gustafsson研究了滚动轴承振动和缺陷、尺寸不均匀及磨损之间的关系，这与目前诊断滚动轴承故障的方法是基本一致的；1969年，H.L.Balderston根据滚动轴承的运动分析得出了滚动轴承的滚动体在内外滚道上的通过频率和滚动体及保持架的旋转频率的计算公式。

至此，有关滚动轴承监测诊断的理论体系已经基本完成；1976年，日本新日铁株式会社研制了MCV-021A机器检测仪，其方法是通过检测低频、中频和高频段轴承的信号特征来判断轴承的工作状态；1976～1983年之间，日本精工公司也积极在滚动轴承检测仪器方面做工作，相继推出了NB系列轴承检测仪，利用1～15kHz范围内的轴承振动信号的有效值（rms）和峰峰值（p－p）来诊断轴承的故障；1980年代至今，以改良频率分析的方法来精密诊断滚动轴承的故障、确定故障位置，一直是精密诊断采取的必备方法，其中包括细化谱分析、倒频谱分析、共振解调技术、包络分析技术等。

1．数据导入matlab载入故障数据中的G2015，Workspace窗口出现：1.3取第一组数据G201，命令窗口输入：G201=G2015(1:1:20000);2. 数据预处理在测试中由数据采集所得的原始信号，在分析前需要进展预处理，以提高数据的可靠性和真实性，并检查信号的随机性，以便正确地选择分析处理方法。

预处理工作主要包括三个方面：一是除去信号中的外界干扰信号和剔除异常数据，如趋势项和异点；二是对原始数据进展适当的平滑或拟合；三是对原始信号的特性进展检验。

当然这些处理工作不是全部必需的，可以选—项或两项容，当认为原始信号获取工作十分可靠或原始数据简单可以直接判断的情况下，也可以不进展这些预处理工作。

以下所做数据预处理，故障轴承以G201为例，正常轴承以Z201为例，观察原始数据经过不同方法做处理前后的变化。

1.1零均值化处理〔原理公式见报告P8〕命令窗口输入：G201l=G201-sum(G201)/20000;%G201l为零均值处理后的数据。

“20000〞为采样点数。

sum为求和语句subplot(2,1,1),plot(G201);subplot(2,1,2),plot(G201l);%显示G201与G201l 得到下面图形：从时域图形上看，是波形整体在Y轴的平移。

再看看频域变化，命令窗口输入：N=20000; %采样点数fs=10000; %采样频率f=(0:N-1)'*fs/N; %进展对应的频率转换G201p=abs(fft(G201)); %进展fft变换，G201p为G201进展fft变换后结果G201lp=abs(fft(G201l)); %进展fft变换，G201lp为G201l进展fft变换后结果subplot(2,1,1),plot(f(1:N/2),G201p(1:N/2));subplot(2,1,2),plot(f(1:N/2),G201lp(1:N/2 )); %显示G201与G201p的频谱图得到下面图形：ω处出现一个由直流分量产生的大谱峰〔将从频域图可以明显看出，零均值后消除0=近达到4105.4⨯〕，处理后防止了其对周围小峰值产生的负面影响，便于频域分析。

第二组实验轴承故障数据：数据打开后应采用X105_DE_time作为分析数据，其他可作为参考，转速1797rpm轴承型号：6205-2RS JEM SKF, 深沟球轴承采样频率：12k Hz1、确定轴承各项参数并计算各部件的故障特征频率通过以上原始数据可知次轴承的参数为：轴承转速r=1797r/min；滚珠个数n=9；滚动体直径d=；轴承节径D=39mm；：滚动体接触角α=0由以上数据计算滚动轴承不同部件故障的特征频率为：外圈故障频率f1=r/60 * 1/2 * n(1-d/D *cosα)=内圈故障频率f2=r/60 * 1/2 * n(1+d/D *cosα)=滚动体故障频率f3=r/60*1/2*D/d*[1-(d/D)^2* cos^2(α)]=保持架外圈故障频率f4=r/60 * 1/2 * (1-d/D *cosα)=2.对轴承故障数据进行时域波形分析将轴承数据导入MATLAB中直接做FFT分析得到时域图如下：并求得时域信号的各项特征：（1）有效值：；（2）峰值：；（3）峰值因子：；（4）峭度：；（5）脉冲因子：；（6）裕度因子：：3.包络谱分析对信号做EMD模态分解，分解得到的每一个IMF信号分别和原信号做相关分析，找出相关系数较大的IMF分量并对此IMF分量进行Hilbert变换。

由图中可以看出经过EMD分解后得到的９个IMF分量和一个残余量。

IMF分量分别和原信号做相关分析后得出相关系数如下：由上表得：IMF1的相关系数明显最大，所以选用IMF1做Hilbert包络谱分析。

所得Hilbert包络谱图如下：对包络谱图中幅值较大区域局部放大得到下图由以上包络图的局部放大图中可以看出包络图中前三个峰值最大也最明显，三个峰值频率由小到大排列分别为、、。

把这三个频率数值和前文计算所得的理论值进行比较可知：频率值最大为和内圈的故障理论计算特征频率f2=相近，说明此轴承的故障发生在轴承的内圈。

滚动轴承故障诊断滚动轴承故障诊断初步1、故障原因滚动轴承的早期故障是滚⼦和滚道剥落、凹痕、破裂、腐蚀和杂物嵌⼊。

即主要故障形式：疲劳剥落、磨损、塑性变形、锈蚀、断裂、胶合、保持架损坏。

产⽣主要原因包括搬运粗⼼、安装不当、不对中、轴承倾斜、轴承选⽤不正确、润滑不⾜或密封失效、负载不合适以及制造缺陷。

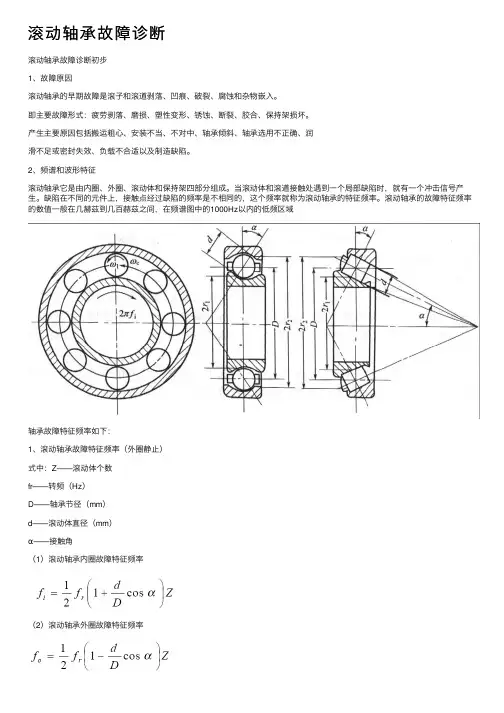
2、频谱和波形特征滚动轴承它是由内圈、外圈、滚动体和保持架四部分组成。

当滚动体和滚道接触处遇到⼀个局部缺陷时，就有⼀个冲击信号产⽣。

缺陷在不同的元件上，接触点经过缺陷的频率是不相同的，这个频率就称为滚动轴承的特征频率。

滚动轴承的故障特征频率的数值⼀般在⼏赫兹到⼏百赫兹之间，在频谱图中的1000Hz以内的低频区域轴承故障特征频率如下：1、滚动轴承故障特征频率（外圈静⽌）式中：Z——滚动体个数fr——转频（Hz）D——轴承节径（mm）d——滚动体直径（mm）α——接触⾓（1）滚动轴承内圈故障特征频率（2）滚动轴承外圈故障特征频率（3）滚动轴承滚动体特征频率（4）滚动轴承保持架特征频率2、滚动轴承故障特征频率的计算经验公式：⼆、滚动轴承故障诊断的要素滚动轴承由内圈、外圈、滚动体和保持架四部分组成，每个轴承部件对应⼀个轴承故障特征频率。

滚动轴承的故障频率分布有⼀个明显的特点，往往在低频和⾼频两个频段内都有表现。

所以在频率分析时，可以选择在这两个频段进⾏分析。

根据滚动轴承的故障形式在频域中的表现形式，将整个频域分为三个频段，既⾼频段、中频段和低频段。

l ⾼频阶段指频率范围处于2000－5000Hz 的频段，主要是轴承固有频率，在轴承故障的早期，⾼频段反映⽐较敏感；中频阶段指频率范围处于800－1600Hz 的频段，⼀般是由于轴承润滑不良⽽引起碰磨产⽣的频率范围；l 低频阶段指频率范围处于0－800Hz 的频段，基本覆盖轴承故障特征频率及谐波；在⾼频段和低频段中所体现的频率是否为轴承故障频率，还要通过其他⽅法进⾏印证加以确认。

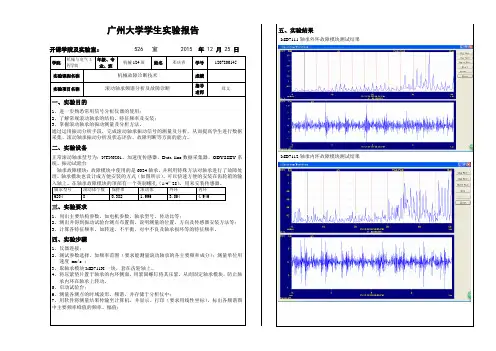
广州大学学生实验报告开课学院及实验室： 526 室2015年 12月25日学院机械与电气工程学院年级、专业、班机械124班姓名邓庆青学号1207200145实验课程名称机械故障诊断技术成绩实验项目名称滚动轴承频谱分析及故障诊断指导老师郑文一、实验目的1、进一步熟悉常用信号分析仪器的使用；2、了解常规滚动轴承的结构、特征频率及安装；3、掌握滚动轴承的振动测量及分析方法。

通过运用振动分析手段，完成滚动轴承振动信号的测量及分析，从而提高学生进行数据采集、滚动轴承振动分析及状态评估、故障判断等方面的能力。

二、实验设备正常滚动轴承型号为：NTN6201、加速度传感器、Data line数据采集器、ODYSSEY系统、振动试验台轴承故障模块：故障模块中使用的是6024轴承，并利用特殊方法对轴承进行了故障处理。

轴承模块也设计成方便安装的方式（如图所示），可以快速方便的安装在齿轮箱的输入轴上。

在轴承故障模块的顶部有一个英制螺孔（1/4”-28），用来安装传感器。

轴承型号滚动体个数保持架滚动体外环内环6204 8 0.382 1.996 3.054 4.946三、实验要求1、列出主要结构参数，如电机参数、轴承型号、传动比等；2、测出并得到振动试验台测点布置图，说明测量的位置、方向及传感器安装方法等；3、计算各特征频率，如转速，不平衡、对中不良及轴承损坏等的特征频率。

四、实验步骤1、仪器连接；2、测试参数选择，如频率范围（要求能测量滚动轴承的各主要频率成分）；测量单位用速度 mm/s ；3、取轴承模块MD711X一块，套在齿轮轴上。

4、将压紧垫片置于轴承的内环侧面，用紧固螺钉将其压紧，从而固定轴承模块，防止轴承内环在轴承上转动。

5、启动试验台；6、测量各测点的时域波形、频谱，并存储于分析仪中；7、用软件将测量结果传输至计算机，并显示、打印（要求用线性坐标），标出各频谱图中主要频率峰值的频率、幅值；五、实验结果MD7111轴承外环故障模块测试结果MD7112轴承内环故障模块测试结果MD7113轴承滚动体故障模块的测试结果MD7114轴承保持架故障模块的测试结果六、分析1、测量对象的结构简图2、计算滚动轴承的特征频率外环fi=Zn/2（1-dcos fi=Zn/2（1-dcosąß/D）ß--接触角fo--外环频率内环fo=Zn/2（1+dcos ß /D）fb--滚动体频率f--保持架频率保持架f=n/2（1-dcos ß /D）d--滚动体直径D--节园直径滚动体fb=D/2d（1-d²cos² ß /D）Z--滚动体数n--轴频3、综合判断滚动轴承的运行状态及存在的问题。

作业名称：傅里叶分析滚动轴承的故障诊断院系：机械工程系学号：姓名：指导教师：20XX年XX月XXXXXXXXX校区傅里叶分析滚动轴承的故障诊断摘要：简要介绍了快速傅里叶变换（FFT）在滚动轴承故障分析中的应用，滚动轴承在机械设备中使用非常广泛，其工作状态直接影响整个设备的运行品质。

对滚动轴承进行状态监测与故障诊断，能够避免重大事故的发生，获得较大的经济和社会效益。

通过快速傅里叶变换（FFT）对滚动轴承运行时的实时数据信号进行分析，可以实现对滚动轴承的状态监测和故障诊断。

同时，采用对正常轴承和故障轴承信号对比分析、各种故障轴承之间信号的对比分析，加深了快速傅里叶变换（FFT）对轴承实时信号分析的运用和理解，能够更好的对轴承进行状态监测和故障分析。

关键词：快速傅里叶变换（FFT）；滚动轴承；故障诊断；状态监测Abstract:This paper describes a fast Fourier transform (FFT) in the rolling bearing failure analysis applications, bearing in machinery and equipment is widely used, and its working status directly affects the quality of the operation of the entire device. Rolling element bearing condition monitoring and fault diagnosis, able to avoid major accidents and achieve greater economic and social benefits. Through Fast Fourier Transform (FFT) for real-time data bearing signal runtime analysis can be achieved on the rolling bearing condition monitoring and fault diagnosis. Meanwhile, the use of normal bearings and bearing fault signal comparative analysis of various fault signals comparative analysis between the bearings and deepened the fast Fourier transform (FFT) of the bearing using real-time signal analysis and understanding of the bearing can be better condition monitoring and fault analysis.Keywords: fast Fourier transform (FFT); Rolling; fault diagnosis; condition monitoring一、概述通过对快速傅里叶变换（FFT）的原理的理解和学习，利用MATLAB软件编程应用快速傅里叶变换（FFT）的方法，对滚动轴承的1组正常数据和2组故障数据（故障类型不同）进行信号分析和处理，并对正常轴承和故障轴承信号对比分析、各种故障轴承之间信号的对比分析，并得出结论，实现对滚动轴承的状态监测和故障分析。

滚动轴承故障诊断初步1、故障原因滚动轴承的早期故障是滚子和滚道剥落、凹痕、破裂、腐蚀和杂物嵌入。

即主要故障形式：疲劳剥落、磨损、塑性变形、锈蚀、断裂、胶合、保持架损坏。

产生主要原因包括搬运粗心、安装不当、不对中、轴承倾斜、轴承选用不正确、润滑不足或密封失效、负载不合适以及制造缺陷。

2、频谱和波形特征滚动轴承它是由内圈、外圈、滚动体和保持架四部分组成。

当滚动体和滚道接触处遇到一个局部缺陷时，就有一个冲击信号产生。

缺陷在不同的元件上，接触点经过缺陷的频率是不相同的，这个频率就称为滚动轴承的特征频率。

滚动轴承的故障特征频率的数值一般在几赫兹到几百赫兹之间，在频谱图中的1000Hz以内的低频区域轴承故障特征频率如下：1、滚动轴承故障特征频率（外圈静止）式中：Z——滚动体个数fr——转频（Hz）D——轴承节径（mm）d——滚动体直径（mm）α——接触角（1）滚动轴承内圈故障特征频率（2）滚动轴承外圈故障特征频率（3）滚动轴承滚动体特征频率（4）滚动轴承保持架特征频率2、滚动轴承故障特征频率的计算经验公式：二、滚动轴承故障诊断的要素滚动轴承由内圈、外圈、滚动体和保持架四部分组成，每个轴承部件对应一个轴承故障特征频率。

滚动轴承的故障频率分布有一个明显的特点，往往在低频和高频两个频段内都有表现。

所以在频率分析时，可以选择在这两个频段进行分析。

根据滚动轴承的故障形式在频域中的表现形式，将整个频域分为三个频段，既高频段、中频段和低频段。

l 高频阶段指频率范围处于2000－5000Hz 的频段，主要是轴承固有频率，在轴承故障的早期，高频段反映比较敏感；中频阶段指频率范围处于800－1600Hz 的频段，一般是由于轴承润滑不良而引起碰磨产生的频率范围；l 低频阶段指频率范围处于0－800Hz 的频段，基本覆盖轴承故障特征频率及谐波；在高频段和低频段中所体现的频率是否为轴承故障频率，还要通过其他方法进行印证加以确认。

根据滚动轴承的故障特征频率在频域和时域中的表现，可将滚动轴承的诊断方法总结为三个频段；八个确认，简称三八诊断法。

滚动轴承故障诊断现代工业通用机械都配备了相当数量的滚动轴承。

一般说来，滚动轴承都是机器中最精密的部件。

通常情况下，它们的公差都保持在机器的其余部件的公差的十分之一。

但是，多年的实践经验表明，只有10%以下的轴承能够运行到设计寿命年限。

而大约40%的轴承失效是由于润滑引起的故障，30%失效是由于不对中或“卡住”等装配失误，还有20%的失效是由过载使用或制造上缺陷等其它原因所致。

如果机器都进行了精确对中和精确平衡，不在共振频率附近运转，并且轴承润滑良好，那么机器运行就会非常可靠。

机器的实际寿命也会接近其设计寿命。

然而遗憾的是，大多数工业现场都没有做到这些。

因此有很多轴承都因为磨损而永久失效。

你的工作是要检测出早期症状并估计故障的严重程度。

振动分析和磨损颗粒分析都是很好的诊断方法。

故障轴承会产生与1X基频倍数不完全相同的振动分量——换言之，它们不是同步的分量。

对振动分析人员而言，如果在振动频谱中发现不同步分量那么极有可能是轴承出现故障的警告信号。

振动分析人员应该马上诊断并排除是否是其它故障引起的这些不同步分量。

(非转频的倍数峰值疑似为故障信息)如果看到不同步的波峰，那极有可能与轴承磨损相关。

如果同时还有谐波(基频的倍频)和边频带出现，那么轴承磨损的可能性就非常大——这时候你甚至不需要再去了解轴承准确的扰动频率。

率(BPO)、保持架频率(FT)和球的自旋频率(BS)(外圈，内圈，保持架，滚动体特征频率)。

轴承的四个物理参数：球的数量、球的直径、节径(滚柱圆心对应轴承的半径D)和接触角。

其中，BPI和BPO的和等于滚珠/滚柱的数量。

例如，如果BPO等于3.2 X(转频)，BPI等于4.8 X，那么滚珠/滚柱的数量必定是8。

轴承扰动频率的计算公式如下：注意：BS的值可能会加倍，因为所给的公式针对的是球撞击内圈或外圈的情况。

如果有庇点的滚球/滚柱同时撞击内圈和外圈，那么其频率值应该加倍。

需要说明的是由于受到各种实际情况如滑动、打滑、磨损、轴承各参数的不精确(如直径可能不完全精确)等的影响，我们所计算出来的频率值可能会与真实值有小范围的差异。

基于经验模态分解的轴承故障诊断方法Xx(大连大学，大连，116622)摘要：针对轴承故障诊断问题,提出一种基于经验模态分解( EMD, Emp iricalModeDecomposition)与切片双谱分析相结合的新方法. 将原始信号分解成不同尺度的固有模态函数( IMF, IntrinsicMode Function) ,求取IMF分量的包络,计算其对角切片双谱,提取由于二次相位耦合产生的非线性特征,得到轴承的故障特征频率. 通过对仿真信号进行分析,表明该方法克服了传统的基于EMD的包络功率谱方法不能抑制噪声的缺点,同时较传统高阶谱方法计算量更小. 给出了瑞典进口620522RS JEM SKF深沟球轴承诊断实例,说明了该方法的可用性.关键词: 故障诊断; 轴承; EMD; MATLABFault diagnosis approach for bearing based on EMDlichengchao(Dalian University, Dalian 116622)Abstract:A new ap roach based on the em irical mode decomposition ( EMD) and slicebi-spectrumwas presented for fault diagnosis on roller bearings. Original signalswere decomposed into a series of intrinsicmode functions ( IMFs) of different scales. Envelopes of the IMFswere extracted and a diagonal slice bi-spectrum for the envelopeswas computed to extract the non-linear feature deriving from the quadratic phase coupling, as well as the fault characteristic frequencies. An analysis on simulation signals shows that the drawback that traditional envelope spectrum methods based on EMD cannot inhibit the noise can be overcome by this app roach. Meanwhile, its computation load is less than traditionalhigh-order spectrum methods. A diagnosis instance of the bearing Sweden imports 6205-2RS JEM SKF was p resented to show the feasibility of this app roach.Key words:: fault diagnosis; bearings; emp iricalmode decomposition;matlab基于经验模态分解( EMD, Emp irical ModeDecomposition)的时频分析方法是1998年Norden E. Huang 等人创立的一种时频信号分析方法[ 1 - 3 ] ,尤其适用于非线性、非稳态的信号序列处理. 同时,该方法可自适应地提取故障冲击信号,避免了共振解调中心频率选择和多个固有频率共存的问题;此外,与小波分析技术相比,该方法不存在难于选取小波函数的问题,表现出更强的易用性.高阶谱分析技术[ 4 - 6 ]是近年来信号处理的新技术,是对非高斯、非线性、非因果信号处理和高斯噪声处理非常有用的分析工具,在理论上可以完全抑制噪声的影响,提高分析和辨识精度,同时更容易获得相位信息.传统的基于EMD的轴承故障诊断方法大多是利用包络的功率谱分析技术来实现的[ 7 ] ,但是,功率谱方法不能够抑制噪声对EMD方法的影响,使得EMD在工程中的使用受到了很大局限.为此,本文引入了切片双谱方法, 提出了基于EMD与切片双谱的轴承故障诊断方法.1 EMD方法的基本原理EMD 方法[ 1 ]的目的是通过对非线性、非平稳信号的分解获得一系列表征信号特征时间尺度的固有模态函数( IMF,Intrinsic Mode Function) ,使得各个IMF 是单分量的幅值或频率调制信号.IMF 要满足2个条件: ①整个数据序列的极值点与过零点的个数相等或最多相差一个; ②在任意时刻,由局部极大值点形成的上包络与由局部极小值点形成的下包络的均值为零. 这2个条件实际上使得分解得到的IMF 是窄带信号. 同时,EMD 分解方法还建立在以下假设上: ①信号至少有2个极点,一个最大值和一个最小值; ②特征时间尺度通过2个极值点之间的时间定义; ③若数据缺乏极值点但有形变点,则可通过微分数据一次或几次获得极值点,然后再通过积分来获得分解结果. 对任意一个实信号x ( t)进行EMD 的具体步骤是: 1) 确定x ( t)上的所有极大值点和极小值点;然后,将所有极大值点和所有极小值点分别用三次样条曲线连接起来, 将这两条曲线分别作为x( t) 的上下包络线. 计算出它们的平均值曲线m 1 ( t) ,用x ( t)减去m 1 ( t)得h 1 ( t) = x ( t) - m 1 ( t) (1) 如果h 1 ( t)不满足IMF 的条件,需要把h 1 ( t)作为 原信号重复上面的步骤得到h 11 ( t) h 11 ( t) = h 1 ( t) - m 11 ( t) (2) 筛选k 次直到h 1k ( t)变为一个IMF ,即 h 1k ( t) = h 1 ( k - 1) ( t) - m 1k ( t) (3) 这样就从原信号中分解出了第一个IMF,称为第一阶IMF,记作 c 1 ( t) = h 1k ( t) (4) 2) 从原信号中减去c 1 ( t)得第一阶剩余信号r 1 ( t)r 1 ( t) = x ( t) - c 1 ( t) (5) 由于第一阶剩余信号r 1 ( t)还包含着更长周期的分量,因此,把r 1 ( t)作为新的原信号,重复步骤1,对后面的也进行同样的筛选,这样依次分解得到r 2 ( t) = r 1 ( t) - c 2 ( t)r 3 ( t) = r 2 ( t) - c 3 ( t)(6)… rn ( t) = rn - 1 ( t) - cn ( t) 直至剩余信号rn ( t)中的信息对所研究内容意义很小,或者变成一个单调函数不能再筛选出基本模式分量为止. 至此, 信号x ( t)已被分解成n 个基本模式分量ci ( t)和一个剩余信号rn (t) . 这样,由式(5)和式(6)得到: )()()(1t r t c t x n ni i +=∑- (7) 进一步,各个IMF 分量可通过Hilbert 变换进行包络解调. 但是,由于所分析信号的有限长度、信号的两端点不能确定是极点,那么,在进行三次样条插值的时候,必然使得信号的上下包络在信号的两端附近严重扭曲,即产生端点效应. 本文使用了文献[ 8 ]中的极值点对称延拓法来处理该问题. 2 双谱分析 2. 1 双谱的概念 高阶谱分析技术[ 4 ]是现代信号处理的新技 术,与功率谱相比具有如下特点: ①功率谱是实数,不包含相位信息,而高阶谱是复数,因而保留了相位信息; ②能抑制噪声的影响; ③保留了系统的非线性信息. 因此,用高阶谱分析振动信号更容易获得特征信息. 定义零均值平稳随机过程x ( t) ,其三阶累积量为 )()()([),(21213ττττ++=t x t x t x E c x (8)相应的累积量谱定义为x ( t)的k 阶累积量的k - 1维傅里叶变换,则三阶谱定义为双谱: )(exp[),(),(221121321321ττττττw w j c w w s x x +-=∑∑∞-∞=∞-∞=(9)本文采用双谱估计的直接法进行计算, 即将观测数据分段,利用FFT 计算数据段的离散傅里叶变换,进而估计各阶频域矩,利用累积量谱与矩谱之间的关系求得双谱估计]4[21^),(3w w xs 2. 2 切片双谱检测二次相位耦合现象 当机械系统发生故障时, 系统往往表现出较强的非线性,产生二次相位耦合现象. 对于这种非线性耦合现象,仅用二阶统计信息如功率谱是很难从根本上解决问题的, 而双谱则可以定量描述二次相位耦合[ 5 ] . 但是用双谱计算二次相位耦合计算量大,不便于定量分析且二维图不够直观.当轴承发生故障时, 采样信号的特征为受干扰的冲击调制信号,即 )cos()]cos([)(01t w t w b t x Ni i ∑=+= (10) 式中,ωi 为调制源(包括轴承故障特征频率及其谐波频率) ;ω0 为载波频率; b 为任意常数. 因此故障轴承振动信号解调后的信号包含了故障特征频率的一簇谐波,且相位是互相关联的,即存在二次相位耦合现象[ 5 ] . 若设ωF 为轴承的故障特征频率,则双谱的(ωF ,ωF )处必然出现相位耦合现象,从而双谱在(ωF ,ωF )处会有明显的谱峰. 根据以上分析, 本文将切片双谱分析引入轴承的故障诊断方法之中,即记ω1 =ω2 =ω,则对角切片双谱估计为)(3),(3^21^w x w w x s s =. 当ω =ωF 时,必然出现明显的峰值,将峰值对应的频率与理论计算的轴承的故障特征频率相比较, 就可以得出正确的结论,同时减小计算量,增强频谱图的可视性.3 切片双谱抑制噪声对EMD 影响一般情况下,轴承的故障振动信号都带有大量高斯噪声,而传统的功率谱分析方法不能抑制高斯噪声对EMD 方法的影响.考察如下仿真信号: x ( t) = x 1 ( t) + x 2 ( t) + k ·n ( t) (11) 其中x 1 ( t) = co s (30π·t) cos (400π·t) (12) x 2 ( t) = co s (10π·t) cos (200π·t) (13) n ( t)为功率是1的高斯白噪声; k 为调节噪声大小的常数. 图1为无噪声时,即k = 0时信号x ( t)经EMD 分解得到的前2个IMF 分量的包络功率谱. 此时,可以清晰地观察到包络谱在30 Hz 和10Hz ,即相应调制频率2倍处有明显的峰值, 可以很好地分辨出调制频率. 图2为k = 3, 信噪比为1: 18时信号x ( t)经EMD 分解得到的前2个IMF分量的包络功率谱. 此时, IMF 包络谱在噪声的干扰下已经失去了意义. 图3 为无噪声时, 即k = 0时x ( t)的前2个IMF 分量的包络切片双谱图,从中可以观察到切片双谱在15 Hz 和5 Hz ,即相应调制频率处有明显峰值, 可以很好地分辨出 调制频率. 图4为k = 3,信噪比为1: 18时x ( t)的前2个IMF 分量的包络切片双谱图, 此时, 仍然可以清楚的观察到15Hz 和5Hz 2处的峰值. 以上分析说明,切片双谱可以有效抑制噪声对EMD 方法的干扰. 这是因为高斯白噪声的功率谱密度在整个频域是均匀分布的, EMD 对高斯白噪声来说是一个二分滤波器组,分解所得的每一IMF 分量都服从高斯分布,且其IMF 的能量谱与相应的平均周期之积是一个常数;而且EMD 分解所得的IMF 分量的平均频率是严格从高到低排列的;因此,它会影响到所有的IMF 分量,并且对图1 无噪声时x( t)前2个IM F 分量的包络功率谱图2 k = 3时x( t)的前2个IM F 分量的包络功率谱图3 无噪声时x( t)前2个IM F 分量的包络切片双谱图4 k = 3时x( t)前2个IM F 分量的包络切片双谱IM F 分量的影响是从高到低逐渐减弱的. 而对于零均值的高斯过程,其三阶累积量和双谱为零,切片双谱作为双谱的一种特例, 其值也为零[ 3 ] . 在机械故障诊断中,故障信号常常是非高斯的,非故障信号往往是高斯的,因此通过切片双谱分析,可以降低高斯噪声的影响,更好地将EMD 方法应用于工程之中.4 轴承故障诊断实例此数据来美国西储大学轴承数据中心，测试实验台由一个1 491W 的电机,一个扭矩传感器/编码器,一个功率计和控制电路组成,选用620522RS JEM SKF 轴承进行测试,利用电蚀加工在测试轴承内圈引入单点故障,故障直径为0. 177 8mm,故障频率为129. 964 8Hz.振动数据被用连接在磁基外壳上的一个加速度传感器收集. 加速度传感器被安装在电机外壳上驱动端和风扇端的12点方向位置. 振动信号用一个16通道的DAT 记录仪收集,在Matlab 环境下做进一步处理,使所有数据保存为Matlab 文件格式( 1 . mat). 采样数据为驱动端轴承数据,采样频率为12 000Hz,电机转速为1 772 r /min.本文中使用Matlab 编程实现,首先对原始振动信号进行零均值化处理,并实施EMD 分解,对分解后IMF 分量进行包络解调,最后利用对角切片双谱分析提取轴承的故障特征. 具体流程如图5所示.图5 基于EMD与切片双谱的振动信号处理流程图6为故障轴承利用上述方法得到的切片双谱图. 该图显示,当轴承存在内圈存在点蚀时,最终得到的对角切片双谱在频率130 Hz处有明显的谱峰存在,这与数据中心提供的故障频率一致.图6内圈振动信号前2个IMF分量的包络切片双谱图7 钢球故障信号时域波形图5 结论本文将切片双谱分析引入了轴承的故障诊断,提出了一种基于EMD与切片双谱的轴承故障诊断方法. 通过对实例验证分析,得出如下结论:①切片双谱方法将双谱的二维函数计算转换为一维函数,减小了谱分析的计算量,同时增强了二维谱图的可视性. ②切片双谱可以有效抑制噪声对EMD方法的干扰,对于低信噪比的振动信号,亦可准确有效地提取故障信息. 因此通过切片双谱分析,可以更好的将EMD方法应用于工程之中.③该方法将EMD与切片双谱相结合,用以提取由于二次相位耦合产生的非线性特征,能较准确地提取到轴承的故障特征频率.参考文献(References)[1] 黄志坚,高立新,廖一凡. 机械设备振动故障检测与诊断[M ]. 化学工业出版社, 2010.6[2] 陈姗姗，李刚燕，何立波．滚动轴承现场故障诊断实用方法[J]．轴承，2008(5)：39—42．[3] 王超，罗允同，许凌祥．滚动轴承故障的Walsh诊断法[J]．应用力学学报，1994，1l(2)：33—39．[4] 徐晖，王丽丽，罗允同．滚动轴承早期故障振动信号的分离与诊断[J]．西安交通大学学报，1997，31(8)：99—104．[5] 李辉,郑海起,唐力伟. 基于EMD和包络谱分析的轴承故障诊断研究[ J ]. 河北工业大学学报,) [6] 肖洁，刘树林，上官长存，赵海峰. Walsh变换在滚动轴承早期故障特征提取中的应用.<轴承> 2010附件一程序：%采样频率fs=12000;load 1.mat;%故障xdata=X224_BA_time(1:1024); xdata=(xdata-mean(xdata))/std(xdata, 1);%时域波形figure(1);N=1024;plot(1:N,xdata,'k-');xlabel('时间 t/n');ylabel('电压 V/v');%db10小波进行4层分解%一维小波分解[c,l]=wavedec(xdata,4,'db10');%重构第1~4层细节信号d4=wrcoef('d',c,l,'db10',4);d3=wrcoef('d',c,l,'db10',3);d2=wrcoef('d',c,l,'db10',2);d1=wrcoef('d',c,l,'db10',1);%显示细节信号figure(2);subplot(4,1,1);plot(d4,'k-','LineWidth',2);ylabel('d4');subplot(4,1,2);plot(d4,'k-','LineWidth',2);ylabel('d3');subplot(4,1,3);plot(d4,'k-','LineWidth',2);ylabel('d2');subplot(4,1,4);plot(d4,'k-','LineWidth',2);ylabel('d1');xlabel('时间 t/s');%第1层细节信号的包络谱y=hilbert(d1);ydata=abs(y);y=y-mean(y);nfft=10240;p=abs(fft(ydata,nfft)); figure(3);plot((0:nfft/2-l)/nfft*fs,p(l:nfft/2),'k-'); xlabel('频率 f/Hz');ylabel('功率谱 P/W');功率谱图。

滚动轴承状态检测与故障分析【摘要】滚动轴承是旋转机械中的重要零件,在各个机械部门有着广泛的应用。

然而滚动轴承也是机器中最易损坏的零件之一有资料表明,在旋转机械中有70%的故障是由滚动轴承引起的，故研究滚动轴承的状态检测和故障诊断技术具有重要意义。

本文通过分析研究轴承损坏的原因，选择合适的振动传感器来监测，对采集到的数据信号通过FFT频谱分析，利用MATLAB软件编程处理数据，再利用BP神经网络进行模式识别判断故障类型。

本文的主要研究内容如下：第一部分论述了关于此课题提出的意义，已经现有的监测方法以及信号分析方法。

第二部分是介绍轴承状态监测的装置。

第三部分是介绍对采集到的信号进行分析处理。

第四部分是建立BP神经网络并对其进行训练，从而实现模式识别。

第五部分是总结全文，表明提高对于轴承故障监测的诊断正确率具有重要意义。

关键词：滚动轴承；状态监测；FFT；信号分析处理；BP神经网络；模式识别—关于滚动轴承的状态检测综述1、滚动轴承故障检测的重要性在国民经济中——滚动轴承被称为“工业的关节”。

轴承工业作为机械工业的基础产业和骨干产业，其发展水平的高低，往往代表或制约着一个国家机械工业和其他相关产业的发展水平。

在日本，人们常把轴乘称作工业的食粮，轴承工业被称为“机械工业的核心产业”、“提高国民生活的基础产业“，受到日本政府振兴政策的保护与支持，是14个”特定机械工业“行业之一。

滚动轴承的应用非常广泛, 其状态好坏直接关系到机械设备的运行状态。

有资料表明,在旋转机械中有70%的故障是由滚动轴承引起的,在齿轮箱的各类故障中轴承的故障仅次于齿轮而占到19%,电机故障中有80%表现为电机轴承故障。

而滚动轴承的失效必然导致机械装置运行的不正常,甚至引发灾难性的后果,因此,对滚动轴承常见故障的研究显得十分重要。

2、轴承常见故障和轴承状态信号的采集2.1滚动轴承常见故障以及产生原因滚动轴承常见的故障主要有如下几种：（1）承受负荷的内外圈、滚动体(滚珠、滚柱等)表面磨损和剥落。

摘要滚动轴承和齿轮是煤矿机电设备机械系统中最基本的元件，其出现故障的概率很高，一旦滚动轴承和齿轮出现故障就会造成巨大的经济损失，因此必须对其进行监测和诊断。

目前的故障诊断方法大都以振动理论为基础，振动信号处理技术是设备故障诊断中最有效、最常用的方法。

本文介绍了故障诊断的目的、意义、国内外研究现状、目前常用的故障诊断方法、Matlab小波工具箱、引起滚动轴承及齿轮故障的主要原因等。

对小波分析法的理论部分进行了深入研究，并利用Matlab小波工具箱对滚动轴承及齿轮的故障信号进行小波分解。

通过对分解所得细节信号的分析，可以准确判断出发生故障的部位及时间。

结果表明，小波分析法可以在早期发现故障及其产生原因，减少维修时间，提高维修质量，节约维修费用，是一种行之有效的故障诊断方法。

关键词：故障诊断；小波分析； Matlab仿真Failure diagnosis of electromechanical device incoal mineAbstract: The condition bearing and gear run is relate to the performance which mechanical system run，the probability it appears the breakdown is very high．Once the bearing and the gear appear the breakdown，can cause the mechanical system to be unable work normally．It will create the huge economic loss．The present method of fault diagnosis mostly bases on the vibration theory and the signal processing technology basing on vibration is the most effective and the most commonly used method. The main significance of fault diagnosis of equipment is state of the implementation of planned maintenance，make early warning of the development of equipment failure. Identificate and evaluate of the reasons，location and degree of risk identification of the fault .Forecast the development trend of the fault. Forecast the development trend of the fault and quickly find fault source. Put forward countermeasures and suggestions. And rapid to the specific circumstances to make response troubleshooting，to avoid or reduce accident，and ensure the smooth progress of production。

摘要滚动轴承是旋转机械中应用最广泛的一种通用部件，也是机械设备中的易损零件，许多机械的故障都与滚动轴承的状态有关。

据统计，在使用滚动轴承的旋转机械中，大约30％的机械故障是由于滚动轴承的损坏造成的。

可见，滚动轴承的好坏对机械系统工作状况的影响极大。

由于设计不当和安装工艺不好或轴承的使用条件不佳，或突发载荷的影响，使轴承运转一段时间后会产生各种各样的缺陷，并且在继续运行中进一步扩大，使轴承运行状态发生变化。

因此，滚动轴承的故障诊断一直是研究的热点。

本文首先从理论上分析了滚动轴承的失效形式、振动机理、振动类型、及发生故障的原因、振动频率；然后在理论基础上提出了滚动轴承的时域、频域的诊断方法；最后搭建了基于Matlab的滚动轴承故障诊断系统，并通过Matlab仿真轴承故障信号，在软件中进行信号分析和处理，验证各种诊断方法的优劣和滚动轴承的故障特征。

本论文按照预定的要求完成了设计任务，研究了滚动轴承的故障诊断方法，完成了故障诊断系统的设计，通过仿真验证了滚动轴承的故障诊断方法。

关键词：滚动轴承；故障诊断；时域分析；频域分析；MatlabAbstractRolling element bearing is one of the most widely used general part of rotating machinery,and one of the most easily damaged parts of mechanical equipment. A lot of mechanical failure is relevant to the state of rolling element bearings. It is estimated that about 30 percent of mechanical failure is caused by its fault in the rotating machine with rolling element bearings. It is obvious that the quality of rolling element bearings has a great impact on the working condition of electromechanical systems. Because of wrong design, poor working condition or a jump heavy load, bearing will be damaged and worse during the running time. So at present, the fault diagnosis of rolling element bearings is a research hotspot.Firstly, the failure forms, the vibration mechanism, vibration type, and the failure cause, vibration frequency of bearing are analyzed in theory.Secondly, based on the theory put forward the time domain, frequency domain diagnostic methods.Finally, the software for the fault diagnosis system of the rolling bearings is designed by Matlab,along with the simulation of bearing fault signals by Matlab.To analysis and processing the signal in software. Verify the merits of various diagnostic methods and characteristics of rolling bearing faults.The paper successfully completed the design task and the result meets the expectation. We researched the fault diagnosis methods and completed the fault diagnosis system design and simulation shows the fault diagnosis methods of rolling element bearings.KeyWords：rolling element bearings,fault diagnosis,time-domain analysis,frequency-domain analysis,Matlab目录摘要 (I)Abstract (II)第一章绪论 ...........................................................................................................- 1 -1.1 本课题研究的主要意义 ...........................................................................- 1 -1.2 滚动轴承故障诊断方法 ...........................................................................- 2 -1.3 滚动轴承故障诊断技术的发展概况 .......................................................- 3 -1.4 滚动轴承故障诊断技术的发展方向 .......................................................- 5 -1.5 本课题主要研究内容 ...............................................................................- 5 -第二章滚动轴承的故障特征分析 .......................................................................- 6 -2.1 概述 ...........................................................................................................- 6 -2.2 滚动轴承的典型结构 ...............................................................................- 6 -2.3 滚动轴承的主要失效形式及原因 ...........................................................- 7 -2.4 滚动轴承的几何参数 ...............................................................................- 8 -2.5 滚动轴承的特征频率 ...............................................................................- 9 -2.6 滚动轴承的振动特性 .............................................................................- 10 -2.6.1 滚动轴承的固有振动 ...................................................................- 11 -2.6.2 轴承构造引起的振动 ...................................................................- 12 -2.6.3 轴承装配不正确、轴颈偏斜产生的振动 ...................................- 13 -2.6.4 精加工波纹度引起的振动 ...........................................................- 13 -2.6.5 滚动轴承的故障引起振动 ...........................................................- 13 -第三章滚动轴承故障诊断方法研究 .................................................................- 16 -3.1 概述 .........................................................................................................- 16 -3.2 时域分析的特征参数 .............................................................................- 16 -3.3 频域分析的特征参数 .............................................................................- 18 -第四章轴承故障诊断系统总体设计 .................................................................- 22 -4.1 概述 .........................................................................................................- 22 -4.2 Matlab软件简介......................................................................................- 22 -4.3 滚动轴承故障诊断系统总体设计 .........................................................- 24 -4.3.1 系统界面子系统 ...........................................................................- 24 -4.3.2 轴承特征频率计算子系统 ...........................................................- 25 -4.3.3 数据加载子系统 ...........................................................................- 26 -4.3.4 信号模拟子系统 ...........................................................................- 27 -4.3.5 时域分析子系统 ...........................................................................- 28 -4.3.6 频域分析子系统 ...........................................................................- 31 -4.3.7 打印子系统 ...................................................................................- 32 -第五章轴承实测信号处理 .................................................................................- 33 -5.1 概述 .........................................................................................................- 33 -5.2 模拟合成信号 .........................................................................................- 33 -5.3 模拟合成信号分析 .................................................................................- 34 -5.4 轴承实测信号分析 .................................................................................- 35 -结论 .....................................................................................................................- 38 -参考文献 .................................................................................................................- 39 -致谢 .....................................................................................................................- 41 -附录A 频域分析系统程序 ..................................................................................- 42 -第一章绪论1.1 本课题研究的主要意义机械故障诊断技术是近40年来发展起来的识别机器或机组运行状态的科学。

第二组实验轴承故障数据：Test2.mat 数据打开后应采用X105_DE_time作为分析数据，其他可作为参考，转速1797rpm轴承型号：6205-2RS JEM SKF, 深沟球轴承采样频率：12k Hz1、确定轴承各项参数并计算各部件的故障特征频率通过以上原始数据可知次轴承的参数为：轴承转速r=1797r/min；滚珠个数n=9；滚动体直径d=7.938mm；轴承节径D=39mm；：滚动体接触角α=0由以上数据计算滚动轴承不同部件故障的特征频率为：外圈故障频率f1=r/60 * 1/2 * n(1-d/D *cosα)=107.34Hz内圈故障频率f2=r/60 * 1/2 * n(1+d/D *cosα)=162.21Hz滚动体故障频率f3=r/60*1/2*D/d*[1-(d/D)^2* cos^2(α)]=70.53Hz 保持架外圈故障频率f4=r/60 * 1/2 * (1-d/D *cosα)=11.92Hz2.对轴承故障数据进行时域波形分析将轴承数据Test2.mat导入MATLAB中直接做FFT分析得到时域图如下：并求得时域信号的各项特征：（1）有效值：0.2909；（2）峰值：1.5256；（3）峰值因子：5.2441；（4）峭度：5.2793；（5）脉冲因子：7.2884；（6）裕度因子：9.1083：3.包络谱分析对信号做EMD 模态分解，分解得到的每一个IMF 信号分别和原信号做相关分析，找出相关系数较大的IMF 分量并对此IMF 分量进行Hilbert 变换。

s i g n a lEmpirical Mode Decompositioni m f 1i m f 2i m f 3i m f 4i m f 5i m f 6i m f 7i m f 8r e s .由图中可以看出经过EMD 分解后得到的９个IMF 分量和一个残余量。

IMF 分量分别和原信号做相关分析后得出相关系数如下：由上表得：IMF1的相关系数明显最大，所以选用IMF1做Hilbert 包络谱分析。

基于C#和Matlab混合编程的轴承故障诊断系统刘亚;王静;田新诚【摘要】为提高系统的开发效率和功能完整性,以.NET为开发平台,实现C#和Matlab混合编程;同时,C#通过XAMPP与MySQL数据库进行通信,实现实时数据的存储.针对轴承故障信号非平稳性问题,采用小波包分解(WPD)和自回归(AR)谱分析方法进行特征提取;考虑到神经网络具有强大的自学习能力,采用反向传播(BP)神经网络实现故障诊断.采用美国凯斯西储大学提供的旋转轴承数据集进行轴承故障诊断实验.实验结果表明,系统可以有效地实现特征提取、故障诊断以及数据存储,从而验证了故障诊断算法的可行性及系统的有效性.【期刊名称】《计算机应用》【年(卷),期】2018(038)0z2【总页数】4页(P236-238,242)【关键词】C#;Matlab;数据库;混合编程;故障诊断【作者】刘亚;王静;田新诚【作者单位】山东大学控制科学与工程学院,济南250061;潍柴动力股份有限公司企业管理与信息化部,山东潍坊261061;山东大学控制科学与工程学院,济南250061【正文语种】中文【中图分类】TP311.50 引言滚动轴承是机电设备中应用最广泛的机械部件，同时它也是最易损坏的部件之一，因此对轴承的状态监测和故障诊断尤为重要[1-2]。

由于轴承的原始振动信号中存在许多噪声，而且实际振动信号在运行过程中表现出明显的非线性和非平稳性特点[3-4]，因此，能否从原始振动信号中提取全面且有效的特征信号将直接影响故障诊断结果的准确性。

傅里叶变换适用于平稳信号分析，难以准确提取轴承故障状态信息。

经验模式分解(Empirical Mode Decomposition, EMD)方法虽然理论上适用于非线性非平稳过程，但是其显著的“模态混叠”问题，使其存在一定局限性[5]。

小波包分解可以对检测信号进行多通道滤波，将信号划分成不同的频段，减少信号间干扰。

同时，AR谱分析具有外推功能，可以有效分析短样本信号[6]。