5大物机械波 习题及答案

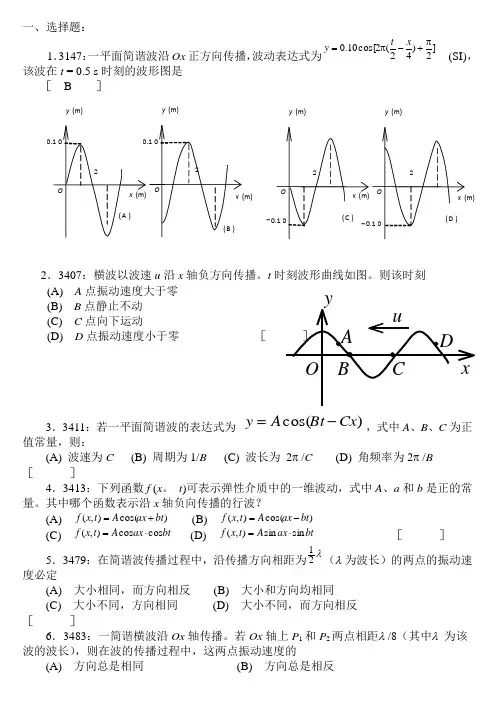
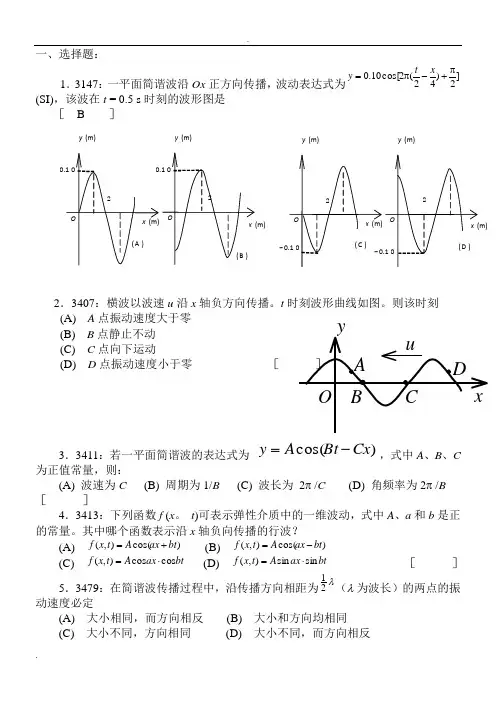
一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) btax A t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C)大小不同，方向相同 (D) 大小不同，而方向相反 ［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反y (m) y (m) - y (m) y (m)(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长(B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。

机械波试题(含答案)一、机械波选择题1．由波源S形成的简谐横波在均匀介质中向左、右传播．波源振动的频率为20Hz，波速为16m/s．已知介质中P、Q两质点位于波源S的两侧，且P、Q和S的平衡位置在一条直线上，P、Q的平衡位置到S的平衡位置之间的距离分别为15. 8 m，14.6m．P、Q开始振动后，下列判断正确的是( )A．P、Q两质点运动的方向始终相同B．P 、Q两质点运动的方向始终相反C．当S恰好通过平衡位置时，P、Q两点也正好通过平衡位置D．当S恰好通过平衡位置向上运动时，P在波峰E.当S恰好通过平衡位置向下运动时，Q在波峰2．如图所示分别为一列横波在某一时刻的图像和在x=6m 处的质点从该时刻开始计时的振动图像，则这列波（）A．沿x 轴的正方向传播，波速为2.5m/sB．沿x 轴的负方向传播，波速为2.5m/sC．沿x 轴的正方向传播，波速为100m/sD．沿x轴的负方向传播，波速为100m/s3．一列简谐横波沿x轴正方向传播，频率为5Hz，某时刻的波形如图所示，介质中质点A 在距原点8cm处，质点B在距原点16cm处，从图象对应时刻算起，质点A的运动状态与图示时刻质点B的运动状态相同需要的最短时间为（）A．0.08s B．0.12s C．0.14s D．0.16s4．如图所示，实线是沿x轴传播的一列简谐横波在t="=" 0时刻的波形图，虚线是这列波在t="=" 0.2 s时刻的波形图．已知该波的波速是0.8 m／s ，则下列说法正确的是A．这列波的波长是14 ㎝B．这列波的周期是0.125 sC．这列波可能是沿x轴正方向传播的D ．t =0时，x = 4 ㎝处的质点速度沿y 轴负方向 5．利用发波水槽得到的水面波形如图所示，则( )A ．图a 、b 均显示了波的干涉现象B ．图a 、b 均显示了波的衍射现象C ．图a 显示了波的干涉现象，图b 显示了波的衍射现象D ．图a 显示了波的衍射现象，图b 显示了波的干涉现象6．如图所示，某一均匀介质中有两列简谐横波A 和B 同时沿x 轴正方向传播了足够长的时间，在t =0时刻两列波的波峰正好在12m x =处重合，平衡位置正好在216m x =处重合，则下列说法中正确的是（ ）A ．横波A 的波速比横波B 的波速小 B ．两列波的频率之比为A B :11:7f f =C ．在0x >的区间，t =0时刻两列波另一波峰重合处的最近坐标为(586)，D ．2m x =处质点的振动始终加强7．一根长20m 的软绳拉直后放置在光滑水平地板上，以绳中点为坐标原点，以绳上各质点的平衡位置为x 轴建立图示坐标系。

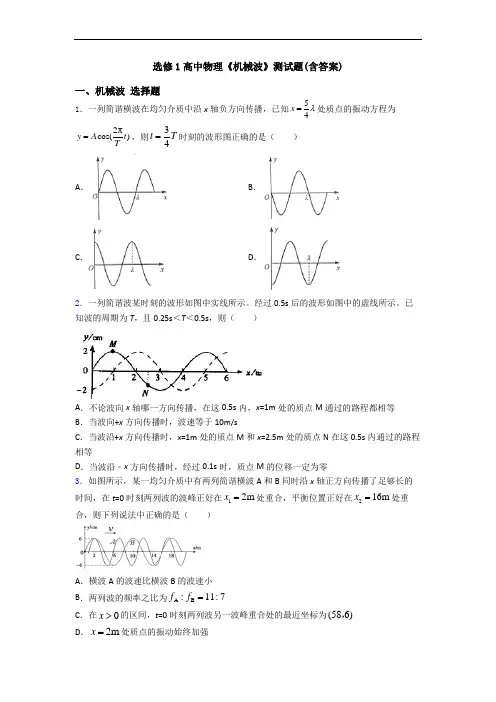
选修1高中物理《机械波》测试题(含答案)一、机械波 选择题1．一列简谐横波在均匀介质中沿x 轴负方向传播，已知54x λ=处质点的振动方程为2πcos()y A t T =，则34t T =时刻的波形图正确的是（ ） A ． B ．C ．D ．2．一列简谐波某时刻的波形如图中实线所示。

经过0.5s 后的波形如图中的虚线所示。

已知波的周期为T ，且0.25s ＜T ＜0.5s ，则（ ）A ．不论波向x 轴哪一方向传播，在这0.5s 内，x =1m 处的质点M 通过的路程都相等B ．当波向+x 方向传播时，波速等于10m/sC ．当波沿+x 方向传播时，x =1m 处的质点M 和x =2.5m 处的质点N 在这0.5s 内通过的路程相等D ．当波沿﹣x 方向传播时，经过0.1s 时，质点M 的位移一定为零3．如图所示，某一均匀介质中有两列简谐横波A 和B 同时沿x 轴正方向传播了足够长的时间，在t =0时刻两列波的波峰正好在12m x =处重合，平衡位置正好在216m x =处重合，则下列说法中正确的是（ ）A ．横波A 的波速比横波B 的波速小 B ．两列波的频率之比为A B :11:7f f =C ．在0x >的区间，t =0时刻两列波另一波峰重合处的最近坐标为(586)，D ．2m x =处质点的振动始终加强4．甲、乙两列横波在同一介质中分别从波源M、N两点沿x轴相向传播，波速为2m/s，振幅相同；某时刻的图像如图所示。

则。

A．甲、乙两波的起振方向相同B．甲、乙两波的频率之比为3:2C．甲、乙两波在相遇区域会发生干涉D．再经过3s，平衡位置在x=6m处的质点处于平衡位置E.再经过3s，平衡位置在x=7m处的质点加速度方向向上5．如图，一列简谐横波沿x轴传播，P、Q是x轴上相距2m的两点，均沿y轴做简谐运动，t=0时刻，P点处于波峰，Q点在平衡位置且速度方向向上；已知波的周期为T=4s，振幅为A=l0cm。

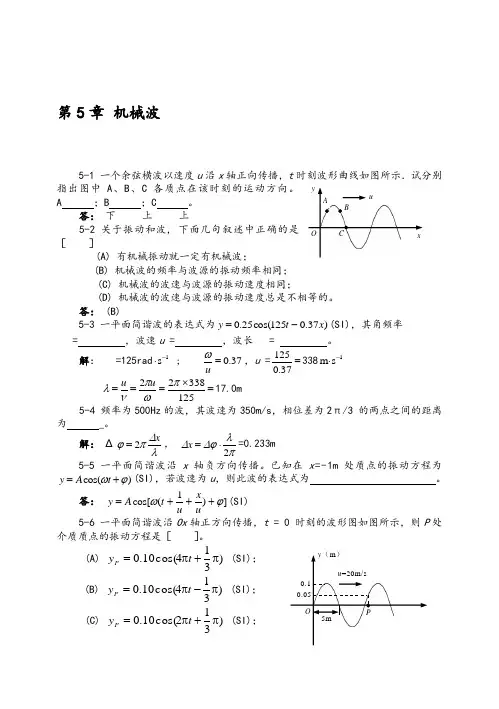
第5章 机械波5-1 一个余弦横波以速度u 沿x 轴正向传播，t 时刻波形曲线如图所示．试分别指出图中A 、B 、C 各质点在该时刻的运动方向。

A ；B ；C 。

答： 下 上 上5-2 关于振动和波, 下面几句叙述中正确的是［ ］(A) 有机械振动就一定有机械波；(B) 机械波的频率与波源的振动频率相同；(C) 机械波的波速与波源的振动速度相同；(D) 机械波的波速与波源的振动速度总是不相等的。

答： (B)5-3 一平面简谐波的表达式为)37.0125cos(25.0x t y -=(SI)，其角频率 = ，波速u = ，波长 = 。

解： =125rad 1s -⋅ ; 37.0=u ω，u ==37.01253381s m -⋅=⨯===12533822πωπνλu u 17.0m5-4 频率为500Hz 的波，其波速为350m/s ，相位差为2π/3 的两点之间的距离为 _。

解： ∆λ∆πϕx 2=， πλϕ∆∆2⋅=x =0.233m5-5 一平面简谐波沿x 轴负方向传播。

已知在x =-1m 处质点的振动方程为cos()y A t ωϕ=+(SI)，若波速为u ，则此波的表达式为 。

答： ])1(cos[ϕω+++=uxu t A y (SI)5-6 一平面简谐波沿Ox 轴正方向传播，t = 0 时刻的波形图如图所示，则P 处介质质点的振动方程是［ ］。

(A) )314cos(10.0π+π=t y P (SI)； (B) )314cos(10.0π-π=t y P (SI)；(C) )312cos(10.0π+π=t y P (SI)；yxA BC O uOPy （m ）5mu =20m/s0.05 0.1(D) )612cos(10.0π+π=t y P (SI)。

解：答案为 (A)确定圆频率：由图知10=λm ，u =20m/s ，得πλππνω422===u确定初相：原点处质元t =0时，205.00A y P ==、00<v ，所以3πϕ= 5-7 一平面简谐波的表达式为)]/(cos[u x t A y -=ω，其中u x /-表示 ；u x /ω-表示 ；y 表示 。

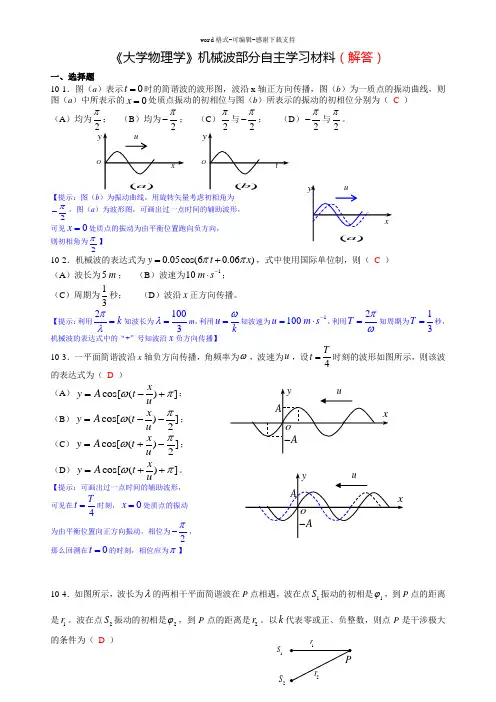
《大学物理学》机械波部分自主学习材料（解答）一、选择题10-1．图（a ）表示0t =时的简谐波的波形图，波沿x 轴正方向传播，图（b ）为一质点的振动曲线，则图（a ）中所表示的0x =处质点振动的初相位与图（b ）所表示的振动的初相位分别为（ C ） （A ）均为2π； （B ）均为π-； （C ）π与π-； （D ）2π-与2π。

【提示：图（b ）为振动曲线，用旋转矢量考虑初相角为2π-，图（a ）为波形图，可画出过一点时间的辅助波形，可见0x =处质点的振动为由平衡位置跑向负方向，则初相角为2π】10-2．机械波的表达式为0.05cos(60.06)y t x ππ=+，式中使用国际单位制，则（ C ） （A ）波长为5m ； （B ）波速为110m s -⋅；（C ）周期为13秒； （D ）波沿x 正方向传播。

【提示：利用2k πλ=知波长为1003λ=m ，利用u k ω=知波速为1100u m s -=⋅，利用2T πω=知周期为13T =秒，机械波的表达式中的“+”号知波沿x 负方向传播】10-3．一平面简谐波沿x 轴负方向传播，角频率为ω，波速为u ，设4Tt =时刻的波形如图所示，则该波的表达式为（ D ）（A ）cos[()]xy A t u ωπ=-+； （B ）cos[()]2x y A t u πω=--；（C ）cos[()]2x y A t u πω=+-；（D ）cos[()]xy A t uωπ=++。

【提示：可画出过一点时间的辅助波形，可见在4Tt =时刻，0x =处质点的振动为由平衡位置向正方向振动，相位为2π-，那么回溯在0t=的时刻，相位应为π】10-4．如图所示，波长为λ的两相干平面简谐波在P 点相遇，波在点1S 振动的初相是1ϕ，到P 点的距离是1r 。

波在点2S 振动的初相是2ϕ，到P 点的距离是2r 。

以k 代表零或正、负整数，则点P 是干涉极大的条件为（ D ）OO1S 2S r（A ）21r r k π-=； （B ）212k ϕϕπ-=； （C ）212122r r k ϕϕππλ--+=；（D ）122122r r k ϕϕππλ--+=。

机械波试题(含答案)一、机械波 选择题1．1S 为振源，由平衡位置开始上下振动，产生一列简谐横波沿12S S 直线传播，1S 、2S 两点之间的距离为9m ．2S 点的左侧为一种介质，右一侧为另一种介质，波在这两种介质中传播的速度之比为3：4．某时刻波正好传到2S 右侧7m 处，且1S 、2S 均在波峰位置．则（ ）A ．2S 开始振动时方向可能向下也可能向上B ．波在2S 左侧的周期比在右侧时大C ．右侧的波长为()228=m 012341n n λ=+，，，，… D ．左侧的波长为()13=m 0123421n n λ=+，，，，… 2．一列波长大于3.6m 的简谐横波沿直线方向由a 向b 传播，a 、b 相距6m ， a 、b 两质点的振动图象如图所示．由此可知A ．3 s 末a 、b 两质点的位移相同B ．该波的波速为2 m/sC ．该波的波长为4mD ．该波由a 传播到b 历时1.5s3．一列简谐横波沿直线由A 向B 传播，A 、B 相距0.45m ，右图是A 处质点的震动图像．当A 处质点运动到波峰位置时，B 处质点刚好到达平衡位置且向y 轴正方向运动，这列波的波速可能是A ．4.5m/sB ．3.0m/sC ．1.5m/sD ．0.7m/s4．声波能绕过某一建筑物传播而光波却不能绕过该建筑物，这是因为A．声波是纵波，光波是横波B．声波振幅大，光波振幅小C．声波波长较长，光波波长很短D．声波波速较小，光波波速很大5．如图所示，质点0在垂直x轴方向上做简谐运动，形成了沿x轴传播的横波．在t＝0时刻，质点0从平衡位置开始向上运动，经0.2s第一次形成图示波形，则下列判断正确的是()A．t＝0.4 s时，质点A第一次到达波峰B．t＝1.2 s时，质点A在平衡位置，速度沿y轴正方向C．t＝2 s时，质点B第一次到达波谷D．t＝2.6 s时，质点B的加速度达到最大6．如图，一列简谐横波沿x轴传播，P、Q是x轴上相距2m的两点，均沿y轴做简谐运动，t=0时刻，P点处于波峰，Q点在平衡位置且速度方向向上；已知波的周期为T=4s，振幅为A=l0cm。

习题五一、选择题1．已知一平面简谐波的表达式为 )cos(bx at A y -=（a 、b 为正值常量），则 ［ ］（A ）波的频率为a ； （B ）波的传播速度为 b/a ； （C ）波长为 π / b ； （D ）波的周期为2π / a 。

答案：D解：由22cos()cos()2/2/y A at bx A t x a b ππππ=-=-，可知周期2T aπ=。

波长为b π2。

2．如图，一平面简谐波以波速u 沿x 轴正方向传播，O 为坐标原点．已知P 点的振动方程为cos y A t ω=，则 ［ ］（A ）O 点的振动方程为 cos ()ly A t u ω=-；（B ）波的表达式为 cos ()l xy A t u u ω=--；（C ）波的表达式为 cos ()l xy A t u uω=+-；（D ）C 点的振动方程为 3cos ()ly A t uω=-。

答案：C解：波向右传播，原O 的振动相位要超前P 点luω，所以原点O 的振动方程为cos ()ly A t uω=+，因而波方程为cos ()x l y A t u u ω=-+，可得答案为C 。

3．一平面简谐波以速度u 沿x 轴正方向传播，在t t '=时波形曲线如图所示．则坐标原点O 的振动方程为［ ］（A ）]2)(cos[π+'-=t t b u a y ； （B ）]2)(2cos[π-'-π=t t b u a y ；（C ）]2)(cos[π+'+π=t t b u a y ；（D ）]2)(cos[π-'-π=t t b u a y 。

答案：D解：令波的表达式为 cos[2()]xy a t νϕλ=-+πxO u 2l lyC P当t t '=， cos[2()]xy a t νϕλ'=-+π由图知，此时0x =处的初相 22t νϕ'+=-ππ， 所以 22t ϕν'=--ππ，由图得 b 2=λ， buu2==λν故0x =处 cos[2]cos[()]2u y a t a t t b νϕ'=+=--πππ4．当一平面简谐机械波在弹性媒质中传播时，下述各结论哪个是正确的？［ ］（A ）媒质质元的振动动能增大时，其弹性势能减小，总机械能守恒； （B ）媒质质元的振动动能和弹性势能都作周期性变化，但二者的相位不相同； （C ）媒质质元的振动动能和弹性势能的相位在任一时刻都相同，但二者的数值不等；（D ）媒质质元在其平衡位置处弹性势能最大。

机械波试题(含答案)一、机械波 选择题1．如图所示，位于介质Ⅰ和Ⅱ分界面上的波源S ，产生两列分别沿x 轴负方向与正方向传播的机械波．若在两种介质中波的频率及传播速度分别为f 1、f 2和v 1、v 2，则A ．f 1＝2f 2，v 1＝v 2B ．f 1＝f 2，v 1＝2v 2C ．f 1＝f 2，v 1＝0.5v 2D ．f 1＝0.5f 2，v 1＝v 22．如图所示，某一均匀介质中有两列简谐横波A 和B 同时沿x 轴正方向传播了足够长的时间，在t =0时刻两列波的波峰正好在12m x =处重合，平衡位置正好在216m x =处重合，则下列说法中正确的是（ ）A ．横波A 的波速比横波B 的波速小 B ．两列波的频率之比为A B :11:7f f =C ．在0x >的区间，t =0时刻两列波另一波峰重合处的最近坐标为(586)，D ．2m x =处质点的振动始终加强3．一列简谐横波沿x 轴正方向传播，t ＝0时波形图如图中实线所示，此时波刚好传到c 点，t ＝0.6s 时波恰好传到e 点，波形如图中虚线所示，a 、b 、c 、d 、e 是介质中的质点，下列说法正确的是（ ）A ．当t ＝0.5s 时质点b 和质点c 的加速度相同B ．该波的传播速度为6.7m/sC ．质点b 在0～0.6s 时间内通过的路程为30cmD ．质点d 在0～0.6s 时间内通过的路程为2m E.质点e 开始运动时方向沿y 轴正方向4．两列简谐波的振幅都是20cm ，传播速度大小相同，实线波的频率为2Hz ，沿x 轴正方向传播，虚线波沿x 轴负方向传播，某时刻两列波在如图所示区域相遇，则（ ）．A ．平衡位置为x =6cm 的质点此刻速度为零B ．平衡位置为x =8.5cm 处的质点此刻位移y >20cmC ．从图示时刻起再经过0.25s ，平衡位置为x =4cm 处的质点的位移y =0D ．随着波的传播，在相遇区域会出现某质点的振动位移达到y =40cm5．位于x =0m 、x =18m 的波源P 、Q 在同一介质中分别产生两列横波甲、乙，传播方向相反，某时刻两列波的波形图如图所示，此时x =1m 处的质点振动了5s 时间。

第5章 机械波5.1基本要求1．理解描述简谐波的各物理量的意义及相互间的关系.2．理解机械波产生的条件．掌握由已知质点的简谐振动方程得出平面简谐波的波函数的方法．理解波函数的物理意义．理解波的能量传播特征及能流、能流密度概念．3．了解惠更斯原理和波的叠加原理.理解波的相干条件，能应用相位差和波程差分析、确定相干波叠加后振幅加强和减弱的条件. 4．理解驻波及其形成。

5．了解机械波的多普勒效应及其产生的原因.5.2基本概念 1．机械波机械振动在弹性介质中的传播称为机械波，机械波产生的条件首先要有作机械振动的物体，即波源；其次要有能够传播这种机械振动的弹性介质。

它可以分为横波和纵波。

2.波线与波面 沿波的传播方向画一些带有箭头的线，叫波线。

介质中振动相位相同的各点所连成的面，叫波面或波阵面。

在某一时刻，最前方的波面叫波前。

3．波长λ 在波传播方向上，相位差为2π的两个邻点之间的距离称为波长，它是波的空间周期性的反映。

4．周期T 与频率ν 一定的振动相位向前传播一个波长的距离所需的时间称为波的周期，它反映了波的时间周期性，波的周期与传播介质各质点的振动周期相同。

周期的倒数称为频率，波的频率也就是波源的振动频率。

5．波速u 单位时间里振动状态（或波形）在介质中传播的距离。

它与波动的特性无关，仅取决于传播介质的性质。

6．平面简谐波的波动方程 在无吸收的均匀介质中沿x 轴传播的平面简谐波的波函数为()2cos y A tx ωϕπλ=+或s )co (x y A tu ωϕ⎡⎤=+⎢⎥⎣⎦其中，“-”表示波沿x 轴正方向传播；“+”表示波沿x 轴负方向传播。

波函数是x 和t 的函数。

给定x ，表示x 处质点的振动，即给出x 处质点任意时刻离开自己平衡位置的位移；给定t ，表示t 时刻的波形，即给出t 时刻质点离开自己平衡位置的位移。

7．波的能量 波动中的动能与势能之和，其特点是同体积元中的动能和势能相等。

一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y (SI)，该波在t = 0.5 s 时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 ［3．3411：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B ［］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为λ21（λ 为波长）的两点的振动速度必定(A) 大小相同，而方向相反 (B) 大小和方向均相同(C) 大小不同，方向相同(D) 大小不同，而方向相反y (m) y (m) - y (m) y (m)［ ］6．3483：一简谐横波沿Ox 轴传播。

若Ox 轴上P 1和P 2两点相距λ /8（其中λ 为该波的波长），则在波的传播过程中，这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同，有时相反 (D) 大小总是不相等 ［ ］7．3841：把一根十分长的绳子拉成水平，用手握其一端。

维持拉力恒定，使绳端在垂直于绳子的方向上作简谐振动，则 (A) 振动频率越高，波长越长 (B) 振动频率越低，波长越长(C) 振动频率越高，波速越大 (D) 振动频率越低，波速越大 ［ ］ 8．3847：图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。

物理机械波各地方试卷集合及解析一、机械波 选择题1．一简谐横波沿水平绳向右传播，波速为v ，周期为T ，振幅为A ．绳上两质点M 、N 的平衡位置相距四分之三波长，N 位于M 右方．设向上为正，在t =0时刻M 位移为2A +，且向上运动；经时间t （t T <），M 位移仍为2A+，但向下运动，则（ ） A ．在t 时刻，N 恰好在波谷位置 B ．在t 时刻，N 位移为负，速度向上 C ．在t 时刻，N 位移为负，速度向下 D ．在2t 时刻，N 位移为2A-，速度向下 2．如图所示，实线是沿x 轴传播的一列简谐横波在t ="=" 0时刻的波形图，虚线是这列波在t ="=" 0.2 s 时刻的波形图．已知该波的波速是0.8 m ／s ，则下列说法正确的是A ．这列波的波长是14 ㎝B ．这列波的周期是0.125 sC ．这列波可能是沿x 轴正方向传播的D ．t =0时，x = 4 ㎝处的质点速度沿y 轴负方向3．一列简谐横波在t =0时刻的波形如图中的实线所示，t =0.02s 时刻的波形如图中虚线所示．若该波的周期T 大于0.02s ，则该波的传播速度可能是（ ）A ．2m/sB ．3m/sC ．4m./sD ．5m/s4．一列简谐横波沿x 轴负方向传播，波速v =4m/s ，已知坐标原点（x =0）处质点的振动图象如图所示，在下列幅图中能够正确表示t =0.15s 时波形的图是A ．B ．C ．D ．5．一列简谐横波在t =13s 时的波形图如图a 所示，P 、Q 是介质中的两个质点，图b 是质点Q 的振动图象。

则（ ）A ．该列波沿x 轴负方向传播B ．该列波的波速是1.8m/sC ．在t =13s 时质点Q 的位移为3A D ．质点P 的平衡位置的坐标x =3cm6．如图所示，两列简谐横波分别沿x 轴正方向和负方向传播。

已知两波源分别位于0.2m x =-和 1.0m x =处，振幅均为0.5cm A =，波速均为0.2m/s v =。

一、选择题：一、选择题：1．3147：一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0p+-p =x t y (SI)，该波在t = 0.5 s 时刻的波形图是时刻的波形图是［ B ］2．3407：横波以波速u 沿x 轴负方向传播。

t 时刻波形曲线如图。

则该时刻时刻波形曲线如图。

则该时刻 (A) A 点振动速度大于零点振动速度大于零 (B) B 点静止不动点静止不动(C) C 点向下运动点向下运动 (D) D 点振动速度小于零点振动速度小于零 ［ ］3．3411：若一平面简谐波的表达式为：若一平面简谐波的表达式为 )cos(Cx Bt A y -=，式中A 、B 、C 为正值常量，则：为正值常量，则：(A) 波速为C (B) 周期为1/B (C) 波长为波长为 2p /C C (D) 角频率为2p /B ［ ］4．3413：下列函数f (x 。

t )可表示弹性介质中的一维波动，式中A 、a 和b 是正的常量。

其中哪个函数表示沿x 轴负向传播的行波？轴负向传播的行波？(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(×= (D) bt ax A t x f sin sin ),(×= ［ ］5．3479：在简谐波传播过程中，沿传播方向相距为l21（l 为波长）的两点的振动速度必定动速度必定(A) 大小相同，而方向相反大小相同，而方向相反 (B) 大小和方向均相同大小和方向均相同 (C) 大小不同，方向相同大小不同，方向相同 (D) 大小不同，而方向相反大小不同，而方向相反xu A y B C D Ox (m) O 2 0.1 0y (m)( A ) x (m)O 2 0.1 0y (m) ( B )x (m) O 2- 0.1 0 y (m) ( C ) x (m)O 2 y (m)( D )- 0.1 0［ ］6．3483：一简谐横波沿Ox 轴传播。

一、 选择题1、一简谐波波动方程为0.03cos6(0.01)()y t x SI π=+则 （A ）其振幅为3m (B)周期为1/3s [ C ] （C ）波速为10m/s (D)波沿X 轴正方向传播2、如图为0t =时刻沿X 负方向传播的平面全余弦简谐波的波形曲线，则O 点处质点振动的初相为： [ D] （A ）0 (B)π (C)2π (D)32π3、一平面简谐波，沿x 轴负方向传播，角频率为ω，波速为u ，设4Tt =时刻的波形如图所示，则该波的波动方程为 [ D ](A);)(cos uxt A y -=ω(B) ;]2)(cos[πω+-=u x t A y(C) ;)(cos u xt A y +=ω(D) ].)(cos[πω++=uxt A y4、两列相干波沿同一直线反向传播形成驻波，则两相邻波节之间各点的相位及振幅的关系为 【C 】（A ）振幅全相同，相位全相同； （B ）振幅不全相同，相位全相同； （C ）振幅全相同，相位不全相同； （D ）振幅不全相同，相位不全相同。

5、一平面简谐波在弹性媒质中传播，在媒质质元从平衡位置运动到 最大位移处的过程中 [ D ]（A ）它的动能转换为势能； （B ）它的势能转换为动能；（C ）它从相邻的一段质元获得能量，其能量逐渐增加； （D ）它的能量传给相邻的另一质元，其能量逐渐减小。

6、以平面余弦波波源得周期为s T 5.0=，它所激发得波得振幅为m 1.0，波长为m 10，取波源振动得位移恰好在正方向最大值时开始计时，波源所在处为原点，沿波传播方向为x 轴正方向，则2λ=x 处质点振动得表示式为[ A ] （A ）;)()4cos(1.0m t y ππ-= (B) ;)()22cos(1.0m t y ππ-=(C) ;)()(4cos 1.0m t y ππ-= (D) .)()2cos(1.0m t y ππ-=7、一平面简谐波沿Ox 正方向传播，波动表达式为]2)42(2cos[10.0π+-π=x t y(SI)，该波在t = 0.5 s 时刻的波形图是 ［ B ］8、横波以波速u 沿x 轴负方向传播．t 时刻波形曲线如图．则该时刻 ［ D ］ (A) A 点振动速度大于零． (B) B 点静止不动． (C) C 点向下运动． (D) D 点振动速度小于零．二、填空题（共18分，每题3分）。

机械波1．提示：1(,)cos[2()]t xy x t A T πϕλ=-+，2012(,)cos[2()]x t y x t A T λπϕλ+=-+，1sin[2()],dy t xv A dtTωπϕλ==--+2112sin[2()]x dy t v A v dtTλωπϕλ+==--+=-2．提示：波速取决于媒质的性质，振动速度是媒质中质元的运动速度3．提示：由图可知O 点处质元的运动方向向下，00,0,,t t y v A ω===-sin[2],dy t v A dtTωπϕ==-+0sin(0),2v A A πωϕωϕ=-+=-=4．提示：由图可知：8,160/,3,m u m s A m λ===则120,240uH Z v T νωππλ=====由图可知O 点处质元的运动方向向上，则当0,0,sin[2()],dy t xt x v A A dtT ωπϕωλ====--+=时可得2πϕ=-5．提示：在最大位移处，胁变最小，它的速度为0，因此动能为0，对于简谐波动能等于势能。

6．提示：对于A 点的上下运动可当作机械振动，在其偏离平衡位置最大位移处其动能为0，因此A 点在向平衡位置方向运动，则可知波沿X 轴负方向传播 7．提示：12,2πϕϕ-=2121122224r r πϕϕπϕπππλλ⎛⎫⎛⎫∆=---=--⨯=- ⎪ ⎪⎝⎭⎝⎭8．提示：由波腹条件22xk k x πλπλ=±⇒=±二、填空题 １．CB ，Bπ2，Cπ2，lC ，lC -提示：将已知波的方程与波的标准方程2(,)cos[]xy x t A t πωϕλ=-+或(,)cos[()]xy x t A t uωωϕ=-+对比可得波长和波速，位相差为：222[()][]t r d t r d cdπππωϕωϕλλλ-++--+==２．Lλπϕ2-；Nk k x x ∈±=,1λ；zk k x x ∈++=,)21(1λ。

机械波试题(含答案)一、机械波选择题1．如图所示，S1和S2是两个相干波源，其振幅均为A，周期均为T．实线与虚线分别表示两列波的波峰和波谷．此刻，c是波谷与波谷的相遇点，下列说法中正确的是( )A．a处质点始终处于离平衡位置2A处B．随着时间的推移，c处的质点将向右移动C．从该时刻起，经过14T，c处的质点将通过平衡位置D．若S2不动，S1沿S1b连线向b运动，则b处质点仍然始终处于平衡位置2．振源以原点O为平衡位置，沿y轴方向做简谐运动，它激发的简谐波在x轴上沿正负两个方向传播，在某一时刻沿x轴正向传播的波形如图所示．图中所示的各个质点中，振动情况始终与原点的左方的质点P的振动情况相同的是 ( )A．a点B．b点C．c点D．d点3．一列简谐横波沿x轴负方向传播，波速v=4m/s，已知坐标原点（x=0）处质点的振动图象如图所示，在下列幅图中能够正确表示t=0.15s时波形的图是A．B．C．D．4．如图，a b c d、、、是均匀媒质中x轴上的四个质点，相邻两点的间距依次为2m4m、和6m。

一列简谐横波以2m/s的波速沿x轴正向传播，在0t=时刻到达质点a处，质点a由平衡位置开始竖直向下运动，3st=时a第一次到达最高点。

下列说法正确的是（）t=时刻波恰好传到质点d处A．在6st=时刻质点c恰好到达最高点B．在5sC．质点b开始振动后，其振动周期为4st<<的时间间隔内质点c向上运动D．在4s6sE.当质点d向下运动时，质点b一定向上运动5．一列简谐横波沿x轴正方向传播，在x=2m处的质点的振动图象如图1所示，在x=8m 处的质点的振动图象如图2所示，下列说法正确的是（）A．该波的传播速度可能为2m/sB．x=2m处的质点在平衡位置向+y方向振动时，x=8m处的质点在波峰C．该波的波长可能为8mD．在0～4s内x=2m处和x=8m处的质点通过的路程均为6cm6．一列简谐横波沿直线传播，该直线上的a、b两点相距4.42m。

选修1高中物理《机械波》测试题(含答案)一、机械波 选择题1．一列简谐横波在均匀介质中沿x 轴负方向传播，已知54x λ=处质点的振动方程为2πcos()y A t T =，则34t T =时刻的波形图正确的是（ ） A ． B ．C ．D ．2．一列简谐横波沿直线传播，该直线上的a 、b 两点相距4.42m 。

图中实、虚两条曲线分别表示平衡位置在a 、b 两点处质点的振动曲线。

从图示可知（ ）A ．此列波的频率一定是10HzB ．此列波的波长一定是0.1mC ．此列波的传播速度可能是34m /sD ．a 点一定比b 点距波源近3．如图所示，坐标原点处的波源0t =时开始从平衡位置沿y 轴做简谐运动，0.5s t =时在0cm x =和7cm x =之间第一次出现了如图所示的波形，7cm x >部分的波形图没有画出，则下列说法正确的是 。

A ．0.5s t =时，这列波一定刚好传到8cm x =处B ．这列波的周期可能为0.25s T =C ．这列波的波速可能为0.2m/s v =D ．0.5s t =时，3cm x =处的质点一定是第二次位于波谷E.若此波传入另一介质中其波速变为0.4m/s，则它在该介质中的波长一定为8cm4．处于坐标原点的波源产生一列沿x轴正方向传播的简谐横波,波速v=200m/s．已知t=0时,波刚传播到x=40m处,波形如图所示．在x=400m处有一接收器(图中未画出),则下列说法正确的是．A．波源开始振动时方向沿y轴负方向B．接收器在t=2s时才能接收此波C．若波源向x轴正方向匀速运动,接收器收到波的频率大于10HzD．从t=0开始经0.15s,x=40m的质点运动的路程为0.6mE.当t=0.75s时，x=40m的质点恰好到达波谷的位置5．一列沿x轴传播的简谐横波，t=0时刻的波形如图中实线所示，t=0.2s时刻的波形如图中的虚线所示，则：（）A．各质点均沿x轴方向运动B．波的周期可能为4 15sC．波的频率可能为1.25HzD．波的传播速度可能为4.5m/s6．一列横波沿x轴传播，图中实线表示t=0时刻的波形，虚线表示从该时刻起经0.005s 后的波形______．A．该横波周期为0.02秒B．t=0时刻，x=4m处的质点的振动方向一定与x=8m处的质点振动方向相反C．t=0时刻，x=4m处的质点向上运动D．如果周期大于0.005s，波向右传播时，波速为400m/sE.如果周期小于0.005s，则当波速为6000m/s时，该波向左传播7．一列向右传播的横波在t=0时的波形如图所示，A、B两质点间距为8m，B、C两质点在平衡位置的间距为3m，当t=1s时，质点C恰好通过平衡位置，该波的波速可能为（）A ．1/3m s B ．3m/s C ．13m/s D ．27m/s8．甲、乙两列简谐横波在同一介质中同向独立传播，传播方向沿x 轴正方向。