C16055 课后测验90分

上海市初三数学二模虹口区学年度第二学期期中教学质量监控测试初三数学考试及评分标准————————————————————————————————作者：————————————————————————————————日期：虹口区2017学年度第二学期期中教学质量监控测试初三数学 试卷（满分150分，考试时间100分钟）2018.04考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计 算的主要步骤．一、选择题：（本大题共6题，每题4分，满分24分）[下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．]1．下列实数中，有理数是 A ．3； B ．39； C ．π； D ．0．2．如果关于x 的一元二次方程220x x k -+=有两个不相等的实数根，那么k 的取值范围是A ．1k <；B ．10k k <≠且；C ．1k >；D ．10k k >≠且.3．如果将抛物线2y x =向左平移1个单位，那么所得新抛物线的表达式是 A ．21y x =+；B ．21y x =-；C ．2(1)y x =+；D ．2(1)y x =-.4．如图，是某中学九（3）班学生外出方式（乘车、步行、骑车）的不完整频数（人数）分布直方图．如果乘车的频率是0.4，那么步行的频率为 A ．0.4；B ．0.36；C ．0.3；D ．0.24.5．数学课上，小明进行了如下的尺规作图（如图所示）：（1）在△AOB （OA <OB ）边OA 、OB 上分别截取OD 、OE ，使得OD=OE ；（2）分别以点D 、E 为圆心，以大于12DE 为半径作弧，两弧交于△AOB 内的一点C ；（3）作射线OC 交AB 边于点P ．那么小明所求作的线段OP 是△AOB 的 A ．一条中线；B ．一条高；C ．一条角平分线；D ．不确定．6．如图，在矩形ABCD 中，点E 是CD 的中点，联结BE ，如果AB =6，BC =4，那么分别以AD 、BE 为直径的⊙M 与⊙N 的位置关系是 A ．外离；B ．外切；C ．相交；D ．内切．人数 出行方式 0乘车 步行 骑车 12 20 第4AO B DECP 第5A CD B第6E二、填空题：（本大题共12题，每题4分，满分48分）[请将结果直接填入答题纸的相应位置] 7．计算：26a a ÷= ▲ .8. 某病毒的直径是0.000 068毫米，这个数据用科学记数法表示为 ▲ 毫米.9．不等式组1,2 4.x x ->⎧⎨<⎩的解集是 ▲ .10．方程2x x -+=的解为 ▲ ． 11．已知反比例函数3ay x-=，如果当0x >时，y 随自变量x 的增大而增大，那么a 的取值范围为 ▲ ．12．请写出一个图像的对称轴为y 轴，开口向下，且经过点（1，-2）的二次函数解析式，这个二次函数的解析式可以是 ▲ ． 13. 掷一枚材质均匀的骰子，掷得的点数为素数的概率是 ▲ ．14. 在植树节当天，某校一个班的学生分成10个小组参加植树造林活动，如果10个小组植树的株数情况见下表，那么这10个小组植树株数的平均数是 ▲ 株．15．如果正六边形的两条平行边间的距离是23,那么这个正六边形的边长为 ▲ ． 16．如图，在□ABCD 中，对角线AC 与BD 相交于点O ，如果AC a =，BD b =，那么用向量a 、b 表示向量AB 是 ▲ ．17．如图，在Rt △ABC 中，∠ACB =90°，AB=10，sin A =35，CD 为AB 边上的中线，以点B 为圆心，r 为半径作⊙B ．如果⊙B 与中线CD 有且只有一个公共点，那么⊙B 的半径r 的取值范围为 ▲ ．18．如图，在△ABC 中，AB ＝AC ，BC=8，tan B 32=，点D 是AB 的中点，如果把△BCD 沿直线CD 翻折，使得点B 落在同一平面内的B ′处，联结A B ′，那么A B ′的长为 ▲ ．三、解答题（本大题共7题，满分78分） 19．（本题满分10分）先化简，再求值：2344(1)11a a a a a -+--÷++，其中3a =．植树株数（株） 5 6 7 小组个数343A C D第17BAB C第18DA CO第16B D① ②EG第23CABD Fx （小y （千O 604第22题AB20．（本题满分10分）解方程组：22444,2 6.x xy y x y ⎧-+=⎨+=⎩21．（本题满分10分）如图，在△ABC 中，4sin 5B =，点F 在BC 上，AB=AF=5，过点F 作EF ⊥CB 交AC 于点E ，且:3:5AE EC =，求BF 的长与sin C 的值．22．（本题满分10分，第（1）小题6分，第（2）小题4分）甲、乙两车需运输一批货物到600公里外的某地，原计划甲车的速度比乙车每小时多10千米，这样甲车将比乙车早到2小时．实际甲车以原计划的速度行驶了4小时后，以较低速度继续行驶，结果甲、乙两车同时到达． （1）求甲车原计划的速度； （2）如图是甲车行驶的路程y （千米）与时间x （小时） 的不完整函数图像，那么点A 的坐标为 ▲ ， 点B 的坐标为 ▲ ，4小时后的y 与x 的函数关 系式为 ▲ （不要求写定义域）．23．（本题满分12分，第（1）小题6分，第（2）小题6分）如图，四边形ABCD 是矩形，E 是对角线AC 上的一点，EB =ED 且∠ABE =∠ADE ． （1）求证：四边形ABCD 是正方形；（2）延长DE 交BC 于点F ，交AB 的延长线于点G ，求证：EF AG BC BE ⋅=⋅．C第21题BFE第25CA BDM G 24．（本题满分12分，第（1）小题4分，第（2）小题4分，第（3）小题4分）如图，在平面直角坐标系xOy 中，抛物线22y ax x c =-+与直线132y x =-+分别交于x 轴、y 轴上的B 、C 两点，抛物线的顶点为点D ，联结CD 交x 轴于点E ． （1）求抛物线的解析式以及点D 的坐标； （2）求tan ∠BCD ；（3）点P 在直线BC 上，若∠PEB=∠BCD ，求点P 的坐标．25．（本题满分14分，第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在梯形ABCD 中，AD ∥BC ，∠C =90°，DC =5，以CD 为半径的⊙C 与以AB 为半径的⊙B 相交于点E 、F ，且点E 在BD 上，联结EF 交BC 于点G ． （1）设BC 与⊙C 相交于点M ，当BM=AD 时，求⊙B 的半径；（2）设BC= x ，EF=y ，求y 关于x 的函数关系式，并写出它的定义域；（3）当BC =10时，点P 为平面内一点，若⊙P 与⊙C 相交于点D 、E ，且以A 、E 、P 、D 为顶点的四边形是梯形，请直接写出⊙P 的面积．（结果保留π）第24xB y OC DE虹口区2017学年度第二学期期中教学质量监控测试初三数学评分参考建议2018.4说明：1．解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照解答中评分标准相应评分；2．第一、二大题若无特别说明，每题评分只有满分或零分；3．第三大题中各题右端所注分数，表示考生正确做对这一步应得分数；4．评阅试卷，要坚持每题评阅到底，不能因考生解答中出现错误而中断对本题的评阅．如果考生的解答在某一步出现错误，影响后继部分而未改变本题的内容和难度，视影响的程度决定后继部分的给分，但原则上不超过后继部分应得分数的一半； 5．评分时，给分或扣分均以1分为基本单位．一、选择题（本大题共6题，每题4分，满分24分）1．D 2．A 3．C 4．B 5．C 6．B二、填空题本大题共12题，每题4分，满分48分） 7．4a8．56.810-⨯9．1x <- 10．1x =11．3a > 12． 21y x =-- 等（答案不唯一） 13．12 14．615．216．1122a b - 17．56r <≤或245r =18．255三、解答题（本大题共7题，满分78分）19．解：原式=22131144a a a a a --+⋅+-+ ………………………………………………………（3分） 2(2)(2)11(2)a a a a a +-+=⋅+- ………………………………………………………（3分）22a a +=-…………………………………………………………………………… （2分） 当3a =时, 原式=3274332+=---…………………………………………… （2分）．20．解：由①得，22x y -=或22x y -=-……………………………………………（2分） 将它们与方程②分别组成方程组，得： ,262;2x x y y ⎧⎨+=-=⎩22,2 6.y y x x ⎧⎨+=-=-⎩……………………………………………………（4分）分别解这两个方程组， 得原方程组的解为114,1;x y =⎧⎨=⎩ 222,2.x y =⎧⎨=⎩． …………………………………………（4分）（代入消元法参照给分）21．解：过点A 作AD ⊥CB ，垂足为点D∵4sin 5B =∴3cos 5B =……………………………………………………（1分） 在Rt △ABD 中，3cos 535BD AB B =⋅=⨯=…………………………………（2分）∵AB=AF AD ⊥CB ∴BF =2BD =6 ………………………………………（1分）∵EF ⊥CB AD ⊥CB ∴EF ∥AD ∴DF AECF EC= …………………（2分）∵:3:5AE EC = DF=BD=3 ∴CF=5 ∴CD=8………………………（1分）在Rt △ABD 中，4sin 545AD AB B =⋅=⨯=……………………………………（1分）在Rt △ACD 中，2245AC AD CD =+= ……………………………………（1分）∴5sin 5AD C AC ==………………………………………………………………（1分）22．解：（1）设甲车原计划的速度为x 千米/小时由题意得600600210x x -=-…………………………………………………………（3分）解得150x =- 260x = 经检验，150x =- 260x =都是原方程的解，但150x =-不符合题意，舍去 ∴60x = ……………………………………………………………………………（2分）答：甲车原计划的速度为60千米/小时．………………………………………（1分） （2）（4，240） （12，600） …………………………………………………（1分，1分）4560y x =+…………………………………………………………………………（2分）23．（1）证明：联结BD …………………………………………………………………（1分）∵EB =ED ∴∠EBD =∠EDB …………………………………………………（2分） ∵∠ABE =∠ADE ∴∠ABD =∠ADB …………………………………………（1分） ∴AB=AD …………………………………………………………………………（1分） ∵四边形ABCD 是矩形 ∴四边形ABCD 是正方形………………………（1分） （2）证明：∵四边形ABCD 是矩形∴AD ∥BC ∴EF ECDE EA =………………………………………………（2分）同理 DC EC AG EA =……………………………………………………………（2分）∵DE=BE∵四边形ABCD 是正方形 ∴BC=DC …………………………………………（1分） ∴EF BC BE AG =∴EF AG BC BE ⋅=⋅ ……………………………………………………………（1分）24．解：（1）由题意得B （6，0） C （0，3） ………………………………………（1分） 把B （6，0） C （0，3）代入22y ax x c =-+得03612,3.a c c =-+⎧⎨=⎩ 解得1,43.a c ⎧=⎪⎨⎪=⎩ ∴21234y x x =-+……………………………………………………………（2分）∴D （4，-1） ………………………………………………………………（1分）（2）可得点E （3,0） ………………………………………………………………（1分）OE=OC=3，∠OEC =45°过点B 作BF ⊥CD ，垂足为点F在Rt △OEC 中，32cos OE EC CEO ==∠在Rt △BEF 中，3sin 22BF BE BEF =∠= ……………………………………（1分）同理，322EF =∴39322222CF =+=……………………………………·（1分）在Rt △CBF 中，1tan 3BF BCD CF ∠==…………………………………………（1分）（3）设点P （m ，132m -+）∵∠PEB=∠BCD ∴tan ∠PEB= tan ∠BCD 13=①点P 在x 轴上方∴131233m m -+=-解得245m = ………………………………………………（1分） ∴点P 243(,)55 ………………………………………………………………………（1分）②点P 在x 轴下方 ∴131233m m -=- 解得12m =…………………………………………………（1分） ∴点P (12,3)- ………………………………………………………………………（1分）综上所述，点P 243(,)55或(12,3)-25．（1）联结DM在Rt △DCM 中，2252DM DC CM =+= …………………………………（2分）∵AD ∥BC BM =AD ∴四边形ABMD 为平行四边形……………………（1分） ∴AB= DM =52即⊙B 的半径为52……………………………………………………………（1分） （2）过点C 作CH ⊥BD ，垂足为点H在Rt △BCD 中，22225BD BC CD x =+=+∴25sin 25DBC x ∠=+可得∠DCH =∠DBC ∴25sin 25DCH x ∠=+在Rt △DCH 中，225sin 25DH DC DCH x =⋅∠=+…………………………（1分）∵CH ⊥BD ∴250225DE DH x ==+…………………………………………（1分） ∴22225025252525x BE x x x -=+-=++ ………………………………………（1分）∵⊙C 与⊙B 相交于点E 、F ∴EF=2EG BC ⊥EF在Rt △EBG 中，225125sin 25x EG BE DBC x -=⋅∠=+ …………………………（1分）∴221025025x y x -=+（53x >）…………………………………………（1分，1分）（3）254π或(2985)π-或(75+305)π………………………………………（做对一个得2分，其余1分一个）。

2025届吉林省延边物理九年级第一学期期末达标检测模拟试题请考生注意：1．请用2B铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题1．以下的四个实例中，机械能正在减小的是A．蓄势待发的火箭B．水平匀速飞行的小鸟C．匀速下降的气球D．加速上升的飞艇2．如图所示的电路中，闭合开关S后电路正常工作。

一段时间后发现电流表的示数变成了0A而电压表的示数变大。

假定电路中只有一处故障，则故障可能是A．R1断路B．R2断路C．电流表断路D．电压表断路3．下列做法中容易发生危险的是（）A．不靠近高压带电体B．雷雨天在大树下避雨C．把电热水器的金属外壳接地D．发现有人触电时先切断电源4．一个电炉的电阻是200Ω，通电10s产生8×103J的热量，那么通过这只电炉的电流是（）A．2A B．4A C．20A D．40A5．如图所示的电路图，电源电压不变，闭合开关S，当滑动变阻器滑片P向右移动时，下列判断正确的是（）A．电流表A的示数变大B．电压表V1示数变大C．电路中消耗的总功率变小D．电压表V2与电流表A的示数之比变大6．在家庭电路中，可能会出现这些情况（1）开关中的两个线头相碰（2）插头中的两个线头相碰（3）电路中增加了大功率的用电器（4）户外输电线绝缘皮损坏在上述情况中，可能引起家庭电路中保险丝熔断的是A．（1）、（2）B．（2）、（3）C．（2）、（4）D．（1）、（4）7．烈日炎炎的夏季，白天海滩上的沙子热得烫脚，海水却很凉爽，傍晚，沙子很快凉了，但海水却仍然暖暖的。

同样的日照条件下，沙子和海水的温度不一样的原因（）A．沙子的密度比海水的密度大B．沙子的比热容比海水的比热容大C．沙子的比热容比海水的比热容小D．沙子的质量比海水的质量小8．如图所示，几个同学在只有电流表或电压表时，利用一个已知阻值的电阻R0设计了四个测未知电阻R x的电路，其中不可行的是（）A．B．C．D．9．科学家探索自然界的秘密，要付出艰辛的努力，十九世纪英国科学家法拉第，经过十年坚持不懈的努力，发现了电磁感应现象，下图中能表明这一现象的实验是（）A．B．C．D．10．如图所示，先后将不同材料接在电路的A、B两点间，闭合开关，能使小灯泡发光的是A．干木条B．铜丝C．塑料棒D．陶瓷棒11．关于磁场与磁感线的描述错误的是（）A．磁感线是磁场中真实存在的一些曲线B．磁感线分布越密集的地方表示磁场越强C．奥斯特实验表明通电导体周围存在磁场D．通电螺线管外部的磁场与条形磁铁的磁场分布相似12．如图所示，将一圆柱体从水中匀速提起直至下表面刚好离开水面，此过程容器底受到水的压强p随时间t变化的图像大致如下列图中的（）A．B． C．D．二、填空题13．一遥控小电动车在平直的路面上做直线运动，其速度v随时间t变化的图象如图所示。

自评量表[指导语]以下列出了有些人可能会有的问题，请仔细阅读每一条，然后根据最近一星期来自己的实际感觉，选择最符合您的一种情况，在5个方格中选择一格，画一个“”号。

然后将每题得分填在测验答案纸中相应题号的评分栏中，其中“无”记0分，“轻度”记1分，“中度”记2分，“相当重”记3分，“严重”记4分。

无轻中比严较度度重重0 1 2 3 41.头痛□□□□□2.；3.神经过敏，心中不踏实□□□□□4.头脑中有不必要的想法或字句盘旋□□□□□5.头晕或晕倒□□□□□6.对异性的兴趣减退□□□□□7.对旁人责备求全□□□□□8.感到别人能控制您的思想□□□□□9.责怪别人制造麻烦□□□□□10.《11.忘性大□□□□□12.担心自己的衣饰整齐及仪态的端正□□□□□13.容易烦恼和激动□□□□□14.胸痛□□□□□15.害怕空旷的场所或街道□□□□□16.感到自己的精力下降，活动减慢□□□□□17.想结束自己的生命□□□□□~18.听到旁人听不到的声音□□□□□19.发抖□□□□□20.感到大多数人都不可信任□□□□□21.胃口不好□□□□□22.容易哭泣□□□□□23.同异性相处时感到害羞不自在□□□□□24.；25.感到受骗、中了圈套或有人想抓住您□□□□□26.无缘无故地突然感到害怕□□□□□27.自己不能控制地发脾气□□□□□28.怕单独出门□□□□□29.经常责怪自己□□□□□30.腰痛□□□□□31.感到难以完成任务□□□□□#无轻中比严较度度重重0 1 2 3 4 32.感到孤独□□□□□33.感到苦闷□□□□□34.过分担忧□□□□□35.~36.对事物不感兴趣□□□□□37.感到害怕□□□□□38.感情容易受到伤害□□□□□39.旁人能知道您的私下想法□□□□□40.感到别人不理解您、不同情您□□□□□41.感到人们对您不友好，不喜欢您□□□□□42.做事必须做得很慢以保证做得正确□□□□□43.{44.心跳得很厉害□□□□□45.恶心或胃部不舒服□□□□□46.感到比不上他人□□□□□47.肌肉酸痛□□□□□48.感到有人在监视您、谈论您□□□□□49.难以入睡□□□□□50.做事必须反复检查□□□□□【51.难以作出决定□□□□□52.怕乘电车、公共汽车、地铁或火车□□□□□53.呼吸有困难□□□□□54.一阵阵发冷或发热□□□□□55.因为感到害怕而避开某些东西、场合或活动□□□□□56.脑子变空了□□□□□57.>58.身体发麻或刺痛□□□□□59.喉咙有梗塞感□□□□□60.感到没有前途没有希望□□□□□61.不能集中注意力□□□□□62.感到身体的某一部分软弱无力□□□□□63.感到紧张或容易紧张□□□□□64.感到手或脚发重□□□□□65.《66.想到死亡□□□□□67.吃得太多□□□□□68.当别人看着您或谈论您时感到不自在□□□□□无轻中比严较度度重重0 1 2 3 469.）70.有一些不属于您自己的想法□□□□□71.有想打人或伤害他人的冲动□□□□□72.醒得太早□□□□□73.必须反复洗手、点数目或触摸某些东西□□□□□74.睡得不稳不深□□□□□75.有想摔坏或破坏东西的冲动□□□□□76.有一些别人没有的想法或念头□□□□□77.&78.感到对别人神经过敏□□□□□79.在商店或电影等人多的地方感到不自在□□□□□80.感到任何事情都很困难□□□□□81.一阵阵恐惧或惊恐□□□□□82.感到在公共场合吃东西很不舒服□□□□□83.经常与人争论□□□□□84.单独一人时神经很紧张□□□□□~85.别人对您的成绩没有作出恰当的评价□□□□□86.即使和别人在一起也感到孤单□□□□□87.感到坐立不安心神不定□□□□□88.感到自己没有什么价值□□□□□89.感到熟悉的东西变成陌生或不像是真的□□□□□90.大叫或摔东西□□□□□91.\92.害怕会在公共场合晕倒□□□□□93.感到别人想占您的便宜□□□□□94.为一些有关“性”的想法而很苦恼□□□□□95.您认为应该因为自己的过错而受到惩罚□□□□□96.感到要赶快把事情做完□□□□□97.感到自己的身体有严重问题□□□□□98.从未感到和其他人很亲近□□□□□99.。

2025 IHC 6培训题答案1. 计算：12111413171111141100⎡⎤⎛⎫⎢⎥ ⎪÷+-÷÷=⎢⎥ ⎪⎢⎥ ⎪-⎢⎥⎝⎭⎣⎦________。

答案：32. 求下面式子的值。

211221122112++++++答案：4 3. 计算：777101515203540=________。

答案：212004. 计算：2222222235719122334910++++⨯⨯⨯⨯=________。

答案：0.995. 定义运算22*4a b a b m =+，594*312=，则3*4=________。

答案：1126. 定义新运算“⊕”：, (), ()a ab a b b a b ≥⎧⊕=⎨<⎩若若，例如：6.52 6.5⊕=，177⊕=。

则712.3+0.13640.59⊕⊕⊕=________。

答案：57. 一个最简分数，分子和分母的和是38，如果分子和分母都减去5，得到的分数化简后是34，则原分数是________。

答案：17218. 将a 的小数部分记为{a }，如{5.3}=0.3。

若3{x }+5x =9，则x =________。

答案：1.59. 已知x ，y 满足[]2024x y +=，{}20.24x y +=，其中[]x 表示不大于x 的最大整数，{}x 表示x 的小数部分，即{}[]x x x =-，那么x =________。

答案：200410. 当自然数n 的值依次取1，2，3，…，2015时，算式[][][]235n n n++有________个不同的值。

（注：[]x 表示不超过x 的最大的自然数） 答案：147911. 在算式（A □B ）△（C ○D ）中，□、△、○分别代表三个互不相同的四则运算符号（加减乘除），A ，B ，C ，D 是4个互不相同的非零整数。

如果无论□、△、○是什么符号，计算结果都是整数，那么四位数ABCD 是________。

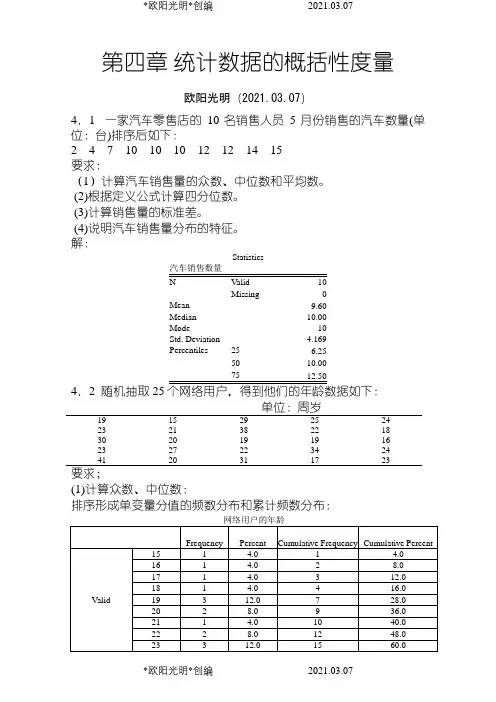
第四章统计数据的概括性度量欧阳光明（2021.03.07）4．1 一家汽车零售店的10名销售人员5月份销售的汽车数量(单位：台)排序后如下：2 4 7 10 10 10 12 12 14 15要求：（1）计算汽车销售量的众数、中位数和平均数。

(2)根据定义公式计算四分位数。

(3)计算销售量的标准差。

(4)说明汽车销售量分布的特征。

解：StatisticsMissing0Mean9.60Median10.00Mode10Std. Deviation 4.169Percentiles25 6.255010.007512.504．2 随机抽取25个网络用户，得到他们的年龄数据如下：单位：周岁19 15 29 25 2423 21 38 22 1830 20 19 19 1623 27 22 34 2441 20 31 17 23要求；(1)计算众数、中位数：排序形成单变量分值的频数分布和累计频数分布：网络用户的年龄从频数看出，众数Mo 有两个：19、23；从累计频数看，中位数Me=23。

(2)根据定义公式计算四分位数。

Q1位置=25/4=6.25，因此Q1=19，Q3位置=3×25/4=18.75，因此Q3=27，或者，由于25和27都只有一个，因此Q3也可等于25+0.75×2=26.5。

(3)计算平均数和标准差；Mean=24.00；Std. Deviation=6.652 (4)计算偏态系数和峰态系数： Skewness=1.080；Kurtosis=0.773(5)对网民年龄的分布特征进行综合分析：分布，均值=24、标准差=6.652、呈右偏分布。

如需看清楚分布形态，需要进行分组。

为分组情况下的直方图：为分组情况下的概率密度曲线： 分组：1、确定组数：()lg 25lg() 1.398111 5.64lg(2)lg 20.30103n K =+=+=+=，取k=62、确定组距：组距＝( 最大值 最小值)÷ 组数=（4115）÷6=4.3，取53、分组频数表网络用户的年龄 (Binned)分组后的均值与方差：分组后的直方图：4．3 某银行为缩短顾客到银行办理业务等待的时间。

北京市西城区北京师范大附属中学2025届九年级数学第一学期期末质量跟踪监视模拟试题注意事项1．考生要认真填写考场号和座位序号。

2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。

第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。

3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题(每小题3分,共30分)1．如图，AB 是O 的弦，半径OC AB ⊥于点D ，且8,O 5,AB cm C cm DC ==的长是（ ）A ．4cmB ．3cmC ．2cmD ．1cm2．下图中，不是中心对称图形的是（ ）A ．B ．C ．D ．3．如图直线y ＝mx 与双曲线y=kx 交于点A 、B ，过A 作AM ⊥x 轴于M 点，连接BM ，若S △AMB ＝2，则k 的值是()A ．1B ．2C ．3D ．44．使分式有意义的x 的取值范是（ ）A ．x ≠3B ．x ＝3C ．x ≠0D ．x ＝05．将抛物线23y x =-的图象向右平移1个单位，再向下平移两个单位后，则所得抛物线解析式为（ ） A ．23(1)2y x =--- B ．23(1)2y x =--+ C ．23(1)2y x =-+- D ．23(1)2y x =-++6．将抛物线22y x =-通过一次平移可得到抛物线2(3)2y x =--．对这一平移过程描述正确的是（ ） A ．沿x 轴向右平移3个单位长度B ．沿x 轴向左平移3个单位长度C ．沿y 轴向上平移3个单位长度D ．沿y 轴向下平移3个单位长度7．下列说法正确的是（ ）A ．“任意画出一个等边三角形，它是轴对称图形”是随机事件B ．某种彩票的中奖率为11000，说明每买1000张彩票，一定有一张中奖C ．抛掷一枚质地均匀的硬币一次，出现正面朝上的概率为13D ．“概率为1的事件”是必然事件8．将抛物线y ＝2x 2向左平移3个单位得到的抛物线的解析式是( )A ．y ＝2x 2+3B ．y ＝2x 2﹣3C ．y ＝2(x+3)2D ．y ＝2(x ﹣3)29．如图，等边△ABC 的边长为6，P 为BC 上一点，BP=2，D 为AC 上一点，若∠APD=60°，则CD 的长为（ ）A ．2B ．C ．D ．110．在△ABC 中，若|sinA ﹣12|+（22﹣cosB ）2=0，则∠C 的度数是（ ） A ．45° B ．75°C ．105°D ．120° 二、填空题(每小题3分,共24分)11．有五张分别印有等边三角形、正方形、正五边形、矩形、正六边形图案的卡片（这些卡片除图案不同外，其余均相同）．现将有图案的一面朝下任意摆放，从中任意抽取一张，抽到卡片的图案既是中心对称图形，又是轴对称图形的概率为_____．12．如图，在等腰直角△ABC 中，∠C ＝90°，将△ABC 绕顶点A 逆时针旋转80°后得到△AB′C′，则∠CAB′的度数为_____．13．如图，△ABC 是直角三角形，BC 是斜边，将△ABP 绕点A 逆时针旋转后，恰好能与△ACP ′完全重合，如果AP =8，则PP ′的长度为___________．14．将二次函数y ＝2x 2的图像向上平移3个单位长度，再向右平移2个单位长度，得到的图像所对应的函数表达式为____．15．如图，将ABC ∆绕点A 逆时针旋转140，得到ADE ∆，这时点,,B C D 恰好在同一直线上，则B 的度数为______．16．如图所示，在平面直角坐标系中，正方形OABC 的顶点O 与原点重合，顶点A ，C 分别在x 轴、y 轴上，双曲线y ＝kx ﹣1（k≠0，x ＞0）与边AB 、BC 分别交于点N 、F ，连接ON 、OF 、NF ．若∠NOF ＝45°，NF ＝2，则点C 的坐标为_____．17．将抛物线 y ＝（x+2）2-5向右平移2个单位所得抛物线解析式为_____．18．如图，已知ABC ∆的面积为48，将ABC ∆沿BC 平移到'''A B C ∆，使'B 和C 重合，连结'AC 交AC 于D ，则'C DC ∆的面积为__________．三、解答题(共66分)19．（10分）（1）（教材呈现）下图是华师版九年级上册数学教材第77页的部分内容．请根据教材提示，结合图23.4.2，写出完整的证明过程．（2）（结论应用）如图，△ABC是等边三角形，点D在边AB上（点D与点A、B不重合），过点D作DE∥BC交AC 于点E，连结BE，M、N、P分别为DE、BE、BC的中点，顺次连结M、N、P．①求证：MN＝PN；②∠MNP的大小是．20．（6分）解方程：（1）x2﹣4x﹣1＝0；（2）5x（x﹣1）＝x﹣1．21．（6分）如图1，抛物线y=﹣x2+bx+c交x轴于点A(- 4，0)和点B，交y轴于点C(0，4)．(1)求抛物线的函数表达式；(2)如图2，设点Q是线段AC上的一动点，作DQ⊥x轴，交抛物线于点D，当△ADC面积有最大值时，在抛物线对称轴上找一点M，使DM+AM的值最小，求出此时M的坐标；(3)点Q在直线AC上的运动过程中，是否存在点Q，使△BQC为等腰三角形？若存在，直接写出点Q的坐标；若不存在，请说明理由.22．（8分）定义：有一组邻边相等的凸四边形叫做“准菱形”，利用该定义完成以下各题：（1）理解：如图1，在四边形ABCD中，若__________（填一种情况），则四边形ABCD是“准菱形”；（2）应用：证明：对角线相等且互相平分的“准菱形”是正方形；（请画出图形，写出已知，求证并证明）（3）拓展：如图2，在Rt△ABC中，∠ABC=90°，AB=2，BC=1，将Rt△ABC沿∠ABC的平分线BP方向平移得到△DEF，连接AD，BF，若平移后的四边形ABFD是“准菱形”，求线段BE的长．23．（8分）如图，Rt△ABC中，∠ABC＝90°，以AB为直径作⊙O交AC于点D，连接BD．（1）求证：∠A＝∠CBD．（2）若AB＝10，AD＝6，M为线段BC上一点，请写出一个BM的值，使得直线DM与⊙O相切，并说明理由．24．（8分）如图1，在矩形ABCD中，AE⊥BD于点E.（1）求证：BE⋅BC＝AE⋅CD．（2）如图2，若点P是边AD上一点，且PE⊥EC，求证：AE⋅AB＝DE⋅AP.25．（10分）作出函数y＝2x2的图象，并根据图象回答下列问题：（1）列表：x ……y … …（2）在下面给出的正方形网格中建立适当的平面直角坐标系，描出列表中的各点，并画出函数y ＝2x 2的图象：（3）观察所画函数的图象，当﹣1＜x ＜2时，y 的取值范围是 （直接写出结论）．26．（10分）解方程：（1）2410x x -=+（2）2(2)3(2)0x x x ---=参考答案一、选择题(每小题3分,共30分)1、C【分析】利用勾股定理和垂径定理即可求解．【详解】∵OC AB ⊥，8AB cm =∴AD=4cm在Rt △AOD 中，OA 2＝OD 2＋AD 2，∴25＝（5−DC ）2＋16，∴DC ＝2cm ．故选：C ．【点睛】主要考查了垂径定理的运用．垂径定理：垂直于弦的直径平分这条弦，并且平分这条弦所对的两条弧．解此类题一般要把半径、弦心距、弦的一半构建在一个直角三角形里，运用勾股定理求解．2、D【解析】根据把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形可得答案．【详解】A、是中心对称图形，故此选项不合题意；B、是中心对称图形，故此选项不合题意；C、是中心对称图形，故此选项不合题意；D、不是中心对称图形，故此选项符合题意；故选：D．【点睛】考查了中心对称图形，关键是掌握中心对称图形定义．3、B【解析】此题可根据反比例函数图象的对称性得到A、B两点关于原点对称，再由S△ABM=1S△AOM并结合反比例函数系数k的几何意义得到k的值．【详解】根据双曲线的对称性可得：OA=OB,则S△ABM＝1S△AOM＝1，S△AOM＝12|k|＝1，则k＝±1．又由于反比例函数图象位于一三象限，k＞0，所以k＝1．故选B．【点睛】本题主要考查了反比例函数y＝kx中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点．4、A【解析】直接利用分式有意义的条件进而得出答案．【详解】分式有意义，则1-x≠0，解得：x≠1．故选A．【点睛】此题主要考查了分式有意义的条件，正确把握分式的定义是解题关键．5、A【分析】根据二次函数图像左加右减，上加下减的平移规律即可确定答案．【详解】解：抛物线y=-3x 2向右平移1个单位的解析式为：y=-3（x-1）2；再向下平移2个单位，得：y=-3（x-1）2-2.故选：A ．【点睛】本题主要考查了二次函数图像的平移，掌握“左加右减，上加下减”的平移规律是解答本题的关键．6、A【分析】分别确定出两个抛物线的顶点坐标，再根据左减右加，确定平移方向即可得解．【详解】解：抛物线22y x =-的顶点坐标为（0，−2），抛物线2(3)2y x =--的顶点坐标为（3，-2），所以，向右平移3个单位，可以由抛物线22y x =-平移得到抛物线2(3)2y x =--．故选：A ．【点睛】本题考查了二次函数图象与几何变换，利用点的平移规律左减右加，上加下减解答是解题的关键．7、D【解析】试题解析：A 、“任意画出一个等边三角形，它是轴对称图形”是必然事件，选项错误；B. 某种彩票的中奖概率为11000，说明每买1000张，有可能中奖，也有可能不中奖，故B 错误； C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为12.故C 错误； D. “概率为1的事件”是必然事件,正确.故选D.8、C 【解析】按照“左加右减，上加下减”的规律，从而选出答案.【详解】y ＝2x 2向左平移3个单位得到的抛物线的解析式是y ＝2（x ＋3）2，故答案选C.【点睛】本题主要考查了抛物线的平移以及抛物线解析式的变换规律，解本题的要点在于熟知“左加右减，上加下减”的变化规律.9、B【解析】由等边三角形的性质结合条件可证明△ABP ∽△PCD ，由相似三角形的性质可求得CD ．【详解】∵△ABC 为等边三角形，∴又∵∠APD+∠DPC=∠B+∠BAP,且∴∠BAP=∠DPC，∴△ABP∽△PCD，∴∵AB=BC=6，BP=2，∴PC=4，∴∴故选:B.【点睛】考查相似三角形的判定与性质，掌握相似三角形的判定定理是解题的关键.10、C【解析】根据非负数的性质列出关系式，根据特殊角的三角函数值求出∠A、∠B的度数，根据三角形内角和定理计算即可．【详解】由题意得，sinA-12=0，22-cosB=0，即sinA=12，22=cosB，解得，∠A=30°，∠B=45°，∴∠C=180°-∠A-∠B=105°，故选C．【点睛】本题考查的是非负数的性质的应用、特殊角的三角函数值的计算和三角形内角和定理的应用，熟记特殊角的三角函数值是解题的关键．二、填空题(每小题3分,共24分)11、3 5【解析】判断出即是中心对称，又是轴对称图形的个数，然后结合概率计算公式，计算，即可．【详解】解：等边三角形、正方形、正五边形、矩形、正六边形图案中既是中心对称图形，又是轴对称图形是：正方形、矩形、正六边形共3种， 故从中任意抽取一张，抽到卡片的图案既是中心对称图形，又是轴对称图形的概率为：． 故答案为．【点睛】考查中心对称图形和轴对称图形的判定，考查概率计算公式，难度中等．12、125°【分析】根据等腰直角三角形的性质得到∠CAB ＝45°，根据旋转的性质得到∠BAB′＝80°，结合图形计算即可．【详解】解：∵△ABC 是等腰直角三角形，∴∠CAB ＝45°，由旋转的性质可知，∠BAB′＝80°，∴∠CAB′＝∠CAB+∠BAB′＝125°，故答案为：125°．【点睛】本题考查旋转的性质,关键在于熟练掌握基础性质.13、82【分析】通过旋转的性质可以得到，'90BAC PAP ∠=∠=，'AP AP =，从而可以得到'PAP 是等腰直角三角形，再根据勾股定理可以计算出PP '的长度．【详解】解：根据旋转的性质得：'90BAC PAP ∠=∠=，'AP AP =∴'PAP 是等腰直角三角形，∴'8AP AP ==∴()()222AP AP PP '='+ ∴228882PP =+='故答案为：82【点睛】本题主要考查了旋转的性质以及勾股定理的应用，其中根据旋转的性质推断出'PAP 是等腰直角三角形是解题的关键．14、y ＝2(x －2)2＋3【分析】根据平移的规律：左加右减，上加下减可得函数解析式．【详解】解：将抛物线y=2x2向上平移3个单位长度，再向右平移2个单位长度后，得到的抛物线的表达式为y=2（x-2）2+3，故答案为：y＝2(x－2)2＋3.【点睛】此题主要考查了二次函数图象与几何变换，关键是掌握平移的规律．15、20°【解析】先判断出∠BAD=140°，AD=AB，再判断出△BAD是等腰三角形，最后用三角形的内角和定理即可得出结论．【详解】∵将△ABC绕点A逆时针旋转140°，得到△ADE，∴∠BAD=140°，AD=AB，∵点B，C，D恰好在同一直线上，∴△BAD是顶角为140°的等腰三角形，∴∠B=∠BDA，∴∠B=12(180°−∠BAD)=20°，故答案为：20°【点睛】此题考查旋转的性质，等腰三角形的判定与性质，三角形内角和定理，解题关键在于判断出△BAD是等腰三角形16、(0，2+1)【分析】将△OAN绕点O逆时针旋转90°，点N对应N′，点A对应A′，由旋转和正方形的性质即可得出点A′与点C 重合，以及F、C、N′共线，通过角的计算即可得出∠N'OF＝∠NOF＝45°，结合ON′＝ON、OF＝OF即可证出△N'OF≌△NOF（SAS），由此即可得出N′M＝NF＝1，再由△OCF≌△OAN即可得出CF＝N，通过边与边之间的关系即可得出BN＝BF，利用勾股定理即可得出BN＝BF＝2，设OC＝a，则N′F＝1CF＝1（a﹣2），由此即可得出关于a的一元一次方程，解方程即可得出点C的坐标．【详解】将△OAN绕点O逆时针旋转90°，点N对应N′，点A对应A′，如图所示．∵OA＝OC，∴OA′与OC重合，点A′与点C重合．∵∠OCN′+∠OCF ＝180°，∴F 、C 、N′共线．∵∠COA ＝90°，∠FON ＝45°，∴∠COF+∠NOA ＝45°．∵△OAN 旋转得到△OCN′，∴∠NOA ＝∠N′OC ，∴∠COF+∠CON'＝45°，∴∠N'OF ＝∠NOF ＝45°．在△N'OF 与△NOF 中，ON ON N OF NOF OF OF '∠'∠⎧⎪⎨⎪⎩＝＝＝，∴△N′OF ≌△NOF （SAS ），∴NF ＝N'F ＝1．∵△OCF ≌△OAN ，∴CF ＝AN ．又∵BC ＝BA ，∴BF ＝BN ．又∠B ＝90°，∴BF 1+BN 1＝NF 1，∴BF ＝BN＝．设OC ＝a ，则CF ＝AN ＝a．∵△OAN 旋转得到△OCN′，∴AN ＝CN'＝a，∴N'F ＝1（a），又∵N'F ＝1，∴1（a）＝1，解得：a，∴C （0+1）．故答案是：（0+1）．【点睛】本题考查了反比例函数综合题，涉及到了全等三角形的判定与性质、旋转的性质以及勾股定理，解题的关键是找出关于a的一元一次方程．本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边角关系是关键．17、y＝x2−1【分析】根据平移规律“左加右减”解答．【详解】按照“左加右减，上加下减”的规律可知：y＝（x＋2）2−1向右平移2个单位，得：y＝（x＋2−2）2−1，即y＝x2−1．故答案是：y＝x2−1．【点睛】考查了抛物线的平移以及抛物线解析式的变化规律：左加右减，上加下减．18、24【解析】根据平移变换只改变图形的位置，不改变图形的形状与大小,可得∠B=∠A´CC´,BC=B´C´，再根据同位角相等，两直线平行可得CD∥ AB,然后求出CD=12AB，点C"到A´B´的距离等于点C到AB的距离，根据等高的三角形的面积的比等于底边的比即可求解.也可用相似三角形的面积比等于相似比的平方来求．【详解】解：根据题意得∠B=∠A´CC´,BC=B´C´,∴CD//AB,CD= 12AB(三角形的中位线)，点C´到A´C´的距离等于点C到AB的距离，∴△CDC´的面积=12△ABC的面积，=12×48=24故答案为：24【点睛】本题考查的是三角形面积的求法之一，等高的三角形的面积比等于底的比，也可用相似三角形的面积比等于相似比的平方来求得．三、解答题(共66分)19、（1）见详解；（2）①见详解；②120°【分析】教材呈现：证明△ADE∽△ABC即可解决问题．结论应用：（1）首先证明△ADE是等边三角形，推出AD＝AE，BD＝CE，再利用三角形的中位线定理即可证明．（2）利用三角形的中位线定理以及平行线的性质解决问题即可．【详解】教材呈现：证明：∵点D，E分别是AB，AC的中点，∴12 AD AEAB AC==，∵∠A＝∠A，∴△ADE∽△ABC，∴∠ADE＝∠ABC，12 DE ADBC AB==，∴DE∥BC，DE＝12 BC．结论应用：（1）证明：∵△ABC是等边三角形，∴AB＝AC，∠ABC＝∠ACB＝60°，∵DE∥AB，∴∠ABC＝∠ADE＝60°，∠ACB＝∠AED＝60°，∴∠ADE＝∠AED＝60°，∴△ADE是等边三角形，∴AD＝AE，∴BD＝CE，∵EM＝MD，EN＝NB，∴MN＝12 BD，∵BN＝NE，BP＝PC，∴PN＝12 EC，∴NM＝NP．（2）∵EM＝MD，EN＝NB，∴MN∥BD，∵BN＝NE，BP＝PC，∴PN∥EC，∴∠MNE∠ABE，∠PNE＝∠AEB，∵∠AEB ＝∠EBC+∠C ，∠ABC ＝∠C ＝60°，∴∠MNP ＝∠ABE+∠EBC+∠C ＝∠ABC+∠C ＝120°．【点睛】本题考查了三角形中位线定理，，平行线的性质、相似三角形的判定与性质，综合性较强，难度适中．熟练掌握各定理是解题的关键．20、（1）x 1＝7，x 2＝27；（2）x 1＝1，x 2＝0.2【分析】（1）利用配方法求解，可得答案；（2）利用因式分解法求解，可得答案．【详解】（1）∵x 2﹣4x ＝1，∴x 2﹣4x +4＝1+4，即（x ﹣2）2＝7，则x ﹣2＝±7，解得：x 1＝7x 2＝27；（2）∵5x （x ﹣1）﹣（x ﹣1）＝0，∴（x ﹣1）（5x ﹣1）＝0，则x ﹣1＝0或5x ﹣1＝0，解得：x 1＝1，x 2＝0.2．【点睛】本题主要考查一元二次方程的解法，掌握配方法和因式分解法解方程，是解题的关键.21、 (1)2y 34x x =--+；(2)点M 的坐标为M(32-，5)；(3)存在，34，344+或(34，34)或(-3，1)或(177-66，). 【分析】（1）将A(- 4，0)、C(0，4)代入y=﹣x 2+bx+c 中即可得；（2）直线AC 的解析式为：4AC y x =+，表达出DQ 的长度，及△ADC 的面积，根据二次函数的性质得出△ADC 面积的最大值，从而得出D 点坐标，作点D 关于对称轴对称的点，确定点M ，使DM+AM 的值最小；（3）△BQC 为等腰三角形，则表达出三边，并对三边进行分类讨论，计算得出Q 点的坐标即可.【详解】解：(1)将A(- 4，0)、C(0，4)代入y=﹣x 2+bx+c 中得16404b c c --+=⎧⎨=⎩ ，解得3,4b c =-= ， ∴2y 34x x =--+，(2)直线AC 的解析式为：4AC y x =+设Q(m ，m+4) ，则 D(m ，234m m --+)DQ=(234m m --+)- (m+4)= 24m m -- 2214-m 42(2)82ADC S m m ∆=⨯-=-++（） 当m=-2时，面积有最大值此时点D 的坐标为D(-2，6)，D 点关于对称轴32x =-对称的点D 1(-1，6) 直线AD 1的解析式为：128AD y x =+ 当32x =-时，32()852M y =⨯-+= 所以，点M 的坐标为M(32-，5) (3)∵4AC y x =+，∴设Q(t,t+4)，由2340x x --+=得14x =-，21x =，∴B(1,0)，∴BC =QC ==BQ ==△BQC 为等腰三角形①当BC=QC =1t =，2t =∴Q(2，4+或(，)；②当BQ=QC =176t =-， ∴Q(17766-，)；③当BQ=BC =t=-3,∴Q(-3，1)；综上所述，若△BQC 为等腰三角形，则Q(2，4+或(，或(-3，1)或(177-66，). 【点睛】本题考查二次函数与最短路径，面积最大值，动点存在性等几何的综合应用，难度较大，解题的关键是能够灵活运用二次函数的性质及几何知识．22、 (1)答案不唯一，如AB ＝BC.（2）见解析;(3) BE=2【解析】整体分析：(1)根据“准菱形”的定义解答，答案不唯一；(2)对角线相等且互相平分的四边形是矩形，矩形的邻边相等时即是正方形；(3)根据平移的性质和“准菱形”的定义，分四种情况画出图形，结合勾股定理求解.解：(1)答案不唯一，如AB ＝BC.(2)已知：四边形ABCD 是“准菱形”，AB=BC ，对角线AC ，BO 交于点O ，且AC=BD ，OA=OC ，OB=OD. 求证：四边形ABCD 是正方形.证明：∵OA=OC，OB=OD ，∴四边形ABCD 是平行四边形.∵AC=BD，∴平行四边形ABCD 是矩形.∵四边形ABCD 是“准菱形”，AB=BC ，∴四边形ABCD 是正方形.(3)由平移得BE=AD ，DE=AB ＝2，EF=BC ＝1，DF=AC 由“准菱形”的定义有四种情况：①如图1，当AD ＝AB 时，BE ＝AD ＝AB ＝2.②如图2，当AD＝DF时，BE＝AD＝DF＝5.③如图3，当BF＝DF＝5时，延长FE交AB于点H，则FH⊥AB.∵BE平分∠ABC，∴∠ABE＝12∠ABC＝45°.∴∠BEH＝∠ABE＝45°.∴BE＝2BH.设EH＝BH＝x，则FH＝x＋1，BE＝2x.∵在Rt△BFH中，BH2＋FH2＝BF2，∴x2＋(x＋1)2＝(5)2，解得x1＝1，x2＝－2(不合题意，舍去)，∴BE＝2x＝2.④如图4，当BF＝AB＝2时，与③)同理得：BH2＋FH2＝BF2. 设EH＝BH＝x，则x2＋(x＋1)2＝22，解得x1＝172-+，x2＝172--(不合题意，舍去)，∴BE＝2x＝1422-.综上所述，BE=252142-23、（1）证明见解析；（2）BM＝203，理由见解析．【分析】（1）利用圆周角定理得到∠ADB＝90°，然后就利用等角的余角相等得到结论；（2）如图，连接OD，DM，先计算出BD＝8，OA＝5，再证明Rt△CBD∽Rt△BAD，利用相似比得到BC＝403，取BC的中点M，连接DM、OD，如图，证明∠2＝∠4得到∠ODM＝90°，根据切线的判定定理可确定DM为⊙O的切线，然后计算BM的长即可．【详解】（1）∵AB为⊙O直径，∴∠ADB＝90°，∴∠A+∠ABD＝90°．∵∠ABC＝90°，∴∠CBD+∠ABD＝90°，∴∠A＝∠CBD；（2）BM＝203．理由如下：如图，连接OD，DM，∵∠ADB＝90°，AB＝10，AD＝6，∴BD＝8，OA＝5，∵∠A＝∠CBD，∵Rt△CBD∽Rt△BAD，∴BCAB＝BDAD，即BC10＝86，解得BC＝403取BC的中点M，连接DM、OD，如图，∵DM为Rt△BCD斜边BC的中线，∴DM＝BM，∵∠2＝∠4，∵OB＝OD，∴∠1＝∠3，∴∠1+∠2＝∠3+∠4＝90°，即∠ODM＝90°，∴OD⊥DM，∴DM为⊙O的切线，此时BM ＝12BC ＝203．【点睛】本题考查了切线的判定定理：经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了圆周角定理，掌握切线的判定定理及圆周角定理是关键．24、（1）详见解析；（2）详见解析. 【分析】（1）根据两角对应相等证AEB BCD ∆∆，由对应边成比例得比例式，化等积式即可；（2）根据两角对应相等证EAP EDC ∆∆，由对应边成比例得比例式后化等积式，再由AB=CD 进行等量代换即可得结论.【详解】解：（1）∵四边形ABCD 是矩形，∴∠ABC=∠C=90°,90ABE DBC ∴∠+∠=︒∵AE ⊥BD∴ 90ABE BAE ∠+∠=︒DBC BAE ∴∠=∠∵ ∠AEB=∠C=90°AEB BCD ∴∆∆AE BE BC CD∴= BE BC AE CD ∴⋅=⋅(2) 90AEP PED ∠+∠=︒90PED DEC ∠+∠=︒AEP DEC ∴∠=∠ 又90EAD ADE ∠+∠=︒90ADE EDC ∠+∠=︒EAD EDC ∴∠=∠EAP EDC ∴∆∆AE AP ED CD∴= AE CD AP DE ∴⋅=⋅AB CD =AE AB DE AP ∴⋅=⋅【点睛】本题考查相似三角形的判定及性质，正确找出相似条件是解答此题的关键.25、（1）见解析；（2）见解析；（3）08y ≤<【分析】（1）根据函数的解析式，取x ，y 的值，即可．（2）描点、连线，画出的函数图象即可；（3）结合函数图象即可求解．【详解】（1）列表： x … ﹣2 ﹣1 0 1 2 … y … 8 2 0 2 8 … （2）画出函数y ＝2x 2的图象如图：（3）观察所画函数的图象，当﹣1＜x ＜2时，y 的取值范围是08y ≤<，故答案为：08y ≤<．26、（1）125x =-，225x =-（2）x 1=2，x 2=-1．【分析】（1）方程移项后，利用完全平方公式配方，开方即可求出解；（2）提取公因式化为积的形式，然后利用两因式相乘积为0，两因式中至少有一个为0，转化为两个一元一次方程来求解．【详解】解：（1）方程整理得：241x x +=，配方得：2445x x ++=，即2(2)5x +=，开方得：2x +=解得：12x =-22x =-（2）方程变形得：(2)[(2)3]0x x x ---=，即(2)(22)0x x ---=，即20x -=或220x --=，解得122,1x x ==-．【点睛】本题考查解一元二次方程．熟练掌握解一元二次方程的方法，并能结合实际情况选择合适的方法是解决此题的关键．。

SCL-90测验专家诊断意见：[说明][说明]1.SCL-90是进行个体心理健康状况鉴别及团体心理卫生普查时实用、简便而有价值的量表，广泛地应用于心理咨询中。

2.按答卷表1计算出结果，其判断方法是：看因子分（Fn）是否超过3分，若超过3分，即表明该项症状已达中等以上严重程度。

3.将计算出的结果与常模表2比较，从而判断自己的心理健康状态水平。

4.各因子的意义：F1－躯体化；F2－强迫；F3－人际敏感；F4－抑郁；F5－焦虑；F6－敌意；F7－恐怖；F8－妄想F9 _ 精神病性；F10－其他。

5.这个自测仅仅是根据最近一周的感觉，其结果也只是表明短期内的心理健康状态，很容易进行调整，不必产生心理负担。

SCL-90自评量表解释及评分标准一、躯体化：体现心血管、胃肠道、呼吸系统、头痛、肌肉等方面最近有无问题二、强迫症：明知没有必要，但又控制不住自己，反复出现为特征，主要表现在思想观念上和行为上。

三、人际关系敏感：与他人交往不自在，人际交往能力低下，害怕与人交往，表现出自卑感，严重的导致自闭。

四、抑郁：对生活的兴趣减退，缺乏活动的愿望和动力，表现出悲观失望。

其特点是以消极的心态看待问题和自己，严重的产生死亡和自杀的念头。

五、焦虑：表现出紧张、神经过敏，严重的惊恐发作。

*焦虑是指当前的或某一特定事物引起的，有明确的对象，时间较短。

一般来说，焦虑发展成抑郁时要以药物治疗和心理咨询相结合。

六、敌对：从思想、情感和行为三方面分析，爱争论、冲动、爆发、摔东西。

七、恐怖：分为社交恐怖和广场恐怖。

以社交恐怖居多，表现出内向、害怕与人交往、自卑感强。

广场恐怖是指到空旷的地方无缘无故地感到恐怖。

八、偏执：敌对、猜疑和妄想。

九、精神病性：各种急性的症状和行为，轻度以上的具有分裂性行为方式的特征，表现出精神病性的症状和行为。

十、其他：睡眠障碍和饮食不良。

评分标准：1、总分超过160的，提示阳性症状。

2、阳性项目数超过43的（43项2分——原始分以上），提示有问题。

2025届四川省绵阳宜溪中学心学校九上数学期末达标检测试题注意事项1．考试结束后，请将本试卷和答题卡一并交回．2．答题前，请务必将自己的姓名、准考证号用0．5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置．3．请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符．4．作答选择题，必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑；如需改动，请用橡皮擦干净后，再选涂其他答案．作答非选择题，必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效．5．如需作图，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗．一、选择题（每题4分，共48分）1．一个布袋里装有2个红球、3个黄球和5个白球，除颜色外其它都相同．搅匀后任意摸出一个球，是黄球的概率为( )A ．12B ．310C ．15D ．7102．如图，AB 与⊙O 相切于点A ，BO 与⊙O 相交于点C ，点D 是优弧AC 上一点，∠CDA ＝27°，则∠B 的大小是（ ）A ．27°B ．34°C ．36°D ．54°3．如图，⊙O 是正方形ABCD 与正六边形AEFCGH 的外接圆．则正方形ABCD 与正六边形AEFCGH 的周长之比为（ ）A ．22 3B 2∶1C 23D ．134．若将抛物线23y x =的函数图象先向右平移1个单位，再向下平移2个单位后，可得到一个新的抛物线的图象，则所得到的新的抛物线的解析式为( )A ．23(1)2y x =-+B ．23(1)2y x =+-C ．23(1)2=--y xD ．23(1)2y x =-+5．已知二次函数y ＝ax 2＋bx ＋c(a≠0)的图象如图所示，当y ＞0时，x 的取值范围是( )A ．－1＜x ＜2B ．x ＞2C ．x ＜－1D ．x ＜－1或x ＞26．如图所示的几何体是由一些小立方块搭成的，则这个几何体的俯视图是（ ）A ．B ．C ．D ．7．抛物线的()213y x =-+顶点坐标是（ ）A ．(1,3)B ．(1,3)-C ．(1,3)--D ．(1,3)- 8．一个正五边形和一个正六边形按如图方式摆放，它们都有一边在直线l 上，且有一个公共顶点O ，则AOB ∠的度数是( )A ．83︒B ．84︒C ．85︒D ．94︒9．已知mx ny =，则下列各式中不正确的是（ ）A ．y m x n =B ．m n y x= C ．m x n y = D ．x y n m = 10．一元二次方程2(21)(21)(1)x x x +=+-的解为（ ）A ．1x =B ．112x =- ，21x =C ．112x =- ，22x =-D ．112x =-，22x = 11．如图，已知二次函数()20y ax bx c a =++≠的图象与x 轴交于点A （-1，0），与y 轴的交点在B （0，-2）和（0，-1）之间（不包括这两点），对称轴为直线1x =，下列结论不正确的是（ ）A ．930a b c ++=B ．430b c ->C ．244ac b a -<-D ．1536a << 12．某商场将进货价为30元的台灯以40元售出，平均每月能售出600个．这种台灯的售价每上涨1元，其销售量就将减少10个．为了实现平均每月10000元的销售利润，台灯的售价是多少？若设每个台灯涨价为x 元，则可列方程为（ ）A ．()()40306001010000x x +--=B ．()()40306001010000x x +-+=C ．()()30600104010000x x ---=⎡⎤⎣⎦D ．()()30600104010000x x ⎡⎤=⎦+⎣--二、填空题（每题4分，共24分）13．一个正多边形的每个外角都等于60︒，那么这个正多边形的中心角为______．14．已知关于x 的一元二次方程2230x x k -+=有两个不相等的实数根，则k 的取值范围是________．15．关于x 的方程2x 2x m 0-+=有一个根10x =，则另一个根2x =________.16．在平面直角坐标系中，点(3，－4)关于原点对称的点的坐标是____________．17．二次函数2(0)y ax bx c a =++≠的部分图象如图所示，图象过点(4,0)-，对称轴为直线1x =-，下列结论：①0abc >；②20a b -=；③一元二次方程20ax bx c ++=的解是14x =-，21x =；④当0y >时，42x -<<，其中正确的结论有__________．18．如图，在平行四边形ABCD 中，AE ：BE ＝2：1，F 是AD 的中点，射线EF 与AC 交于点G ，与CD 的延长线交于点P ，则AG GC的值为_____．三、解答题（共78分）19．（8分）如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．（1）求灯杆CD的高度；（2）求AB的长度（结果精确到0.1米）．（参考数据：3=1.1．sin37°≈060，cos37°≈0.80，tan37°≈0.75）20．（8分）如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D，E两点分别在AC，BC上，且DE∥AB，将△CDE 绕点C按顺时针方向旋转，记旋转角为α．（1）问题发现：当α＝0°时，ADBE的值为；（2）拓展探究：当0°≤α＜360°时，若△EDC旋转到如图2的情况时，求出ADBE的值；（3）问题解决：当△EDC旋转至A，B，E三点共线时，若设CE＝5，AC＝4，直接写出线段BE的长．21．（8分）如图，点C在以AB为直径的O上，ACB的平分线交O于点D，过点D作AB的平行线交CA的延长线于点E.（1）求证：DE 是O 的切线；（2）若6AC =，8BC =，求DE 的长度.22．（10分）根据广州市垃圾分类标准，将垃圾分为“厨余垃圾、可回收垃圾、有害垃圾、其它垃圾”四类．小明将分好类的两袋垃圾准确地投递到小区的分类垃圾桶里．请用列举法求小明投放的两袋垃圾是“厨余垃圾和有害垃圾”的概率．23．（10分）小明投资销售一种进价为每件20元的护眼台灯．销售过程中发现：每月的销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数y ＝－10x ＋500，在销售过程中销售单价不低于成本价，而每件的利润不高于成本价的60%.(1)设小明每月获得利润为w(元)，求每月获得利润w(元)与销售单价x(元/件)之间的函数表达式，并确定自变量x 的取值范围；(2)当销售单价定为多少元/件时，每月可获得最大利润？每月的最大利润是多少？24．（10分）先化简：248211m m m m ⎛⎫÷+- ⎝-⎪⎭，再求代数式的值，其中m 是方程224x x -=的一个根． 25．（12分）如图，平面直角坐标中，把矩形OABC 沿对角线OB 所在的直线折叠，点A 落在点D 处，OD 与BC 交于点E ．OA 、OC 的长是关于x 的一元二次方程x 2﹣9x +18＝0的两个根（OA ＞OC ）．（1）求A 、C 的坐标．（2）直接写出点E 的坐标，并求出过点A 、E 的直线函数关系式．（3）点F 是x 轴上一点，在坐标平面内是否存在点P ，使以点O 、B 、P 、F 为顶点的四边形为菱形？若存在请直接写出P 点坐标；若不存在，请说明理由．26．在⊙O 中，AB 为直径，C 为⊙O 上一点．（1）如图1，过点C作⊙O的切线，与AB延长线相交于点P，若∠CAB=27°，求∠P的度数；（2）如图2，D为弧AB上一点，OD⊥AC，垂足为E，连接DC并延长，与AB的延长线交于点P，若∠CAB=10°，求∠P的大小．参考答案一、选择题（每题4分，共48分）1、B【分析】用黄色小球的个数除以总个数可得．【详解】解：搅匀后任意摸出一个球，是黄球的概率为33 23510=++故答案为B．【点睛】本题考查了概率公式,解答的关键在于确定发生事件的总发生数和所求事件发生数.2、C【分析】由切线的性质可知∠OAB=90°，由圆周角定理可知∠BOA=54°，根据直角三角形两锐角互余可知∠B=36°．【详解】解：∵AB与⊙O相切于点A，∴OA⊥BA．∴∠OAB=90°．∵∠CDA=27°，∴∠BOA=54°．∴∠B=90°-54°=36°．故选C．考点：切线的性质．【分析】计算出在半径为R 的圆中，内接正方形和内接正六边形的边长即可求出．【详解】解：设此圆的半径为R ，R ，它的内接正六边形的边长为R ，内接正方形和内接正六边形的周长比为：R ：6R ＝ 1．故选：A ．【点睛】本题考查了正多边形和圆，找出内接正方形与内接正六边形的边长关系，是解决问题的关键．4、C【分析】根据函数图象平移的法则“左加右减，上加下减”的原则进行解答即可．【详解】由“左加右减”的原则可知，将抛物线23y x =先向右平移1个单位可得到抛物线()231y x =-；由“上加下减”的原则可知，将抛物线()231y x =-先向下平移2个单位可得到抛物线23(1)2=--y x ． 故选：C ．【点睛】本题考查的是二次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．5、D【分析】根据已知图象可以得到图象与x 轴的交点是（-1，0），（2，0），又y ＞0时，图象在x 轴的上方，由此可以求出x 的取值范围．【详解】依题意得图象与x 轴的交点是（-1，0），（2，0），当y ＞0时，图象在x 轴的上方，此时x ＜－1或x ＞2，∴x 的取值范围是x ＜－1或x ＞2，故选D ．【点睛】本题考查了二次函数与不等式，解答此题的关键是求出图象与x 轴的交点，然后由图象找出当y ＞0时，自变量x 的范围，注意数形结合思想的运用.6、D【解析】试题分析：根据三视图中，从左边看得到的图形是左视图,因此从左边看第一层是两个小正方形，第二层左边一个小正方形，考点：简单组合体的三视图7、A【分析】根据二次函数的性质，利用顶点式即可得出顶点坐标．【详解】解：∵抛物线()213y x =-+，∴抛物线()213y x =-+的顶点坐标是：（1，3），故选：A ．【点睛】本题主要考查了利用二次函数顶点式求顶点坐标．能根据二次函数的顶点式找出抛物线的对称轴及顶点坐标是解题的关键．8、B【分析】利用正多边形的性质求出∠AOE ，∠BOF ，∠EOF 即可解决问题；【详解】由题意：∠AOE=108°，∠BOF=120°，∠OEF=72°，∠OFE=60°，∴∠EOF=180°−72°−60°=48°，∴∠AOB=360°−108°−48°−120°=84°，故选：B ．【点睛】本题考查正多边形的性质、三角形内角和定理，解题关键在于掌握各性质定义.9、C【分析】依据比例的基本性质，将比例式化为等积式，即可得出结论．【详解】A. 由y m x n=可得mx ny =，变形正确，不合题意； B. 由m n y x=可得mx ny =，变形正确，不合题意； C. 由m x n y=可得my nx =，变形不正确，符合题意；D. 由x y n m=可得mx ny =，变形正确，不合题意． 故选C ．【点睛】本题考查了比例的性质，此题比较简单，解题的关键是掌握比例的变形．10、C【分析】通过因式分解法解一元二次方程即可得出答案.【详解】2(21)(21)(1)0x x x +-+-= (21)(211)0x x x ++-+=∴210x +=或2110x x +-+= ∴112x =-，22x =- 故选C【点睛】本题主要考查解一元二次方程，掌握因式分解法是解题的关键.11、D【分析】根据二次函数的图象和性质、各项系数结合图象进行解答．【详解】∵A （-1，0），对称轴为1x =∴二次函数与x 轴的另一个交点为()3,0将()3,0代入()20y ax bx c a =++≠中 093a b c =++，故A 正确将()()1,0,3,0-代入()20y ax bx c a =++≠中0093a b c a b c =-+⎧⎨=++⎩①② ②9-⨯①0128b c =-23c b = ∴8143333b c c c c -=-=- ∵二次函数与y 轴的交点在B （0，-2）和（0，-1）之间（不包括这两点）∴21c -<<- ∴14303b c c -=->∴430b c ->，故B 正确；∵二次函数与y 轴的交点在B （0，-2）和（0，-1）之间（不包括这两点） ∴抛物线顶点纵坐标2414ac b a-<- ∵抛物线开口向上∴0a >∴244ac b a -<-，故C 正确∵二次函数与y 轴的交点在B （0，-2）和（0，-1）之间（不包括这两点）∴21c -<<-将()()1,0,3,0-代入()20y ax bx c a =++≠中0093a b c a b c =-+⎧⎨=++⎩①② ①3⨯+②0124a c =+3c a =-∴231a -<-<- ∴1233a <<，故D 错误，符合题意 故答案为：D ．【点睛】本题主要考查了二次函数的图象与函数解析式的关系，可以根据各项系数结合图象进行解答． 12、A【分析】设这种台灯上涨了x 元，台灯将少售出10x ，根据“利润=（售价-成本）×销量”列方程即可.【详解】解：设这种台灯上涨了x 元，则根据题意得，（40+x-30）（600-10x ）=10000.故选：A.【点睛】解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程．二、填空题（每题4分，共24分）13、60°【分析】根据题意首先由多边形外角和定理求出正多边形的边数n ，再由正多边形的中心角=360n ︒，即可得出结果． 【详解】解：正多边形的边数为360606÷=，故这个正多边形的中心角为360660.故答案为：60°. 【点睛】本题考查正多边形的性质和多边形外角和定理以及正多边形的中心角的计算方法，熟练掌握正多边形的性质，并根据题意求出正多边形的边数是解决问题的关键．14、3k <【分析】根据一元二次方程的根的判别式，建立关于k 的不等式，求出k 的取值范围．【详解】根据一元二次方程的根的判别式，建立关于k 的不等式，求出k 的取值范围.1a ，b =-，c k =方程有两个不相等的实数根，241240b ac k ∴∆=-=->，3k ∴<.故答案为：3k <．【点睛】本题考查了根的判别式．总结：一元二次方程根的情况与判别式△的关系：（1）△＞0⇔方程有两个不相等的实数根；（2）△＝0⇔方程有两个相等的实数根；（3）△＜0⇔方程没有实数根．15、2【分析】由根与系数的关系，根据两根之和为-b a计算即可． 【详解】∵关于x 的方程2 20x x m -+=有一个根10x =，∴202x +=解得：22x =；故答案为：22x =．【点睛】本题考查了一元二次方程根与系数的关系，熟记根与系数的关系的结构是解题的关键．16、 (－3，4)【详解】在平面直角坐标系中，点(3，－4)关于原点对称的点的坐标是(－3，4).故答案为(－3，4).【点睛】本题考查关于原点对称的点的坐标，两个点关于原点对称时，它们的坐标符号相反.17、①②④【分析】①由抛物线的开口向下知a ＜0，与y 轴的交点在y 轴的正半轴上得到c ＞0，由对称轴为12b x a =-=-，得到b ＜0，可以①进行分析判断； ②由对称轴为12b x a=-=-，得到2a=b ，b-2a=0，可以②进行分析判断； ③对称轴为x=-1，图象过点（-4，0），得到图象与x 轴另一个交点（2，0），可对③进行分析判断；④抛物线开口向下，图象与x 轴的交点为（-4，0），（2，0），即可对④进行判断．【详解】解：①∵抛物线的开口向下，∴a ＜0，∵与y 轴的交点在y 轴的正半轴上，∴c ＞0， ∵对称轴为12b x a =-=-＜0 ∴b ＜0，∴abc ＞0，故①正确； ②∵对称轴为12b x a=-=-， ∴2a=b ，∴2a-b=0，故②正确；③∵对称轴为x=-1，图象过点A （-4，0），∴图象与x 轴另一个交点（2，0），∴关于x 的一元二次方程ax 2+bx+c=0的解为x=-4或x=2，故③错误；④∵抛物线开口向下，图象与x 轴的交点为（-4，0），（2，0），∴当y ＞0时，-4＜x ＜2，故④正确；∴其中正确的结论有：①②④；故答案为：①②④.【点睛】本题考查了二次函数的图象与系数的关系，解答此类问题的关键是掌握二次函数y=ax 2+bx+c 系数符号由抛物线开口方向、对称轴、抛物线与y 轴的交点、抛物线与x 轴交点的个数确定，解题时要注意数形结合思想的运用． 18、25【分析】设2x AE =则BE x =，根据ABCD 是平行四边形，可得//AB CP ，即=AEF DPF ∠∠，EAF PDF =∠∠和EAG PCG =∠∠，可得AEG CPG △∽△，由于F 是AD 的中点，可得AF DF =，因此AEF DPF △≌△，=2x AE DP =，5x CP DP DC DP AE BE =+=++=，再通过AG AE GC CP =便可得出2=5AG GC ． 【详解】解：∵2AE BE =：：1∴设2x AE =，BE x =，则3x AB =∵ABCD 是平行四边形∴//AB CP ，3x DC AB ==∴=AEF DPF ∠∠，EAF PDF =∠∠，EAG PCG =∠∠∴AEG CPG △∽△ ∴AG AE GC CP= 又∵F 是AD 的中点∴AF DF =∴()AEF DPF AAS △≌△∴=2x DP AE =∴2x+3x 5x CP DP DC =+== ∴2x 2==5x 5AG AE GC CP = 故答案为：25 【点睛】本题主要考查了平行四边形的性质，全等三角形的判定和性质，相似三角形的判定和性质，求证两个三角形相似，再通过比值等量代换表示出边的数量关系是解题的关键．三、解答题（共78分）19、（1）10米；（2）11.4米【解析】（1）延长DC 交AN 于H ．只要证明BC=CD 即可；（2）在Rt △BCH 中，求出BH 、CH ，在 Rt △ADH 中求出AH 即可解决问题.【详解】（1）如图，延长DC 交AN 于H ，∵∠DBH=60°，∠DHB=90°， ∴∠BDH=30°， ∵∠CBH=30°， ∴∠CBD=∠BDC=30°， ∴BC=CD=10（米）；（2）在Rt △BCH 中，CH=12BC=5，3， ∴DH=15，在Rt △ADH 中，AH=tan 37DH ︒≈150.75=20， ∴AB=AH ﹣BH=20﹣8.65=11.4（米）．【点睛】本题考查解直角三角形的应用﹣坡度坡角问题，解题的关键是学会添加常用辅助线，构造直角三角形解决问题.20、（1）22；（2）22；（3）7或1． 【分析】（1）先证△DEC 为等腰直角三角形，求出2CD CE =AD BE 的值； （2）证△BCE ∽△ACD ，由相似三角形的性质可求出AD BE的值； （3）分两种情况讨论，一种是点E 在线段BA 的延长线上，一种是点E 在线段BA 上，可分别通过勾股定理求出AE 的长，即可写出线段BE 的长．【详解】（1）∵∠BAC =90°，AB =AC ，∴△ABC 为等腰直角三角形，∠B =45°．∵DE ∥AB ，∴∠DEC =∠B =45°，∠CDE =∠A =90°，∴△DEC 为等腰直角三角形，∴cos ∠C 2CD CE ==． ∵DE ∥AB ，∴2AD CD BE CE ==．故答案为：2； （2）由（1）知，△BAC 和△CDE 均为等腰直角三角形，∴AC DC BC EC ==． 又∵∠BCE =∠ACD =α，∴△BCE ∽△ACD ，∴2AD AC BE BC ==，即2AD BE =； （3）①如图3﹣1，当点E 在线段BA 的延长线上时．∵∠BAC =90°，∴∠CAE =90°，∴AE ===3，∴BE =BA +AE =4+3=7；②如图3﹣2，当点E 在线段BA 上时，AE ===3，∴BE =BA ﹣AE =4﹣3=1．综上所述：BE 的长为7或1．故答案为：7或1．【点睛】本题考查了等腰直角三角形的性质，锐角三角函数，相似三角形的判定与性质等，解答本题的关键是注意分类讨论思想在解题过程中的运用．21、（1）见解析；（2）354【分析】（1）连接OD ，由AB 为O 的直径得到∠ACB=90︒，根据CD 平分∠ACB 及圆周角定理得到∠AOD=90︒，再根据DE ∥AB 推出OD ⊥DE ，即可得到DE 是O 的切线； （2）过点C 作CH ⊥AB 于H ，CD 交AB 于M ，利用勾股定理求出AB ，再利用面积法求出CH ，求出OH ，根据△CHM ∽△DOM 求出HM 得到AM ，再利用平行线证明△CAM ∽△CED ，即可求出DE.【详解】（1）如图，连接OD ，∵AB 为O 的直径，∴∠ACB=90︒，∵CD 平分∠ACB ，∴∠ACD=45︒，∴∠AOD=90︒，即OD ⊥AB ，∵DE ∥AB ，∴OD ⊥DE ,∴DE 是O 的切线；（2）过点C 作CH ⊥AB 于H ，CD 交AB 于M ，∵∠ACB=90︒，6AC =，8BC =，∴22226810AC BC +=+=,∵S△ABC=1122AC BC AB CH ⋅⋅=⋅⋅,∴CH=684.8 10⨯=,∴AH=22226 4.8 3.6AC CH-=-=, ∴OH=OA-AH=5-3.6=1.4，∵∠CHM=∠DOM=90︒，∠HMC=∠DMO, ∴△CHM∽△DOM,∴CH HM CM DO OM DM==∴CMDM=4.824525HMOM==，2449CMCD=，∴HM=24 35,∴AM=AH+HM=30 7,∵AB∥DE,∴△CAM∽△CED,∴2449 AM CMED CD==,∴DE=35 4.【点睛】此题考查圆的性质，圆周角定理，切线的判定定理，三角形相似，勾股定理，（2）是本题的难点，利用平行线构建相似三角形求出DE的长度，根据此思路相应的添加辅助线进行证明.22、见解析，1 6【分析】首先利用树状图法列举出所有可能，进而利用概率公式求出答案．【详解】解：分别记厨余垃圾、可回收垃圾、有害垃圾、其它垃圾为A、B、C、D，画树状图如下：由树状图知，共有12种等可能结果，其中小明投放的两袋垃圾是“厨余垃圾和有害垃圾”的结果有2种，所以小明投放的两袋垃圾是“厨余垃圾和有害垃圾”的概率为212＝16． 【点睛】本题主要考查的是利用树状图求解概率，解此题需要正确的运用树状图，所以掌握树状图是解此题的关键.23、 (1)w ＝－10x 2＋700x －10000(20≤x ≤32)；(2)当销售单价定为32元/件时，每月可获得最大利润，最大利润是2160元．【解析】分析：（1）由题意得，每月销售量与销售单价之间的关系可近似看作一次函数，利润=（定价-进价）×销售量，从而列出关系式；（2）首先确定二次函数的对称轴，然后根据其增减性确定最大利润即可；详解：（1）由题意，得：w=（x-20）•y=（x-20）•（-10x+500）=-10x 2+700x-10000，即w=-10x 2+700x-10000（20≤x≤32）.(2)w ＝－10x 2＋700x －10000＝－10(x －35)2＋2250.对称轴为：x=35，又∵a ＝－10＜0，抛物线开口向下， ∴当20≤x ≤32时，w 随着x 的增大而增大，∴当x ＝32时，w 最大＝2160.答：当销售单价定为32元/件时，每月可获得最大利润，最大利润是2160元．点睛：二次函数的应用.重点在于根据题意列出函数关系式. 24、228m m-；1． 【分析】首先对括号内的分式进行通分，然后把除法转化为乘法即可化简，最后整体代值计算． 【详解】解：248211m m m m ⎛⎫÷+- ⎝-⎪⎭， ()()24228m m m m m m --+=-÷， ()()24222m m m m -=+， ()224m m =-，228m m =-； ∵m 是方程224x x -=的一个根，∴224m m -=，∴242m m -=，∴2284m m -=，∴原式=44m m == 【点睛】本题考查了分式的化简求值和一元二次方程的根，熟知整体代入是解答此题关键．25、（1）A （6，0），C （0，3）；（2）E （94，3），y ＝﹣45x +245；（3）满足条件的点P 坐标为（6﹣35，3）或（6+35，3）或（94，3）或（6，﹣3）． 【解析】（1）解方程求出OA 、OC 的长即可解决问题；（2）首先证明EO ＝EB ，设EO ＝EB ＝x ，在Rt △ECO 中，EO 2＝OC 2＋CE 2，构建方程求出x ，可得点E 坐标，再利用待定系数法即可解决问题；（3）分情形分别求解即可解决问题；【详解】（1）由x 2﹣9x ＋18＝0可得x ＝3或6，∵OA 、OC 的长是关于x 的一元二次方程x 2﹣9x ＋18＝0的两个根（OA ＞OC ），∴OA ＝6，OC ＝3，∴A （6，0），C （0，3）．（2）如图1中，∵OA ∥BC ，∴∠EBC ＝∠AOB ，根据翻折不变性可知：∠EOB ＝∠AOB ，∴∠EOB ＝∠EBO ，∴EO＝EB，设EO＝EB＝x，在Rt△ECO中，∵EO2＝OC2＋CE2，∴x2＝32＋（6﹣x）2，解得x ＝154，∴CE＝BC﹣EB＝6﹣154＝94，∴E（94，3），设直线AE的解析式为y＝kx＋b，则有6093 4k bk b⎧⎪⎨⎪⎩＋＝＋＝，解得45245kb⎧-⎪⎪⎨⎪⎪⎩＝＝，∴直线AE的函数解析式为y＝﹣45x＋245．（3）如图，OB＝2236＋＝35．①当OB为菱形的边时，OF1＝OB＝BP1＝3＝5，故P1（6﹣35，3），OF3＝P3F3＝BP3＝35，故P3（6＋35，3）．②当OB为菱形的对角线时，∵直线OB的解析式为y＝12x，∴线段OB的垂直平分线的解析式为y＝﹣2x＋152，可得P2（94，3），③当OF4问问对角线时，可得P4（6，﹣3）综上所述，满足条件的点P坐标为（6﹣35，3）或（6＋35，3）或（94，3）或（6，﹣3）．【点睛】本题考查的是一次函数的综合题，熟练掌握一次函数是解题的关键.26、（1）∠P =36°；（2）∠P=30°．【分析】（1）连接OC，首先根据切线的性质得到∠OCP=90°，利用∠CAB=27°得到∠COB=2∠CAB=54°，然后利用直角三角形两锐角互余即可求得答案；（2）根据E为AC的中点得到OD⊥AC，从而求得∠AOE=90°﹣∠EAO=80°，然后利用圆周角定理求得∠ACD=∠AOD=40°，最后利用三角形的外角的性质求解即可．【详解】解：（1）如图，连接OC，∵⊙O与PC相切于点C，∴OC⊥PC，即∠OCP=90°，∵∠CAB=27°，∴∠COB=2∠CAB=54°，在Rt△AOE中，∠P+∠COP=90°，∴∠P=90°﹣∠COP=36°；（2）∵E为AC的中点，∴OD⊥AC，即∠AEO=90°，在Rt△AOE中，由∠EAO=10°，得∠AOE=90°﹣∠EAO=80°，∴∠ACD=∠AOD=40°，∵∠ACD是△ACP的一个外角，∴∠P=∠ACD﹣∠A=40°﹣10°=30°．【点睛】本题考查切线的性质．。

2025届四川绵阳富乐国际学校数学七年级第一学期期末学业质量监测试题请考生注意：1．请用2B 铅笔将选择题答案涂填在答题纸相应位置上，请用0．5毫米及以上黑色字迹的钢笔或签字笔将主观题的答案写在答题纸相应的答题区内。

写在试题卷、草稿纸上均无效。

2．答题前，认真阅读答题纸上的《注意事项》，按规定答题。

一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．在3，0，6，－2这四个数中，最大的数为（ ）A ．0B ．6C ．－2D ．32．倒数是它本身的数是（ ）A ．1B ．﹣1C ．1或﹣1D ．0 3．单项式33xy 的次数是（ ）．A ．3B ．4C ．5D ．64．下列各组数中，数值相等的是( )A ．23和32B ．3(2)-和32-C ．23-和2(3)-D ．(2)--和|2|--5．下列变形一定正确的是（ ）A ．若x ＝y ，则x ﹣6＝y +6B ．若x ＝y ，则3x ﹣2＝3y ﹣2C ．若2x ＝2y +1，则x ＝y +1D ．若x 2＝y 2，则x ＝y6．关于代数式232a b -，下列表述正确的是（ ） A ．单项式，次数为1B ．单项式，次数为2C ．多项式，次数为2D ．多项式，次数为37．已知x ＝﹣2是方程x+4a ＝10的解，则a 的值是（ ）A ．3B ．C ．2D ．﹣38．16的平方根为（ ）A ．4B ．﹣4C ．±2D ．29．如图，小明将自己用的一副三角板摆成如图形状，如果∠AOB=155°，那么∠COD 等于（ ）A ．15°B ．25°C ．35°D ．45°10．下列说法中①a -是负数；②9ab 是二次单项式；③倒数等于它本身的数是±1；④若||a a =-，则0a <；⑤由()41x --=变形成()41x -=-，正确个数是() A ．1个 B ．2个C ．3个D ．4个 11．下列说法错误的是（ ）A ．平移不改变图形的形状和大小B ．对顶角相等C ．两个直角一定互补D ．同位角相等12．设一列数1a 、2a 、3a 、…、2014a 、…中任意三个相邻数之和都是20，已知22a x =，1813a =，656a x =-，那么2020a =（ ）A ．2B ．3C ．4D ．13二、填空题（每题4分，满分20分，将答案填在答题纸上）13．已知 A 、B 、C 三点在同一条直线上，M 、N 分别为线段 AB 、BC 的中点，且 AB=60，BC=40， 则 MN 的长为 ______14．下图所示的网格是正方形网格，BAC ∠________DAE ∠．（填“>”，“=”或“<”）15．如图，数轴上A 、B 两点表示的数互为相反数，且点A 与点B 之间的距离是5个单位长度，则点A 表示的数是_________．16．若a 、b 互为倒数，则2ab=___．17．如图，在一个长方形草坪ABCD 上，放着一根长方体的木块，已知9AD =米，10AB =米，该木块的较长边与AD 平行，横截面是边长为1米的正方形，一只蚂蚁从点A 爬过木块到达C 处需要走的最短路程是______米．三、解答题 （本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18．（5分）某养鸡场有2500只鸡准备对外出售，从中随机抽取了一部分鸡，根据它们的质量（单位：kg）绘制出如图所示的统计图（不完整）．（1）求抽取的质量为1.5kg的鸡有多少只？（2）质量为1.8kg鸡对应扇形圆心角的度数是多少？（3）估计这2500只鸡中，质量为2.0kg的鸡约有多少只？19．（5分）化简后求值：3（x2y+xy2）﹣3（x2y﹣1）﹣4xy2﹣3，其中x、y满足|x﹣2|+（y+）2＝1．20．（8分）已知下图为从正面、左面、上面看到的一个几何体的形状图.（1）写出这个几何体的名称；（2）若从正面看到的长方形的宽为3cm，从上面看到的正方形的边长为8cm，求这个几何体的表面积．21．（10分）计算：16（x2-2x+3）-（12-13x2-x）．22．（10分）若中学生体质健康综合评定成绩为x分，满分为100分．规定：85≤x≤100为A级，75≤x＜85为B级，60≤x＜75为C级，x＜60为D级．现随机抽取某中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图．请根据图中的信息，解答下列问题：（1）在这次调查中，一共抽取了名学生；（2）a＝%；C级对应的圆心角为度．（3）补全条形统计图；（4）若该校共有2000名学生，请你估计该校D级学生有多少名？23．（12分）已知如图，∠1=∠2，∠C=∠D．（1）求证：BD∥CE；（2）说明∠A=∠F的理由．参考答案一、选择题：本大题共12个小题，每小题3分，共36分.在每小题给出的四个选项中，只有一项是符合题目要求的.1、B【详解】把所给出的4个数表示在数轴上，位于最右边的数6最大；故选B.2、C【详解】倒数是它本身的数是1或﹣1，0没有倒数．故选：C．3、B【分析】根据单项式的定义分析，即可得到答案．3xy的次数是：4【详解】单项式3故选：B．【点睛】本题考查了单项式的知识；解题的关键是熟练掌握单项式的定义，从而完成求解．4、B【分析】求出各选项中两式的结果，即可做出判断．【详解】23=9≠32=8；3(2)-=-8=32-=-8；23-=-9≠2(3)-=-9；(2)--=2≠|2|--=-2故选B【点睛】考核知识点：有理数计算. 此题考查了有理数的混合运算，有理数的混合运算首先弄清运算顺序，先乘方，再乘除，最后算加减，有括号先算括号里边的，同级运算从左到右依次进行计算，然后利用各种运算法则计算，有时可以利用运算律来简化运算．5、B【分析】根据等式是性质进行计算．【详解】解：A 、若x ＝y ，则x +6＝y +6，原变形错误，故本选项不符合题意；B 、若x ＝y ，则3x ﹣2＝3y ﹣2，原变形正确，故本选项符合题意；C 、若2x ＝2y +1，则x ＝y +12，原变形错误，故本选项不符合题意； D 、若x 2＝y 2，则x ＝y 或x ＝﹣y ，原变形错误，故本选项不符合题意；故选：B ．【点睛】此题主要考查等式的性质，解题的关键是熟知等式的变形方法.6、C【分析】利用多项式的定义，变化代数式解出答案. 【详解】2233222a b a b -=- ， 故此代数式是多项式，次数为2.所以C 选项是正确的.【点睛】此题主要考查多项式，正确把握多项式的定义是解题的关键.7、A【解析】把x=-2代入方程，即可求出答案．【详解】把x=-2代入方程x+4a=10得：-2+4a=10，解得：a=3，故选：A．【点睛】本题考查了一元一次方程的解和解一元一次方程，能得出关于a的方程是解题的关键．8、C.==±，4,2±2.故选C.【点睛】此题主要考查了平方根算术平方根定义，解题时注意：本题求的是4的平方根，不是16的平方根．9、B【分析】利用直角和角的组成即角的和差关系计算．【详解】解：∵三角板的两个直角都等于90°，所以∠BOD+∠AOC=180°，∵∠BOD+∠AOC=∠AOB+∠COD，∵∠AOB=155°，∴∠COD等于25°．故选B．【点睛】本题考查角的计算，数形结合掌握角之间的数量关系是本题的解题关键．10、C【分析】根据正负数的意义、单项式的概念、倒数的定义、绝对值的定义以及等式的性质逐条分析即可. 【详解】解：①-a不一定是负数，例如a=0时，-a=0，不是负数，错误；②9ab是二次单项式，正确；③倒数等于它本身的数是±1，正确；④若|a|=-a，则a≤0，错误；x-=-，正确，⑤由-（x-4）=1变形成()41则其中正确的选项有3个．故选：C．【点睛】此题考查了等式的性质，相反数，绝对值，倒数，以及单项式的知识，熟练掌握各自的定义是解本题的关键． 11、D【解析】根据平移的性质判断A ；根据对顶角的性质判断B ；根据互补的定义判断C ；根据同位角的定义判断D ．【详解】解：A 、平移不改变图形的形状和大小，说法正确，故本选项不符合题意；B 、对顶角相等，说法正确，故本选项不符合题意；C 、两个直角一定互补，说法正确，故本选项不符合题意；D 、同位角不一定相等，要有平行的条件，说法错误，故本选项符合题意；故选：D ．【点睛】本题考查了平移的性质，对顶角的性质，互补的定义，同位角的定义，是基础知识，需熟练掌握．12、B【分析】首先根据任意三个相邻数之和都是20，推出a 1=a 4，a 2=a 5，a 1=a 6，总结规律为a 1=a 1n+1，a 2=a 1n+2，a 1=a 1n ，即可推出a 18=a 1=11，a 65=a 2=6-x=2x ，求出a 2=4，即可推出a 1=1，推出a 2020=a 1=1．【详解】∵任意三个相邻数之和都是20，∴a 1=a 4，a 2=a 5，a 1=a 6，故a 1=a 1n+1，a 2=a 1n+2，a 1=a 1n ，∴a 18=a 1=11，a 65=a 2=6-x=2x ，∴a 2=4，∴a 1=1，∴a 2020=a 1=1．故选：B ．【点睛】此题考查数字的变化规律，掌握数字之间的运算规律，利用规律解决问题是解答此题的关键．二、填空题（每题4分，满分20分，将答案填在答题纸上）13、10或50【解析】试题解析：(1)当C 在线段AB 延长线上时,如图1，∵M 、N 分别为AB 、BC 的中点，1130,2022BM AB BN BC ；∴==== ∴MN =50.(2)当C 在AB 上时，如图2，同理可知BM =30，BN =20，∴MN =10，所以MN =50或10，故答案为50或10.14、>【分析】构造等腰直角三角形，根据等腰直角三角形的性质即可进行比较大小.【详解】解：如下图所示，AFG 是等腰直角三角形，∴45FAG BAC ∠=∠=︒，∴BAC DAE ∠>∠．故答案为.>另：此题也可直接测量得到结果．【点睛】本题考查等腰直角三角形的性质，构造等腰直角三角形是解题的关键.15、－2.5【分析】根据相反数在数轴上的分布特点求解即可.【详解】∵5÷2＝2.5，点A 在原点的左边，∴点A 表示的数是－2.5，故答案为－2.5.【点睛】本题考查了相反数的几何意义，在数轴上，表示互为相反数的两个点，分别位于原点的两旁，并且它们与原点的距离相等.16、1【分析】根据乘积为1的两个数互为倒数，可得互为倒数的两个数的积是1，可得答案．【详解】解；∵a、b互为倒数，则ab=1，∴1ab=1；故答案为：1．【点睛】本题考查了倒数的定义，解题的关键是熟练掌握倒数的定义.17、15【分析】解答此题要将木块展开，然后根据两点之间线段最短解答．【详解】由题意可知，将木块展开，如图所示：长相当于增加了2米，∴长为10+2=12米，宽为9米，22+=．91215故答案为：15．【点睛】本题主要考查了平面展开-最短路径问题，两点之间线段最短，勾股定理的应用，要注意培养空间想象能力．三、解答题（本大题共7小题，共64分.解答应写出文字说明、证明过程或演算步骤.）18、（1）13只；（2）115.2︒；（3）200只【分析】（1）根据1.2kg的鸡的百分比和数量求出抽取的总数量，然后求出1.0kg的鸡的数量，再求出1.5kg的鸡的数量即可；（2）利用1.8kg的鸡的数量除以抽取的总数量，然后乘以360°，即可得到答案；（3）先求出抽取的鸡中2.0kg的鸡的百分比，然后估计总体的数量即可.÷=（只），【详解】解：（1）1224%50⨯（只），∴1.0kg的鸡的数量为：5010%=5----=（只）；∴1.5kg的鸡的数量为：5051216413∴抽取的质量为1.5kg的鸡有13只．（2）16 360115.250︒⨯=︒；∴质量为1.8kg的鸡对应扇形圆心角为115.2︒；（3）4250020050⨯=（只）；∴质量为2.0kg的鸡大约有200只．【点睛】本题考查了条形统计图和扇形统计图的联合应用，以及用样本数量估计总体数量，解题的关键是熟练掌握条形统计图和扇形统计图的联系进行解题.19、-．【解析】先去括号、合并同类项化简原式，再根据非负数的性质得出x，y的值，继而将x，y的值代入计算可得．【详解】原式∵|x-2|+（y+）=1，∴x-2=1，y+=1，于是x=2，y=-，当x=2，y=-时，原式=-xy2=-2×（-）2=-．【点睛】本题主要考查非负数的性质与整式的加减-化简求值，解题的关键是掌握整式的加减的本质即为去括号、合并同类项．20、（1）长方体（四棱柱）；（2）s=224【分析】（1）根据长方体的定义和三视图，即可判定；（2）该长方体由四个长方形和两个相对的面是正方形围成，即可求解其表面积.【详解】（1）由题意，得该几何体是长方体（四棱柱）；（2）由题意，得s=64×2＋24×4=224.【点睛】此题主要考查长方体的特征以及表面积的求解，熟练掌握，即可解题.21、21223x x + 【分析】根据单项式乘多项式的法则先运算，然后去括号再合并同类项即可. 【详解】()2211123623x x x x ⎛⎫-+--- ⎪⎝⎭=221111163223x x x x -+-++ =21223x x + 【点睛】本题主要考查了合并同类项，根据去括号的法则先去括号是解题的关键.22、（1）50；（2）24，72；（3）见解析（4）160人．【分析】（1）根据B 级的人数和所占的百分比求出抽取的总人数，（2）再用A 级的人数除以总数即可求出α；用抽取的总人数减去A 、B 、D 的人数，求出C 级的人数，用360度乘以C 级所占的百分比即可求出扇形统计图中C 级对应的圆心角的度数；（3）根据所求各组的人数补全统计图；（4）用D 级所占的百分比乘以该校的总人数，即可得出该校D 级的学生数．【详解】（1）在这次调查中，一共抽取的学生数是：24÷48%＝50（人），故答案为：50；（2）α＝1250×100%＝24%；等级为C 的人数是：50−12−24−4＝10（人） 扇形统计图中C 级对应的圆心角为1050×360°＝72°； 故答案为：24，72；（3）补图如下：（4）根据题意得：2000×450＝160（人）， 答：该校D 级学生有160人．【点睛】此题考查了是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．23、（1）详见解析；（2）详见解析【分析】（1）证明∠3=∠2，问题得证；（2）根据BD∥C E，得到∠C=∠DBA，进而证明DF∥AC，问题得证．【详解】解：（1）证明：∵∠1=∠2，∠1=∠3，∴∠3=∠2；∴BD∥C E（同位角相等，两直线平行）（2）由（1）可知：BD∥CD，∴∠C=∠DBA（两直线平行，同位角相等），又∵∠C=∠D，∴∠D=∠DBA，∴DF∥AC（内错角相等，两直线平行），∴∠A=∠F（两直线平行，内错角相等）．【点睛】本题考查了平行线的判定与性质，解答此题的关键是注意平行线的性质和判定定理的综合运用．平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系.应用平行线的判定和性质定理时，一定要弄清题设和结论，切莫混淆．。

北京市第六十六中学2015—2016学年第一学期期中检测初三年级数学学科答案及评分标准2015.11一、选择题(每小题3分，共30分)二、填空题（每小题3分，共18分） 11．25 12．75°13．32+-=x y (答案不唯一) 14．∠ABC= ∠ACD 15．3y < 1y <2y 16．②④⑤ 三、填空题（每小题5分，共30分） 17．解：原式 21=+ ……………………………………4分 = ……………………………………………………………5分18. 解：在BDC ∆中，090=∠C ， 045=∠BDC ，6=DC∴tan 451BCDC︒== ∴6BC = …………………………………2分 在ABC ∆中，52sin =A ，∴25BC AB =，............3分 ∴15AB = (5)分19.证明：∵AB ＝2，BC ＝4 BD ＝1 ,2142==∴CB AB ,21=BA BD ……………………2分 ,BABDCB AB =∴………………3分 ∵CBA ABD ∠=∠， …………………4分 ∴△ABD ∽△CBA ； ……………………………5分20. 解：（1）∵抛物线)(022≠++=a bx ax y 过点A (-1，0)，B (1，6)∴a - b= -2 a + b= 4 ∴a=1,b=3∴抛物线的函数关系式为232++=x x y . …………2分 （1） ∵2494932+-++=x x y …………3分 41232-⎪⎭⎫ ⎝⎛+=x …………4分∴抛物线的顶点坐标是（23-，41） …………5分 21. 解：过点A 做AD BC 于D …………1分 则 在Rt中∴sinC= …………2分∵sinC= ,AC=10∴∴AD=8 …………3分 在Rt中∴sinB= …………4分∵sinB=∴∴AB=24 …………5分22. 解：由题意，可得∠P AC =30°，∠PBC =60°．………………………………………… 2分 ∴ 30APB PBC PAC ∠=∠-∠=︒．∴ ∠P AC=∠APB ．∴ PB =AB = 200．…………………………… 3分在Rt △PBC 中，∠PCB =90°，∠PBC =60°，PB =200， ∴)米(1732.173310023200sin ≈==⨯=∠=PBC PB PC ………4分 答：灯塔P 到环海路的距离PC 约等于173米． …………………………………… 5分23.解 (1) W= (x-20)(-2x+80) ……………… 1分 =-2x ²+120x-1600 ……………… 2分 (2) W=-2(x-30)²+200 ……………… 4分 ∵a=-2<0∴当x=30元时，每天利润最大，最大利润是200元。

2016 年黄埔区初中毕业班综合测试 数学参考答案与评分标准说明：1．参考答案与评分标准给出了一种或几种解法供参考，如果考生的解法与参考答案不同，可根据试题主要考 查的知识点和能力要求参照评分标准给分． 2． 对解答题中的计算题， 当考生的解答在某一步出现错误时， 如果后继部分的解答未改变该题的内容和难度， 可视影响的程度决定后继部分的得分， 但所给分数不得超过该部分正确解答应得分数的一半； 如果后继部分的 解答有较严重的错误，就不再给分． 3．解答右端所注分数，表示考生正确做到这一步应得的累加. 4．只给整数分数，选择题和填空题不给中间分． 一、选择题： （本大题考查基本知识和基本运算．共 10 小题，每小题 3 分，满分 30 分． ） 1 2 3 4 5 题号 二、 填空 C A A B C 答案 大题查 识和基本运算．共 6 小题，每小题 3 分，满分 18 分． ） 题号 答案 11 12 13 6 C 7 D 8 D 9 B 10 D 题： （本 基本知1415161000130( x  2 y)( x  2 y)318 3三、解答题：(本大题共9小题，满分102 分．解答应写出文字说明、证明过程或演算步骤．) 17． （本小题满分 9 分） （本小题考查目标与要求：会解由两个一元一次不等式组成的不等式组，并会用数轴确定其解集.）–2–101234x解：解不等式 (1) ，得 x  1 ， ……………………………………………3 分 解不等式 (2) ，得 x  4 ， …………………………………………………6 分把不等式 (1) 和 (2) 的解集在数轴上表示出来，如上图所示. ……………8 分 从上图可以找出两个不等式解集的公共部分，得不等式组的解集为：1  x  4 . …………………………………………………………………9 分18． （本小题满分 9 分） （本小题考查目标与要求：会解可化为一元一次方程的分式方程） 解：方程两边乘 ( x  1)( x  1) ， ……………………………………………3 分得： x  1  2 . 解得： x  3 .…………………………………………………………5 分 …………………………………………………………6 分 …………………………7 分检验：当 x  3 时， ( x  1)( x  1)  8  0 . 因此 x  3 是原分式方程的解. 所以，原分式方程的解为 x  3 .……………………………………8 分 ……………………………………9 分19． （本小题满分 10 分） （本小题考查目标与要求：会作一条线段的垂直平分线；会判断点与圆的位置关系； 会运用勾股定理解决简单问题.） 解答：⑴如图所示； ①作 AC 的垂直平分线，交 AB 于点 O ，交 AC 于点 D ； ……………………3 分 ②以 O 为圆心， OA 为半径作圆，交 OD 的延长线于点 E . …………………4 分（每一步的作图痕迹及点的标签各占 0.5 分，按四舍五入给整数分） ⑵①填“点 B 在 O 上”,或填“ O 经过点 B ”. …………………………5 分 ②∵ OD  AC ,且点 D 是 AC 的中点, ∴ AD 1 AC  4 ,设 O 的半径为 r ， ………………………………………6 分 2则 OA  OE  r , OD  OE  DE  r  2 . ……………………………………7 分 在 Rt AOD 中，由勾股定理，得OA2  AD2  OD2 ,………………………………………………………………8 分即 r  4  (r  2) ,………………………………………………………………9 分2 2 2解得 r  5 .∴ O 的半径为 5 ……………………………………………………10 分E DCAOB图720． （本小题满分10分） （本小题考查目标与要求：能根据已知条件确定一次函数表达式；能根据已知条件确定反比例函数表达式； 考查运算求解能力.） 解： （1）∵直线 y  3 x  b 与 y 轴交于点 B ， 2∴点 B 的坐标为 (0, b) . …………………………………………………2 分 ①作 AC  y 轴, C 为垂足，则 AC 是 OB 边上的高，………………3 分 ②∵点 A 的坐标为 (2, m) ，∴ AC  2 . ………………………………4 分 ③又∵ AOB 的面积等于 2 ，∴ ∴b  2 .1 b  2  2 ， ………………………5 分 2………………………………………………………………6 分（说明：第①、②二步省略，只要第③步正确，不扣分.） (2)∵点 A(2, m) 在直线 y   ∴m  3 x  2 上， 23  2  2  1，…………………………………………………7 分 2∴ A 的坐标为 (2, 1) . ……………………………………………………8 分 又∵反比例函数 y  ∴ 1 k （ k 是常量， k  0 ）的图像经过点 A ， xk ，即 k  2 , …………………………………………………9 分 2 2 ∴这个反比例函数的解析式为 y   . ………………………………10 分 xyBO C1 A 图8x21． （本小题满分12分） （本小题考查目标与要求：会用列举法（包括列表、画树形图）计算简单事件发生的概率.） 解：⑴从 O 、 A 、 B 、 C 、 D 五点中任取两点，所有等可能出现的结果有：AB、AC、AD、BC、BD、CD、OA、OB、OC、OD，共有 10 种.（写对一个结果给 0.5 分，四舍五入，给整数分） 满足两点间的距离为 2 的结果有 AB 、BC、CD、AD 这 4 种.………5 分………7 分（写对一个结果给 0.5 分，四舍五入，给整数分） 所以 P(两点间的距离为 2 ) 4 2  . 10 5………8 分 ………9 分⑵满足两点间的距离为 2 2 的结果有 AC 、BD 这 2 种. （写对一个结果给 0.5 分，四舍五入，给整数分） 所以 P(两点间的距离为 2 2 ) 2 1  . 10 5………10 分 ………12 分⑶满足两点间的距离为 2 的结果有 OA 、OB、OC、OD 这 4 种. （写对一个结果给 0.5 分，四舍五入，给整数分） 所以 P(两点间的距离为 2 ) 4 2  . 10 5………12 分22.（本小题满分12分） （本小题考查目标与要求：能用一元一次方程解决实际问题，能用二元一次方程组解决实际问题；考查解决 简单实际问题的能力；考查运算求解能力.） 解法 1：设甲加工 30 个零件需 t 小时， 依题意，乙加工 30 个零件需 t+1 小时. ………1 分 ………2 分 ………3 分 ………4 分30 个零件， t 30 乙原来每小时加工 个零件. t+1甲原来每小时加工 乙改进操作方法后，每小时加工 乙完成 30 个零件的时间是60 个零件， t+1………5 分 ………7 分30 1 ， = （t  1 ） 60 2 t+1 24 4 甲完成 24 个零件的时间是 = t， 30 5 t 4 1 依题意得， t  (t  1)  1 ， 5 2解得， t=5 . 答：甲乙两人原来每小时各加工零件分别为 6 个、5 个． 解法 2：设甲乙两人原来每小时各加工零件分别为 x 个、 y 个，………9 分………10 分 ………11 分 ………12 分 ………1 分 30 30   1,  x y ∴  24  30  1,   x 2y………7 分 x  6, 解得   y  5.………11 分经检验它是原方程的组解，且符合题意． 答：甲乙两人原来每小时各加工零件分别为 6 个、5 个． 23. （本小题满分12分） 性质；考查推理能力、转化思想）………12 分（本小题考查目标与要求：掌握两个三角形全等的条件；掌握菱形的性质；理解等边三角形的概念并掌握其D E A 图10 F CD E A 备用图………1 分F CBB解： （1）BE=BF，证明如下： 如图 10，∵四边形 ABCD 是边长为 4 的菱形，BD=4， ∴ΔABD、ΔCBD 都是边长为 4 的正三角形， 在 ΔBDE 与 ΔBCF 中， ∵AE+CF=4，∴CF=4-AE=AD-AE=DE， 又∵BD=BC=4，∠BDE=∠C=60° ， ∴ΔBDE≅ΔBCF，∴BE=BF. （2）∵ΔBDE≅ΔBCF，∴∠EBD=∠FBC， ∴∠EBD+∠DBF=∠FBC+∠DBF， ∴∠EBF=∠DBC=60° 又∵BE=BF，∴ΔBEF 是正三角形， ∴EF=BE=BF. 在备用图中，当动点 E 运动到点 D 或点 A 时，BE 的最大值为 4， 当 BE⊥AD，即 E 为 AD 的中点时，BE 的最小值为 2 3 ， ∵EF=BE，∴EF 的最大值为 4，最小值为 2 3………2 分………3 分 ………4 分 ………4 分 ………5 分 ………6 分 ………6 分 ………7 分 ………7 分 ………9 分 ………11 分 ………12 分24.（本小题满分14分） （本小题考查目标与要求：能判定一条直线是否为圆的切线；掌握切线与过切点的半径之间的关系；会运用 三角函数解决与直角三角形有关的简单问题；考查推理能力、转化思想考查运算求解能力.）C D AEC D O 图11 B AEC D O 图11 B AEO 图11B证明： （1）解法 1:连接 OE， ∵AB 是⊙O 的直径，AC 是圆⊙O 的切线， ∴AE⊥BC，AC⊥AB. 在直角 ΔAEC 中， ∵D 为 AC 的中点， ∴DE=DC，∴∠DEC=∠DCE. ∵∠OEB=∠OBE，∠ABC+∠ACB=90° ， ∴∠DEC+∠OEB=∠DCE+∠OBE=90° ， ∴∠DEO=180° -90° =90° ，∴OE⊥DE， ∴DE 是⊙O 的切线. 解法 2: 连接 OE，OD. AC 是圆⊙O 的切线， ∴AE⊥BC，AC⊥AB. 在直角 ΔAEC 中， ∵D 为 AC 的中点，∴DE=DA=DC， 在 ΔDEO 与 ΔDAO 中， ∵OA=OE, OD=OD, DE=DA, ∴ΔDEO≌ΔDAO, ∴∠DEO=∠DAO=90° ，∴OE⊥DE， ∴DE 是⊙O 的切线. （2）解法 1：在直角 ΔEAC 与直角 ΔEBA 中， ∵∠EAC+∠EAB=90° ，∠EBA+∠EAB=90° ， ∴∠EAC=∠EBA， ∴ΔEAC∼ΔEBA，……… 1 分 ………2 分……… 3 分 ……… 4 分 ……… 5 分 ………6 分 ………1 分∵AB 是⊙O 的直径， ………2 分 ………3 分………4 分 ………5 分 ………6 分 ………7 分 ………8 分 ………9 分 ………10 分 ………11 分 ………12 分EA EB  ， EA2  EB  EC . EC EA 设 EC  1 ，则 EB  3 ，∴EA2  EB  EC  3 ， EA  3 .在直角 ΔAEB 中， tan ABC  （2）解法 2 设 AE  x ， CE  1 ，则 BE  3 ， BC  4 . 在直角 ΔAEB 与直角 ΔAEC 中，由勾股定理得：EA 3 ,  EB 3………14 分………7 分AB  9  x2 ， AC  1  x2 ．∵………9 分 ………10 分 ………10 分 ………11 分 ………11 分 ………12 分1 1 AC  AB  AE  BC ， 2 2∴ 1  x2  9  x2  4 x ， ∴ 9  x2  9 x2  x4  16 x2 ，4 2 ∴ x  6x  9  0 ，∴ ( x  3)  0 ，∴ x  3 .2 2在直角 ΔAEB 中， tan ABC EA 3 ，  EB 3………14 分25. （本小题满分14分） （本小题考查目标与要求： 能根据已知条件确定二次函数的表达式； 会应用配方法或公式法确定图象的顶点、 开口方向和对称轴；会用描点法画出二次函数的图象；掌握四边形是平行四边形的条件；考查待定系数法、 数形结合、转化、分类讨论的思想方法，以及运算求解能力）解： （1）根据题意得： 9-3b+c=0, -1+b+c=0.………1 分解得： a  1, ， b  2.2………2 分∴解析式为 y   x  2 x  3 . 当x………2 分 ………3 分 ………3 分 ………4 分 ………5 分b  1 时， y  4 ， 2a∴顶点 D 的坐标为 (1, 4) ， ∴点 F 的坐标为 (1, 4) . 此抛物线的草图如右图所示 （2）若以 O 、 F 、 P 、 Q 为顶点的平行四边形存在， 则点 Q( x, y) 必须满足 y  EF  4 .………6 分2 ①当 y  4 时，  x  2 x  3  4 .………7 分 ………8 分 ， ………8 分 ………9 分 ………12 分 ………13 分 ………13 分 ………14 分解得， x  1  2 2 ， ∴ Q1 (1  2 2, 4), Q2 (1  2 2, 4) ∴P 1 (2 2,0), P 2 (2 2,0) .2 ②当 y  4 时，  x  2 x  3  4 ，解得， x  1 ， ∴ Q3 (1, 4) ， ∴P 3 (2,0) . 综上所述，符合条件的点有三个即：P 1 (2 2,0), P 2 (2 2,0), P 3 (2,0) .………14 分。

1、答题前填写好自己的姓名、班级、考号等信息2、请将答案正确填写在答题卡上2023-2024学年新疆图木舒克高中数学人教A 版 必修二第九章 统计强化训练(15)姓名：____________ 班级：____________ 学号：____________考试时间：120分钟满分：150分题号一二三四五总分评分*注意事项：阅卷人得分一、选择题（共12题，共60分）99.5%99.9%97.5%95%1. 某学校课题组为了研究学生的数学成绩和物理成绩之间的关系，随机抽取高二年级20名学生某次考试成绩（百分制）如表所示：序号1234567891011121314151617181920数学成绩9575809492656784987167936478779057837283物理成绩9063728791715882938177824885699161847886若数学成绩90分（含90分）以上为优秀，物理成绩85（含85分）以上为优秀．有多少把握认为学生的数学成绩与物理成绩之间有关系（ ）A. B. C. D. 6810122. 某校选修乒乓球课程的学生中，高一年级有30名，高二年级有40名，现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为（ ）A. B. C. D. 141832503. 在新冠疫苗试验初期，某居民区有5000人自愿接种了新冠疫苗，其中60~70岁的老年人有1400人，16~19岁的中学生有400人，其余为符合接种条件的其它年龄段的居民.在一项接种疫苗的追踪调查中，要用分层抽样的方法从该居民区5000名接种疫苗的人群中抽取部分人作为样本进行追踪调查，已知老年人中抽取了14人，则从其余符合接种条件的其它年龄段的居民中抽取的人数为（ ）A. B. C. D. 甲、乙两个街道的测评分数的极差相等甲、乙两个街道的测评分数的平均数相等街道乙的测评分数的众数为87甲、乙两个街道测评分数的中位数中，乙的中位数较大4. 某区创建全国文明城市，指挥部办公室对所辖街道当月文明城市创建工作进行考评．工作人员在本区选取了甲、乙两个街道，并在这两个街道各随机抽取10个地点进行现场测评，下表是两个街道的测评分数（满分100分），则下列说法正确的是（ ）甲75798284868790919398乙73818183878895969799A. B. C. D.020714015. 总体由编号为01，02，…，19，20的20个个体组成，利用下面的随机数表选取容量为6的样本，选取方法是从随机数表第1行的第5列开始，依次向右读取．一行结束后，转至下一行从第一列开始，直到取足样本，则选出来的第6个样本的编号为（ ）32 04 34 12 49 35 82 00 36 23 48 69 69 38 74 8178 07 65 72 06 02 63 14 07 64 43 01 69 97 28 98A. B. C. D. ①用简单随机抽样法 ②用分层抽样法①用分层抽样法 ②用简单随机抽样法①、②都用简单随机抽样法①、②都用分层抽样法6. 要完成下列2项调查，应采用的抽样方法是（ ）①从某社区125户高收入家庭，280户中等收入家庭，95户低收入家庭中选出100户调查社会购买力的某项指标；②从某中学高一年级的12名体育特长生中选出3人调查学习负担情况.A. B. C. D. 讲座后问卷答题的正确率的中位数为87.5%讲座后问卷答题的正确率的众数为85%讲座后问卷答题的正确率的第75百分位数为95%讲座前问卷答题的正确率的标准差小于讲座后问卷答题的正确率的标准差7. 某社区通过公益讲座以普及社区居民的垃圾分类知识；为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷．这10位社区居民在讲座前和讲座后问卷答题的正确率如下：则下列说法错误的是（ ）A. B. C. D. 34568. 如果个数的平均数为，则的平均数为（ ）．A. B. C. D. 50，0.1550，0.75100，0.15100，0.759. 某中学举办电脑知识竞赛，满分为100分，80分以上为优秀（含80分），现将高一两个班参赛学生的成绩进行整理后分成5组；第一组[50，60），第二组[60，70），第三组[70，80），第四组[80，90），第五组[90，100]，其中第一、三、四、五小组的频率分别为0.30、0.15、0.10、0.05，而第二小组的频数是40，则参赛的人数以及成绩优秀的概率分别是（ ）A. B. C. D. 10. 在一组样本数据中，1，2，3，4出现的频率分别为，且，则下面四种情形中，对应样本的标准差最大的一组是（ ）A.B.C. D.4125811. 一个单位有职工120人，其中业务人员60人，管理人员40人，后勤人员20人，为了了解职工健康情况，要从中抽取一个容量为24的样本，如用分层抽样，则管理人员应抽到的人数为 A. B. C. D. 频数众数平均数频率12. 频率分布直方图中每个矩形的面积所对应的数字特征是（ ）A. B. C. D. 13. 某校随机抽取100名同学进行“垃圾分类”的问卷测试，测试结果发现这100名同学的得分都在内，按得分分成5组：，，，，， 得到如图所示的频率分布直方图，则估计这100名同学的得分的中位数为 .14. 已知总体的各个体的值由小到大依次为2，3，3，7，a ，b ，12，13.7，18.3，20，且总体的中位数为10.5，平均数为10．若要使该总体的方差最小，则a 、b 的取值分别是 ．15. 若数据 ， ， ，…， 的方差为3，则数据 ， ， ，…， 的方差为 ．16. 某牧草种植基地2019年种植 三种牧草共50亩，种植比例如图所示.该基地计划在2020年扩大 品种和 品种的种植面积，同时保持 品种的种植面积不变，这样 品种的种植面积比例下降为 .若C 品种的种植面积比例保持不变，那么2020年，C 品种的种植面积是 亩.17. 根据某水文观测点的历史统计数据，得到某河流水位（单位：米）的频率分布直方图如下.将河流水位在 ，，，，，，各段内的频率作为相应段的概率，并假设每年河流水位变化互不影响.(1) 求未来4年中，至少有2年该河流水位的概率（结果用分数表示）.(2) 已知该河流对沿河工厂的影响如下：当时，不会造成影响；当时，损失50000元；当时，损失300000元.为减少损失，工厂制定了三种应对方案.方案一：不采取措施；方案二：防御不超过30米的水位，需要工程费用8000元；方案三：防御34米的最高水位，需要工程费用20000元.试问哪种方案更好，请说明理由.18. 投资人甲为预测某行业的发展前景，对100位从事该行业的人进行了访问，根据被访问者的问卷评分（满分100分）得到如下频率分布直方图．将该行业发展前景预期分为三个等级，评分不超过40分认为悲观，大于40分不超过60分认为尚可，超过6 0分认为乐观．将这100人预测各等级的频率估计为未来该行业各等级发生的可能性．(1) 估计这100个人评分的平均值和中位数；(2) 投资人甲在该行业有A，B两个备选投资项目，投资回报率都与该行业发展前景等级有关，根据分析，大致关系如下：行业发展前景等级乐观尚可悲观项目A年回报率（）168-16项目B年回报率（）139-3根据以上信息，分别计算这两个备选投资项目的年回报率的期望与方差，并用统计学的知识给甲投资建议．19. 某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计，绘制了频率分布直方图（如图所示），规定80分及以上者晋级成功，否则晋级失败．晋级成功晋级失败合计男16女50合计（参考公式：，其中）0.400.250.150.100.050.0250.780 1.323 2.072 2.706 3.841 5.024(1) 求图中a的值；(2) 根据已知条件完成下面列联表，并判断能否有85%的把握认为“晋级成功”与性别有关？(3) 将频率视为概率，从本次考试的所有人员中，随机抽取4人进行约谈，记这4人中晋级失败的人数为X，求X的分布列与数学期望．20. 从一批苹果中，随机抽取50个，其重量（单位：克）的频数分布表如下：(1) 根据频数分布表计算苹果的重量在的频率；(2) 用分层抽样的方法从重量在和的苹果中共抽取4个，其中重量在的有几个？(3) 在（2）中抽出的4个苹果中，任取2个，写出所有可能的结果，并求重量在和中各有1个的概率.21. 旨在全面提高国民体质和健康水平，1995年国务院颁布了《全民健身计划纲要》，并在2009年将每年8月8日设置为“全民健身日”，倡导全民做到每天参加--次以上的体育健身活动，学会两种以上健身方法，每年进行一次体质测定．某小区为了调查居民的体育运动情况，从该小区随机抽取了100位成年人，记录了他们某天的锻炼时间，其频率分布直方图如下：(1) 求的值，并求这100位居民锻炼时间的中位数；(2) 若规定为第一组，依次往下，现采用分层抽样的方法从第三组和第五组随机抽取6名成年人进行体质测定，再从这6人中随机抽取2人进行跟踪调查，求这2人中，两组各有1人的概率．答案及解析部分1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.(1)(2)18.(1)(2)19.(1)(2)(3)20.(1)(2)(3)21.(1)(2)。

四川省绵阳市江油市2025届九上数学期末质量跟踪监视模拟试题注意事项：1．答卷前，考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。

用2B铅笔将试卷类型（B）填涂在答题卡相应位置上。

将条形码粘贴在答题卡右上角"条形码粘贴处"。

2．作答选择题时，选出每小题答案后，用2B铅笔把答题卡上对应题目选项的答案信息点涂黑；如需改动，用橡皮擦干净后，再选涂其他答案。

答案不能答在试题卷上。

3．非选择题必须用黑色字迹的钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上；如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

4．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

一、选择题（每题4分，共48分）1．已知在直角坐标平面内，以点P（﹣2，3）为圆心，2为半径的圆P与x轴的位置关系是（）A．相离B．相切C．相交D．相离、相切、相交都有可能2．在半径为3cm的⊙O中，若弦AB＝32，则弦AB所对的圆周角的度数为（）A．30°B．45°C．30°或150°D．45°或135°3．一组数据0、－1、3、2、1的极差是（）A．4 B．3 C．2 D．14．已知点A、B、C、D、E、F是半径为r的⊙O的六等分点，分别以A、D为圆心，AE和DF长为半径画圆弧交于点P．以下说法正确的是( )①∠PAD=∠PDA=60º；②△PAO≌△ADE；③PO=2r；④AO∶OP∶PA=1∶2∶3.A．①④B．②③C．③④D．①③④5．如图，已知////AB CD EF，直线AF与直线BE相交于点O，下列结论错误的是（）A．AD BCDF CE=B．OA OBOC OD=C ．CD OC EF OE = D ．OA OB OF OE = 6．在平面直角坐标系中，二次函数22y x x =-的图象可能是（ ）A ．B ．C ．D ．7．下列事件为必然事件的是（ ）A ．打开电视机，正在播放新闻B ．任意画一个三角形，其内角和是180︒C ．买一张电影票，座位号是奇数号D ．掷一枚质地均匀的硬币，正面朝上8．下列几何体中，主视图和左视图都为矩形的是（ ）A ．B ．C ．D ．9．已知二次函数y ＝ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c ＜0；②b 2﹣4ac ＞0；③b ＞0；④4a ﹣2b+c ＜0；⑤a+c ＜23，其中正确结论的个数是（ ）A ．②③④B ．①②⑤C ．①②④D ．②③⑤ 10．如图，AB 为O 的直径，,C D 为O 上两点，若40BCD ∠︒＝，则ABD ∠的大小为（ ）．A ．60°B ．50°C ．40°D ．20°11．如图，一次函数1(0)y kx b k =+≠的图象与反比例函数2m y x=（m 为常数且0m ≠）的图象都经过()()1,2,2,1A B --，结合图象，则不等式m kx b x+>的解集是（ ）A ．1x <-B ．10x -<<C ．1x <-或02x <<D ．10x -<<或2x >12．若将抛物线y=5x 2先向右平移2个单位，再向上平移1个单位，得到的新抛物线的表达式为（ ） A ．y=5（x ﹣2）2+1 B ．y=5（x+2）2+1 C ．y=5（x ﹣2）2﹣1 D ．y=5（x+2）2﹣1二、填空题（每题4分，共24分）13．如图，Rt △ABC 中，∠A ＝90°，CD 平分∠ACB 交AB 于点D ，O 是BC 上一点，经过C 、D 两点的⊙O 分别交AC 、BC 于点E 、F ，AD ＝3，∠ADC ＝60°，则劣弧CD 的长为_____．14．某工厂去年10月份机器产量为500台，12月份的机器产量达到720台，设11、12月份平均每月机器产量增长的百分率为x ，则根据题意可列方程_______________15．只请写出一个开口向下，并且与x 轴有一个公共点的抛物线的解析式__________．16．一个圆锥的母线长为5cm ，底面圆半径为3 cm ，则这个圆锥的侧面积是____ cm ²．（结果保留）．17．定义：在平面直角坐标系中，我们将横、纵坐标都是整数的点称为“整点”．若抛物线y ＝ax 2﹣2ax +a +3与x 轴围成的区域内(不包括抛物线和x 轴上的点)恰好有8个“整点”，则a 的取值范围是_____．18．如图，AB 为O 的直径，弦CD ⊥AB 于点E ，点F 在圆上，且DF ＝CD ，BE ＝2，CD ＝8，CF 交AB 于点G ，则弦CF 的长度为__________，AG 的长为____________.三、解答题（共78分）19．（8分）如图：在Rt△ABC中，∠C=90°，∠ABC=30°。