数学卷

高中数学卷试题及答案一、选择题（每题3分，共30分）1. 若函数\( f(x) = 2x^2 - 3x + 1 \)，求\( f(-1) \)的值。

A. 0B. 2C. 4D. 62. 已知数列\( \{a_n\} \)的通项公式为\( a_n = 3n - 1 \)，求\( a_5 \)的值。

A. 14B. 12C. 16D. 183. 圆的方程为\( (x-3)^2 + (y-4)^2 = 25 \)，求圆心坐标。

A. (-3, 4)B. (3, 4)C. (4, 3)D. (4, -3)4. 已知\( \sin \theta = \frac{3}{5} \)，求\( \cos \theta \)的值（假设\( \theta \)在第一象限）。

A. \( \frac{4}{5} \)B. \( -\frac{4}{5} \)C.\( \frac{3}{5} \) D. 05. 若\( \log_{10}100 = 2 \)，求\( \log_{10}1000 \)的值。

A. 3B. 4C. 5D. 66. 已知\( \frac{1}{x} + \frac{1}{y} = 5 \)，且\( xy = 6 \)，求\( x + y \)的值。

A. 3B. 6C. 9D. 127. 函数\( y = \sqrt{x} \)的定义域是：A. \( x \geq 0 \)B. \( x > 0 \)C. \( x \leq 0 \)D. \( x < 0 \)8. 已知\( \tan \alpha = 2 \)，求\( \sin \alpha \)的值（假设\( \alpha \)在第一象限）。

A. \( \frac{2}{\sqrt{5}} \)B. \( \frac{1}{\sqrt{5}} \)C. \( \frac{2}{3} \)D. \( \frac{1}{2} \)9. 已知\( |a| < 1 \)，求\( 1 - a \)的值的范围。

2024新课标卷数学试卷一、选择题：本大题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设集合A = {xx^2-3x + 2 = 0}，B={x∈ Z - 1≤slant x≤slant3}，则A∩ B = (_ )A. {1}B. {2}C. {1,2}D. {1,2,3}2. 已知复数z = 1 + i（i为虚数单位），则frac{z^2}{z - 1}=(_ )A. 2B. 2iC. -2D. -2i3. 已知向量→a=(1,2)，→b=(x,1)，若→a⊥→b，则x = (_ )A. -2B. -(1)/(2)C. (1)/(2)D. 24. 在等差数列{a_n}中，a_1=1，公差d = 2，则a_5=(_ )A. 9B. 10C. 11D. 125. 函数y=sin(2x+(π)/(3))的最小正周期是(_ )A. πB. 2πC. (π)/(2)D. (2π)/(3)6. 从5名男生和3名女生中任选3人参加志愿者活动，则所选3人中至少有1名女生的选法有(_ )种。

A. 46B. 56C. 70D. 807. 已知双曲线frac{x^2}{a^2}-frac{y^2}{b^2} = 1(a>0,b>0)的一条渐近线方程为y=(3)/(4)x，且过点(4,3√(3))，则双曲线的方程为(_ )A. frac{x^2}{16}-frac{y^2}{9}=1B. frac{x^2}{9}-frac{y^2}{16}=1C. frac{x^2}{4}-frac{y^2}{3}=1D. frac{x^2}{3}-frac{y^2}{4}=18. 若x,y满足约束条件x + y≤slant3 x - y≥slant - 1 y≥slant0，则z = 2x + y的最大值为(_ )A. 3B. 4C. 5D. 6二、多项选择题：本大题共4小题，每小题5分，共20分。

数学试题及标准答案大全一、选择题（每题2分，共10分）1. 下列哪个数不是实数？A. √2B. πC. iD. 0答案：C2. 一个等差数列的首项是2，公差是3，那么第5项是多少？A. 17B. 14C. 11D. 8答案：A3. 函数f(x) = 2x^2 - 3x + 1的顶点坐标是？A. (3/4, -1/8)B. (3/2, -1/4)C. (1/2, -1/8)D. (1/4, -1/8)答案：C4. 一个圆的半径是5，那么它的面积是多少？A. 25πC. 75πD. 100π答案：B5. 以下哪个是偶函数？A. f(x) = x^2 + 1B. f(x) = x^3 - 3xC. f(x) = cos(x)D. f(x) = sin(x)答案：C二、填空题（每题3分，共15分）6. 一个直角三角形的两个直角边长分别是3和4，那么斜边的长度是________。

答案：57. 函数y = 2^x的反函数是________。

答案：log2(y)8. 已知集合A = {1, 2, 3}，集合B = {2, 3, 4}，那么A∩B =________。

答案：{2, 3}9. 一个等比数列的首项是2，公比是2，那么第4项是多少？10. 一个抛物线方程是y = ax^2 + bx + c，如果它经过点(1, 2)和(2, 3)，那么a + b + c = ________。

答案：3三、解答题（每题10分，共20分）11. 已知函数f(x) = x^3 - 3x^2 + 2，求它的导数f'(x)。

答案：f'(x) = 3x^2 - 6x12. 一个长方体的长、宽、高分别是a、b、c，求它的体积。

答案：体积 V = abc结束语：以上是数学试题及标准答案大全，希望这些题目能帮助你更好地理解和掌握数学知识。

一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 若函数f(x) = ax^2 + bx + c在x=1时取得最小值，则下列选项中正确的是（）A. a > 0, b = 0, c = 0B. a > 0, b = 0, c ≠ 0C. a < 0, b ≠ 0, c ≠ 0D. a ≠ 0, b ≠ 0, c ≠ 02. 已知等差数列{an}的前n项和为Sn，若S10 = 100，S20 = 200，则第10项a10的值为（）A. 10B. 20C. 30D. 403. 下列函数中，在其定义域内连续的是（）A. y = |x|B. y = x^2C. y = 1/xD. y = √x4. 已知向量a = (1, 2)，向量b = (2, -1)，则向量a·b的值为（）A. 5B. -3C. 0D. 15. 在三角形ABC中，角A、B、C的对边分别为a、b、c，若a=5，b=7，c=8，则角C的余弦值为（）A. 1/2B. 1/3C. 2/3D. 3/46. 已知函数f(x) = x^3 - 3x + 1，则f'(1)的值为（）A. 1B. -1C. 0D. 37. 下列命题中，正确的是（）A. 对于任意的实数x，都有x^2 ≥ 0B. 对于任意的实数x，都有x^3 ≥ 0C. 对于任意的实数x，都有x^4 ≥ 0D. 对于任意的实数x，都有x^5 ≥ 08. 在直角坐标系中，点P(2, 3)关于直线y = x的对称点为（）A. (2, 3)B. (3, 2)C. (3, 3)D. (2, 2)9. 下列复数中，属于第二象限的是（）A. 1 + iB. -1 + iC. 1 - iD. -1 - i10. 已知等比数列{an}的公比为q，若a1 = 2，a3 = 16，则q的值为（）A. 2B. 4C. 8D. 16二、填空题（本大题共10小题，每小题5分，共50分。

２０２３年高考文科数学试卷（全国乙卷）一、选择题1.232i 2i ++=（）A.1B.2C.D.52.设全集{}0,1,2,4,6,8U =，集合{}{}0,4,6,0,1,6M N ==，则U M N ⋃=ð（）A.{}0,2,4,6,8 B.{}0,1,4,6,8 C.{}1,2,4,6,8 D.U3.如图，网格纸上绘制的一个零件的三视图，网格小正方形的边长为1，则该零件的表面积为（）A .24B.26C.28D.304.在ABC 中，内角,,A B C 的对边分别是,,a b c ，若cos cos a B b A c -=，且5C π=，则B ∠=（）A.10π B.5π C.310π D.25π5.已知e ()e 1xaxx f x =-是偶函数，则=a （）A.2- B.1- C.1 D.26.正方形ABCD 的边长是2，E 是AB 的中点，则EC ED ⋅=（）A.B.3C. D.57.设O 为平面坐标系的坐标原点，在区域(){}22,14x y xy ≤+≤内随机取一点A ，则直线OA 的倾斜角不大于π4的概率为（）A.18B.16C.14D.128.函数()32f x x ax =++存在3个零点，则a 的取值范围是（）A.(),2-∞- B.(),3-∞- C.()4,1-- D.()3,0-9.某学校举办作文比赛，共6个主题，每位参赛同学从中随机抽取一个主题准备作文，则甲、乙两位参赛同学抽到不同主题概率为（）A.56B.23C.12D.1310.已知函数()sin()f x x ωϕ=+在区间π2π,63⎛⎫⎪⎝⎭单调递增，直线π6x =和2π3x =为函数()y f x =的图像的两条对称轴，则5π12f ⎛⎫-= ⎪⎝⎭（）A.32B.12-C.12D.3211.已知实数,x y 满足224240x y x y +---=，则x y -的最大值是（）A.3212+B.4C.1+D.712.设A ，B 为双曲线2219y x -=上两点，下列四个点中，可为线段AB 中点的是（）A.()1,1 B.()1,2- C.()1,3 D.()1,4--二、填空题13.已知点(A 在抛物线C ：22y px =上，则A 到C 的准线的距离为______.14.若π10,,tan 22⎛⎫∈= ⎪⎝⎭θθ，则sin cos θθ-=________．15.若x ，y 满足约束条件312937x y x y x y -≤-⎧⎪+≤⎨⎪+≥⎩，则2z x y =-的最大值为______.16.已知点,,,S A B C 均在半径为2的球面上，ABC 是边长为3的等边三角形，SA ⊥平面ABC ，则SA =________．三、解答题17.某厂为比较甲乙两种工艺对橡胶产品伸缩率的处理效应，进行10次配对试验，每次配对试验选用材质相同的两个橡胶产品，随机地选其中一个用甲工艺处理，另一个用乙工艺处理，测量处理后的橡胶产品的伸缩率．甲、乙两种工艺处理后的橡胶产品的伸缩率分别记为i x ，()1,2,,10i y i =⋅⋅⋅．试验结果如下：试验序号i 12345678910伸缩率i x 545533551522575544541568596548伸缩率iy 536527543530560533522550576536记()1,2,,10i i i z x y i =-=⋅⋅⋅，记1210,,,z z z ⋅⋅⋅的样本平均数为z ，样本方差为2s ．（1）求z ，2s ；（2）判断甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率是否有显著提高（如果z ≥，则认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高，否则不认为有显著提高）18.记n S 为等差数列{}n a 的前n 项和，已知21011,40a S ==．（1）求{}n a 的通项公式；（2）求数列{}n a 的前n 项和n T ．19.如图，在三棱锥-P ABC 中，AB BC ⊥，2AB =，BC =PB PC ==,,BP AP BC 的中点分别为,,D E O ，点F 在AC 上，BF AO ⊥．（1）求证：EF //平面ADO ；（2）若120POF ∠=︒，求三棱锥-P ABC 的体积．20.已知函数()()1ln 1f x a x x ⎛⎫=++⎪⎝⎭．（1）当1a =-时，求曲线()y f x =在点()()1,f x 处的切线方程．（2）若函数()f x 在()0,∞+单调递增，求a 的取值范围．21.已知椭圆2222:1(0)C b b x a a y +>>=的离心率是3，点()2,0A -在C 上．（1）求C 的方程；（2）过点()2,3-的直线交C 于,P Q 两点，直线,AP AQ 与y 轴的交点分别为,M N ，证明：线段MN 的中点为定点．【选修4-4】（10分）22.在直角坐标系xOy 中，以坐标原点O 为极点，x 轴正半轴为极轴建立极坐标系，曲线1C 的极坐标方程为2sin 42ππρθθ⎛⎫=≤≤ ⎪⎝⎭，曲线2C ：2cos 2sin x y αα=⎧⎨=⎩（α为参数，2απ<<π）.（1）写出1C 的直角坐标方程；（2）若直线y x m =+既与1C 没有公共点，也与2C 没有公共点，求m 的取值范围．【选修4-5】（10分）23.已知()22f x x x =+-（1）求不等式()6x f x ≤-的解集；（2）在直角坐标系xOy 中，求不等式组()60f x yx y ⎧≤⎨+-≤⎩所确定的平面区域的面积．２０２３年高考文科数学试卷（全国乙卷）答案一、选择题【1题答案】【答案】C【2题答案】【答案】A【3题答案】【答案】D【4题答案】【答案】C【5题答案】【答案】D【6题答案】【答案】B【7题答案】【答案】C【8题答案】【答案】B【9题答案】【答案】A【10题答案】【答案】D【11题答案】【答案】C【12题答案】【答案】D二、填空题【13题答案】【答案】94【14题答案】【答案】5-【15题答案】【答案】8【16题答案】【答案】2三、解答题【17题答案】【答案】（1）11z =，261s =；（2）认为甲工艺处理后的橡胶产品的伸缩率较乙工艺处理后的橡胶产品的伸缩率有显著提高.【18题答案】【答案】（1）152n a n=-（2）2214,71498,8n n n n T n n n ⎧-≤=⎨-+≥⎩【19题答案】【答案】（1）证明见解析（2）3【20题答案】【答案】（1）()ln 2ln 20x y +-=；（2）1|2a a ⎧⎫≥⎨⎬⎩⎭.【21题答案】【答案】（1）22194y x +=（2）证明见详解【选修4-4】（10分）【22题答案】【答案】（1）()[][]2211,0,1,1,2x y x y +-=∈∈（2）()(),0-∞+∞【选修4-5】（10分）【23题答案】【答案】（1）[2,2]-；（2）6.。

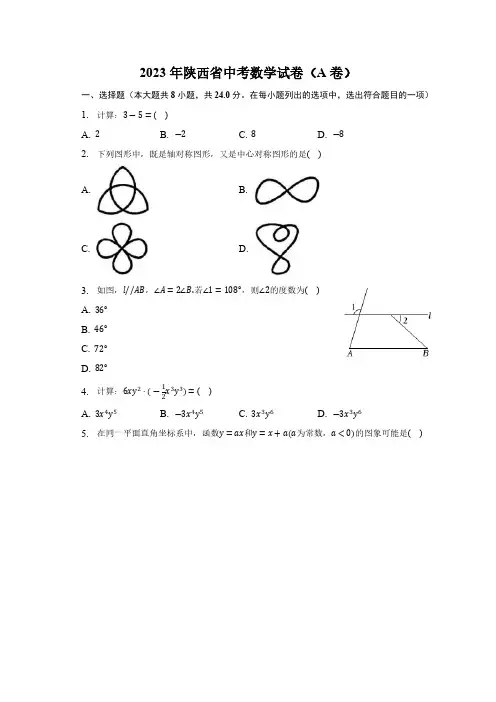
2023年陕西省中考数学试卷（A卷）一、选择题（本大题共8小题，共24.0分。

在每小题列出的选项中，选出符合题目的一项）1. 计算：3―5=( )A. 2B. ―2C. 8D. ―82. 下列图形中，既是轴对称图形，又是中心对称图形的是( )A. B.C. D.3.如图，l//AB，∠A=2∠B.若∠1=108°，则∠2的度数为( )A. 36°B. 46°C. 72°D. 82°4. 计算：6xy2⋅(―1x3y3)=( )2A. 3x4y5B. ―3x4y5C. 3x3y6D. ―3x3y65. 在同一平面直角坐标系中，函数y=ax和y=x+a(a为常数，a<0)的图象可能是( )A. B.C. D.6.如图，DE 是△ABC 的中位线，点F 在DB 上，DF =2BF.连接EF 并延长，与CB 的延长线相交于点M.若BC =6，则线段CM 的长为( )A. 132B. 7C. 152D. 87. 陕西饮食文化远流长，“老碗面”是陕西地方特色美食之一.图②是从正面看到的一个“老碗”(图①)的形状示意图．AB 是⊙O 的一部分，D 是AB 的中点，连接OD ，与弦AB 交于点C ，连接OA ，OB.已知AB =24cm ，碗深CD =8cm ，则⊙O 的半径OA 为( )A. 13cmB. 16cmC. 17cmD. 26cm8. 在平面直角坐标系中，二次函数y =x 2+mx +m 2―m(m 为常数)的图象经过点(0,6)，其对称轴在y 轴左侧，则该二次函数有( )A. 最大值5B. 最大值154C. 最小值5 D. 最小值154二、填空题（本大题共5小题，共15.0分）9. 如图，在数轴上，点A表示3，点B与点A位于原点的两侧，且与原点的距离相等.则点B 表示的数是______ ．10.如图，正八边形的边长为2，对角线AB、CD相交于点E.则线段BE的长为______ ．11. 点E是菱形ABCD的对称中心，∠B=56°，连接AE，则∠BAE的度数为______ ．12.如图，在矩形OABC和正方形CDEF中，点A在y轴正半轴上，点C，F均在x轴正半轴上，点D在边BC上，BC=2CD，AB=3.若点B，E在同一个反比例函数的图象上，则这个反比例函数的表达式是______ ．13.如图，在矩形ABCD中，AB=3，BC=4.点E在边AD上，且ED=3，M、N分别是边AB、BC上的动点，且BM=BN，P是线段CE上的动点，连接PM，PN.若PM+PN=4.则线段PC的长为______ ．三、解答题（本大题共13小题，共81.0分。

一年级上册数学期末试卷（一）班级姓名得分一、看谁算得又对又快。

（20分）7+1= 6-1= 9-3= 3+4=1+2= 5-5= 1+7= 9-5=8-4= 2+2= 6-4= 3+3=1+3= 3+5= 2+3= 0+9=3-1= 8-0= 6+0= 7-6=二、填空。

（30分）1、在○里填上“+”或“—”。

（6分）5○1=6 9○9=0 7○2=94○3=1 5○3=2 0○5=52、在○里填上“＞”“＜”或“=”。

（6分）8○7 9○10 3+1○3-19○6 2○5 2+5○8-13、填上合适的数。

（8分）2 5 □∧∧∧□□3□ 5 289 10∧∧∧3□ 1 □□□4、（10分）（1）（ ）。

（2）我还能给它们排排队呢。

（ ）＞（ ）＞（）＞（ ）＞（ ）＞（）＞（ ） 三、接着画一画，填一填。

（6分）（13+□=7 （2 4+□=8四、涂一涂。

（3分）把左边9只小象圈起，给从左数第10只小象涂上颜色。

五、他们说的话对吗？对的打“√”，错的打“×”。

（8分）（ （ ）（ ） （ ）六、数一数。

（11分）七、看图列式计算。

（22分前面4小题各3分，最后1题10分）□○□=□（只）□○□=□（枝）一年级上册数学期末试卷（三）一年级上册数学期末试卷（二）2019—2020学年上学期期中测试卷年级：一年级 科目：数学 考试时间：90分钟1、划一划。

（划去多余的o)2、①、从左数，排在第（ ）；排在第（ ）。

②、从右数，（ ）排在第4；（ ）排在第6。

3、4、什么也没有用（ ）表示。

53： 。

画多2个：。

6、在Ο里填上“＞”“＜”或“＝”。

5Ο3＋2 10－7Ο46＋2Ο8－1 5＋2Ο97、分类（是同一类的圈起）二、小法官判案（对的打“√”，错的打“×”）（5分）1、比3多4的数是6。

（）2、与8相邻的数是7和8。

（）3不是圆柱。

（）4、□○△☆，○排第1。

（）5、这两根绳子不一样长。

2022年全国统一高考数学试卷（新高考Ⅰ）一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）若集合{|4}M x =<，{|31}N x x =，则(M N = )A ．{|02}x x <B ．1{|2}3x x <C ．{|316}x x <D ．1{|16}3x x <2．（5分）若(1)1i z -=，则(z z +=)A ．2-B ．1-C ．1D ．23．（5分）在ABC ∆中，点D 在边AB 上，2BD DA =．记CA m = ，CD n = ，则(CB = )A ．32m n- B ．23m n-+C ．32m n+ D ．23m n+ 4．（5分）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库．已知该水库水位为海拔148.5m 时，相应水面的面积为2140.0km ；水位为海拔157.5m 时，相应水面的面积为2180.0km ．将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5m 上升到157.5m 时，增加的水量约为2.65)(≈)A ．931.010m ⨯B ．931.210m ⨯C ．931.410m ⨯D ．931.610m ⨯5．（5分）从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为()A ．16B ．13C ．12D ．236．（5分）记函数()sin()(0)4f x x b πωω=++>的最小正周期为T ．若23T ππ<<，且()y f x =的图像关于点3(2π，2)中心对称，则()(2f π=)A ．1B ．32C ．52D ．37．（5分）设0.10.1a e =，19b =，0.9c ln =-，则()A ．a b c<<B ．c b a <<C ．c a b <<D ．a c b<<8．（5分）已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且3l ，则该正四棱锥体积的取值范围是()A ．[18，81]4B ．27[4，81]4C ．27[4，64]3D ．[18，27]二、选择题：本题共4小题，每小题5分，共20分。

数学试卷本卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟。

第Ⅰ卷一、选择题（每题5分，共60分）1、设0a b <<，则下列不等式中正确的是 （ ）A. 2a b a b ab +<<<B ． 2a b a ab b +<<<C ．2a b a ab b +<<<D ． 2a b ab a b +<<<2、已知等比数列{}n a 的公比2=q ，前n 项和为n S ，则42S a = （ ）A. 2B. 4C.152D. 1723、已知向量→a ，→b 满足,2b ,1a ,0b a ===∙→→→→则 =→→b -a 2 （ ）A. 0B. 22C. 4D. 84、有一个几何体的正视、侧视、俯视图分别如下，则该几何体的表面积为 （ ）A.π12B.π24C.π36D.π48 5、已知函数()42322+++=kx kx x x f 的定义域是R ，则k 的取值范围是 （ ）A. ()4,0B. [)4,0C. (]4,0D. []4,0 6、=-+oooo oo7sin 15sin 8cos 7sin 15cos 8sin （ ）A.32-B.32+C. 32±D.23-5565567、设n S 为等差数列{}n a 的前n 项和，若11a =，公差2d =，362=-+k k S S ，则k = （ ）A ． 8B ． 7C ． 6D ． 5 8、已知{}n a 为等比数列，472a a +=，568a a =-，则110a a +=（ ）A. 7B. 5C. -5D. -79、在ABC ∆中，,30A ,100b ,80a o ===则角B 的解得个数是 （ ） A.0个 B.1个 C.2个 D.不确定的10、已知()x f y =是开口向上的二次函数，且()()x f x f -11=+恒成立.若()()2-31x f x f <+，则x 的取值范围是 （ ） A. ⎪⎭⎫⎝⎛2343， B. ⎪⎭⎫⎝⎛∞43-，∪⎪⎭⎫⎝⎛∞+，23C. ⎪⎭⎫ ⎝⎛43-23-， D. ⎪⎭⎫ ⎝⎛∞23--，∪⎪⎭⎫⎝⎛∞+，43- 11、已知⎥⎦⎤⎝⎛∈20πθ，，则函数()θθθsin 2sin +=f 的最小值为 （ ）A ．22 B. 3 C. 32 D. 212、定义在R 上的偶函数()x f 满足()()x f x f =+2，且在[]2,-3-上是减函数.若B A 、是锐角三角形的两内角，则有 （ ） A. ()()B cos A sin f f > B. ()()sinB A sin f f > C. ()()B cos A sin f f < D. ()()B cos A cos f f >第Ⅱ卷二、填空题（共4个小题，每小题5分，共20分；把答案填答题纸上）13、在ABC ∆中，3B π=中，且34B C B A =⋅,则ABC ∆的面积是___________.14、设,x y 满足约束条件：⎪⎪⎩⎪⎪⎨⎧≥≥-≥-≤+.0y 0x ,1y x ,3y x 则y 2x z -=的取值范围为 .15、已知0,0x y >>，若2282y x m m xy+>+恒成立，则实数m 的取值范围是 .16、 若)y ,x (P 在圆()()63y 3x 22=-+-上运动，则xy 的最小值为__________.三、解答题（共6小题，17题10分，18—22题各12分，共70分；解答应写出文字说明，证明过程或演算步骤）17、已知a 千克的糖水中含有b 千克的糖；若再加入m 千克的糖()0,0>>>m b a ，则糖水变甜了.请你根据这个事实，写出一个不等式 ； 并证明不等式ma mb a b ++<()0,0>>>m b a 成立，请写出证明的详细过程.18、如图,正三棱柱111C B A AB C -的底面边长为3，侧棱233AA 1=,D 是CB 延长线上一点，且BD=BC（1）求证：直线1B C //平面D AB 1； （2）求二面角B AD B 1--的大小； （3）求三棱锥11AB B C -的体积.19、已知△ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c ，并且有c b C a C a +=+sin 3cos 。

2024年普通高等学校招生全国统一考试数学（Ⅰ卷）一、选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.已知集合{}{}355,3,1,0,2,3A x x B =-<<=--,则A B = （）A.{}1,0-B.{}2,3 C.{}3,1,0-- D.{}1,0,2-2.若z1i 1z =+-,则z =（）A.1i-- B.1i-+ C.1i- D.1i+3.已知向量()()0,1,2,x ==a b ,若()4⊥-b b a ,则x =（）A.-2B.-1C.1D.24.已知()cos m αβ+=,tan tan 2αβ=,则()cos αβ-=（）A.3m- B.3m -C.3m D.3m,则圆锥的体积为（）A. B. C. D.6.已知函数()()22,0e ln 1,0x x ax a x f x x x ⎧---<⎪=⎨++≥⎪⎩在R 上单调递增,则a 的取值范围是（）A.(],0-∞B.[]1,0-C.[]1,1-D.[)0,∞+7.当[]0,2x π∈时,曲线sin y x =与2sin 36y x π⎛⎫=- ⎪⎝⎭的交点个数为（）A.3B.4C.6D.88.已知函数()f x 的定义域为R，()()()12f x f x f x >-+-,且当3x <时,()f x x =,则下列结论中一定正确的是（）A.()10100f > B.()201000f > C.()101000f < D.()2010000f <二、多项选择题:本大题共3个小题，每小题6分，满分18分。

每小题给出的备选答案中，有多个选项是符合题意的。

全部选对得6分，部分选对得3分，选错或不选得0分。

9.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1X =,样本方差20.01S =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设失去出口后的亩收入Y 服从正态分布()2,N X S ,则（）(若随机变量Z 服从正态分布()2,N μσ,则()0.8413P Z μσ<+≈)A.()20.2P X >>B.()0.5P X Z ><C.()0.5P Y Z >> D.()0.8P Y Z ><10.设函数()()()214f x x x =--,则（）A.3x =是()f x 的极小值点B.当01x <<时,()()2f x f x <C.当12x <<时,()4210f x -<-<D.当10x -<<时,()()2f x f x ->11.造型可以看作图中的曲线C 的一部分,已知C 过坐标原点O ,且C 上的点满足横坐标大于2-,到点()2,0F 的距离与到定直线()0x a a =<的距离之积为4,则（）A.2a =-B.点()在C 上C.C 在第一象限的点的纵坐标的最大值为1D.当点()00,x y 在C 上时,0042y x ≤+三、填空题:本大题共3个小题，每小题5分，共15分。

小学数学试卷测试大全及答案(全国通用)小学数学试卷测试大全及答案一、选择题1. 以下数字哪一个是偶数？A. 3B. 5C. 8D. 9答案：C2. 下面哪个图形是正方形？A. ○B. △C. □D. ●答案：C3. 对于下列运算式：5 + 7 x 2 = ？A. 12B. 14C. 19D. 24答案：D4. 选择下列数字中的最小值：A. 0.5B. 0.9C. 0.1D. 0.8答案：C5. 在一小时内，钟表指针会经过多少次重合？A. 0B. 1C. 2D. 3答案：C二、填空题1. 36 ÷ 4 = ________ 。

答案：92. 30 - ________ = 13 。

答案：173. 值得注意的是，1 千米 = ________ 米。

答案：10004. 12 颗葡萄分给 4 个小朋友，每个小朋友分到 ________ 颗葡萄。

答案：35. 星期一到星期天一共有 ________ 天。

答案：7三、计算题1. 一辆公交车上有 36 名乘客，下车后只剩下 18 名乘客，那么这辆公交车上原本有多少人？答案：542. 小明有 16 支铅笔，他送了朋友 5 支，还剩下多少支铅笔？答案：113. 小红有 2 张 5 元的纸币和 3 张 10 元的纸币，她想买一本 25 元的书，她还需要多少钱？答案：5四、应用题1. 一袋苹果有 5 公斤，小明吃掉了其中的 1.5 公斤，那么剩下的苹果还有多重？答案：3.5 公斤2. 小华每天步行上学需要 15 分钟，周一到周五上学日一共需要多少分钟？答案：75 分钟3. 如果一根绳子的长度是 80 厘米，小明需要使用这根绳子来围成一个正方形，每条边的长度是多少厘米？答案：20 厘米五、解答题1. 请计算 13 加上 8 的和，并写出运算步骤。

答案：13 + 8 = 21运算步骤：13+ 8------212. 请画出一个边长为 5 厘米的正方形。

答案：____| || ||____|3. 请说明什么是等于号（=）的作用。

一、选择题（每题5分，共25分）1. 下列哪个数是质数？A. 14B. 17C. 18D. 202. 一个长方形的长是6厘米，宽是3厘米，它的周长是多少厘米？A. 12B. 15C. 18D. 213. 小明有10个苹果，他给小红3个，又给小刚2个，小明还剩多少个苹果？A. 5B. 7C. 9D. 104. 一个圆的半径是5厘米，它的周长是多少厘米？A. 15B. 25C. 30D. 505. 小华有20元，她买了一个文具盒花了10元，还剩多少元？A. 5C. 15D. 20二、填空题（每题5分，共25分）6. 25 + 35 = _______（用加法计算）7. 48 - 27 = _______（用减法计算）8. 3 × 4 = _______（用乘法计算）9. 8 ÷ 2 = _______（用除法计算）10. 一个正方形的边长是4厘米，它的面积是多少平方厘米？_______（用公式计算）三、应用题（每题10分，共30分）11. 小明骑自行车去学校，他骑了15分钟，平均速度是每分钟200米，他一共骑了多少米？12. 一本书有100页，小明已经看了40页，还剩下多少页没看？13. 一个长方形的面积是36平方厘米，如果长是9厘米，宽是多少厘米？四、解答题（每题15分，共30分）14. 请用分数和小数表示下列各数：A. 五分之四B. 三又二分之一15. 一个梯形的上底是5厘米，下底是10厘米，高是6厘米，求这个梯形的面积。

五、附加题（20分）16. 小明和小红一起去商店，小明买了3个苹果，小红买了4个苹果，共花费了12元，苹果的单价是多少元？17. 小华有一个正方体，它的边长是2厘米，求这个正方体的体积。

一、选择题1. B2. B3. C4. B5. B二、填空题6. 607. 218. 129. 410. 16平方厘米三、应用题11. 3000米12. 60页13. 6厘米四、解答题14. A. 4/5，0.8；B. 5/2，2.515. 30平方厘米五、附加题16. 2元17. 8立方厘米。

2023全国三卷数学2023年全国三卷数学试卷一、选择题（每小题5分，共25分）1、已知函数$f(x)=\frac{2x+1}{x-3}$，则$f(-\frac{1}{2})$的值为（）。

A. $-5$B. $-\frac{3}{7}$C. $5$D. $\frac{7}{3}$2、四棵树分别在下午2：00、2：30、3：00和3：30分别开始按1小时、$\frac{3}{4}$小时、$\frac{2}{3}$小时和$\frac{1}{2}$小时的速度升高，如果四棵树同时到达了相同的高度，那么它们一起升高的总时长是（）。

A. $\frac{51}{8}$小时B. $\frac{19}{3}$小时C.$\frac{53}{6}$小时 D. $\frac{133}{12}$小时3、下列选项中，不是二次函数的是（）。

A. $y=2x^2+3x+4$B. $y=-x^2+3x-2$C.$y=\frac{1}{2}x^2+2$ D. $y=\sqrt{x}$4、过$\bigtriangledown ABC$的外心的直线交$AC$、$AB$分别于$D$、$E$，则$BD$、$CE$两线段的长度之比是（）。

A. $AB:AC$B. $AC:AB$C. $BD:CE$D. $CE:BD$5、已知$\log_3 a=\frac{1}{2}$，则$\frac{1}{a^2}-\frac{3}{a}+\frac{2}{3}$的值为（）。

A. $0$B. $-\frac{1}{6}$C. $\frac{1}{12}$D. $\frac{5}{18}$二、填空题（每小题6分，共30分）6、在$\bigtriangleup ABC$中，$AB=10$，$AC=12$，$BC=8$，则$\sin A=$__________。

7、已知函数$f(x)=\frac{5}{x-2}+\frac{3}{x-1}$，则$f(-\frac{1}{2})=$__________。