第二编 专题三 第3讲

人教版数学四升五衔接讲义（复习进阶）专题03 运算定律知识互联网知识导航知识点一：.加法运算定律1.加法交换律（1）两个数相加.交换加数的位置.它们的和不变。

这叫做加法交换律。

用字母表示：a+b=b+a。

（2）加法交换律中变化的只是两个加数的位置.不变的是这两个加数及它们的和。

2.加法结合律三个数相加.先把前两个数相加.或者先把后两个数相加.和不变。

这叫做加法结合律。

用字母表示；：（a+b）+c=a+（b+c）。

3.运用加法运算定律进行简便计算在计算几个数连加的算式时.可以利用加法交换律和加法结合律.使计算简便。

4.连减的简便计算（1）一个数减去几个数的和.可以从这个数里依次减去各个加数。

用字母可表示：a-（b +c）=a-b-c。

（2）一个数连续减去几个数.可以先把所有的减数加起来.再从被减数里减去所有减数的和。

用字母可表示：a -b-c=a-（b+c）。

知识点二：.乘法交换律1.乘法交换律两个数相乘.交换两个因数的位置.积不变。

这叫做乘法交换律。

用字母表示：a×b=b×ag2.乘法结合律三个数相乘.先乘前两个数.或者先乘后两个数.积不变。

这叫做乘法结合律。

用字母表示：（a×b）×c=a×（b×c）。

3.乘法分配律（两个数的和与一个数相乘.可以先把它们与这个数分别相乘.再相加。

这叫做乘法分配律。

用字母表示：（a+b）×c=a×c+b×c 知识点三：乘法及连除的简便计算1.同一道乘法算式的不同简算方法：计算某些特殊的乘法算式时.可以将其中一个因数折分成两个数的积.再运用乘法交换律和乘法结合律来进行简算；也可以将其中一个因数折分成两个数的和.再运用乘法分配律来进行简算。

2.连除的简便计算（1）一个数连续除以两个数.可以改为除以两个数的积。

用字母可表示为：a÷b÷c=a÷（b ×c）。

三 、《研究匀变速直线运动》实验专题[实验目的]①练习使用电火花计时器或电磁打点计时器，利用打上点的纸带研究物体的运动情况。

②掌握判断物体是否做匀变速运动方法； ③测定匀变速直线运动的加速度。

[实验原理和方法] 1．打点计时器的使用（1）电磁打点计时器（2）电火花计时器阅读课本，需要掌握两种打点计时器的构造、原理、工作电压、打点时间间隔 2．由纸带判断物体是否做匀变速直线运动的方法。

如图所示： （1）s n 是相邻两记数点间的距离；（2）△s 是两个连续相等的时间里的位移之差；⋯⋯-=∆-=∆,,232121s s s s s s（3）T 是相邻两记数点间的时间间隔：T =0.02ns （n 为两记数点间点子的间隔数）； 由运动学有关公式得：20121aT T v s +=，……① 21221aT T v s +=，……② aT v v +=01，……③所以212aT s s s =-=∆因为时间T 是个恒量，匀变速运动小车的加速度a 也是个恒量。

因此△s 必然是个恒量。

这表明，只要小车做匀加速运动，它在任意两个连续相等的时间里的位移之差就一定相等。

3．由纸带求物体运动加速度的方法。

（方法一）逐差法：取偶数段位移因为()()().3214122334aT s s s s s s s s =-=-+-+- 同理有236253aT s s s s =⋯⋯=-=-所以，我们可以由测得的各段位移s 1，s 2……求出⋯⋯-=-=225221413,3T s s a T s s a 再算出a 1，a 2……的平均值()()()23216543T s s s s s s a ++-++=这样使所给的数据得到有效利用，达到减小误差的目的。

（方法二）图象法： 由Ts s v n n n 21++=求出各个计数点的瞬时速度，作t v -图象，图线的斜率即为物体的加速度。

4．求物体在打下某记数点时瞬时速度的方法： 由以上①②③式得：Ts s v 2211+=（时间2T 内的平均速度等于该段时间中点T 时刻的瞬时速度）。

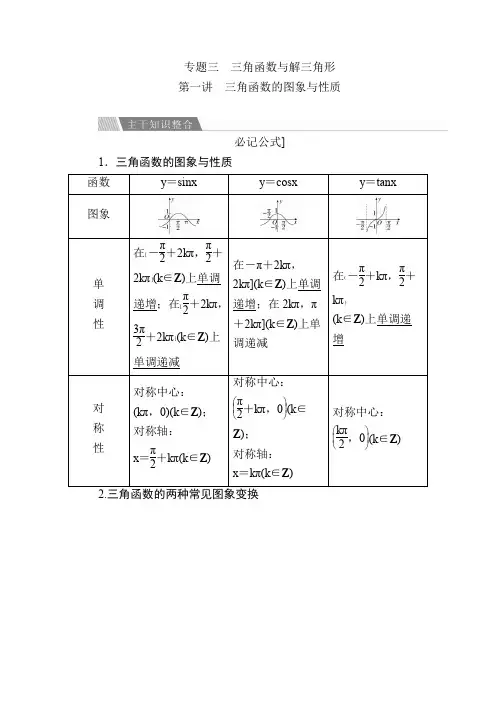
专题三三角函数与解三角形第一讲三角函数的图象与性质必记公式]1．三角函数的图象与性质重要结论]1．三角函数的奇偶性(1)函数y ＝A sin(ωx ＋φ)是奇函数⇔φ＝k π(k ∈Z )，是偶函数⇔φ＝k π＋π2(k ∈Z )；(2)函数y ＝A cos(ωx ＋φ)是奇函数⇔φ＝k π＋π2(k ∈Z )，是偶函数⇔φ＝k π(k ∈Z )；(3)函数y ＝A tan(ωx ＋φ)是奇函数⇔φ＝k π(k ∈Z )． 2．三角函数的对称性(1)函数y ＝A sin(ωx ＋φ)的图象的对称轴由ωx ＋φ＝k π＋π2(k ∈Z )解得，对称中心的横坐标由ωx ＋φ＝k π(k ∈Z )解得；(2)函数y ＝A cos(ωx ＋φ)的图象的对称轴由ωx ＋φ＝k π(k ∈Z )解得，对称中心的横坐标由ωx ＋φ＝k π＋π2(k ∈Z )解得；(3)函数y ＝A tan(ωx ＋φ)的图象的对称中心由ωx ＋φ＝k π2(k ∈Z )解得．失分警示]1．忽视定义域求解三角函数的单调区间、最值(值域)以及作图象等问题时，要注意函数的定义域．2．重要图象变换顺序在图象变换过程中，注意分清是先相位变换，还是先周期变换．变换只是相对于其中的自变量x 而言的，如果x 的系数不是1，就要把这个系数提取后再确定变换的单位长度和方向．3．忽视A ，ω的符号在求y ＝A sin(ωx ＋φ)的单调区间时，要特别注意A 和ω的符号，若ω<0，需先通过诱导公式将x 的系数化为正的．4．易忽略对隐含条件的挖掘，扩大角的范围导致错误．考点三角函数的定义域、值域(最值)典例示法典例1 (1)2016·合肥一模]函数y ＝lg (2sin x －1)＋1－2cos x 的定义域是________．解析] 由题意，得⎩⎪⎨⎪⎧2sin x －1＞0，1－2cos x ≥0，即⎩⎪⎨⎪⎧sin x ＞12，cos x ≤12，首先作出sin x ＝12与cos x ＝12表示的角的终边(如图所示)．由图可知劣弧和优弧的公共部分对应角的范围是⎣⎢⎡2k π＋π3，2k π＋⎭⎪⎫5π6(k ∈Z )． 所以函数的定义域为⎣⎢⎡⎭⎪⎫2k π＋π3，2k π＋5π6(k ∈Z )．答案] ⎣⎢⎡⎭⎪⎫2k π＋π3，2k π＋5π6(k ∈Z ) (2)已知函数f (x )＝－2sin ⎝⎛⎭⎪⎫2x ＋π4＋6sin x cos x －2cos 2x ＋1，x ∈R .①求f (x )的最小正周期；②求f (x )在区间⎣⎢⎡⎦⎥⎤0，π2上的最大值和最小值． 解] ①f (x )＝－sin2x －cos2x ＋3sin2x －cos2x ＝2sin2x －2cos2x ＝22sin ⎝ ⎛⎭⎪⎫2x －π4.所以f (x )的最小正周期T ＝2π2＝π. ②由①知f (x )＝22sin ⎝ ⎛⎭⎪⎫2x －π4.因为x ∈⎣⎢⎡⎦⎥⎤0，π2， 所以2x －π4∈⎣⎢⎡⎦⎥⎤－π4，3π4，则sin ⎝ ⎛⎭⎪⎫2x －π4∈⎣⎢⎡⎦⎥⎤－22，1.所以f (x )在⎣⎢⎡⎦⎥⎤0，π2上最大值为22，最小值为－2.1．三角函数定义域的求法求三角函数的定义域实际上是解简单的三角不等式，常借助三角函数线或三角函数图象来求解．2．三角函数值域(最值)的三种求法 (1)直接法：利用sin x ，cos x 的值域．(2)化一法：化为y ＝A sin(ωx ＋φ)＋k 的形式逐步分析ωx ＋φ的范围，根据正弦函数单调性写出函数的值域(最值)．(3)换元法：把sin x 或cos x 看作一个整体，可化为求函数在给定区间上的值域(最值)问题．针对训练2015·天津高考]已知函数f (x )＝sin 2x －sin 2⎝ ⎛⎭⎪⎫x －π6，x ∈R . (1)求f (x )的最小正周期；(2)求f (x )在区间⎣⎢⎡⎦⎥⎤－π3，π4上的最大值和最小值．解 (1)由已知，有f (x )＝1－cos2x 2－1－cos ⎝⎛⎭⎪⎫2x －π32＝12⎝ ⎛⎭⎪⎫12cos2x ＋32sin2x －12cos2x＝34sin2x －14cos2x ＝12sin ⎝ ⎛⎭⎪⎫2x －π6.所以，f (x )的最小正周期T ＝2π2＝π.(2)解法一：因为f (x )在区间⎣⎢⎡⎦⎥⎤－π3，－π6上是减函数，在区间⎣⎢⎡⎦⎥⎤－π6，π4上是增函数，f ⎝ ⎛⎭⎪⎫－π3＝－14，f ⎝ ⎛⎭⎪⎫－π6＝－12，f ⎝ ⎛⎭⎪⎫π4＝34.所以，f (x )在区间－π3，π4]上的最大值为34，最小值为－12.解法二：由x ∈⎣⎢⎡⎦⎥⎤－π3，π4得2x －π6∈⎣⎢⎡⎦⎥⎤－5π6，π3，故当2x －π6＝－π2，x ＝－π6时，f (x )取得最小值为－12，当2x －π6＝π3，x ＝π4时，f (x )取最大值为34.考点三角函数的性质典例示法典例2 2015·山东枣庄质检]已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6＋sin ⎝⎛⎭⎪⎫ωx －π6－2cos 2ωx2，x ∈R (其中ω＞0)．(1)求函数f (x )的值域；(2)若函数f (x )的图象与直线y ＝－1的两个相邻交点间的距离为π2，求函数f (x )的单调递增区间．解] (1)f (x )＝32sin ωx ＋12cos ωx ＋32sin ωx －12cos ωx －(cos ωx ＋1)＝2⎝ ⎛⎭⎪⎫32sin ωx －12cos ωx －1 ＝2sin ⎝ ⎛⎭⎪⎫ωx －π6－1 由－1≤sin ⎝ ⎛⎭⎪⎫ωx －π6≤1，得－3≤2sin ⎝ ⎛⎭⎪⎫ωx －π6－1≤1， 所以函数f (x )的值域为－3,1]．(2)由题设条件及三角函数的图象和性质可知， f (x )的周期为π，所以2πω＝π，即ω＝2. 所以f (x )＝2sin ⎝⎛⎭⎪⎫2x －π6－1，再由2k π－π2≤2x －π6≤2k π＋π2(k ∈Z )， 解得k π－π6≤x ≤k π＋π3(k ∈Z )．所以函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－π6，k π＋π3 (k ∈Z )．1．求解函数y ＝A sin(ωx ＋φ)的性质问题的三种意识(1)转化意识：利用三角恒等变换将所求函数转化为f (x )＝A sin(ωx ＋φ)的形式．(2)整体意识：类比y ＝sin x 的性质，只需将y ＝A sin(ωx ＋φ)中的“ωx ＋φ”看成y ＝sin x 中的“x ”，采用整体代入求解．①令ωx ＋φ＝k π＋π2(k ∈Z )，可求得对称轴方程． ②令ωx ＋φ＝k π(k ∈Z )，可求得对称中心的横坐标．③将ωx ＋φ看作整体，可求得y ＝A sin(ωx ＋φ)的单调区间，注意ω的符号．(3)讨论意识：当A 为参数时，求最值应分情况讨论A >0，A <0. 2．求解三角函数的性质的三种方法 (1)求单调区间的两种方法①代换法：求形如y ＝A sin(ωx ＋φ)(或y ＝A cos(ωx ＋φ))(A ，ω，φ为常数，A ≠0，ω＞0)的单调区间时，令ωx ＋φ＝z ，则y ＝A sin z (或y ＝A cos z )，然后由复合函数的单调性求得．②图象法：画出三角函数的图象，结合图象求其单调区间． (2)判断对称中心与对称轴：利用函数y ＝A sin(ωx ＋φ)的对称轴一定经过图象的最高点或最低点，对称中心一定是函数的零点这一性质，通过检验f (x 0)的值进行判断．(3)三角函数周期的求法 ①利用周期定义．②利用公式：y ＝A sin(ωx ＋φ)和y ＝A cos(ωx ＋φ)的最小正周期为2π|ω|，y ＝tan(ωx ＋φ)的最小正周期为π|ω|.③利用图象． 针对训练1．2015·湖南高考]已知ω＞0，在函数y ＝2sin ωx 与y ＝2cos ωx 的图象的交点中，距离最短的两个交点的距离为23，则ω＝________.答案 π2解析 由题意，两函数图象交点间的最短距离即相邻的两交点间的距离，设相邻的两交点坐标分别为P (x 1，y 1)，Q (x 2，y 2)，易知|PQ |2＝(x 2－x 1)2＋(y 2－y 1)2，其中|y 2－y 1|＝2－(－2)＝22，|x 2－x 1|为函数y ＝2sin ωx －2cos ωx ＝22sin ⎝⎛⎭⎪⎫ωx －π4的两个相邻零点之间的距离，恰好为函数最小正周期的一半，所以(23)2＝⎝ ⎛⎭⎪⎫2π2ω2＋(22)2，ω＝π2. 2．2014·北京高考]设函数f (x )＝A sin(ωx ＋φ)(A ，ω，φ是常数，A >0，ω>0)．若f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝f ⎝⎛⎭⎪⎫2π3＝－f ⎝ ⎛⎭⎪⎫π6，则f (x )的最小正周期为________．答案 π解析 由f (x )在区间⎣⎢⎡⎦⎥⎤π6，π2上具有单调性，且f ⎝ ⎛⎭⎪⎫π2＝－f ⎝ ⎛⎭⎪⎫π6知，f (x )有对称中心⎝ ⎛⎭⎪⎫π3，0，由f ⎝ ⎛⎭⎪⎫π2＝f ⎝ ⎛⎭⎪⎫23π知f (x )有对称轴x ＝12(π2＋23π)＝712π.记f (x )的最小正周期为T ，则12T ≥π2－π6，即T ≥23π.故712π－π3＝π4＝T4，解得T ＝π.考点三角函数的图象及应用典例示法题型1 利用图象求y ＝A sin(ωx ＋φ)的解析式典例3 函数f (x )＝2sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω>0，－π2<φ<π2的部分图象如图所示，则ω，φ的值分别是( )A ．2，－π3 B ．2，－π6 C ．4，－π6D ．4，π3解析] 从图中读出此函数的周期情况为34T ＝34·2πω＝5π12－⎝ ⎛⎭⎪⎫－π3＝3π4，所以ω＝2.又读出图中最高点坐标为⎝ ⎛⎭⎪⎫5π12，2，代入解析式f (x )＝2sin(2x ＋φ)，得到2＝2sin ⎝ ⎛⎭⎪⎫2×5π12＋φ，所以2×5π12＋φ＝2k π＋π2(k ∈Z )，则φ＝2k π－π3.因为－π2<φ<π2，所以令k ＝0，得到φ＝－π3，故选A. 答案] A题型2 函数y ＝A sin(ωx ＋φ)的图象变换典例4 2015·山东高考]要得到函数y ＝sin ⎝⎛⎭⎪⎫4x －π3的图象，只需将函数y ＝sin4x 的图象( )A ．向左平移π12个单位 B ．向右平移π12个单位 C ．向左平移π3个单位D ．向右平移π3个单位解析] 因为y ＝sin ⎝ ⎛⎭⎪⎫4x －π3＝sin ⎣⎢⎡⎦⎥⎤4⎝ ⎛⎭⎪⎫x －π12，所以只需将y ＝sin4x的图象向右平移π12个单位，即可得到函数y ＝sin ⎝ ⎛⎭⎪⎫4x －π3的图象，故选B.答案] B题型3 函数y ＝A sin(ωx ＋φ)的图象和性质的综合应用 典例5 2016·太原一模]已知函数f (x )＝sin(ωx ＋φ)⎝ ⎛⎭⎪⎫ω>0，|φ|<π2的最小正周期是π，若将其图象向右平移π3个单位后得到的图象关于原点对称，则函数f (x )的图象( )A ．关于直线x ＝π12对称B ．关于直线x ＝5π12对称C ．关于点⎝ ⎛⎭⎪⎫π12，0对称D ．关于点⎝ ⎛⎭⎪⎫5π12，0对称解析] ∵f (x )的最小正周期为π，∴2πω＝π，ω＝2，∴f (x )的图象向右平移π3个单位后得到g (x )＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π3＋φ＝sin ⎝ ⎛⎭⎪⎫2x －2π3＋φ的图象，又g (x )的图象关于原点对称，∴－2π3＋φ＝k π，k ∈Z ，φ＝2π3＋k π，k ∈Z ，又|φ|<π2，∴⎪⎪⎪⎪⎪⎪2π3＋k π<π2，∴k ＝－1，φ＝－π3，∴f (x )＝sin ⎝⎛⎭⎪⎫2x －π3，当x ＝π12时，2x －π3＝－π6，∴A ，C 错误，当x ＝5π12时，2x －π3＝π2，∴B 正确，D 错误．答案] B本例中条件不变，若平移后得到的图象关于y 轴对称，则f (x )的图象又关于谁对称？( )答案 D解析 g (x )的图象关于y 轴对称，则－2π3＋φ＝π2＋k π，k ∈Z ，可求φ＝π6，∴f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π6，2x ＋π6＝k π，可得x ＝k π2－π12，令k ＝1，则x ＝5π12，故选D.1．函数表达式y ＝A sin(ωx ＋φ)＋B 的确定方法2.三角函数图象平移问题处理策略(1)看平移要求：首先要看题目要求由哪个函数平移得到哪个函数，这是判断移动方向的关键点．(2)看移动方向：移动的方向一般记为“正向左，负向右”，看y ＝A sin(ωx ＋φ)中φ的正负和它的平移要求．(3)看移动单位：在函数y ＝A sin(ωx ＋φ)中，周期变换和相位变换都是沿x 轴方向的，所以ω和φ之间有一定的关系，φ是初相，再经过ω的压缩，最后移动的单位是⎪⎪⎪⎪⎪⎪φω.3．研究三角函数图象与性质的常用方法(1)求三角函数的周期、单调区间、最值及判断三角函数的奇偶性，往往是在定义域内，先化简三角函数式，尽量化为y ＝A sin(ωx ＋φ)的形式，然后再求解．(2)对于形如y ＝a sin ωx ＋b cos ωx 型的三角函数，要通过引入辅助角化为y ＝a 2＋b 2sin(ωx ＋φ)⎝⎛cos φ＝a a 2＋b 2，⎭⎪⎫sin φ＝b a 2＋b 2的形式来求．全国卷高考真题调研]1．2016·全国卷Ⅱ]若将函数y ＝2sin2x 的图象向左平移π12个单位长度，则平移后图象的对称轴为( )A ．x ＝k π2－π6(k ∈Z ) B ．x ＝k π2＋π6(k ∈Z ) C ．x ＝k π2－π12(k ∈Z ) D ．x ＝k π2＋π12(k ∈Z )答案 B解析 函数y ＝2sin2x 的图象向左平移π12个单位长度，得到的图象对应的函数表达式为y ＝2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x ＋π12，令2⎝⎛⎭⎪⎫x ＋π12＝k π＋π2(k ∈Z )，解得x ＝k π2＋π6(k ∈Z )，所以所求对称轴的方程为x ＝k π2＋π6(k ∈Z )，故选B.2．2015·全国卷Ⅰ]函数f (x )＝cos(ωx ＋φ)的部分图象如图所示，则f (x )的单调递减区间为( )A.⎝ ⎛⎭⎪⎫k π－14，k π＋34，k ∈Z B.⎝⎛⎭⎪⎫2k π－14，2k π＋34，k ∈ZC.⎝ ⎛⎭⎪⎫k －14，k ＋34，k ∈ZD.⎝⎛⎭⎪⎫2k －14，2k ＋34，k ∈Z答案 D解析 由图象可知ω4＋φ＝π2＋2m π，5ω4＋φ＝3π2＋2m π，m ∈Z ，所以ω＝π，φ＝π4＋2m π，m ∈Z ，所以函数f (x )＝cos ⎝⎛⎭⎪⎫πx ＋π4＋2m π＝cos ⎝ ⎛⎭⎪⎫πx ＋π4的单调递减区间为2k π<πx ＋π4<2k π＋π，k ∈Z ，即2k －14<x <2k ＋34，k ∈Z ，故选D.其它省市高考题借鉴]3．2016·北京高考]将函数y ＝sin ⎝ ⎛⎭⎪⎫2x －π3图象上的点P ⎝ ⎛⎭⎪⎫π4，t 向左平移s (s >0)个单位长度得到点P ′.若P ′位于函数y ＝sin2x 的图象上，则( )A ．t ＝12，s 的最小值为π6 B ．t ＝32，s 的最小值为π6 C ．t ＝12，s 的最小值为π3 D ．t ＝32，s 的最小值为π3 答案 A解析 因为点P ⎝ ⎛⎭⎪⎫π4，t 在函数y ＝sin ⎝ ⎛⎭⎪⎫2x －π3的图象上，所以t ＝sin ⎝ ⎛⎭⎪⎫2×π4－π3＝sin π6＝12.又P ′⎝ ⎛⎭⎪⎫π4－s ，12在函数y ＝sin2x 的图象上，所以12＝sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫π4－s ，则2⎝ ⎛⎭⎪⎫π4－s ＝2k π＋π6或2⎝ ⎛⎭⎪⎫π4－s ＝2k π＋5π6，k ∈Z ，得s ＝－k π＋π6或s ＝－k π－π6，k ∈Z .又s >0，故s 的最小值为π6.故选A.4．2015·陕西高考]如图，某港口一天6时到18时的水深变化曲线近似满足函数y ＝3sin ⎝ ⎛⎭⎪⎫π6x ＋φ＋k .据此函数可知，这段时间水深(单位：m)的最大值为( )A ．5B ．6C ．8D ．10答案 C解析 由题图可知－3＋k ＝2，k ＝5，y ＝3sin ⎝ ⎛⎭⎪⎫π6x ＋φ＋5，∴y max＝3＋5＝8.5．2015·湖南高考]将函数f (x )＝sin2x 的图象向右平移φ⎝ ⎛⎭⎪⎫0<φ<π2个单位后得到函数g (x )的图象．若对满足|f (x 1)－g (x 2)|＝2的x 1，x 2，有|x 1－x 2|min ＝π3，则φ＝( )A.5π12B.π3C.π4D.π6答案 D解析 由已知得g (x )＝sin(2x －2φ)，满足|f (x 1)－g (x 2)|＝2，不妨设此时y ＝f (x )和y ＝g (x )分别取得最大值与最小值，又|x 1－x 2|min ＝π3，令2x 1＝π2，2x 2－2φ＝－π2，此时|x 1－x 2|＝⎪⎪⎪⎪⎪⎪π2－φ＝π3，又0<φ<π2，故φ＝π6，选D.6．2015·湖北高考]某同学用“五点法”画函数f (x )＝A sin(ωx ＋φ)⎝⎛⎭⎪⎫ω>0，|φ|<π2在某一个周期内的图象时，列表并填入了部分数据，如下表：(2)将y ＝f (x )图象上所有点向左平行移动θ(θ>0)个单位长度，得到y ＝g (x )的图象．若y ＝g (x )图象的一个对称中心为⎝ ⎛⎭⎪⎫5π12，0，求θ的最小值．解 (1)根据表中已知数据，解得A ＝5，ω＝2，φ＝－π6.数据补全如下表： 且函数表达式为f (x )＝5sin ⎝⎛⎭⎪⎫2x －π6.(2)由(1)知f (x )＝5sin ⎝ ⎛⎭⎪⎫2x －π6，得g (x )＝5sin ⎝ ⎛⎭⎪⎫2x ＋2θ－π6.因为y ＝sin x 的对称中心为(k π，0)，k ∈Z . 令2x ＋2θ－π6＝k π，解得x ＝k π2＋π12－θ，k ∈Z .由于函数y ＝g (x )的图象关于点⎝ ⎛⎭⎪⎫5π12，0成中心对称，令k π2＋π12－θ＝5π12，解得θ＝k π2－π3，k ∈Z .由θ>0可知，当k ＝1时，θ取得最小值π6.一、选择题1．2016·贵阳监测]下列函数中，以π2为最小正周期的奇函数是( )A ．y ＝sin2x ＋cos2xB ．y ＝sin ⎝ ⎛⎭⎪⎫4x ＋π2C ．y ＝sin2x cos2xD ．y ＝sin 22x －cos 22x答案 C解析 A 中，y ＝sin2x ＋cos2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π4，为非奇非偶函数，故A 错；B 中，y ＝sin ⎝⎛⎭⎪⎫4x ＋π2＝cos4x ，为偶函数，故B 错；C 中，y＝sin2x cos2x ＝12sin4x ，最小正周期为π2且为奇函数，故C 正确；D 中，y ＝sin 22x －cos 22x ＝－cos4x ，为偶函数，故D 错，选C.2．2016·唐山统考]将函数y ＝3cos2x －sin2x 的图象向右平移π3个单位长度，所得图象对应的函数为g (x )，则g (x )＝( )A ．2sin2xB ．－2sin2xC ．2cos ⎝ ⎛⎭⎪⎫2x －π6D ．2sin ⎝ ⎛⎭⎪⎫2x －π6答案 A解析 因为y ＝3cos2x －sin2x ＝2sin ⎝⎛⎭⎪⎫π3－2x ＝－2sin ( 2x －π3 )，将其图象向右平移π3个单位长度得到g (x )＝－2sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π3－π3＝－2sin(2x －π)＝2sin2x 的图象，所以选A.3．2016·武昌调研]已知函数f (x )＝2sin ⎝ ⎛⎭⎪⎫ωx ＋π6－1(ω＞0)的图象向右平移2π3个单位后与原图象重合，则ω的最小值是( )A ．3 B.32 C.43 D.23答案 A解析 将f (x )的图象向右平移2π3个单位后得到图象的函数解析式为2sin ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x －2π3＋π6－1＝2sin ⎝ ⎛⎭⎪⎫ωx －2ωπ3＋π6－1，所以2ωπ3＝2k π，k∈Z ，所以ω＝3k ，k ∈Z ，因为ω＞0，k ∈Z ，所以ω的最小值为3，故选A.4．2016·沈阳质检]某函数部分图象如图所示，它的函数解析式可能是( )A ．y ＝sin ⎝ ⎛⎭⎪⎫－56x ＋3π5B ．y ＝sin ⎝ ⎛⎭⎪⎫65x －2π5C ．y ＝sin ⎝⎛⎭⎪⎫65x ＋3π5D ．y ＝－cos ⎝⎛⎭⎪⎫56x ＋3π5答案 C解析 不妨令该函数解析式为y ＝A sin(ωx ＋φ)(ω＞0)，由图知A ＝1，T 4＝3π4－π3＝5π12，于是2πω＝5π3，即ω＝65，π3是函数的图象递减时经过的零点，于是65×π3＋φ＝2k π＋π，k ∈Z ，所以φ可以是3π5，选C.5．2016·广州模拟]已知sin φ＝35，且φ∈⎝ ⎛⎭⎪⎫π2，π，函数f (x )＝sin(ωx ＋φ)(ω＞0)的图象的相邻两条对称轴之间的距离等于π2，则f ⎝ ⎛⎭⎪⎫π4的值为( )A ．－35 B ．－45 C.35 D.45答案 B解析 由函数f (x )＝sin(ωx ＋φ)的图象的相邻两条对称轴之间的距离等于π2，得到其最小正周期为π，所以ω＝2，f ⎝ ⎛⎭⎪⎫π4＝sin ⎝ ⎛⎭⎪⎫2×π4＋φ＝cos φ＝－1－sin 2φ＝－45.6．2016·重庆测试]设x 0为函数f (x )＝sinπx 的零点，且满足|x 0|＋f ⎝⎛⎭⎪⎫x 0＋12＜33，则这样的零点有( )A ．61个B ．63个C ．65个D ．67个答案 C解析 依题意，由f (x 0)＝sinπx 0＝0得，πx 0＝k π，k ∈Z ，x 0＝k ，k ∈Z .当k 是奇数时，f ⎝ ⎛⎭⎪⎫x 0＋12＝sin ⎣⎢⎡⎦⎥⎤π⎝ ⎛⎭⎪⎫k ＋12＝sin ⎝ ⎛⎭⎪⎫k π＋π2＝－1，|x 0|＋f ⎝ ⎛⎭⎪⎫x 0＋12＝|k |－1＜33，|k |＜34，满足这样条件的奇数k 共有34个；当k 是偶数时，f ⎝⎛⎭⎪⎫x 0＋12＝sin ⎣⎢⎡⎦⎥⎤π⎝⎛⎭⎪⎫k ＋12＝sin ⎝⎛⎭⎪⎫k π＋π2＝1，|x 0|＋f ⎝⎛⎭⎪⎫x 0＋12＝|k |＋1＜33，|k |＜32，满足这样条件的偶数k 共有31个．综上所述，满足题意的零点共有34＋31＝65个，选C.二、填空题7．函数f (x )＝sin(ωx ＋φ)(x ∈R )⎝⎛⎭⎪⎫ω>0，|φ|<π2的部分图象如图所示，如果x 1，x 2∈⎝ ⎛⎭⎪⎫－π6，π3，且f (x 1)＝f (x 2)，则f (x 1＋x 2)＝________.答案 32解析 由题图可知，T 2＝π3－⎝ ⎛⎭⎪⎫－π6＝π2，则T ＝π，ω＝2，又∵－π6＋π32＝π12，∴f (x )的图象过点⎝ ⎛⎭⎪⎫π12，1，即sin ⎝ ⎛⎭⎪⎫2×π12＋φ＝1，得φ＝π3，∴f (x )＝sin ⎝ ⎛⎭⎪⎫2x ＋π3. 而x 1＋x 2＝－π6＋π3＝π6，∴f (x 1＋x 2)＝f ⎝ ⎛⎭⎪⎫π6＝sin ⎝ ⎛⎭⎪⎫2×π6＋π3＝sin 2π3＝32.8．2016·贵阳监测]为得到函数y ＝sin ⎝ ⎛⎭⎪⎫x ＋π3的图象，可将函数y＝sin x 的图象向左平移m 个单位长度，或向右平移n 个单位长度(m ，n 均为正数)，则|m －n |的最小值是________．答案 2π3解析 由题意可知，m ＝π3＋2k 1π，k 1为非负整数，n ＝－π3＋2k 2π，k 2为正整数，∴|m －n |＝⎪⎪⎪⎪⎪⎪2π3＋2(k 1－k 2)π，∴当k 1＝k 2时，|m －n |min ＝2π3.9．2016·湖南岳阳质检]已知函数f (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π4的图象向左平移π6个单位后与函数g (x )＝sin ⎝ ⎛⎭⎪⎫ωx ＋π6的图象重合，则正数ω的最小值为________．答案 232解析 将f (x )＝sin ⎝⎛⎭⎪⎫ωx ＋π4的图象向左平移π6个单位后，得到函数f 1(x )＝sin ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x ＋π6＋π4的图象．又f 1(x )＝sin ⎣⎢⎡⎦⎥⎤ω⎝ ⎛⎭⎪⎫x ＋π6＋π4的图象与g (x )＝sin ( ωx ＋π6 )的图象重合，故ωx ＋π6ω＋π4＝2k π＋ωx ＋π6，k ∈Z .所以ω＝12k －12(k ∈Z )．又ω＞0，故当k ＝1时，ω取得最小值，为12－12＝232.三、解答题10．2014·山东高考]已知向量a ＝(m ，cos2x )，b ＝(sin2x ，n )，函数f (x )＝a ·b ，且y ＝f (x )的图象过点⎝ ⎛⎭⎪⎫π12，3和点⎝ ⎛⎭⎪⎫2π3，－2.(1)求m ，n 的值；(2)将y ＝f (x )的图象向左平移φ(0＜φ＜π)个单位后得到函数y ＝g (x )的图象，若y ＝g (x )图象上各最高点到点(0,3)的距离的最小值为1，求y ＝g (x )的单调递增区间．解 (1)由题意知f (x )＝a ·b ＝m sin2x ＋n cos2x .因为y ＝f (x )的图象过点⎝ ⎛⎭⎪⎫π12，3和⎝ ⎛⎭⎪⎫2π3，－2， 所以⎩⎪⎨⎪⎧3＝m sin π6＋n cos π6，－2＝m sin 4π3＋n cos 4π3，即⎩⎨⎧3＝12m ＋32n ，－2＝－32m －12n ，解得⎩⎪⎨⎪⎧m ＝3，n ＝1.(2)由(1)知f (x )＝3sin2x ＋cos2x ＝2sin ⎝ ⎛⎭⎪⎫2x ＋π6.由题意知g (x )＝f (x ＋φ)＝2sin ⎝ ⎛⎭⎪⎫2x ＋2φ＋π6. 设y ＝g (x )的图象上符合题意的最高点为(x 0,2)， 由题意知x 20＋1＝1，所以x 0＝0， 即到点(0,3)的距离为1的最高点为(0,2)． 将其代入y ＝g (x )得sin ⎝ ⎛⎭⎪⎫2φ＋π6＝1， 因为0＜φ＜π，所以φ＝π6， 因此g (x )＝2sin ⎝ ⎛⎭⎪⎫2x ＋π2＝2cos2x . 由2k π－π≤2x ≤2k π，k ∈Z 得k π－π2≤x ≤k π，k ∈Z ， 所以函数y ＝g (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－π2，k π，k ∈Z. 11．2016·天津五区县调考]已知函数f (x )＝3sin x cos x －cos 2x ＋12(x∈R )．(1)求函数f (x )的单调递增区间；(2)函数f (x )的图象上所有点的横坐标扩大到原来的2倍，再向右平移π6个单位长度，得到g (x )的图象，求函数y ＝g (x )在x ∈0，π]上的最大值及最小值．解 (1)f (x )＝3sin x cos x －cos 2x ＋12＝32sin2x －12cos2x ＝sin ⎝⎛⎭⎪⎫2x －π6由2k π－π2≤2x －π6≤2k π＋π2得k π－π6≤x ≤k π＋π3(k ∈Z )， 所以函数f (x )的单调递增区间为⎣⎢⎡⎦⎥⎤k π－π6，k π＋π3(k ∈Z )．(2)函数f (x )的图象上所有点的横坐标扩大到原来的2倍，再向右平移π6个单位，得g (x )＝sin ⎝ ⎛⎭⎪⎫x －π3， 因为x ∈0，π]得：x －π3∈⎣⎢⎡⎦⎥⎤－π3，2π3，所以sin ⎝ ⎛⎭⎪⎫x －π3∈⎣⎢⎡⎦⎥⎤－32，1所以当x ＝0时，g (x )＝sin ⎝ ⎛⎭⎪⎫x －π3有最小值－32， 当x ＝5π6时，g (x )＝sin ⎝⎛⎭⎪⎫x －π3有最大值1.12．2016·福建质检]已知函数f (x )＝sin x cos x ＋12cos2x . (1)若tan θ＝2，求f (θ)的值；(2)若函数y ＝g (x )的图象是由函数y ＝f (x )的图象上所有的点向右平移π4个单位长度而得到，且g (x )在区间(0，m )内是单调函数，求实数m 的最大值．解 (1)因为tan θ＝2，所以f (θ)＝sin θcos θ＋12cos2θ＝sin θcos θ＋12(2cos 2θ－1)＝sin θcos θ＋cos 2θ－12＝sin θcos θ＋cos 2θsin 2θ＋cos 2θ－12＝tan θ＋1tan 2θ＋1－12＝110.(2)由已知得f (x )＝12sin2x ＋12cos2x ＝22sin ⎝ ⎛⎭⎪⎫2x ＋π4.依题意，得g (x )＝22sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x －π4＋π4，即g (x )＝22sin ⎝⎛⎭⎪⎫2x －π4. 因为x ∈(0，m )，所以2x －π4∈⎝⎛⎭⎪⎫－π4，2m －π4.又因为g (x )在区间(0，m )内是单调函数，所以2m －π4≤π2，即m ≤3π8，故实数m 的最大值为3π8.。

高考历史二轮复习专题微讲之国家制度与社会治理第3讲法律与教化一、专题主线线索1：中国古代法律起源很早，起初以习惯法为主，春秋后期开始出现成文法，战国时期逐渐复杂化。

在这个过程中，围绕法律与教化，亦即法治与德治的关系问题，各派思想家展开了热烈的讨论。

线索2：秦以法家思想治国，推动了律的编撰。

汉承秦制，同时吸取秦期速亡的教训，在治国方针上采取“霸王道杂之”的统治策略，实际上就是法律与礼教并用。

自西晋起，礼教内容直接渗人法律条文，出现“法律儒家化”的趋势，至唐律的礼法结合臻于完善。

线索3：宋朝以后，理学在社会上广泛传播，深入社会基层，并以乡约形式直接面向底层百姓宣讲，乡约经政府利用推广而具有约束力，并与法律合流。

线索4：西方法律发展有自己的路径，在罗马法的基础上，英国和法国分别发展了英美法系和大陆法系。

近代西方法律强调司法独立、保护个人权利。

线索5：基督教的宗教伦理不仅强化了教会对人们的控制，同时具有一定的社会教化功能。

基督教的伦理和教化深刻影响了人们的思想意识和日常行为。

线索6：新中国成立后，法治建设取得显著成就，形成了中国特色社会主义法律体系。

党的领导是中国特色社会主义法治建设的本质特征，是社会主义法治建设最根本的保证。

二、模拟练习1.商汤伐夏时说：“有夏多罪，天命極(jí)之”；周武王伐纣时也曾说：“商罪贯盈，天命诛之”，并产生了“民之所欲，天必从之”“天视自我民视，天听自我民听”的思想。

这反映出先秦时期( )A.神权统治的思想根深蒂固B.统治阶层等级意识淡薄C.敬天保民的民本观念萌发D.儒学深受天人感应影响2.汉代名臣黄霸在任职颍川太守期间“力行教化而后诛罚”。

治颍川八年“田者让畔，道不拾遗，养视鳏寡，赡助贫穷，狱或八年亡重罪囚”。

据此可知，汉代( )A.社会治理渗透德治教化思想B.重视家训，强化基层教化C.地方治理形成了统一的标准D.社会道德伦理水平普遍提高3.魏晋南北朝时期不同政权颁布的部分律令内容，这体现出当时( )政权律令内容曹魏贼斗杀人，以劾而亡，许依古义，听子弟得追杀之西晋子不孝父母，子弃市北魏居三年之丧而冒哀求仕，五岁刑A.北方游牧民族封建化进程完成B.儒家思想作为主流思想开始融入法典C.凸显出严刑峻法治国理念盛行D.法律、礼教并用成为重要统治手段4.唐宋时期对奴婢、牲畜等“活口”交易有严格规定。

专题三第三讲断句与翻译知能演练场一、阅读下面的文言文，完成后面的题目。

丁氏穿井宋之丁氏，家无井而出溉汲，常一人居外。

及其家穿井，告人曰：“吾穿井得一人。

”有闻而传之者曰丁氏穿井得一人国人道之闻之于宋君宋君使人问之于丁氏丁氏对曰得一人之使非得一人于井中也求闻之若此不若不闻给上面文言文语段中的文字断句：有闻而传之者曰丁氏穿井得一人国人道之闻之于宋君宋君使人问之于丁氏丁氏对曰得一人之使非得一人于井中也求闻之若此不若不闻答案：有闻而传之者曰/丁氏穿井得一人/国人道之/闻之于宋君/宋君使人问之于丁氏/丁氏对曰/得一人之使/非得一人于井中也/求闻之若此/不若不闻[参考译文]宋国有一个姓丁的人，家里没有井就出去洗东西和取水，常常一个人住在外面。

等到他的家里打了井时，他告诉别人说：“我打井得一人。

”有的人听了他的话然后转述道：“丁氏打井得一人。

”国人谈论这件事，宋国的国君听到了这件事。

他就派人去问姓丁的。

姓丁的回答说：“得到一个人使用，不是在井里得到一个人。

”听话听成这样，不如不听。

二、用斜线(/)给下面文言文断句。

天之道其犹张弓与高者抑之下者举之有馀者损之不足者补之天之道损有馀而补不足人之道则不然损不足以奉有馀孰能有馀以奉天下唯有道者是以圣人为而不恃功成而不处。

(取材于《老子·七十七章》) 答案：天之道其犹张弓与/高者抑之/下者举之/有馀者损之/不足者补之/天之道损有馀而补不足/人之道则不然/损不足以奉有馀/孰能有馀以奉天下/唯有道者/是以圣人为而不恃/功成而不处。

[参考译文]天道，就像是把弦绷在弓上射箭一样，弦位高了就要压低一些，弦位低了就要抬高一些。

多出来的时候，就要加以减损，不足的时候，就要加以补足。

天道，是减损有余的用来补给不足的。

但人之道却不是这样，总是减损不足的用来供给有余的。

有谁能够把有余的拿来补给天下不足的呢，只有能够观天之道、执天之行的道者才能做得到。

因此，圣人有所作为却不会自恃，有功劳却不居功自傲。