05博弈论—多重均衡与制度和文化

博弈论知识总结博弈论概述：1、博弈论概念： 博弈论：就是研究决策主体的行为发生直接相互作用时的决策以及这种决策的均衡问题。

博弈论研究的假设：1、 决策主体是理性的，最大化自己的收益。

2、 完全理性是共同知识3、 每个参与人被假定为可以对所处环境以及其他参与者的行为形成正确的信念与预期2、和博弈有关的变量：博弈参与人：博弈中选择行动以最大化自己受益的决策主体。

行动：参与人的决策选择 战略：参与人的行动规则，即事件与决策主体行动之间的映射，也是参与人行动的规则。

信息：参与人在博弈中的知识，尤其是其他决策主体的战略、收益、类型（不完全信息）等的信息。

完全信息：每个参与人对其他参与人的支付函数有准确的了解；完美信息：在博弈过程的任何时点每个参与人都能观察并记忆之前各局中人所选择的行动，否则为不完美信息。

不完全信息：参与人没有完全掌握其他参与人的特征、战略空间及支付函数等信息，即存在着有关其他参与人的不确定性因素。

支付：决策主体在博弈中的收益。

在博弈中支付是所有决策主题所选择的行动的函数。

从经济学的角度讲，博弈是决策主体之间的相互作用，因此和传统个人决策存在着区别： 3、博弈论与传统决策的区别：1、 传统微观经济学的个人决策就是在给定市场价格、消费者收入条件下，最大化自己效用，研究工具是无差异曲线。

可表示为：maxU(P ,I)，其中P 为市场价格，I 为消费者可支配收入。

2、 其他消费者对个人的综合影响表示为一个参数——市场价格，所以在市场价格既定下，消费者效用只依赖于自己的收入和偏好，不用考虑其他消费者的影响。

但是在博弈论理个人效用函数还依赖于其他决策者的选择和效用函数。

4、博弈的表示形式：战略式博弈和扩展式博弈战略式博弈：是博弈问题的一种规范性描述，有时亦称标准式博弈。

战略式博弈是一种假设每个参与人仅选择一次行动或战略，并且参与人同时进行选择的决策模型，因此，从本质上来讲战略式博弈是一种静态模型，一般适用于描述不需要考虑博弈进程的完全信息静态博弈问题。

博弈论知识点总结完整版博弈论是数学和经济学中一个重要的分支，研究决策制度下的相互作用和决策策略。

它是通过数学模型来描述和分析不同参与者的决策行为和决策结果，并找到最优的决策策略。

下面是博弈论中的一些重要知识点的总结。

1.博弈的定义和基本概念：-博弈是指参与者在一定的规则下做出决策，并根据其他参与者的决策结果来确定自己的收益或损失。

-参与者称为博弈者，他们的决策称为策略，策略的组合称为策略组合。

-博弈可以是合作博弈或非合作博弈，合作博弈强调协作，非合作博弈强调竞争。

2.标准博弈：-标准博弈是博弈论中最基础的形式，参与者之间的策略和收益都是确定的。

-标准博弈可以是零和博弈（总收益为零）或非零和博弈（总收益不为零）。

3.纳什均衡：-纳什均衡是指在博弈中，不存在一个参与者可以通过改变自己的策略来获得更高收益的情况。

-纳什均衡是博弈论中的核心概念，它描述了博弈中的稳定状态。

-一个博弈可能有一个或多个纳什均衡，也可能没有纳什均衡。

4.基本博弈：-二人零和博弈是一种特殊的博弈，其中一个参与者的利益是另一个参与者的损失。

-石头、剪刀、布是一个典型的二人零和博弈，存在一个纳什均衡策略。

-行棋游戏如国际象棋、围棋也是二人零和博弈，但策略空间较复杂。

5.博弈理论的扩展：-广义博弈是对博弈理论的扩展，考虑了更复杂的情况，如多人博弈、不完全信息博弈等。

-多人博弈是指博弈中有多个参与者，每个参与者都会影响其他参与者的决策。

-不完全信息博弈是指博弈中参与者对其他参与者的信息是不完全的。

6.博弈论在经济学中的应用：-博弈论在经济学中有广泛的应用，如市场竞争、拍卖等。

-例如，决定定价策略的厂商可以使用博弈论来确定最优的定价策略。

-拍卖是一种常见的博弈形式，在博弈过程中参与者可以选择不同的竞标策略。

7.演化博弈：-演化博弈是博弈论的一个重要分支，研究博弈在一定的演化过程中的演化规律。

-演化博弈通过数学模型来描述和分析参与者的策略演化和演化结果。

博弈均衡和机制设计概述解释及说明1. 引言1.1 概述博弈均衡和机制设计是博弈论和经济学中的两个重要概念，它们在分析和解决各种经济、社会和政治问题中起着关键作用。

博弈均衡是指在多方参与者之间进行策略选择时达到一种相对稳定状态的理论概念，而机制设计则是为了实现特定目标而设计出合适的规则和激励机制。

本文将对博弈均衡和机制设计进行总结、解释和说明。

1.2 文章结构本文将分为六个部分进行讨论。

首先，在引言部分对博弈均衡和机制设计进行介绍，并说明它们的关系。

接着，我们将详细探讨不同类型的博弈均衡及其特点，包括完全信息博弈和不完全信息博弈，以及纳什均衡与其他类型的博弈均衡之间的比较。

然后，我们将深入研究机制设计的原理与方法，包括契约理论在机制设计中的应用、声明式机制设计与计算式机制设计的对比分析，以及公共品和外部性问题中的机制设计策略。

接下来，我们将探讨博弈论在经济领域中的应用实例以及社会公共资源配置中的机制设计案例，并讨论机制设计在社会政策决策中的意义和作用。

最后，我们将给出结论部分对全文进行总结。

1.3 目的本文的目的是介绍和解释博弈均衡和机制设计的概念，并探讨它们之间的关系。

通过对不同类型博弈均衡及其特点、机制设计的原理与方法以及应用案例进行分析，我们希望读者能够更好地理解博弈论和机制设计，并认识到它们在经济、社会和政治问题中起到的重要作用。

同时，本文还旨在提供一些思考和启发，为相关领域研究者提供理论依据和实践指导。

2. 博弈均衡和机制设计2.1 博弈均衡的概念博弈均衡是博弈论中一个重要的概念，指的是在一个博弈过程中，各参与者通过采取最佳策略而达到的一种稳定状态。

在博弈均衡中，不存在任何一个参与者可以通过改变自己的策略来获取更好的结果，即没有人单方面改变策略可以获得更高效益。

博弈均衡可以分为纯策略均衡和混合策略均衡两种形式。

2.2 机制设计的概念机制设计是经济学中研究如何设计合适机制以实现某种特定目标或解决某个问题的理论框架。

不管一种文明的内部具体如何，封建主义也好，资本主义也好，专制也好，民主也好，科学也好，愚昧也好，有宗教也好，无信仰也好，黑人种也好，白人种也好，大陆型也好，海洋型也好，内省文化也好，外向文化也好，窝里斗也好，不窝里斗也好，其他种种也好，我们完全可以对这一些纷争置之不理，但我们都可以肯定，该一文明的总格局是人与人的博弈——只要是人的文明，任一文明的总格局都是人与人的博弈；这一总格局与任何其他因素无关，唯一只与人性人心人情紧密相关。

如果我们从外部看到某一文明长时间大体稳定，甚至一直处于大体稳定的状态，那我们应该可以肯定，该一文明内部格局已经达到博弈均衡，要不然，它不可能老是大体稳定！对这样的文明，我们应该表示尊重！而如果这样的文明不属于小文明——小文明可能会存在特殊性——而是巨型文明，甚至是超巨型文明，那我们更应该表示尊重！中华文明正是这样的文明，一者五千年绵延不绝，大体一直稳定；一者超巨型，人口和面积都是超巨型的——所以我们绝对应该尊重中华文明！按：在“中外名家系列讲座”第191讲上，着名环保活动家廖晓义女士除了振聋发馈的“谁更需要脱贫”的质问之外，饭间还提到一个鲜明的观点：“气候变化标志西方文化的破产！”深表赞同，在“全球变暖”成为舆论热点的2007年中，曾撰写《气候变暖：中国软崛起的重大契机》的专门文章，内中有这样一段话：全球变暖正可能意味着“风水轮流转”的时候到了，它从最高也最硬的层面反映了西方文化的危机，再不深刻反省西方文化已经不行了，它已经触底！中华文明或许“古道西风瘦马，小桥流水人家”，物质上不怎么让人刺激，但中华文明经受了时间和历史的考验——五千年延绵不绝，是古代文明中惟一幸存下来的超巨型文明！仅仅凭这一点，就值得今天陷于天诛地灭之境的人类深刻反思和借鉴。

鸦片战争以来，特别是五四运动以后，一部分国人，而且多为精英分子，开始对自己的文化失去自信。

首先得承认，这是完全可以理解的，毕竟“落后就要挨打”的达摩克利斯剑高悬在我们的头上。

从博弈论谈制度建设戴兴邦(中国人寿保险股份有限公司研发中心，北京，100033)摘要博弈论是现代数学的一个新分支，是运筹学的重要组成内容，是研究理性人的互动(interactive)决策理论。

本文从博弈论基本思想出发，对纳什均衡、智猪博弈、猎鹿博弈、七人分粥案例进行了深入阐述分析，指出了制度建设中所涉及的激励策略、分配合作、可操作的重要性。

最后，深入分析了制度建设和博弈论之间的关系，提出了基于博弈论思想进行制度建设的实施方法和策略。

关键词博弈论；纳什均衡；智猪博弈；猎鹿博弈；七人分粥；制度建设中文分类号：文献标识码：1前言博弈论（Game Theory）是现代数学的一个新分支，是运筹学的重要组成内容。

按照Robert Aumann 教授的说法（注：2005年其因对博弈论的贡献而获得诺贝尔经济学奖），博弈论就是研究理性人的互动(interactive)决策理论，即各行动方的决策是相互影响的，每个人在决策的时候必须将他人的决策纳入自己的决策考虑之中，当然也需要把别人对于自己的考虑纳入决策依据之中，迭代考虑情形进行决策，选择最有利于自己的战略。

`与博弈论密切相关的一个经济学理论为纳什均衡(Nash Equilibrium)，纳什均衡即在一策略组合中，所有的参与者面临这样一种情况，当其他人不改变策略时，他此时的策略是最好的。

任何改变策略的人其收益将会降低。

在纳什均衡点上，每一个理性的参与者都不会有单独改变策略的冲动。

制度，是国家机关、社会团体、企事业单位，为了维护正常的工作、劳动、学习、生活的秩序，保证各项政策的顺利执行和各项工作的正常开展，依照法律、法令、政策而制订的具有法规性、指导性以及约束力的文件总称。

制度建设是抓好工作的根本，其在企业发展中起着举足轻重的作用。

随着企业规模发展壮大，受到管理者自身管理幅度的限制，企业只能依靠制度来管理，也籍此，才能实现由“人治”向“法治”的转变。

制度建设和博弈论有什么关系？制度是政策（制度设计者）、制度参与人相互博弈的结果。

博弈论（一）：基本知识1.1定义:博弈论，又称对策论，是使用严谨的数学模型研究冲突对抗条件下最优决策问题的理论，是研究竞争的逻辑和规律的数学分支。

即，博弈论是研究决策主体在给定信息结构下如何决策以最大化自己的效用，以及不同决策主体之间的均衡。

1.2基本要素：参与人、各参与人的策略集、各参与人的收益函数，是博弈最重要的基本要素。

1.3博弈的分类：博弈论根据其所采用的假设不同而分为合作博弈理论和非合作博弈理论。

两者的区别在于参与人在博弈过程中是否能够达成一个具有约束力的协议（binding agreement）。

倘若不能，则称非合作博弈（Non-cooperative game）。

合作博弈强调的是集体主义，团体理性，是效率、公平、公正；而非合作博弈则主要研究人们在利益相互影响的局势中如何选择策略使得自己的收益最大，强调个人理性、个人最优决策，其结果有时有效率，有时则不然。

目前经济学家谈到博弈论主要指的是非合作博弈，也就是各方在给定的约束条件下如何追求各自利益的最大化，最后达到力量均衡。

博弈的划分可以从参与人行动的次序和参与人对其他参与人的特征、战略空间和支付的知识、信息，是否了解两个角度进行。

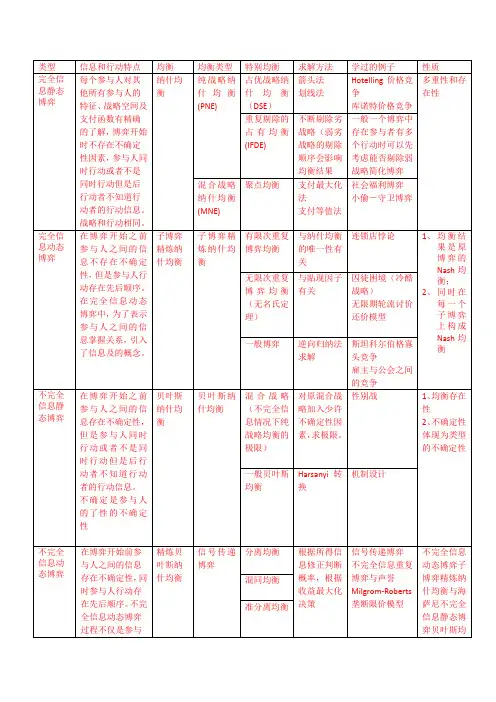
把两个角度结合就得到了4种博弈：a、完全信息静态博弈，纳什均衡，Nash(1950)b、完全信息动态博弈，子博弈精炼纳什均衡，泽尔腾（1965）c、不完全信息静态博弈，贝叶斯纳什均衡，海萨尼（1967-1968）d、不完全信息动态博弈，精炼贝叶斯纳什均衡，泽尔腾（1975）Kreps, Wilson(1982) Fudenberg, Tirole(1991)1.4课程主要内容：完全信息静态博弈完全信息动态博弈不完全信息静态博弈机制设计合作博弈1.5博弈模型的两种表示形式：策略式表述(Strategic form), 扩展式表述（Extensive form）1.6占优均衡：a、占优策略：在博弈中如果不管其他参与人选择什么策略，一个参与人的某个策略给他带来的支付值始终高于其他策略，或至少不劣于其他策略，则称该策略为该参与人的严格占优策略或占优策略。

理论探讨摘要：制度的诞生都与博弈论的出现息息相关。

主观博弈论是制度赖以生存的规则，其将制度与参与者之间的默契配合联合，形成一套行之有效的共同遵守规则。

制度变迁过程中产生的激励约束与共同塑造两种功能时刻调整与完善参与者自身的主观博弈论。

通过学习与反学习两种驱动力共同作用下，使得参与者自身主观博弈论的均衡，最终达到共同信念。

关键词：制度变迁；主观博弈论；均衡一、制度产生与主观博弈论的关系制度常被称作博弈的原则，甚至说是博弈之后的产物，因此，很多制度的诞生都与博弈论的出现息息相关，或是博弈的结果，或是博弈的平衡点。

在博弈论的视觉下，制度更像是博弈的一种规则。

黄凯南等认为，制度的产生过程是博弈的结果，这也是为何制度的变化过程中需要多方主观博弈斗争而来。

这个观点解释了制度产生已经发展的问题[1]。

制度在表面上的理解更多是传统的规则的延续，包括信念的存续、习俗的继承和组织的形成等系统组合，是一种规则制定的规律社会行为。

实际上，主观博弈论更多是将博弈作为制度赖以生存的规则，将制度与参与者之间的默契配合联合，形成一套行之有效的共同遵守规则，共同描述博弈进行的场景与内在联系。

无论是主观博弈论还是博弈均衡观都追求制度由内而外的相生，共同描述制度进行及施放的基本原则。

主观博弈论本身在制度变迁过程中着重均衡制度[2]。

每个博弈论参与者其实际都是制度变化的参与人，若将制度作为一个独立的参与者融会其中，就会改变其他参与者的参与行为，例如策略适应、支付集合、信息集合等等，随之改变的是制度的外在规则，重新形成一套新的制度。

这也就是制度变迁过程中的体现。

在主观博弈之中，参与者无论针对的是客观还是主观的博弈场景都会依靠自身主观的博弈模型，这种模型是由参与者自发内在生成的博弈模型，来源于参与者本身。

因此，制度变迁过程中也是参与者自身调整模型的过程，是将博弈内生规则外表露的一种方式。

在参与过程中会形成一种针对于博弈环境的共同认知行为，共同施行同等概念，逐步形成博弈的均衡，这也是主观博弈论均衡原理的体现之一。

第五章重复博弈在这一章中，我们将围绕着人类的合作为什么产生这一命题来展开。

人与人之间合作生产的一个原因（从经济学的角度来看）是这种做法对于参与者双方而言是一个有利可图的事，为什么说明这一点我们将用到重复博弈。

另一个解释合作生产的方法就是引入信息不对称，在这种情况下，一个人装作是好人是有利可图的（因为好名声能够给他带来收益），这在信息不对称中会加以介绍。

第一节 重复博弈的定义及扩展式 给出重复博弈定义之前，需要做若干准备，一个准备就是由于重复博弈有可能会进行一个很长的时期，甚至是无穷期，因而必须考虑收益的时间价值。

相应的表达偏好的收益函数也需要给出一定的限制。

一、贴现因子与偏好明天的一元钱和今天的一元钱价值是不一样的，最简单的理由是今天的一元钱如果存入银行那么在明天会变成1+ r ，所以明天的一元钱只相当于今天的1/(1+ r )元钱，1/(1+ r )实际上就是经济学中的贴现率。

如果假设未来没有不确定性，定义11r δ=+，未来存在收益流R 1，R 2，R 3，…，那么这个未来收益流的贴现值之和就为V =211231t t t R R R R δδδ∞-=+++=∑L(5-1)其中(0,1)δ∈称为贴现因子(Discount factor)。

严格讲，贴现因子并不等于贴现率，但贴现因子与贴现率一定是同方向变动的。

例如，我们考虑一个特殊的重复博弈，其结束之前重复进行的次数是随机的，即在博弈的每一阶段完成之后，都要通过抛若干枚（加权的）硬币的方式来决定博弈是否结束，如果硬币朝上那么博弈结束（即概率为p），如果是其他情况，那么博弈继续（即概率为1 –p）。

如果下一阶段能得到的收益为R1，那么在当前阶段硬币未抛之前的价值（即贴现后的期望值）为(1 –p)R1/(1+ r)；如果下两阶段能得到的收益为R2，在当前阶段硬币未抛之前的价值为(1 –p)2R2/(1+ r)2；下三阶段、四阶段等等的收益，照此类推。