《数学实验》曲线绘制实验报告

实验一 曲线绘图【实验目的】1.了解曲线的几种表示方法。

2.学习、掌握MATLAB 软件有关命令。

【实验内容】绘制下列四种曲线：1.以直角坐标方程sin ,cos y x y x ==表示的正、余弦曲线。

2.以参数方程cos ,sin ,[0,2]x t y t t π==∈表示的平面曲线(单位圆)。

3.以参数方程0.20.2cos ,sin ,,[0,20]22t t x e t y e t z t t ππ--===表示的空间曲线。

4.以极坐标方程(1cos ),1,[0,2]r a a ϕϕπ=+=∈表示的心脏线。

【实验准备】1.平面、空间曲线的表示形式2.曲线绘图的MATLAB 命令MATLAB 中主要用plot,fplot,plot3三种命令绘制不同的曲线 matlab 绘图命令比较多,我们选编一些常用命令,并简单说明其作用,这些命令的调用格式,可参阅例题及使用帮助help 查找.表1.1 二维绘图函数表1.2 基本线型和颜色表1.3 二维绘图工具表1.4 axis命令linspace 创建数组命令,调用格式为:x=linspace(x1,x2,n),创建了x1到x2之间有n个数据的数组.funtool 函数工具,在matlab指令窗键入funtool可打开“函数计算器”图形用户界面.【实验重点】1.一维函数的绘制2.各种曲线的实现方法 【实验难点】1.各种曲线的实现方法 【实验方法与步骤】练习１ 作出函数sin ,cos y x y x ==的图形，并观察它们的周期性。

先作函数sin y x =在[4,4]ππ-上的图形，用MATLAB 作图的程序代码为>>x=linspace(-4*pi,4*pi,300); %产生300维向量x >>y=sin(x)>>plot(x,y) %二维图形绘图命令 运行结果如图1.1。

-15-10-551015-1-0.8-0.6-0.4-0.200.20.40.60.81图1.1此图也可以用fplot 命令,相应的 MATLAB 程序代码为 >>clear;close; %clear 清理内存；close 关闭已有窗口． >>fplot('sin(x)',[-4*pi,4*pi]) 运行结果如图1.2。

高中数学实验报告标题：高中数学实验报告引言数学实验作为一种创新性的教育方式，旨在通过实际操作来增强学生对数学概念的理解和应用能力。

本文将以高中数学实验为主题，从实验目的、实验方法、实验结果等方面展开回答，旨在探讨实验对学生数学学习的促进作用。

实验目的本次实验的主要目的是通过实践来加深学生对函数、几何、概率等数学概念的理解，并培养学生的分析和解决问题的能力。

同时，实验也旨在激发学生对数学的兴趣，提高他们的学习积极性。

实验方法在本次实验中，我们采用了以小组合作为基础的学习方式。

学生们分成小组，在老师的指导下进行实验，通过互相合作和讨论，提高了学生们的思维能力和团队合作意识。

实验一：函数图像绘制在这个实验中，学生们利用软件绘制了函数的图像。

通过改变函数中的系数和常量，他们可以直观地观察到图像的变化，并将其与数学公式相联系。

这样一来，学生们不仅可以更好地理解函数的性质，还能够培养他们的图形直观能力。

实验结果显示，学生们在绘制函数图像的过程中，逐渐掌握了函数图像的规律，提高了图像的准确性。

通过实验，学生们深入了解了函数的概念，从而更好地掌握了相关的求导和导数概念。

实验二：几何问题求解在这个实验中，学生们通过模拟实际生活中的几何问题，运用数学知识解决实际问题。

比如，他们用测量工具测量物体的高度，然后根据测量结果计算物体的体积。

这样的实践操作能够帮助学生将抽象的数学概念与实际问题联系起来，提高解决实际问题的能力。

实验结果表明，学生们在几何问题求解中，通过实践操作掌握了几何图形的性质和计算方法，提高了他们的空间想象和逻辑思维能力。

实验三：概率实验在这个实验中，学生们利用随机事件的模拟实验来研究概率。

例如，他们通过投掷骰子的实验来研究点数的分布规律，并运用概率理论对实验结果进行分析。

这样的实践操作可以帮助学生更好地理解概率的概念和计算方法。

实验结果显示，学生们通过概率实验加深了对概率的理解，提高了他们的分析和推理能力。

高等数学实验报告实验七：空间曲线与曲面的绘制一、 实验目的1、利用数学软件Mathematica 绘制三维图形来观察空间曲线和空间曲面图形的特点，以加强几何的直观性。

2、学会用Mathematica 绘制空间立体图形。

二、实验题目利用参数方程作图，做出由下列曲面所围成的立体图形：(1)xy x y x z =+--=2222,1及xOy 平面；(2) 01,=-+=y x xy z 及.0=z三、实验原理空间曲面的绘制作参数方程],[],,[,),(),(),(max min max min v v v u u v u z z v u y y v u x x ∈∈⎪⎩⎪⎨⎧===所确定的曲面图形的Mathematica 命令为：ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},{u,umin,umax}, {v,vmin,vmax},选项]四、程序设计(2)五、程序运行结果（2）六、结果的讨论和分析1、通过参数方程的方法做出的图形，可以比较完整的显示出空间中的曲面和立体图形。

2、可以通过mathematica 软件作出多重积分的积分区域，使积分能够较直观的被观察。

3、从(1)中的实验结果可以看出，所围成的立体图形是球面和圆柱面所围成的立体空间。

4、从(2)中的实验结果可以看出围成的立体图形的上面曲面的方程是xy z =，下底面的方程是z=0，右边的平面是01=-+y x 。

实验八 无穷级数与函数逼近一、 实验目的(1) 用Mathematica 显示级数部分和的变化趋势； (2) 展示Fourier 级数对周期函数的逼近情况;(3) 学会如何利用幂级数的部分和对函数进行逼近以及函数值的近似计算。

二、实验题目（1）、观察级数∑∞=1!n nnn 的部分和序列的变化趋势，并求和。

（2）、观察函数⎩⎨⎧<≤<≤--=ππx x x x f 0,10,)(展成的Fourier 级数的部分和逼近)(x f 的情况。

线路测设实习报告实训起止时间：班级：组号：姓名：学号:指导教师:一、实验内容1．在实地测设出圆曲线主点。

2．根据计算的测设数据及转折点里程，推算各主点里程。

3．用极坐标法测设每弧长为10m加密圆曲线。

二、目的与要求1．熟悉圆曲线各元素计算方法。

2．掌握各主点里程推算方法及主点测设程序。

3．掌握用极坐标法加密曲线的计算与实测方法。

三、预习内容1．路线交点和转点的测设及转折角的测定。

2．圆曲线主点测设。

3．用极坐标法测设圆曲线的计算与实例。

四、人员组织与仪器********************************************************五、实验步骤1．在实验场地上，先布置一折线JD2-JD1为路线方向，各点钉以木桩，JD2点为转折点，并设其桩号为（K2+204.73）。

2．在JD2点设站，布置JD3位置，以测回法一个测回测转折角。

3．视现场情况选定半径R,计算设置主点所需各曲线元素值。

并推算各主点里程桩号。

4.主点放样方法：课本157页******************************************************************************** ******************************************************************************** *********************************************************************5.测设细部点方法：课本160页极坐标法及全站仪放样方法**************************************************************************************************************************************************************** *****************************************************************************************************************六、数据计算及放样：1、转折角及JD1-JD2和JD2-JD3距离测量记录与计算。

数值分析课程设计报告学生姓名学生学号所在班级指导教师一、课程设计名称函数逼近与曲线拟合二、课程设计目的及要求实验目的：⑴学会用最小二乘法求拟合数据的多项式，并应用算法于实际问题。

⑵学会基本的矩阵运算，注意点乘和叉乘的区别。

实验要求：⑴编写程序用最小二乘法求拟合数据的多项式，并求平方误差，做出离散函数（x i ,y i ）和拟合函数的图形；⑵用MATLAB 的内部函数polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差，并用MATLAB 的内部函数plot 作出其图形，并与（1）结果进行比较。

三、课程设计中的算法描述用最小二乘法多项式曲线拟合，根据给定的数据点，并不要求这条曲线精确的经过这些点，而是拟合曲线无限逼近离散点所形成的数据曲线。

思路分析：从整体上考虑近似函数)(x p 同所给数据点）（i i y x ,误差i i i y x p r -=)(的大小，常用的方法有三种：一是误差i i i y x p r -=)(绝对值的最大值i mi r ≤≤0max ，即误差向量的无穷范数；二是误差绝对值的和∑=mi i r 0，即误差向量的1范数；三是误差平方和∑=mi i r 02的算术平方根，即类似于误差向量的2范数。

前两种方法简单、自然，但不便于微分运算，后一种方法相当于考虑2范数的平方，此次采用第三种误差分析方案。

算法的具体推导过程： 1.设拟合多项式为：y =a 0+a 1x +a 2x 1+⋯+a k x k2.给点到这条曲线的距离之和，即偏差平方和：R 2=∑[y i −(a 0+a 1x +⋯+a k x i k )]2ni=13.为了求得到符合条件的a 的值，对等式右边求a i 偏导数，因而我们得到了：−2∑[y −(a 0+a 1x +⋯+a k x i k )]ni=1x =0−2∑[y −(a 0+a 1x +⋯+a k x i k )]ni=1=0⋯⋯−2∑[y −(a 0+a 1x +⋯+a k x i k )]x k ni=1=04.将等式左边进行一次简化，然后应该可以得到下面的等式a 0n +a 1∑x i +⋯+a k ∑x i k ni=1ni=1a 0∑x i +a 1∑x i 2+⋯+∑x i k+1ni=1ni=1ni=1a 0∑x i k +a 1∑x i k+1+⋯+a k ∑x i 2k ni=1ni=1ni=15.把这些等式表示成矩阵的形式，就可以得到下面的矩阵：⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∑∑∑∑∑∑∑∑∑∑∑=====+==+====n i i n i n i i k n i k i ni k ini k i n i k i ni in i ini k ini iy y y a a x xx x xxx x 11i 110121111112111a n M MΛM O MM ΛΛ 6. 将这个范德蒙得矩阵化简后得到⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡n k k n n k k y y y a a a x x x x x x M M ΛMOM M ΛΛ21102211111 7.因为Y A X =*,那么X Y A /=,计算得到系数矩阵，同时就得到了拟合曲线。

工作曲线图的绘制实验报告
一、课程设计名称
函数逼近与曲线拟合
二、课程设计目的及要求
实验目的:
⑴学会用最小二乘法求拟合数据的多项式,并应用算法于实际问
题。

⑵学会基本的矩阵运算,注意点乘与叉乘的区别。

实验要求:
⑴编写程序用最小二乘法求拟合数据的多项式,并求平方误差,做出离散函数与拟合函数的图形;
⑵用 MATLAB 的内部函数 polyfit 求解上面最小二乘法曲线拟合多项式的系数及平方误差,并用MATLAB的内部函数plot作出其图形,并与(1)结果进行比较。

三、课程设计中的算法描述用最小二乘法多项式曲线拟合,根据给定的数据点,并不要求这条曲线精确的经过这些点,而就是拟合曲线无限逼近离散点所形成的数据曲线。

范数;三就是误差平方与miir02的算术平方根,即类似于误差向量的 2 范数。

前两种方法简单、自然,但不便于微分运算,
后一种方法相当于考虑 2 范数的平方,此次采用第三种误差分析方案。

为乘法的算法就需要进一步的细化。

例如在进行数据采集时,由于数据采集器(各种传感器)或机器自身的原因及其外部各种因素的制约,导致数据偶尔会有大幅度的波动,及产生一些偏差极大的数据,不能真实反映数据的可靠性,所以会对数据进行筛选或修正。

而此时就可应用曲线拟合。

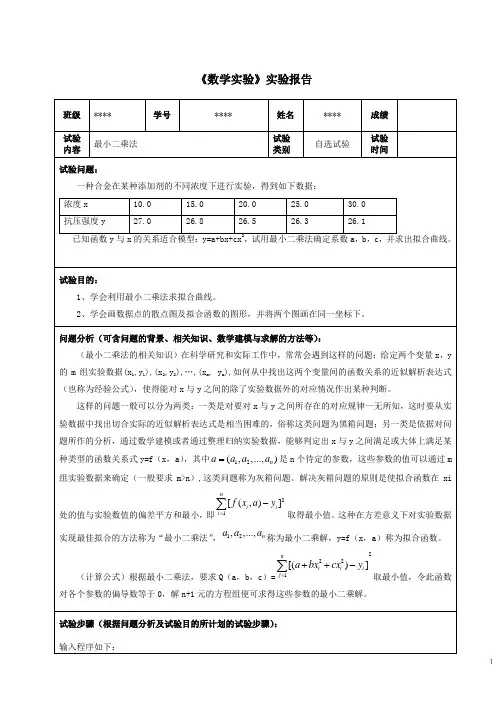
《数学实验》实验报告１x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02]];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25}];Show[t1,t2]首先得到a，b，c三个值： {{a->27.56,b->-0.0574286,c->0.000285714}}然后得到同一坐标系下的数据点散点图及拟合函数的图形：试验过程（含详细试验步骤、程序清单及异常情况记录等）输入以下mathematica语句求解参数a,b,c:运行后可得解：２为求得数据点的散点图及拟合函数的图形，输入以下语句，并将两个图画在同一坐标下：运行得：３在最开始时，我输入的程序是这样的：x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02],DisplayFunction->Identity];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25},DisplayFunction->Identity];Show[t1,t2, DisplayFunction->$ DisplayFunction]然而得到的结果没有图形（如下）：我比照了老师的讲义，改动了“DisplayFunction->Identity”，可是，结果还是一样，没有图形。

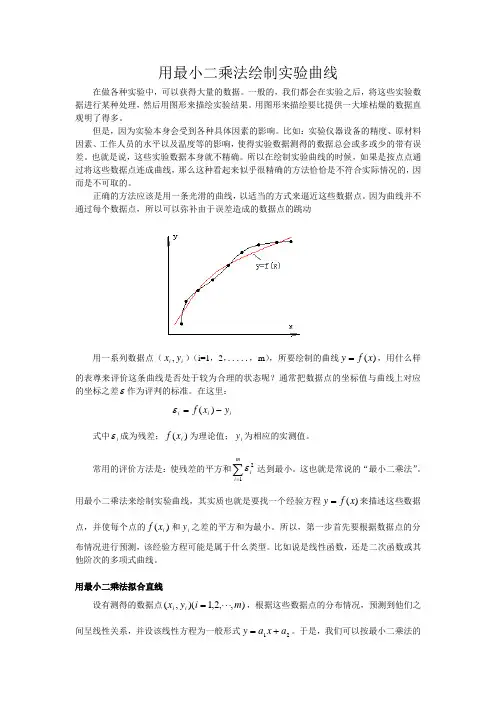
用最小二乘法绘制实验曲线在做各种实验中，可以获得大量的数据。

一般的，我们都会在实验之后，将这些实验数据进行某种处理，然后用图形来描绘实验结果。

用图形来描绘要比提供一大堆枯燥的数据直观明了得多。

但是，因为实验本身会受到各种具体因素的影响。

比如：实验仪器设备的精度、原材料因素、工作人员的水平以及温度等的影响，使得实验数据测得的数据总会或多或少的带有误差。

也就是说，这些实验数据本身就不精确。

所以在绘制实验曲线的时候，如果是按点点通过将这些数据点连成曲线，那么这种看起来似乎很精确的方法恰恰是不符合实际情况的，因而是不可取的。

正确的方法应该是用一条光滑的曲线，以适当的方式来逼近这些数据点。

因为曲线并不通过每个数据点，所以可以弥补由于误差造成的数据点的跳动用一系列数据点（i i y x ,）（i=1，2，．．．．．，m ），所要绘制的曲线)(x f y =，用什么样的表尊来评价这条曲线是否处于较为合理的状态呢？通常把数据点的坐标值与曲线上对应的坐标之差ε作为评判的标准。

在这里：i i i y x f -=)(ε式中i ε成为残差；)(i x f 为理论值；i y 为相应的实测值。

常用的评价方法是：使残差的平方和∑=mi i 12ε达到最小。

这也就是常说的“最小二乘法”。

用最小二乘法来绘制实验曲线，其实质也就是要找一个经验方程)(x f y =来描述这些数据点，并使每个点的)(i x f 和i y 之差的平方和为最小。

所以，第一步首先要根据数据点的分布情况进行预测，该经验方程可能是属于什么类型。

比如说是线性函数，还是二次函数或其他阶次的多项式曲线。

用最小二乘法拟合直线设有测得的数据点),,2,1)(,(m i y x i i ⋅⋅⋅=，根据这些数据点的分布情况，预测到他们之间呈线性关系，并设该线性方程为一般形式21a x a y +=。

于是，我们可以按最小二乘法的原理建立起下面的式子：∑∑==-+=mi i i mi iy a x a122112)(ε其中i i y x ,为测得的已知数据点的值，故这个方程可以看成是关于1a 和2a 的函数，即有两个未知数1a 和2a 。

目录第一部分非完整、非对称缓和曲线要素计算及测设 (2)1.实验目的及要求 (2)2.前期实验准备和相关安排 (2)2.1实验人员及仪器 (2)2.2实验内容 (2)3.实验原理 (3)4.计算过程 (4)5.运行结果 (7)5.小结 (10)第二部分圆曲线和缓和曲线的实地放样 (11)1.实习目的及要求 (11)2.前期实习准备和相关安排 (11)2.1实习人员及仪器 (11)2.2实习内容 (11)2.3放样元素计算软件设计 (11)2.3.1放样元素计算原理及过程 (11)2.3.2 软件设计程序 (14)2.3.3程序运行结果及检核 (16)2.4 曲线测设方案及施测过程 (18)2.4.1曲线测设方案 (18)2.4.2 施测过程 (20)2.5 小结 (20)第一部分非完整、非对称缓和曲线要素计算及测设随着短程光电测距仪和全站仪在道路勘测中的应用越来越普及，利用极坐标法测设曲线将越来越重要。

这种测设曲线的方法，其优点是测量误差不累计，测设的点位精度高。

尤其是测站设置在中线外任意一点测设曲线，将给现场的工作带来很大的方便。

极坐标测设曲线主要是曲线测设资料的计算问题，该方法的计算原理及思路为：把由直线段、圆曲线段、缓和曲线段组合而成的曲线归算到统一的导线测量坐标系统中，这样就便于计算放样的元素了。

1.实验目的及要求1.学会非完整、非对称缓和曲线要素计算方法；2.学会编写偏角法、极坐标法非完整、非对称缓和曲线要素计算程序；3.实地放样非完整、非对称缓和曲线；4.在实习前预先算出实测数据；5.各小组做好测设过程的人员安排。

2.前期实验准备和相关安排2.1实验人员及仪器组长：杨威副组长：张懂庆组员：杨永强张文超范龙强赵晨亮子丽天实习仪器：全站仪一台，三脚架两个，棱镜两个，卷尺一个2.2实验内容1. 根据自己设计的数据计算测设要素和主点里程；2. 设置非完整、非对称曲线的主点；3. 根据书上P169页的曲线测设程序框图(图1)，编写一般缓和曲线的程序，并进行调试和检核；4. 可以查资料，学习非完整、非对称曲线的计算方法和测设方法，并和自己设计的程序相结合，计算各个放样点的坐标等内容；5. 在内业计算的基础上，选取合适的控制点和位置进行曲线测设；6. 直接根据课本实例，进行相应元素的计算和检核，最后安排具体的实习过程，进行现场曲线放样；7.书写实习报告书。