(格利森)弧齿锥齿轮几何尺寸计算(EXCEL)
- 格式：xls
- 大小：138.50 KB
- 文档页数：1
下载文档原格式
合集下载
弧齿锥齿轮几何参数设计
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动，一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
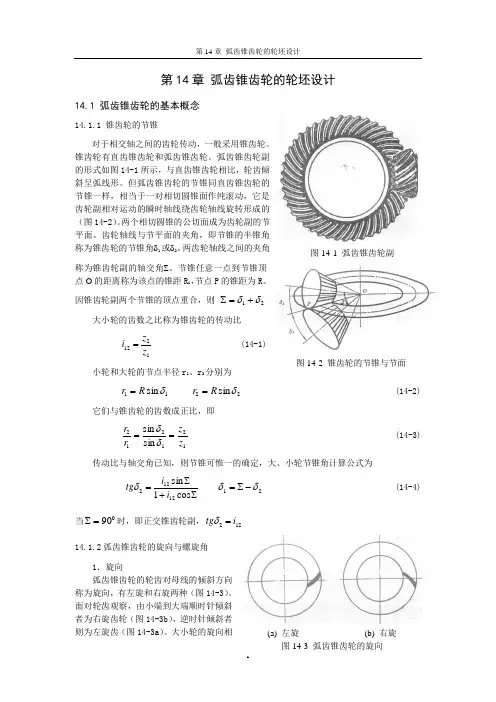
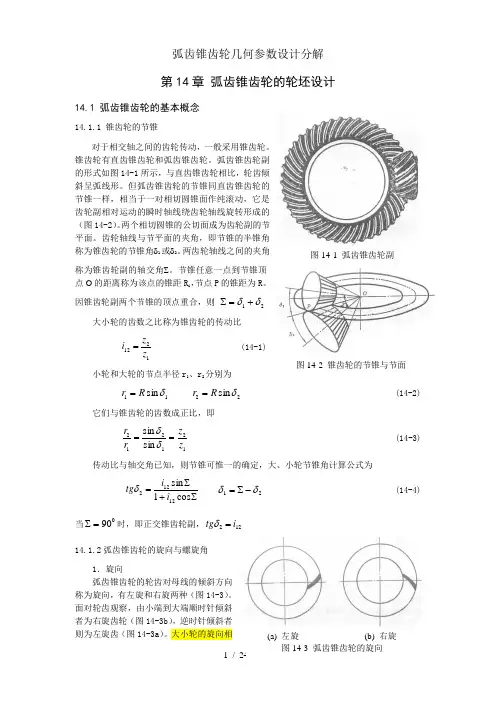
弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比，轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样，相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的（图14-2）。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ，节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合，则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比，即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时，即正交锥齿轮副，122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向，有左旋和右旋两种（图14-3）。
面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮（图14-3b ），逆时针倾斜者则为左旋齿（图14-3a ）。
大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-3 弧齿锥齿轮的旋向图14-1 弧齿锥齿轮副反时，才能啮合。
一般情况下，工作面为顺时针旋转的（从主动轮背后看，或正对被动轮观察），主动锥齿轮的螺旋方向为左旋，被动轮为右旋（图14-1）；工作面为逆时针旋转的，情况相反。
弧齿锥齿轮几何参数设计
弧齿锥齿轮几何参数设计————————————————————————————————作者: ————————————————————————————————日期：ﻩ第14章 弧齿锥齿轮的轮坯设计１４.1 弧齿锥齿轮的基本概念1４．1.1 锥齿轮的节锥对于相交轴之间的齿轮传动，一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图１4－2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角δ１或δ２。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合，则21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(１４-1）小轮和大轮的节点半径r １、r 2分别为11sin δR r = 22sin δR r =（14－2）它们与锥齿轮的齿数成正比，即121212sin sin z z r r ==δδ （14-3）传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑=（14-4)当090=∑时，即正交锥齿轮副,122i tg =δ图14-2 锥齿轮的(a) 左旋图14-1 弧齿锥１４.1．２弧齿锥齿轮的旋向与螺旋角ﻩ1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图１4-３)。
面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮(图１4-3b ），逆时针倾斜者则为左旋齿(图14-3ａ)。
大小轮的旋向相反时，才能啮合。
一般情况下，工作面为顺时针旋转的(从主动轮背后看，或正对被动轮观察）,主动锥齿轮的螺旋方向为左旋，被动轮为右旋(图14-1)；工作面为逆时针旋转的，情况相反。
弧齿、零度弧齿锥齿轮计算-任意轴交角
14 齿宽中点螺旋角 15 中点模数 16 中点法向模数 17 中点锥距 18 小端锥距 19 切向变位系数 20 径向变位系数 21 齿顶高 22 齿根高 23 顶隙 24 全齿高 25 工作齿高 26 27 28 齿顶角（不等顶隙） 齿顶角（等顶隙） 齿根角
m em m nm Rm Ri xt x ha hf C
K ψ mn S mn
h am d0
β β
e i
533.4 39.87016633 30.84621438 48.69468613 29.79729163 22.24976736 18.51003688 18.8973945 14.27481083 8.179908056
Pe
se s ne h ne
ht h
θ
a
θ δ δ
f
2.165679711 27.27235224 21.0329108 265.7804032 184.6753387
29 顶锥角(等顶隙） 30 根锥角 31 大端齿顶圆直径 32 小端齿顶圆直径
a
f
d ae d ai
33 冠顶距 34 中点法向齿厚 35 中点法向齿厚半角 36 中点齿厚角系数 37 中点分度圆弦齿厚 38 中点分度圆弦齿高 39 铣刀盘名义直径 40 大端螺旋角 41 小端螺旋角 42 齿距 43 大端分度圆理论弧齿厚 44 大端理论弦齿厚 45 大端理论弦齿高 46 当量齿数 47 48 49 50 51 端面重合度 52 纵向重合度 53 总重合度 54 不根切的许用最大齿根角 55 不产生根切的最少齿数
Zv
at
α
vat
α β
29.69023654 161.6468434 23.95680324 0.418125095 36.92510996 0.644464745 25.43970428 0.4440066
运用Excel计算螺旋锥齿轮的加工参数
3结语为了快速准确地编制铣齿机调整卡采用了新的计算方法和算法程序改变了以往用200多个公式进行大量复杂运算的传统计算方法大大提高了计算效率和数据准确率有效缩短了产品的制造周期同时提高了齿轮副的啮合精度提升了螺旋锥齿轮的制造精度和产品质量
104
工具技术
运用 Excel 计算螺旋锥齿轮的加工参数
朱玉胜
太原重型机械集团公司
以保护 ,设定为不可修改项 ,以避免误操作 。 ③最后进行整理 、编辑 ,确认打印输出结果 。
2 应用实例与效果
加工某一对 GB/ T11365 —89 五级精度的弧齿锥 齿轮副 ,大 、小轮的齿数分别为 86 齿和 34 齿 ,模数 为 7. 569 ,中点螺旋角为 35°,轴交角为 90°。输入参 数进行运算后 ,得到表 3 所示铣齿调整数据卡 (打印 输出结果) 。
的计算方法和算法程序 ,改变了以往用 200 多个公 式进行大量复杂运算的传统计算方法 ,大大提高了 计算效率和数据准确率 ,有效缩短了产品的制造周 期 ,同时提高了齿轮副的啮合精度 ,提升了螺旋锥齿 轮的制造精度和产品质量 。
3 结语
为了快速 、准确地编制铣齿机调整卡 ,采用了新
小轮粗切跳齿数
17
小轮精切跳齿数
13
大轮粗切跳齿数
1
大轮精切跳齿数
13
机床调整数据
大齿轮粗切
大齿轮精切
粗切
小齿轮 精切凹面
精切凸面
水平轮位
- 3142585
513295
垂直轮位
- 14169741
141373
根角 (安装角)
66°44′
20°41′
滚比
011893
01492228896
016435
104
工具技术
运用 Excel 计算螺旋锥齿轮的加工参数
朱玉胜
太原重型机械集团公司
以保护 ,设定为不可修改项 ,以避免误操作 。 ③最后进行整理 、编辑 ,确认打印输出结果 。
2 应用实例与效果
加工某一对 GB/ T11365 —89 五级精度的弧齿锥 齿轮副 ,大 、小轮的齿数分别为 86 齿和 34 齿 ,模数 为 7. 569 ,中点螺旋角为 35°,轴交角为 90°。输入参 数进行运算后 ,得到表 3 所示铣齿调整数据卡 (打印 输出结果) 。
的计算方法和算法程序 ,改变了以往用 200 多个公 式进行大量复杂运算的传统计算方法 ,大大提高了 计算效率和数据准确率 ,有效缩短了产品的制造周 期 ,同时提高了齿轮副的啮合精度 ,提升了螺旋锥齿 轮的制造精度和产品质量 。
3 结语
为了快速 、准确地编制铣齿机调整卡 ,采用了新
小轮粗切跳齿数
17
小轮精切跳齿数
13
大轮粗切跳齿数
1
大轮精切跳齿数
13
机床调整数据
大齿轮粗切
大齿轮精切
粗切
小齿轮 精切凹面
精切凸面
水平轮位
- 3142585
513295
垂直轮位
- 14169741
141373
根角 (安装角)
66°44′
20°41′
滚比
011893
01492228896
016435
格里森弧齿锥齿轮建模
格里森弧齿锥齿轮建模
格里森弧齿锥齿轮是一种用于调节行星齿轮系统和机械传动系统的齿轮系统。
它能有
效地变换行星齿轮系统中两个轴之间的动力传递比率。
格里森弧齿锥齿轮主要包括两个锥齿轮和半节圆环，正反两个锥齿轮是几何同心，通
常支承轴的外表面上安装半节圆环，用于连接两个锥齿轮，以达到调整轴之间扭矩传递比
率的作用。
我们以中心点为参考，首先确定锥齿轮上的螺旋线的方向，然后对锥齿轮的数
量进行确定和计算，并在根据螺旋线方向将一齿宽绘制成弧齿形状。
设计一个高效率的格里森弧齿锥齿轮要考虑几个方面的因素。
首先，正反两个锥齿轮
之间的节圆环和锥齿轮之间的精度要高，以便把几何同心的特性发挥出来，减少传动系统
的损耗；其次，对螺旋线参数的角度来变化，这样可以调整齿轮减速效率；第三，齿面的
精度和材料硬度也很重要，齿面精度高可以减少噪音及损耗；最后，设计格里森弧齿锥齿
轮时也要注意重力影响，将重力影响因素考虑在设计之中。
建模可以采用三维CAD/CAE软件进行建模，利用软件表达出各个零件几何尺寸、材料
特性等重要因素。
首先，利用软件的三维建模功能，建立出正向和反向的锥齿轮，结合其
精度要求，确定其螺旋线参数；接下来，将其与轴结合，将节圆环以紧定螺丝连接；最后，根据重力影响、材料特性等其他参数，对总体的齿轮参数进行规划，以满足齿轮的精度及
高效的减速效果。
总之，格里森弧齿锥齿轮是一款具有调节性能好、减振阻尼好、损耗小、质量轻的齿轮，具有重要的应用价值，在行星齿轮传动系统和机械传动系统中具有很大的发挥空间，
但要想达到最佳性能，就必须要正确设计并进行精确建模，以满足传动系统效率、精度和
损耗的要求。
弧齿锥齿轮几何参数设计分解
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动，一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示，与直齿锥齿轮相比，轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样，相当于一对相切圆锥面作纯滚动，它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的（图14-2）。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角，即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ，节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合，则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比，即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知，则节锥可惟一的确定，大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时，即正交锥齿轮副，122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1．旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向，有左旋和右旋两种（图14-3）。
面对轮齿观察，由小端到大端顺时针倾斜者为右旋齿轮（图14-3b ），逆时针倾斜者则为左旋齿（图14-3a ）。
大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-1 弧齿锥齿轮副反时，才能啮合。
一般情况下，工作面为顺时针旋转的（从主动轮背后看，或正对被动轮观察），主动锥齿轮的螺旋方向为左旋，被动轮为右旋（图14-1）；工作面为逆时针旋转的，情况相反。
这样可保证大小轮在传动时具有相互推开的轴向力，从而使主被动轮互相推开以避免齿轮承载过热而咬合。
弧齿锥齿轮设计计算2
ห้องสมุดไป่ตู้
名
准双曲面齿轮计算结果 称 小轮 16
大轮 41 4.646
齿数 模数 压力角 小轮偏置 外锥距 齿顶高 齿根高 工作齿高 全齿高 节锥定点到交错点的距离 面锥顶点到交错点的距离 根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径 侧隙 刀具直径 外径
19 下38.6 107.52 2.7719 6.668 8.5281 9.440 -3.543 15.51547 -4.812 23.86825 -1.819 89.93 50.973 60.46 25.63205 62.3573 29.79222 64.44521 23.63867 58.02087 54.49766 30.86347 0 右旋 190.5 0.20--0.30 190.5 120.7404 193.0721
准双曲面齿轮设计计算
小轮齿数 16 小轮螺旋角 54 大轮齿数 41 工作齿高系数 4.000 输入齿轮基本参数 大轮齿面宽 偏置距 29.2 38.6 锥度系数 压力角和 0.788532 38 大轮节径 刀盘半径 190.5 95.25 大轮齿顶高系数 齿侧间隙 0.325 0.20--0.30 计算刀盘半径 95.24998171 旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250
名
准双曲面齿轮计算结果 称 小轮 16
大轮 41 4.646
齿数 模数 压力角 小轮偏置 外锥距 齿顶高 齿根高 工作齿高 全齿高 节锥定点到交错点的距离 面锥顶点到交错点的距离 根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径 侧隙 刀具直径 外径
19 下38.6 107.52 2.7719 6.668 8.5281 9.440 -3.543 15.51547 -4.812 23.86825 -1.819 89.93 50.973 60.46 25.63205 62.3573 29.79222 64.44521 23.63867 58.02087 54.49766 30.86347 0 右旋 190.5 0.20--0.30 190.5 120.7404 193.0721
准双曲面齿轮设计计算
小轮齿数 16 小轮螺旋角 54 大轮齿数 41 工作齿高系数 4.000 输入齿轮基本参数 大轮齿面宽 偏置距 29.2 38.6 锥度系数 压力角和 0.788532 38 大轮节径 刀盘半径 190.5 95.25 大轮齿顶高系数 齿侧间隙 0.325 0.20--0.30 计算刀盘半径 95.24998171 旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250
弧齿锥齿轮副参数计算(格里森制等顶隙收缩齿)
弧齿锥齿轮副参数计算（格里森制等顶隙收缩齿）
名 称 齿数 旋向 大端端面模数 齿形角 齿顶高系数 顶隙系数 轴交角 齿宽中点螺旋角 大端螺旋角 齿数比 变位系数 切向变为系数 分锥角 分度圆直径 分度圆锥距 齿宽系数 齿宽 铣刀盘名义直径 齿顶高 全齿高 符号 Z1 Z2 主动轮 从动轮 m α ha* c* ∑ β m β μ x1 x2 xt δ δ
备
注
单位° 单位° 单位° 单位° 单位° 单位° 单位° 单位°
δ a1 δ a2 δ f1 δ f2 Ak1 Ak2 A1 A2 H1 H2 Rm s1 s2 Zv1 Zv2
按结构确定，一般凑成整数
A1-Ak1 A2-Ak2 19.27414012 2.395974063 1.923715762 28.10354121 42.19802237
f1 f2 a1 a2
数值 1.182150 1.672350 21.81275382 27.63823083 2.971416149 4.199805087 4.199805087 2.971416149 29.20045046 37.97077078 22.02922922 30.79954954 20.04273869 18.12585546
1 2
数值 14 19 左旋 右旋 1.375 20 0.85 0.188 60 35 40.92242589 1.357143 0.18 -0.18 0.00 25.00064537 34.99935463 19.25 26.125 22.77414012 R/3.5～R/3 7 38.1 1.413850 0.923650 2.596000
ε α 端面重合度 1.222798812 对于α =20°可查表 注：只要填写黄色区域，其余将自动生成
名 称 齿数 旋向 大端端面模数 齿形角 齿顶高系数 顶隙系数 轴交角 齿宽中点螺旋角 大端螺旋角 齿数比 变位系数 切向变为系数 分锥角 分度圆直径 分度圆锥距 齿宽系数 齿宽 铣刀盘名义直径 齿顶高 全齿高 符号 Z1 Z2 主动轮 从动轮 m α ha* c* ∑ β m β μ x1 x2 xt δ δ
备
注
单位° 单位° 单位° 单位° 单位° 单位° 单位° 单位°
δ a1 δ a2 δ f1 δ f2 Ak1 Ak2 A1 A2 H1 H2 Rm s1 s2 Zv1 Zv2
按结构确定，一般凑成整数
A1-Ak1 A2-Ak2 19.27414012 2.395974063 1.923715762 28.10354121 42.19802237
f1 f2 a1 a2
数值 1.182150 1.672350 21.81275382 27.63823083 2.971416149 4.199805087 4.199805087 2.971416149 29.20045046 37.97077078 22.02922922 30.79954954 20.04273869 18.12585546
1 2
数值 14 19 左旋 右旋 1.375 20 0.85 0.188 60 35 40.92242589 1.357143 0.18 -0.18 0.00 25.00064537 34.99935463 19.25 26.125 22.77414012 R/3.5～R/3 7 38.1 1.413850 0.923650 2.596000
ε α 端面重合度 1.222798812 对于α =20°可查表 注：只要填写黄色区域，其余将自动生成
弧齿锥齿轮主要参数的测绘计算
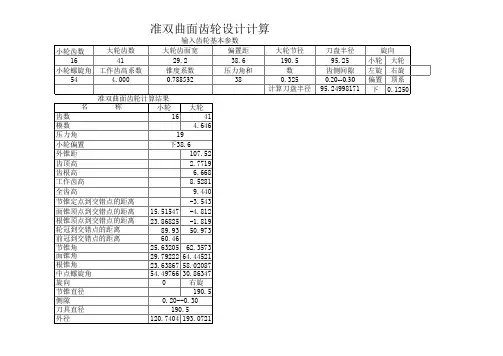
弧齿锥齿轮主要参数的测绘计算零部件加工部 麻俊方弧齿锥齿轮具有承载能力高、运转平稳、噪音低等特点，在汽车行业中得到了广泛的应用。
通常由一对弧齿锥齿轮组成汽车驱动桥主减速器的主要传动机构。
弧齿锥齿轮的设计与测绘计算均比较复杂，下面仅介绍几种主要参数的测绘计算方法。
1.轴交角一对弧齿锥齿轮副的住从动齿轮中心轴线交于一点。
轴线间的交角∑可成任意角度，但在绝大多数汽车驱动桥上，主减速齿轮副都采用90°相交的布置。
2.齿制渐开线锥齿轮的齿制很多,多达40多种,我国常用的齿制有Gleason(格利森）制、Oerlikon(奥利康)制、Kingelnberg(克林贝格）制三种。
其中应用最广泛也是最常见到的是Gleason(格利森）制弧齿锥齿轮。
不同的齿制，对应不同的参数计算方法与计算公式，在测量齿轮时一定要注意区分。
3.模数弧齿锥齿轮模数是一个变值，由大端向小端与锥距成比例缩小，通常以大端面模数s m 来计算。
GB12368-90规定了锥齿轮大端端面模数，其中以≥1为例，有1、1.125、1.375、1.5、1.75、2等等。
但是所测量的齿轮模数不一定为整数，也不一定符合标准模数系列。
对于模数的测绘与计算，有以下方式：⒈由测量的锥距R ，可初步估算锥齿轮的大端模数s m 。
因为2212mR z z z =+，于是便可确定锥齿轮大端模数22122/m R z z =+。
然后实测齿高h(用深度尺来测量)加以复核。
对于等顶隙收缩齿(格里森制)，齿顶高系数*a h ＝0.85，顶隙系数C *=0.188,则齿高h=(2*a h +C *)m 。
由此得出模数m=h(2*a h +C *)，进而复核模数m s。
⒉ 测量出锥齿轮的周节t ，根据公式s tm π=来进行计算，这种方法要求测量数据准确无误，且被测绘齿轮无磨损现象。
⒊ 由齿顶圆直径反求模数。
首先测绘出齿顶圆的直径尺寸，利用齿顶圆计算公式，然后反求模数。
弧齿锥齿轮的几何尺寸计算表
2
13.09189306 76.90810694 33.11061008 33.11061008 4.71238898 0.16 0.37 4.71238898 -0.16 -0.37
xt1查表23.4-9 x1=0.39(1-1/u²)或查表23.4-10
xt2=-xt1 x2=-x1
hf=h-ha c=h-h′ θ f=arctan(பைடு நூலகம்f/Re) δ δ
s2=p/2-(ha1-ha2)tanα /cosβ m-xt1m
Smn1=(0.5πcosβm+2x1tanα+xt1)mm ψmn=Smn*cosδ*cos²βm/(mmZ) Kψ mn=1-ψ mn²/6 S′mn=SmnKψmn h′am1=ha1-0.5b*tanθf2+0.25Smn1ψmn1 查表23.4-11 N0=（θ
f1+θf2）sinβm/20
Smn2=πmmcosβm-Smn1
h′am2=ha2-0.5b*tanθf1+0.25Smn2ψmn2
1.472078944 0.525395815 9.262878463 9.262878463
设定值 传动比 4.3 齿顶高系数 顶隙系数 0.85 0.188
da1=d1+2ha1*cosδ
da2=d2+2ha2*cosδ
21 锥点至轮冠距离 22 理论弧齿厚 23 侧隙 24 中点螺旋角 25 齿宽系数 26 中点模数 27 中点法向模数 28 中点法向齿厚 29 中点法向齿厚半角 30 中点齿厚角系数 31 中点分度圆弦齿厚 32 中点分度圆弦齿高 33 刀盘直径 34 刀号
表5.4-1 序号 1 齿数 2 大端模数 3 齿宽 4 工作齿高 5 齿高 6 压力角 7 轴交角 8 分度圆直径 9 分锥角 10 锥距 11 周节 12 切向变位系数 13 径向变位系数 14 齿顶高 15 齿根高 16 顶隙 17 齿根角 18 顶锥角 19 根锥角 20 顶圆直径 δ δ
13.09189306 76.90810694 33.11061008 33.11061008 4.71238898 0.16 0.37 4.71238898 -0.16 -0.37
xt1查表23.4-9 x1=0.39(1-1/u²)或查表23.4-10
xt2=-xt1 x2=-x1
hf=h-ha c=h-h′ θ f=arctan(பைடு நூலகம்f/Re) δ δ
s2=p/2-(ha1-ha2)tanα /cosβ m-xt1m
Smn1=(0.5πcosβm+2x1tanα+xt1)mm ψmn=Smn*cosδ*cos²βm/(mmZ) Kψ mn=1-ψ mn²/6 S′mn=SmnKψmn h′am1=ha1-0.5b*tanθf2+0.25Smn1ψmn1 查表23.4-11 N0=（θ
f1+θf2）sinβm/20
Smn2=πmmcosβm-Smn1
h′am2=ha2-0.5b*tanθf1+0.25Smn2ψmn2
1.472078944 0.525395815 9.262878463 9.262878463
设定值 传动比 4.3 齿顶高系数 顶隙系数 0.85 0.188
da1=d1+2ha1*cosδ
da2=d2+2ha2*cosδ
21 锥点至轮冠距离 22 理论弧齿厚 23 侧隙 24 中点螺旋角 25 齿宽系数 26 中点模数 27 中点法向模数 28 中点法向齿厚 29 中点法向齿厚半角 30 中点齿厚角系数 31 中点分度圆弦齿厚 32 中点分度圆弦齿高 33 刀盘直径 34 刀号
表5.4-1 序号 1 齿数 2 大端模数 3 齿宽 4 工作齿高 5 齿高 6 压力角 7 轴交角 8 分度圆直径 9 分锥角 10 锥距 11 周节 12 切向变位系数 13 径向变位系数 14 齿顶高 15 齿根高 16 顶隙 17 齿根角 18 顶锥角 19 根锥角 20 顶圆直径 δ δ
格里森弧齿锥齿轮校核_V0.1
hf
齿顶圆直径 da
齿根角
θf
齿顶角
θa
顶锥角
δa
11.310
12.000
1.476
0.790
14.895 1.478 3.183 14.493
几何输出 78.690 齿数比
60.000 锥距
0.564 齿宽
1.702 齿高
60.221 3.183 1.478 80.168
根锥角
δf 9.832 75.507
润滑油膜影响系数 Zlvr
工作硬化系数 Zw
尺寸系数Zx 最小安全系数S 齿形系数Yfa 应力修正系数Ysa
1 0.905 0.8
0.95
1
0.982
1 1.25 2.7 2.05
重合度系数Yε
0.625
锥齿轮系数Yk 载荷分担系数Yls 应力修正系数 Yst
寿命系数Ynt
齿根圆角敏感系数 Yδr 齿根表面状况系数 Yrr 尺寸系数Yx 最小安全系数S
计算根据GB10062-2003（正交情况）
切向力Fmt 齿轮计算接触应力 许用接触应力 小齿轮计算齿根应力
100 363.46319 1231.8706 66.271104
小齿轮许用齿根应力
712.5
作用力——主动轮：右旋左转
小齿轮径向力
57.301911
大齿轮径向力
59.947056
小齿轮轴向力
10.198 10.355 134.614 12.783 0.418 9.463 0.494 3.276 0.779 1.432
1.630
5.109
4.497
254.951 258.873 259.758 236.572
圆弧齿锥齿轮传动设计几何计算过程
17
中点分度圆法向齿厚smn
smn=(0.5πcosβm+2xtanα+xt)mm
smn1=7.962mm,smn2=5.851mm
18
中点法向齿厚半角ψmn
ψmn=smnsinδcos2βm/dm
ψmn1=1.803°,
ψmn2=.147°
19
中点分圆法向弦齿厚smn
smn=smn(1-ψmn2/6)
Ak1=d2/2-ha1sinδ1,=d1/2-ha2sinδ2
Ak1=267.73,Ak2=87.14mm
15
齿宽中点分度圆直径dm
dm1=d1-bsinδ1,dm2=d2-bsinδ2
dm1=161.026mm,dm2=483.079mm
16
齿宽中点模数mm
mm=dm1/z1=dm2/z2
mm=5.368mm
8
顶隙c
c=c*m
c=1.13mm
9
齿根角θf
θf1=arctg(hf1/R),θf2=arctg(hf2/R)
θf1=.835°,θf2=1.672°
10
齿顶角θa
θa1=θf2,θa2=θf1(等顶隙收缩齿)
θa1=1.672°,θa2=.835°
11
顶锥角δa
δa1=δ1+θf2,δa2=δ2+θf1
+Z2(tanαvat2-tanαt)/cosδ2]/2π
其中:tanαt=(tanα/cosβm)
cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]
εα=1.317
23
齿线重合度εβ
εβ=btanβmπ/mm
εβ=2.491
中点分度圆法向齿厚smn
smn=(0.5πcosβm+2xtanα+xt)mm
smn1=7.962mm,smn2=5.851mm
18
中点法向齿厚半角ψmn
ψmn=smnsinδcos2βm/dm
ψmn1=1.803°,
ψmn2=.147°
19
中点分圆法向弦齿厚smn
smn=smn(1-ψmn2/6)
Ak1=d2/2-ha1sinδ1,=d1/2-ha2sinδ2
Ak1=267.73,Ak2=87.14mm
15
齿宽中点分度圆直径dm
dm1=d1-bsinδ1,dm2=d2-bsinδ2
dm1=161.026mm,dm2=483.079mm
16
齿宽中点模数mm
mm=dm1/z1=dm2/z2
mm=5.368mm
8
顶隙c
c=c*m
c=1.13mm
9
齿根角θf
θf1=arctg(hf1/R),θf2=arctg(hf2/R)
θf1=.835°,θf2=1.672°
10
齿顶角θa
θa1=θf2,θa2=θf1(等顶隙收缩齿)
θa1=1.672°,θa2=.835°
11
顶锥角δa
δa1=δ1+θf2,δa2=δ2+θf1
+Z2(tanαvat2-tanαt)/cosδ2]/2π
其中:tanαt=(tanα/cosβm)
cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]
εα=1.317
23
齿线重合度εβ
εβ=btanβmπ/mm
εβ=2.491
弧齿锥齿轮设计计算
齿侧间隙 0.20--0.30 95.24998171
旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250
准双曲面齿轮设计计算
输入齿轮基本参数
小轮齿数
大轮齿数
大轮齿面宽
偏置距
大轮节径
16
41
小轮螺旋角 工作齿高系数
54
4.000
29.2 锥度系数 0.788532
38.6 压力角和
38
大轮1齿90顶.5高系 数
0.325
计算刀盘半径
准双曲面齿轮计算结果
名
称
小轮 大轮
齿数
16
41
模数
4.646
压力角
19
小轮偏置
23.86825 -1.819
89.93 50.973
60.46
25.63205 62.3573
29.79222 64.44521
23.63867 58.02087
54.49766 30.86340--0.30 190.5
外径
120.7404 193.0721
刀盘半径 95.25
下38.6
外锥距
107.52
齿顶高
2.7719
齿根高 工作齿高
6.668 8.5281
全齿高
9.440
节锥定点到交错点的距离
-3.543
面锥顶点到交错点的距离 15.51547 -4.812
根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径
旋向 小轮 大轮 左旋 右旋 偏置 顶系 下 0.1250
准双曲面齿轮设计计算
输入齿轮基本参数
小轮齿数
大轮齿数
大轮齿面宽
偏置距
大轮节径
16
41
小轮螺旋角 工作齿高系数
54
4.000
29.2 锥度系数 0.788532
38.6 压力角和
38
大轮1齿90顶.5高系 数
0.325
计算刀盘半径
准双曲面齿轮计算结果
名
称
小轮 大轮
齿数
16
41
模数
4.646
压力角
19
小轮偏置
23.86825 -1.819
89.93 50.973
60.46
25.63205 62.3573
29.79222 64.44521
23.63867 58.02087
54.49766 30.86340--0.30 190.5
外径
120.7404 193.0721
刀盘半径 95.25
下38.6
外锥距
107.52
齿顶高
2.7719
齿根高 工作齿高
6.668 8.5281
全齿高
9.440
节锥定点到交错点的距离
-3.543
面锥顶点到交错点的距离 15.51547 -4.812
根锥顶点到交错点的距离 轮冠到交错点的距离 前冠到交错点的距离 节锥角 面锥角 根锥角 中点螺旋角 旋向 节锥直径
弧齿锥齿轮的加工调整计算
第15章 弧齿锥齿轮的加工调整计算弧齿锥齿轮的切齿是按照“假想齿轮”的原理进行的，而采用的切齿方法要根据具体情况而定。
15.1 弧齿锥齿轮的切齿原理与刀号对于收缩齿弧齿锥齿轮的加工，通常采用平顶齿轮原理进行加工。
就是在切齿的过程中，假想有一个平顶齿轮与机床摇台同心，它通过机床摇台的转动而与被切齿轮做无隙的啮合。
这个假想平顶齿轮的轮齿表面，是由安装在机床摇台上的铣刀盘刀片切削刃的相对于摇台运动的轨迹表面所代替,如图15-1中所示。
在这个运动过程中，代表假想平顶齿轮轮齿的刀片切削刃就在被切齿轮的轮坯上逐渐地切出齿形。
YS2250(Y225)和Y2280等机床就是按“假想平顶齿轮”原理设计的。
在调整切齿机床的时候，必须使被切齿轮的节锥面与假想平顶齿轮的节锥面相切并做纯滚动。
而切齿时刀顶旋转平面则需和被切齿轮的根锥相切，也就是说，刀盘轴线与根锥母线垂直，而非与节锥母线垂直，如图15-2所示。
所以铣刀盘轴线与被切齿轮的节锥面倾斜了一个大小等于被切齿轮齿根角θf 的角度，使被切齿轮两则齿面的压力角出现了误差，这样就产生了刀号修正问题。
如图15-2，用螺旋角接近900时的情况予以说明刀号与压力角的关系。
由于在切齿时采用了“平顶产形轮”原理，工件是按照根锥角进行安装的，铣刀盘轴线垂直于根锥母线，因而和节锥母线倾斜一个齿根角θf 。
这样，当外切刀片与内切刀片使用相同的压力角时，切出来的齿轮凹面与凸面在节锥上的压力角是不相等的（α”≠α’）。
如果要使轮齿中点处的两侧压力角相等，就需要对刀具的两个侧刃的压力角进行修图15-1弧齿锥齿轮的切齿原理摇台刀盘 被加工齿轮正。
修正时，外侧刃齿形角减少α∆，内侧刃增加α∆。
α∆的确定可按以下公式计算βθαsin f ≈∆ (15-1)其中β代表螺旋角。
由于大轮与小轮具有不同齿根角θf ，所以从严格意义上来讲，在加工大轮与小轮时，相应的切齿刀盘的刀刃修正量α∆也应不同。
按照现有的刀号制度，将α∆的单位设置为分，并规定10分为一号，则刀号的计算公式为小轮理论刀盘刀号βθβθαsin 610sin 6010c 111*1f f ==∆= (15-2a)大轮理论刀盘刀号βθβθαsin 610sin 6010c 222*2f f ==∆=(15-2b) 所以，在用双面法分别加工大轮与小轮时，应该用不同刀号的刀盘。
弧齿锥齿齿轮计算
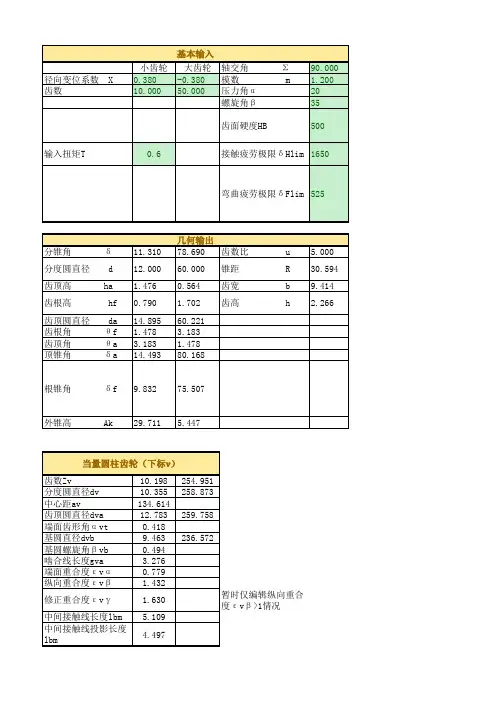
齿数大端模数齿宽螺旋角压力角轴交角齿数比小轮338513520900.787879大轮268513520900.787879小轮209.551352090 1.45大轮299.551352090 1.45 103.2897528206.579505580141.2018164282.4036327160小轮228.453352090 1.590909大轮358.453352090 1.590909 100.1518042200.30360858070149.726847299.453694160小轮208.452352090 1.8大轮368.452352090 1.892.22407165184.44814338070153.5660524307.1321047160小轮178.651352090 2.058824大轮358.651352090 2.05882481.99613569163.99227148070152.5665557305.1331115160小轮158.850352090 2.266667大轮348.850352090 2.26666775.41999368150.83998748070151.4825779302.9651558160小轮158******** 2.533333大轮38850352090 2.53333368.78066529137.56133068070153.5274128307.0548256160小轮147.849352090 2.785714大轮397.849352090 2.78571463.33616893126.67233798070153.444026306.888052160小轮137.549352090 3.153846大轮417.549352090 3.15384657.32907574114.65815158070154.8834145309.766829160小轮117.848352090 3.545455大轮397.848352090 3.54545551.98360004103.96720018070153.1375208306.2750415160小轮117483520904大轮44748352090446.7850169593.57003398070154.8149197309.6298394160小轮228.553352090 1.590909大轮358.553352090 1.590909 101.3440876202.68817538070151.5093095303.0186189160小轮178.550352090 2.058824大轮358.550352090 2.05882481.04269225162.0853*******150.792526301.5850521160小轮147.748352090 2.785714大轮397.748352090 2.78571462.52416677125.0483*******151.4767949302.9535898160小轮317.75513520901大轮317.75513520901 124.8378667249.67573348070124.7282651249.4565303160大端分度圆直径分锥角外锥距齿宽系数中点模数26451.76617482168.04761230.303485 6.78605820838.23382518168.04761230.303485 6.78605819034.59228869167.33219210.3047838.052281 275.555.40771131167.33219210.3047838.052281184.832.152********.62822350.305257.11795 29457.84770486173.62822350.305257.1179516829.0546041172.96658640.3006367.137328 302.460.9453959172.96658640.3006367.137328146.225.906508167.31365750.3048177.289288 30164.093492167.31365750.3048177.28928813223.80594352163.51195670.3057887.454533 299.266.19405648163.51195670.3057887.454533 12021.54097592163.41358570.305972 6.77611230468.45902408163.41358570.305972 6.776112 109.219.74683661161.6031250.303212 6.617473304.270.25316339161.6031250.303212 6.61747397.517.59242456161.29359880.303794 6.360773 307.572.40757544161.29359880.303794 6.36077385.815.75117366158.03423680.303732 6.615447 304.274.24882634158.03423680.303732 6.6154477714.03624347158.73956660.302382 5.941663 30875.96375653158.73956660.302382 5.941663 18732.152********.69522620.3016597.21795 297.557.84770486175.69522620.3016597.21795 144.525.906508165.36814990.3023567.214988 297.564.093492165.36814990.3023567.214988 107.819.74683661159.531290.300881 6.541607300.370.25316339159.531290.300881 6.541607 240.2545169.88240420.300208 6.586695 240.2545169.88240420.300208 6.586695中点法向模数切向变位系数径向变位系数齿顶高齿根高齿全高顶隙5.558813549#N/A06.88.30415.104 1.5045.558813549#N/A06.88.30415.104 1.5046.59604241200.2110.077.86617.936 1.786 6.5960424120-0.21 6.0811.85617.936 1.786 5.83068359500.249.156 6.703215.8592 1.5792 5.8306835950-0.24 5.12410.735215.8592 1.5792 5.8465571320.0150.279.408 6.451215.8592 1.5792 5.846557132-0.015-0.27 4.87210.987215.8592 1.5792 5.9710352580.0250.39.89 6.346816.2368 1.6168 5.971035258-0.025-0.3 4.7311.506816.2368 1.61686.1063956550.0550.3210.296 6.318416.6144 1.6544 6.106395655-0.055-0.32 4.66411.950416.6144 1.6544 5.5506656290.060.339.44 5.66415.104 1.504 5.550665629-0.06-0.33 4.1610.94415.104 1.5045.4207168330.0750.349.282 5.444414.7264 1.4664 5.420716833-0.075-0.34 3.97810.748414.7264 1.46645.2104403210.0850.359 5.1614.16 1.41 5.210440321-0.085-0.35 3.7510.4114.16 1.415.4190565670.140.369.438 5.288414.7264 1.4664 5.419056567-0.14-0.36 3.82210.904414.7264 1.46644.8671251690.150.378.54 4.67613.216 1.3164.867125169-0.15-0.37 3.369.85613.216 1.3165.912598800.249.2656.78316.048 1.598 5.91259880-0.24 5.18510.86316.048 1.598 5.9101724520.0250.39.775 6.27316.048 1.598 5.910172452-0.025-0.3 4.67511.37316.048 1.5985.3585703860.0750.349.163 5.374614.5376 1.44765.358570386-0.075-0.34 3.92710.610614.5376 1.4476 5.39550491600.016.6657.96714.632 1.457 5.3955049160-0.01 6.518.12214.632 1.457齿根角齿顶角顶锥角根锥角齿顶圆直径2.828945 2.82894554.5951198848.93722976272.4166623 2.828945 2.82894541.0627702435.40488012218.6826867 2.691395 4.05280938.6450978731.90089344206.5795055 4.052809 2.69139558.0991065651.35490213282.40363272.2108993.53801735.6903125129.94139636200.30360853.538017 2.21089960.0586036454.30968749299.4536942.1359923.63466532.6892686326.91861189184.44814333.634665 2.13599263.0813881157.31073137307.13210472.172393.93425529.8407628523.73411761163.99227143.934255 2.1723966.2658823960.159********.1331115 2.2129124.18007527.9860185421.59303117150.8399874 4.180075 2.21291268.4069688362.01398146302.9651558 1.985107 3.83144425.372420319.55586904137.5613306 3.831444 1.98510770.4441309664.6275797307.0548256 1.929562 3.805223.5520369117.81727489126.67233793.80521.92956272.1827251166.44796309306.8880521.832344 3.69278721.285211915.76008015114.6581515 3.692787 1.83234474.2399198568.7147881309.7668291.916613.94716619.6983398413.83456382103.9672001 3.947166 1.9166176.1654361870.30166016306.27504151.687277 3.55288417.5891271612.3489665193.5700339 3.552884 1.68727777.6510334972.41087284309.62983942.2108993.53801735.6903125129.94139636202.68817533.538017 2.21089960.0586036454.30968749303.01861892.172393.93425529.8407628523.73411761162.08538453.934255 2.1723966.2658823960.159********.5850521 1.929562 3.805223.5520369117.81727489125.04833353.80521.92956272.1827251166.44796309302.9535898 2.685041 2.73720147.7372007542.31495872249.6757334 2.737201 2.68504147.6850412842.26279925249.4565303锥顶到轮冠距离中点法向齿厚中点法向齿厚半角中点齿厚角系数中点分度圆弦尺厚98.65865663#N/A#N/A#N/A#N/A127.7916689#N/A#N/A#N/A#N/A132.032929111.591971240.0397602880.9997365211.5889169989.994866269.1301071450.0148947120.9999630259.129769555142.127437310.402362960.0377381340.99976263910.3998938588.061834327.9152697840.0113454940.9999785477.915099975146.631071310.693608940.0439417390.99967818710.690167679.741105757.6738919980.0097324820.9999842137.673770851146.179019811.153362790.0543257760.99950811811.1478766668.845326417.6051977070.0087392140.9999872717.605100901145.444120411.738369080.0644476660.9993077511.7302431961.732823377.4454386540.007956360.9999894497.4453601148.533947910.753291790.0660319450.99927329710.7454773556.13055428 6.6846385690.0063959630.999993182 6.684592993148.963939410.648975660.0725932260.99912170410.639622750.8559276 6.3807085230.0056051090.999994764 6.380675112151.029805310.34579870.0800272320.99893260710.33475566 45.17538511 6.023*******.0046840980.999996343 6.023260312149.53795911.172031120.0991487760.99836158711.15372672 39.22151734 5.852*******.0041318840.999997155 5.852420526151.928745810.136827140.1009638560.9983010510.11960518 35.2403212 5.1536975320.003208210.999998285 5.153688691 143.819430610.548505640.0377381340.99976263910.54600183 89.110189498.0264713150.0113454940.9999785478.02629912 144.479263811.039676490.0543257760.99950811811.03424627 68.044799367.5276778710.0087392140.9999872717.527582052 147.054145310.526889220.0725932260.99912170410.5176434950.20392853 6.3075561380.0056051090.999994764 6.30752311 115.41213338.5231865240.0198055440.9999346238.522629308 115.52173498.4272920830.0195827110.9999360868.426753463中点分度圆弦尺高查表L中点分度圆直径#N/A351.7640106223.9399246#N/A277.1474023176.43751648.378471671252.9698668161.04561924.915286215366.8063068233.51614787.615682012245.978706156.5949084.123375055391.3297596249.12826287.873899463224.2257836142.74656753.920939699403.6064106256.94382158.287746265194.6497785123.91789783.779310489400.749544255.12508388.657982955175.6432872111.81798963.712764086398.1247842253.45410987.943235796159.6583668101.64167323.304175653404.4678624257.49223887.845739167145.525839792.644627033.161537548405.3934105258.0814617.625739527129.889227982.69005078 2.973265332409.6506418260.79169868.058917583114.306710472.76991204 3.024*********.269246258.00241547.305724409102.664561765.35828997 2.657164238410.6582467261.4331599 7.7260608249.434458158.794908 4.184690464396.8275467252.6282628 8.205589153192.6657119122.6548018 3.743107895396.664701252.5245919 7.75777905143.857441591.582491783.127280012400.74573255.1226557 5.488058255320.7370595204.18755415.355380071320.7370595204.1875541。