高中数学第三章三角恒等变换3.2两角和与差的三角函数2自我小测北师大版

学习资料课时素养评价二十五两角和与差的正切函数(20分钟35分)1.若tan=2,则= （）A。

B。

2 C.-2 D。

—【解析】选D。

已知tan=2，所以=2,则=2，所以==—=-。

【补偿训练】已知cos=2cos，则tan= ( )A。

B.—3 C。

D.3【解析】选B。

由cos=2cos（π-α），可得—sin α=—2cos α，所以tan α=2，则tan===-3.2.已知tan α，tan β是方程x2+3x+4=0的两个根,且α、β∈，则α+β的值是（)A。

B.—C。

或— D。

—或【解析】选B。

由题意得tan α+tan β=—3，tan αtan β=4,所以tan α<0,tan β〈0，所以α,β∈，因为tan（α+β)===，α+β∈（—π，0）,所以α+β=—.3。

已知tan α+tanβ=2，tan（α+β）=4，则tan α·tan β等于( )A.4 B。

2 C。

1 D。

【解析】选D。

因为tan(α+β）=，又tan α+tan β=2,tan（α+β)=4，所以4=,所以tan αtan β=.4。

已知tan=7，α∈,则cos α=。

【解析】因为tan α=tan==,又α∈,由tan α〉0可得α∈，所以cos α== ===。

答案：5。

若（tan α—1）（tan β-1）=2，则α+β= .【解析】(tan α-1）（tan β-1)=2⇒tan αtan β-tan α—tan β+1=2⇒tan α+tan β=tan αtan β—1⇒=—1,即tan（α+β)=-1，所以α+β=kπ-，k∈Z。

答案：kπ—，k∈Z6。

已知α是第二象限角，其终边上的一点为P,且cos α=.（1）求x的值。

(2)求tan的值。

【解析】(1）由P得cos α=,由cos α=得=,解得x=0或x=12或x=—12。

α是第二象限角,则x〈0，所以x=—12。

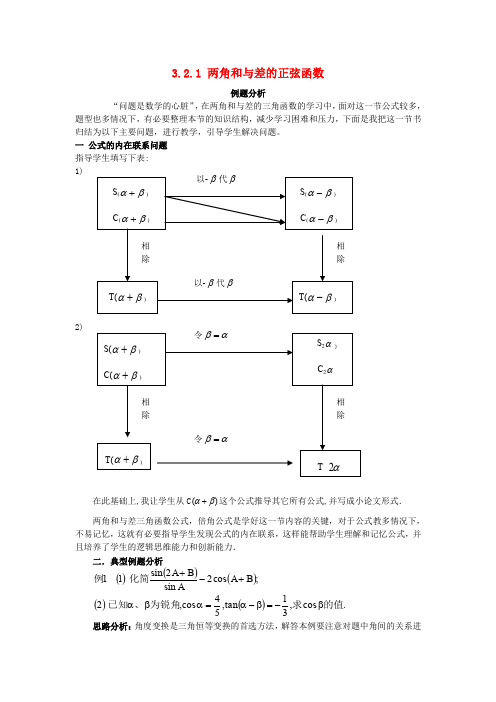
3.2.1 两角和与差的正弦函数例题分析“问题是数学的心脏”，在两角和与差的三角函数的学习中，面对这一节公式较多，题型也多情况下，有必要整理本节的知识结构，减少学习困难和压力，下面是我把这一节书归结为以下主要问题，进行教学，引导学生解决问题。

一 公式的内在联系问题1)2)在此基础上,我让学生从C )(βα+这个公式推导其它所有公式,并写成小论文形式． 两角和与差三角函数公式，倍角公式是学好这一节内容的关键，对于公式教多情况下，不易记忆，这就有必要指导学生发现公式的内在联系，这样能帮助学生理解和记忆公式，并且培养了学生的逻辑思维能力和创新能力．二．典型例题分析()()();22 1 1B A cos Asin B A sin +-+化简例 ()().cos ,tan ,cos ,的值求为锐角、已知β-=β-α=αβα3154 2 思路分析：角度变换是三角恒等变换的首选方法，解答本例要注意对题中角间的关系进行分析，如（1）中有2A ＋B ＝（A ＋B ）＋A ，（2）中有β＝α－（α－β），抓住了这些关系后，再恰当地运用公式，问题便不难解决了．（2）解法一：.sin ,cos ,53 54=α∴=αα是锐角 .,22 π<β-α<π-∴βα为锐角、又 ()可求出,31tan -=-βα ()(),1010sin ,10103cos -=-=-βαβα ()[]()().10509 1010531010354 sin sin cos cos cos cos =⎪⎪⎭⎫ ⎝⎛-+⋅=-+-=--=∴βααβααβααβ,54cos , :=αα是锐角解法二 .tan ,sin 4353=α=α∴ ()[]()().913314313143 tan tan 1tan tan tan tan =⋅-+=-+--=--=∴βααβααβααβ 又∵β是锐角，.10509cos =∴β 点评：对角间的关系进行分析，主要是分析它们之间的和、差、倍、分关系，以便通过角度变换，减少不同角的个数．它实际上是一种基本量方法，即把题中某些角作为基本量，其他角用基本量表示出来，达到变形的目的．()()()()()()sin 2cos sin : 1 sin sin cos cos sin sin sin sin sin .sin A B A A B A A A B A A B A A A B A A BA ++-+=+-+=+-==⎡⎤⎣⎦⎡⎤⎣⎦解原式例2 （1）如果方程()102≠=++c c bx x 的两根为tan α、tan β，求()()()()βαβαβαβα++++++22cos cos sin sin c b 的值；（2）在非直角△ABC 中，求证：tanA ＋tanB ＋tanC ＝tanA ·tanB ·tanC ．思路分析：观察（1）中待求式特点，须先求出α＋β的一个三角函数值，由韦达定理和和角正切公式特点，可先求tan （α＋β）．根据（2）中恒等式的结构特点，可利用和角正切公式的变形tan α＋tan β＝tan （α＋β）（1－tan αtan β）将左边的正切和转化为右边的正切积．解：（1）由韦达定理，得⎩⎨⎧=⋅-=+.tan tan ,tan tan c b βαβα ().1 tan tan 1tan tan tan cb --=-+=+∴βαβαβα ()()()[]()()()[]()()()()()[](). 1111 1111 tan tan tan 11tan tan cos 222222222222222c c c b c b c c c c b c b b c c c b cb =--+⋅+--=⎥⎥⎦⎤⎢⎢⎣⎡+--⎪⎭⎫ ⎝⎛--+--=++++⋅++=++++⋅+=∴βαβαβαβαβαβα原式 （2）∵A ＋B ＋C ＝π，∴A ＋B ＝π－C ，()()().tan tan tan tan tan tan 1tan tan tan tan 1tan tan tan tan C B A CB AC CB A B A CB A ⋅⋅=+⋅--=+⋅-+=++∴点评：含α、β两角的正切和与正切积的式子，用和、差角正切公式的变形比较容易处理．例3 化简().8sin 15sin 7sin 8sin 15cos 7sin 1︒︒-︒︒︒+︒ ()().50cos 50sin 2110tan 3180sin 50sin 2 2︒︒+︒+︒+︒思路分析：对于（1），三个角的关系非常明显，结合和、差角三角函数公式的特点，易进行角度变换7°＝15°－8°．对于（2），一方面应由诱导公式将80°角变换成10°的角，另一方面应将切化成弦．()()()().323113 45tan 60tan 145tan 60tan 4560tan 15tan 8cos 15cos 8cos 15sin 8sin 15sin 815cos 8sin 15cos 815sin 1 :-=+-=︒︒+︒-︒=︒-︒=︒=︒︒︒︒=︒︒-︒-︒︒︒+︒-︒=原式解()()()().323113 45tan 60tan 145tan 60tan 4560tan 15tan 8cos 15cos 8cos 15sin 8sin 15sin 815cos 8sin 15cos 815sin 1 :-=+-=︒︒+︒-︒=︒-︒=︒=︒︒︒︒=︒︒-︒-︒︒︒+︒-︒=原式解点评：数值角三角式的化简，在变形过程中应注意产生特殊角，并设法将非特殊的三角函数值约掉或消掉．例4 已知△ABC 中的三内角A 、B 、C 成等差数列，且B C A cos 2cos 1cos 1-=+，求2c o s C A -的值．思路分析：本题中角间关系较为隐蔽，注意到260C A B +=︒=，而22C A C A A -++=，22C A C A C --+=．取2C A -作为基本量，就找到了解决本题的突破口． 解：由已知，B ＝60°，A ＋C ＝120°则设,2α=-C A ,6022α+︒=-++=C A C A A .6022α-︒=--+=C A C A C ()().43cos cos sin 43cos 41cos sin 23cos 211sin 23cos 211 60cos 160cos 1 cos 1cos 1 222-=-=++-=-︒++︒=+αααααααααααCA 故22cos 243cos cos 2-=-=-Bαα依题设有 ,cos cos :023224 2=-α+α整理得()().cos cos 032222=+α-α ,cos 0322≠+α.cos 022=-α∴.C A cos 222=-故 点评：本题实际上是把题设等式看成一个方程，上述解法体现了方程思想的应用．例5 已知21cos cos ,31sin sin =--=-βαβα，α、β都是锐角，求tan （α－β）的值．⎪⎪⎩⎪⎪⎨⎧=--=-21cos cos 31sin sin :βαβα由错解 ⎪⎪⎩⎪⎪⎨⎧=β+βα-α=β+βα-α②①得 412 912 2222cos cos cos cos sin sin sin sin ()361322 =β-α-+cos ②得①()7259cos =-∴βα 22πβαπ<-<-又()()721703cos 1sin 2±=--±=-∴βαβα ()()()591703cos sin tan ±=--=-βαβαβα故 点评：上述错解未挖掘出角的隐含条件．事实上，由于α、β为锐角，且031sin sin <-=-βα，可知α－β＜0，于是有02<-<-βαπ． ()591703 :-=β-αtan 正解。

3.2 两角和与差的三角函数自我小测1．sin 12°cos 48°＋cos 12°sin 48°的值是( ) A ．12 B ．22 C ．32 D ．－322．若cos α＝－12，sin β＝－32，α∈⎝ ⎛⎭⎪⎫π2，π，β∈⎝ ⎛⎭⎪⎫3π2，2π，则sin(α＋β)的值是( )A ．32 B ．－32C ．－1D ．0 3．已知a ＝(2sin 35°，2cos 35°)，b ＝(cos 5°，－sin 5°)，则a ·b ＝( ) A ．12 B ．1 C ．2 D ．2sin 40° 4．在△ABC 中，A ＝π4，cos B ＝1010，则sin C ＝( )A ．－55 B ．55 C ．－255 D ．2555．在△ABC 中，cos A ＝35，且cos B ＝513，则cos C 等于( )A ．－3365B ．3365C ．－6365D ．63656．化简sin(α＋30°)＋cos(α＋60°)2cos α＝__________.7．函数y ＝cos x ＋cos ⎝⎛⎭⎪⎫x ＋π3的最大值是__________．8．若cos α＝15，α∈⎝ ⎛⎭⎪⎫0，π2，则cos ⎝ ⎛⎭⎪⎫α＋π3＝______. 9．化简下列各式：(1)sin ⎝ ⎛⎭⎪⎫x ＋π3＋2sin ⎝ ⎛⎭⎪⎫x －π3－3cos ⎝ ⎛⎭⎪⎫2π3－x ；(2)sin(2α＋β)sin α－2cos(α＋β)．10．如图，设A 是单位圆和x 轴正半轴的交点，P ，Q 是单位圆上的两点，O 是坐标原点，且∠AOP ＝π6，∠AOQ ＝α，α∈[0，π)．(1)若点Q 的坐标是⎝ ⎛⎭⎪⎫35，45，求cos ⎝ ⎛⎭⎪⎫α－π6的值； (2)设函数f (α)＝OP OQ ⋅，求f (α)的值域．参考答案1．解析：原式＝sin(12°＋48°)＝sin 60°＝32. 答案：C2．解析：∵α∈⎝ ⎛⎭⎪⎫π2，π，β∈⎝ ⎛⎭⎪⎫3π2，2π，cos α＝－12，sin β＝－32， ∴sin α＝1－cos 2α＝1－⎝ ⎛⎭⎪⎫－122＝32，cos β＝1－sin 2β＝1－⎝ ⎛⎭⎪⎫－322＝12， ∴sin(α＋β)＝sin αcos β＋cos αsin β ＝32×12＋⎝ ⎛⎭⎪⎫－12×⎝ ⎛⎭⎪⎫－32＝32. 答案：A3．解析：a ·b ＝2sin 35°cos 5°－2cos 35°sin 5° ＝2sin(35°－5°)＝2sin 30°＝1. 答案：B4．解析：∵cos B ＝1010＞0，B ∈(0，π)，∴B ∈⎝⎛⎭⎪⎫0，π2，∴sin B ＝1－cos 2B ＝1－⎝⎛⎭⎪⎫10102＝31010， ∴sin C ＝sin[π－(A ＋B )]＝sin(A ＋B )＝sin A ·cos B ＋cos A sin B ＝22×⎝⎛⎭⎪⎫1010＋31010＝255.答案：D5．解析：∵cos A ＝35＞0，cos B ＝513＞0，且A ，B ∈(0，π)，∴A ，B ∈⎝⎛⎭⎪⎫0，π2， ∴sin A ＝1－cos 2A ＝1－⎝ ⎛⎭⎪⎫352＝45，sin B ＝1－cos 2B ＝1－⎝ ⎛⎭⎪⎫5132＝1213. ∴cos C ＝cos (180°－A －B )＝－cos(A ＋B ) ＝sin A sin B －cos A cos B ＝45×1213－35×513＝3365.答案：B6．解析：∵sin(α＋30°)＋cos(α＋60°)＝sin αcos 30°＋cos αsin 30°＋cos αcos 60°－sin α·sin 60°＝32sin α＋12cos α＋12cos α－32sin α＝cos α， ∴原式＝cos α2cos α＝12.答案：127．解析：y ＝cos x ＋cos ⎝ ⎛⎭⎪⎫x ＋π3＝cos x ＋12cos x －32sin x ＝3⎝ ⎛⎭⎪⎫32cos x －12sin x ＝3sin ⎝⎛⎭⎪⎫π3－x ，故函数的最大值是 3.答案： 38．解析：由cos α＝15，α∈⎝ ⎛⎭⎪⎫0，π2，得sin α＝265.所以cos ⎝ ⎛⎭⎪⎫α＋π3＝cos αcos π3－sin αsin π3 ＝15×12－265×32＝1－6210. 答案：1－62109．解：(1)原式＝sin x cos π3＋cos x sin π3＋2sin x cos π3－2cos x sin π3－3cos 2π3cosx －3sin2π3sin x ＝⎝ ⎛⎭⎪⎫cos π3＋2cos π3－3sin 2π3sin x ＋⎝ ⎛⎭⎪⎫sin π3－2sin π3－3cos 2π3cos x＝⎝ ⎛⎭⎪⎫12＋1－3×32sin x ＋⎝ ⎛⎭⎪⎫32－3＋32cos x＝0.(2)原式＝sin[(α＋β)＋α]－2cos(α＋β)sin αsin α＝sin(α＋β)cos α－cos(α＋β)sin αsin α＝sin[(α＋β)－α]sin α＝解：(1)由已知，可得cos α＝35，sin α＝45.所以cos ⎝ ⎛⎭⎪⎫α－π6＝cos αcos π6＋sin αsin π6＝35×32＋45×12＝33＋410.(2)f (α)＝OP OQ ⋅＝⎝ ⎛⎭⎪⎫cos π6，sin π6·(cos α，sin α)＝32cos α＋12sin α＝sin ⎝⎛⎭⎪⎫α＋π3.因为α∈[0，π)，所以α＋π3∈⎣⎢⎡⎭⎪⎫π3，4π3，所以－32＜sin ⎝⎛⎭⎪⎫α＋π3≤1，故f (α)的值域是⎝ ⎛⎦⎥⎤－32，1.。

3.2 两角和与差的三角函数自我小测1．若tan α＝2，tan β＝3，且α，β∈⎝⎛⎭⎪⎫0，π2，则α＋β的值为( ) A ．π6 B ．π4 C ．3π4 D ．5π42．设A ，B ，C 是△ABC 的三个内角，且tan A ，tan B 是方程3x 2－5x ＋1＝0的两个实数根，则△ABC 是( )A ．等边三角形B ．等腰直角三角形C ．锐角三角形D ．钝角三角形3．若tan α＝3，tan β＝43，则tan(α＋β)＝( ) A ．－3 B ．3C ．－139D ．1394．tan 20°＋tan 40°＋3tan 20°tan 40°的值为( )A ．－ 3B ． 3C ．3D ．33 5．若tan 28°tan 32°＝m ，则tan 28°＋tan 32°的值为( ) A ．3m B ．3(1－m ) C ．3(m －1) D ．3(m ＋1)6．已知tan ⎝ ⎛⎭⎪⎫π4＋α＝2，则12sin αcos α＋cos 2α＝__________. 7．若A ＝15°，B ＝30°，则(1＋tan A )(1＋tan B )的值为__________．8．已知sin α＝35⎝ ⎛⎭⎪⎫π2<α<π，tan(π－β)＝12，则tan(α－β)＝__________. 9．已知tan α＝12，tan β＝13，0＜α＜π2，π＜β＜3π2，求α＋β 的值． 10．已知tan α＝－13，cos β＝55，α，β∈(0，π)． (1)求tan(α＋β)的值；(2)求函数f (x )＝2sin(x －α)＋cos(x ＋β)的最大值．参考答案1．解析：∵tan(α＋β)＝tan α＋tan β1－tan αtan β＝2＋31－2×3＝－1，0＜α＋β＜π， ∴α＋β＝3π4. 答案：C2．解析：由题意知，tan A ＋tan B ＝53，tan A tan B ＝13. ∴tan C ＝tan[π－(A ＋B )]＝－tan(A ＋B )＝－tan A ＋tan B 1－tan A tan B ＝－531－13＝－52＜0. ∴π2＜C ＜π. ∴△ABC 为钝角三角形．答案：D3．解析：tan(α＋β)＝tan α＋tan β1－tan αtan β＝3＋431－3×43＝－139. 答案：C4．解析：原式＝tan 60°(1－tan 20°tan 40°)＋3tan 20°tan 40°＝tan 60°＝ 3.答案：B5．解析：∵tan(28°＋32°)＝tan 28°＋tan 32°1－tan 28°tan 32°， ∴tan 28°＋tan 32°＝tan 60°(1－tan 28°tan 32°) ＝3(1－m )．答案：B6．解析：由tan ⎝ ⎛⎭⎪⎫π4＋α＝2，得1＋tan α1－tan α＝2， ∴tan α＝13. ∴12sin αcos α＋cos 2α＝sin 2α＋cos 2α2sin αcos α＋cos 2α＝tan 2α＋12tan α＋1＝19＋123＋1＝23.答案：237．解析：∵tan(A ＋B )＝tan 45°＝1，∴tan A ＋tan B 1－tan A tan B＝1. ∴tan A ＋tan B ＝1－tan A tan B .∴(1＋tan A )(1＋tan B )＝1＋tan A ＋tan B ＋tan A tan B ＝2.答案：28．解析：∵sin α＝35，且π2＜α＜π， ∴cos α＝－1－sin 2α＝－45.∴tan α＝sin αcos α＝－34. 又∵tan(π－β)＝－tan β＝12，∴tan β＝－12. ∴ta n(α－β)＝tan α－tan β1＋tan αtan β＝－34＋121＋⎝ ⎛⎭⎪⎫－34×⎝ ⎛⎭⎪⎫－12 ＝－211. 答案：－2119．解：∵tan α＝12，tan β＝13， ∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝12＋131－12×13＝1. ∵0＜α＜π2，π＜β＜3π2， ∴π＜α＋β＜2π.∴α＋β＝5π4. 10．解：(1)∵cos β＝55，β∈(0，π)， ∴sin β＝255， ∴tan β＝2，∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝－13＋21－⎝ ⎛⎭⎪⎫－13×2＝1.(2)∵tan α＝－13，α∈(0，π)， ∴sin α＝1010，cos α＝－31010， ∴f (x )＝2(sin x cos α－cos x sin α)＋(cos x cos β－sin x sin β)＝－355sin x －55cos x ＋55cos x －255sin x ＝－5sin x . 又∵－1≤sin x ≤1，∴f (x )的最大值为 5.。

3.2 两角和与差的三角函数自我小测1．sin 12°cos 48°＋cos 12°sin 48°的值是( ) A ．12 B ．22 C ．32 D ．－322．若cos α＝－12，sin β＝－32，α∈⎝ ⎛⎭⎪⎫π2，π，β∈⎝ ⎛⎭⎪⎫3π2，2π，则sin(α＋β)的值是( )A ．32 B ．－32C ．－1D ．0 3．已知a ＝(2sin 35°，2cos 35°)，b ＝(cos 5°，－sin 5°)，则a ·b ＝( ) A ．12 B ．1 C ．2 D ．2sin 40° 4．在△ABC 中，A ＝π4，cos B ＝1010，则sin C ＝( )A ．－55 B ．55 C ．－255 D ．2555．在△ABC 中，cos A ＝35，且cos B ＝513，则cos C 等于( )A ．－3365B ．3365C ．－6365D ．63656．化简sin(α＋30°)＋cos(α＋60°)2cos α＝__________.7．函数y ＝cos x ＋cos ⎝⎛⎭⎪⎫x ＋π3的最大值是__________．8．若cos α＝15，α∈⎝ ⎛⎭⎪⎫0，π2，则cos ⎝ ⎛⎭⎪⎫α＋π3＝______. 9．化简下列各式：(1)sin ⎝ ⎛⎭⎪⎫x ＋π3＋2sin ⎝ ⎛⎭⎪⎫x －π3－3cos ⎝ ⎛⎭⎪⎫2π3－x ；(2)sin(2α＋β)sin α－2cos(α＋β)．10．如图，设A 是单位圆和x 轴正半轴的交点，P ，Q 是单位圆上的两点，O 是坐标原点，且∠AOP ＝π6，∠AOQ＝α，α∈[0，π)．(1)若点Q 的坐标是⎝ ⎛⎭⎪⎫35，45，求cos ⎝ ⎛⎭⎪⎫α－π6的值； (2)设函数f (α)＝OP OQ ⋅，求f (α)的值域．参考答案1．解析：原式＝sin(12°＋48°)＝sin 60°＝32. 答案：C2．解析：∵α∈⎝ ⎛⎭⎪⎫π2，π，β∈⎝ ⎛⎭⎪⎫3π2，2π，cos α＝－12，sin β＝－32， ∴sin α＝1－cos 2α＝1－⎝ ⎛⎭⎪⎫－122＝32，cos β＝1－sin 2β＝1－⎝ ⎛⎭⎪⎫－322＝12， ∴sin(α＋β)＝sin αcos β＋cos αsin β ＝32×12＋⎝ ⎛⎭⎪⎫－12×⎝ ⎛⎭⎪⎫－32＝32. 答案：A3．解析：a ·b ＝2sin 35°cos 5°－2cos 35°sin 5° ＝2sin(35°－5°)＝2sin 30°＝1. 答案：B4．解析：∵cos B ＝1010＞0，B ∈(0，π)，∴B ∈⎝⎛⎭⎪⎫0，π2，∴sin B ＝1－cos 2B ＝1－⎝⎛⎭⎪⎫10102＝31010， ∴sin C ＝sin[π－(A ＋B )]＝sin(A ＋B )＝sin A ·cos B ＋cos A sin B ＝22×⎝ ⎛⎭⎪⎫1010＋31010＝255. 答案：D5．解析：∵cos A ＝35＞0，cos B ＝513＞0，且A ，B ∈(0，π)，∴A ，B ∈⎝⎛⎭⎪⎫0，π2， ∴sin A ＝1－cos 2A ＝1－⎝ ⎛⎭⎪⎫352＝45，sin B ＝1－cos 2B ＝1－⎝ ⎛⎭⎪⎫5132＝1213. ∴cos C ＝cos (180°－A －B )＝－cos(A ＋B ) ＝sin A sin B －cos A cos B ＝45×1213－35×513＝3365.答案：B6．解析：∵sin(α＋30°)＋cos(α＋60°)＝sin αcos 30°＋cos αsin 30°＋cos αcos 60°－sin α·sin 60°＝32sin α＋12cos α＋12cos α－32sin α＝cos α，∴原式＝cos α2cos α＝12.答案：127．解析：y ＝cos x ＋cos ⎝ ⎛⎭⎪⎫x ＋π3＝cos x ＋12cos x －32sin x ＝3⎝ ⎛⎭⎪⎫32cos x －12sin x ＝3sin ⎝ ⎛⎭⎪⎫π3－x ，故函数的最大值是 3.答案： 38．解析：由cos α＝15，α∈⎝ ⎛⎭⎪⎫0，π2，得sin α＝265.所以cos ⎝ ⎛⎭⎪⎫α＋π3＝cos αcos π3－sin αsin π3＝15×12－265×32＝1－6210. 答案：1－62109．解：(1)原式＝sin x cosπ3＋cos x sin π3＋2sin x cos π3－2cos x sin π3－3cos 2π3cos x －3sin 2π3sin x ＝⎝ ⎛⎭⎪⎫cos π3＋2cos π3－3sin 2π3sin x ＋⎝ ⎛⎭⎪⎫sin π3－2sin π3－3cos 2π3cos x＝⎝ ⎛⎭⎪⎫12＋1－3×32sin x ＋⎝ ⎛⎭⎪⎫32－3＋32cos x＝0.(2)原式＝sin[(α＋β)＋α]－2cos(α＋β)sin αsin α＝sin(α＋β)cos α－cos(α＋β)sin αsin α＝sin[(α＋β)－α]sin α＝解：(1)由已知，可得cos α＝35，sin α＝45.所以cos ⎝⎛⎭⎪⎫α－π6＝cos αcos π6＋sin αsin π6＝35×32＋45×12＝33＋410.(2)f (α)＝OP OQ ⋅＝⎝ ⎛⎭⎪⎫cos π6，sin π6·(cos α，sin α)＝32cos α＋12sin α＝sin ⎝ ⎛⎭⎪⎫α＋π3.因为α∈[0，π)，所以α＋π3∈⎣⎢⎡⎭⎪⎫π3，4π3，所以－32＜sin ⎝⎛⎭⎪⎫α＋π3≤1，。