八年级数学下册第19章四边形19.1多边形内角和练习新版沪科版

(完整版)2019年春八年级数学下册第19章四边形19.1多边形内角和练习新版沪科版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)2019年春八年级数学下册第19章四边形19.1多边形内角和练习新版沪科版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)2019年春八年级数学下册第19章四边形19.1多边形内角和练习新版沪科版的全部内容。

课时作业(十九）[19。

1 多边形内角和]一、选择题1．八边形的内角和为（)A．180° B．360° C．1080° D．1440°2．正十边形的每个外角都等于（)A．18° B．36° C．45° D．60°3．2018·乌鲁木齐一个多边形的内角和是720°,这个多边形的边数是（）A．4 B．5 C．6 D．74．从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点．若把这个n边形分割成6个三角形，则n的值是( ）A．6 B．7 C．8 D．95．设四边形的内角和等于a，五边形的外角和等于b，则a与b的关系是( )A．a>b B．a＝bC．a<b D．b＝a＋180°6．若一个多边形有9条对角线，则这个多边形的边数是错误!( ）A．6 B．7 C．8 D．97．2018·济宁如图K－19－1，在五边形ABCDE中，∠A＋∠B＋∠E＝300°,DP,CP分别平分∠EDC，∠BCD，则∠P的度数为（）A．50° B．55° C．60° D．65°K－19－1K－19－28．如图K－19－2所示，小华从A点出发，沿直线前进10米后左转24°，再沿直线前进10米,又向左转24°……照这样走下去，她第一次回到出发地A点时，一共走的路程是( ) A．140米 B．150米C．160米 D．240米9．一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为( )A．7 B．7或8C．8或9 D．7或8或9二、填空题10．五边形的内角和是________．错误!11．2018·怀化一个多边形的每一个外角都是36°，则这个多边形的边数是________．12．学校门口的电动伸缩门能伸缩的几何原理是四边形具有________．13．若一个多边形的内角和是外角和的3倍,则这个多边形的边数是________．14．若n边形的内角和为1260°，则从一个顶点出发引出对角线的条数是________．错误!15．如图K－19－3,∠1是五边形ABCDE的一个外角．若∠1＝60°,则∠A＋∠B＋∠C＋∠D的度数为________．K－19－3K－19－416．如图K－19－4，在四边形ABCD中，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN.若MF∥AD，FN∥DC，则∠B＝________°.三、解答题17．在四边形ABCD中，∠D＝60°，∠B比∠A大20°，∠C是∠A的2倍,求∠A,∠B，∠C的度数．18．如果一个正多边形的每个内角都比它相邻的外角的4倍多30°，求这个正多边形的内角和及对角线的总条数。

19.1 多边形内角和一．选择题1．若一个多边形截去一个角后，变成十四边形，则原来的多边形的边数可能为（）A．14或15B．13或14C．13或14或15D．14或15或16 2．把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（）A．六边形B．五边形C．四边形D．三角形3．下列图形为正多边形的是（）A．B．C．D．4．从六边形的一个顶点出发，可以画出m条对角线，它们将六边形分成n个三角形．则m、n的值分别为（）A．4，3B．3，3C．3，4D．4，45．从n边形一个顶点出发，可以作（）条对角线．A．n B．n﹣1C．n﹣2D．n﹣36．从一个多边形的任何一个顶点出发都只有5条对角线，则它的边数是（）A．6B．7C．8D．97．过多边形的一个顶点的所有对角线把多边形分成8个三角形，这个多边形的边数是（）A．8B．9C．10D．118．如图，正四边形有2条对角线，正五边形有5条对角线，正六边形有9条对角线，则正十边形有（）条对角线．A．27B．35C．40D．449．已知一个多边形的内角和是900°，则这个多边形是（）A．五边形B．六边形C．七边形D．八边形10．一个多边形的内角和是外角和的2倍，这个多边形是（）A．四边形B．五边形C．六边形D．八边形二．填空题11．若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．12．一个多边形的内角和是外角和的2倍，则这个多边形的边数为．13．如图，五边形ABCDE是正五边形．若l1∥l2，则∠1﹣∠2＝°．14．如图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1+∠2+∠3+∠4+∠5＝．15．如图所示，已知O是四边形ABCD内一点，OB＝OC＝OD，∠BCD＝∠BAD＝75°，则∠ADO+∠ABO＝度．16．如图，四边形ABCD中，∠A＝100°，∠C＝70°．将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，则∠B＝度．三．解答题17．乐乐和数学小组的同学们研究多边形对角线的相关问题，邀请你也加入其中！请仔细观察下面的图形和表格，并回答下列问题：多边形的顶45678……n点数12345……①从一个顶点出发的对角线的条数多边形对角2591420……②线的总条数（1）观察探究请自己观察上面的图形和表格，并用含n的代数式将上面的表格填写完整，其中①；②；（2）实际应用数学社团共分为6个小组，每组有3名同学．同学们约定，大年初一时不同组的两位同学之间要打一个电话拜年，请问，按照此约定，数学社团的同学们一共将拨打电话多少个？（3）类比归纳乐乐认为（1）、（2）之间存在某种联系，你能找到这两个问题之间的联系吗？请用语言描述你的发现．18．“转化”是数学中的一种重要思想，即把陌生的问题转化成熟悉的问题，把复杂的问题转化成简单的问题，把抽象的问题转化为具体的问题．（1）请你根据已经学过的知识求出下面星形图（1）中∠A+∠B+∠C+∠D+∠E的度数；（2）若对图（1）中星形截去一个角，如图（2），请你求出∠A+∠B+∠C+∠D+∠E+∠F 的度数；（3）若再对图（2）中的角进一步截去，你能由题（2）中所得的方法或规律，猜想图3中的∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N的度数吗？只要写出结论，不需要写出解题过程）19．已知n边形的内角和θ＝（n﹣2）×180°．（1）甲同学说，θ能取360°；而乙同学说，θ也能取630°．甲、乙的说法对吗？若对，求出边数n．若不对，说明理由；（2）若n边形变为（n+x）边形，发现内角和增加了360°，用列方程的方法确定x．20．动手操作，探究：探究一：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图（1），在△ADC中，DP、CP分别平分∠ADC和∠ACD，试探究∠P与∠A 的数量关系．探究二：若将△ADC改为任意四边形ABCD呢？已知：如图（2），在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．（写出说理过程）探究三：若将上题中的四边形ABCD改为六边形ABCDEF（图（3））呢？请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：．参考答案一．选择题1．C．2．A．3．D．4．C．5．D．6．C．7．C．8．B．9．C．10．C．二．填空题11．八．12．6．13．72．14．360°．15．135．16．95．三．解答题17．解：（1）由题可得，当多边形的顶点数为n时，从一个顶点出发的对角线的条数为n﹣3，多边形对角线的总条数为n（n﹣3）；故答案为：n﹣3，n（n﹣3）；（2）∵3×6＝18，∴数学社团的同学们一共将拨打电话为×18×（18﹣3）＝135（个）；（3）每个同学相当于多边形的一个顶点，则共有n个顶点；每人要给不同组的同学打一个电话，则每人要打（n﹣3）个电话；两人之间不需要重复拨打电话，故拨打电话的总数为n（n﹣3）；数学社团有18名同学，当n＝18时，×18×（18﹣3）＝135．18．解：（1）∵∠1＝∠2+∠D＝∠B+∠E+∠D，∠1+∠A+∠C＝180°，∴∠A+∠B+∠C+∠D+∠E＝180°；（2）∵∠1＝∠2+∠F＝∠B+∠E+∠F，∠1+∠A+∠C+∠D＝360°，∴∠A+∠B+∠C+∠D+∠E+∠F＝360°；（3）根据图中可得出规律∠A+∠B+∠C+∠D+∠E＝180°，每截去一个角则会增加180度，所以当截去5个角时增加了180×5度，则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N＝180°×5+180°＝1080°．19．解：（1）∵360°÷180°＝2，630°÷180°＝3…90°，∴甲的说法对，乙的说法不对，360°÷180°+2＝2+2＝4．答：甲同学说的边数n是4；（2）依题意有（n+x﹣2）×180°﹣（n﹣2）×180°＝360°，解得x＝2．故x的值是2．20．解：探究一：∵DP、CP分别平分∠ADC和∠ACD，∴∠PDC＝∠ADC，∠PCD＝∠ACD，∴∠DPC＝180°﹣∠PDC﹣∠PCD，＝180°﹣∠ADC﹣∠ACD，＝180°﹣（∠ADC+∠ACD），＝180°﹣（180°﹣∠A），＝90°+∠A；探究二：∵DP、CP分别平分∠ADC和∠BCD，∴∠PDC＝∠ADC，∠PCD＝∠BCD，∴∠DPC＝180°﹣∠PDC﹣∠PCD，＝180°﹣∠ADC﹣∠BCD，＝180°﹣（∠ADC+∠BCD），＝180°﹣（360°﹣∠A﹣∠B），＝（∠A+∠B）；探究三：六边形ABCDEF的内角和为：（6﹣2）•180°＝720°，∵DP、CP分别平分∠EDC和∠BCD，∴∠PDC＝∠EDC，∠PCD＝∠BCD，∴∠P＝180°﹣∠PDC﹣∠PCD，＝180°﹣∠EDC﹣∠BCD，＝180°﹣（∠EDC+∠ACD），＝180°﹣（720°﹣∠A﹣∠B﹣∠E﹣∠F），＝（∠A+∠B+∠E+∠F）﹣180°，即∠P＝（∠A+∠B+∠E+∠F）﹣180°．。

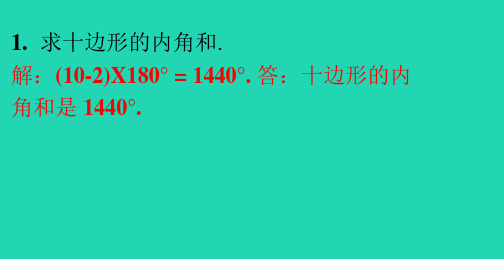
1.求十边形的内角和.解：(10-2)X180° = 1440°. 答：十边形的内角和是1440°.2.求正五边形的每一个外角的度数. 解：360。

+ 5 = 72。

・答：正五边形的每一个外角的度数是72。

.3.一个多边形，每一个外角都等于45。

，这个多边形是几边形，它的内角和是多少? 解：多边形的边数是360+45 = 8,其内角和是(8-2)X180° = 1080°.答：这个多边形是八边形，它的内角和为1080。

.4.一个多边形的内角和等于它的外角和，求这个多边形的边数.解：设这个多边形的边数为〃.由题意得：(〃—2)X180。

= 360。

, 解得〃=4.答：这个多边形的边数是4.5.(1)过四边形的一个顶点有条对角线，四边形共有2条对角线：(2)过五边形的一个顶点有卷条对角线，五边形共有5条对角线；(3)过〃边形的一个顶点有(〃 - 3)条对角线,〃(〃■ 3)n边形共有；条对角线・6.假设一个多边形的边数与对角线的条数相等, 求这个多边形的边数.解：设多边形有〃条边，那么依题意得〃次〃I）,2解得〃i = 0 （不合题意，舍去），n2 = 5. 答：这个多边形的边数为5.7.如果一个〃边形的边数增加1,那么它的内角和增加多少度？如果〃边形的边数增加到原来的2倍，那么它的内角和增加多少度？解：[(〃 + 1)- 2]>180°— (〃— 2)*180° = 180°.(2n— 2)*180°— (〃— 2)*180° = n*180°. 答：一个〃边形的边数增加1,那么它的内角和增加180°；如果n边形的边数增加到原来的2倍, 那么它的内角和增加^180°.。

19.1 多边形内角和练习1 .下列角度中，是多边形内角和的只有 （）.A . 6B . 7C . 84.如图，/ A +Z B+Z C +Z D +Z E +Z F +Z G+Z H=■r.5. 小华从A 点出发向前直走50 m 向左转18，继续向前走 50 m 再左转18°,他以同样走6 .一个多边形每一个外角都等于 40°,则这个多边形的边数是7 •如图所示，分别以 n 边形的顶点为圆心，以 1个单位为半径画圆，则图中阴影部分的面积之8•已知一个多边形的 每个内角都为钝角，则这样的多边形有多少个？边数最少的一个是几边 形？ 9.已知：四边形 ABCD 中, Z ABC= 70°,Z C= 90°, BC= CD AB= AD 求Z A 的度数.D法回到A 点时，共走了m. A . 270° B . 56 0° C . 630° D . 1 440°2 •多边形的每一个内角都等于 150°,则从此多边形一个顶点出发引出的对角线有 （）.A . 7 条B . 8 条C .9条D . 10条3 .若一个多边形的内角和为1 080。

，则这个多边形的边数为（）.和为 个平方单位.10 .如图，求/ 冊/ B+Z C+Z D+Z E+Z F的度数.参考答案1. 答案：D点拨：要判断四个选项中哪个是多边形的内角和，我们需要知道多边形内角和的特点•由多边形的内角和公式(n—2) • 180°可知，多边形的内角和是180°的倍数，观察验算四个选项知选D.2. 答案：C点拨：由每一内角都等于150°得每一外角为30°,得边数为360=12.而从n30边形的一个顶点可以引(n—3)条对角线，即可引出12— 3 = 9条对角线.3. 答案：C4. 答案:360° 点拨：把多个角的和转化为一个多边形的内角和或外角和.•••/ 1 = Z A^Z B,Z2 =Z C+Z D, Z 3=Z E+Z F,Z 4=Z G^Z H,又T Z 1 + Z 2+Z 3+Z 4= 360°,•••Z A+Z B+Z C+Z D+Z E+Z F+Z G+Z H= 360°.5. 答案：1 000点拨：转回原方向转过的角度和为360°,即多边形外角和为360°,所以边数为20,小华共走了20 X 50= 1 000(m).6. 答案：97. 答案：n 点拨：阴影部分的角是n边形的外角，其和为360°,故所有的阴影组成一个圆，其面积为n 个平方单位.8. 解：设多边形的边数为n,则每一个内角为(n —2) 180 .由题意，得n(n—2) 18090 < < 180 .n• n>4. •内角都为钝角的多边形有无数个.T n>4,• n的最小值为5,即边数最少的一个是五边形.点拨：根据内角和表示出一个内角，确定它的范围是大于90°且小于180°,从而求出边数n的范围.9. 解：方法一：如图1,连接BD •/ Rt△ BCD中, Z C= 90°, BC= CD •Z DB(= 45°.又T Z ABC= 70°,•Z AB=Z ABC-Z DBC= 70°—45°= 25°.•••△ABD中, AB= AD A Z ABD-Z ADB= 25°,「・Z A= 180°—Z AB亠ADB= 130° .(三角形内角和为180°)方法二：如图2,连接AC 在厶 ABCm ADC 中,•/ AB= AD BC= CD AC= AC •••△ ABC^A ADC SSS),•••/ ABC=/ ADC= 70°.•••/ BAD= 360°—/ B-Z D-Z BCD= 360°— 70°点拨：当题目中有线段长度时，一般利用勾股定理的逆定理判定某三角形是否为直角三角形.四边形问题通常转化为三角形问题来解决，在构造三角形时必须同已知条件结合起来，不要随意连 线.本题认真分析条件，很容易想到构造等腰三角形或全等三角形.10.解：如图，连接 BE 在四边形 ABEF 中,/ A +Z ABEF / BEFF / F = 360°.¥ ----- //\ D 匚•••/ 1 + Z 2=Z C +Z D,• Z A +Z AB(+Z C +Z D+Z DEF +Z F =Z A +Z AB(+Z 1 + Z 2+Z DEF +Z F=360°点拨：此题的关键是将不规则图形中的角转移到常见图形中，把多个角的和转化为一个多边形 的内角和或外角和.*rlBCri—70°- 90°= 130°。

19.1 多边形内角和练习基础巩固1．下列角度中，是多边形内角和的只有（）．A．270° B．560° C．630° D．1 440°2．多边形的每一个内角都等于150°，则从此多边形一个顶点出发引出的对角线有（）．A．7条 B．8条 C．9条 D．10条3．若一个多边形的内角和为1 080°,则这个多边形的边数为（）．A．6 B．7 C．8 D．94．如图,∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＝__________。

5．小华从A点出发向前直走50 m，向左转18°,继续向前走50 m，再左转18°,他以同样走法回到A点时，共走了__________m.6．一个多边形每一个外角都等于40°,则这个多边形的边数是__________．7．如图所示,分别以n边形的顶点为圆心，以1个单位为半径画圆，则图中阴影部分的面积之和为__________个平方单位．8．已知一个多边形的每个内角都为钝角，则这样的多边形有多少个？边数最少的一个是几边形？9．已知：四边形ABCD中，∠ABC＝70°，∠C＝90°,BC＝CD，AB＝AD。

求∠A的度数．10．如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．参考答案1。

答案：D 点拨:要判断四个选项中哪个是多边形的内角和,我们需要知道多边形内角和的特点．由多边形的内角和公式（n －2）·180°可知，多边形的内角和是180°的倍数，观察验算四个选项知选D 。

2。

答案:C 点拨：由每一内角都等于150°得每一外角为30°,得边数为3601230︒︒＝.而从n 边形的一个顶点可以引（n －3)条对角线，即可引出12－3＝9条对角线．3. 答案：C4。

答案：360° 点拨：把多个角的和转化为一个多边形的内角和或外角和．∵∠1＝∠A ＋∠B ,∠2＝∠C ＋∠D ,∠3＝∠E ＋∠F ，∠4＝∠G ＋∠H ，又∵∠1＋∠2＋∠3＋∠4＝360°，∴∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＋∠H ＝360°。

第19章四边形19.1 多边形内角和一、选择题1．如果一个多边形的每一个内角都是108°，那么这个多边形是( )A．四边形B．五边形C．六边形D．七边形2．已知一个多边形的内角和是540°，则这个多边形是( )A．四边形B．五边形C．六边形D．七边形3．如果一个多边形的边数增加1倍，它的内角和是2160°，那么原来的多边形的边数是( )A．5 B．6 C．7 D．84．一个多边形最少可分割成五个三角形，则它是________边形（）A．8 B．7 C．6 D．55．一个多边形的外角和是内角和的一半，则它的边数为（）A．7 B．6 C．5 D．46．一个多边形的内角和与外角和共为540°，则它的边数为（）A．5 B．4 C．3 D．不确定7．若等角n边形的一个外角不大于40°，则n的值为（）A．n＝8 B．n＝9 C．n＞9 D．n≥98．中华人民共和国国旗上的五角星，它的五个锐角的度数和是（）A．50°B．100°C．180°D．200°9．用三块正多边形的木板铺地，拼在一起并相交于一点的各边完全吻合，其中两块木板的边数都是8，则第三块木板的边数应是（）A．4 B．5 C．6 D．810．如果只用正三角形作平面镶嵌（要求镶嵌的正三角形的边与另一正三角形有边重合），则在它的每一个顶点周围的正三角形的个数为（）A．3 B．4 C．5 D．6二、填空题11．在四边形ABCD中，∠A＝∠D，∠A∶∠B∶∠C＝3∶2∶1，则∠A＝．12．一个多边形的内角和与外角和的比是4：1，它的边数是，顶点的个数是，对角线的条数是．13．若四边形ABCD的相对的两个内角互补，且满足∠A∶∠B∶∠C＝2∶3∶4，则∠A＝________°，∠B＝________°，∠C＝________°，∠D＝________°．14．若一个n边形的内角都相等，且内角的度数与和它相邻的外角的度数比为3∶1，那么，这个多边形的边数为________．15．若一个十边形的每个外角都相等，则它的每个外角的度数为________°，每个内角的度数为________°．16．如果一个多边形的每个内角都等于108°，那么这个多边形是_____边形．17.一个正多边形的内角和为720°，则这个正多边形的每一个内角等于____ ___°．18．若一个多边形的各边都相等，它的周长是63，且它的内角和为900°，则它的边长是_____．19．多边形的内角中，最多有________个直角．20．已知一个多边形的内角和与外角和共2160°，则这个多边形的边数是21．用正三角形和正方形能够铺满地面，每个顶点周围有_____个正三角形和_____个正方形三、解答题22．如图所示，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．23．一个凸多边形的内角的度数从小到大排列起来，恰好依次增加相同的度数，其中最小角是100°，最大角是140°，求这个多边形的边数．24．已知多边形内角和与外角和的和为2160°，求多边形对角线的条数．25．在四边形ABCD中，∠A＝∠C＝90°，∠B与∠D的度数比是3：2，求∠B，∠D 的度数．26．已知和多边形一个内角相邻的外角与其余各内角度数总和为600°，求该多边形的边数．27．过n边形的一个顶点有7条对角线，m边形有m条对角线，p边形没有对角线，q 边形的内角和与外角和相等，求q(n－m)p的值．28．如图所示，已知六边形ABCDEF中，∠A＝∠B=∠C＝∠D＝∠E＝∠F＝120°．试说明AB＋BC=EF＋ED．29．某科技小组制作了一个机器人，它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米?30．我们知道过n边形的一个顶点可以做（n－3）条对角线，这（n－3）条对角线把三角形分割成（n－2）个三角形，想一想这是为什么？如图1．图1如图2，在n边形的边上任意取一点，连结这点与各顶点的线段可以把n边形分成几个三角形？图2想一想，利用这两个图形，怎样证明多边形的内角和定理．********************************************************************。

2019-2020学年度初中八年级下册数学第19章四边形19.1 多边形内角和沪科版习题精选第四篇第1题【单选题】从六边形的一个顶点作对角线，把这个六边形分成三角形的个数是( )A、3个B、4个C、5个D、6 个【答案】：【解析】：第2题【单选题】已知一个多边形的内角和是外角和的2倍，则此多边形的边数为( )A、6B、7C、8D、9【答案】：【解析】：第3题【单选题】如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3=( )A、90°B、180°C、120°D、270°【答案】：【解析】：第4题【单选题】把边长相等的正五边形ABCDE和正方形ABFG，按照如图所示的方式叠合在一起，连结AD，则∠DAG=( )A、18°B、20°C、28°D、30°【答案】：【解析】：第5题【单选题】一个多边形的外角和与它的内角和的比为1：3，这个多边形的边数是( )A、9B、8C、7D、6【答案】：【解析】：第6题【单选题】如果一个多边形的内角和等于720°，那么这个多边形是( )．A、四边形B、五边形C、六边形D、七边形【答案】：【解析】：第7题【单选题】过一个正多边形的某个顶点的所有对角线，将这个正多边形分成了4个三角形，则这个正多边形的每一个内角的度数是( )A、120°B、90°C、60°D、30°【答案】：【解析】：第8题【填空题】如图，以五边形的每个顶点为圆心，以1为半径画圆,求圆与五边形重合（即阴影部分）的面积为______【答案】：【解析】：第9题【填空题】已知正n边形的一个内角为135°，则边数n的值是?______【答案】：【解析】：第10题【填空题】如图，在四边形ABCD中，∠α，∠β分别是∠BAD、∠BCD相邻的补角，且∠B＋∠CDA＝140°，则∠α＋∠β等于______．【答案】：【解析】：第11题【填空题】已知任意三角形的内角和为180°，试利用多边形中过某一点的对角线条数，寻求多边形内角和的公式．根据上图所示，一个四边形可以分成2个三角形；于是四边形的内角和为360度；一个五边形可以分成3个三角形，于是五边形的内角和为540度，…，按此规律n边形的内角和为______度．【答案】：【解析】：第12题【填空题】已知多边形的每个内角都等于135°，求这个多边形的边数是______．（用两种方法解决问题）A、9【答案】：【解析】：第13题【解答题】已知一个四边形的第二个内角是第一个内角的3倍，第三个内角是第二个内角的一半，第四个内角比第三个内角大10^°．求它的第一个内角．【答案】：【解析】：第14题【解答题】一个凸多边形共有20条对角线，它是几边形？是否存在有15条对角线的多边形？如果存在，它是几边形？如果不存在，说明得出结论的过程．【答案】：【解析】：第15题【解答题】一个多边形的外角和是内角和的有误，求这个多边形的边数．【答案】：【解析】：。

19.1 多边形内角和练习1．下列角度中，是多边形内角和的只有( )．A．270° B．560° C．630° D．1 440°2．多边形的每一个内角都等于150°，则从此多边形一个顶点出发引出的对角线有( )．A．7条 B．8条 C．9条 D．10条3．若一个多边形的内角和为1 080°，则这个多边形的边数为( )．A．6 B．7 C．8 D．94．如图，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＋∠G＋∠H＝__________.5．小华从A点出发向前直走50 m，向左转18°，继续向前走50 m，再左转18°，他以同样走法回到A点时，共走了__________m.6．一个多边形每一个外角都等于40°，则这个多边形的边数是__________．7．如图所示，分别以n边形的顶点为圆心，以1个单位为半径画圆，则图中阴影部分的面积之和为__________个平方单位．8．已知一个多边形的每个内角都为钝角，则这样的多边形有多少个？边数最少的一个是几边形？9．已知：四边形ABCD中，∠ABC＝70°，∠C＝90°，BC＝CD，AB＝AD.求∠A的度数．10．如图，求∠A＋∠B＋∠C＋∠D＋∠E＋∠F的度数．参考答案1. 答案：D 点拨：要判断四个选项中哪个是多边形的内角和，我们需要知道多边形内角和的特点．由多边形的内角和公式(n －2)·180°可知，多边形的内角和是180°的倍数，观察验算四个选项知选D.2. 答案：C 点拨：由每一内角都等于150°得每一外角为30°，得边数为3601230︒︒＝.而从n 边形的一个顶点可以引(n －3)条对角线，即可引出12－3＝9条对角线．3. 答案：C4. 答案：360° 点拨：把多个角的和转化为一个多边形的内角和或外角和．∵∠1＝∠A ＋∠B ，∠2＝∠C ＋∠D ，∠3＝∠E ＋∠F ，∠4＝∠G ＋∠H ，又∵∠1＋∠2＋∠3＋∠4＝360°，∴∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＋∠H ＝360°.5. 答案：1 000 点拨：转回原方向转过的角度和为360°，即多边形外角和为360°，所以边数为20，小华共走了20×50＝1 000(m)．6. 答案：97. 答案：π 点拨：阴影部分的角是n 边形的外角，其和为360°，故所有的阴影组成一个圆，其面积为π个平方单位．8. 解：设多边形的边数为n ，则每一个内角为(2)180n n⋅︒－.由题意，得(2)18090<<180n n⋅︒︒︒－. ∴n ＞4.∴内角都为钝角的多边形有无数个．∵n ＞4，∴n 的最小值为5，即边数最少的一个是五边形．点拨：根据内角和表示出一个内角，确定它的范围是大于90°且小于180°，从而求出边数n 的范围．9. 解：方法一：如图1，连接BD .∵Rt△BCD 中，∠C ＝90°，BC ＝CD ，∴∠DBC ＝45°. 又∵∠ABC ＝70°，∴∠ABD ＝∠ABC －∠DBC ＝70°－45°＝25°.∵△ABD 中，AB ＝AD ，∴∠ABD ＝∠ADB ＝25°，∴∠A ＝180°－∠ABD －ADB ＝130°.(三角形内角和为180°)方法二：如图2，连接AC.在△ABC和△ADC中，∵AB＝AD，BC＝CD，AC＝AC，∴△ABC≌△ADC(SSS)，∴∠ABC＝∠ADC＝70°.∴∠BAD＝360°－∠B－∠D－∠BCD＝360°－70°－70°－90°＝130°.点拨：当题目中有线段长度时，一般利用勾股定理的逆定理判定某三角形是否为直角三角形．四边形问题通常转化为三角形问题来解决，在构造三角形时必须同已知条件结合起来，不要随意连线．本题认真分析条件，很容易想到构造等腰三角形或全等三角形．10.解：如图，连接BE，在四边形ABEF中，∠A＋∠ABE＋∠BEF＋∠F＝360°.∵∠1＋∠2＝∠C＋∠D，∴∠A＋∠ABC＋∠C＋∠D＋∠DEF＋∠F＝∠A＋∠ABC＋∠1＋∠2＋∠DEF＋∠F＝360°.点拨：此题的关键是将不规则图形中的角转移到常见图形中，把多个角的和转化为一个多边形的内角和或外角和．本文档仅供文库使用。

最新精选初中数学八年级下册第19章四边形19.1 多边形内角和沪科版课后练习第五十篇第1题【单选题】下列说法中正确的是( )A、两条对角线垂直的四边形的菱形B、对角线垂直且相等的四边形是正方形C、两条对角线相等的四边形是矩形D、两条对角线相等的平行四边形是矩形【答案】：【解析】：第2题【单选题】一个正多边形的每个外角都是36有误，这个正多边形是( )A、正六边形B、正八边形C、正十边形D、正十二边形【答案】：【解析】：第3题【单选题】如图，在四边形ABCD中，点F，E分别在边AB，BC上，将△BFE沿FE翻折，得△GFE，若GF∥AD，GE∥DC，则∠B的度数为( )?A、95°B、100°C、105°D、110°【答案】：【解析】：第4题【单选题】若从一多边形的一个顶点出发，最多可引10条对角线，则它是( )A、十三边形B、十二边形C、十一边形D、十边形【答案】：【解析】：第5题【单选题】如图，五边形ABCDE中，AB∥CD，∠1，∠2，∠3分别是∠BAE，∠AED，∠EDC的外角，则∠1+∠2+∠3=( )A、90°B、180°C、120°D、270°【答案】：【解析】：第6题【单选题】若一个正多边形的一个外角是45°，则这个正多边形的边数是( )A、10B、9C、8D、6【答案】：【解析】：第7题【单选题】如果一个多边形的内角和等于1260°，那么这个多边形的边数为( )A、7B、8C、9D、10【答案】：【解析】：第8题【单选题】一个多边形有20条对角线，则这个多边形的边数是( )A、6B、7C、8D、9【答案】：【解析】：第9题【单选题】已知四边形ABCD中，∠A与∠B互补，∠D=70°，则∠C的度数为( )A、70°B、90°C、110°D、140°【答案】：【解析】：第10题【填空题】正五边形每个外角的度数是?______．A、72°【答案】：【解析】：第11题【填空题】一个多边形截去一个角后，形成另一个多边形的内角和为720°，那么原多边形的边数为______．A、5或6或7【答案】：【解析】：第12题【填空题】若一个多边形的内角和等于720°，则这个多边形是______边形．A、n=6【答案】：【解析】：第13题【填空题】若一个凸n边形的内角和为1080°，则边数n=?______【答案】：【解析】：第14题【解答题】已知从n边形的一个顶点出发共有4条对角线，其周长为56，且各边长是连续的自然数，求这个多边形的各边长．【答案】：【解析】：第15题【综合题】如图所示，一个四边形纸片ABCD，∠D=90°把纸片按如图所示折叠，使点B落在AD上的B′处，AE是折痕．若B′E∥CD，求∠B的度数．在（1）的条件下，如果∠C=128°，求∠EAB的度数．【答案】：【解析】：。

2019-2020学年度沪科版初中数学八年级下册第19章四边形19.1 多边形内角和习题精选七十三第1题【单选题】如果n边形每一个内角等于与它相邻外角的2倍，则n的值是( )A、4B、5C、6D、7【答案】：【解析】：第2题【单选题】如果一个多边形的内角和是720°，那么这个多边形是( )A、四边形B、五边形C、六边形D、七边形【答案】：【解析】：第3题【单选题】已知一个多边形的内角和是外角和的4倍，则这个多边形是( )A、八边形B、十二边形C、十边形D、九边形【答案】：【解析】：第4题【单选题】一个多边形的内角和是720°，则这个多边形的边数为( )A、4B、5C、6D、7【答案】：【解析】：第5题【单选题】如图，一个等边三角形纸片，剪去一个角后得到一个四边形，则图中有误的度数是( )A、180°B、220°C、240°D、300°【答案】：【解析】：第6题【单选题】若一个多边形的内角和与它的外角和相等，则这个多边形是( )A、三角形B、四边形C、五边形D、六边形【答案】：【解析】：第7题【填空题】若正多边形的内角和是1080°，则该正多边形的边数是______．【答案】：【解析】：第8题【填空题】如图，小明在操场上从A点出发，沿直线前进10米后向左转40°，再沿直线前进10米后，又向左转40°，照这样走下去，他第一次回到出发地A点时，一共走了______米．【答案】：【解析】：第9题【填空题】如图所示，正六边形ABCDEF内接于⊙O，则∠ADF的度数为______．A、30°【答案】：【解析】：第10题【填空题】已知一个正多边形的内角是140°，则这个正多边形的边数是______．A、9【答案】：【解析】：第11题【填空题】从一个多边形的某个顶点出发，分别连接这个点和其余各顶点，可以把这个多边形分割成15个三角形，则这个多边形的边数为______．【答案】：【解析】：第12题【解答题】已知一个多边形的边数增加一倍后，内角和增加1980°，求原多边形的边数．【答案】：【解析】：第13题【综合题】如图，四边形ABCD的内角∠BAD、∠CDA的角平分线交于点E，∠ABC、∠BCD的角平分线交于点F．若∠F＝70°，则∠ABC＋∠BCD＝______°；∠E＝______°；探索∠E与∠F有怎样的数量关系，并说明理由；给四边形ABCD添加一个条件，使得∠E＝∠F，所添加的条件为______．【答案】：【解析】：第14题【综合题】如图，已知△BAD和△BCE均为等腰直角三角形，∠BAD=∠BCE=90°，点M为DE的中点，过点E与AD平行的直线交射线AM于点N．当A，B，C三点在同一直线上时（如图1），求证：M为AN的中点；将图1中的△BCE绕点B旋转，当A，B，E三点在同一直线上时（如图2），求证：△ACN为等腰直角三角形；将图1中△BCE绕点B旋转到图3位置时，（2）中的结论是否仍成立？若成立，试证明之，若不成立，请说明理由．【答案】：【解析】：第15题【综合题】动手操作，探究：探究一：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图（1），在△ADC中，DP，CP分别平分∠ADC和∠ACD，试探究∠P与∠A的数量关系．探究二：若将△ADC改为任意四边形ABCD呢？已知：如图（2），在四边形ABCD中，DP，CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A+∠B的数量关系．（写出说理过程）探究三：若将上题中的四边形ABCD改为六边形ABCDEF（图（3））呢？请直接写出∠P与∠A+∠B+∠E+∠F的数量关系：______．【答案】：无【解析】：。