下载文档原格式
六年级微专题复习之一元一次不等式的解法在本单元中，我们将梳理不等式及其基本性质(II)、一元一次不等式及其解得概念(II)、一元一次不等式的解法(III)及数轴表示不等式的解集(III)。
1、不等式的定义用不等号“>”“<”“≥”或“≤”表示的关系式，叫做不等式。
(1)方程与不等式的区别：方程表示的是相等关系，不等式表示的是不等关系.(2)常用的不等号有“>”“<”“≥”“≤”和“≠”五种，在“≥”和“≤”中，只要有一个符号成立，该不等式就成立，如3≥2，2≤2，而“≠”仅表示左、右两边不相等。
1、“不小于”、“不低于”、“不少于”等表示“≥”；2、“不超过”、“不大于”、“不多于”等表示“≤”；3、“非负数”→“≥0”、“非正数”→“≤0”、“正数”→“＞0”、“负数”→“<0”.2、不等式的性质运用不等式的性质进行不等式变形时，要特别注意性质2和性质3的区别，在乘以或除以同一个数时，必须先弄清楚这个数是正数还是负数，如果是负数，不等号要改变方向！不等式的其他性质：(1)反对称性：若a>b，则b<a；(2)传递性：若a>b，b>c，则a>c.1、不等式解得定义在含有未知数的不等式中，能使不等式成立的未知数的值，叫做不等式的解。
(如不等式x<4的解有1、1.5、0.3、-5、-10...等数).2、不等式的解集的定义不等式的解的全体叫做不等式的解集. 一般情况下，一元一次方程的解只有一个，一元一次不等式的解可以有无数个.3、一元一次不等式的定义只含有一个未知数且未知数的次数是一次的不等式叫做一元一次不等式.(如：12+x>2x就是一元一次不等式).4、在数轴上表示不等式的解集用数轴表示不等式的解集时，应注意两点：一是确定“端点”，二是确定方向.若解集包含“端点”，则用实心圆点；若解集不包含“端点”，则用空心圆圈.对于方向，相对于“端点”而言，大于向右画，小于向左画。
第三讲 二元一次方程及方程组一元一次不等式及不等式组。
本讲课程目标知识与技能熟练掌握方程的解法，提高分析问题的能力及解题能力，着重训练实际问题的审题、找相等关系并正确地列出方程的能力。
过程与方法 系统复习初一下册、一元一次方程、二元一次方程组、一元一次不等式及不等式组等三章内容，讲练结合。
情感态度价值观本讲课程的重点1．一元一次方程的解法。
2．二元一次方程组的解法。
3．一元一次不等式及不等式组的解法本讲课程的难点1．应用一元一次方程解决实际问题。
2．二元一次方程组的消元技巧。
3．不等式的性质3的符号变换，不等式组的解集的分类。
教学方法建议精讲多练，讲练结合 选材程度及数量课堂精讲例题 搭配课堂训练题 课后作业 A 类（ ）道（ ）道（ ）道B 类 （ ）道 （ ）道 （ ）道C 类（ ）道（ ）道（ ）道—、回顾上一讲知识一：有理数知识的复习★第一步：要点一知识规律或思维方法、解题方法梳理1．正数、负数、有理数、数轴、相反数、绝对值及倒数的概念。
2．有理数的加减法、乘除法、以及乘方的运算法则及运算律（交换律、结合律、分配律）。
3．科学记数法及近似数，以及有理数混合运算的运算顺序。
★第二步：要点一经典例题讲解1．(－61＋43－125)⨯)12(-； （ 用分配律）2．B.⎥⎦⎤⎢⎣⎡-÷--⨯---3210)2(322)32(31(答案：0 )★第三步：要点一课堂巩固练习1．B.（－1）2009－（43－61－83）×24－（－2）2×3 （答案：-18 ） 2．B.20103)1(|52|)3(2)2(---+-⨯--。
（答案：0 ）二、整式的加减★第一步：要点二知识规律或思维方法、解题方法梳理1．单项式、多项式的概念。
2．整式加减的去括号的方法。
3．合并同类项的方法。
★第二步：要点二经典例题讲解1．B.已知一个多项式与x x 932+的和等于1432-+x x ，则此多项式是 （ B ）A ．1562---x xB ．15--xC ．1562++-x x D ．15+-x2. C. 已知5,4=-=+c b b a ，则代数式222222a b c ab bc +++-= 41 。
六年级数学一元一次不等式组和它的解法；一元一次不等式（组）的应用人教四年制【同步教育信息】一. 本周教学内容1. 一元一次不等式组和它的解法2. 一元一次不等式（组）的应用二. 教学目标和要求1. 知道一元一次不等式组的解集的含义2. 会借助数轴解一元一次不等式组3. 会利用一元一次不等式（组）解决简单的实际问题三. 教学重、难点1. 重点：一元一次不等式组的解法2. 难点：不等式组的解集的确定四. 知识要点1. 一元一次不等式组的有关概念（1）一元一次不等式组：含有相同未知数的几个一元一次不等式所组成的不等式组，叫做一元一次不等式组。
（2）一元一次不等式组的解集：一般地，几个一元一次不等式的解集的公共部分，叫做由它们所组成的一元一次不等式组的解集。
（3）解不等式组：求不等式组的解集的过程，叫做解不等式组。
2. 解一元一次不等式组的步骤（1）分别求出这个不等式组中各个不等式的解集。
（2）利用数轴求出这些不等式的解集的公共部分，即求出了这个不等式组的解集。
3. 确定由两个一元一次不等式所组成的不等式组的解集，有以下四种基本情况：（设【典型例题】[例1] 解不等式组⎪⎩⎪⎨⎧≤-+<--)2(12312)1(7)14(x x x x解：解不等式（1），得174-<-x x 63<-x 2->x解不等式（2），得63)12(2≤-+x x 2634-≤-x x 4≤x在数轴上表示不等式（1）和（2）的解集为∴ 原不等式组的解集为42≤<-x [例2] 解不等式53123<-≤-x 解法一：解：把原不等式写成不等式组⎪⎪⎩⎪⎪⎨⎧<--≤-)2(5312)1(3123x x解不等式（1），得4-≥x ，解不等式（2），得8<x ∴ 不等式组的解集为84<≤-x ∴ 原不等式的解集为84<≤-x解法二：解：去分母，得15129<-≤-x移项，得1628<≤-x 系数化为1，得84<≤-x ∴ 原不等式的解集为84<≤-x [例3] 解不等式组⎩⎨⎧->+>-)2(11)1(2)1(0xx a x解：解不等式（1），得a x > 解不等式（2），得3>x∴ ⎩⎨⎧>>3x ax当3>a 时，原不等式组的解集为a x >。
第三节：二元一次不等式组与简单的线性规划1、二元一次不等式表示的区域：二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
注意：由于对直线同一侧的所有点(x,y)，把它代入Ax+By+C，所得实数的符号都相同，所以只需在此直线的某一侧取一个特殊点(x0,y0) ，从Ax0+By0+C的正负可以判断出Ax+By+C>0表示哪一侧的区域（一般在C≠0时，取原点作为特殊点）2、二元一次不等式组表示的区域：二元一次不等式表示平面的部分区域，所以二元一次方程组表示各个区域的公共部分。
（二元一次不等式表示的区域）例1、画出不等式2x+y-6<0表示的平面区域。
（跟踪训练）画出不等式４ｘ－３ｙ≤１２表示的平面区域。
（点的分布）例2、已知点P(x 0,y 0)与点A(1,2)在直线l:3x+2y-8=0的两侧，则( ) A 、3x 0+2y 0>0 B 、3x 0+2y 0<0 C 、3x 0+2y 0>8 D 、3x 0+2y 0<8（跟踪训练）已知点（3 ，1）和点（－4 ，6）在直线 3x –2y + m = 0 的两侧，则（ ） A ．m ＜－7或m ＞24 B ．－7＜m ＜24 C ．m ＝－7或m ＝24D ．－7≤m ≤ 24（二元一次不等式组表示的平面区域） 例3、画出不等式组表示的区域。
（1） （2）⎪⎩⎪⎨⎧-≥≤+<242y y x xy ⎪⎪⎩⎪⎪⎨⎧+<≥+≥<9362323x y y x x y x(已知区域求不等式)例4、求由三直线x-y=0；x+2y-4=0及y+2=0所围成的平面区域所表示的不等式。
（跟踪训练）下图所示的阴影区域用不等式组表示为（已知不等式组求围成图形的面积）例5、求不等式组3,0,20xx yx y≤⎧⎪+≥⎨⎪-+≥⎩表示的平面区域的面积（跟踪训练）在直角坐标系中，由不等式组230,2360,35150,x yx yx yy->⎧⎪+-<⎪⎨--<⎪⎪<⎩所确定的平面区域内整点个数（绝对值不等式的画法）例6、画出不等式|x|+|y|<1所表示的区域。
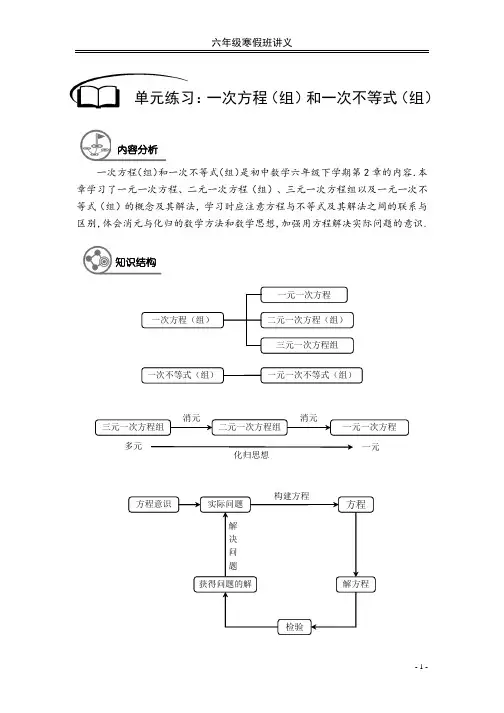
- 1 -一次方程（组）和一次不等式（组）是初中数学六年级下学期第2章的内容．本章学习了一元一次方程、二元一次方程（组）、三元一次方程组以及一元一次不等式（组）的概念及其解法，学习时应注意方程与不等式及其解法之间的联系与区别，体会消元与化归的数学方法和数学思想，加强用方程解决实际问题的意识．单元练习：一次方程（组）和一次不等式（组）内容分析知识结构一次方程（组）一次不等式（组）三元一次方程组一元一次方程二元一次方程（组） 一元一次不等式（组） 三元一次方程组一元一次方程二元一次方程组 消元消元多元一元化归思想实际问题检验解方程方程获得问题的解构建方程解决 问 题 方程意识- 2 -【练习1】 下列各式中，方程有（ ）个（1）633-+=-；（2）35x +=；（3）22ππ⨯=；（4）38a =；（5）7y =；（6）32p q -；（7）719nm +=；（8）1a a =+． A ．3B ．4C ．5D ．6【练习2】 下列各式中，一元一次方程有（ ）个（1）30x =；（2）437x y -=；（3）21303x -=；（4）()397y y --=；（5）23x -；（6）4x ≠． A ．1B ．2C ．3D ．4【练习3】 下列各式中，二元一次方程有（ ）个（1）2311x y -=；（2）23xy =-；（3）35m y+=；（4）25p q ->；（5）221x x +=；（6）21953m n -=．A ．1B ．2C ．3D ．4【练习4】 下列各式中，二元一次方程组有（ ）个（1）()()23111x y xy x y +=-⎧⎪⎨=+-⎪⎩；（2）31230x y x y +=⎧⎨-=⎩；（3）235x x y =⎧⎨+=-⎩；（4）3227x y x y -=+=+．A ．1B ．2C ．3D ．4【练习5】 二元一次方程组324526x y x y -=⎧⎨-=⎩的解是（ ）A ．11x y =⎧⎨=-⎩B ．112x y =-⎧⎪⎨=⎪⎩C ．112x y =-⎧⎪⎨=-⎪⎩D ．112x y =⎧⎪⎨=-⎪⎩【练习6】 如果0m n <<，那么下列各式中正确的是（ ）A ．0.30.3m n <B ．22m n <C ．11m n <D ．m n m n -<+选择题- 3 -【练习7】 下列判断中正确的是（ ）A ．如果0x <，那么15x x <B ．不等式35x ->-的解集是53x <C ．如果113x <-，那么3x >-D ．不等式组11x x >⎧⎨<⎩的解集为1x =【练习8】 若方程()2210a x bx c +++=是表示字母x 的一元一次方程，则（ ）A ．12a =，0b ≠，c 为任意数 B ．12a ≠，0b ≠，0c = C ．12a =-，0b ≠，0c ≠D ．12a =-，0b ≠，c 为任意数【练习9】 下列式子中一定正确的是（ ）A ．23a a< B ．a b a -< C ．2a a >D ．322x x-< 【练习10】 下列说法中错误的是（ ）A ．方程ax b =的解是bx a=（0a ≠）B ．如果ax b ->，则bx a<-（0a ≠）C ．若2k =时，方程()22k x k -=无解D ．8-是不等式32x ->一个解【练习11】 下列各对数值，是方程342x y +=的解的为（ ）A ．012x y =⎧⎪⎨=-⎪⎩B ．22x y =-⎧⎨=⎩C ． 114x y =⎧⎪⎨=-⎪⎩D ． 21x y =-⎧⎨=⎩【练习12】 某运输队运煤，第一天运了总量的27，第二天运煤恰好是第一天的23，还剩14 吨，设一共运煤x 吨，则可列出方程（ ）A ．22214773x x x +⨯=-B ．221473x x x ++=C ．222114737x x x ⎛⎫+-=- ⎪⎝⎭D ．22214773x x x +÷+=【练习13】 学校的篮球数比排球数的2倍少3个，篮球数与排球数的比是3 : 2，求两种球各有多少个？若设篮球有x 个，排球有y 个，则根据题意得到的方程组是（ ） A ．2332x y x y =-⎧⎨=⎩B ．2332x y x y =+⎧⎨=⎩C ．2323x y x y =-⎧⎨=⎩D ．2323x y x y =+⎧⎨=⎩【练习14】 已知不等式组00x a x b -<⎧⎨-<⎩的解集为x a <，则不等式组00x a x b +>⎧⎨+>⎩的解集为（ ）A ．x a <-B ．x a >-C ．x b >-D ．x b <-- 4 - 【练习15】 323x y+=的正整数解的个数为（ ）个A ．1B ．2C ．3D ．4【练习16】 观察下列方程组，无解的是（ ）A ．61x y x y -=⎧⎨+=-⎩B ．52210x y x y -=-⎧⎨-=⎩C ．5229x y x y -=⎧⎨+=⎩D ．423x y x y +=⎧⎨-=⎩【练习17】 已知不等式组5x x m >⎧⎨>⎩的解集为5x >，则m 的取值范围是（ ）A ．5m >B ．5m ≥C ．5m <D ．5m ≤【练习18】 已知方程组35223x y k x y k+=+⎧⎨+=⎩，其中x 是y 的2倍，则k 的值是（ ）A ．72-B ．72C ．0D ．以上都不对【练习19】 如果关于x 的不等式32x a ->的所有正整数解之和为6，则a 的取值范围为（ ） A ．5a ≥-B ．3a <-C ．53a -<<-D ．53a -≤<-【练习20】 如果关于x 的不等式组30310x m x m -->⎧⎨-+<⎩无解，那么m 的取值范围是（ ）A ．2m <B ．2m ≤C ．2m >D ．2m ≥【练习21】 若3350m x ---=是一元一次方程，则m =______．【练习22】 把方程5239x y -+=化成用含x 的式子表示y 的形式，得______________．【练习23】 用不等式表示：2x y+减去()21x --所得的差是非负数________________． 填空题- 5 -【练习24】 用不等号填空，并说明不等式变形过程．（1）若x y >，则4x -______4y -； （2）若235x +≤-，则3x ______7-； （3）若1233x x -≥-，则x ______2； （4）若x y >，则6x -______6y -； （5）若x y >，则2x -______2y -； （6）若x y >，0m >，则mx ______my ； （7）若m n ≥，20k +<，则mk ______nk ．【练习25】 解集32x -≤<中的整数解为__________________．【练习26】 不等式组340731x x +>⎧⎨-≥-⎩的解集为____________________．【练习27】 判断：（1）如果a b >，那么3232a b ->-；（ ） （2）如果a b <，那么22a b <；（ ） （3）如果22a b >，那么a b >；（ ） （4）如果a b >，那么a b >；（ ） （5）如果1a >，那么a 比1a大；（ ） （6）如果5a >，那么55a a -=-；（ ） （7）如果144m <-，那么1m <-；（ ）（8）如果x y >，那么()()2211m x m y -->--．（ ） 【练习28】 若0a b +<，且0ab >，则a ______0，b ______0．- 6 - 【练习29】 满足不等式()10484x x ++≤的最大整数解是_______．【练习30】 当x ______时，52x -的值是正的，此时最小的整数x =_______．【练习31】 如果43x y =⎧⎨=-⎩是方程436x ay -=的一个解，则a =______．【练习32】 如果3235351m n m n x y +--++=-是二元一次方程，那么m =______，n =_______．【练习33】 若357x -+=，则x =______．- 7 -【练习34】 若:5:3x y =，且x 与y 的和是10，则x =______，y =______．【练习35】 已知1y =是方程()1223m y y --=的解，那么关于x 的方程 ()()3225m x m x --=-的解是______．【练习36】 若关于x 、y 方程组352278x y ax y a -=⎧⎨+=-⎩的解互为相反数，则a =______．【练习37】 如果()222303x y x ⎛⎫+++-= ⎪⎝⎭，那么2016y =______．- 8 - 【练习38】 甲、乙两班共有88名学生，若从乙班调25人到甲班，则甲班人数是乙班人数的3倍，设甲班x 人，乙班y 人，可列出方程组_______________________，并解得甲班有______人，乙班有______人．【练习39】 有一个两位数，个位数字和十位数字之和是9，且这个两位数不大于63，求这个两位数．可设这个两位数的个位数字为x ，根据题意，可列不等式 ________________________，最后这个两位数为_______________________．【练习40】 若关于x 的不等式()22a x a +>+的解集是1x <，则a 的取值范围是______．- 9 -【练习41】 解方程：（1）1071253x x x +=--；（2）()()160%2180%22x x +-+=；（3）111257918643x ⎧⎫⎡+⎤⎛⎫+-+=⎨⎬⎪⎢⎥⎝⎭⎣⎦⎩⎭； （4）1.88 1.5350.401.220.3x x x -----=．【练习42】 解不等式：（1）()23213x x +-≤；（2）()30%151%x x +<+；（3）()()11221225x x x ⎡⎤-+≤-⎢⎥⎣⎦； （4）()()0.20.30.40.50.10.21110.030.066x x --->+．解答题【练习43】解不等式组：（1）()()3241353324x xx x⎧-->-⎪⎨+≤+⎪⎩；（2）()210381274332xxxxx⎧---≤-⎪⎪⎨⎪-<+⎪⎩；（3）13222364553522x xx xx x⎧+>+⎪⎪+>+⎨⎪⎪-<-⎩；（4）()1226323112184xxx xx x⎧+>⎪⎪⎪+≥+⎨⎪+-⎪-<-⎪⎩．【练习44】解方程组：（1）521347a ba b+=-⎧⎨+=⎩；（2）5.3 4.7804.75.320x yx y+=⎧⎨+=⎩；- 10 -- 11 -（3）34135353x y z x y z x y z +-=⎧⎪-+=⎨⎪+-=⎩；（4）2636315764949x y z x y z x y z ++=⎧⎪++=⎨⎪-+=⎩．【练习45】 关于x 的方程()143321223x x x a x x +----=-的解是最小的质数的倒数，求a 的值．【练习46】 解方程：2015122320152016x x x +++=⨯⨯⨯．【练习47】若关于x、y的方程组2323ax byx y-=⎧⎨-=-⎩和3424y xax by-=⎧⎨+=-⎩有相同的解，求a、b的值．【练习48】甲、乙两人同时求7mx ny-=的整数解，甲求出一组解为34xy=⎧⎨=⎩，而乙把7mx ny-=中的7看成1，求出一组解为12xy=⎧⎨=⎩，求m、n的值．【练习49】已知关于x、y的方程组321431x y px y p+=+⎧⎨+=-⎩满足x > y，求p的取值范围．【练习50】解方程组：252821126x yy zz uu x+=⎧⎪+=⎪⎨+=⎪⎪+=⎩．- 12 -。
六年级一元一次方程、二元一次方程组的解法及应用学生编号学生姓名授课教师辅导学科六年级数学教材版本上教课题名称一元一次方程、二元一次方程组的应用课时进度总第（）课时授课时间5月26日教学目标1.熟练掌握一元一次不等式和一元一次方程的解法和应用；2.会解二元一次方程组；能够熟练的运用二元一次方程组解决实际问题；3.使学生掌握三元一次方程、三元一次方程组和它的解的含义；重点难点1.二元一次方程组和三元一次方程组的解题技巧；2.根据应用题的题意列出二元一次方程组。
同步教学内容及授课步骤一、一知识梳理1.列二元一次方程组解应用题的步骤①弄清题意和题目中的数量关系，用字母（如x、y）表示题目中的两个未知数；②找出能够表示应用题全部含意的两个相等关系；③根据两个相等关系列出代数式，从而列出两个方程并组成方程组；④解这个二元一次方程组，求出未知数的值；⑤检查所得结果的正确性及合理性；⑥写出答案．2.设未知数的几种常见方法（1）设直接未知数：即题目里要求的未知量是什么，就把它设做方程里的未知数，并且求几个设几个．（2）设间接未知数：即设的不是所求量．有些应用题，若设直接未知数，则所列的方程比较复杂；若改设间接未知数，则能列出既简单又易解的方程．（3）少设未知数：有些应用题，要求两个或更多个未知数，但根据各未知数之间的关系，只需设一个或少数几个未知数就可以求解．（4）多设未知数：有些应用题，不仅要设直接未知数，而且要增设辅助未知数，但这些辅助未知数本身并不需要求出，它们的作用只是为了帮助列方程，同时为了求出真正的未知数．3.应用题常见的几种类型：（1）行程问题：①基本量之间的关系：路程＝速度×时间②解题时一般应画线段示意图。
（2）工程问题①基本量之间的关系：工作量＝工作效率×工作时间甲、乙合做的工作效率＝甲的工作效率＋乙的工作效率②解题时，若工作总量是抽象的，通常把它设为单位1。
（3）浓度问题①基本量之间的关系：溶液＝溶质＋溶剂（指体积或质量）溶液的浓度＝溶质溶液×100% ②解题时应注意配制前后溶液中的不变量和变化量分别是什么？（4）利润问题：①有关量的关系：利润＝售价－进价利润率＝售价进价进价-×100% 利息＝本金×利率×期数1. 已知 z y x z y x 26=-=+)0(≠xyz ，则z y x ::= ；2. 解方程组：⎩⎨⎧=++=20233:2:1::z y x z y x3. 解方程组：435:4:3)(:)(:)(-=-+=+++z y x x z z y y x4.⎪⎩⎪⎨⎧=++==355:4:3:2:z y x z y y x【拓展题】方程组⎩⎨⎧-=--=+322m y x m y x 的解满足32=+y x ，求m 的值. 解法指导 把m 看作已知字母.求出的x 与y 的值是含有m 的式子，再把求出的x 与y 的值代入32=+y x ，得到关于m 的一元一次方程，再求出m 的值；也可以把这三个方程组成三元一次方程组，求出m 的值.【典型例题5】六年级（2）班去春游，全班分成若干个小组进行活动，其中女同学分成2组，第一组人数的2倍比第二组人数多4人；如果从第二组调2人到第一组，那么两个小组的人数相等，求女同学的第一组、第二组人数分别是多少人？解法指导 设第一组的人数是x 人，第二组的人数是y 人.根据“第一组人数的2倍比第二组多4人”列出第一个方程，“第二组调2人到第一组，那么两个小组的人数相等”列出第二个方程.【基础习题限时训练】 1. 西部山区某县响应国家“退耕还林”号召，将该县一部分耕地改还为林地。
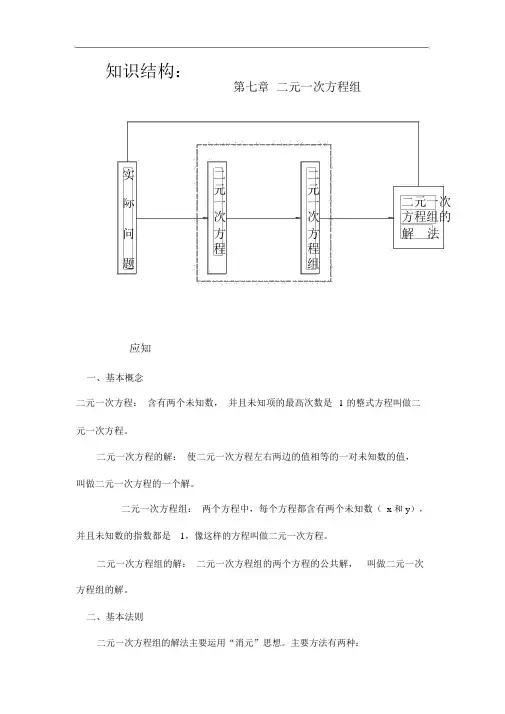
知识结构：第七章二元一次方程组实二二元元二元一次际一一次次方程组的问方方解法程程题组应知一、基本概念二元一次方程：含有两个未知数，并且未知项的最高次数是 1 的整式方程叫做二元一次方程。
二元一次方程的解：使二元一次方程左右两边的值相等的一对未知数的值，叫做二元一次方程的一个解。
二元一次方程组：两个方程中，每个方程都含有两个未知数（x 和 y），并且未知数的指数都是1，像这样的方程叫做二元一次方程。
二元一次方程组的解：二元一次方程组的两个方程的公共解，叫做二元一次方程组的解。
二、基本法则二元一次方程组的解法主要运用“消元”思想。
主要方法有两种：代入消元法： 将一个未知数用另一个未知数来表示， 然后代入方程中， 消去一个未知数，得到一个一元一次方程。
这种方法叫做代入消元法，简称代入法。
加减消元法：两个二元一次方程中同一未知数的系数相反或相等时，将两个方程的两边分别相加或相减， 就能消去这个未知数， 得到一个一元一次方程， 这种方法叫做加减消元法，简称加减法。
【注意】更多时候同一未知数的系数需经简单变形后， 才成为相反数或相等。
应会1. 列二元一次方程式 (组)。
2. 解二元一次方程组。
3. 用二元一次方程组解实际问题。
例题1. 下列方程组是不是二元一次方程组。
不是的请说明理由。
x 3y 4 xy 4 (1)5y 7 (2)5y72x2xx 3y 4 x 2 3y 4(3)z7(4)5y72x2x2. （ 1）方程（ a ＋2）x +( b-1) y =3 是二元一次方程，试求 a 、b 的取值范围 .a –1 是二元一次方程，试求 a 的值 .（ 2）方程 x∣ ∣+( a-2) y = 2 3. 已知下列三对值：x ＝－ 6 x ＝ 10 x ＝10y ＝－ 9y ＝－ 6y ＝－ 1（1）哪几对数值使方程1x－y＝6 的左、右两边的值相等？2（2）哪几对数值是方程组1 x y6的解？231y2x114.x a是方程 2x+y=2 的解，求 8a+4b-3 的值。
二元一次方程组教学目标：1、灵活运用代入消元法和加减消元法解解二元一次方程组。
2、会用二元一次方程组解决数学实际问题。
3、培养学生分析问题解决问题的能力，训练学生运用多种方法解题的能力，加强学生的数学逻辑思维。
教学重点：1、灵活运用代入消元法和加减消元法解解二元一次方程组。
2、会用二元一次方程组解决实际问题。
教学难点：会用二元一次方程组解决实际问题。
教学过程：一、旧知铺垫，引入新知幻灯：古老的“鸡兔同笼问题”“今有鸡兔同笼，上有三十五头，下有九十四足。
问鸡、兔各几何？”师：同学们还记得有关鸡兔同笼的数学问题吗？（记得）我们是用什么方法来解决这类问题的呢？生：假设法。
师：除了假设法，还有其他的方法吗？生：用一元一次方程。
师：很好，同学们说的都很正确。
今天我们就一起先来看一个中国古代的算术问题：鸡兔同笼（PPT课件展示问题）。
用你们刚刚说到的两种方法来解答（学生自主完成，展示完成情况）算术方法：假设都是鸡一元一次方程：设鸡有x只，则列方程得35×2=70（条） 2x+4（35-x）= 9494-70=24（条） 2x+140-4x = 944-2=2（条） 2x = 46兔子的只数：24÷2=12（只）鸡的只数： x = 23 鸡的只数： 35-12=23（只）兔子的只数： 24÷2=12（只）师：同学们非常棒！除了这两种方法外，还有其他方法吗？今天这节课我们就一起来探究。
（板书课题）二、思维探索（一）出示例1展示例题：例1：今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何？师：分析刚刚的数学问题，问题中要求什么呢？生：鸡和兔的只数各有几只。
（若学生想不到，教师要引导学生，要求的是两个未知数，能否设两个未知数列方程求解呢？让学生自己设未知数，列方程）师：问题中要求两个未知量，我们不妨设这两个量分别为x和y，那我们可以得到哪些等量关系呢？生：鸡的只数+兔的只数=35只，可以得到x+y=35。
