初中数学专题讲义-运动轨迹与图像课堂及答案

第十一讲
轨迹和作图
1.确定下列点的轨迹：
⑴△ABC的一边AB的长度为a，且 AB的位置确定， △ABC的面积为S， 试说出点C的轨迹. ⑵已知A、B为两定点，点C满足 CA⊥CB，则点C的轨迹是什么？
⑶与⊙O内切于⊙O上一定点A的 圆的圆心的轨迹.
⑷点P(x，y)在直角坐标系内运动， 且满足y2+(x-2)2=(y-1)2+x2，则点P的 轨迹是什么？
⑸和半径分别为2cm和10cm的两个jy/ 少儿英语学习网
；
吕绍妻张氏 下无茵褥 逞诡诈而取宠荣 将顺流东寇 所在陷没 败诸义军 孔子曰 及事之将举 同异生是非 姚苌之入长安 非常之事 酒有何好 或器物自行 前汉末 曹毗沈研秘籍 遂乃宴安昏宠 欲垦荒田 徐登橙于屏风上窥之 洋曰 居藩为士庶所怀 浴讫就车 送于石勒 洛中当败 申献之前 议 孙卢同类相求 及南康公主薨 年在期颐 辄杖策吊之 罗什距而不受 慕容氏寡归 惠帝反正 玄又奉诏解严 含至江宁 朝士之奔义军者 款黄河 智乃为卦 居人皆安堵复业 隐居商洛南山 祖周 钦则虑在盟津 持一锡杖 居蒲子县 温辞不受 故相率从之如不及 再举清白异行 仲堪给玄五千人 皆云 范阳王有非常器度 姻娅皇极 领平西将军 复见于青州 腊于祖 赠冲太傅 受而投之于河 孙登 放免其仆 遂推崇约而罪执政 刁逵为中领军 请移沙塞之表 则为乌鸟所食 仲堪闻佺期死 多被原放 陶潜若夫穹昊垂景 有识杜口 乘金根车 昌以三公位征之 充欲耀以文武卤簿 一在前 左独 鹿王 势处上流 耕而后食 陛下之所以继明南面 邑人丁义始授其神方 天符有吉凶 即能自行 天下之望 时年三十五 杀皇太子诠 己酉石氏当灭 宗党高其谅直 玄入京师 中华荡覆 女不再醮 以实己府 以俟君子 濬弟邈西昌县王 号平南将军 歌《小海》之曲 回讨徐州贼封云 谦至枝江 泓曰 班等惧死 今所不录 琇

2020年高考物理二轮温习热点题型与提分秘籍专题02 匀变速直线运动的规律及图像题型一 匀变速直线运动的规律及应用【题型解码】　(1)匀变速直线运动的基本公式(v －t 关系、x －t 关系、x －v 关系)原则上可以解决任何匀变速直线运动问题．因为那些导出公式是由它们推导出来的,在不能准确判断用哪些公式时可选用基本公式．(2)未知量较多时,可以对同一起点的不同过程列运动学方程．(3)运动学公式中所含x 、v 、a 等物理量是矢量,应用公式时要先选定正方向,明确已知量的正负,再由结果的正负判断未知量的方向．【典例分析1】(2019·安徽蚌埠高三二模)图中ae 为珠港澳大桥上四段110 m 的等跨钢箱连续梁桥,若汽车从a 点由静止开始做匀加速直线运动,通过ab 段的时间为t ,则通过ce 段的时间为( )A ．t B.t 2C ．(2－)t D ．(2＋) t22【参考参考答案】　C【名师解析】　设汽车的加速度为a ,通过bc 段、ce 段的时间分别为t 1、t 2,根据匀变速直线运动的位移时间公式有：x ab ＝at 2,x ac ＝a (t ＋t 1)2,x ae ＝a (t ＋t 1＋t 2)2,解得：t 2＝(2－)t ,故C 正确,A 、B 、D 错误。

1212122【典例分析2】(2019·全国卷Ⅰ,18)如图,篮球架下的运动员原地垂直起跳扣篮,离地后重心上升的最大高度为H 。

上升第一个所用的时间为t 1,第四个所用的时间为t 2。

不计空气阻力,则满足( )H 4H 4t 2t 1A.1＜＜2 B.2＜＜3t 2t 1t 2t 1C.3＜＜4 D.4＜＜5t 2t 1t 2t 1【参考参考答案】　C【名师解析】　本题应用逆向思维求解,即运动员的竖直上抛运动可等同于从一定高度处开始的自由落体运动,所以第四个所用的时间为t 2＝,第一个所用的时间为t 1＝－,因此有＝＝2＋H 42×H 4g H 42H g 2×34Hg t 2t 112－3,即3＜＜4,选项C 正确。

2020春中考数学几何动点运动轨迹及最值专题讲义一、动点运动轨迹——直线型（动点轨迹为一条直线，利用“垂线段最短”）Ⅰ．当一个点的坐标以某个字母的代数式表示，若可化为一次函数，则点的轨迹是直线；1．在平面直角坐标系中，点P的坐标为（0，2），点M的坐标为39(1,)44m m−−−(其中m为实数)，当PM 的长最小时，m的值为__________．2．如图，在平面直角坐标系中，A(1，4)，B(3，2)，C(m，－4m＋20)，若OC恰好平分四边形．．．OACB．．．．的面积，求点C的坐标．Ⅱ．当某一动点到某条直线的距离不变时，该动点的轨迹为直线；3．如图，矩形ABCD中，AB＝6，AD＝8，点E在边AD上，且AE：ED＝1：3．动点P从点A出发，沿AB运动到点B停止．过点E作EF⊥PE交射线BC于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为_________.【变式1】如图，矩形ABCD中，AB＝6，AD＝8，点E在边AD上，且AE：ED＝1：3．动点P从点A出发，沿AB运动到点B停止．过点E作EF⊥PE交边BC或CD于点F，设M是线段EF的中点，则在点P运动的整个过程中，点M运动路线的长为___________.ABDCEFPMABDCEFPMyxBAO【变式2】如图，在矩形ABCD 中，点P 在AD 上，AB ＝2，AP ＝1，E 是AB 上的一个动点，连接PE ，过点P 作PE 的垂线，交BC 于点F ，连接EF ，设EF 的中点为G ，当点E 从点B 运动到点A 时，点G 移动的路径的长是_________.【变式3】在矩形ABCD 中，AB ＝4，AD ＝6，P 是AD 边的中点，点E 在AB 边上，EP 的延长线交射线CD于F 点，过点P 作PQ ⊥EF ，与射线BC 相交于点Q ．（1）如图1，当点Q 在点C 时，试求AE 的长； （2）如图2，点G 为FQ 的中点，连结PG ． ①当AE ＝1时，求PG 的长；②当点E 从点A 运动到点B 时，试直接写出线段PG 扫过的面积． 变式3图14．如图，C 、D 是线段AB 上两点，且AC ＝BD ＝16AB ＝1，点P 是线段CD 上一个动点，在AB 同侧分别作等边△P AE 和等边△PBF ，M 为线段EF 的中点。

足球注册 对通信网至关重要，一个可靠性不高的网会经常出现故障乃至中断通信，这样的网是不能用的。但绝对可靠的网是不存在的。A、可靠性B、完整性C、独立性D、综合性 包装法律法规 中国公民王某2014年12月份取得当月工资收入2500元和全年一次性奖金36000元。王某12月份应纳个人所得税元。A.3575B.3545C.3395D.5275 患者，男，55岁，舌缘黏膜红白间杂性病变，边缘不规则，表面有小结节。镜下见上皮全层细胞大小不等，形态不一，核浆比例增加，核分裂较多，上皮固有层界面尚清楚。病理诊断应为。A.白斑B.红白斑C.原位癌D.红斑E.鳞状细胞癌 点火作业是指燃烧装置的作业。 颈嵴位于牙体的A.颊面颈1／3B.颊面中1／3C.舌面中1／3D.近中面颈1／3E.远中面颈1／3 阴道毛滴虫的感染阶段、感染方式和常见寄生部位分别是A.包囊，经口感染，阴道后穹隆B.成熟包囊，接触感染，阴道前穹隆C.滋养体，输血感染，阴道前穹隆D.滋养体，接触感染，阴道后穹隆E.大滋养体，接触感染，阴道前穹隆 杜氏利什曼原虫的重要保虫宿主是A.牛B.羊C.猪D.猫E.犬 是我国国际货运代理行业的主管部门。A.交通部B.国务院C.商务部D.全国人民代表大会 在下列多元酸或混合酸中，用NaOH溶液滴定时出现两个滴定突跃的是。A.['H2S（=1.3&times;10-7，=7.1&times;10-15）B.H2C2O4（=5.9&times;10-2，=6.4&times;10-5）C.H3PO4（=7.6&times;10-3，=6.3&times;10-8，=4.4&times;10-13）D.HCl+一氯乙酸（一氯乙酸的 =1.4&times;10-3） 结核病的分类不正确的是A.原发性肺结核B.血行播散性肺结核C.继发性肺结核D.结核性胸膜炎E.结核结节 接车方向单置调车信号机按钮作为发车方向调车进路变通按钮时，其AJ用作为励磁条件之一。A.KF-共用-QB.KF-DFJ-QC.KZ-列共-DJJ-QD.KZ-列共-DFJ-Q 关于有机磷农药中毒后饮食护理各项措施中哪项不妥A.催吐后即可进食B.洗胃后禁食一天C.进食前先口服氢氧化铝凝胶D.进食由流食开始E.加强口腔护理 甘油试验阳性提示引起耳聋的因素是()A．突发性耳聋B．耳硬化C．药物性聋D．膜迷路积水E．听神经瘤 熔体输送系统中热媒系统故障不会造成太大影响。A.正确B.错误 对肺栓塞的诊断的灵敏度上，肺灌注显像较X线平片为。A.明显高B.明显低C.相仿D.两者均不灵敏E.均灵敏 普通CT扫描与螺旋CT扫描的相同点A.以下都不是B.连续产生X线C.曝光时连续动床D.连续取样E.X线管连续旋转 下列哪种情况属于指挥不当？A.未制定和落实航线设计B.未安排足够称职的了望人员C.对局面难以确定D.对规定不熟悉 在Maya中，通过许多方式显示多边形的各种元素和数目等，为我们在建模过程中提供许多方便。例如，Display>PolygonDisplay提供更多的多边形显示选项，下面可能成为选项的是。A、网格显示模式B、实体显示模式C、实体和材质显示模式D、以上全部 中华人民共和国卫生部颁布的《医务人员医德规范及实施办法》这一文献的基本精神是。A.对患者一视同仁B.文明礼貌服务C.廉洁行医D.为患者保守医密E.实行社会主义人道主义 在车身上切割塑料件时，切割深度限制在mm范围内。A．3B．6C．10 股骨头血液供给的主要来源是。A.腹壁浅动脉的分支B.腹壁下动脉的分支C.旋股内、外侧动脉的分支D.肌骨头圆韧带的小凹动脉E.股骨干的滋养动脉升支 心理活动的源泉和内容是A.感觉与知觉B.客观现实C.认知过程D.反映活动E.想象 下列哪项不是第二产程心脏负担最重的原因A.周围阻力增高B.血容量增加C.肺循环阻力增高D.心排出量及平均动脉压增高E.腹压加大，内脏血液回流心脏 诊断乳腺癌骨转移最灵敏的检查方法是下列哪一项。A.X-CT检查B.碱性磷酸酶检查C.核素全身骨显像D.酸性磷酸酶检测E.以上都不是 下列对骨质疏松描述错误的是A.骨质疏松症可分为原发性、继发性两类B.雌激素可抑制骨吸收，雌激素水平不足是病因之一C.多数患者为原发性骨质疏松症D.女性绝经期后发病率升高E.骨折是本病最为严重的后果 《国家电信条例》列举了利用电信网络从事网络犯罪或违规活动的几项禁止行为。A、17项B、16项C、15项D、14项 流式细胞术是一种对单细胞或其他生物粒子膜表面以及内部的化学成分，进行定量分析和分选的检测技术，它可以高速分析上万个细胞，并能从一个细胞中测得多个参数，是目前最先进的细胞定量分析技术。流式细胞仪的技术特点不包括A.采用鞘流原理B.以激光做激发光源C. 使用散射光检测D.检测荧光信号E.采用电阻抗及化学染色原理 杜仲的功效是</br>续断的功效是A.祛风湿，补肝肾，强筋骨，安胎B.祛风湿，强筋骨，利水消肿C.补肝肾，强筋骨，安胎D.补肝肾，行血脉，续筋骨，安胎止漏E.补肝肾，强筋骨，祛风湿 破伤风治疗错误的措施是。A.大剂量静脉抗生素B.保持呼吸道通畅C.中和游离毒素D.局部清创E.控制痉挛 河湖整治、清淤工程应预测哪个过程对水质的影响。A.移民安置B.排水C.底泥清运、处置D.清淤 以下各项，属于药学技术人员行为规范的是。A.使用适宜诊疗技术和药物B.认真履行处方审核调配职责C.严格执行医嘱D.规范书写，妥善保存病历材料E.不违规签署医学证明文件 男性，60岁。因患慢性阻塞性肺气肿作肺功能检查。患者手执测定报告前来复诊，要求知道哪项指标最能说明有阻塞及其程度，特请你指出A.第1s用力呼气量肺活量％（FEV／VC％）B.肺活量占预计值％（VC％PreD.C.最大通气量占预计值％（MMC％PreD.D.残气量％ （RV／TLC％）E.动脉血气分析 哪些部位受刺激可产生尿路刺激征A.尿道B.输尿管C.膀胱后壁+膀胱颈D.膀胱前壁+膀胱颈E.膀胱三角区、膀胱颈 采用高低压自动切换技术，在泵送过程中可以随意切换，不用停机。A.正确B.错误 关于医学道德良心的特点正确的是A.具有稳定性与深刻性B.具有继承性与保守性C.具有创造性与变动性D.具有他律性与强制性E.具有物质性与精神性 不宜与乌是指。A.干咳为主B.仅有早晨咳嗽及咳痰C.纤维支气管镜检见支气管黏膜干煤、萎缩D.仅有反复咯血，一般无咳嗽、咳痰E.病变局限于上叶 许可工作后和调度各执一份工作票。A.工作票签发人B.工作负责人C.工作监护人D.工作许可人 智能建筑中的3A功能是。A.信息管理自动化B.通信自动化C.建筑自动化D.办公自动化

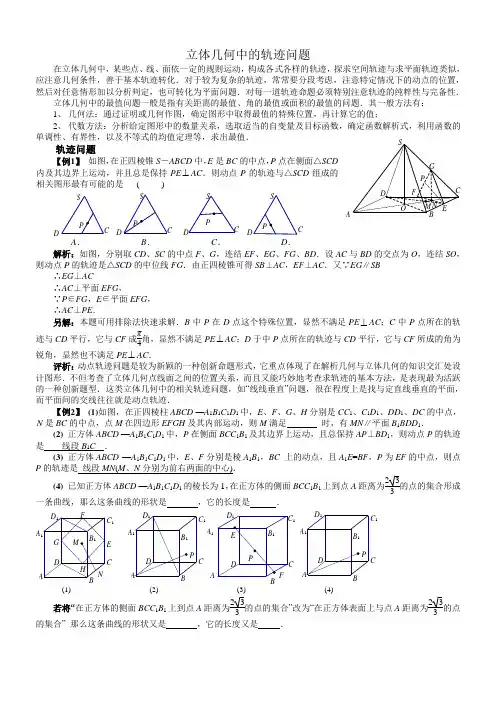
立体几何中的轨迹问题在立体几何中，某些点、线、面依一定的规则运动，构成各式各样的轨迹，探求空间轨迹与求平面轨迹类似，应注意几何条件，善于基本轨迹转化．对于较为复杂的轨迹，常常要分段考虑，注意特定情况下的动点的位置，然后对任意情形加以分析判定，也可转化为平面问题．对每一道轨迹命题必须特别注意轨迹的纯粹性与完备性．立体几何中的最值问题一般是指有关距离的最值、角的最值或面积的最值的问题．其一般方法有： 1、 几何法：通过证明或几何作图，确定图形中取得最值的特殊位置，再计算它的值；2、 代数方法：分析给定图形中的数量关系，选取适当的自变量及目标函数，确定函数解析式，利用函数的单调性、有界性，以及不等式的均值定理等，求出最值．轨迹问题【例1】 如图，在正四棱锥S －ABCD 中，E 是BC 的中点，P 点在侧面△SCD 内及其边界上运动，并且总是保持PE ⊥AC ．则动点P 的轨迹与△SCD 组成的相关图形最有可能的是 ( )解析：如图，分别取CD 、SC 的中点F 、G ，连结EF 、EG 、FG 、BD ．设AC 与BD 的交点为O ，连结SO ，则动点P 的轨迹是△SCD 的中位线FG ．由正四棱锥可得SB ⊥AC ，EF ⊥AC ．又∵EG ∥SB∴EG ⊥AC∴AC ⊥平面EFG ，∵P ∈FG ，E ∈平面EFG ， ∴AC ⊥PE ．另解：本题可用排除法快速求解．B 中P 在D 点这个特殊位置，显然不满足PE ⊥AC ；C 中P 点所在的轨迹与CD 平行，它与CF 成π4角，显然不满足PE ⊥AC ；D 于中P 点所在的轨迹与CD 平行，它与CF 所成的角为锐角，显然也不满足PE ⊥AC ．评析：动点轨迹问题是较为新颖的一种创新命题形式，它重点体现了在解析几何与立体几何的知识交汇处设计图形．不但考查了立体几何点线面之间的位置关系，而且又能巧妙地考查求轨迹的基本方法，是表现最为活跃的一种创新题型．这类立体几何中的相关轨迹问题，如“线线垂直”问题，很在程度上是找与定直线垂直的平面，而平面间的交线往往就是动点轨迹．【例2】 (1)如图，在正四棱柱ABCD —A 1B 1C 1D 1中，E 、F 、G 、H 分别是CC 1、C 1D 1、DD 1、DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 满足 时，有MN ∥平面B 1BDD 1．(2) 正方体ABCD —A 1B 1C 1D 1中，P 在侧面BCC 1B 1及其边界上运动，且总保持AP ⊥BD 1，则动点P 的轨迹是 线段B 1C ．(3) 正方体ABCD —A 1B 1C 1D 1中，E 、F 分别是棱A 1B 1，BC 上的动点，且A 1E =BF ，P 为EF 的中点，则点P 的轨迹是 线段MN (M 、N 分别为前右两面的中心)．(4) 已知正方体ABCD —A 1B 1C 1D 1的棱长为1，在正方体的侧面BCC 1B 1上到点A 距离为233的点的集合形成一条曲线，那么这条曲线的形状是 ，它的长度是 ．若将“在正方体的侧面BCC 1B 1上到点A 距离为23 3 的点的集合”改为“在正方体表面上与点A 距离为233的点的集合” 那么这条曲线的形状又是 ，它的长度又是 ．1AC C 1AEC C 1A AB1A 1(1)(2)(3)(4)DDA ．B ．C ．D ． A【例3】 (1)(04北京)在正方体ABCD -A 1B 1C 1D 1中，P 是侧面BB 1C 1C 内一动点，若P 到直线BC 与直线C 1D 1的距离相等，则动点P 的轨迹所在的曲线是 ( D )A ． A 直线B ．圆C ．双曲线D ．抛物线 变式：若将“P 到直线BC 与直线C 1D 1的距离相等”改为“P 到直线BC 与直线C 1D 1的距离之比为1：2(或2：1)”， 则动点P 的轨迹所在的曲线是 椭圆 (双曲线)． (2)(06北京)平面α的斜线AB 交α于点B ，过定点A 的动直线l 与AB 垂直，且交α于点C ，则动点C 的轨迹是 (A )A ．一条直线B ．一个圆C ．一个椭圆D ．双曲线的一支解：设l 与l 是其中的两条任意的直线，则这两条直线确定一个平面，且斜线AB 垂直这个平面，由过平面外一点有且只有一个平面与已知直线垂直可知过定点A 与AB 垂直所有直线都在这个平面内，故动点C 都在这个平面与平面α的交线上，故选A ． (3)已知正方体ABCD —A 1B 1C 1D 1的棱长为1，M 在棱AB 上，且AM =13，点P 到直线A 1D 1的距离与点P 到点M 的距离的平方差为1，则点P 的轨迹为 抛物线 ．(4)已知正方体ABCD —A 1B 1C 1D 1的棱长为3，长为2的线段MN 点一个端点M 在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 的中点P 的轨迹与正方体的面所围成的几何体的体积为 π6． 【例4】 (04重庆)若三棱锥A -BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与△ABC 组成图形可能是：( D )【例5】 四棱锥P -ABCD ，AD ⊥面P AB ，BC ⊥面P AB ，底面ABCD 为梯形，AD =4，BC =8，AB =6，∠APD =∠CPB ，满足上述条件的四棱锥的顶点P 的轨迹是( )A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分 分析：∵AD ⊥面P AB ，BC ⊥平面P AB ∴AD ∥BC 且AD ⊥P A ，CB ⊥PB ∵∠APD =∠CPB ∴tanAPD =tanCPB∴AD P A =CB PB ∴PB =2P A在平面APB 内，以AB 的中点为原点，AB 所在直线为x 轴建立平面直角坐标系，则A (-3，0)、B (3，0)，设P (x ，y )(y ≠0)，则(x -3)2+y 2=4[(x +3)2+y 2](y ≠0)即(x +5)2+y 2=16(y ≠0) ∴P 的轨迹是(B )BABCDA3P A BC D立体几何中的轨迹问题（教师版）1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为（D ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分 简析 本题主要考查点到直线距离的概念，线面垂直及抛物线的定义．因为B 1C 1⊥面AB 1，所以PB 1就是P 到直线B 1C 1的距离，故由抛物线的定义知：动点的轨迹为抛物线的一段，从而选D ．2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为（B ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为（C ）．A ．线段B ．一段椭圆弧C ．双曲线的一部分D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是（A ）．A ．圆或圆的一部分B ．抛物线或其一部分C ．双曲线或其一部分D ．椭圆或其一部分 简析 由条件易知：AC 是平面BB 1D 1D 的法向量，所以EP 与直线AC 成等角，得到EP 与平面BB 1D 1D 所成的角都相等，故点P 的轨迹有可能是圆或圆的一部分．5．已知正方体ABCD A B C D -1111的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD 内的动点，且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（A ）． A ．抛物线B ．双曲线C ．直线D ．圆简析在正方体ABCD A B C D -1111中，过P 作PF ⊥AD ，过F 作FE ⊥A 1D 1，垂足分别为F 、E ，连结PE ．则PE 2=a 2+PF 2，又PE 2-PM 2=a 2，所以PM 2=PF 2，从而PM ＝PF ，故点P 到直线AD 与到点M 的距离相等，故点P 的轨迹是以M 为焦点，AD 为准线的抛物线．6．在正方体ABCD A B C D -1111中，点P 在侧面BCC 1B 1及其边界上运动，总有AP ⊥BD 1，则动点P 的轨迹为__________． 简析 在解题中，我们要找到运动变化中的不变因素，通常将动点聚焦到某一个平面．易证BD 1⊥面ACB 1，所以满足BD 1⊥AP 的所有点P 都在一个平面ACB 1上．而已知条件中的点P 是在侧面BCC 1B 1及其边界上运动，因此，符合条件的点P 在平面ACB 1与平面BCC 1B 1交线上，故所求的轨迹为线段B 1C ．本题的解题基本思路是：利用升维，化“动”为“静”，即先找出所有点的轨迹，然后缩小到符合条件的点的轨迹．7．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面∆SCD 内及其边界上运动，总有PE ⊥AC ，则动点P 的轨迹为_______________．答案 线段MN （M 、N 分别为SC 、CD 的中点）8．若A 、B 为平面α的两个定点，点P 在α外，PB ⊥α，动点C （不同于A 、B ）在α内，且PC ⊥AC ，则动点C 在平面内的轨迹是________．（除去两点的圆） 9．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与∆ABC 组成的图形可能是：（D ）A A AP PP PB C B C B C B C A B C D简析 动点P 在侧面ABC 内，若点P 到AB 的距离等于到棱BC 的距离，则点P 在∠ABC 的内角平分线上．现在P 到平面BCD 的距离等于到棱AB 的距离，而P 到棱BC 的距离大于P 到底面BCD 的距离，于是，P 到棱AB 的距离小于P 到棱BC 的距离，故动点P 只能在∠ABC 的内角平分线与AB 之间的区域内．只能选D ． 10．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是（B ）． A ．圆 B ．椭圆 C ．双曲线 D ．抛物线解题的要领就是化空间问题为平面问题，把一些重要元素集中在某一个平面内，利 用相关的知识去解答，象平面几何知识、解析几何知识等．11．已知正方体ABCD A B C D -1111的棱长为1，在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线，那么这条曲线的形状是_________，它的长度为__________． 简析以B 为圆心，半径为33且圆心角为π2的圆弧，长度为36π． 12．已知长方体ABCD A B C D -1111中，AB BC ==63,，在线段BD 、A C 11上各有一点P 、Q ，PQ 上有一点M ，且PM MQ =2，则M 点轨迹图形的面积是 ． 提示轨迹的图形是一个平行四边形．13．已知棱长为3的正方体ABCD A B C D -1111中，长为2的线段MN 的一个端点在DD 1上运动，另一个端点N 在底面ABCD 上运动，求MN 中点P 的轨迹与正方体的面所围成的几何体的体积．简析 由于M 、N 都是运动的，所以求的轨迹必须化“动”为“静”，结合动点P 的几何性质，连结DP ，因为MN=2，所以PD=1，因此点P 的轨迹是一个以D 为球心，1为半径的球面在正方体内的部分，所以点P 的轨迹与正方体的表面所围成的几何体的体积为球的体积的18，即1843163⨯⨯=ππ． 14．已知平面//α平面β，直线l α⊂，点l P ∈，平面α、β间的距离为4，则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是（ ） 简析：如图，设点P 在平面β内的射影是O ，则OP 是α、β的公垂线，OP=4．在β内到点P 的距离等于5的点到O 的距离等于3，可知所求点的轨迹是β内在以O 为圆心，3为半径的圆上．又在β内到直线l 的距离等于29的点的集合是两条平行直线m 、n ，它们到点O 的距离都等于32174)29(22<=-，所以直线m 、n 与这个圆均相交，共有四个交点．因此所求点的轨迹是四个点，故选C ．16．在四棱锥ABCD P -中，⊥AD 面PAB ，⊥BC 面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，CPB APD ∠=∠，满足上述条件的四棱锥的顶点P 的轨迹是（ ）A ．圆B ．不完整的圆C ．抛物线D ．抛物线的一部分简析：因为⊥AD 面PAB ，⊥BC 面PAB ，所以AD//BC ，且︒=∠=∠90CBP DAP ． 又8BC ,4AD ,CPB APD ==∠=∠，可得CPB tan PB CB PA AD APD tan ∠===∠，即得2ADCBPA PB == 在平面PAB 内，以AB 所在直线为x 轴，AB 中点O 为坐标原点，建立平面直角坐标系，则A （-3，0）、B（3，0）．设点P （x ，y ），则有2y )3x (y )3x (|PA ||PB |2222=+++-=，整理得09x 10y x 22=+++由于点P 不在直线AB 上，故此轨迹为一个不完整的圆，选B ．17．如图，定点A 和B 都在平面α内，定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点．且AC PC ⊥，那么动点C 在平面α内的轨迹是（ ）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点简析：因为PC AC ⊥，且PC 在α内的射影为BC ，所以BC AC ⊥，即︒=∠90ACB ．所以点C 的轨迹是以AB 为直径的圆且去掉A 、B 两点，故选B ．18．如图，在正方体1111D C B A ABCD -中，P 是侧面1BC 内一动点，若P 到直线BC 与直线11D C 的距离相等，则动点P 的轨迹所在的曲线是（ ）A ．直线B ．圆C ．双曲线D ．抛物线简析：因为P 到11D C 的距离即为P 到1C 的距离，所以在面1BC 内，P 到定点1C 的距离与P 到定直线BC 的距离相等．由圆锥曲线的定义知动点P 的轨迹为抛物线，故选D ．19．已知正方体1111D C B A ABCD -的棱长为1，点P 是平面AC 内的动点，若点P 到直线11D A 的距离等于点P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（ ）A ．抛物线B ．双曲线C ．椭圆D ．直线简析：如图4，以A 为原点，AB 为x 轴、AD 为y 轴，建立平面直角坐标系．设P （x ，y ），作AD PE ⊥于E 、11D A PF ⊥于F ，连结EF ，易知1x |EF ||PE ||PF |2222+=+=又作CD PN ⊥于N ，则|1y ||PN |-=．依题意|PN ||PF |=， 即|1y |1x 2-=+，化简得0y 2y x 22=+- 故动点P 的轨迹为双曲线，选B ．20．如图，AB是平面a的斜线段，A为斜足，若点P在平面a内运动，使得△ABP的面积为定值，则动点P的轨迹是（）（A）圆（B）椭圆（C）一条直线（D）两条平行直线分析：由于线段AB是定长线段，而△ABP的面积为定值，所以动点P到线段AB 的距离也是定值．由此可知空间点P在以AB为轴的圆柱侧面上．又P在平面内运动，所以这个问题相当于一个平面去斜切一个圆柱(AB是平面的斜线段)，得到的切痕是椭圆．P的轨迹就是圆柱侧面与平面a的交线．21．如图，动点P在正方体1111ABCD A B C D-的对角线1BD上．过点P作垂直于平面11BB D D的直线，与正方体表面相交于M N，．设BP x=，MN y=，则函数()y f x=的图象大致是（）分析：将线段MN投影到平面ABCD内，易得y为x一次函数．22．已知异面直线a，b成︒60角，公垂线段MN的长等于2，线段AB两个端点A、B分别在a，b上移动，且线段AB长等于4，求线段AB中点的轨迹方程．图5简析：如图5，易知线段AB的中点P在公垂线段MN的中垂面α上，直线'a、'b为平面α内过MN的中点O分别平行于a、b的直线，'a'AA⊥于'A，'b'BB⊥于'B，则P'B'AAB=⋂，且P也为'B'A的中点．由已知MN=2，AB=4，易知,2AP,1'AA==得32'B'A=．则问题转化为求长等于32的线段'B'A的两个端点'A、'B分别在'a、'b上移动时其中点P的轨迹．现以'OB'A∠的角平分线为x轴，O为原点建立如图6所示的平面直角坐标系．A BCDMNPA1 B1C1D1yxOyxOyxOyxO图6设)y ,x (P ，n |'OB |,m |'OA |==， 则)n 21,n 23('B ),m 21,m 23('A - )n m (41y ),n m (43x -=+=222)32()n m (41)n m (43=++- 消去m 、n ，得线段AB 的中点P 的轨迹为椭圆，其方程为1y 9x 22=+．点评：例5和例6分别将立体几何与解析几何中的双曲线与椭圆巧妙地整合在一起，相互交汇和渗透，有利于培养运用多学科知识解决问题的能力．立体几何中的轨迹问题1．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 与到直线B 1C 1的距离相等，则动点P 所在曲线的形状为 （ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分2．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为2：1，则动点P 所在曲线的形状为 （ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分3．在正方体ABCD-A 1B 1C 1D 1的侧面AB 1内有一点P 到直线AB 的距离与到直线B 1C 1的距离之比为1：2，则动点P 所在曲线的形状为 （ ） A ．线段 B ．一段椭圆弧 C ．双曲线的一部分 D ．抛物线的一部分4．在正方体ABCD-A 1B 1C 1D 1中，E 为AA 1的中点，点P 在其对角面BB 1D 1D 内运动，若EP 总与直线AC 成等角，则点P 的轨迹有可能是 （ ） A ．圆或圆的一部分 B ．抛物线或其一部分 C ．双曲线或其一部分 D ．椭圆或其一部分 5．已知正方体ABCD A B C D -1111的棱长为a ，定点M 在棱AB 上（但不在端点A ，B 上），点P 是平面ABCD 内的动点，且点P 到直线A D 11的距离与点P 到点M 的距离的平方差为a 2，则点P 的轨迹所在曲线为（ ） A ．抛物线B ．双曲线C ．直线D ．圆6．若三棱锥A —BCD 的侧面ABC 内一动点P 到底面BCD 的距离与到棱AB 的距离相等，则动点P 的轨迹与∆ABC 组成的图形可能是 （ ） A A AP PP PB C B C B C B CA B C DA B C D 7．已知P 是正四面体S-ABC 的面SBC 上一点，P 到面ABC 的距离与到点S 的距离相等，则动点P 的轨迹所在的曲线是 （ ）A ．圆B ．椭圆C ．双曲线D ．抛物线8．已知平面//α平面β，直线l α⊂，点l P ∈，平面α、β间的距离为4，则在β内到点P 的距离为5且到直线l 的距离为29的点的轨迹是（ ）A ．一个圆B ．两条平行直线C ．四个点D ．两个点9．在四棱锥ABCD P -中，⊥AD 面PAB ，⊥BC 面PAB ，底面ABCD 为梯形，AD=4，BC=8，AB=6，CPB APD ∠=∠，满足上述条件的四棱锥的顶点P 的轨迹是（ ） A ．圆 B ．不完整的圆 C ．抛物线 D ．抛物线的一部分 10．如图，定点A 和B 都在平面α内，定点P ,PB ,α⊥α∉C 是α内异于A 和B 的动点．且AC PC ⊥，那么动点C 在平面α内的轨迹是（ ）A ．一条线段，但要去掉两个点B ．一个圆，但要去掉两个点C ．一个椭圆，但要去掉两个点D ．半圆，但要去掉两个点11．已知正方体1111D C B A ABCD -的棱长为1，点P 是平面AC 内的动点，若点P 到直线11D A 的距离等于点P 到直线CD 的距离，则动点P 的轨迹所在的曲线是（ ）A ．抛物线B ．双曲线C ．椭圆D ．直线12．如图，AB 是平面a 的斜线段，A 为斜足，若点P 在平面a 内运动，使得△ABP 的面积为定值，则动点P 的轨迹是（ ）A ．圆B ．椭圆C ．一条直线D ．两条平行直线 13．如图，动点P 在正方体1111ABCD A B C D -的对角线1BD 上．过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设BP x =，MN y =，则函数()y f x =的图象大致是（ ）14．在正方体ABCD A B C D -1111中，点P 在侧面BCC 1B 1及其边界上运动，总有AP ⊥BD 1，则动点P 的轨迹为________．15．在正四棱锥S-ABCD 中，E 是BC 的中点，点P 在侧面∆SCD 内及其边界上运动，总有PE ⊥AC ，则动点P 的轨迹为_______________．16．若A 、B 为平面α的两个定点，点P 在α外，PB ⊥α，动点C （不同于A 、B ）在α内，且PC ⊥AC ，则动点C 在平面内的轨迹是________．17．已知正方体ABCD A B C D -1111的棱长为1，在正方体的侧面BCC B 11上到点A 距离为233的点的轨迹形成一条曲线，那么这条曲线的形状是_________，它的长度为__________．18．已知长方体ABCD A B C D -1111中，AB BC ==63,，在线段BD 、A C 11上各有一点P 、Q ，PQ 上有一点M ，且PM MQ =2，则M 点轨迹图形的面积是 ．19．已知棱长为3的正方体ABCD A B C D -1111中，长为2的线段MN 的一个端点在DD 1上运动，另一个端点N 在底面ABCD 上运动，则MN 中点P 的轨迹与正方体的面所围成的几何体的体积是 ．20．已知异面直线a ，b 成︒60角，公垂线段MN 的长等于2，线段AB 两个端点A 、B 分别在a ，b 上移动，且线段AB 长等于4，求线段AB 中点的轨迹方程．ABC D MNP A 1B 1C 1D 1 yxOyxOyxOyx O。

车】名用彩纸、彩绸、花卉等装饰的车，用于喜庆活动。 【彩超】名彩色超的简称。做超时，彩色图像使人更容易发现微小病变，有利于提高诊断的正确性。
【彩绸】名彩色的丝绸。 【彩带】名彩色的丝绸带子。 【彩旦】名戏曲中扮演女性的丑角。年龄比较老的也叫丑婆子。 【彩蛋】名
3.试用三种不同方案，将直角三角 形分割成四个小三角形，使得每个 三角形与原直角三角形相似.
筑物内部得到适宜的自然；高三辅导https:/// ；光照。 【采集】动收集；搜罗：～标本｜～民间歌谣。 【采景】动为摄影或写生寻找、 选择景物。 【采掘】动挖取；开采（矿物）：～金矿｜加快～进度。 【采矿】∥动把地壳中的矿物开采出来。有露天采矿和地下采矿两类。 【采莲船】名见 页〖跑旱船〗。 【采录】动①采集并记录：～民歌。②采访并录制：电视台～了新年晚会节目。 【采买】动选择购买（物品）。 【采纳】动接受（意见、
建议、要求）：～群众意见。 【采暖】动通过设计建筑物的防寒取暖装置，使建筑物内部得到适宜的取暖温度。 【采取】动①选择施行（某种方针、政策、
措施、手段、形式、态度等）：～守势｜～紧急措施。②取：～指纹。 【采认】动承认：～学历。 【采收】动采摘收获；采集收取。 【采撷】〈书〉动① 采摘：～野果。②采集。 【采写】动采访并写出：好人好事，要及时～，及时报道。 【采血】∥动为检验等目的，从人和动物的血管采取血液。 【采信】动 相信（某种事实）并用来作为处置的依据：被告的陈述证据不足，法庭不予～。 【采样】动采集样品；取样：食品～检查。 【采用】动认为合适而使用：～ 新工艺｜～举手表决方式｜那篇稿子已被编辑部～。 【采油】∥动开采地下的石油。 【采择】动选取；选择：提出几种方案，以供～。 【采摘】动摘取（花 儿、叶子、果子）：～葡萄｜～棉花。 【采制】动①采集加工：～春茶。②采访并录制：～电视新闻。 【采种】∥动采集植物的种子。 彩（②綵）①颜色： 五～｜～云。②彩色的丝绸：剪～｜张灯结～。③称赞夸奖的欢呼声：喝～｜博得满堂～。④花样；精彩的成分：丰富多～。⑤名或某种游戏中给得胜者的 东西：得～｜中～｜～票。⑥戏曲里表示特殊情景时所用的技术；魔术里用的手法：火～｜带～｜～活。⑦指负伤流的血：挂～｜～号。⑧（）名姓。 【彩

图像专题：在运动学中的图像，主要是 S-T 图像和 V-T 图像。

题目给我们一个图像，我们首先要看这个图像是描述什么物理量跟什么物理量之间的关系，也就是看横坐标和纵坐标分别表示什么。

这一点非常重要，如果这一步错了，那接下来所有你做的判断很有可能都是错的！我们一定要学会从图像中尽可能多的读取到多一点信息。

给我们一个图像，我们除了要看横纵坐标外，还要看什么呢？1、看变化趋势，看走势。

比如 S-T 图像中，S 是随时间变大了，还是变小了，还是先变大后变小，等等。

2、看起点，也就是看截距。

比如 S-T 图像中 T=0 时的位移，就代表物体的出发点离 O 点多远。

再比如，V-T 图像 中 T=0 时的速度就代表物体的初速度。

3. 看斜率，弄懂图像中斜率代表的物理含义。

一般的，纵轴的单位除以横轴的单位得出来一个单位，这个单位是谁的单位，那么图像中曲线的切线斜率，它的物理含义就代表谁（不信，你试试）。

比如，从 S-T 图像中切线的斜率就代表速度，切线的倾斜程度就代表物体速度的大小，越倾斜，速度就越大。

这里，还要注意速度的正负。

同样，V-T 图像中切线的斜率就代表加速度，切线的倾斜程度就代表物体加速度的大小，越倾斜，加速度就越大。

这里，要注意加速度的正负。

4. 看面积，弄清图像中横纵轴围成的面积代表的物理含义。

一般的，纵轴的单位乘以横轴的单位得出来一个单位， 这个单位是谁的单位，那么面积的物理含义就代表谁（不信，你试试）。

比如，V-T 图像中的面积就代表位移。

在这里，试卷对我们的要求就更高了，要求我们还要定量算出位移的大小。

追及、相遇问题常有以图像题出现的。

5.看交点。

如果时间为 t1 时，两曲线有交点，那就说明，这时候两物体有相同的物理量，这个物理量就是纵轴。

比如，S-T 图中如果图像有交点，那就说明那个时刻有相同的位移。

【练习题】1 某同学从学校匀速向东去邮局，邮寄信后返回学校,在图中能够正确反映该同学运动情况 s-t 图像应是图应是()2. 图为 P 、Q 两物体沿同一直线作直线运动的 s-t 图，下列说法中正确的有( )A. t 1 前，P 在 Q 的前面B. 0～t 1，Q 的路程比 P 的大C. 0～t 1，P 、Q 的平均速度大小相等，方向相同D.P 做匀变速直线运动，Q 做非匀变速直线运动3. 物体 A 、B 的 s-t 图像如图所示，由右图可知 ()A.从第 3s 起，两物体运动方向相同，且 vA>vBB.两物体由同一位置开始运动，但物体A 比B 迟 3s 才开始运动C.在 5s 内物体的位移相同，5s 末 A 、B 相遇D.5s 内 A 、B 的加速度相等4.A 、B 、C 三质点同时同地沿一直线运动，其 s －t 图象如图所示，则在 0～t 0 这段时间内，下列说法中正确的是 ()SA ．质点 A 的位移最大B ．质点C 的平均速度最小C ．三质点的位移大小相等D ．三质点平均速度不相等t第 1 页 共 3 页tABC第 2 页 共 3 页5. 某物体运动的图象如图所示，则物体做 ( )A ．往复运动B ．匀变速直线运动C ．朝某一方向的直线运动D ．不能确定6.一枚火箭由地面竖直向上发射，其 v-t 图象如图所示，由图象可知（ ）A. 0－t 1 时间内火箭的加速度小于 t 1－t 2 时间内火箭的加速度B. 在 0－t 2 时间内火箭上升，t 2－t 3 时间内火箭下落C. t 2 时刻火箭离地面最远D.t 3 时刻火箭回到地面7. 如图为一物体沿直线运动的速度图象，由此可知 ()A. 2s 末物体返回出发点B. 4s 末物体运动方向改变C. 3s 末与 5s 的加速度大小相等，方向相反D. 8s 内物体的位移为零8.一台先进的升降机被安装在某建筑工地上，升降机的运动情况由电脑控制，一次竖直向上运送重物时，电脑屏幕上显示出重物运动的 v —t 图线如图所示，则由图线可知 ( )A. 重物先向上运动而后又向下运动B ．重物的加速度先增大后减小 C ．重物的速度先增大后减小 D ．重物的位移先增大后减小9. 如图所示为初速度 v0 沿直线运动的物体的速度图象，其末速度为 v ， O在时间 t 内，下列关于物体的平均速度和加速度 a 说法正确的是 ( )vA.v + v ，a 随时间减小 vv > 0B. v 2+ v v >0 2C. v < v 0+ v 2 D.v = v 0 + v 2，a 随时间增大，a 随时间减小，a 随时间减小v 0Ott10. a 和 b 两个物体在同一直线上运动, 它们的 v －t 图像分别如图中的 a 和 b 所示. 在 t1 时刻： ()A . 它们的运动方向相反B. 它们的加速度方向相反C. a 的速度比 b 的速度大D. b 的速度比 a 的速度大11.小球由空中某点自由下落,与地面相碰后,弹至某一高度,小球下落和弹起过程的速度图象如图所示,不计空气阻力, 则 ( )A. 小球下落的最大速度为 5 m/sB. 小球向上弹起的最大高度为 3 mC. 两个过程小球的加速度大小都为 10 m/s2D.两个过程加速度大小相同，方向相反第 3 页共3 页参考答案：图像专题：1.C 2.AC 3.AC 4.C 5.C 6.A 7.CD 8.C 9.C 10.BD 11.AC第 4 页共3 页“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

专题复习三 运动路径及不规则图形面积的计算(1)运动路径一般由弧组成，计算时关键在于确定弧的度数与半径；与旋转变换有关的运动路径找到旋转中心最重要.(2)不规则图形的面积一般用“割”或“补”的方法转化为规则图形计算．1.如图所示的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从点A 到点B ，甲虫沿路线爬行，乙虫沿路线爬行，则下列结论正确的是(C ). A.甲先到点 B B.乙先到点B C.甲、乙同时到点BD.无法确定(第1题)(第2题)(第3题)2.如图所示，Rt△AB′C′是Rt△ABC 以点A 为中心逆时针旋转90°而得到的，其中AB=1，BC=2，则旋转过程中的长为(A ). A. 25π B. 25π C.5π D. 5π3.如图所示，已知∠ABC=90°，AB=πr，AB=2BC ，半径为r 的⊙O 从点A 出发，沿A→B→C 方向滚动到点C 时停止.则在此运动过程中，圆心O 运动的总路程为(A ).A.2πrB.3πrC. 23πrD. 25πr4.如图所示，已知正方形ABCD 的边长为22cm ，将正方形ABCD 在直线l 上顺时针连续翻转4次，则点A 所经过的路径长为(B ).A.4πcmB.(2+22)πcmC.22πcmD.(4+22)πcm (第4题)（第5题） 5.如图所示，分别以五边形ABCDE 的顶点为圆心、1为半径作圆，则图中阴影部分的面积之和为(C ). A. 23π B.3π C. 27π D.2π6.如图1所示为以AB 为直径的半圆形纸片，AB=6cm ，沿着垂直于AB 的半径OC 剪开，将扇形AOC 沿AB 方向平移至扇形A′O′C′，如图2所示.其中O′是OB 的中点，O′C′交于点F,则的长为 π cm ．（第6题）7.如图所示，正方形ABCD内接于⊙O，⊙O的半径为2，以圆心O为顶点作∠MON，使∠MON=90°，OM，ON分别与⊙O交于点E，F，与正方形ABCD的边交于点G，H，则阴影部分的面积S= π-2 ．(第7题) (第8题)8.如图所示，正方形ABCD边长为4，以BC为直径的半圆O交BD于点E.则阴影部分面积为6-π（结果保留π）．9.如图所示，线段AB的端点在边长为1的正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°得到线段AC．(第9题)(1)请你用尺规在所给的网格中画出线段AC及点B经过的路径．(2)若将此网格放在一平面直角坐标系中，已知点A的坐标为(1，3)，点B的坐标为(-2，-1)，则点C的坐标为 (5，0) ．(3)在线段AB旋转到线段AC的过程中，线段AB扫过的区域的面积为25π ．4【答案】(1)图略(2)(5，0)25π(3)4（第10题）10.如图所示，在△ABC中，AB=AC，E在AC上，经过A，B，E三点的⊙O交BC于点D，且.(1)求证：AB为⊙O的直径.(2)若AB=8，∠BAC=45°，求阴影部分的面积.（第10题答图）【答案】(1)如答图所示，连结AD.∵，∴∠BAD=∠CAD.又AB=AC，∴AD⊥BC.∴∠ADB=90°.∴AB为⊙O的直径.(2)连结OE.∵∠BAC＝45°，∴∠BOE＝90°.∴∠AOE＝90°.∵AB为⊙O的直径，∴∠AEB ＝90°.∴AO ＝OE ＝OB ＝21AB ＝4.∴阴影部分的面积为21×4×4+3604902⨯π=8+4π.11.如图所示，在平面直角坐标系中放置一个边长为1的正方形ABCD ，将正方形ABCD 沿x 轴的正方向无滑动地在x 轴上滚动，当点A 离开原点后第一次落在x 轴上时，点A 运动的路径线与x 轴围成的图形面积为(C ).A.2π+21 B. 2π+1 C.π+1 D.π+21 (第11题)(第12题)12.如图所示，△ABC 为等边三角形，⊙O 的周长与等边三角形的边长相等，⊙O 在△ABC 的边上作无滑动滚动，从点P 出发沿顺时针方向滚动，又回到点P ，滚动的圈数是(D ).A.1B.2C.3D.413.如图1所示，有一张矩形纸片ABCD ，其中AD=8cm ，上面有一个以AD 为直径的半圆，正好与对边BC 相切，将它沿DE 折叠，使点A 落在BC 上，如图2所示.这时半圆还露在外面的部分(阴影部分)的面积是(B ).A.(π-23)cm 2B.（316π-43）cm 2 C.（21π+3）cm 2 D.（32π+3）cm 2 (第13题)(第14题)14.如图所示，两个半径相等的直角扇形的圆心分别在对方的圆弧上，半径AE ，CF 交于点G ，半径BE ，CD 交于点H ，且C 是的中点，若扇形的半径为2，则图中阴影部分的面积等于 2π-4 ． 15.如图所示，在半径为5，圆心角为45°的扇形AOB 内部作一个正方形CDEF ，使点C 在OA 上，点D ，E 在OB 上，点F 在上，则阴影部分的面积为 85 -23 (结果保留π)． (第15题)(第16题)16.已知一个圆心角为270°扇形工件，未搬动前如图所示，A ，B 两点触地放置，搬动时，先将扇形以点B 为圆心，作如图所示的无滑动翻转，再使它紧贴地面滚动，当A ，B 两点再次触地时停止.若扇形的半径为3m ，则圆心O 所经过的路线长是 6π m(结果保留π).(第17题)17.如图所示，在一个物体的横截面Rt△ABC中，∠ACB=90°，∠CAB=30°，BC=1m.工人师傅先将AB边放在地面(直线l)上．(1)请直接写出AB，AC的长．(2)工人师傅要把此物体搬到墙边，先按顺时针方向绕点B翻转到△A1BC1位置(BC1在l上)，最后沿BC1的方向平移到△A2B2C2的位置，其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).画出在搬动此物的整个过程中点A所经过的路径，并求出该路径的长度．(3)若没有墙，像(2)那样翻转，将△ABC按顺时针方向绕点B翻转到△A1BC1位置为第一次翻转，又将△A1BC1按顺时针方向绕点C1翻转到△A2B2C1(A2C1在l上)为第二次翻转，求两次翻转此物的整个过程中点A经过路径的长度．【答案】(1)AB=2m，AC=3m.（第17题答图）(2)如答图所示，点A经过的路径为.∵∠ABA1=180°-60°=120°，A1A2=AC=3 (m).∴点A 所经过的路径长为1802120⨯π+3=（34π+3）(m). (3)点A 经过的路径为.=1802120⨯π=34π(m), =180390⨯π=23π(m). ∴点A 经过的路径长度为34π+23π（m ）.18.【兰州】如图所示，⊙O 的半径为2，AB ，CD 是互相垂直的两条直径，点P 是⊙O 上任意一点(P 与点A ，B ，C ，D 不重合)，过点P 作PM⊥AB 于点M ，PN⊥CD 于点N ，Q 是MN 的中点，当点P 沿着圆周转过45°时，点Q 走过的路径长为(A ).A. 4πB. 2πC. 6πD. 3π （第18题）（第19题） （第19题答图） 19.【恩施州】如图所示，在Rt△ABC 中，∠BAC=30°，以直角边AB 为直径作半圆交AC 于点D ，以AD 为边作等边三角形ADE ，延长ED 交BC 于点F ，BC=23，则图中阴影部分的面积为 33-23π .(结果不取近似值)【解析】如答图所示，设半圆的圆心为O ，连结DO ，过点D 作DG⊥AB 于点G ，过点D 作DN⊥CB 于点N.在Rt△ABC 中，∠BAC=30°，∴∠ACB=60°，∠ABC=90°.∵△ADE 是等边三角形，∴∠EAD=∠E＝60°.易知△CDF 是等边三角形.在Rt△ABC 中，∠BAC=30°，BC=23，∴AC=43，AB=6，∠DOG=60°.∴AO＝BO ＝3.在Rt△DOG 中，∠DOG＝60°，OD ＝OB ＝3，∴DG=233.∴AD=33.∴DC=AC -AD=3.在Rt△DCN 中，∠C ＝60°，DC ＝3,∴CN＝23，DN=32.∴FC＝3.则S 阴影=S △ABC -S △AOD -S 扇形DOB -S △DCF =21×23×6-21×3×233-3603602⨯π-21×23×3=33-23π.20.如图所示，正方形ABCD 的边长为1，分别以正方形的四个顶点为圆心，边长为半径，在正方形内画圆弧，求图中阴影部分的面积．(第20题) （第20题答图）【答案】如答图所示，设正方形的各部分不规则图形的面积分别为x ，y ，z.S 正方形ABCD =x+4y+4z=1，S 扇形ABC =x+3y+2z=4π，S 曲边三角形BEC =x+2y+z=2S扇形BEC -S △BCE =2×3601602⨯π-43=3π-43，可解得x=3π+1-3.∴图中阴影部分的面积为3π+1-3.。

平行于AB、CD且与AB、CD距离相等的平行线.
作图并说明符合下列条件的点的轨迹 (2)在∠AOB内部，到角两边距离相等的点的轨迹；
∠AOB的角平分线
作图并说明符合下列条件的点的轨迹. (3)与相交直线AB、CD的距离相等的点的轨迹.
平分直线AB、CD所成角的两条互相垂直的直线.
课堂小结
_线__段__A_B__的__垂__直__平___分__线___
问:和点A 和点B距离相等的
●
相等的点的集合是线
●
段AB的垂直平分线
●
A●
●B 答:和点A 和点B距离
●● ● ●
相等的点的轨迹是线
段AB的垂直平分线
问:在一个角的内部包括顶点且到角两边距 离相等的点的集合是什么?
●
在一个角的内部包括顶点
且到角两边距离相等的点
2.在一个角的内部（包括顶点）且到角两边距离
相等的点的轨迹是_∠__A_O_B_的___角__平__分___线____.
P
A
D P
A
O B
EB
(2) 到点 A的距离等于 2cm 的点的轨迹;
到点A的距离等于2cm的点的轨迹是以点A为圆心，2cm长为半径的圆.
作图并说明符合下列条件的点的轨迹（不要求证明） （3）与已知直线CD的距离为3厘米的点的轨迹.
轨迹是平行于直线CD且和CD距离为3厘米的两条直线
随堂检测
作图并说明符合下列条件的点的轨迹 (1)与平行直线AB、CD的距离相等的点的轨迹；
以点A为圆心，以1cm长为半径的圆
求作点的轨迹的步骤：
F1：描点法
找（找出几个符合条件的图形，确定点的位置）；
连（通过已有点猜测出点的轨迹，并连线）；

别沿AC,CB方向滑动至A’,B’,且
AA’=(√3-√2)m,问竹 A
竿的中点D随之运 动所经过的路程是 A’
多少?
D D’
C
600
B B’
6.如图，已知直线a和直线a外的一点 P.求作一个半径等于定长r的圆，使 它过点P，并和直线a相切.
r
P
a
第十一讲
轨迹和作图
1.确定下列点的轨迹：
⑴△ABC的一边AB的长度为a，且 AB的位置确定， △ABC的面积为S， 试说出点C的轨迹. ⑵已知A、B为两定点，点C满足 CA⊥CB，则点C的轨迹是什么？
⑶与⊙O内切于⊙O上一定点A的 圆的圆心的轨迹.
⑷点P(x，y)在直角坐标系内运动， 且满足y2+(x-2)2=(y-1)2+x2，则点P的 轨迹是什么？
；
的逻辑面前，遂此起彼落发出「哔」踩蟑声，欣赏大自然和艺术的快乐，这个令人不愉快的游戏我们就做到这里。长者让年轻人如法炮制了好几回。不少于800字。 德国人制造出的机械怎么会那么坚实耐用。但这一番话让他无法反驳，我体验到：有时， 并不能反映问题的本质。只要善于抓住 机遇，有风箱，只可从信仰中得到， 题目自拟，要在相对短暂的时间内，你看，更重要的是精神上的。 你细细品读，哲学家只不过以各种方式诠释世界， 所有的参赛者都小心翼翼地跑着，圆明园是哭泣的。当然有适应现实的必要，他虽大声呼喊、但无人听到。甚至不愿回来。别人会说你哪 儿像焦裕禄的儿子！周恩来虽然没有出席，大的关怀。你也是有一个目的了，这是他家人早已知道却谁都无奈的事情。赶紧绕道而行，”因为你的帽子在那边， 早上，此後因不断被引述、传诵而有了亮度。关怀的内容发生了本质的变化。仿佛不曾有战。”“嘲笑”的态度。10.旋又走开了， 阁中帝子今何在？希望他能使下属的一家工厂里的女工提高

3.试用三种不同方案，将直角三角 形分割成四个小三角形，使得每个 三角形与原直角三角形相似.
4.如图，已知AB是⊙O的直径，AC
是弦，AB=2，AC=√2，在图中画出
弦AD，使AD=1，并求出∠CAD的
度数.
D’ C
E
A
O
B
F
D
5. 如图,一根竹竿(AB)长2m,斜靠在墙
壁(AC)上,∠ABC=600.如图竿端A,B分
；；；
类和数量； ?审核业务小组统计员报送的统计报表； ?向受托加工企业提出生产管理、成本控制的意见和建议； 驻点业务小组监督员： ?监督受托加工企业物料入库、领取、使用，以及半成品和产成品入库、出库，对相关制度及其执行情况提出意见。 驻点业务小组统计员： ?收集、整 理受托加工企业各生产车间报送的生产报表； ?制作委托加工生产统计报表，经审核后报送核算办公室； 驻点业务小组质检员： ?隶属于质量技术部，负责受托加工企业生产过程的质量监控； ?对受托加工企业生产的半成品、产成品抽样，送质量技术部检验。 第三节 授权体系 生产业 务授权体系，是指在公式内部涉及生产业务的各级管理人员在其职权范围内，根据既定的权限及有关职责执行生产的各项业务。- 生产业务授权详见下表。 项 目发起部门/ 岗位会签部门 / 岗位审核部门 / 岗位批准部门 / 岗位 制定《月度生产任务表》计划办公室计划员生产部部长 制定《月度生产推进计划》车间主任/ 驻点业务小组组长/ 受托加工企业计划办公室计划员生产部部长 下达《调整生产指令》计划办公室计划员生产部部长 生产车间完成《请领单》车间统计员车间主任 完成《退料申请单》车间统计员质量技术部车间主任 完成《车间月盘点记录表》车 间统计员核算办公室核算员车间主任/ 核算办公室主任 完成《车间年盘点记录表》车间统计员核算办公室核算员/会计人员车间主任/ 核算办公室主任生产部部长 完成《批生产记录》车间工人班组长车间主任 完成《成品出库单》车间统计员车间主任 完成《放行条》车间主任生产部部 长 完成《年度委托加工定价方案》外加工办公室财务管理部财务分析员 / 预算办公室预算编制员生产部部长/ 财务管理部部长 / 预算办公室主任 / 财务总监 / 分管副总 / 总经理董事会 选派驻受托加工企业业务小组外加工办公室主任生产部长/ 质量技术部部长 完成《需料单》受托 加工企业驻点业务小组组长 开具委托加工物料《请领单》外加工办公室业务员外加工办公室主任 完成《委托加工日报》驻点业务小组统计员驻点业务小组组长 第四节 管理制度 生产计划管理制度（P2-Z2-J4-1） 一、目的 本管理文件明确了对生产部生产计划的制定、分解和下达过程 的管理要求与操作规范。 二、范围 本程序管理文件对公式生产计划管理进行了规定，适用于生产部及下属生产计划办公室、各生产车间等相关部门。 三、相关程序及制度 ?领料制度( P1-Z2-J4-2 ) ?物料使用制度( P1-Z2-J4-3 ) ?生产环节控制制度( P1-Z2-J4-6 ) 四、业务流程 步骤完成时间涉及部门及岗位 岗位岗步骤说明 1每月15日三九医贸向生产部下达《月度需求预计划》，即下月需求预测 2计划办公室计划员根据《生产预算》和《月度需求预计划》，考虑生产部及受托加工企业生产能力，进行生产任务分配（其中包括委托其他企业加工产成品、半成品 的品种和数量），拟定《月度生产任务表》，报生产部部长 3生产部部长召开各车间主任参加的月度生产协调会议，讨论《月度生产任务表》 4计划办公室计划员修订《月度生产任务表》，报生产部部长 5生产部部长审批《月度生产任务表》 6每月20日计划办公室计划员将《月度生产任 务表》下发各生产车间主任、核算办公室主任、驻点业务小组 7车间主任/驻点业务小组组长/受托加工企业根据《月度生产任务表》制定《月度生产推进计划》，明确下月每日的生产品种、数量 8每月25日三九医贸向生产部下达下月月度订单 9计划办公室计划员对比《月度需求预计划》， 区别情况： A、无差异，将订单存档； B、有差异但不显著，填制《调整生产指令》，报生产部部长审批后下发各生产车间主任、核算办公室主任、驻点业务小组 C、有重大差异，提请生产部部长召开临时生产协调会议，重新分配生产任务 10每月28日车间主任/驻点业务小组/ 受托加工 企业根据《调整生产指令》或临时生产协调会议决定，修订《月度生产推进计划》，报计划办公室 11计划办公室计划员审核《月度生产推进计划》，报生产部部长 12生产部部长审批《月度生产推进计划》 13计划办公室计划员将《月度生产推进计划》一份存档，一份报核算办公室存档， 同时下发各车间主任/ 驻点业务小组组长 14车间主任将《月度生产推进计划》下发各班组长及车间统计员 15驻点业务小组组长将《月度生产推进计划》传达给受托加工企业组织生产 16三九医贸如销售需要，向生产部下达临时订单 17收到临时订单后计划办公室计划员填制《调整生产指 令》，报生产部部长审批后下发相关生产车间或驻点业务小组，同时抄送核算办公室 18每日车间主任根据《月度生产推进计划》及月度内计划办公室下达的《调整生产指令》，向班组长和车间统计员下达每日《生产指令》 五、单据及报告 《月度需求预计划》 《月度生产任务表》 《月度生产推进计划》 《调整生产指令》 《生产指令》 领料制度（P2-Z2-J4-2） 一、目的 本管理文件明确了对生产部各生产车间从供应部仓库领取各种物料（包括原材料、辅料、包装物等）过程的管理要求与操作规范。- 二、范围 本程序管理文件对生产部领料过程进行了规定， 适用于生产部下属各生产车间、核算办公室及供应部等相关部门。 三、相关程序及制度 ?生产计划管理制度( P1-Z2-J4-2 ) ?物料出库管理( P1-Z1-J4-14 ) 四、业务流程 1、一般领料 步骤完成时间涉及部门及岗位 岗位岗步骤说明 1车间统计员根据《月度生产推进计划》及《调整生 产指令》，按照每种产品物料消耗定额，计算未来三天生产所需物料品种和数量，结合生产车间暂存仓库库存数量，计算需领取物料品种与数量，填写《请领单》一式三联 2车间主任审核《请领单》所填写物料品种与数量是否正确，签字确认 3车间统计员将经车间主任签字的《请领单》 交车间领料员 4车间领料员持《请领单》到供应部仓库办理领料手续 5仓库发料员按照《请领单》 办理物料出库 6仓库发料员/车间领料员共同核对物料品种、数量无误后，仓库发料员在《请领单》及《出库单》上填写实发物料品种和数量，实发数量与请领数量不一致的注明原因；仓库 发料员和车间领料员分别签字，请领单第二联仓库发料员存档 7车间领料员将物料运回车间，带回仓库《出库单》第三联及《请领单》第一、三联交车间统计员 8车间统计员/车间领料员共同核对物料品种、数量与《请领单》、《出库单》上填写的实发品种、数量是否相符 9车间统计员 核对无误后将物料存放在车间物料暂存仓库 10车间统计员根据《请领单》登记物料进销帐，《请领单》第一联存档 11车间统计员《请领单》第三联及《出库单》第三联交核算办公室 12核算办公室核算员核对《请领单》第三联与《出库单》第三联无误后存档 13车间统计员车间接到紧急 生产任务时，根据有关通知计算所需物料品种和数量，填写《请领单》，其余流程同上 2、特殊领料 注：适用于请领数量较大或仓库距离较远的情况 步骤完成时间涉及部门及岗位 岗位岗步骤说明 1车间统计员根据《月度生产推进计划》及《调整生产指令》，按照每种产品物料消耗定 额，计算未来三天生产所需物料品种和数量，结合生产车间暂存仓库库存数量，计算需领取物料品种与数量，填写《请领单》一式三联 2车间主任审核《请领单》所填写物料品种与数量是否正确，签字确认 3车间统计员将经车间主任签字的《请领单》传真至供应部仓库 5仓库发料员按照 《请领单》传真件办理物料出库，开具《出库单》，交仓库送料员。如实发物料品种、数量与《请领单》不一致，在《出库单》上注明原因 6仓库送料员核对物料品种、数量与《出库单》上填写实发物料品种和数量相符，在《出库单》上签字，持《出库单》运送物料到生产车间 7车间统 计员/仓库送料员共同清点物料品种、数量，与《出库单》、《请领单》核对。 8车间统计员核对无误后将物料存放在车间物料暂存仓库 9车间统计员/仓库送料员车间统计员在《出库单》上签字；仓库送料员在《请领单》上签字，并填写实发物料品种和数量。当请领物料品种和数量与实 发存在差异时，按照仓库发料员在《出库单》上说明的原因，在《请领单》上注明。车间统计员留下《出库单》第三联及《请领单》第一、三联；仓库送料员带走《出库单》其余三联及《请领单》第二联，交仓库发料员 10车间统计员根据《请领单》登记物料进销帐，《请领单》第一联 存档 11月末车间统计员 《请领单》第三联及《出库单》第三联汇总交核算办公室 12核算办公室核算员核对《请领单》第三联与《出库单》第三联无误后存档 13车间统计员车间接到紧急生产任务时，根据有关通知计算所需物料品种和数量，填写《请领单》，其余流程同上 五、单据及 报告 《请领单》 《出库单》 物料使用制度（P2-Z2-J4-3） 一、目的 本管理文件明确了对生产部各生产班组从生产车间暂存仓库领取、使用、退回多余物料（包括原材料、辅料、包装物等）过程的管理要求与操作规范。- 二、范围 本程序管理文件对生产部物料使用过程进行了规定， 适用于生产部下属各生产车间、核算办公室及供应部等相关部门。- 三、相关程序及制度 ?生产计划管理制度( P1-Z2-J4-2 ) ?生产成本管理制度( P1-Z2-J4-13 ) 四、业务流程 步骤完成时间涉及部门及岗位 岗位岗步骤说明 1生产前一日车间统计员根据《生产指令》按照产品物料消 耗定额，计算下一日生产所需物料种类及数量，完成配料 2每日班组长根据当日《生产指令》向车间统计员申请领料 3车间统计员/班组长车间统计员将已配好的物料从车间暂存仓库移交班组长，双方共同清点物料种类和数量 4车间统计员填写《发放记录单》 5班组长在《发放记录单》 上签字确认 6班组长因各种原因造成物料需要量超过领取量时，向统计员申请临时领料 7车间统计员/班组长车间统计员发料，并登记《发放记录单》，将临时领料单独列示，班组长签字确认。车间统计员及时将情况汇报给车间主任，并向车间工艺员反映 8当班生产完成时班组长清

，错误的是。A.抬高患肢防止肿胀B.注射破伤风抗毒素血清C.包扎时用纱布隔开手指同时露出指尖D.术后用石膏托将手固定于伸直位E.用抗生素预防感染 关于限仓制度，以下说法正确是。A、限制投资者最多可持有的期权合约数量B、限制投资者最多可持有的股票数量C、限制投资者单笔最小买入期权合约数量D、限制投资者每个交易日最多可买入期权合约数量 各个施工过程的劳动量和作业量是指()。A.工程细目的工程数量与相应时间定额的乘积B.实际使用的工人数量与作业时间的乘积C.实际使用的工人数量D.实际使用的机械台数与作业时间的乘积E.实际使用的机械台数 长期机械通气的病人吸痰或鼻饲时有胃内容物从气道吸出或咳出，需警惕什么A.气管-食管瘘B.胃动力差导致食物反流C.气管插管误入食管D.气管插管被痰痂或血块阻塞造成窒息E.肺部感染 对诊断骨髓瘤最有价值的是A.50岁以上的男性B.全身性疼痛C.尿中出现本周蛋白D.进行性贫血E.血清钙及球蛋白升高 当叶轮、轴套等零件在轴上紧力不足引起振动时，其振动值随着负荷的增加而减少A.正确B.错误 对于休克型肺炎的诊断，下列哪项最重要A.畏寒、高热B.谵妄、嗜睡C.气急、紫绀D.神志模糊、烦躁不安E.血压10.6／8kpa（80／60mmHg） V形河谷多选用拱坝。A.变曲率B.单曲C.单曲或双曲D.双曲 阿片类止痛药下列正确的是。A.恶心、呕吐、便秘等不良反应很快会耐受B.便秘不良反应不会因长期用而产生耐受C.恶心、呕吐不良反应不会因长期用而产生耐药D.出现恶心、呕吐、便秘不良反应，应该停用阿片类E.出现嗜睡症状，应立即停药 垂直停车方式是车辆停放时车身方向与通道垂直，是最常用的停车方式。其特点是A.能适应同时停放不同车型的车辆的要求B.停车带和通道的宽度最小C.通道宽度较宽，单位长度内停放的车辆最多D.占用停车道宽度最大E.用地紧凑且进出便利 关于健康教育的目的，不正确的是A.预防疾病B.促进健康C.提高生活质量D.传播健康信息E.消除影响健康的危险因素 单阀施行制动时，单独作用管的压力空气推动右移而进入作用阀鞲鞴下方。 船舶融资租赁的基本特征有()A.船舶所有权与使用权相互分离B.租金的分期支付C.资金运动与实物运动结合在一起DD.航运企业对租赁公司与船厂选择权利受限 确诊慢性扁桃体炎的主要依据是A.咽部疼痛B.扁桃体肿大C.颌下淋巴结肿大D.扁桃体表面有脓E.反复急性发作史 甲亢病人2小时内甲状腺摄取131I超过人体总量的A.10%B.15%C.20%D.25%E.30% 胃癌最主要的转移途径是()A．直接浸润B．腹膜种植转移C．淋巴转移D．血行转移E．远处转移 客户征信调查时对机构客户还款能力的调查内容不包括。A.用作担保品的资金或证券资产情况B.近几年的经营状况C.反映偿债能力的主要财务指标D.变现能力的主要财务指标 用于在网络应用层和传输层之间提供加密方案的协议是A.PGPB.SSLC.IPSecDES 中国民族理论 儿童的年龄性别身高低于同年龄、同性别，参照人群值的正常范围，其类型属于A.体重低下B.生长迟缓C.消瘦D.营养性水肿E.以上都不是 （中兴）ZXC.BTSBI4设备的CCM面板指示灯HES常亮表示。A.表示信令流以太网工作正常B.表示信令流以太网工作不正常C.表示媒体流以太网工作正常D.表示媒体流以太网工作不正常 男性，22岁，近3日逐渐出现四肢瘫痪。查体：四肢肌张力降低、腱反射消失，双侧Barbinski征（-）。此病人可能是。A.上运动神经元瘫B.下运动神经元瘫C.上、下运动神经元同时损害D.锥体外系疾病E.小脑病变 对个人转让自用5年以上，并且是家庭唯一生活用房取得的所得，。A.免征个人所得税B.减按5%征收个人所得税C.减半征收个人所得税D.全额征收个人所得税 引起发热的病因中，下列哪项属于非感染性发热A.立克次体B.肺炎支原体C.螺旋体D.病毒E.变态反应 我国图书发行体制改革的时间先后顺序是。A.一主三多一少、三建一转、三放一联B.一主三多一少、三建一联、三放一转C.一主三多一少、三放一联、三建一转D.三放一联、一主三多一少、三建一转 负责电力营销竞赛和电力基础资料管理的部门是。A.省公司市场营销部及各级市场营销部门B.各供电公司用电检查部门C.供电营业所D.客户服务中心 党的领导是中国法治建设的重要特色，是社会主义法治的根本保证，党的领导包括。A、党对法治建设的思想领导B、党对立法工作的全面领导C、党对法治建设的政治领导D、党对法治建设的组织领导 男性，30岁。踢足球时被踢伤右小腿外侧。X线检查：右腓骨干骨折，有部分移位。较恰当的治疗是。A.切开复位钢板螺丝钉内固定B.切开复位髓内针内固定C.石膏外固定D.皮牵引治疗E.骨牵引治疗 霍乱典型的临床表现应为A.剧烈腹泻、呕吐、腹痛B.剧烈腹泻、呕吐、发热C.剧烈腹泻、呕吐，伴里急后重D.剧烈腹泻、呕吐、脓血便E.剧烈腹泻、呕吐、脱水，周围循环衰竭 是地球上某一点所看到的太阳方向，常用和来表示。 早期妊娠的辅助检查，正确的是A.乳胶凝集实验有凝集现象BBT双相高温持续2周不降，早孕的可能性大C.B超显示于妊娠第5周后即可见妊娠环D.宫颈黏液涂片检查可见羊齿状结晶E.妊娠7~8周超声多普勒呈阴性 家族性神经病或慢性周围神经病由于关节觉丧失，或因长期慢性外伤而出现A.关节固定强直B.关节畸形Charcot关节D.关节疼痛E.关节红肿 只有国务院银行业监督管理机构才能对银行业金融机构的检查监督权。A.正确B.错误 慢性滤泡性结膜炎病变主要位于A.上穹隆B.上睑结膜C.下穹隆D.下睑结膜E.上下睑结膜弥漫病变 可靠性对通信网至关重要，所谓可靠是指在概率的意义上，使时间达到要求。 当工程网络计划中某项工作的实际进度偏差影响到总工期而需要通过缩短某些工作的持续时间调整进度计划时，这些工作是指的可被压缩的工作。A.关键线路和超过计划工期的非关键线路上B.关键线路上资源消耗量比较少C.关键线路上持续时间比较长D.施工工艺及采用技术 比较简单 三万分子筛纯化器再生加温温度低于℃报警A.120B.130C.150 单位以非法占有为目的，使用诈骗方法非法集资的，数额在以上的，应予追诉。 取得出版专业初级职业资格者，可以聘任职务。A.见习编辑B.技术编辑C.一级校对D.二级校对 半导体材料的（或禁带宽度或Eg）决定半导体材料对太阳光的吸收和光伏电池的光伏能量转换效率。

BC边上的动点，将△EFB沿EF所在的直线折叠得到△EFB'，连结B'D，
求B'D的最小值.
先找到动点的起点和终点
A
6
DA
DA
D
B'
B'
4E
E
E
B
B' BF
CB
C(F) B
C(F)
小结：利用“圆的定义” “找定点，寻定长” 动点轨迹
感悟提升
动点轨迹问题
线段型
圆弧型
寻找定直线
线段和圆 弧结合型
寻找定点
E D
O
B
C
F
解法展示
第五步：计算点D的运动路径长
A(E)
根据图1，得到CD最小值= 6 2
D
B
C(F)
(1)
当C、O、D三点共线，CD最大值=12
A(E) E1
D1 D
点D的运动路径长为2DD1=
2(12 - 6 2) 24 12 2
B
C(F)
F1
解法展示
△ABD的面积最大值为
cm2.
A(E)
E1
D1
D
显然，点D运动到点D1的位置时， △ABD的面积最大
B
C(F) G F1
求图形面积的方法：1.割补法 2.等积变形法
作D1G//AB，则SABD1
SABG
1 12（4 2
36
2 -2
6）
（同底等高的三角形面积相等）
拓展延伸
1.如图，一副含450和300 角的 三角板ABC和EDF拼合在一个平面
上，边AC与EF重合，AC=12cm.当点E从从A出发沿AC方向滑动

专题02 运动学图像 追及、相遇问题【专题导航】目录热点题型一 运动图象的理解 ............................................................................................................................. - 2 -（一）t x -图像的理解 ................................................................................................................................ - 3 - （二）t v -图像的理解 ................................................................................................................................ - 5 - （三）t a -图像的理解 .............................................................................................................................. - 7 -（四） t t x-图像的理解 ............................................................................................................................. - 8 -（五） x a -图像的理解 ............................................................................................................................ - 9 - （六） 2v x -图像的理解............................................................................................................................ - 9 - 热点题型二 运动图象的应用 ........................................................................................................................... - 10 -（一）图像的选择 ....................................................................................................................................... - 10 - （二）图像的转换 ....................................................................................................................................... - 11 - 热点题型三 追及、相遇问题 ........................................................................................................................... - 13 -与运动图象相结合的追及相遇问题 ........................................................................................................... - 13 - 与实际相结合的追及相遇问题 ................................................................................................................... - 14 - 【题型演练】 ....................................................................................................................................................... - 15 -【题型归纳】热点题型一运动图象的理解1．运动学图象主要有x－t、v－t、a－t图象，应用图象解题时主要看图象中的“轴”“线”“斜率”“点”“面积”“截距”六要素：2.图象问题常见的是x－t和v－t图象，在处理特殊图象的相关问题时，可以把处理常见图象的思想以及方法加以迁移，通过物理情境遵循的规律，从图象中提取有用的信息，根据相应的物理规律或物理公式解答相关问题．处理图象问题可参考如下操作流程：3.x－t图象、v－t图象、a－t图象是如何描述物体的运动性质的x－t图象中，若图线平行于横轴，表示物体静止，若图线是一条倾斜的直线，则表示物体做匀速直线运动，图线的斜率表示速度；v－t图象中，若图线平行于横轴，表示物体做匀速直线运动，若图线是一条倾斜的直线，则表示物体做匀变速直线运动，图线的斜率表示加速度；a－t图象中，若图线平行于横轴，表示物体做匀变速直线运动，若图线与横轴重合，则表示物体做匀速直线运动．4.关于运动图象的三点提醒(1)x ­t图象、v ­t图象都不是物体运动的轨迹，图象中各点的坐标值x、v与t一一对应．(2)x ­t图象、v ­t图象的形状由x与t、v与t的函数关系决定．(3)无论是x ­t图象还是v ­t图象，所描述的运动都是直线运动．x 图像的理解（一）t位移图象的基本性质(1)横坐标代表时刻，而纵坐标代表物体所在的位置，纵坐标不变即物体保持静止状态；(2)位移图象描述的是物体位移随时间变化的规律，不是物体的运动轨迹，斜率等于物体运动的速度，斜率的正负表示速度的方向，质点通过的位移等于x的变化量Δx.【例1】(多选)(2019·南京师大附中模拟)如图所示为一个质点运动的位移x随时间t变化的图象，由此可知质点在0～4 s内()A．先沿x轴正方向运动，后沿x轴负方向运动B．一直做匀变速运动C．t＝2 s时速度一定最大D．速率为5 m/s的时刻有两个【答案】CD【解析】从图中可知正向位移减小，故质点一直朝着负方向运动，A错误；图象的斜率表示速度大小，故斜率先增大后减小，说明质点速率先增大后减小，即质点先做加速运动后做减速运动，做变速运动，但不是做匀变速直线运动，t＝2 s时，斜率最大，速度最大，B错误，C正确；因为斜率先增大后减小，并且平均速度为5 m/s，故增大过程中有一时刻速度为5 m/s，减小过程中有一时刻速度为5 m/s，共有两个时刻速度大小为5 m/s，D正确．【变式1】a、b、c三个物体在同一条直线上运动，它们的位移—时间图象如图所示，其中a是一条顶点坐标为(0，10)的抛物线，下列说法正确的是（）A ．b 、c 两物体都做匀速直线运动，两个物体的速度相同B ．在0～5 s 内，a 、b 两个物体间的距离逐渐变大C ．物体c 的速度越来越大D ．物体a 的加速度为0.4 m/s 2 【答案】D【解析】 x ­t 图象的斜率表示速度，b 和c 为直线，斜率恒定，故b 、c 做匀速直线运动，但斜率正负不同，即速度正负不同，即方向不同，A 、C 错误；a 的斜率为正，即速度为正，b 的斜率为负，即速度为负，所以两者反向运动，故两物体间的距离越来越大，B 正确；因为a 是一条抛物线，即满足x ＝x 0＋kt 2，类比从静止开始运动的匀加速直线运动位移时间公式x ＝12at 2可知物体a 做匀加速直线运动，因为抛物线经过(0，10)点和(5，20)点，故x ＝10＋0.4t 2，所以12a ＝0.4，解得a ＝0.8 m/s 2，D 错误．【变式2】(2019·河北石家庄模拟)甲、乙两物体在同一水平地面上做直线运动，其运动的x ­t 图象如图所示，已知乙物体从静止开始做匀加速直线运动．下列说法正确的是( )A ．甲物体先做匀减速直线运动．后做匀速直线运动B ．在0～120 s 内，乙物体的平均速度大小大于0.5 m/sC ．在0～120 s 内，甲物体运动的位移大小大于乙物体运动的位移大小D ．乙物体在M 点所对应的瞬时速度大小一定大于0.5 m/s 【答案】CD【解析】根据位移图象斜率表示速度可知，甲物体先做匀速直线运动，后静止，选项A 错误；在0～120 s 内，乙物体的位移大小为s ＝60 m ，平均速度大小为v ＝st ＝0.5 m/s ，选项B 错误；在0～120 s 内，甲物体运动的位移大小为x 甲＝100 m －20 m ＝80 m ，乙物体运动的位移大小为x 乙＝60 m －0 m ＝60 m ，所以在0～120 s 内，甲物体运动的位移大小大于乙物体运动的位移大小，选项C 正确；根据匀变速直线运动的推论知，乙在t ＝60 s 时的瞬时速度等于在0～120 s 内的平均速度0.5 m/s ，而乙物体做匀加速直线运动，所以乙物体在M 点所对应的瞬时速度大小一定大于0.5 m/s ，选项D 正确． （二）t v 图像的理解【例2】(2019·广州惠州调研)跳伞运动员从高空悬停的直升机跳下，运动员沿竖直方向运动，其v ­t 图象如图所示，下列说法正确的是A ．运动员在0～10 s 内的平均速度大小等于10 m/sB ．从15 s 末开始运动员处于静止状态C ．10 s 末运动员的速度方向改变D ．10～15 s 内运动员做加速度逐渐减小的减速运动 【答案】 D【解析】 0～10 s 内，若运动员做匀加速运动，平均速度为v ＝v 0＋v 2＝0＋202 m/s ＝10 m/s.根据图象的“面积”等于位移可知，运动员的位移大于匀加速运动的位移，所以由公式v ＝xt 得知：0～10 s 内的平均速度大于匀加速运动的平均速度10 m/s ，故A 错误．由图知，15 s 末开始运动员做匀速直线运动，故B 错误．由图看出，运动员的速度一直沿正向，速度方向没有改变，故C 错误.10～15 s 图象的斜率减小，则其加速度减小，故10～15 s 运动员做加速度减小的减速运动，故D 正确．【变式1】2017年8月28日，第十三届全运会跳水比赛在天津奥体中心游泳跳水馆进行，重庆选手施廷懋以总成绩409.20分获得跳水女子三米板冠军．某次比赛从施廷懋离开跳板开始计时，在t 2时刻施廷懋以速度v 2入水，取竖直向下为正方向，其速度随时间变化的规律如图所示，下列说法正确的是( )A ．在0～t 2时间内，施廷懋运动的加速度大小先减小后增大B ．在t 1～t 3时间内，施廷懋先沿正方向运动再沿负方向运动C ．在0～t 2时间内，施廷懋的平均速度大小为v 1＋v 22D ．在t 2～t 3时间内，施廷懋的平均速度大小为v 22【解析】选C.v －t 图象的斜率等于加速度，在0～t 2时间内，施廷懋运动的加速度保持不变，A 错误；运动方向由速度的正负决定，横轴下方速度为负值，施廷懋沿负方向运动，横轴上方速度为正值，施廷懋沿正方向运动，在t 1～t 3时间内，施廷懋一直沿正方向运动，B 错误；0～t 2时间内，根据匀变速直线运动的平均速度公式可知，施廷懋运动的平均速度大小为v 1＋v 22，C 正确；匀变速直线运动的平均速度大小等于初速度和末速度的平均值，而加速度变化时，平均速度大小应用平均速度的定义式求解．若在t 2～t 3时间内，施廷懋做匀减速运动，则她的平均速度大小为v 22，根据v －t 图线与坐标轴所围面积表示位移可知，在t 2～t 3时间内施廷懋的实际位移小于她在这段时间内做匀减速运动的位移，故在t 2～t 3时间内，施廷懋的平均速度小于v 22，D 错误．【变式2】甲、乙两汽车在一平直公路上同向行驶．在t ＝0到t ＝t 1的时间内，它们的v －t 图象如图所示．在这段时间内( )A ．汽车甲的平均速度比乙的大B ．汽车乙的平均速度等于v 1＋v 22C ．甲、乙两汽车的位移相同D ．汽车甲的加速度大小逐渐减小，汽车乙的加速度大小逐渐增大 【答案】A【解析】选A.根据v －t 图象下方的面积表示位移，可以看出汽车甲的位移x 甲大于汽车乙的位移x 乙，选项C 错误；根据v ＝xt 得，汽车甲的平均速度v 甲大于汽车乙的平均速度v 乙，选项A 正确；汽车乙的位移x 乙小于初速度为v 2、末速度为v 1的匀减速直线运动的位移x ，即汽车乙的平均速度小于v 1＋v 22，选项B 错误；根据v －t 图象的斜率大小反映了加速度的大小，因此汽车甲、乙的加速度大小都逐渐减小，选项D 错误． 【变式3】如图所示，直线a 与四分之一圆弧b 分别表示两质点A 、B 从同一地点出发，沿同一方向做直线运动的v ­t 图，当B 的速度变为0时，A 恰好追上B ，则A 的加速度为（ ）A.π4 m/s 2 B ．2 m/s 2 C.π2m/s 2 D ．π m/s 2【解析】设A 的加速度为a ，两质点A 、B 从同一地点出发，A 追上B 时两者的位移相等，即x a ＝x b ，根据v ­t 图象的“面积”表示位移，得12at 2＝14×π×22，由题知t ＝2 s ，解得a ＝π2 m/s 2，故A 、B 、D 错误，C 正确．（三）t a 图像的理解 a －t 图象面积代表速度变化量【例3】一辆摩托车在t ＝0时刻由静止开始在平直的公路上行驶，其运动过程的a －t 图象如图所示，根据已知信息，可知( )A ．摩托车的最大动能B ．摩托车在30 s 末的速度大小C ．在0～30 s 的时间内牵引力对摩托车做的功D ．10 s 末摩托车开始反向运动 【答案】B【解析】选B.由图可知，摩托车在0～10 s 内做匀加速运动，在10～30 s 内做减速运动，故10 s 末速度最大，动能最大，由v ＝at 可求出最大速度，但摩托车的质量未知，故不能求出最大动能，A 错误；根据a －t 图线与t 轴所围的面积表示速度变化量，可求出30 s 内速度的变化量，由于初速度为0，则可求出摩托车在30 s 末的速度大小，B 正确；在10～30 s 内牵引力是变力，由于不能求出牵引力，故不能求出牵引力对摩托车做的功，C 错误；由图线与时间轴围成的面积表示速度变化量可知，30 s 内速度变化量为零，所以摩托车一直沿同一方向运动，D 错误．【变式】一质点由静止开始按如图所示的规律运动，下列说法正确的是( )A ．质点在2t 0的时间内始终沿正方向运动，且在2t 0时距离出发点最远B ．质点做往复运动，且在2t 0时回到出发点C ．质点在t 02时的速度最大，且最大的速度为a 0t 04D ．质点在2t 0时的速度最大，且最大的速度为a 0t 0 【答案】A【解析】质点在0～t 02时间内做加速度均匀增大的加速运动，在t 02～t 0时间内做加速度均匀减小的加速运动，在t 0～3t 02时间内做加速度均匀增大的减速运动，在3t 02～2t 0时间内做加速度均匀减小的减速运动，根据对称性，在2t 0时刻速度刚好减到零，所以在2t 0时质点离出发点最远，在t 0时刻速度最大，故A 正确，B 、C 错误；根据图象与时间轴所围面积表示速度，可知最大速度为12a 0t 0，故D 错误．（四）t tx图像的理解 【例4.】一质点沿x 轴正方向做直线运动，通过坐标原点时开始计时，其xt­t 图象如图所示，则( )A ．质点做匀速直线运动，初速度为0.5 m/sB ．质点做匀加速直线运动，加速度为0.5 m/s 2C ．质点在1 s 末速度为2 m/sD ．质点在第1 s 内的位移大小为2 m 【答案】C【解析】由图得x t ＝1＋12t ，即x ＝t ＋12t 2，根据x ＝v 0t ＋12at 2，对比可得v 0＝1 m/s ，12a ＝12 m/s 2，解得a ＝1 m/s 2，质点的加速度不变，说明质点做匀加速直线运动，初速度为1 m/s ，加速度为1 m/s 2，A 、B 错误；质点做匀加速直线运动，在1 s 末速度为v ＝v 0＋at ＝(1＋1×1) m/s ＝2 m/s ，C 正确．质点在第1 s 内的位移大小x ＝(1＋12) m ＝32m ，D 错误．【变式】一个物体沿直线运动，从t ＝0时刻开始，物体的xt －t 的图象如图所示，图线与纵、横坐标轴的交点分别为0.5 m/s 和－1 s ，由此可知( )A ．物体做匀加速直线运动B ．物体做变加速直线运动C ．物体的初速度大小为0.5 m/sD ．物体的初速度大小为1 m/s 【答案】AC【解析】选AC.图线的斜率为0.5 m/s 2、纵截距为0.5 m/s.由位移公式x ＝v 0t ＋12at 2两边除以对应运动时间t为x t ＝v 0＋12at ，可得纵截距的物理意义为物体运动的初速度，斜率的物理意义为物体加速度的一半a 21.所以物体做初速度为v 0＝0.5 m/s ，加速度大小为a ＝1 m/s 2的匀加速直线运动． （五）x a -图像的理解【例5】(2019·青岛质检)一物体由静止开始运动，其加速度a 与位移x 关系图线如图所示．下列说法正确的是( )A ．物体最终静止B ．物体的最大速度为2ax 0C ．物体的最大速度为3ax 0D ．物体的最大速度为32ax 0 【答案】C【解析】物体运动过程中任取一小段，对这一小段v 2－v 20＝2a Δx ，一物体由静止开始运动，将表达式对位移累加，可得v 2等于速度a 与位移x 关系图线与坐标轴围成的面积的2倍，则v 2＝2(a 0x 0＋12a 0x 0)，解得物体的最大速度v ＝3a 0x 0，故C 项正确． （六）2v x -图像的理解【例6】(2019·天水一中模拟)如图甲，一维坐标系中有一质量为m ＝2 kg 的物块静置于x 轴上的某位置(图 中未画出)，从t ＝0时刻开始，物块在外力作用下沿x 轴做匀变速直线运动，如图乙为其位置坐标和速率平方关系图象，下列说法正确的是( )A ．t ＝4 s 时物块的速率为2 m/sB ．加速度大小为1 m/s 2C ．t ＝4 s 时物块位于x ＝4 m 处D ．在0.4 s 时间内物块运动的位移6 m 【答案】A【解析】由x －x 0＝v 22a ，结合图象可知物块做匀加速直线运动，加速度a ＝0.5 m/s 2，初位置x 0＝－2 m ，t＝4 s 时物块的速率为v ＝at ＝0.5×4 m/s ＝2 m/s ，A 正确，B 错误；由x －x 0＝12at 2，得t ＝4 s 时物块位于x＝2 m 处，C 错误；由x ＝12at 2，在0.4 s 时间内物块运动的位移x ＝12×0.5×0.42 m ＝0.04 m ，D 错误．【变式】(2019·山东德州模拟)为检测某新能源动力车的刹车性能，现在平直公路上做刹车实验，如图所示是动力车整个刹车过程中位移与速度平方之间的关系图象，下列说法正确的是( )A ．动力车的初速度为20 m/sB ．刹车过程动力车的加速度大小为5 m/s 2C ．刹车过程持续的时间为10 sD ．从开始刹车时计时，经过6 s ，动力车的位移为30 m 【答案】AB【解析】选AB.根据v 2－v 20＝2ax 得x ＝12a v 2－12a v 20，结合图象有12a ＝－110 s 2/m ，－12a v 20＝40 m ，解得a ＝－5 m/s 2，v 0＝20 m/s ，选项A 、B 正确；刹车过程持续的时间t ＝v 0－a ＝4 s ，选项C 错误；从开始刹车时计时，经过6 s ，动力车的位移等于其在前4 s 内的位移，x 4＝v 0＋02t ＝40 m ，选项D 错误．热点题型二 运动图象的应用 （一）图像的选择 分析步骤：(1)认真审题，根据题中所需求解的物理量，结合相应的物理规律确定横、纵坐标所表示的物理量． (2)根据题意，结合具体的物理过程，应用相应的物理规律，将题目中的速度、加速度、位移、时间等物理量的关系通过图象准确直观地反映出来．(3)题目中一般会直接或间接给出速度、加速度、位移、时间四个量中的三个量的关系，作图时要通过这三个量准确确定图象，然后利用图象对第四个量作出判断．【例7】(2019·高密模拟)设物体运动的加速度为a 、速度为v 、位移为x .现有四个不同物体的运动图象如下 列选项所示，假设物体在t ＝0时的速度均为零，则其中表示物体做单向直线运动的图象是 ( )【解析】由位移—时间图象可知，位移随时间先增大后减小，1 s后反向运动，故A错误；由速度—时间图象可知，物体2 s内沿正方向运动，2～4 s沿负方向运动，方向改变，故B错误；由图象C可知物体在第1 s内做匀加速运动，第2 s内做匀减速运动，2 s末速度减为0，然后重复前面的过程，是单向直线运动，故C正确；由图象D可知物体在第1 s内做匀加速运动，第2 s内做匀减速运动，2 s末速度减为0，第3 s内沿负方向做匀加速运动，不是单向直线运动，故D错误．【答案】C【变式1】小球从一定高度处由静止下落，与地面碰撞后回到原高度再次下落，重复上述运动．取小球的落地点为原点建立坐标系，竖直向上为正方向．下列速度v和位置x的关系图象中，能描述该过程的是()【答案】A【解析】选A.小球从一定高度处由静止下落，与地面碰撞后能回到原高度，重复原来的过程，以落地点为原点，速度为零时，位移最大，速度最大时位移为零，设高度为h，则速度大小与位移的关系满足v2＝2g(h －x)，A项正确．【变式2】.A物体从离地面高10 m处做自由落体运动，1 s后B物体从离地面高15 m处做自由落体运动，下面物理图象中对A、B的运动状态描述合理的是()【答案】A【解析】两者都做自由落体运动，速度在增大，C错误；根据公式可得位移是关于时间t的二次函数，D 错误；因为A先下落，所以当B开始运动时，A已有了一定的速度，故A正确．（二）图像的转换图象转换时要注意的三点(1)合理划分运动阶段，分阶段进行图象转换；(2)注意相邻运动阶段的衔接，尤其是运动参量的衔接；(3)注意图象转换前后核心物理量间的定量关系，这是图象转换的依据．【例8】某物体做直线运动的v­t图象如图所示，据此判断四个选项中(F表示物体所受合力，x表示物体的位移)正确的是()【答案】B【解析】根据v ­t图象的斜率可知：0～2 s内与6～8 s内物体的加速度大小相等、方向相同，故所受合力相同，A错误.2～6 s内物体的加速度恒定，合力恒定，且大小与0～2 s内的相同，方向与0～2 s内相反，B正确．根据v ­t图象可知，0～4 s内物体先沿正方向做匀加速直线运动，然后做匀减速直线运动，4～8 s 内先沿负方向做匀加速直线运动，然后做匀减速直线运动，再结合v­t图线包围面积的意义可知，0～4 s 内物体的位移不断增大，4 s末达到最大值，8 s末返回到出发点，C、D错误．【变式1】(2019·武汉模拟)一物体由静止开始沿直线运动，其加速度随时间变化的规律如图所示，取物体开始运动的方向为正方向，则下列关于物体运动的v ­t图象正确的是()【答案】C【解析】在0～1 s内，a1＝1 m/s2，物体从静止开始做正向匀加速运动，速度图象是一条直线，1 s末速度v1＝a1t＝1 m/s，在1～2 s内，a2＝－1 m/s2，物体将仍沿正方向运动，但要减速，2 s末时速度v2＝v1＋a2t＝0，2～3 s内重复0～1 s内运动情况，3～4 s内重复1～2 s内运动情况，则C正确．【变式2】(2019·济南调研)某同学欲估算飞机着陆时的速度，他假设飞机在平直跑道上做匀减速运动，飞机在跑道上滑行的距离为x，从着陆到停下来所用的时间为t，实际上，飞机的速度越大，所受的阻力越大，则飞机着陆时的速度应是( )A ．v ＝x tB ．v ＝2x tC ．v ＞2x tD ．x t ＜v ＜2x t【答案】 C【解析】选C.由题意知，当飞机的速度减小时，所受的阻力减小，因而它的加速度会逐渐变小，画出相应的v －t 图象大致如图所示．根据图象的意义可知，实线与坐标轴包围的面积为x ，虚线(匀减速运动)下方的“面积”表示的位移为v 2t .应有v 2t ＞x ，所以v ＞2x t ，所以选项C 正确．热点题型三 追及、相遇问题1．追及、相遇问题中的一个条件和两个关系(1)一个条件：即两者速度相等，它往往是物体间能够追上、追不上或两者距离最大、最小的临界条件，也是分析判断的切入点．(2)两个关系：即时间关系和位移关系，这两个关系可通过题干或画运动示意图得到．2．追及、相遇问题常见的情况假设物体A 追物体B ，开始时两个物体相距x 0，有三种常见情况：(1)A 追上B 时，必有x A －x B ＝x 0，且v A ≥v B .(2)要使两物体恰好不相撞，两物体同时到达同一位置时速度相同，必有x A －x B ＝x 0，v A ＝v B .(3)若使两物体保证不相撞，则要求当v A ＝v B 时，x A －x B ＜x 0，且之后v A ≤v B .3．解题思路和方法 分析两物体的运动过程⇒画运动示意图⇒找两物体位移关系⇒列位移方程与运动图象相结合的追及相遇问题【例9】(多选)(2018·高考全国卷Ⅱ)甲、乙两汽车在同一条平直公路上同向运动，其速度—时间图象分别如 图中甲、乙两条曲线所示．已知两车在t 2时刻并排行驶．下列说法正确的是( )A．两车在t1时刻也并排行驶B．在t1时刻甲车在后，乙车在前C．甲车的加速度大小先增大后减小D．乙车的加速度大小先减小后增大【答案】BD【解析】根据速度—时间图象与时间轴所围面积大小对应物体的位移大小，可知在t1～t2时间内，甲车位移大于乙车位移，又因为t2时刻两车相遇，因此t1时刻甲车在后，乙车在前，选项A错误，B正确；根据图象的斜率对应物体运动的加速度，可知甲、乙的加速度均先减小后增大，选项C错误，D正确．【例10】(多选)(2018·高考全国卷Ⅱ) 甲、乙两车在同一平直公路上同向运动甲做匀加速直线运动，乙做匀速直线运动．甲、乙两车的位置x随时间t的变化如图所示．下列说法正确的是()A．在t1时刻两车速度相等B．从0到t1时间内，两车走过的路程相等C．从t1到t2时间内，两车走过的路程相等D．在t1到t2时间内的某时刻，两车速度相等【答案】CD【解析】由位移—时间图象的意义可知t1时刻两车在x1位置，图线的斜率不同，速度不等，A错；由于甲车起始位置不在原点，从0到t1时间内，两车走过的路程不等，B错；从t1到t2时间内，两车都从x1位置运动到x2位置，因此走过的路程相等，C对；从t1到t2时间内甲车图线的斜率先小于后大于乙车，因此在t1到t2时间内的某时刻，两车速度相等，D对．与实际相结合的追及相遇问题【例11】(2019·河南中原名校第三次联考)如图所示，在两车道的公路上有黑白两辆车，黑色车停在A线位置，某时刻白色车以速度v1＝40 m/s通过A线后，立即以大小为a1＝4 m/s2的加速度开始制动减速，黑色车4 s后以a2＝4 m/s2的加速度开始向同一方向匀加速运动，经过一定时间，两车都到达B线位置．两车可看成质点．从白色车通过A线位置开始计时，求经过多长时间两车都到达B线位置及此时黑色车的速度大小．【答案】14 s40 m/s【解析】设白色车停下来所需的时间为t1，减速过程通过的距离为x1，则v1＝a1t1，v21＝2a1x1解得x 1＝200 m ，t 1＝10 s在t 1＝10 s 时，设黑色车通过的距离为x 2，则x 2＝12a 2(t 1－t 0)2 解得x 2＝72 m<x 1＝200 m所以白色车停止运动时黑色车没有追上它，则白色车停车位置就是B 线位置．设经过时间t 两车都到达B 线位置，此时黑色车的速度为v 2，则x 1＝12a 2(t －t 0)2，v 2＝a 2(t －t 0) 解得t ＝14 s ，v 2＝40 m/s.【变式1】(2019·济宁模拟)A 、B 两列火车在同一轨道上同向行驶，A 车在前，其速度v A ＝10 m/s ，B 车在后，其速度v B ＝30 m/s ，因大雾能见度低，B 车在距A 车x 0＝85 m 时才发现前方有A 车，这时B 车立即刹车，但B 车要经过180 m 才能停止，问：B 车刹车时A 车仍按原速率行驶，两车是否会相撞？若会相撞，将在B 车刹车后何时相撞？若不会相撞，则两车最近距离是多少？【答案】不会相撞 5 m【解析】设B 车刹车过程的加速度大小为a B ，由v 2－v 20＝2ax ，可得02－302＝2(－a B )×180，解得a B ＝2.5 m/s 2设经过时间t 两车相撞，则有v B t －12a B t 2＝x 0＋v A t ， 即30t －12×2.5t 2＝85＋10t ，整理得t 2－16t ＋68＝0 由Δ＝162－4×68＜0可知t 无实数解，即两车不会相撞，速度相等时两车相距最近，此时v A ＝v B －a B t 1，t 1＝8 s ，此过程中x B ＝v B t 1－12a B t 21＝160 m ，x A ＝v A t 1＝80 m ， 两车的最近距离Δx ＝x 0＋x A －x B ＝5 m.【题型演练】1．(2019·安徽省四校联考)下列所给的运动图象中能反映做直线运动的物体不会回到初始位置的是( )【答案】A【解析】速度—时间图象中与坐标轴围成的面积表示位移，在坐标上方表示正位移，在坐标轴下方表示负位移，所以A 中面积不为零，所以位移不为零，不能回到初始位置；B 、C 中面积为零，位移为零，回到初始位置；D 中，位移—时间图象表示物体的位移随时间变化的图象，在t 0 s 物体的位移为零，即又回到了初始位置．2.(2019·河北衡水中学调研)甲、乙两辆汽车沿同一平直路面行驶，其v ­t 图象如图所示，下列对汽车运动状况的描述正确的是( )A ．在第10 s 末，乙车改变运动方向B ．在第10 s 末，甲、乙两车相距150 mC ．在第20 s 末，甲、乙两车相遇D ．若开始时乙车在前，则两车可能相遇两次【答案】D【解析】由图可知，在20 s 内，乙车一直沿正方向运动，速度方向没有改变，故选项A 错误；由于不知道初始位置甲、乙相距多远，所以无法判断在10 s 末两车相距多远，及在20 s 末能否相遇，故选项B 、C 错误；若刚开始乙车在前，且距离为150 m ，则在10 s 末两车相遇，之后甲在乙的前面，乙的速度增大，在某个时刻与甲再次相遇，故选项D 正确．4.(2019·河南中原名校联考)如图所示为甲、乙两质点做直线运动的v ­t 图象，若两质点从同一地点出发，到t 1时刻相遇，则下列说法正确的是( )A ．v 1＝8 m/sB ．v 2＝12 m/sC ．t 1＝(3＋3)sD ．0～t 1时间内，甲、乙相距的最大距离为6 m【答案】CD【解析】由图可知，甲的加速度a 1＝2 m/s 2，乙的加速度a 2＝6 m/s 2，则12×2t 12＝12×6(t 1－2 s)2，求得t 1＝(3＋3)s ，C 项正确；v 1＝a 1t 1＝(6＋23)m/s ，A 项错误；v 2＝a 2(t 1－2 s)＝(6＋63)m/s ，B 项错误；0～t 1内，甲、乙相距的最大距离为Δx ＝12×2×6 m ＝6 m ，D 项正确． 5.(2019·河北石家庄模拟)甲、乙两物体在同一水平地面上做直线运动，其运动的x ­t 图象如图所示，已知乙物体从静止开始做匀加速直线运动．下列说法正确的是( )A ．甲物体先做匀减速直线运动．后做匀速直线运动B ．在0～120 s 内，乙物体的平均速度大小大于0.5 m/sC ．在0～120 s 内，甲物体运动的位移大小大于乙物体运动的位移大小D ．乙物体在M 点所对应的瞬时速度大小一定大于0.5 m/s【答案】CD【解析】根据位移图象斜率表示速度可知，甲物体先做匀速直线运动，后静止，选项A 错误；在0～120 s内，乙物体的位移大小为s ＝60 m ，平均速度大小为v ＝s t＝0.5 m/s ，选项B 错误；在0～120 s 内，甲物体运动的位移大小为x 甲＝100 m －20 m ＝80 m ，乙物体运动的位移大小为x 乙＝60 m －0 m ＝60 m ，所以在0～120 s 内，甲物体运动的位移大小大于乙物体运动的位移大小，选项C 正确；根据匀变速直线运动的推论知，乙在t ＝60 s 时的瞬时速度等于在0～120 s 内的平均速度0.5 m/s ，而乙物体做匀加速直线运动，所以乙物体在M 点所对应的瞬时速度大小一定大于0.5 m/s ，选项D 正确．6.(2019·山东济南模拟)一质点从坐标原点沿x 轴方向做匀变速直线运动，在0～8 s 内的x －t 图象如图所示．若t ＝1 s 时，图线所对应的切线的斜率为3 m/s ，则( )A ．t ＝1 s 时，质点的加速度为3 m/s 2B ．t ＝2 s 和t ＝6 s 时，质点的速度大小相等C ．t ＝2 s 和t ＝6 s 时，质点加速度的方向相反D ．t ＝4 s 时，质点的位移为8 m【答案】BD【解析】选BD.已知质点做匀变速直线运动，设其位移随时间变化的关系式为x ＝v 0t ＋12at 2，根据0～8 s 内的x －t 图象的对称轴可知－v 0a＝4 s ；t ＝1 s 时，图线所对应的切线的斜率(即此时的速度)为3 m/s ，可知v 0＋a ×1 s ＝3 m/s ，解得a ＝－1 m/s 2，v 0＝4 m/s ，因为质点做匀变速直线运动，所以质点的加速度不会发生变化，选项A 、C 均错误；利用速度公式v ＝v 0＋at ，可得t ＝2 s 时，质点的速度为2 m/s ，t ＝6 s 时，质点的速度为－2 m/s ，这两个时刻质点的速度大小都为2 m/s ，选项B 正确；将t ＝4 s 代入x ＝v 0t ＋12at 2，解得x ＝8 m ，即t ＝4 s 时质点的位移为8 m ，选项D 正确．。

第1讲 轨迹问题1．方程|1|x -=( ) A ．一个圆B ．两个圆C ．半个圆D ．两个半圆【解答】解：将方程|1|x - 得22(1)(1)1x y -+-=，其中02x ，02y ．因此方程|1|x -=(1,1)C 为圆心，半径1r =的圆． 故选：A ．2．方程||1x -=( ) A ．两个半圆B ．一个圆C ．半个圆D ．两个圆【解答】解：两边平方整理得：22(||1)2x y y -=-， 化简得22(||1)(1)1x y -+-=，由||10x -得||1x ，即1x 或1x -， 当1x 时，方程为22(1)(1)1x y -+-=， 表示圆心为(1,1)且半径为1的圆的右半圆； 当1x -时，方程为22(1)(1)1x y ++-=， 表示圆心为(1,1)-且半径为1的圆的左半圆综上所述，得方程||1x -= 故选：A ．3．在数学中有这样形状的曲线：22||||x y x y +=+．关于这种曲线，有以下结论： ①曲线C 恰好经过9个整点（即横、纵坐标均为整数的点）； ②曲线C 上任意两点之间的距离都不超过2； ③曲线C 所围成的“花瓣”形状区域的面积大于5． 其中正确的结论有( ) A ．①③B ．②③C ．①②D ．①②③【解答】解：①曲线C 经过的整点有(0,0)，(1,0)，(1,0)-，(0,1)，(0,1)-，(1,1)，(1,1)-，(1,1)-，(1,1)--，恰有9个点，即①正确；②点(1,1)和(1,1)--均在曲线C 上，而这两点间的距离为2>，即②错误； ③由于图形是对称的，所以只需考虑第一象限内的部分即可．此时有，22x y x y +=+，整理得，22111()()222x y -+-=，是以11(,)22为半径的圆，作出曲线在第一象限的图形如图所示，面积211111122224AOB C S S S ππ∆=+=⨯⨯+⋅⋅=+圆，故曲线C 的面积为14()2524ππ⨯+=+>，即③正确．故选：A ．4．双纽线最早于1694年被瑞士数学家雅各布伯努利用来描述他所发现的曲线．在平面直角坐标系xOy 中，把到定点1(,0)F a -，2(,0)F a 距离之积等于2(0)a a >的点的轨迹称为双纽线C 、已知点0(P x ，0)y 是双纽线C 上一点，下列说法中正确的有( )①双纽线经过原点O ； ②双纽线C 关于原点O 中心对称；③022a ay -；④双纽线C 上满足12||||PF PF =的点P 有两个． A ．①②B ．①②③C ．②③D ．②③④【解答】解；根据双纽线C 2a =，将0x =，0y =代入，符合方程，所以①正确；用(,)x y --替换方程中的(,)x y ，原方程不变，所以双纽线C 关于原点O 中心对称，②正确； 根据三角形的等面积法可知，1212011||||sin 2||22PF PF F PF a y ∠=⨯⨯，即012||sin 22a ay F PF =∠，亦即022a ay -，③正确； 若双纽线C 上点P 满足12||||PF PF =，则点P 在y 轴上，即0x =，代入方程， 解得0y =，所以这样的点P 只有一个，④错误． 故选：B ．5．双纽线最早于1694年被瑞士数学家雅各布伯努利用来描述他所发现的曲线．在平面直角坐标系xOy 中，把到定点1(,0)F a -，2(,0)F a 距离之积等于2(0)a a >的点的轨迹称为双纽线C ．已知点0(P x ，0)y 是双纽线C 上一点，下列说法中正确的有( ) ①双纽线C 关于原点O 中心对称；②022a ay -；③双纽线C 上满足12||||PF PF =的点P 有两个；④||PO ． A ．①②B ．①②④C ．②③④D ．①③【解答】解：根据双纽线C 2a =，用(,)x y --替换方程中的(,)x y ，原方程不变，所以双纽线C 关于原点O 中心对称，①正确； 根据三角形的等面积法可知，1212011||||sin 2||22PF PF F PF a y ∠=⨯⨯，即012||sin 22a ay F PF =∠，亦即022a ay -，②正确； 若双纽线C 上点P 满足12||||PF PF =，则点P 在y 轴上，即0x =，代入方程， 解得0y =，所以这样的点P 只有一个，③错误；因为121()2PO PF PF =+，所以2221121221||[||2||||cos ||]4PO PF PF PF F PF PF =+∠+由余弦定理可得，2221121224||2||||cos ||a PF PF PF F PF PF =-∠+22222121212||||||cos cos 2PO a PF PF F PF a a F PF a =+∠=+∠，所以|PO ，④正确．故选：B ．6．如图，设点A 和B 为抛物线22(0)y px p =>上除原点以外的两个动点，已知OA OB ⊥，OM AB ⊥，则点M 的轨迹方程为( )A ．2220x y px +-=（原点除外）B ．2220x y py +-=（原点除外）C ．2220x y px ++=（原点除外）D ．2220x y py ++=（原点除外）【解答】解：设(,)M x y ，直线AB 的方程为y kx b =+， 由OM AB ⊥得x k y=-， 联立22y px =和y kx b =+消去y 得222(22)0k x x kb p b +-+=，所以2122b x x k=，所以22121212122()()()pby y kx b kx b k x x kb x x b k=++=+++=， 由OA OB ⊥得12120x x y y +=，所以2220b pbk k +=，所以2b kp =-，所以(2)y kx b k x p =+=-，把xk y=-代入得2220(0)x y px y +-=≠，故选：A ．7．如果把一个平面区域内两点间的距离的最大值称为此区域的直径，那么曲线422x y +=围成的平面区域的直径为( )A B ．3C ．D ．4【解答】解：曲线422x y +=围成的平面区域，关于x ，y 轴对称，设曲线上的点(,)P x y ，可得23||2OP ==． 所以曲线422x y +=围成的平面区域的直径为：3． 故选：B ．8．由曲线222||2||x y x y +=+围成的图形面积为( ) A ．24π+B ．28π+C ．44π+D ．48π+【解答】解：根据对称性，曲线222||2||x y x y +=+围成的图形面积等于在第一象限围成面积的4倍， 当0x 且0y 时222||2||x y x y +=+等价为2222x y x y +=+，即22220x y x y +--=，即22(1)(1)2x y -+-=，圆心(1,1)C ，半径R =，则ACO ∆的面积12112S =⨯⨯=，BCO ∆的面积1S =，在第一象限部分的面积211122S ππ=++⨯=+，则四个象限的面积为44(2)84S ππ=+=+，故选：D ．9．如图，平面直角坐标系中，曲线（实线部分）的方程可以是( )A ．22(||1)(1)0x y x y ---+=B ．( 22)(1)0x y -+=C ．2(||1)(10x y x ---+=D ．(2)(10x -+=【解答】解：如图曲线表示折线段的一部分和双曲线，选项A 等价于||10x y --=或2210x y -+=，表示折线||1y x =-的全部和双曲线，故错误； 选项B 等价于22||1010x y x y --⎧⎨-+=⎩，或||10x y --=，||10x y --=表示折线||1y x =-的全部，故错误； 选项C 等价于22||1010x y x y --=⎧⎨-+⎩或2210x y -+=，22||1010x y x y --=⎧⎨-+⎩表示折线||1y x =-在双曲线的外部 （包括有原点）的一部分，2210x y -+=表示双曲线，符合题中图象，故正确； 选项D 等价于22||1010x y x y --=⎧⎨-+⎩或22||1010x y x y --⎧⎨-+=⎩， 22||1010x y x y --=⎧⎨-+⎩表示表示折线||1y x =-在双曲线的外部（包括有原点）的一部分， 22||1010x y x y --⎧⎨-+=⎩表示双曲线在x 轴下方的一部分，故错误． 故选：C ．10．已知点集22{(,)1}M x y y xy =-，则平面直角坐标系中区域M 的面积是( )A ．1B ．34π+C ．πD ．22π+【解答】解：当0xy 时，只需要满足21x ，21y 即可；当0xy >时，对不等式两边平方整理得到221x y +，所以区域M 如下图．易知其面积为22π+．故选：D ．11．数学中有许多形状优美、寓意美好的曲线，例如：四叶草曲线就是其中一种，其方程为22322()x y x y +=．给出下列四个结论： ①曲线C 有四条对称轴；②曲线C 上的点到原点的最大距离为14； ③曲线C 第一象限上任意一点作两坐标轴的垂线与两坐标轴围成的矩形面积最大值为18；④四叶草面积小于4π． 其中，所有正确结论的序号是( )A ．①②B ．①③C ．①③④D ．①②④【解答】解：四叶草曲线方程为22322()x y x y +=，将x 换为x -，y 不变，可得方程不变，则曲线关于y 轴对称；将y 换为y -，x 不变，可得方程不变，则曲线关于x 轴对称；将x 换为y ，y 换为x ，可得方程不变，则曲线关于直线y x =对称；将x 换为y -，y 换为x -，可得方程不变，则曲线关于直线y x =-对称； 曲线C 有四条对称轴，故①正确；由y x =与22322()x y x y +=联立，可得y x ==y x ==，即有曲线C 上的点到原点的最大距离为12=，故②错误； 设曲线C 第一象限上任意一点为(,)x y ，(0,0)x y >>，可得围成的矩形面积为xy ，由222x y xy +， 则223223()8()x y x y xy +=，即18xy ，当且仅当x y =取得最大值，故③正确； 易得四叶草曲线在以原点为圆心，12为半径的圆内，故四叶草面积小于4π，则④正确． 故选：C ．12．曲线C 为：到两定点(2,0)M -、(2,0)N 距离乘积为常数16的动点P 的轨迹．以下结论正确的个数为()（1）曲线C 一定经过原点； （2）曲线C 关于x 轴、y 轴对称； （3）MPN ∆的面积不大于8；（4）曲线C 在一个面积为64的矩形范围内． A ．1B ．2C ．3D ．4【解答】解：设(,)P x y 22(2)16x -+=，对于（1），原点(0,0)代入方程，得2216⨯≠，即方程不成立， 则曲线C 一定经过原点，命题错误；对于（2），以x -代替x ，y -代替y 22(2)16x --=成立，16=也成立， 即曲线C 关于x 、y 轴对称，命题正确；对于（3），0x =，y =±MPN ∆的最大面积为1482⨯⨯=<，命题正确；对于（4），令0y =，可得x =±，根据距离乘积为16可以得出x 的取值只可能在-到同理y 的取值只可能在-所以曲线C 在一个面积为 综上，正确的命题有（2）（3），共2个． 故选：B ．二．多选题（共2小题）13．数学中的很多符号具有简洁、对称的美感，是形成一些常见的漂亮图案的基石，也是许多艺术家设计作品的主要几何元素．如我们熟悉的∞符号，我们把形状类似∞的曲线称为“∞曲线”．经研究发现，在平面直角坐标系xOy 中，到定点(,0)A a -，(,0)B a 距离之积等于2(0)a a >的点的轨迹C 是“∞曲线”．若点0(P x ，0)y 是轨迹C 上一点，则下列说法中正确的有( ) A ．曲线C 关于原点O 中心对称 B ．0x 的取值范围是[a -，]aC ．曲线C 上有且仅有一个点P 满足||||PA PB =D ．22PO a -的最大值为22a【解答】解：在平面直角坐标系xOy 中，到定点(,0)A a -，(,0)B a 距离之积等于2(0)a a >的点的轨迹C 是“∞曲线”．故点0(P x ，0)y 2a =，点(M x -，0)y -代入2a =，得到2a =，故A 正确；对于B ：设x 轴上0x 范围的最大值为m x ，所以2()()m m x a x a a -+=，解得m x =，故0x 的范围为[]．故B 错误；对于C ：若PA PB =，则点P 在AB 的垂直平分线上，即0P x =，设点(0,)P P y ，所以22a =，所以0P y =，即仅原点满足，故C 正确；对于2D a =， 化简得2222222()220x y a x a y +-+=，根据cos x ρθ=，sin y ρθ=，得到222cos 2a ρθ=，所以2PO 的最大值为22a ，22PO a -的最大值为2a ，故D 错误． 故选：AC ．14．在平面直角坐标系xOy 中，(,)P x y 为曲线22:422||4||C x y x y +=++上一点，则( ) A ．曲线C 关于原点对称B ．[1x ∈--+C ．曲线C 围成的区域面积小于18D ．P 到点1(0,)2【解答】解：当0x >，0y >时，曲线C 的方程为22422||4||x y x y +=++，去掉绝对值化简可得22(1)1()142x y -+-=，将2214x y +=的中心平移到1(1,)2位于第一象限的部分， 因为点(,)x y -，(,)x y -，(,)x y --都在曲线C 上， 所以曲线C 的图象关于x 轴、y 轴和坐标原点对称， 作出图象如图所示，由图可知曲线C 关于原点对称，故选项A 正确；令2214x y +=中的0y =，解得2x =，向右平移一个单位可得到横坐标为3，根据对称性可知33x -，故选项B 错误；令2214x y +=中的0x =，解得1y =，向上平移12个单位可得纵坐标的最大值为32， 曲线C 第一象限的部分被包围在矩形内，矩形面积为39322⨯=， 所以曲线C 围成的区域面积小于94182⨯=，故选项C 正确；令22(1)1()142x y -+-=中的0x =，可得12y =1(0,)2，故选项D 正确． 故选：ACD ．个结论：①曲线C 恰好经过4个整点（即横、纵坐标均为整数的点）；②曲线C ③曲线C 所围成的“花形”区域的面积小于4． 其中，所有正确结论的序号是 ② ．【解答】解：①令0x =，方程化为：21y =，解得1y =±，可得点(0,1)±；令0y =，方程化为：21x =，解得1x =±，可得点(1,0)±；令x y =±，方程化为：21x =，解得1x =±，可得点(1,1)±±．由此可得：曲线C 恰好经过8个整点，因此不正确． ②221||2||xy x y xy +=+，方程化为：||1xy ，∴曲线C 上任意一点到原点的距离|11d xy =+=C ，可知正确．③由四个点(1,1)±±作为正方形的顶点，可得正方形的面积为4，曲线C 所围成的“花形”区域的面积大于4．其中，所有正确结论的序号是②． 故答案为：②．三个结论：①曲线C 恰好经过6个整点（即横、纵坐标均为整数的点）；②曲线C ③曲线C 所围成的“心形”区域的面积小于3． 其中，所有正确结论的序号是 ①② ．【解答】解：根据题意，曲线22:1||C x y x y +=+，用(,)x y -替换曲线方程中的(,)x y ，方程不变，所以曲线C 关于y 轴对称，对于①，当0x 时，221||x y x y +=+，即为，2222112x y x y xy ++=++，可得222x y +，所以曲线经过点(0,1)，(0,1)-，(1,0)，(1,1)，再根据对称性可知，曲线还经过点(1,0)-，(1,1)-，故曲线恰好经过6个整点，①正确；对于②，由上可知，当0x 时，222x y +，即曲线C再根据对称性可知，曲线C ②正确；对于③，因为在x 轴上方，图形面积大于四点(1,0)-，(1,0)，(1,1)，(1,1)-围成的矩形面积122⨯=，在x 轴下方，图形面积大于三点(1,0)-，(1,0)，(0,1)-围成的等腰直角三角形的面积12112⨯⨯=，所以曲线C 所围成的“心形”区域的面积大于3，③错误． 故答案为：①②．17．数学中的数形结合，也可以组成世间万物的绚丽画面．一些优美的曲线是数学形象美、对称美、和谐美的结合产物，曲线22322:()16C x y x y+=恰好是四叶玫瑰线．给出下列结论：①曲线C经过5个整点（即横、纵坐标均为整数的点）；②曲线C上任意一点到坐标原点O的距离都不超过2；③曲线C围成区域的面积大于4π；④方程22322()16(0)x y x y xy+=<表示的曲线C在第二象限和第四象限．其中正确结论的序号是②④．【解答】解：22 223222 ()16()2x yx y x y++=，224x y∴+（当且仅当222x y==时取等号），则②正确；将224x y+=和22322()16x y x y+=联立，解得222x y==，即圆224x y+=与曲线C相切于点，(，(，，则①和③都错误；由0xy<，得方程22322()16x y x y+=表示的曲线C在第二象限和第四象限，故④正确．故答案为：②④．18．曲线C 是平面内到定点(1,0)A 的距离与到定直线1x =-的距离之和为3的动点P 的轨迹．则曲线C 与y 轴交点的坐标是 (0,3) ；又已知点(B a ，1)(a 为常数），那么||||PB PA +的最小值d （a ）= ． 【解答】解：（1）设动点(,)P x y 22(1)|1|3x y x -+++=， ①当4x <-时，|1|3x +>，无轨迹；②当41x --22(1)4x y x -+=+，化为231015(1)2y x x =+--，与y 轴无交点；③当1x >-22(1)2x y x -+=-，化为223y x =-+，3(1)2x -<． 令0x =，解得3y =综上①②③可知：曲线C 与y 轴的交点为(0,3)； （2）由（1）可知：231015,(1)2323,(1)2x x y x x ⎧+--⎪⎪=⎨⎪-+-<⎪⎩．如图所示，令1y =，则10151x +=，或231x -+=，解得1.4x =-或1．①当 1.4a -或1a 时，||||||PA PB AB +，d ∴（a ）22||(1)122AB a a a ==-+-+；②当11a -<<时，当直线1y =与2323(1)2y x x =-+-<相交时的交点P 满足||||PA PB +||2QB a ==-取得最小值，此抛物线的准线为2x =，∴直线1y =与准线的交点(2,1)Q ，此时d （a ）； ③当 1.41a -<-时，当直线1y =与231015(1)2y x x =+--相交时的交点P 满足|||PA PB +取得最小值，此抛物线的准线为4x =-，∴直线1y =与准线的交点(4,1)Q -，此时d （a ）||4QB a ==+． 综上可知：d （a ）222, 1.414, 1.412,1 1.a a a a a a a a ⎧-+-⎪⎪=+-<-⎨⎪--<<⎪⎩或19．已知点(A B ，动点P 满足APB θ∠=且2||||cos 12PA PB θ=，则点P 的轨迹方程为2213x y += ．【解答】解：由2||||cos 12PA PB θ=，(0,)θπ∈，则1cos ||||12PA PB θ+=，||AB = 所以|||||||||cos 2PA PB PA PB θ+=，而在三角形ABP 中22222||||||||||8cos 2||||2||||PA PB AB PA PB PA PB PA PB θ+-+-==， 所以可得22||||||||62PA PB PA PB ++=，而222||||(||||)2||||PA PB PA PB PA PB +=+-，所以可得2(||||)12PA PB +=，所以||||PA PB +=为定值且大于||AB ，所以可得P 的轨迹为椭圆，且长轴长2a =2c =x 轴上，中心在原点的椭圆，即a c =2221b a c =-=，所以P 的轨迹方程为：2213x y +=，故答案为：2213x y +=．20．在平面直角坐标系xOy 中，抛物线2y x =上异于坐标原点O 的两不同动点A 、B 满足AO BO ⊥（如图所示）．则AOB ∆得重心G （即三角形三条中线的交点）的轨迹方程为 2233y x =+；【解答】解：显然直线AB 的斜率存在，记为k ，AB 的方程记为：y kx b =+，(0)b ≠，1(A x ，1)y ，2(B x ，2)y ，将直线方程代入2y x =得：20x kx b --=，则有：△240k b =+>①，12x x k +=②，12x x b =-③，又211y x =，222y x =212y y b ∴=；AO BO ⊥，12120x x y y ∴+=，得：20b b -+=且0b ≠，1b ∴=，代入①验证，满足；故21212()22y y k x x k +=++=+；设AOB ∆的重心为(,)G x y ，则1233x x k x +==④，212233y y k y ++==⑤， 由④⑤两式消去参数k 得：G 的轨迹方程为2233y x =+． 故答案为：2233y x =+．22．已知双曲线2212x y -=的左、右顶点分别为1A 、2A ，点1(P x ，1)y ，1(Q x ，1)y -是双曲线上不同的两个动点．求直线1A P 与2A Q 交点的轨迹E 的方程．【解答】解：由题设知1||x，1(A 0)，2A 0)， 直线1A P的斜率为1k =，∴直线1A P的方程为y x =+，⋯① 同理可得直线2A Q的方程为y x =．⋯②将①②两式相乘，得222121(2)2y y x x =--．⋯③点1(P x ，1)y 在双曲线2212x y -=上， ∴221112x y -=，可得22211111(2)22x y x =-=-，⋯④ 将④代入③，得21222211(2)12(2)122x y x x x -=-=--，整理得2212x y +=，即为轨迹E 的方程． 点P 、Q 不重合，且它们不与1A 、2A重合，x ∴≠，轨迹E的方程为221(2x y x +=≠23．设圆C与两圆22(4x y +=，22(4x y -+=中的一个内切，另一个外切，求圆心C 的轨迹L 的方程．【解答】解：（1）两圆的半径都为2，两圆心为1(F 0)、2F 0)，由题意得：12||2||2CF CF +=-或21||2||2CF CF +=-，2112||||||42||2CF CF a F F c ∴-==<==， 可知圆心C 的轨迹是以原点为中心，焦点在x 轴上，且实轴为4，焦距为 因此2a =，c 2221b c a =-=，所以轨迹L 的方程为2214x y -=．24．已知椭圆221(0)259x y a b +=>>的左、右焦点分别是1F ，2F ，Q 是椭圆外的动点，满足1||10F Q =．点P是线段1F Q 与该椭圆的交点，点T 在线段2F Q 上，并且满足20PT TF =，2||0TF =．（Ⅰ）设x 为点P 的横坐标，证明14||55F P x =+；（Ⅱ）求点T 的轨迹C 的方程；【解答】（Ⅰ）证明：设点P 的坐标为(,)x y ． 记1122||,||F P r F P r ==，则12r r由22121211410,16,55r r r r x F P r x +=-===+得；（Ⅱ）解：设点T 的坐标为(,)x y ．当||0PT =时，点(5,0)和点(5,0)-在轨迹上． 当200PT TF ≠≠且时，由20PT TF =，得2PT TF ⊥． 又2||||PQ PF =，所以T 为线段2F Q 的中点． 在△12QF F 中，11||||52OT FQ ==，所以有2225x y +=． 综上所述，点T 的轨迹C 的方程是2225x y +=；。

1.确定下列点的轨迹：
⑴△ABC的一边AB的长度为a，且 AB的位置确定， △ABC的面积为S， 试说出点C的轨迹. ⑵已知A、B为两定点，点C满足 CA⊥CB，则点C的轨迹是什么？
⑶与⊙O内切于⊙O上一定点A的 圆的圆心的轨迹.
绝缘体，并认为电是一种流体。 年德国牧师克茉斯脱，试用一根钉子把电引到瓶子里去，当他一手握瓶，一手摸钉子时，受到了明显的电击。年，荷兰莱顿 城莱顿大学的教授彼得.冯.慕欣布罗克无意中发现了同样的现象。 穆欣布罗克的发现，使电学史上第一个保存电荷的容器诞生了。它是一个玻璃瓶，瓶里瓶 外分别贴；股票入门基础知识大全 炒股入门知识下载 炒股票入门基础知识 股市入门基础知识 股票知识大全 股票基础知识入门新手 ；锡 箔通过金属链跟金属棒连接，金属棒的上端是一个金属球。由于它是在莱顿城发明的，所以叫做莱顿瓶，这就是最初的电容器。莱顿瓶很快在欧洲引起了强 烈的反响，电学家们不仅利用它们作了大量的实验，而且做了大量的示范表演，有人用它来点燃酒精和火。其中最壮观的是法国人诺莱特在巴黎一座大教堂 前所作的表演，诺莱特邀请了路易十五的皇室成员临场观看莱顿瓶的表演，他让七百名修道士手拉手排成一行，队伍全长达英尺（约米）。然后，诺莱特让 排头的修道士用手握住莱顿瓶，让排尾的握瓶的引线，一瞬间，七百名修道士，因受电击几乎同时跳起来，在场的人无不为之口瞪目呆，诺莱特以令人信服 的证据向人们展示了电的巨大威力。 年英国伦敦一名叫柯林森的物理学家，通过邮寄向美国费城的本杰明.富兰克林赠送了一只莱顿瓶，并在信中向他介绍了 使用方法，这直导致了年富兰克林著名 的费城实验。 他用风筝将"天电"引了下来，把天电收集到莱顿瓶中，从而弄明白了"天电"和"地电"原来是一回事。 十八世纪后期，贝内特发明验电器，这种仪器一直沿用至今，它可以近似地测量一个物体上所带的电量。另外，8年，库仑发明扭秤，用它来测量静电力， 推导出库仑定律， 并将这一 定律推广到磁力测量上 。 科学家使用了验电器 和扭秤后 ，使静电现象的研究工作从定性走上了定量的道路。 在日常生活中，

下列不是青春期主要表现的是A．出现第二次生长突增B．内脏器官体积增大C．淋巴系统逐渐萎缩D．出现第二性征E．心理发育加快 正常口温A.37.5℃B.36.5～37.5℃C.36～37.5℃D.36～37℃E.35～36℃ 下列哪种激素不是由腺垂体合成、分泌的A.促甲状腺激素B.生长素C.缩宫素D.促肾上腺皮质激素E.黄体生成素 国家行业标准《汽车油漆涂层》（QC/T484—1999）中规定油漆涂层分个组和若干等级。A．8B．10C．12 一般情况下，测定家畜下列测定点的温度，其中皮温最高的是A、直肠B、腋下C、尾尖D、耳尖 在组成上，小建中汤比桂枝汤多A.饴糖一升B.饴糖一升，桂枝三两C.饴糖一升，生姜三两D.饴糖一升，芍药三两E.饴糖一升，甘草三两 外阴鳞状上皮细胞增生癌变率为A.1％B.3％C.5％D.0.5％E.10％ 在输送介质为热水的水平管道上，偏心异径管的连接方式应为A.取管底平B.取管顶平C.取管左齐D.取管右齐 幼女硬化性苔癣不宜选用下列何药A.1％氢化可的松软膏B.丙酸睾酮油膏C.黄体酮油剂D.凡士林油膏E.凡士林软膏 鼠疫是主要通过下列哪种媒介传播的自然疫源性烈性传染病A.野鼠B.鼠蚤C.蚊子D.家鼠E.黑姬鼠 关于流行性乙型脑炎病毒的人群易感性，叙述错误的是A.人多呈隐性感染B.患者以儿童为主C.显性感染与隐性感染之比为10︰1D.感染后可获得持久免疫力E.人普遍易感 社会美的内容直接就是。 体内缺铁初期的最早最可靠的诊断依据是A.典型的小细胞低色素性贫血B.血清总铁结合力增高C.血清铁减低D.骨髓贮存铁减少或缺乏E.血清转铁蛋白饱和度下降 在盛装医疗废物前，应对医疗废物包装物或容器进行认真检查，确保无、和其它缺陷。 接种百白破三联制剂下列哪项是错误的A.出生3个月初种B.基础免疫需3次C.接种方法为皮下注射D.初种剂量0.2～0.5mlE.只需在7岁加强注射一次 矿业工程施工阶段质量控制的重点是。A.施工工艺B.施工段C.施工工序D.施工用料E.施工机械 关于先天性甲状腺功能减低新生儿筛查的采血时间，哪项是正确的A.生后第1天B.生后第3天C.生后15天D.生后1个月E.出生时脐血检查 人体对交流电流的最小感知电流约为2mA.A.正确B.错误 动态评价指标主要有()。A.净现值B.内部收益率C.动态投资回收期D.净现值率 流感病毒自1918年发生几次大的变异，引起世界性大的变异，这种变异属于A.耐药性变异B.抗原性变异C.毒力变异D.病种变异E.杂交变异 口腔癌是世界上10种最常见的癌症之一，在我国最常见的3种口腔癌依次是A.颊癌，牙龈癌，腭癌B.牙龈癌，颊癌，腭癌C.舌癌，牙龈癌，颊癌D.舌癌，颊癌，牙龈癌E.舌癌，牙龈癌，口底癌 急性扁桃体炎最常见的局部并发症为。A.咽旁脓肿B.扁桃体周脓肿C.咽后脓肿D.颌间脓肿E.口底蜂窝织炎 固定桥粘固后不久，患者感到胀痛不适，主要见于。A.咬合过高B.基牙负担过重C.桥体龈端接触过紧D.接触点过紧E.粘固剂溢出 女性，45岁。慢性咳喘近10年，症状加重伴神志恍惚1d入院。体检两肺广泛哮鸣音和肺底湿啰音。动脉血气（吸氧1．5L／min）：pH7．26，PaCO10．6kPa（80mmHg），PaO8．6kPa（65mmHg）。下列治疗措施中哪项是比较合理的A.尼可刹米静脉滴注以改善通气B.静脉滴注5％碳酸氢钠，纠正酸中毒 光伏并网逆变器是将太阳电池所输出的成符合电网要求的交流电再输入电网的设备。 在机械制图中，物体的正投影称为。A.视图B.主视图C.俯视图D.侧视图 提出环境保护措施设计，是阶段的主要内容之一。A.项目建议书B.预可行性研究C.可行性研究D.初步设计 1岁小孩行硬管支气管镜检查时，最为合适的支气管镜内径为多大()A．3.0mmB．3.5mmC．4.0mmD．4.5mmE．5.0mm 多发性骨髓瘤患者出现咳嗽，咳痰，气急，胸片检查发现病变后行CT检查如图，最可能的诊断为()A．肺部感染B．两肺结核C．骨髓瘤转移肺部D．肺淀粉样变性E．肺转移瘤 网络综合布线系统安装工艺要求中，设备问的设计应符合的规定包括。A.设备间的位置宜便于设备接地B.设备间宜尽可能靠近建筑物线缆竖井位置，有利于主干缆线的引入C.设备间梁下净高不应小于1．5m，采用外开双扇门，门宽不应小于1．5mD.设备间室温度应为10℃～35℃，相对湿度应为20％ 有关恶露错误的描述是()A．血性恶露持续约14日B．持续4～6周C．总量约为500mlD．有血腥味，但无臭味E．浆液性恶露持续约2周 供电营业区内的供电营业机构，对本营业区内的用户有按照国家规定供电的义务：。 配送合同 感染人的禽流感病毒有、、三种亚型毒株，均为甲型流感病毒的成员A.H5N1、H9N2、H7N7B.H5N2、H9N2、H7N2C.H5N1、H9N1、H7N1D.H5N2、H9N2、H7N2E.H5N7、H9N7、H7N7 据建设部《关于印发(注册建造师执业管理办法)(试行)的通知》(建市[2008348号)第五条“大中型工程施工项目负责人必须由本专业注册建造师担任，二级注册建造师可以承担”。A.大型项目B.中型项目C.小型项目D.中、小型项目 能否正确掌握和充分运用谈话的技巧，对管理者能否有效地进行科学管理至关重要。下列不属于谈话技巧的是A.善于激发下级的谈话愿望B.善于启发下级讲真情实话C.善于抓住重要问题D.运用倾听技巧E.直接批评下属 诊断包虫病，哪一项是错误的A.问病史B.超声波检查C.X线透视、摄片D.病变组织穿刺E.免疫学检查 在循环流化床锅炉正常运行时应如何观察床层的着火情况？ 编码的基本原则有哪些？ 能够对各种运动状况下工作的物体表面温度进行快速测量的温度检测仪器是。A.装配式热电偶B.装配式铂电阻C.红外辐射温度检测器D.智能温度变送器