重复测量方差分析报告模板

第1篇一、实验目的本次实验旨在学习计量资料分析方法，通过具体案例，掌握重复测量方差分析（Repeated Measures ANOVA）和广义估计方程（Generalized Estimating Equations，GEE）在处理重复测量数据中的应用。

同时，通过实际操作，加深对数据分析过程的理解。

二、实验内容1. 实验背景选取某高校20名大学生，随机分为两组，分别进行为期三个月的体育锻炼。

分别在锻炼开始后第一个月（time1）、第二个月（time2）、第三个月（time3）测量两组学生的体重变化（kg），以研究体育锻炼对体重变化的影响。

2. 数据整理将数据整理为长型格式，包含以下变量：- ID：研究对象编号- group：分组（1为对照组，2为实验组）- time：不同时点的测量次数（time1、time2、time3）- weight：相应时间点测量的体重增量（kg）3. 实验步骤（1）重复测量方差分析使用SPSS软件进行重复测量方差分析，比较两组学生在三个月内的体重变化是否存在显著差异。

（2）广义估计方程使用GEE方法，对重复测量数据进行统计分析，进一步探讨体育锻炼对体重变化的影响。

三、实验结果与分析1. 重复测量方差分析（1）结果重复测量方差分析结果显示，组间效应显著（F=5.678，p<0.05），说明两组学生在三个月内的体重变化存在显著差异。

（2）分析根据结果，可以得出结论：体育锻炼对体重变化具有显著影响，实验组学生在三个月内的体重变化明显优于对照组。

2. 广义估计方程（1）结果GEE分析结果显示，体育锻炼对体重变化具有显著正向影响（β=0.25，p<0.05），说明体育锻炼能够有效降低体重。

（2）分析GEE分析结果与重复测量方差分析结果一致，进一步证实了体育锻炼对体重变化具有显著影响。

四、实验结论通过本次实验，我们得出以下结论：1. 重复测量方差分析和广义估计方程在处理重复测量数据方面具有较好的应用效果。

1、利用SAS PROC GLM程序进行重复测量的方差分析本手册描述了如何利用SAS PROC GLM 程序进行重复测量的方差分析，包括对象间变量（a between-subjects variable）的分析。

首先解释了何时该使用改方法；描述了本手册中用到的术语；给出了研究问题；最后，用一个详细的例子阐述了如何使用改程序。

假定你知道如何书写SAS的程序和导入数据文件以及运行SAS命令。

此外，我们还假定你熟悉方差分析（ANOVA）的基本方法和假定。

2、何时使用重复测量的方差分析任何方差分析都一样，重复测量的方差分析也是用来检验平均值的差别的。

当在许多不同的条件下测量随机取样的所有成员时，使用重复测量的方差分析。

由于样本是依次曝光于各个条件的，所以对因变量的测量是重复的。

对此使用标准的ANOVA分析是不合适的，因为它不符合标准方差分析的前提假定：数据之间的独立性。

需要注意的是，有些ANOVA设计综合了重复测量因子和非重复测量因子。

只要有一个重复测量因子存在，就应该考虑使用重复测量的方差分析。

使用该方法有以下几个原因：1)、一些研究的假说要求重复测量。

比如，经度研究测量几个年龄的样本成员。

在这个例子中，年龄应该是重复的因子。

2)、当取样成员之间存在很大的变异时，按标准方法得到的误差变异很大。

对每个取样成员的重复测量可以减小改误差变异。

3）、当取样成员不宜获取时，重复测量的设计显得经济实惠，因为每个成员都可以用来曝光于所有的条件。

4）、注意的是重复测量的方差分析不能检验随机效应！5)、当取样成员根据一些重要的特征配对后，也可使用重复测量方差分析。

这里，每个配对的组具有相同的成员，组内每个成员都曝光于某个因子的不同的随机水平。

当取样成员配对了，不同条件下的测量可以当作重复测量来看待。

比如，假定你选择了一组低气压对象，测量他们的气压水平，然后将那些具有相似气压水平的进行配对。

然后给予每对中的一个成员低压处理，再次测量所有成员的低压水平。

重复测量方差分析1. 引言重复测量方差分析（Repeated Measures Analysis of Variance, RM-ANOVA）是一种统计方法，用于分析在不同时间点或不同处理条件下对同一组个体或样本进行多次测量的数据。

通过比较不同时间点或处理条件下的测量结果，我们可以确定是否存在显著的差异，并了解时间或处理对测量结果的潜在影响。

本文档将介绍重复测量方差分析的基本原理、假设条件、计算方法和结果解读，并提供使用Markdown格式编写重复测量方差分析报告的示例。

2. 基本原理重复测量方差分析的基本原理是基于方差分析（ANOVA）方法，但相对于普通的单因素方差分析，重复测量方差分析考虑了测量数据间的相关性。

在重复测量设计中，同一个个体或样本在不同时间点或处理条件下进行多次测量，因此测量数据之间存在一定的相关性。

为了解决相关性的问题，重复测量方差分析使用了独特的矩阵分解方法，将总体方差分解为组内方差和组间方差。

通过计算组间方差与组内方差的比值，可以判断不同时间点或处理条件下的测量结果是否存在显著差异。

3. 假设条件在进行重复测量方差分析之前，需要满足以下假设条件：•正态性假设：每个时间点或处理条件下的测量结果应当服从正态分布。

•同方差性假设：每个时间点或处理条件下的测量结果应具有相同的方差。

•相关性假设：各个时间点或处理条件下的测量结果之间应具有一定的相关性。

如果数据不满足正态性、同方差性或相关性假设，需要采取适当的数据转换、方差齐性检验或相关性分析等方法进行处理。

4. 计算方法重复测量方差分析的计算方法可以通过计算F统计量来进行。

具体步骤如下：步骤1：计算总体方差首先计算总体方差SSTotal，即测量数据的总体波动情况。

步骤2：计算组间方差然后计算组间方差SSBetween，即不同时间点或处理条件下的测量结果之间的差异。

步骤3：计算组内方差接下来计算组内方差SSWithin，即测量数据在同一个时间点或处理条件下的波动情况。

重复测量的方差分析 (Repeated-measures ANOVA)研究情境:重复测量的ANOVA能够处理数据的类型：在上例中有一个自变量 (称为组内因素): 时间.ANOVA 亦可用于分析同时包含组间和组内因素的混合设计1.ANOVA的逻辑ANOVA 非常类似两个相关样本的 t检验对于 ANOVA检验统计量 (称为 F比率) 类似F = 样本均值间方差误差方差和方的分解分两个阶段首先考虑方差的来源.a)处理间变异i.处理效应 - 处理造成的差异ii.实验误差b)处理内变异i.被试间方差ii.实验误差F比率可以表达为:F比率 =处理效应方差+实验误差实验误差2.重复测量ANOVA的专用符号K = 处理条件(或组)的数目n = 每一个组的数目(如果它们相等)N = ∑n i = 总的观察数目T i = ∑X ijG = ∑X ij =总的和G-bar = G / N = 总的均值SS i = 每一个组的和方 = ∑(X ij - i)2P = 每一个被试的观察数目在上例中：∑X2G = 36K = 3， n=4， N=123.和方的分解步骤第1阶段：SS和 = SS组间 + SS组内SS和 = ∑X2 - (G2/N)SS和 = 140 - (362/12) =140 - 108 = 32需要将其分解为组间变异和组内变异.SS组间= ∑(T2/n i) - G2/N= 82/4 + 202/4 + 182/4–108 = 14SS组内= ∑SS每一个处理内部 = ∑SS i= 2 + 5 + 11 = 18第2阶段：SS组内 = SS被试间 + SS误差SS被试间= ∑(P2/k) - G2/N= 122/3 + 62/3 + 62/3 + 122/3–108 = 12 SS误差= SS组内-SS被试间= 18-12=64.自由度共有5个自由度, 2个计算均方时要用到1）总的 df = N-12）组间方差df = k-13）组内方差df = N-k4）被试间方差df = n-15）误差方差df = （N-k） -（n-1）均方和F值的计算.MS = SS/dfMS组间= SS组间/df组间--> 上例中 = 14/2 = 7MS误差 = SS误差/df误差--> 上例中 = 6/6 = 1F比率 = 处理间方差误差方差将结果总结到方差分析表中：来源SS df MS处理间14 2 7 F = 7处理内18 9被试内12 3误差 6 6 1总的32 11查 F表确定 Fcrit 对假设作出结论df组间 = 分子的dfdf组内 = 分母的df (误差) --> 上例中:df误差 = 6; df组间= 3假设中选择α = .05, Fcrit = 4.76（如果选择α = .01, Fcrit = 9.78）F比率的观测值6大于 F.05., 所以拒绝 H0 (μ1 = μ2 = μ3).报告结果F(df组间,df误差) = Fobs, p < ?各练习次数的均值和标准差列在表1中。

SPSS学习笔记之重复测量的多因素方差分析报告学习笔记之重复测量的多因素方差分析报告SPSS（Statistical Package for the Social Sciences，社会科学统计软件包）是一款功能强大的数据分析工具，广泛应用于各个领域的研究。

在SPSS中，重复测量的多因素方差分析被视为一项重要的统计方法，用于研究相同参与者在不同条件下的测试结果。

本篇学习笔记以重复测量的多因素方差分析为主题，将介绍如何使用SPSS进行该项分析，并给出详细的分析报告。

1. 研究目的和问题描述2. 数据采集和处理3. 研究设计和假设4. 数据分析5. 结果解释与讨论1. 研究目的和问题描述本次研究的目的是考察不同刺激条件对参与者注意力的影响。

具体而言，我们想了解参与者在三种刺激条件下的注意力水平是否存在显著差异。

2. 数据采集和处理我们招募了40位参与者，并随机将其分为三组。

每组参与者分别接受三次测试，每次测试采用不同的刺激条件。

我们记录了每位参与者的测试结果，并进行数据整理和清洗。

3. 研究设计和假设本研究采用的是重复测量的多因素方差分析设计。

考察因素为刺激条件，对应的水平为A、B和C。

我们的研究假设如下：- H0（零假设）：不同刺激条件下的注意力水平无显著差异。

- H1（备择假设）：不同刺激条件下的注意力水平存在显著差异。

4. 数据分析为了进行重复测量的多因素方差分析，我们打开SPSS软件，并导入数据集。

接下来，我们按照以下步骤进行分析：步骤一：打开SPSS软件，点击“打开”按钮，导入数据集。

步骤二：选择“分析”菜单，然后选择“一般线性模型”和“重复测量”。

步骤三：将待分析的因子变量（刺激条件）拖动到“因子”框中，并设置不同刺激条件的水平。

步骤四：选择适当的因变量（注意力水平），并将其拖动到“依赖变量”框中。

步骤五：点击“选项”按钮，可以对分析进行更多设置，比如是否计算偏斜度和峰度等。

步骤六：点击“确定”按钮，SPSS将自动进行重复测量的多因素方差分析，并生成分析结果。

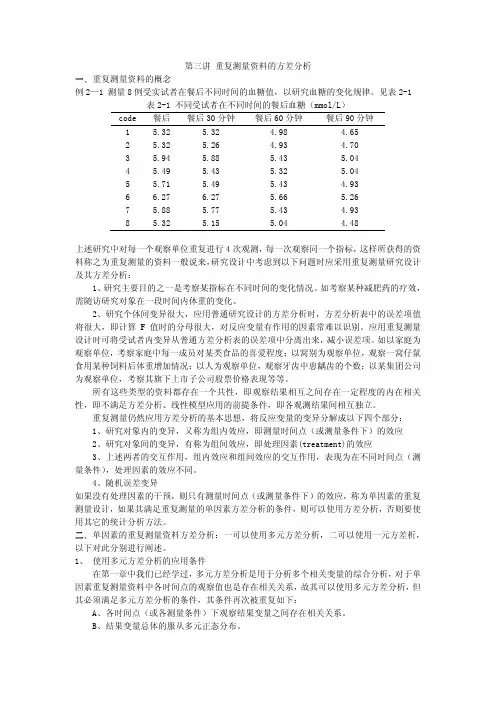
第三讲 重复测量资料的方差分析一、重复测量资料的概念例2—1 测量8例受实试者在餐后不同时间的血糖值，以研究血糖的变化规律。

见表2-1 表2-1 不同受试者在不同时间的餐后血糖（mmol/L）code 餐后 餐后30分钟 餐后60分钟 餐后90分钟1 5.32 5.32 4.98 4.652 5.32 5.26 4.93 4.703 5.94 5.88 5.43 5.044 5.49 5.43 5.32 5.045 5.71 5.49 5.43 4.936 6.27 6.27 5.66 5.267 5.88 5.77 5.43 4.938 5.32 5.15 5.04 4.48上述研究中对每一个观察单位重复进行4次观测，每一次观察同一个指标，这样所获得的资料称之为重复测量的资料一般说来，研究设计中考虑到以下问题时应采用重复测量研究设计及其方差分析：1、研究主要目的之一是考察某指标在不同时间的变化情况。

如考察某种减肥药的疗效，需随访研究对象在一段时间内休重的变化。

2、研究个体间变异很大，应用普通研究设计的方差分析时，方差分析表中的误差项值将很大，即计算F值时的分母很大，对反应变量有作用的因素常难以识别。

应用重复测量设计时可将受试者内变异从普通方差分析表的误差项中分离出来，减小误差项。

如以家庭为观察单位，考察家庭中每一成员对某类食品的喜爱程度；以窝别为观察单位，观察一窝仔鼠食用某种饲料后体重增加情况；以人为观察单位，观察牙齿中患龋齿的个数；以某集团公司为观察单位，考察其旗下上市子公司股票价格表现等等。

所有这些类型的资料都存在一个共性，即观察结果相互之间存在一定程度的内在相关性，即不满足方差分析、线性模型应用的前提条件，即各观测结果间相互独立。

重复测量仍然应用方差分析的基本思想，将反应变量的变异分解成以下四个部分：1、研究对象内的变异，又称为组内效应，即测量时间点（或测量条件下）的效应2、研究对象间的变异，有称为组间效应，即处理因素(treatment)的效应3、上述两者的交互作用，组内效应和组间效应的交互作用，表现为在不同时间点（测量条件），处理因素的效应不同。