数学与应用数学专业《学年论文》指导书(1)

数学与应用数学专业毕业论文选题指南一、引言毕业论文是数学与应用数学专业本科生在毕业阶段完成的一项重要学术任务。

论文选题的好坏直接关系到后续研究工作的展开和论文的质量，因此选题是毕业论文写作过程中的关键步骤。

本指南旨在为数学与应用数学专业的学生提供选题方向和思路，帮助他们找到合适的论文选题，并提供相关的写作指导。

二、选题方向1. 应用数学在应用数学领域，有许多热门的选题方向可供选择。

其中一些方向包括：金融数学、精算学、组合优化、算法设计与分析、数据挖掘与机器学习等。

学生可以选择与自己感兴趣的领域相关的选题，并深入研究该领域中的一个具体问题。

2. 数值计算数值计算是数学与应用数学专业中的重要方向。

在这个领域，有很多有趣和有挑战性的问题可以作为毕业论文的选题，比如：数值解常微分方程、数值微分方程组中的稳定性与收敛性、计算流体力学中的数值模拟等。

学生可以根据自己的研究兴趣和能力选择一个适合的数值计算选题。

3. 纯数学纯数学是数学与应用数学专业中最基础也是最抽象的领域。

在纯数学中，有许多经典和有意思的问题可以作为毕业论文的选题，比如：代数学、几何学、拓扑学等。

学生可以选择一个自己感兴趣的领域，并深入研究该领域中的一个具体问题。

三、选题思路选择一个好的论文选题需要学生充分考虑以下几个方面：1. 兴趣和热情选择一个自己感兴趣的选题是非常重要的，因为在毕业论文的写作过程中需要投入大量的时间和精力。

如果选取一个自己兴趣的选题，不仅可以提高学生的学术研究积极性，还可以使其对该领域的知识有更深入的理解。

2. 研究前沿选择一个研究前沿的选题可以提高论文的学术价值和创新性。

学生可以通过查阅相关文献和与导师交流来了解当前领域的研究进展，选择一个有研究价值的选题进行深入研究。

3. 研究可行性选择一个研究可行的选题是非常重要的，学生在选择选题时应充分考虑自己的时间和能力，并与导师进行充分的讨论。

选择一个研究可行的选题可以保证毕业论文能够按时完成并具备一定的研究成果。

数学与应用数学专业大学毕业论文一、引言数学与应用数学专业涵盖了数学理论和数学应用的学习，旨在培养学生在数学理论和方法上的深入理解和应用能力。

本次毕业论文旨在探究数学与应用数学的重要性以及其在现代社会中的应用。

二、数学的重要性1. 数学理论的推动作用数学理论作为科学发展的基础，对现代科学和技术的发展起到了重要的推动作用。

通过深入理解数学的基本原理和概念，学生可以在未来的职业生涯中运用数学方法解决实际问题。

2. 数学在科学研究中的应用数学在自然科学和社会科学等领域中起到了重要的作用。

在物理学、化学、生物学等自然科学领域，数学模型被广泛运用于预测、解释以及模拟实验。

在经济学、管理学、社会学等社会科学领域，数学方法可以用来分析数据、描述现象以及推理推论。

3. 数学教育的培养能力数学学科的学习不仅仅是为了培养学生的数学知识和技能，更重要的是培养学生的逻辑思维能力、抽象思维能力、创造力以及解决问题的能力。

这些能力在学生的终身学习和职业发展中都起到了重要的作用。

三、数学与应用数学的应用领域1. 工程与技术领域数学在工程和技术领域中应用广泛。

在电子工程、计算机科学和信息技术等领域，数学方法被用于设计和优化算法、模拟和分析电路，以及解决不同领域的工程问题。

2. 金融与经济领域数学在金融与经济领域中起到了重要的作用。

通过建立数学模型和运用数学方法，可以预测市场走势、风险管理和投资决策。

金融数学和金融工程等学科的发展也证明了数学在金融领域中的重要性。

3. 自然科学领域数学在自然科学领域中也有广泛的应用。

在物理学、化学、天文学等领域中，数学方法被用于解决实验数据分析、数值计算和模拟实验等问题。

数学模型和方程式可以帮助科学家理解和解释现象，指导实验和观测。

4. 社会科学领域社会科学领域也离不开数学的应用。

例如，在心理学、社会学和统计学等领域中，数学方法可以帮助研究者分析数据、探索关联性以及验证假设。

数学模型的运用可以揭示出隐藏在数据背后的规律和趋势。

《数学与应用数学专业导论》教学大纲一、课程地位与课程目标（一）课程地位本课程是数学与应用数学专业的专业必修课，是本专业的先导性课程。

通过学习本课程使学生了解数学与应用数学专业的专业背景、人才培养定位、课程设置、毕业生能力和素质要求及毕业去向，从而使学生树立牢固的专业思想，明确的学习目标和努力方向。

（二）课程目标1. 使学生了解本专业的专业背景、人才培养定位、课程设置、毕业生能力和素质要求及毕业去向。

2. 使学生树立牢固的专业思想、明确的学习目标和努力方向。

二、课程目标达成的途径与方法课堂教学、专业调研、课堂讨论、课程论文。

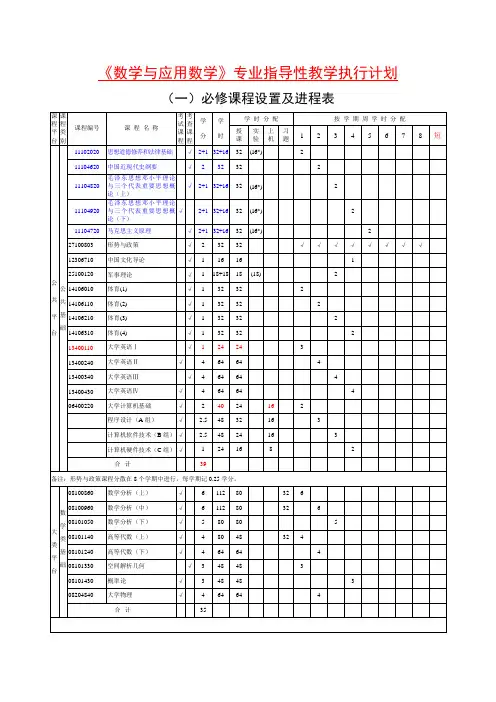
三、课程目标与相关毕业要求的对应关系四、课程主要内容与基本要求第一章数学学科发展历史和现状了解数学学科的学科性质和特点，了解学科发展历史和现状，了解本专业的师资状况和办学条件。

第二章培养目标与课程设置了解本专业的培养目标、课程设置情况，了解必修课和选修课，了解专业方向课，了解各课程在专业培养方案中的地位，能够制订选课方案和学习计划。

第三章人工智能算法及应用初步了解神经网络和深度学习的基本内容与方法，了解神经网络和深度学习的主要应用领域。

第四章数据挖掘理论与技术初步了解数据挖掘的思想和基本理论，了解重要的数据挖掘方法。

第五章金融风险和金融数学初步了解期货证券投资等金融活动的数量特征，了解组合投资中的风险与收益关系，了解常用的统计数据和基本统计分析方法。

第六章软件开发理论展望初步了解常用的程序设计语言，了解软件开发的一般流程，了解大学期间学习的软件，了解程序设计竞赛的举办时间和参加条件。

五、课程学时安排（一）推荐教材：无（二）主要参考书：[1] 数学文化,顾沛,北京：高等教育出版社,2017,第二版.[2]人工神经网络教程,韩力群,北京:邮电大学出版社,2006.。

数学与应用数学专业推荐选读书目第一部分：推荐数学类选读书目一、数学1、《数学分析讲义》，（复旦）陈纪修、於崇华等编，高等教育出版社 ;2、《微积分教程》， [ 苏 ] 菲赫金哥尔茨著，人民教育出版社 ;3、《数学分析题集》， [ 苏 ] 吉米多维奇编，人民教育出版社 ;4、《数学分析中的典型问题与方法》，裴礼文，高等教育出版社 ;5、《数学分析的基本概念与方法》，强文久、李元章、黄雯荣编，6、《实变函数与泛函分析基础》，程其襄等编，高等教育出版社；7、《线性代数 -- 方法导引》，屠伯埙，复旦大学出版社， 1986 年；8、《线性代数解题分析》，胡海清，湖南科学技术出版社， 1984 年；9、《近世代数基础》，张禾瑞，高等教育出版社， 1978 年；10、《点集拓扑讲义》（第二版），熊金城编，高等教育出版社；11、《一般拓扑学》， J.L.Kelly 编，科学出版社 , 1982;12、《概率入门》，杨宗磐著，科学出版社， 1981 ；13、《概率论及数理统计》， M. 费史著，王福保译，上海科技出版社， 1983 ；14、《初等概率论附随机过程》，钟开莱著，魏宗舒等译，人民教育出版社， 1980 ；15、《统计学教学方法》， H 、克拉美著，魏宗舒译，16、《计算数学简明教程》，何旭初等，高等教育出版社；17、《计算方法》，徐萃微等，高等教育出版社；18、《常微分方程数值解法》，南京大学，科学出版社。

19、《离散数学》，耿素云，屈婉玲，高等教育出版社， 1998 ；20、《图论》（第二版），王朝瑞，北京理工大学出版社， 1997 。

21、《数学模型》，姜启源编，高等教育出版社， 1993 ；22、《数学模型及方法》，李火林、邓声南、甘筱青编，23、《微分方程模型》，朱煜民、周宇虹译，国防科技大学出版社。

24、《数值计算方法》，冯康等主编，国防工业出版社；25、《运筹学》，运筹学教材编写组编，清华大学出版社；26、《实用运筹学》，魏国华等编，复旦大学出版社；27、《运筹学入门》， [ 美 ] 罗伯特 . 吉 : 瑟罗夫著，薛华成等译，清华大学出版社；28、《运筹学讲义》，吕立生编，上海工业大学出版社；29、《预测学概论》，孙明玺编，浙江教育出版社；30、《技术经济预测与决策》，张世英编，天津大学出版社；31、《经济预测与决策方法》，暴奉贤编，暨南大学出版社；32、《市场预测与管理决策》，胡玉立等编，中国人民大学出版社；33、《决策分折》，陈珽编著，科学出版社；34、《决策学基础》，姜圣阶等著，中国社会科学出版社。

数学与应用数学专业的毕业论文数学与应用数学专业的毕业论文数学与应用数学专业是一门理论与实践相结合的学科，涉及到数学理论的研究与数学在实际问题中的应用。

而毕业论文是数学与应用数学专业学生完成学业的重要环节，旨在通过独立研究与论文撰写，展示学生在该领域的专业能力和研究成果。

一、选择合适的毕业论文题目选择一个合适的毕业论文题目对于顺利完成论文至关重要。

在选择题目时，学生可以从自己感兴趣的领域出发，结合导师的研究方向进行选择。

同时，要考虑到论文的可行性和实用性，以及对学术界的贡献程度。

一个好的论文题目应该具备研究的深度和广度，能够激发学生的思考和创新。

二、论文的研究方法和理论基础在进行毕业论文的研究过程中，学生需要选择适当的研究方法和理论基础。

研究方法可以包括数学建模、实证研究、理论分析等，而理论基础则是研究的基石。

学生需要通过文献调研和实际操作，选择适合自己研究方向的方法和理论，确保论文的科学性和可信度。

三、数据的收集与分析在进行应用数学专业的毕业论文研究时，数据的收集与分析是一个重要的环节。

学生可以通过实地调研、问卷调查、文献分析等方法收集相关数据，然后运用数学统计学方法进行数据分析。

数据的收集与分析能够为论文的结论提供有力的支持，同时也能够培养学生的实践能力和数据处理能力。

四、论文的撰写与表达毕业论文的撰写与表达是整个研究过程的总结与展示。

学生需要按照学校或学院的要求，规范地撰写论文的各个部分，包括摘要、引言、研究方法、数据分析、结果与讨论等。

同时，学生还需要注重论文的语言表达和逻辑结构，确保论文的可读性和连贯性。

在撰写过程中，学生可以请教导师或其他专业人士的意见和建议，以提高论文的质量。

五、论文的答辩与评审完成毕业论文后，学生还需要进行论文的答辩与评审。

答辩是学生对自己研究成果的展示和解释，评审则是对论文质量的评价和认可。

在答辩和评审过程中，学生需要清晰地陈述自己的研究内容和方法，并回答评委的问题。

《数学与应用数学专业导论》教学大纲课程编号：10180101英文名称：Introduction to Mathematics and Applied Mathematics学分：0.5学时：总学时8学时，其中理论8学时先修课程：无课程类别：专业基础课程授课对象：数学与应用数学(师范)专业学生教学单位：数理信息学院修读学期：第1学期一、课程描述和目标本课程是数学与应用数学(师范)专业基础课，主要介绍数学与应用数学(师范)专业的培养方案、课程设置、课程资源，介绍数学各个分支的发展历史、主要研究成果以及未来的发展趋势。

本课程详细介绍了本科阶段各个课程的内容设置、课程要求以及学习中应注意的地方。

学习本专业导论课程的目的是使学生初步了解数学与应用数学(师范)专业的性质、特点，初步了解并把握学习数学与应用数学(师范)专业各课程的方法，为学好本专业打下导论基础。

【学生学习结果1】：通过课程教学，学生熟悉数学与应用数学(师范)专业的设置情况和专业性质，了解本专业的知识体系，掌握本专业的主要学习方法，了解各学年阶段主要课程的基本内容与特点，为以后学习各门课程做好前期准备。

【学生学习结果2】：了解专业培养方案，具备根据培养方案安排大学四年学习生活的能力。

【学生学习结果3】：具有爱国主义、社会责任感，树立为人师表的理念，能保持严谨细致的科学态度和求实创新的精神，具备自觉学习和终身学习意识。

二、本课程对应的专业毕业要求的内涵分解和支撑关系本课程对应的专业毕业要求内涵和指标，以及所支撑毕业要求指标的程度关系如表2-1和表2-2所示。

表2-1 对应本课程的专业毕业要求内涵分解表2-2课程与毕业要求指标对应的支撑程度矩阵关系三、教学内容、基本要求与学时分配本课程理论教学共8个学时。

四、学生毕业目标的达成途径本课程采用专家报告、教师讲授、案例解读等教学方法，以达到符合毕业要求指标点的教学目的。

表 4-1课程毕业要求和达成途径注: 毕业要求指标下内涵和具体内容参考表2-1。

学号12509013011学年论文（2012级本科）题目: 泊松分布、二项分布、正态分布之间的关系及应用学院：数学与统计学院专业：数学与应用数学作者姓名：柴丽娜指导教师：李劲职称：教授完成日期：2014年12 月20日二○一四年十二月泊松分布、二项分布、正态分布之间的关系及应用柴丽娜 指导教师：李劲（河西学院数学与应用数学专业2012级3班1250901301号, 甘肃张掖 734000）摘 要 二项分布、Poisson 分布与指数分布是概率统计的基础,这3个分布存在密切的关系.本文将通过极限分布的方法讨论二项分布、泊松分布和正态分布三者之间的关系,进一步揭示它们之间的内在联系,并给出有关近似计算公式和应用实例.关键字 泊松分布；二项分布；正态分布；特征函数 中图分类号 O2111 引言许多数学教材中常常只是介绍了二项分布、泊松分布、均匀分布、指数分布、正态分布等重要的概率分布,给出它们的分布列、密度函数、它们的期望和方差,但是很少讨论出这些分布之间的关系.在学习概率统计等时,常常认为这些重要概率分布之间没有什么联系,但是这些分布中间还有很多重要的关系. 本文将通过极限分布的方法讨论二项分布、泊松分布和正态分布三者之间的关系,进一步揭示它们之间的内在联系,并给出有关近似计算公式和应用实例.2 预备知识2.1 相关定义 定义[]11（二项分布）在n 重伯努利试验中,每次试验中事件A 发生的概率为p （0<p<1）,记X 为n 次试验中事件A 发生的次数,则X 的可能取值为0,1,2,…,n.且对每一个k,0≤k ≤n,事件｛X=k ｝即为“在n 次试验中事件A 恰好发生k 次”,根据伯努利概型,有P ｛X=k ｝=()1n kk k n C p p --,k=0,1,2,…,n （1）一般地,如果一个随机变量X 的概率分布由（1）给出,则称X 服从参数为n,p 的二项分布,并记作(,)XB n p ,且记()(;,)1n kk k n B k n p C p p -=-.定义[]12（泊松（poisson ）分布） 如果一个随机变量X 的概率分布为{}(0,1,2,)!k P X k e k k λλ-=== (2)其中0λ>为参数,则称X 服从参数为λ的泊松分布,记作()XP λ.定义[]13(正态分布)一个连续性随机变量X,如果其密度函数为22()2（x）=xeμσϕ--()x-∞<<+∞（3）其中,μ,0σ>为常数,则称X服从参数为μ和0σ>的正态分布,记作2(,)X Nμσ.此时称X为正态变量.特别地,若2(,)X Nμσ,=0，=1μσ,则称X服从标准正态分布(0，1)N,其概率密度函数为22（x）=xϕ-(,)x∈-∞+∞定义[]24(特征函数)若随机变量X的分布函数为F(x),则称()()()()ϕ+∞Ω-∞⎡⎤===⎣⎦⎰⎰itX itX w itxt E e e P dw e dF x（4）为X的特征函数.如果F（x）有密度f(x),则()ϕt就是f(x)的Fourier变换()()ϕ+∞-∞=⎰itxt e f x dx2.2相关定理定理[]31特征函数的一个重要定理（唯一性定理）：分布函数由其特征函数唯一确定.证明设A是F(x)的一切连续点的集合,对任意的x A∈,由逆转公式有[]()lim()()yy AF x F x F y→-∞∈=-1lim()2jty jtxTy Ty Ae et dtjtϕπ--→-∞-∈-=⎰所以,对于一切x A∈,()F x的值唯一的由其特征函数()tϕ所决定.若x A∉,利用分布函数的右连续性,选一列单调下降的趋于x的()F x的连续点12,,x x…,则有1()l i m()l i m l i m l i m()2n nn njty jtxTnx x x x y TTx A x A y Ae eF x F x t dtjtϕπ++--→→→-∞-→∞∈∈∈-==⎰于是,对于一切的x A∉,()F x的值亦唯一的由其特征函数()tϕ所决定.2.3相关结论结论1 二项分布B （n,p ）：其概率分布为()(1)kk n k n P X k P p C -==- 0,1,2,,01k n p =<<…其特征函数为()()(1)nkitXitk k n k X n k t E e e p p C ϕ-===-∑=()(1)nkit k n k n k pe p C -=-∑(1)it n pe p =+-结论2 泊松分布()πλ：设()X πλ,则其概率分布为()!k e P X k k λλ-== 0,1,2,,k λ=>…其特征函数为()()!k itXitxX k e t E e ek λλϕ-∞===∑结论3 正态分布(,)N λλ：其密度函数为22()2（x ）=x eμσϕ--()x -∞<<+∞其特征函数为212()()i t t itXX t E e eλλϕ-==()(1)=!ititite ek e eeee k λλλλλ∞---===∑3 主要结论及证明（三大分布之间的关系）3.1 二项分布与泊松分布的关系（二项分布的poisson 逼近）定理1 二项分布X ：b(n,p),如果n 很大,而P 很小,设0λ>,n 为任意的正整数,n np λ=,则对于任意给定的一个非负整数k,有()lim 1!k kn kkkn n n n ke p p k C λ--→-=.证明 由n p nλ=()(1)11!kn kn kkk nn n n n p p k n n Cλλ---⋅⋅⎛⎫⎛⎫-=- ⎪⎪⎝⎭⎝⎭…(n-k +1)121=1(1)(1)(1)(1)(1)!k n k k k nnnnnλλλ--⎡⎤⋅-----⎢⎥⎣⎦…当,n k →∞固定,1211(1)(1)(1)1,(1),(1)1n k k ke n n n n nλλ---⋅---→-→-→…故有 l i m (1)!k kkkn knnn n e pp k C λ--→∞-=所以当n 很大时,p 很小时有下列近似公式(1)!k kk k n kne p p k Cλ---≈3.2 二项分布和正态分布之间的关系 定理 设随机变量(,)(01,1,2,)nX b n p p n <<=…,则对于任意x,有22lim ()t x n x dt x -→∞⎧⎫⎪≤==Φ⎬⎪⎭⎰由上式可以得出当n 充分大时,二项分布可以用正态分布来近似,即二项分布的正态逼近.例 {}(1)kk n kn n P X k p p C -==-和{}kk n kn na k bP a X b p q C-≤≤≤≤=∑在n 充分大时计算非常困难.N （0,1）或等价地n X 近似服从(,(1))N np np p -,于是可以近似地用正态分布来计算上述概率,即{}(1)kk n k n n P X k p p C -==-()22k np npq--≈⎛⎫={}n P a X b P ⎧⎫≤≤=≤≤⎛⎫⎛⎫≈Φ-Φ只要查一下标准正态分布表就可以得到{}n P a X b ≤≤的相当精确的值.3.3 泊松分布与正态分布之间的关系二项分布可以用泊松分布近似,也可以用正态分布近似.所以泊松分布和正态分布在一定条件下也有近似关系,下面说明泊松分布的正态分布.定理 设()(0)Xπλλ>,泊松分布的分布函数{}!k k xe P X x k λλ-<<=∑与正态分布N λλ（，）的分布函数2()2y xedy λλ---∞⎰是近似相等的.证明 根据特征函数的唯一性定理可以得出分布函数1()F x 和2()F x 恒等的充分必要条件是他们的特征函数1()x ϕ和2()x ϕ恒等.已知正态分布(,)N λλ的特征函数是212()()i t t itXX t E e eλλϕ-==泊松分布的特征函数是(1)()()ititX e X t E e e λϕ-==对于任意的t, it e 的幂级数展开为23123!itt it e it =+--+…,忽略3t 以后的各项,则有212itt e it -≈-,于是2(1)2itt e i t λλλ-≈-2(1)2itt i t ee eλλλ--≈根据唯一性定理可知,泊松分布的分布函数{}!k k xe P X x k λλ-<<=∑与正态分布的分布函数2()2yxe dyλλ---∞⎰近似相等.4 初步应用例1 某大城市有一个繁忙的交通岗,若每天有100000人通过,每人出事故的概率为0. 0001,求该天事故的人数X不超过2人的概率.解法一：由题意可以知道()1000000.0001X B，,由二项分布可以得{}20.002769P X≤=解法二：用泊松分布近似二项分布.即将数据代入(1)!k kk k n knep pkCλ---≈可以得到{}1021020.002769!kkeP Xk-=≤≈=∑解法三：用正态分布的分布函数近似二项分布.即将数据代入{}nP a X b⎛⎫⎛⎫≤≤≈Φ-Φ可以得到{}()()2 2.53 3.160.00501P X≤≈Φ--Φ-=这里直接查标准正态分布的分布函数表求得,其误差为0.00224151,这比用泊松分布产生的误差要大.例2 同类型仪器300台,各仪器的工作相互独立,且发生故障的概率为0.01,通常一台仪器的故障可有一个人来排除.问：（1）至少配备多少维修工人,才能保证当仪器发生故障又不能及时排除的概率小于0.01？（2）若一个人包干20台仪器,求仪器发生故障又不能及时排除的概率.解：设300 台仪器中在同一时刻发生故障的仪器台数为X, 则X~B(300,0.01).设X 表示发生故障的仪器台数,假若至少要配备x个工人,则按题意有P(X＞x)＜0.01,即300300()10.010.99xk k kkP X x C-=>=-⋅⋅∑此时用泊松定理则可以容易计算.(1)有3000.013npλ==⨯=,{}30310.01!k xk e P X x k -=>≈-<∑,查询泊松分布表即可以得到x=8.(2) 记 X 为 20 台仪器中在同一时刻发生故障的仪器台数,则 X~B(20,0.01).(2)1(2)P X P X ≥=-<12020010.010.99kk k k C -==-⋅⋅∑0.20.210.20.017523e e --≈--⨯≈致谢 感谢李劲老师对本论文的指导.参 考 文 献[1]马统一.经济应用数学—概率论与数理统计[M].北京.高等教育出版社,2012.57-65. [2]张波,商豪.应用随机过程[M].第二版.北京.中国人民大学出版社,2013.13-15. [3]田铮,秦超英.随机过程与应用[M].北京.科学出版社,2007.14-21.[4]苏淳,刘杰.现代极限理论及其在随机结构中的应用[M].北京.高等教育出版社,2010.4-5. [5]李裕奇,李玉红.随机过程[M].北京.国防工业出版社,2005.56-65.[6]梁好翠.三种重要概率分布的关系及其应用[J].钦州学院学报,2007,第22卷第3期:9-11 [7]段勇花.概率中伯努利试验问题的解决策略[J].西安文理学院学报,2012,上旬刊：77-78 [8]周桂如.概率分布及其应用的研究[J].赤峰学院学报,2008,第24卷第4期：13-14[9]于洋.浅析二项分布、泊松分和正态分布之间的关系[J].企业科技与发展,2008,第20期：108-110 [10]朱冬梅.谈概率论中三种重要的分布[J].开封教育学院学报,2003,第23卷第4期：42-43[11]张子贤.关于二项分布的正态近似计算问题[J].河北工程技术高等专科学校学报,2002,第1期：20-23[12]李晓辉,任伟和.浅谈二项分布与正态分布之间的关系[J].石家庄理工职业学院学术研究,2014,第9卷第2期:1-3[13]杜勋明,陈冬娥,姚云二项分布和泊松分布的正态近似条件分析[J].湖北医科大学学报,1998,第19卷第2期:123-125。