数学北师大版九年级上册韦达定理

韦达其人一元二次方程的根与系数的关系，常常也称作韦达定理，这是因为该定理一般被认为是16世纪法国最杰出的数学家韦达发现的。

韦达1540年出生在法国东部的普瓦图的韦特奈。

他早年学习法律，曾以律师身份在法国议会里工作，韦达不是专职数学爱，但他非常喜欢在政治生涯的间隙和工作余暇研究数学，并做出了很多重要贡献，成为那个时代最伟大的数学家。

韦达是第一个有意识地和系统地使用字母表示数的人，并且对数学符号进行了很多改进。

他在1591年所写的《分析术引论》是最早的符号代数著作。

是他确定了符号代数的原理与方法，使当时的代数学系统化并且把代数学作为解析的方法使用。

因此，他获得了“代数学之父”之称。

他还写下了《数学典则》（1579年）、《应用于三角形的数学定律》（1579年）等不少数学论著。

韦达的著作，以独特形式包含了文艺复兴时期的全部数学内容。

只可惜韦达著作的文字比较晦涩难懂，在当时不能得到广泛传播。

在他逝世后，才由别人汇集整理并编成《韦达文集》于1646年出版。

韦达1603年卒于巴黎，享年63岁。

下面是关于韦达的两则趣事：一、与罗门的较量比利时的数学家罗门曾提出一个45次方程的问题向各国数学家挑战。

法国国王便把该问题交给了韦达，韦达当时就得出一解，回家后一鼓作气，很快又得出了22解。

答案公布，震惊了数学界。

韦达又回敬了罗门一个问题。

罗门苦思冥想数日方才解出，而韦达却轻而易举地作了出来，为祖国争得了荣誉，他的数学造诣由此可见一斑。

二、韦达的“魔法”在法国和西班牙的战争中，法国人对于西班牙的军事动态总是了如指掌，在军事上总能先发制人，因而不到两年功夫就打败了西班牙。

可怜西班牙的国王对法国人在战争中的“未卜先知”十分脑火又无法理解，认为是法国人使用了“魔法”。

原来，是韦达利用自己精湛的数学方法，成功地破译了西班牙的军事密码，为他的祖国赢得了战争的主动权。

另外，韦达还设计并改进了历法。

所有这些都体现了韦达作为大数学家的深厚功底。

数学韦达定理知识点
数学韦达定理知识点
同学们还记得韦达定理吗，下面我们来学习。

韦达定理
利用韦达定理去了解，韦达定理就是在一元二次方程中，二根之和=-b/a，二根之积=c/a
也可以表示为x1+x2=-b/a,x1x2=c/a。

利用韦达定理，可以求出一元二次方程中的各系数，在题目中很常用
关于韦达定理的知识点，希望同学们能很好的记住，相信同学们对数学的学习是充满信心的。

初中数学知识点总结：平面直角坐标系
下面是对平面直角坐标系的内容学习，希望同学们很好的掌握下面的内容。

平面直角坐标系
平面直角坐标系：在平面内画两条互相垂直、原点重合的`数轴，组成平面直角坐标系。

水平的数轴称为x轴或横轴，竖直的数轴称为y轴或纵轴，两坐标轴的交点为平面直角坐标系的原点。

平面直角坐标系的要素：①在同一平面②两条数轴③互相垂直④原点重合
三个规定：
①正方向的规定横轴取向右为正方向，纵轴取向上为正方向
②单位长度的规定；一般情况，横轴、纵轴单位长度相同；实际有时也可不同，但同一数轴上必须相同。

③象限的规定：右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。

相信上面对平面直角坐标系知识的讲解学习，同学们已经能很好的掌握了吧，希望同学们都能考试成功。

初中数学知识点：平面直角坐标系的构成
对于平面直角坐标系的构成内容，下面我们一起来学习哦。

【数学韦达定理知识点】。

第三讲 一元二次方程之韦达定理一元二次方程的根与系数的关系，通常也称为韦达定理，这是因为该定理是由16世纪法国最杰出的数学家韦达发现的．1.一元二次方程根与系数的关系（韦达定理）对于一元二次方程，如果方程有两个实数根，那么说明：（1）定理成立的条件（2）注意公式重的负号与b的符号的区别2.韦达定理的逆定理给定一个一元二次方程。

如果有两个数，它们的和等于该方程的一次项系数除以二次项系数的相反数，它们的积又等于该方程的常数项除以二次项系数，那么它们就是该方程的两根。

设关于的一元二次方程为，且，，、必定是一元二次方程的两个根。

3.韦达定理简单的形式中包含了丰富的数学内容，应用广泛，主要体现在：运用韦达定理，求方程中参数的值运用韦达定理，求代数式的值；利用韦达定理并结合根的判别式，讨论根的符号特征； 利用韦达定理逆定理，构造一元二次方程辅助解题等． 韦达定理具有对称性，设而不求、整体代入是利用韦达定理解题的基本思路．韦达定理，充满活力，它与代数、几何中许多知识可有机结合，生成丰富多彩的数学问题，而解这类问题常用到对称分析、构造等数学思想方法．佳题新题品味例已知△ABC的边长分别为a,b,c,且a>b>c,2b=a+c,b为正整数,若a2+b2+c2=84,求b的值.热身例题13、（2010·珠海中考）已知x=－1是方程的一个根，求m的值及方程的另一根x2【典型例题】例1 已知关于的方程，根据下列条件，分别求出的值．(1) 方程两实根的积为5； (2) 方程的两实根满足．例2 已知是一元二次方程的两个实数根．(1) 是否存在实数，使成立？若存在，求出的值；若不存在，请您说明理由．(2) 求使的值为整数的实数的整数值．例3 已知关于x的方程x2+2mx+m+2=0,求:(1)m为何值时, 方程的两个根一个大于0,另一个小于0;(2)m为何值时, 方程的两个根都是正数;(3)m为何值时, 方程的两个根一个大于1,另一个小于1.根与系数的关系（韦达定理）提升练习1．已知关于的方程有两个不相等的实数根．(1) 求的取值范围；(2) 是否存在实数，使方程的两实根互为相反数？如果存在，求出的值；如果不存在，请您说明理由．2．已知关于的方程的两个实数根的平方和等于11．求证：关于的方程有实数根．3．若是关于的方程的两个实数根，且都大于1．(1) 求实数的取值范围；(2) 若，求的值．韦达定理中考题练习1、（2010·玉溪中考）一元二次方程x2－5x+6=0 的两根分别是x1,x2,则x1+x2等于（）A. 5B. 6C. －5D. －62、（2008·枣庄中考）已知x1、x2是方程x2－3x－2＝0的两个实根，则(x1－2) (x2－2)= ．3、（2008·中山中考）已知关于x的方程．（1）求证方程有两个不相等的实数根．（2）当m为何值时，方程的两根互为相反数？并求出此时方程的解．4、(2009•鄂州中考)关于x的方程有两个不相等的实数根.(1)求k的取值范围。

一元n次方程根与系数的关系
数学在许多人眼里是很抽象、复杂的，但在这些复杂现象的背后却往往有着
非常和谐、自然的规律，如果能更多地理解和掌握这些规律，就会对数学有更深
刻的认识。

很多迷恋数学的人就是被数学的这一特点所吸引，韦达便是其中的一
员。

韦达于1540年生于法国普瓦图地区，1560年就读于法国普瓦图大学，是大
学法律系的毕业生。

毕业后长期从事法律工作，一直到1603年去世，数学始终
是韦达的业余爱好，并且达到了酷爱的程度。

韦达研究二次方程时，已经注意到，如果一次项的系数是两个数之和的相反数，而常数项是这两个数的乘积，则这两个数就是这个方程的根。

由于时代的局限，他当时没能从理论上证明它，但他的数学思想和他的数学著作都大大充实了数学宝库。

1615年(此时，韦达已逝世12年，这些著作是由后人整理的)发表的韦达的著作《论方程的整数与修正》是一部方程论的专著，书中对一元三次方程、一元四次方程的解法做出了改进，并揭示了方程根与系数的关系。

其中不仅包括一元二次方程的根与系数的关系，还包含了一元n次方程根与系数的关系：
如果一元n次方程a
n x n+a
n-1
x n-1+…+a1x+a0=0的n个根是x
1
, x
2
, …, x
n
, 那么
人们为了纪念他，把这个关系称为“韦达定理”。

一元二次方程根与系数的关系，就是上述定理在n=2时的情况。

一元二次方程根与系数的关系（2）一、知识导航1．如果21x x 、是一个一元二次方程的两根，那么当方程二次项系数为1时，方程应该表示为（构造一个适合的方程） ．2．根的分布情况：如果21x x 、是一元二次方程)0(02≠=++a c bx ax 的两根，则 (1)0,021>>x x 时，有⎪⎪⎪⎩⎪⎪⎪⎨⎧>=⋅>-=+≥∆0002121a c x x a b x x (2)0,021<<x x 时，有⎪⎪⎪⎩⎪⎪⎪⎨⎧>=⋅<-=+≥∆0002121a c x x a b x x (3)0,021<>x x 时，有021<=⋅ac x x (特别注意：利用根的分布时要注意别漏掉考虑根的判别式，只有有根才谈得上考虑根的正负)3．特殊根的表示方法：当x =1时，a+b+c=0，当x=-1时，a-b+c=0，当x =0时，c=0．二、预习反馈1．如果关于x 的一元二次方程ax 2＋bx ＋c ＝0有一正一负根，且负根的绝对值更大，那么（ ）(A) a ，b 同号，且a ，c 同号(B) a ，b 同号，且a ，c 异号(C) a ，b 异号，且a ，c 同号(D) a ，b 异号，且a ，c 异号2．已知一元二次方程012=-+x x 的两根21x x 、 为，则(12x x +－1)(21x x ⋅+2014)= ．3．已知一元二次方程02)2(2=--+x k x 的两根互为相反数，则k 的取值范围是 ．4．写出一个一元二次方程，使它的两根分别是1,2--，方程为 ． 三、例题精析例1、已知关于x 的一元二次方程28(1)70x m x m +++-=有两个负数根，求实数m 取值范围．例2、当n ＞0时，关于x 的一元二次方程21(2)04x m n x mn --+=有两个相等的正实数根，求m n的值．四、课堂过手A 级1．二次函数352+-=x x y 的图象交x 轴于A 、B 两点，交y 轴于点C ，则△ABC 的面积为（ ）（A ）13 （B ）213 （C ）132 （D ）2133 2．以方程3 x 2＋2x －6＝0的各根的负倒数为根的一个一元二次方程是（ ）（A ）6 x 2－2x ＋1＝0 （B ）6 x 2＋2x ＋3＝0（C ）6 x 2＋2x ＋1＝0 （D ）6 x 2＋2x －3＝03． 已知关于x 的方程02)12(22=-+++k x k x 的两实数根的平方和等于11，则k 的值为 ．4．已知21x x 、是方程)53()2(22+++--k k x k x =0的两个实数根（其中k 为实数），则2221x x +的最大值是__________．(不等式0161632≤++x x 解集为344-≤≤-x ) 5．已知一元二次方程01032=+-m x x 有两个正根，求m 的取值范围．B 级6．若a 、b 为方程012682=+++m mx x 的两实数根，且122=+b a ，求m 的值．五、能力提升当所考查的根的分布不仅仅限于正负性时，比如两个实数根都介于2与4之间（不包括2和4），或者两根中一根介于0与1之间，另一个根介于3与4之间，这时用根的判别式及韦达定理解决问题就相当复杂．那么比较朴素的方法就是直接去求出方程的根，但是这一方法有两个弊端：第一，带有参数的方程求根是个较复杂的过程，且涉及较深的不等式解法：第二，抽象数量运算较多，缺乏直观性．这时借助于二次函数图像，就比较直观且容易理解．根据分析解答下列题目:7．若方程03422=-+-a ax x 的两根均大于1，求实数a 的取值范围．。

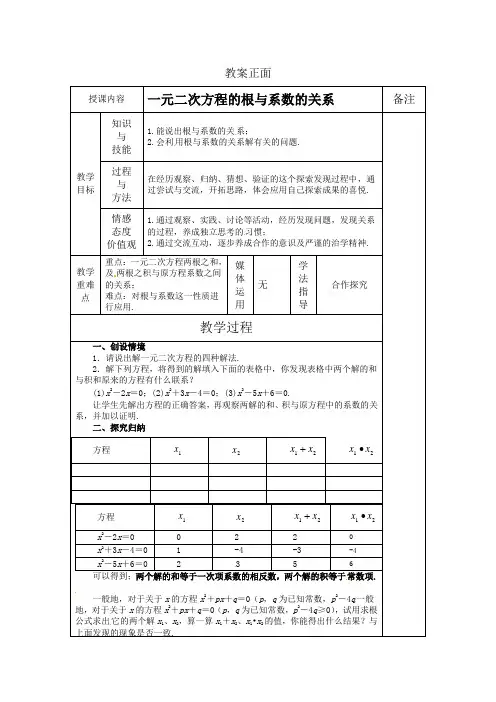
1.能说出根与系数的关系；2.会利用根与系数的关系解有关的问题.价值观 1.通过观察、实践、讨论等活动，经历发现问题，发现关系的过程，养成独立思考的习惯；2.通过交流互动，逐步养成合作的意识及严谨的治学精神.教学重难重点：一元二次方程两根之和，及两根之积与原方程系数之间的关系；难点：对根与系数这一性质进行应用.一、创设情境1．请说出解一元二次方程的四种解法.2．解下列方程，将得到的解填入下面的表格中，你发现表格中两个解的和与积和原来的方程有什么联系？(1)x 2－2x ＝0；(2)x 2＋3x －4＝0；(3)x 2－5x ＋6＝0. 让学生先解出方程的正确答案，再观察两解的和、积与原方程中的系数的关系，并加以证明.二、探究归纳方程1x2x21x x +21x x ∙x 2－2x ＝0 0 2 2 0 x 2＋3x －4＝0 1-4-3-4x 2－5x ＋6＝02 3 56 可以得到；两个解的和等于一次项系数的相反数，两个解的积等于常数项.一般地，对于关于x 的方程x 2＋px ＋q ＝0（p ，q 为已知常数，p 2－4q 一般地，对于关于x 的方程x 2＋px ＋q ＝0（p ，q 为已知常数，p 2－4q ≥0），试用求根公式求出它的两个解x 1、x 2，算一算x 1＋x 2、x 1•x 2的值，你能得出什么结果？与上面发现的现象是否一致.方程 1x2x21x x +21x x ∙qqp p q p p x x pqp p q p p x x q p p x q p p x q p p aac b b x q p ac b q c p b a q px x =---∙-+-=∙-=---+-+-=+---=-+-=-±-=-±-=≥-=-====++24242424242424240441022212221222122222，，，结论：两根之和等于一次项系数的相反数，两根之积等于常数项，这与上面的发现是一致的.三、实践应用例 1 已知关于x 的方程x 2－px ＋q ＝0的两个根是0和－3，求p 和 q 的值.解法一：因为关于x 的方程x 2－px ＋q ＝0的两个根是0和－3，所以有．q p q p q p q p 03030)3()3(00022=-=⎩⎨⎧=-=⎪⎩⎪⎨⎧=+-⨯--=+⨯-，所以解这个方程组得解法二：由q x x p x x =∙-=+2121，，方程x 2－px ＋q ＝0的两个根是0和－3，可得．q p q p 03)3(0)3(0=-==-⨯，即得＝－－＋例2 写出下列方程的两根和与两根积：5)4(032)3(02114)2(017)1(2222=-+-=-+=-+=+-n nx xx xx x x x5)4(2321)3(2114)2(17)1(2121212*********-=∙=+=∙-=+=∙-=+=∙=+n x x nx x x x x x x x x x x x x x ，－，－，，解四、交流反思1.通过这节课的学习，掌握探索的步骤：观察——归纳——猜想——证明；2.通过本节课探索出一元二次方程的根与系数的关系.五、布置作业。

初三数学九年级上《韦达定理》复习一、知识回顾1.一般地，对于关于x 的一元二次方程ax 2＋bx ＋c ＝0(a ≠0) 用求根公式求出它的两个根x 1.x 2 ，由一元二次方程ax 2＋bx ＋c ＝0的求根公式知x 1=a ac b b 242-+-,x 2=aac b b 242---2.能得出以下结果：x 1＋x 2= 即：两根之和等于x 1•x 2= 即：两根之积等于12x x +=a ac b b 242-+-+aac b b 242--- =aac b b ac b b 24422----+- =12.x x =a ac b b 242-+-×aac b b 242--- =2224)4)(4(a ac b b ac b b ----+- =2224)()(a -=由此得出，一元二次方程的根与系数之间存在得关系为x 1+x 2=ab -， x 1x 2=a c 3.韦达定理韦达定理：对于一元二次方程20(0)ax bx c a ++=≠，如果方程有两个实数根12,x x ，那么1212,b c x x x x a a+=-= 4.韦达定理前提（1）定理成立的条件0∆≥（2）注意公式重12b x x a+=-的负号与b 的符号的区别 二、知识学习（1）计算对称式的值 例1. 若12,x x 是方程2220070x x +-=的两个根，试求下列各式的值：(1) 2212x x +； (2)1211x x +； (3) 12(5)(5)x x --； (4) 12||x x -．说明：利用根与系数的关系求值，要熟练掌握以下等式变形： 222121212()2x x x x x x +=+-，12121211x x x x x x ++=，22121212()()4x x x x x x -=+-，12||x x -=2212121212()x x x x x x x x +=+，33312121212()3()x x x x x x x x +=+-+等等．韦达定理体现了整体思想．举一反三1．设x 1，x 2是方程2x 2－6x ＋3＝0的两根，则x 12＋x 22的值为_________2．已知x 1，x 2是方程2x 2－7x ＋4＝0的两根，则x 1＋x 2＝ ，x 1·x 2＝ ， （x 1－x 2）2＝例2．已知方程2x 2－3x+k=0的两根之差为212，则k= ; 例3．若方程x 2+(a 2－2)x －3=0的两根是1和－3，则a= ;例4．若关于x 的方程x 2+2(m －1)x+4m 2=0有两个实数根，且这两个根互为倒数，那么m 的值为 ;例5.设x 1,x 2是方程2x 2－6x+3=0的两个根，求下列各式的值：(1)x 12x 2+x 1x 22 (2) 1x 1 －1x 2例6．已知x 1和x 2是方程2x 2－3x －1=0的两个根，利用根与系数的关系，求下列各式的值： 2221x 1x 1（2）构造新方程例7.理论：以两个数为根的一元二次方程是。

2.5一元二次方程的根与系数的关系知识精讲韦达定理（1）如果20(0)ax bx c a++=≠的两根是1x，2x，则12bx xa+=-，12cx xa=（隐含条件：0∆≥）（2）当二次项系数为1时，20x bx c++=的两个根，则12x x b+=-，12x x c⋅=()221244+=2=b b ac b b acx xaba------＋＋221244=22=b b ac b b acx xa aca----⋅⋅＋－应用（1）已知方程的一个根，求另一个根以及确定方程参数的值；若方程240x x c-+=的一个根为23+，则根据韦达定理，124x x+=，∴()2423=23x=-－＋12x x c⋅=，∴c=1（2）已知方程，求方程的两根；2320x x+=－123x x+=，122x x⋅=1212x x==（3）公式的变形例：x1，x2是一元二次方程x2＋2x＋2m＝0的两个根，且x12＋x22＝8，求m的值x1＋x2＝-2，x1 x2＝2mx12＋x22＝（x1＋x2）2－2x1x2＝4－4m＝8，∴m＝-1，当m＝-1时，△＞0，∴成立，m＝-1（4）已知方程的两根，求作方程；例：已知一元二次方程的两根为1+212、－，求该方程121+2122bx xa+===-+－()()121+212-1cx xa⋅=⋅==－2c a b a∴=-=-令a=1，则方程为2210x x--=（5）结合根的判别式，讨论根的符号特征；若0ca<，0ba-≥，则12x x≥若0ca<，ba-<，则12x x<若0ca>，0ba->，则12x x≥>若0c a >，0ba-<，则210x x ≤< （6）逆用构造一元二次方程辅助解题：当已知等式具有相同的结构时，就可以把代数式看作某个一元二次方程的两根，以便利用韦达定理（a + b ）+（c +d ）=8（a + b ）（c +d ）=16运用韦达定理可得a + b =4， c +d =4易错点：在使用韦达定理的时候没有提前检验0∆≥是否成立三点剖析一．考点：韦达定理二．重难点：韦达定理的应用1．已知方程的一个根，求另一个根以及确定方程参数的值； 2．已知方程，求关于方程的两根的代数式的值； 3．已知方程的两根，求作方程；4．结合根的判别式，讨论根的符号特征；5．逆用构造一元二次方程辅助解题：当已知等式具有相同的结构时，就可以把某两个变元看作某个一元二次方程的两根，以便利用韦达定理．三．易错点：在使用韦达定理的时候没有提前检验0∆≥是否成立韦达定理例题1、 若方程240x x c -+=的一个根为23+，则方程的另一个根为______，c =______． 【答案】 231c =【解析】 根据韦达定理，124x x +=，因为123x =+223x =-(1223231c x x =⋅== 例题2、 设1x 、2x 是方程()222120x k x k -+++=的两个不同的实根，且()()12118x x ++=，则k 的值是 ． 【答案】 1k =【解析】 由根与系数的关系得 ()1221x x k +=+，2122x x k ⋅=+．且有()()224142840k k k ∆=+-+=->，即12k >． 所以()()12118x x ++=． 从而2230k k +-=， 解之得3k =-或1k =．又12k >，所以1k =．例题3、 如果a ，b 都是质数，且2130a a m -+=，2130b b m -+=，求b aa b+的值． 【答案】 当a b =时，2b a a b +=；当a b ≠时，12522b a a b +=【解析】 当a b =时，2b aa b+=；当a b ≠时，a 、b 为方程2130x x m -+=的两个根，所以 13a b +=，则2a =，11b =或2b =，11a =． 所以21112511222b a a b +=+=．例题4、 已知关于x 的一元二次方程x 2﹣4x+m=0． （1）若方程有实数根，求实数m 的取值范围；（2）若方程两实数根为x 1，x 2，且满足5x 1+2x 2=2，求实数m 的值． 【答案】 （1）m≤4 （2）﹣12【解析】 （1）∵方程有实数根， ∴△=（﹣4）2﹣4m=16﹣4m≥0， ∴m≤4；（2）∵x 1+x 2=4，∴5x 1+2x 2=2（x 1+x 2）+3x 1=2×4+3x 1=2， ∴x 1=﹣2，把x 1=﹣2代入x 2﹣4x+m=0得：（﹣2）2﹣4×（﹣2）+m=0， 得：m=﹣12．例题5、 已知关于x 的方程211300x x a -++=的两根都大于5，求a 的取值范围．【答案】 104a <≤【解析】 设1x ，2x 是方程的两根，1212121212(5)(5)5()250301112141200x x x x x x x x a x x a --=-++>⎧⎪=+⎪⎨+=⎪⎪∆=--⎩≥，解得104a <≤．随练1、 已知m ，n 是有理数，并且方程20x mx n ++=2-，那么m n +=_______．【答案】 3【解析】 由于m ，n 是有理数，并且方程20x mx n ++=2-，所以方程的另一个根是2-．由韦达定理知：(2)2)m -=-+-，(2)2)n =-⨯-∴4m =，1n =-，∴4mn =-，3m n +=．随练2、 已知x 1，x 2是关于x 的一元二次方程x 2﹣5x+a=0的两个实数根，且x 12﹣x 22=10，则a=_____．【答案】 214【解析】 由两根关系，得根x 1+x 2=5，x 1•x 2=a ， 由x 12﹣x 22=10得（x 1+x 2）（x 1﹣x 2）=10， 若x 1+x 2=5，即x 1﹣x 2=2，∴（x 1﹣x 2）2=（x 1+x 2）2﹣4x 1•x 2=25﹣4a=4，∴a=214．随练3、 如果实数,a b 分别满足222a a +=，222b b +=，求11a b+的值【答案】 当a b ≠时，111a b +=；当a b =时，当1a b ==-+时，111a b +，当1a b ==--时，111a b+=【解析】 由题意知：,a b 为方程2220x x +-=的两个根，且0,0a b ≠≠，解方程2220x x +-=得：113x =-+213x =--⑴当a b ≠时，有2a b +=-，2ab =-，11212a b a b ab +-∴+===-；⑵当a b =时，方程的根为113x =-+213x =--当13a b ==-+1123131a b a ∴+==-；当13a b ==-1121331a b a ∴+===---随练4、 已知关于x 的方程222(2)50x m x m +++-=有两个实数根，并且这两个根的平方和比这两个根的积大16，求m 的值． 【答案】 -1【解析】 有实数根，则△≥0，且22121216x x x x +=+，联立解得m 的值．依题意有：12212221212222(2)5164(2)4(5)0x x m x x m x x x x m m +=-+⎧⎪=-⎪⎨+=+⎪⎪∆=+--≥⎩由①②③解得：1m =-或15m =-，又由④可知m ≥94-∴15m =-舍去，故1m =-随练5、 已知关于x 的方程24280x x m --+=的一个根大于1，另一个根小于1，求m 的取值范围．【答案】 52m >【解析】 设1x ，2x 是方程的两根，且11x >，21x <，即110x ->，210x -<， 因此1212121212(1)(1)()10284164(28)0x x x x x x x x m x x m --=-++<⎧⎪=-+⎪⎨+=⎪⎪∆=+->⎩，解得52m >．随练6、 关于x 的一元二次方程x 2＋2x ＋2m ＝0有两个不相等的实数根． （1）求m 的取值范围；（2）若x 1，x 2是一元二次方程x 2＋2x ＋2m ＝0的两个根，且x 12＋x 22＝8，求m 的值．【答案】 （1）12m ＜（2）－1【解析】 （1）∵一元二次方程x2＋2x ＋2m ＝0有两个不相等的实数根， ∴△＝b 2－4ac ＝4－8m ＞0，解得：12m ＜∴m 的取值范围为12m ＜．（2）根据根与系数关系得： x 1＋x 2＝－2，x 1x 2＝2mx 12＋x 22＝（x 1＋x 2）2－2x 1x 2＝4－4m ＝8， ∴m ＝－1，当m ＝－1时，△＞0， ∴m 的值为－1．课后练习1、 已知方程22240x mx m -+-=的一个解为1，则另一个解为__________，m =__________．【答案】 0；2【解析】212mx +=，212x m ⋅=-，解得20x =，2m =． 2、 已知方程2230x mx -+=的两根的平方和为5，则m=__________．【答案】 ±【解析】 设2230x mx -+= 的两根分别为12,x x ，则12,2m x x +=123.2x x =而22222121212()23,35,44m m x x x x x x +=+-=-∴-=即232,m m =∴=±3、 已知关于x 的一元二次方程x 2＋2（m ＋1）x ＋m 2－1＝0． （1）若方程有实数根，求实数m 的取值范围；（2）若方程两实数根分别为x 1，x 2，且满足（x 1－x 2）2＝16－x 1x 2，求实数m 的值． 【答案】 （1）m≥－1（2）1【解析】 （1）由题意得△＝[2（m ＋1）]2－4（m 2－1）≥0， 整理得8m ＋8≥0， 解得m≥－1，∴实数m 的取值范围是m≥－1；（2）由两根关系，得x1＋x2＝－（2m ＋1），x 1•x 2＝m 2－1， （x 1－x 2）2＝16－x 1x 2（x 1＋x 2）2－3x 1x 2－16＝0，∴[－2（m ＋1）]2－3（m 2－1）－16＝0， ∴m 2＋8m －9＝0， 解得m ＝－9或m ＝1 ∵m≥1 ∴m ＝1．4、 已知关于x 的一元二次方程x 2﹣4x+m=0． （1）若方程有实数根，求实数m 的取值范围；（2）若方程两实数根为x 1，x 2，且满足5x 1+2x 2=2，求实数m 的值． 【答案】 （1）m ≤4（2）m=﹣12 【解析】 （1）∵方程有实数根， ∴△=（﹣4）2﹣4m=16﹣4m ≥0， ∴m ≤4；（2）∵x 1+x 2=4，∴5x 1+2x 2=2（x 1+x 2）+3x 1=2×4+3x 1=2， ∴x 1=﹣2，把x 1=﹣2代入x 2﹣4x+m=0得：（﹣2）2﹣4×（﹣2）+m=0， 解得：m=﹣12．5、 实数k 为何值时，关于x 的一元二次方程2(23)(24)0x k x k --+-=．（1）有两个正根？（2）两根异号，且正根的绝对值较大？ （3）一根大于3，一根小于3？【答案】 （1）2k >（2）322k <<（3）72k >【解析】 []2(23)(24)0(1)(24)0x k x k x x k --+-=⇒---=，故1x =或24x k =- （1）若两根均为正，则240k ->，故2k >；（2）若两根异号，且正根的绝对值较大，则0421k <-<，故322k <<； （3）由13<可知，72432k k ->⇒>．6、 阅读材料：设一元二次方程20(0)ax bx c a ++=≠的两根是1x 、2x ，则根与系数关系为：12b x x a +=-，12cx x a =．已知210p p --=，210q q --=，且1pq ≠，求1pq q +的值． 【答案】 1【解析】 由210p p --=，210q q --=有0p ≠，0q ≠，又1pq ≠，所以1p q≠则210q q --=可变形为211()10q q --=．由210p p --=及1p q ≠，可知p 与1q是方程210x x --=的根，因此111pq p q q+=+=．。

教学设计一元二次方程的根与系数的关系【学习目标】1、学会用韦达定理求代数式的值。

2、理解并掌握应用韦达定理求待定系数。

3、理解并掌握应用韦达定理构造方程，解方程组。

4、能应用韦达定理分解二次三项式。

【内容分析】韦达定理：对于一元二次方程20(0)ax bx c a ++=≠，如果方程有两个实数根12,x x ，那么1212,b c x x x x a a+=-=说明：（1）定理成立的条件0∆≥（2）注意公式重12bx x a+=-的负号与b 的符号的区别根与系数关系的三大用处 （1）计算对称式的值例 若12,x x 是方程2220070x x +-=的两个根，试求下列各式的值：(1) 2212x x +； (2)1211x x +； (3) 12(5)(5)x x --； (4)12||x x -．解：由题意，根据根与系数的关系得：12122,2007x x x x +=-=- (1) 2222121212()2(2)2(2007)4018x x x x x x +=+-=---= (2)121212112220072007x x x x x x +-+===- (3) 121212(5)(5)5()2520075(2)251972x x x x x x --=-++=---+=-(4) 12||x x -====说明：利用根与系数的关系求值，要熟练掌握以下等式变形：222121212()2x x x x x x +=+-，12121211x x x x x x ++=，22121212()()4x x x x x x -=+-，12||x x -=2212121212()x x x x x x x x +=+，33312121212()3()x x x x x x x x +=+-+等等．韦达定理体现了整体思想．【课堂练习】1．设x 1，x 2是方程2x 2－6x ＋3＝0的两根，则x 12＋x 22的值为_________ 2．已知x 1，x 2是方程2x 2－7x ＋4＝0的两根，则x 1＋x 2＝ ，x 1·x 2＝ ， （x 1－x 2）2＝3．已知方程2x 2－3x+k=0的两根之差为212，则k= ;4．若方程x 2+(a 2－2)x －3=0的两根是1和－3，则a= ;5．若关于x 的方程x 2+2(m －1)x+4m 2=0有两个实数根，且这两个根互为倒数，那么m 的值为 ;6．设x 1,x 2是方程2x 2－6x+3=0的两个根，求下列各式的值： (1)x 12x 2+x 1x 22 (2) 1x 1 －1x 27．已知x 1和x 2是方程2x 2－3x －1=0的两个根，利用根与系数的关系，求下列各式的值：2221x 1x 1+（2）构造新方程理论：以两个数为根的一元二次方程是。

一元二次方程判别式和韦达定理一、知识内容提要1、一元二次方程ax2＋bx＋c＝0(a≠0)，其根的判别式为：△＝b2－4ac（1）△= b2－4ac＞0 一元二次方程ax2＋bx＋c＝0(a≠0)有两个不相等的实数根21242b b acxa-±-=，。

（2）△= b2－4ac＝0 一元二次方程ax2＋bx＋c＝0(a≠0)有两个相等的实数根122bx xa==-。

（3）△= b2－4ac＜0一元二次方程ax2＋bx＋c＝0(a≠0)没有实数根。

2、一元二次方程根的判别式的主要应用方面：（1）判定方程根情况：根据方程或给定的条件，判定方程根的情况（不解方程）；（2）确定字母取值范围：利用判别式建立等式、不等式,确定含字母的一元二次方程中参数值或取值范围；（3）证明、探求参数条件：证明某种条件下方程根情况，或求参数满足条件等；（4）讨论根的性质：构造一元二次方程，把原问题转化为讨论根的性质。

3、韦达定理：一元二次方程)0(02≠=++acbxax的根与系数的关系设方程的两根为1x、2x，则acxxabxx=-=+2121,。

注：现在应用韦达定理的前提条件是042≥-=∆acb，即方程必须有实数解。

4．韦达定理的逆定理: 以两个实数21xx，为根的一元二次方程（二次项系数为1）是：()021212=++-xxxxxx注意：（1）根与系数的关系是以一元二次方程有两个实数根（Δ≥0）为前提的，因此，运用韦达定理判定根具体条件必须考虑Δ≥0这一条件。

（2）运用韦达定理可以不解方程，求含有1x、2x的代数式值，常见变形如下：2122122212)(xxxxxx-+=+，21221221214)()(||xxxxxxxx-+=-=-，)(3)(21213213231xxxxxxxx+-+=+，21212111xxxxxx+=+二、考点分析（一）判别式的运用问题一、利用判别式,判定方程根的个数和情况.例1、不解方程，直接判断下列方程的解的情况：⑴2710x x --=⑵294(31)x x =-（3）22320x x --+= （4）2(1)02m x m x -++=(m 为常数)例2.关于x 的一元二次方程01)12(2=-+++k x k x 的根的情况是（ ）.A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.根的情况无法判断练习：⑴若关于x 的方程x 2－2x －m ＝0有两个相等的实数根，则m ＝__________；⑵若关于x 的方程(x ＋1)2＝1－k 无实根，则k 的取值为__________；⑶若关于x 的一元二次方程21(1)04k x x -+-=有实根，则k 的取值范围为__________；例3.已知关于x 的方程02)22=++-k x k x （. (1)求证：无论k 取任何实数值，方程总有实数根；(2)若等腰三角形ABC 的一边长为a=1,另两边长b 、c 恰好是这个方程的两个根，求△ABC 的周长；练习：已知关于x 的方程 x 2－(k ＋1)x ＋2k －2＝0⑴求证：无论k 为何值，方程总有实根；⑵若等腰△ABC ，底边a ＝3，另两边b 、c 恰好是此方程的两根，求△ABC 的周长。

一个伟大的发现—韦达定理【知识要点】1．若一元二次方程ax 2+bx+c=0(a ≠0)的两根分别为1x , 2x ，则：1x +2x =-b/a ；1x .2x =c/a2．若1x , 2x 是某一元二次方程的两根，则该方程可以写成：x 2-(1x +2x )x+1x 2x =0.【经典例题】【例1】已知1x ,x2为方程x 2+px+q=0的两根，且1x +x 2=6, 1x 2+2x 2=20，求p 和q 的值.【例2】 已知：方程12212+=x x 的两根为1x ，2x ，不解方程求下列各式的值：(1)(x1-x2)2；(2) 321231x x x x +【例3】 已知：关于x 的方程x 2-3x+2k-1=0的两个实数根的平方和不小于这两个根的积，且1+2k>0,求满足上述条件的k 的整数值.【例4】 已知方程组⎪⎩⎪⎨⎧-==+--)12(0212x k y y x kx (x,y 为未知数)，有两个不同的实数解 ⎩⎨⎧==⎩⎨⎧==2211,y y x x y y x x (1)求实数k 的取值范围； (2)若,3112121=++x x y y 求实数k 的值.【例5】 已知，关于x 的方程(n-1)x 2+mx+1=0①有两个相等的实数根.(1)求证：关于y 的方程m 2y 2-2my-m 2-2n 2+3=0②必有两个不相等的实数根；(2)若方程①的一根的相反数恰好是方程②的一个根，求代数式m 2n+12n 的值.【方法总结】1.利用韦达定理求一元二次方程的两根之和与两根之积.(1)容易忘记除以二次项系数；(2)求两根之和时易弄错符号.2.已知两根，求作一元二次方程时，也容易弄错一次项系数的符号.3.应用韦达定理时，注意不要忽略题中的隐含条件，比如隐含的二次方程必有实数根的条件.【经典练习】一、选择题1.下列说法中不正确的是 ( )A.方程x 2+2x-7=0的两实数根之和为2B.方程x 2-3x-5=0的两实数根之积为-5C.方程x 2-2x-7=0的两实数根的平方和为18D.方程x 2-3x-5=0的两实数根的倒数和为3/52.若x1,x2是一元二次方程2x 2-3x+1=0的两个根，则x12+x22 的值是( )A.5/4B.9/4C.11/4D.73.已知关于x 的一元二次方程X 2-mx+2m-1=0的两个实数根的平方和为7，那么m 的值是( )A.5B.-1C.5或-1D.-5或14.方程x 2-3x-6=0与方程x 2-6x+3=0的所有根的乘积为 ( )A.-18B.18C.-3D.35.若一元二次方程ax 2+bx+c=0的两根为-3和-1，则抛物线y=ax 2+bx+c 的顶点横坐标为( )A.-2B.2C.3D.-16.已知：a 、b 、c 是△ABC 的三条边长，那么方程cx 2+(a+b)x+c/4=0的根的情况是 ( )A.无实数根B.有两个不相等的正实根C.有两个不等的负实根D.有两个异号的实根二、填空题1.请写出一个二次项系数为1，两实根之和为3的一元二次方程： 。

北师大版九年级数学上册第二章，第三节一元二次方程根与系数的关系教材分析1.一元二次方程根与系数的关系（也称韦达定理）是在学习了一元二次方程的解法和根的判别式之后引入的，课标要求通过本节内容的学习能运用韦达定理由已知一元二次方程的一个根求出另一个根与未知数，会求一元二次方程两个根的倒数和、两根的平方和及两根之差；教材通过一元二次方程ax2+bx+c=0(a≠0)的根x1、x2推导出韦达定理，以及能够建立以数x1、x2为根的一元二次方程的方程模型；是对前面知识的巩固与深化，又为以后的知识打下基础，它深化了两根与系数之间的关系，是我们今后继续研究一元二次方程根的情况的主要工具，是方程理论的重要组成部分。

2.韦达定理是初中代数中的一个重要定理，这是因为通过韦达定理的学习，把一元二次方程的研究推向了高级阶段，运用韦达定理可以进一步研究数学中的许多问题，通过近些年的中考数学试卷的分析可以得出：韦达定理及其应用是各地市中考数学命题的热点之一。

出现的题型有选择题、填空题和解答题，有的将其与三角函数、几何、二次函数等内容综合起来，形成难度系数较大的压轴题。

通过韦达定理的教学，可以培养学生的创新意识、创新精神和综合分析数学问题的能力，也为学生今后学习方程理论打下基础。

学情分析1．学生已学习用求根公式法解一元二次方程，但是有一部分在把一些较复杂一点的一元二次方程化为一元二次方程的一般形式的时候，要么常在去括号、移项或者合并同类项的时候出问题，要么就在解方程过程中不能正确代入各项系数；或者就在最后不会把计算结果化成最简单的形式；2．本课的教学对象是初中三年级学生，学生对事物的认识多是直观、形象的，他们所注意的多是事物外部的、直接的、具体形象的特征；3．在教学初始，出示一些学生所熟悉和感兴趣的东西，结合一元二次方程求根公式使他们在现代化的教学模式和传统的教学模式相结合的基础上掌握一元二次方程根与系数的关系。

教学目标1、知识目标：要求学生在理解的基础上掌握一元二次方程根与系数的关系式，能运用根与系数的关系由已知一元二次方程的一个根求出另一个根与未知数，会求一元二次方程两个根的倒数和与平方数，两根之差。