确定管道内的气体流速

气力输送最重要的参数：气流速度和输送浓度（气固比）设计一套气力输送系统时气流速度和输送浓度这两个参数并非是能够计算出来的而是依靠经验设定的，最优先的条件就是确定气流速度和输送浓度，这两个参数至关重要，从设计的最初阶段就必须确定这两个参数，他们设定正确的话则气力输送系统已经成功一半了，反之这两个参数不正确的话则气力输送系统完全不可行。

确定气流速度和输送浓度之后即可计算出其他全部的数据。

1，气流速度和输送浓度（物料量）同时变化的情况下水平管道输送状态试验：⑴当管道内气流速度很快远大于悬浮速度，而物料量则相对较少（输送浓度低）时，水平管道内的物料颗粒基本上接近均匀分布，并在气流中呈完全悬浮状态随气流前进。

这就是稀相输送。

⑵气流速度降低同时增加物料量（输送浓度增加）时，气流作用于颗粒上的推力随之减小，颗粒的运行速度相应地减慢，并伴有颗粒之间的相互碰撞。

致使部分较大颗粒趋向于下沉接近管底，水平管道内的物料颗粒分布变得上稀下密，但所有物料仍处于连续前进状态。

这就是密相输送。

2，下面分别对输送浓度和气流速度进行试验：①输送浓度试验：一个动床试验设备，见下图：输送管道的阻力降正比于输送距离而反比于输送物料的浓度，在其他参数相同且气源的输出压力恒定的情况下如果增加输送距离，其阻力也必然相应地增加，使其超出气源的输出额定压力，为了不增加输送管道的阻力就只能降低输送浓度。

换句话说增加输送距离的话就必须降低输送浓度，也就是输送浓度取决于输送距离。

也可以这样理解，针对采用同样输出压力的气源，如果一定浓度的物料能够被输送100米的话，再让其以同等浓度的物料输送200米的话则肯定送不动了，只能降低输送浓度1倍才能送走，因此输送浓度与输送距离有很大关联。

用一个动床试验设备，加入1公斤物料进行吹送30米，大约用30秒将这些物料吹送完毕。

、将管道长度加长一倍则用70秒才能将相同的1公斤物料吹送完毕。

这说明管道长度增加后其输送时间延长了一倍多，这就意味着输送浓度降低了，即输送浓度反比于输送距离。

管道内气体流速计算公式在我们日常生活和各种工程应用中，管道内气体流速的计算可是个相当重要的事儿。

你可能会想，这东西跟我有啥关系？别急，听我慢慢给您唠唠。

就说前阵子，我去一个工厂参观，看到工人们正在调试一个大型的通风系统。

那管道错综复杂，呼呼地往外吹着风。

我就好奇啊，这风在管道里跑得有多快呢？这就涉及到咱们今天要说的管道内气体流速的计算公式啦。

要计算管道内气体的流速，咱们得先搞清楚几个关键的因素。

首先就是管道的横截面积，这就好比是气体流动的通道宽窄。

面积越大，相同流量下流速可能就相对较慢；面积越小，流速就会快一些。

然后呢，还有气体的流量。

想象一下，单位时间内通过管道的气体量越多，流速自然也就越大。

那计算公式到底是啥呢？一般来说，管道内气体流速可以用公式：流速 = 流量 ÷横截面积来计算。

这里面的流量，通常用体积流量来表示，单位可以是立方米每秒（m³/s）。

而横截面积呢，得根据管道的形状来算。

如果是圆形管道，那横截面积就是π乘以半径的平方；要是方形管道，那就是边长乘以边长。

咱们来举个例子瞅瞅。

比如说有一个圆形管道，半径是 0.5 米，气体的流量是 10 立方米每秒。

那先算横截面积，就是 3.14×0.5×0.5 = 0.785 平方米。

然后再用流速 = 流量 ÷横截面积，也就是10÷0.785 ≈ 12.75 米每秒。

这就算出气体在这个管道里的流速啦。

在实际应用中，这个计算公式可太有用了。

比如在空调系统里，要保证室内有合适的风量和风速，就得根据房间大小和需求，通过计算来选择合适的管道和风机。

再比如在化工生产中，控制气体在管道中的流速对于反应的进行、物料的输送都有着至关重要的影响。

回到开头我参观的那个工厂，后来我跟工程师交流，他们就是根据这些计算来优化通风系统，确保工厂里的空气质量和温度都能达到理想的状态。

总之，管道内气体流速的计算公式虽然看起来简单，但其背后的应用却十分广泛。

管内气体流速计算公式好的，以下是为您生成的文章：在咱们的日常生活和科学研究中，管内气体流速的计算可是个相当重要的事儿。

这就好比你在吹气球的时候，想知道气到底跑得多快才能把气球吹大；又或者是在工厂的管道里，工程师得搞清楚气体流速，才能保证生产的顺利进行。

那管内气体流速的计算公式到底是啥呢？其实啊，它和不少因素都有关系。

一般来说，常见的计算公式是：流速 = 流量÷管道截面积。

先来说说流量。

流量就是在单位时间内通过管道某一横截面的气体体积。

比如说，在一分钟内通过管道横截面的气体体积是 10 立方米，那流量就是 10 立方米每分钟。

再讲讲管道截面积。

这就好比是管道的“肚子”大小。

比如说管道的半径是 1 米，那截面积就是π×半径的平方，也就是 3.14 平方米。

我记得有一次，我去参观一个工厂。

那个工厂生产各种塑料制品，其中有一个环节就是通过管道输送压缩气体来推动生产线上的零件。

当时，工程师们就在讨论管道里气体流速的问题。

他们拿着各种测量工具，在本子上写写算算，神情特别专注。

我凑过去看了看，发现他们就是在运用管内气体流速的计算公式来优化生产流程呢。

这计算公式看似简单，但是在实际运用中可得小心谨慎。

比如说，测量流量和管道截面积的时候，数据一定要准确，哪怕是一点点的误差，都可能导致计算结果的大偏差。

还有啊，不同的气体性质也会对流速产生影响。

比如说，密度大的气体和密度小的气体，在相同的条件下，流速可能就不一样。

而且，管道的材质和内壁的光滑程度也会有关系。

内壁粗糙的管道，气体流动的时候会受到更大的阻力，流速可能就会变慢。

总之，管内气体流速的计算可不是个简单的事儿，需要我们综合考虑各种因素，认真测量数据，才能得出准确的结果。

这样，无论是在日常生活中的小发明，还是在大型的工业生产中，我们都能更好地掌控气体的流动，让它们为我们服务，而不是给我们添麻烦。

所以啊，大家可别小看这个管内气体流速的计算公式，它在很多地方都能派上大用场呢！。

空气流速计算公式空气流速计算是气流力学中的一个重要参数，可以用于工程设计、空气流动分析等领域。

空气流速的计算公式主要根据流体力学的基本理论和实验数据得出，并考虑了空气的密度、速度、压力等因素。

下面将介绍几种常见的空气流速计算公式。

1.空气流速计算公式：测压孔法在测流量系统中，常用的一种方法是通过在管道上设有孔或测压孔来测量孔内的静压差，并根据该差值计算空气流速。

具体的计算公式如下：Q=A×C×√(2ΔP/ρ)其中，Q表示空气流量，A表示测压孔面积，C表示流速系数，ΔP表示测压孔内的静压差，ρ表示空气密度。

2.空气流速计算公式：皮托管法皮托管是一种测量气体流速的装置，它通过测量气体通过装置流过的动静压差来估计气体流速。

根据连续方程和动量方程，可以计算空气流速的公式如下：v=√(2ΔP/ρ(1-(A2/A1)^2))其中，v表示空气流速，ΔP表示皮托管内的动静压差，ρ表示空气密度，A2和A1分别表示皮托管截断口的面积和进口截面的面积。

3.空气流速计算公式：直线差压法直线差压法是通过在两个管道之间设置差压孔，将携带流体动能的压力转化为动能差压来测量气体流速。

计算空气流速的公式如下：v=√((2ΔP)/ρ(1+(A2/A1)^2))其中，v表示空气流速，ΔP表示差压孔内的静压差，ρ表示空气密度，A1和A2分别表示差压孔口和管道的截面积。

4.空气流速计算公式：热线法热线法利用传感器中的细热线的电阻值随流体流速的变化而变化的特性，测量空气流速。

在计算公式中，需要考虑风速与细热线电阻值的关系，并进行相应的转换计算。

这些是常见的空气流速计算公式，根据不同的实际应用场景和测量方法，选择合适的计算公式可以准确地计算出空气流速。

实际测量中，还需根据具体设备和条件进行相应的修正和校准，以提高测量的准确性和可靠性。

管道流速V、压力P、流量Q1、在实际工业管道工程设计中，我们经常会根据客户所给的相关技术参数（如： 工作压力、用气量、用气设备参数等等）来设计符合实际生产要求的合理的工 程方案，从而在满足工程合理、安全的前提下最大限度的降低工程成本。

所以 在工程设计时如何确定管道内流速V、压力P、流量Q三者之间的关系变得尤为 重要，现简单从理论上介绍一下三者之间的关系： 例：不锈钢无缝管φ25.4x1.65 、工作介质N2、工作压力P=0.8MPa，工作温度 t=20℃ 求工况流量Q？ 解：取不锈钢管内某一截面为参考面，在1h内有： Q=VπR2 x 3600 式中， Q: 工况流量— m³ V： 介质流速— m/s R: 管道半径 — m所以 ,R = Q /(3600Vπ ) = 9.4 Q / V (mm) D = 18.8 Q / V (mm) ⎛ D ⎞ Q =V⎜ ⎟2(m3) 18.8 ⎠ ⎝管道流速V、压力P、流量Q在实际工程中管道内流速V受很多因素影响（使用压力、管道通径、 使用流量等等），所以合理的流速应根据经济权衡决定，一般液体 流速为0.5~3m/s，气体流速为10~30m/s，需根据具体情况并通过经 济核算来确定适宜流速，使操作费用与设备费用之和为最低! 现在0.8Mpa情况下取流速V=10m/s , 则 Q=10x(22.1/18.8)2=13.8m3 (在工况下每小时流量) 工况流量与标况流量的换算： 在实际生产中气体的使用压力往往不尽相同，所以一般把工况 流量换算成标准状况下的流量，以方便计量使用。

气体在实际使用 过程中受各种因素影响，其相关参数往往在不断变化，所以在工程 实际计算中往往把气体认为理想气体，从而大概计算出其实际流量。

理想气体状态方程： PV=nRT管道流速V、压力P、流量Q式中， P—气体绝对压力 KPa V—气体体积 m3 n—气体的物质的量 kmol R—气体摩尔常数 8.314kj/(kmol .K) T—气体的热力学温度 K t —工作温度 ℃ 所以在工况和标况下有： P0V0=nRT 0（标况） P1V1=nRT 1（工况） 联合两式得：V0=(P1/P0)x(T 0/T 1) = V1(P1/P0)x【273/（273+t)】 注：式中P1绝对压力，P0为标准大气压力 所以例题中换算成标况流量为Q0=（0.9/0.1)x(273/293)Q1 =115.7Nm3管道压力与厚度的简单计算1、例：计算不锈钢无缝管φ25.4x1.65 最高工作压力？ 解：由于介质在管道内流动，管道承受内压作用，故可以将管道 厚度、压力的计算近似认为承受内压圆筒的计算，所以由内 压圆筒计算公式 ：PcDi δ= 2σφ − Pc mm δ = 1.65mm 式中，δ — 计算厚度 Pc — 计算压力 MPa Di — 圆筒内径 mm Di = 22.1mm MPa σ — 材料许用应力 ，查资料得 = 137MPa σ φ — 焊接接头系数取0.85 ,管道压力与厚度的简单计算代入数据得 Pc=16.2MPa 注： 式中的计算压力包括设计压力和液柱静压力，当液柱静压力 少于5%设计压力时，可忽略不计； 厚度为管子实际厚度（除去钢材负偏差，有腐蚀的应考虑腐 蚀裕量）； 该公式只适用于单层薄壁圆筒（ /D≦0.1）的计算.Best wishes for you !。

《大气污染控制工程》课程设计指导书《大气污染控制工程》是环境工程专业的主干课程之一，为了使同学们全面地掌握本课程所学的基本理论知识，学会灵活运用所学知识，进行大气污染控制工程设计，完成环境工程师基本训练，以模拟课题或实际课题为题的课程设计是一个必不可少的教学环节。

为帮助同学们圆满完成这一教学环节，特编写本课程设计指导书。

一、目的与要求1、培养学生严谨的科学态度，严肃认真的学习和工作作风，树立正确的设计思想，形成科学的研究方法。

2、培养学生独立工作的能力，包括收集设计资料、综合分析问题、理论计算、数据处理、工程制图、文字表达等能力。

3、通过课程设计，使学生得到较为全面的大气污染控制工程设计的初级训练。

4、掌握大气污染控制工程设计的一般程序，大气净化系统各部分的有机组合方法，学会灵活处理复杂的实际工程问题。

5、学会编写“设计说明书”和“设计计算书”，按标准绘制有关图件。

6、本设计原则上应由学生在指导教师的指导下，独立完成。

可以讨论，但不得互相抄袭。

7、本设计应提交如下成果：（l）设计项目的设计报告书一份，（包括：设计说明书和设计计算书）（2）净化系统布置图（二视图）。

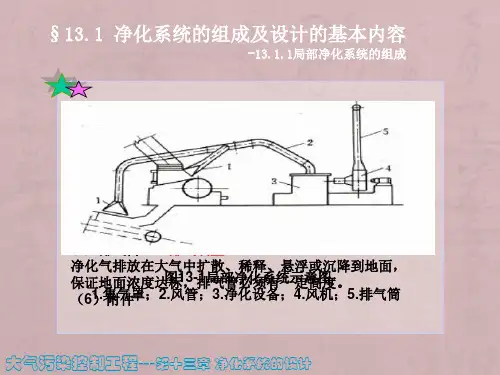
二、工业废气净化系统设计的基本内容工业废气净化系统设计的基本内容包括：根据当地（企业）的总体规划和各种自然条件，合理地确定处理设施规模和处理要求；确定处理工艺流程；进行平面布置；对污染物的捕集装置（集气罩）、输送管道系统、净化设备及排放烟囱设计四个部分进行设计计算；为满足系统正常运行的需要，还应针对所处理污染物的特性，进行上述系统必要配套设备及附件的综合布置和设计。

1、捕集装置的设计污染物的捕集装置通常称为集气罩。

设计内容主要包括集气罩结构形式、安装位置以及性能参数的确定等内容。

2、输送管道设计管道系统设计主要包括管道布置、管道内气体流速确定、管径选择、压力损失计算以及通风机选择等内容。

3、净化设备选择或设计净化设备的选择或设计一般按以下程序进行：①工程调查，认真收集有关资料，全面考虑可能影响设备性能的各种因素；②根据排放标准和生产要求，计算需要达到的净化效率；③根据污染物性质和操作条件确定净化方法（除尘或吸收、吸附等）和净化流程（几级处理，是否预冷，调湿以及吸收剂或吸附剂选择等），在此基础上决定净化设备的选择范围；④对设备的技术指标和经济指标进行全面比较，选定最适宜的净化装置；⑤确定净化设备的型号规格及运行参数。

管内流速的计算公式管内流速是指管道内流体的流动速度。

在流体力学中，计算管内流速的公式有多种，根据不同的情况和假设条件选择不同的公式。

我们来看一种简单的情况，即在水平无重力作用下的圆管内流速。

在这种情况下，流速的计算公式为：v = Q / (π * r^2)其中，v表示流速，Q表示流量，r表示管道半径。

该公式是根据质量守恒定律和圆管截面积的计算得出的。

接下来，我们来看一种更为复杂的情况，即在斜面上的管道内流速。

在这种情况下，流速的计算公式需要考虑斜面的倾角和管道的长度。

假设斜面的倾角为α，管道的长度为L，则流速的计算公式为：v = (Q * sin α) / (π * r^2 * L)其中，v表示流速，Q表示流量，r表示管道半径，α表示斜面的倾角，L表示管道的长度。

这个公式是根据质量守恒定律、斜面倾角和管道长度的计算得出的。

除了上述两种情况外，还有其他一些特殊情况需要特殊考虑。

例如，在液体通过喉管时，流速的计算公式为：v = (2 * g * h) ^ 0.5其中，v表示流速，g表示重力加速度，h表示液体从喉管底部到液面的高度差。

这个公式是根据能量守恒定律和液体静压力的计算得出的。

在气体管道内流动时，流速的计算公式也有所不同。

一般情况下，气体流速的计算公式可以根据质量守恒定律和管道截面积的计算得出。

但在高速气体流动时，需要考虑气体的压缩性，流速的计算公式会更加复杂。

管内流速的计算公式是根据流体力学的基本原理和特定情况下的假设条件得出的。

在实际应用中，我们根据具体情况选择合适的公式进行计算，以便准确地求得管内流速。

管道内气体压力与流速的计算公式在我们日常生活和工业生产中，管道内气体的流动是一个常见的现象。

比如说，家里的天然气通过管道输送到炉灶，工厂里的压缩空气用于驱动各种设备。

而要理解和控制这些气体的流动，就离不开对管道内气体压力与流速计算公式的了解。

想象一下，你正在厨房里准备做一顿美味的晚餐。

当你打开燃气炉灶的瞬间，天然气从管道中涌出，蓝色的火焰欢快地跳跃着。

你有没有想过，这背后其实隐藏着气体压力和流速的秘密？咱们先来说说气体压力。

压力就像是气体的“力量”，它推动着气体在管道中流动。

压力越大，气体流动的动力就越强。

而流速呢，则是气体在单位时间内通过管道某一截面的体积。

那管道内气体压力与流速的计算公式到底是啥呢？一般来说，常用的公式是伯努利方程。

不过，先别被这个高大上的名字吓到，咱们来把它简单化理解。

这个公式可以表示为：$P + \frac{1}{2}\rho v^2 + \rho gh = C$ （其中$P$是压力，$\rho$是气体密度，$v$是流速，$h$是高度，$C$是常数）在实际应用中，我们常常会做一些简化和假设。

比如说，如果管道是水平的，那么高度$h$这一项就可以忽略不计。

这样公式就变成了：$P + \frac{1}{2}\rho v^2 = C$ 。

咱们来举个例子哈。

假设在一个水平的管道中，气体的压力是 10帕斯卡，气体的密度是 1.2 千克/立方米，通过测量和计算，我们知道常数$C$是 20 。

那么，我们就可以通过这个公式来算出流速$v$ 。

先把已知的数值代入公式：$10 + \frac{1}{2}×1.2×v^2 = 20$ 。

接下来就是解方程啦，经过一番计算，我们就能得出流速$v$的值。

再比如说，在汽车的发动机中，燃料和空气混合后进入气缸燃烧，产生的气体要通过排气管排出。

这时候，工程师们就需要精确计算管道内气体的压力和流速，以确保发动机能够高效地工作，同时还能满足环保要求。