八年级数学上册第7讲全等三角形的判定之HL课后练习新版苏科版

苏科版数学八年级上册《全等三角形》课后练习一重难点易错点解析题一：题面：下列说法：①能够完全重合的图形叫做全等形；②全等三角形的对应边相等、对应角相等；③全等三角形的周长相等、面积相等；④所有的等边三角形都全等；⑤面积相等的三角形全等．其中正确的说法有 .题二：题面：如图所示，已知△ABC≌△DCB，是其中AB=DC，试证明∠ABD=∠ACD．金题精讲题一：题面：如图，已知△ABC≌△DCB，∠BDC=35°，∠DBC=50°，则∠ABD= .题二：题面：已知△ABC的三边长分别为3，5，7，△DEF的三边长分别为3，3x2，2x1，若这两个三角形全等，则x为 .题三：题面：在直角坐标系中，有点A（3，0），B（1，0），C（1，3），若有一个直角三角形与Rt△ABC全等，且它们只有一条公共直角边．（1）建立平面直角坐标系并画出这些三角形；（2）写出这些三角形第三个顶点的坐标．题四：题面：如图，Rt△ADE是由Rt△ABC绕点A顺时针旋转得到的，且Rt△ADE≌Rt△ABC，连接CE交斜边AB于点F，CE的延长线交BD于点G．试证明∠ACE=∠ABD思维拓展题面：如图，已知△ABC中，AB=AC=10厘米，BC=8cm，点D为AB的中点，点P在线段BC 上以3厘米/秒的速度由B点向C点运动，同时，点Q在线段CA上由点C向点A点以a厘米/秒运动，设运动的时间为t秒，（1）求CP的长；（2）若以C、P、Q为顶点的三角形和以B、D、P为顶点的三角形全等，且∠B和∠C是对应角，求a的值．课后练习详解重难点易错点解析题一：答案：①②③.详解：①中能够完全重合的图形叫做全等形，正确；②中全等三角形的对应边相等、对应角相等，正确；③全等三角形的周长相等、面积相等，也正确；④中所有的等边三角形角都是60°，但由于边不相等，所以不能说其全等，④错误；⑤中面积相等的三角形并不一定是全等三角形，⑤中说法错误；故题中①②③说法正确，④⑤说法错误题二：答案：∠ABD=∠ACD．详解：∵△ABC≌△DCB，∴∠ABC=∠DCB，∠ACB=∠DBC，∴∠ABC∠DBC=∠DCB∠ACB，即∠ABD=∠ACD．金题精讲题一：答案：45°．详解：∵∠BDC=35°，∠DBC=50°，∴∠BCD=180°∠BDC∠DBC=180°35°50°=95°，∵△ABC≌△DCB，∴∠ABC=∠BCD=95°，∴∠ABD=∠ABC∠DBC=95°50°=45°．故答案为：45°．题二：x2=5x1=7，7代入x1中，3x1≠7，∴3x2与不是对应边，当3x2=7时，x =3，把x =3代入2x 1中，2x 1=5题三：答案：（1）三角形有：△ABD 、△ABE 、△BCF 、△BCE ．（2）点D 的坐标（1，3） 点E 的坐标（3，3）点F 的坐标（1，0）．详解：（1）如图：与Rt△ABC 全等，且它们只有一条公共直角边的三角形有： △ABD 、△ABE 、△BCF 、△BCE ．（2）点D 的坐标（1，3）点E 的坐标（3，3）点F 的坐标（1，0）．题四：答案：∠ACE=∠ABD.详解：∵Rt △ADE ≌Rt △ABC ，∴AC=AE ，AB=AD ，在△ACE 中，∠ACE=12（180°∠CAE ），在△ABD 中，∠ABD=12（180°∠BAD ），∴∠ACE=∠ABD思维拓展答案：83t ；3或154．详解：（1）∵BP =3t ，BC =8，∴CP t ；（2）①BD =CP 时，∵AB =10，D 为AB 的中点，∴t ，解得t =1，∵△BDP ≌△CPQ ，∴BP=CQ，即3×1=a，解得a=3；②BP=CP时，3t t，解得t=4 3，∵△BDP≌△CQP，∴BD=CQ，即5=a×4 3，解得a=15 4，综上所述，a的值为3或15 4．。

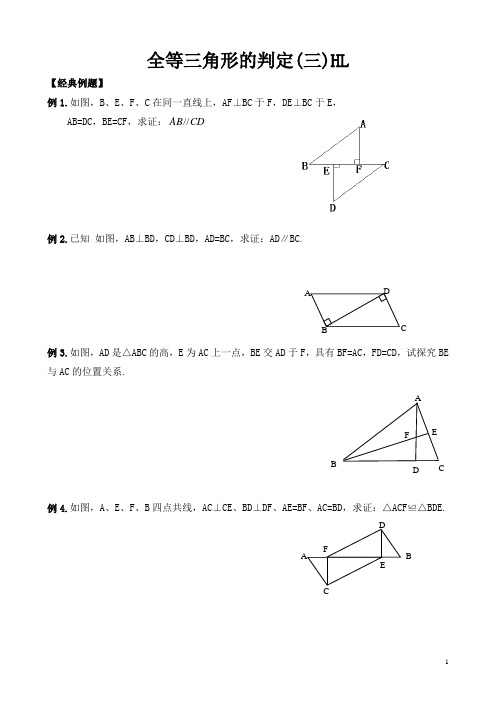
全等三角形的判定(三)HL【经典例题】例1.如图，B 、E 、F 、C 在同一直线上，AF ⊥BC 于F ，DE ⊥BC 于E ，AB=DC ，BE=CF ，求证：CD AB //例2.已知 如图，AB ⊥BD ，CD ⊥BD ，AD=BC ，求证：AD ∥BC.例3.如图，AD 是△ABC 的高，E 为AC 上一点，BE 交AD 于F ，具有BF=AC ，FD=CD ，试探究BE 与AC 的位置关系.例4.如图，A 、E 、F 、B 四点共线，AC ⊥CE 、BD ⊥DF 、AE=BF 、AC=BD ，求证：△ACF ≌△BDE.ADBABEDFABDCEFA【经典练习】1.如图，在△ABC 和△ABD 中，∠C=∠D=90°，若利用“AAS ”证明△ABC ≌△ABD ，则需要加条件或 ； 若利用“HL ”证明△ABC ≌△ABD ，则需要加条件 或 ．2.如图，在△ABC 中，已知D 是BC 中点，DE ⊥AB ，DF ⊥AC ，垂足分别是E 、F ，DE ＝DF . 求证：AB=AC3．如图，CE ⊥AB ，DF ⊥AB ，垂足分别为E 、F ，AC ∥DB ，且AC=BD ，那么Rt △AEC ≌Rt △BFD 的理由是（ ）.A ．SSS B. AAS C. SAS D. HL4.已知：如图，AC 平分∠BAD ，CE ⊥AB 于E ，CF ⊥AD 于F ，且BC ＝DC .你能说明BE 与DF 相等吗？ABCDE F 125.如图，在△ABC 中，AB =AC ，DE 是过点A 的直线，BD ⊥DE 于D ，CE ⊥DE 于E ． （1）若BC 在DE 的同侧（如图①）且AD =CE ，说明：BA ⊥A C ．（2）若BC 在DE 的两侧（如图②）其他条件不变，问AB 与AC 仍垂直吗？若是请予证明，若不是请说明理由．【巩固练习】 基础训练题1．在Rt △ABC 和Rt △DEF 中，∠ACB=∠DFE=︒90，AB=DE ，AC=DF ，那么Rt △ABC 与Rt △DEF（填全等或不全等）2．如图，点C 在∠DAB 的内部，CD ⊥AD 于D ，CB ⊥AB 于B ，CD=CB 那么Rt △ADC ≌Rt △ABC 的理由是（ ）A ．SSS B. ASAC. SASD. HL3．下列说法正确的个数有（ ）.①有一角和一边对应相等的的两个三角形全等； ②有两边对应相等的两个直角三角形全等； ③有两边和一角对应相等的两个直角三角形全等； ④有两角和一边对应相等的两个直角三角形全等. A ．1个B. 2个C. 3个D. 4个4．过等腰△ABC 的顶点A 作底边的垂线，就得到两个全等三角形，其理由是 . 5．如图，△ABC 中，∠C=︒90，AM 平分∠CAB ，CM=20cm ，那么M 到AB 的距离是（ ）cm.6．在△ABC 和△C B A '''中，如果AB=B A ''，∠B=∠B '，AC=C A ''，那么这两个三角形（ ）. A ．全等B. 不一定全等C. 不全等D. 面积相等，但不全等ACDB ┐ ABM C☆7.如果两个三角形中两条边和其中一边上的高对应相等，那么这两个三角形的第三条边所对的角的关系是 （ ）A. 相等B. 不相等C. 互余或相等D. 互补或相等8．如图，∠B=∠D=︒90，要证明△ABC 与△ADC 全等， 还需要补充的条件是 .9．如图，在△ABC 中，∠ACB=︒90，AC=BC ，直线MN 经过点C ，且AD ⊥MN 于D ，BE ⊥MN 于E ，求证：DE=AD+BE.10．如图，已知AC ⊥BC ，AD ⊥BD ，AD=BC ，CE ⊥AB ，DF ⊥AB ，垂足分别为E 、F ，那么，CE=DF 吗？谈谈你的理由DBF11．如图，已知AB=AC，AB⊥BD，AC⊥CD，AD，BC相交于点E，求证：（1）CE=BE；（2）CB⊥AD.能力提高题1.如图①，E、F分别为线段AC上的两个动点，且DE⊥AC于E，BF⊥AC于F，若AB=CD，AF=CE，BD交AC于点M．（1）求证：MB=MD，ME=MF（2）当E、F两点移动到如图②的位置时，其余条件不变，上述结论能否成立？若成立请给予证明；若不成立请说明理由．2.如图，在ABC中，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E、F，且DE=DF，试说明AB=AC.A E DC3.如图：BE ⊥AC ，CF ⊥AB ，BM=AC ，CN=AB 。

苏教科版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！苏科版初中数学和你一起共同进步学业有成！全等三角形的判定重难点易错点解析题一：题面：如图是一个风筝设计图，其主体部分（四边形ABCD）关于BD所在的直线对称，AC与BD相交于点O，且AB≠AD，则下列判断不正确的是（）A.△ABD≌△CBDB.△ABC≌△ADCC.△AOB≌△COBD.△AOD≌△COD金题精讲题一：题面：如图，已知点A、D、C、F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（）A．∠B CA=∠F B．∠B=∠E C．BC∥EF D．∠A=∠EDF题二：题面：如图，小强利用全等三角形的知识测量池塘两端M、N的距离，如果△PQO≌△NMO，则只需测出其长度的线段是（）A．PO B．PQ C．MO D．MQ题三：题面：如图．点D、E在△ABC的边BC上，AB=AC，AD=AE．请写出图中的全等三角形(写出一对即可)．题四：题面：如图，己知AC=BD，要使△ABC≌△DCB，则只需添加一个适当的条件是(填一个即可)思维拓展题面：如图，点A、B、D、E在同一直线上，AD=EB，BC∥DF，∠C=∠F．求证：AC=EF．课后练习详解重难点易错点解析题一：答案：B．详解：根据轴对称的性质，知△ABD≌△CBD，△AOB≌△COB，△AOD≌△COD．由于AB≠AD，从而△ABC和△ADC不全等．故选B．金题精讲题一：答案：B．详解：A．由AB=DE，BC=EF和∠BCA=∠F构成SSA，不符合全等的条件，不能推出△ABC≌△DEF，故本选项错误；B．由AB=DE，BC=EF和∠B=∠E构成SAS，符合全等的条件，能推出△ABC≌△DEF，故本选项正确；C．∵BC∥EF，∴∠F=∠BCA。

由AB=DE，BC=EF和∠F=∠BCA构成SSA，不符合全等的条件，不能推出△ABC≌△DEF，故本选项错误；D．由AB=DE，BC=EF和∠A=∠EDF构成SSA，不符合全等的条件，不能推出△ABC≌△DEF，故本选项错误。

重难点易错点解析题一：题面：有下列说法：①全等三角形的形状相同；②全等三角形的周长和面积相等；③若两个钝角三角形全等，则两个钝角所对应的边是对应边；④两个全等形不论怎样改变位置，都能够完全重合．其中正确的个数是.题二：题面：如图，△ABE≌△ADC≌△ABC，若：∠1=150°，则∠α的度数为.金题精讲题一：题面：如图，△ACE≌△DBF，若∠E=∠F，AD=8，BC=2，则AB等于.题二：题面：已知一个三角形的三边长是10，8，6，另一个三角形的三边长分别为n1．n+1，n+3，如果这两个三角形全等，那么n等于.题三：题面：如图，在平面直角坐标系中，已知点A（1，2），B（3，2），C（4，3），D（2，6），E（3，5）且以点D、E、F为顶点的三角形与△ABC全等，那么点F的坐标为.题四：题面：已知Rt△ABC与Rt△ADE中，△ACE≌△ABD且AB=AC，AD=AE．求证：BD⊥CE．思维拓展题面：如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点．如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C 向点A运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD 与△CQP全等？课后练习详解重难点易错点解析题一：答案：4个.详解：根据全等三角形的性质可知：全等三角形的形状相同，①正确；全等三角形的周长和面积相等，②正确；若两个钝角三角形全等，则两个钝角所对应的边是对应边，③正确；两个全等形不论怎样改变位置，都能够完全重合，④正确．所以说法正确的个数有4个．题二：答案：60°．详解：如图，∵△ABE≌△ADC≌△ABC，∴∠BAE=∠1=150°，∠DCA=∠E，∴∠2=360°∠1∠BAE=360°150°150°=60°，∴∠DFE=180°∠α∠E，∠AFC=180°∠2∠DCA，∵∠DFE=∠AFC（对顶角相等），∴180°∠α∠E=180°∠2∠DCA，∴∠α=∠2=60°．金题精讲题一：答案：3.详解：∵△ACE≌△DBF，∠E=∠F，AD=8，BC=2∴AC=BD，即AB+BC=CD+BC∴AB=CD∴AB=(AD BC)÷2=(82)÷2=3.题二：答案：n=7．详解：n1，n+1，n+3中n+3是最长边，∵这两个三角形全等，∴10=n+3，解得n=7．题三：答案：F1（2，8），F2（0，6），F3（5，5），F4（3，3）．详解：设点F的坐标是（x，y）．∵A（1，2），B（3，2），C（4，3），D（2，6），E（3，5），∴AB=2，BC=2，AC=10，DE=2；①当△FDE≌△ABC时，FE=AC=10，DF=BA=2，则(x2)2+(y6)2＝4，(x3)2+(y5)2＝1，解得：x＝2，y＝8或x＝0，y＝6；∴F1（2，8），F2（0，6）；②当△FED≌△ABC时，FE=AB=2，FD=AC=10，则(x3)2+(y5)2＝4，(x2)2+(y6)2＝1，解得：x＝5，y＝5或x＝3，y＝3，∴F3（5，5），F4（3，3）；综上所述，点F的坐标是：F1（2，8），F2（0，6），F3（5，5），F4（3，3）．故答案是：F1（2，8），F2（0，6），F3（5，5），F4（3，3）．题四：答案：BD⊥CE．详解：如图，BD与CE交于点P，BD交AE于点O，∵△ACE≌△ABD，∴∠CEA=∠BDA，∵∠AOD=∠POE，∴∠OPE=∠OAD=90°，∴BD⊥CE．思维拓展答案：△BPD≌△CPQ；1.5cm/s.详解：①全等，理由如下：∵t=1秒，∴BP=CQ=1×1=1厘米，∵AB=6cm，点D为AB的中点，∴BD=3cm．又∵PC=BC BP，BC=4cm，∴PC=41=3cm，∴PC=BD．又∵AB=AC，∴∠B=∠C，∴△BPD≌△CPQ；②假设△BPD≌△CPQ，∵v P≠v Q，∴BP≠CQ，又∵△BPD≌△CPQ，∠B=∠C，则BP=CP=2，BD=CQ=3，BF=2秒，∴点P，点Q运动的时间t=1=1.5cm/s；∴v Q=CQt。

2022-2023学年八年级数学上册章节同步实验班培优题型变式训练（人教版）12.2 三角形全等的判定【题型1】SSS 证明三角形全等1．（2022·山西·运城市盐湖区教育科技局教学研究室七年级期末）小华在复习用尺规作一个角等于已知角的过程中，回顾了作图的过程，他发现OCD V 与'''O C D V 全等，请你说明小华得到全等的依据是（ ）A ．SSSB ．SASC ．ASAD ．AAS【答案】A 【分析】利用全等三角形的判定定理即可求解．【详解】解：在OCD D 和O C D ¢¢¢D 中，OD O D OC O C DC D C ¢¢¢¢¢=ì¢ï=íï=î，()OCD O C D SSS ¢¢¢\D @D ．故选：A ．【点睛】本题主要考查全等三角形的判定，掌握全等三角形的判定定理是解题的关键．【变式1-1】2．（2021·重庆·华东师范大学附属中旭科创学校八年级期中）已知，如图，AD=AC ，BD=BC ，O 为AB 上一点，那么图中共有___对全等三角形．【答案】3【分析】由已知条件，结合图形可得△ADB ≌△ACB ，△ACO ≌△ADO ，△CBO ≌△DBO 共3对．找寻时要由易到难，逐个验证．【详解】解：∵AD=AC ，BD=BC ，AB=AB，∴△ADB ≌△ACB ；∴∠CAO=∠DAO ，∠CBO=∠DBO ，∵AD=AC ，BD=BC ，OA=OA ，OB=OB∴△ACO ≌△ADO ，△CBO ≌△DBO ．∴图中共有3对全等三角形．故答案为3．【题型2】SAS 证明三角形全等1．（2022·全国·八年级专题练习）如图，已知∠1＝∠2，∠3＝∠4，要证BC ＝CD ，证明中判定两个三角形全等的依据是（ ）A ．角角角B ．角边角C ．边角边D ．角角边【答案】B 【分析】根据已知条件，直接利用ASA 进行证明即可求解．【详解】解：在△ABC 与△ADC 中，1234AC AC Ð=Ðìï=íïÐ=Ðî，则△ABC ≌△ADC （ASA ）．∴BC ＝CD ．故选：B ．【点睛】本题考查了全等三角形的判定，掌握全等三角形的判定方法是解题的关键．【变式2-1】2．（2022·全国·八年级课时练习）如图，BE BA =，//AB DE ，BC DE =，若40BAC Ð=°，25E Ð=°，则BDE Ð=___．【答案】115°【分析】根据//AB DE ，推出Ð=ÐABC BED ，联合题目的条件可证明(SAS)BED ABC ≌△△，进而可求得结论．【详解】解：∵//AB DE ，∴Ð=ÐABC BED ，在BED V 与ABC V 中BE AB BED ABC DE CB =ìïÐ=Ðíï=î，∴(SAS)BED ABC ≌△△，∴40EBD BAC Ð=Ð=°，而180BDE EBD E Ð=°-Ð-Ð，且25E Ð=°，∴1804025115BDE Ð=°-°-°=°，故答案为：115°．【点睛】本题考查利用SAS 判定三角形全等，三角形内角和定理，利用平行推出角等，进而推出三角形全等是解题关键．【题型3】ASA 或AAS 证明三角形全等1．（2022·河北·平乡县第二中学八年级阶段练习）已知如图，要测量水池的宽AB ，可过点A 作直线AC ⊥AB ，再由点C 观测，在BA 延长线上找一点B ¢，使ACB ACB ¢ÐÐ＝，这时只要出AB ¢的长，就知道AB 的长，那么判定ABC D ≌AB C D ¢的理由是（ ）A ．ASAB ．AASC ．SASD ．HL【答案】A 【分析】直接利用全等三角形的判定方法得出答案．【详解】解：∵AC ⊥AB ，∴90CAB CAB Ð=Т=°，在ABC D 和AB C D ¢中，ACB ACB AC ACCAB CAB Ð=Ðìï=íïТ=Ðî¢，∴ABC D ≌()ASA AB C D ¢，∴AB AB ¢=．故选A ．【点睛】本题考查了全等三角形的应用，解题的关键是能够利用ASA 判定两个三角形全等．【变式3-1】2．（2021·江苏南京·八年级阶段练习）如图，AB 、CD 相交于点E ，且AE ＝BE ，AC BD ∥．求证：△AEC ≌△BED ．【答案】见解析【分析】采用“ASA ”的全等三角形的判定方法即可求证．【详解】∵AC BD∥∴∠A ＝∠B ，在△AEC 和△BED 中，A B AE BEAEC BED Ð=Ðìï=íïÐ=Ðî，∴△AEC ≌△BED （ASA ），【点睛】本题考查了全等三角形的判定以及平行线的性质的知识，掌握全等三角形的判定方法是解答本题的关键．【题型4】HL 证明三角形全等1．（2022·全国·八年级专题练习）如图，已知AD BD ^，BC AC ^，AC BD =．则CAB DBA △△≌的理由是（ ）A ．HLB ．SASC ．AASD ．ASA 【答案】A 【分析】利用直角三角形全等的判定方法进行判断．【详解】证明：∵AD ⊥BD ，BC ⊥AC ，∴∠C ＝∠D ＝90°，在Rt △CAB 和Rt △DBA 中，AB BA AC BD =ìí=î，∴Rt △CAB ≌Rt △DBA （HL ）．故选：A ．【点睛】本题考查了全等三角形的判定，熟练掌握直角三角形全等的判定是解决问题的关键．【变式4-1】2．（2022·湖南·新化县东方文武学校八年级期中）如图，AB =AD ，CB ⊥AB 于点B ，CD ⊥AD 于点D ，求证△ABC ≌△ADC ．【答案】见解析【分析】求出∠B =∠D =90°，根据全等三角形的判定定理得出Rt △ABC ≌Rt △ADC ．【详解】解：∵CB ⊥AB ，CD ⊥AD∴∠B =∠D =90°又∵AB =AD ，AC =AC∴Rt △ABC ≌Rt △ADC （HL ）【点睛】本题考查了全等三角形的判定定理和性质定理，能灵活运用定理进行推理是解此题的关键．【题型5】全等三角形判定的灵活应用1．（2021·甘肃·庄浪县阳川中学八年级期中）下列各组条件中，可以判定△ABC ≌△DEF 的条件是（ ）A ．AB =DE 、AC =DF 、BC =EFB ．∠A =∠D 、∠B =∠E 、∠C =∠F C ．AB =DE 、AC =DF 、∠C =∠FD ．BC =EF 、∠A =∠D 【答案】A 【分析】全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，直角三角形全等还有HL ，根据以上定理判断即可【详解】解： A 、符合全等三角形的判定定理SSS ，即能推出△ABC ≌△DEF ，故本选项符合题意；B 、只有角相等，不能判定△ABC ≌△DFE ，故本选项不合题意；C 、只满足SSA ，不符合全等三角形的判定定理，即不能推出△ABC ≌△DEF ，故本选项不合题意；D 、只有一角一边两个条件，不符合全等三角形的判定定理，即不能推出△ABC ≌△DEF ，故本选项不合题意； 故选A ．【点睛】本题考查了全等三角形的判定定理的应用，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，直角三角形全等还有HL ．【变式5-1】2．（2022·浙江·舟山市普陀第二中学八年级期末）如图，在ABC V 中，AD 是BC 边上的高，BE 是AC 边上的高，且AD ，BE 交于点F ，若BF AC =，BD =8，3CD =，则线段AF 的长度为______．【答案】5【分析】首先证明△BDF ≌△ADC ，再根据全等三角形的性质可得FD =CD ，AD =BD ，根据AD =8，DF =3，即可算出AF 的长．【详解】解：∵AD 是BC 边上的高，BE 是AC 边上的高，∴∠ADC =∠FDB =90°，∠AEB =90°，∴∠1+∠C =90°，∠1+∠2=90°，∴∠2=∠C ，∵∠2=∠3，∴∠3=∠C ，在△ADC 和△BDF 中，3C FDB CDA BF AC Ð=ÐìïÐ=Ðíï=î，∴△BDF ≌△ADC （AAS ），∴FD =CD ，AD =BD ，∵CD =3，BD =8，∴AD =8，DF =3，∴AF =8-3=5，故答案为：5．【点睛】本题考查的是全等三角形的判定及性质，熟练掌握性质定理是解题的关键．一．选择题1．（2022·福建·福州十八中八年级期末）如图，已知AC BD ^，垂足为O ，AO CO =，AB CD =，则可得到AOB COD D @D ，理由是( )A ．HLB ．SASC ．ASAD ．AAS【答案】A 【分析】根据全等三角形的判定定理分析即可．【详解】解:∵AC BD^∴∠AOB=∠COD=90°在Rt △AOB 和Rt △COD 中AO CO AB CD=ìí=î∴AOB COD D @D （HL ）故选A ．【点睛】此题考查的是全等三角形的判定定理，掌握用HL 判定两个三角形全等是解决此题的关键．2．（2022·全国·七年级期末）如图，为测量桃李湖两端AB 的距离，南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C ，测得∠ACB 的度数，在AC 的另一侧测得∠ACD =∠ACB ，CD =CB ，再测得AD 的长，就是AB 的长．那么判定△ABC ≌△ADC 的理由是（ ）A ．SASB ．SSSC ．ASAD ．AAS【答案】A【分析】已知条件是∠ACD =∠ACB ，CD =CB ，AC =AC ，据此作出选择．【详解】解：在△ADC 与△ABC 中，CD CB ACD ACB AC AC =ìïÐ=Ðíï=î．∴△ADC ≌△ABC （SAS ）．故选：A ．【点睛】此题考查了全等三角形的应用，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS ，做题时注意选择．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．3．（2021·全国·七年级课时练习）如图，△ABC 和△EDF 中，∠B ＝∠D ＝90°，∠A ＝∠E ，点B ，F ，C ，D 在同一条直线上，再增加一个条件，不能判定△ABC ≌△EDF 的是( )A ．AB ＝EDB ．AC ＝EF C ．AC ∥EFD ．BF ＝DC 【答案】C【分析】根据全等三角形的判定方法即可判断.【详解】A. AB ＝ED ，可用ASA 判定△ABC ≌△EDF ；B. AC ＝EF ，可用AAS 判定△ABC ≌△EDF ；C. AC ∥EF ，不能用AAA 判定△ABC ≌△EDF ，故错误；D. BF ＝DC ，可用AAS 判定△ABC ≌△EDF ；故选C.【点睛】此题主要考查全等三角形的判定，解题的关键是熟知全等三角形的判定方法.4．（2022·全国·八年级课时练习）如图，在ABC V 中，D ，E 是BC 边上的两点，,,12110,60AD AE BE CD BAE ==Ð=ÐÐ=°=°，则BAC Ð的度数为（ ）A ．90°B ．80°C ．70°D ．60°【答案】B 【分析】先证明BD =CE ，然后证明△ADB ≌△AEC ，∠ADE =∠AED =70°，得到∠BAD =∠CAE ，根据三角形内角和定理求出∠DAE =40°，从而求出∠BAD 的度数即可得到答案．【详解】解：∵BE =CD ，∴BE -DE =CD -DE ，即BD =CE ，∵∠1=∠2=110°，AD =AE ，∴△ADB ≌△AEC （SAS ），∠ADE =∠AED =70°，∴∠BAD =∠CAE ，∠DAE =180°-∠ADE -∠AED =40°，∵∠BAE =60°，∴∠BAD =∠CAE =20°，∴∠BAC =80°，故选B ．【点睛】本题主要考查了全等三角形的性质与判定，邻补角互补，三角形内角和定理，熟知全等三角形的性质与判定条件是解题的关键．5．（2022·全国·八年级专题练习）如图，点B ，C ，E 在同一直线上，且AC CE =，90B D Ð=Ð=°，AC CD ^，下列结论不一定成立的是（ ）A ．2A Ð=ÐB ．90A E Ð+Ð=°C ．BC DE =D ．BCD ACEÐ=Ð【答案】D 【分析】根据直角三角形的性质得出∠A =∠2，∠1=∠E ，根据全等三角形的判定定理推出△ABC ≌△CDE ，再逐个判断即可．【详解】解：∵AC ⊥CD ，∴∠ACD =90°，∵∠B =90°，∴∠1+∠A =90°，∠1+∠2=90°，∴∠A =∠2，同理∠1=∠E ，∵∠D =90°，∴∠E+∠2=∠A+∠E=90°，在△ABC 和△CDE 中，2A B D AC CE Ð=ÐìïÐ=Ðíï=î，∴△ABC ≌△CDE （AAS ），∴BC DE =，∴选项A 、选项B ，选项C 都正确；根据已知条件推出∠A =∠2，∠E =∠1，但是∠1=∠2不能推出，而∠BCD =90°+∠1，∠ACE =90°+∠2，所以BCD ACE Ð=Ð不一定成立故选项D 错误；故选：D ．【点睛】本题考查了全等三角形的判定定理和直角三角形的性质，能灵活运用知识点进行推理是解此题的关键，注意：全等三角形的判定定理有：ASA ，SAS ，AAS ，SSS ，两直角三角形全等，还有HL ．6．（2022·江苏·八年级专题练习）如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作等边三角形ABC 和等边三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ ．以下结论错误的是（ ）A ．∠AOB =60°B ．AP =BQC ．PQ ∥AED ．DE =DP 【答案】D【分析】利用等边三角形的性质，BC ∥DE ，再根据平行线的性质得到∠CBE =∠DEO ，于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°，得出A 正确；根据△CQB ≌△CPA （ASA ），得出B 正确；由△ACD ≌△BCE 得∠CBE =∠DAC ，加之∠ACB =∠DCE =60°，AC =BC ，得到△CQB ≌△CPA （ASA ），再根据∠PCQ =60°推出△PCQ 为等边三角形，又由∠PQC =∠DCE ，根据内错角相等，两直线平行，得出C 正确；根据∠CDE =60°，∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，可知∠DQE ≠∠CDE ，得出D 错误．【详解】解：∵等边△ABC 和等边△CDE ，∴AC =BC ，CD =CE ，∠ACB =∠DCE =60°，∴∠ACB +∠BCD =∠DCE +∠BCD ，即∠ACD =∠BCE ，在△ACD 与△BCE 中，AC BC ACD BCE CD CE =ìïÐ=Ðíï=î，∴△ACD ≌△BCE （SAS ），∴∠CBE =∠DAC ，又∵∠ACB =∠DCE =60°，∴∠BCD =60°，即∠ACP =∠BCQ ，又∵AC =BC ，在△CQB 与△CPA 中，ACP BCQ AC BCPAC CBQ Ð=Ðìï=íïÐ=Ðî，∴△CQB ≌△CPA （ASA ），∴CP =CQ ，又∵∠PCQ =60°可知△PCQ 为等边三角形，∴∠PQC =∠DCE =60°，∴PQ ∥AE ，故C 正确，∵△CQB ≌△CPA ，∴AP =BQ ，故B 正确，∵AD =BE ，AP =BQ ，∴AD -AP =BE -BQ ，即DP =QE ，∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，∠CDE =60°，∴∠DQE ≠∠CDE ，故D 错误；∵∠ACB =∠DCE =60°，∴∠BCD =60°，∵等边△DCE ，∠EDC =60°=∠BCD ，∴BC ∥DE ，∴∠CBE =∠DEO ，∴∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°，故A 正确．故选：D ．【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质，利用旋转不变性，解题的关键是找到不变量．二、填空题7．（2022·全国·八年级课时练习）如图，90B D Ð=Ð=°，AB AD =，130BAD Ð=°，则DCA Ð=______°．8．（2020·北京·中考真题）在V ABC 中，AB=AC ，点D 在BC 上（不与点B ，C 重合）．只需添加一个条件即可证明V ABD ≌V ACD ，这个条件可以是________（写出一个即可）【答案】∠BAD=∠CAD （或BD=CD ）【分析】证明V ABD ≌V ACD ，已经具备,,AB AC AD AD == 根据选择的判定三角形全等的判定方法可得答案．【详解】解：,,AB AC AD AD ==Q\ 要使,ABD ACD V V ≌则可以添加：∠BAD=∠CAD ，此时利用边角边判定：,ABD ACD V V ≌或可以添加：,BD CD =此时利用边边边判定：,ABD ACD V V ≌故答案为：∠BAD=∠CAD 或（.BD CD =）【点睛】本题考查的是三角形全等的判定，属开放性题，掌握三角形全等的判定是解题的关键．9．（2022·全国·八年级课时练习）如图，点D 、A 、E 在直线m 上，AB =AC ，BD ⊥m 于点D ，CE ⊥m 于点E ，且BD =AE ．若BD =3，CE =5，则DE =____________【答案】8【分析】根据BD ⊥m ，CE ⊥m ，得∠BDA =∠CEA =90°，再结合已知AB =AC ，BD =AE 可推出Rt △ADB ≌Rt △CEA ，最后由全等三角形的性质，即可计算出结果．【详解】解：∵BD ⊥m ，CE ⊥m ，∴∠BDA =∠CEA =90°，在Rt △ADB 和Rt △CEA 中，∵AB =AC ，BD =AE ，∴Rt △ADB ≌Rt △CEA （HL ），∵BD =3，CE =5，∴AE =BD =3，AD =CE =5，∴DE = AD + AE =8．故答案为：8．【点睛】本题考查了全等三角形的判定与性质，掌握利用HL 判定直角三角形的全等是解题的关键．10．（2022·全国·八年级专题练习）如图，在△ABC 中，∠ABC ＝90°，AB ＝CB ，F 为AB 延长线上一点，点E 在BC 上，且AE ＝CF ，若∠CAE ＝29°，则∠ACF 的度数为________°．【答案】61【分析】由“HL”可证Rt△ABE≌Rt△CBF，可得∠BAE＝∠BCF＝16°，即可求解．【详解】解：∵在△ABC中，∠ABC＝90°，AB＝CB，∴∠BAC＝∠BCA＝45°，∵∠CAE＝29°，∴∠BAE＝16°，在Rt△ABE和Rt△CBF中，AB BC AE CF=ìí=î，∴Rt△ABE≌Rt△CBF（HL），∴∠BAE＝∠BCF＝16°，∴∠ACF＝∠BCA＋∠BCF＝61°，故答案为：61．【点睛】本题考查了全等三角形的判定和性质，证明Rt△ABE≌Rt△CBF是本题的关键．11．（2021·广东·深圳市龙岗区木棉湾实验学校八年级阶段练习）如图，△ABC的面积为25cm2，BP平分∠ABC，过点A作AP⊥BP于点P，则△PBC的面积为________；∵BP 平分ABC Ð，∴ABP EBP Ð=Ð．∵AP BP ^，12．（2022·全国·八年级专题练习）如图，BD 是△ABC 的中线，E 为A B 边上一点，且:2:1AE EB =，连接CE 交BD 于F ，连接AF 并延长交BC 于点G ，则:BGF ADF S S =△△______．【答案】1:3【分析】作//DK EC ，交AB 于K ，作//DH BC ，交AG 于H ．通过平行线的性质证明AH GH =，GF FH =，3AH HF =，即可求出:1:3BGF ADF S S D D =．【详解】解：作//DK EC ，交AB 于K ，作//DH BC ，交AG 于H ，BD Q 是ABC D 的中线，AD CD \=，AK EK \=，AH GH =，:2:1AE EB =Q ，EB EK AK \==，//EF DK Q ，BF DF \=，//DH BC Q ，GBF HDF \Ð=Ð，在GBF D 和HDF D 中，GBF HDF BF DF BFG DFH Ð=Ðìï=íïÐ=Ðî，()GBF HDF ASA \D @D ，GF HF \=，BGF DHF S S D D =，AH GH =Q ，3AH HF \=，33ADF DHF BGF S S S D D D \==，:1:3BGF ADF S S D D \=，故答案为：1:3．【点睛】本题考查三角形的面积，三角形全等，平行线的性质，等高模型等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．三、解答题13．（2022·江苏·八年级专题练习）如图，D 是AB 边上一点，DF 交AC 于点E ，DE ＝FE ，AE ＝CE ．求证：FC //AB ．【答案】见解析【分析】由DE =FE ，AE =CE ，易证得△ADE ≌△CFE ，即可得∠A =∠ECF ，则可证得FC ∥AB ．【详解】证明：在△ADE 和△CFE 中，DE FE AED CEF AE CE =ìïÐ=Ðíï=î，∴△ADE ≌△CFE （SAS ），∴∠A =∠ECF ，∴FC //AB ．【点睛】此题考查了全等三角形的判定与性质以及平行线的判定．此题难度不大，注意掌握数形结合思想的应用．14．（2022·江苏·八年级课时练习）已知：如图AD 为△ABC 的高，E 为AC 上一点BE 交AD 于F 且有BF ＝AC ，FD ＝CD ．求证：Rt △BFD ≌Rt △ACD ．【答案】证明见解析【分析】由题意可知BFD △和ACD △都为直角三角形，即可直接利用“HL ”证明BFD ACD @△△．【详解】证明：∵AD 是ABC V 的高，∴AD BC ^，即BFD △和ACD △都为直角三角形．∴在Rt BFD V 和Rt ACD △中BF AC FD CD =ìí=î，∴()BFD ACD HL @V V ．【点睛】本题考查全等三角形的判定；掌握判定三角形全等的方法是解答本题的关键．15．（2022·陕西·中考真题）如图，在△ABC 中，点D 在边BC 上，CD =AB ，DE ∥AB ，∠DCE =∠A ．求证：DE =BC ．【答案】证明见解析【分析】利用角边角证明△CDE ≌△ABC ，即可证明DE =BC ．【详解】证明：∵DE ∥AB ，∴∠EDC =∠B ．又∵CD =AB ，∠DCE =∠A ，∴△CDE ≌△ABC (ASA)．∴DE =BC ．【点睛】本题考查了全等三角形的判定和性质，掌握全等三角形的判定是本题的关键．16．（2021·广东广州·中考真题）如图，点E 、F 在线段BC 上，//AB CD ，A D Ð=Ð，BE CF =，证明：AE DF =．【答案】见解析【分析】利用AAS 证明△ABE ≌△DCF ，即可得到结论．【详解】证明：∵//AB CD ，∴∠B =∠C ，∵A D Ð=Ð，BE CF =，∴△ABE ≌△DCF （AAS ），∴AE DF =．【点睛】此题考查全等三角形的判定及性质，熟记全等三角形的判定定理是解题的关键．17．（2021·全国·八年级专题练习）如图，已知AB ＝DC ，AC ＝DB ，BE ＝CE,求证：AE ＝DE.【答案】见解析【分析】利用SSS 证明△ABC ≌△DCB ，根据全等三角形的性质可得∠ABC=∠DCB ，再由SAS 定理证明△ABE ≌△CED ，即可证得AE=DE ．【详解】证明：在△ABC 和△DCB 中，AB DC AC DB BC CB ìïíïî＝＝＝ ，∴△ABC ≌△DCB （SSS ）．∴∠ABC=∠DCB ．在△ABE 和△DCE 中，AB DCABC DCB BE CE ＝＝＝ìïÐÐíïî，∴△ABE ≌△DCE （SAS ）．∴AE=DE ．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．18．（2022·江苏泰州·九年级专题练习）如图，V ABC 中，AC ＝BC ，∠ACB ＝90°，AD 平分∠BAC 交BC 于点D ，过点B 作BE ⊥AD ，交AD 延长线于点E ，F 为AB 的中点，连接CF ，交AD 于点G ，连接BG ．（1）线段BE 与线段AD 有何数量关系？并说明理由；（2）判断V BEG的形状，并说明理由．。

苏教科版初中数学重点知识精选掌握知识点，多做练习题，基础知识很重要！苏科版初中数学和你一起共同进步学业有成！全等三角形重难点易错点解析题一：题面：有下列说法：①全等三角形的形状相同；②全等三角形的周长和面积相等；③若两个钝角三角形全等，则两个钝角所对应的边是对应边；④两个全等形不论怎样改变位置，都能够完全重合．其中正确的个数是 .题二：题面：如图，△ABE≌△ADC≌△ABC，若：∠1=150°，则∠α的度数为 .金题精讲题一：题面：如图，△ACE≌△DBF，若∠E=∠F，AD=8，BC=2，则AB等于 .题二：题面：已知一个三角形的三边长是10，8，6，另一个三角形的三边长分别为n 1．n+1，n+3，如果这两个三角形全等，那么n等于 .题面：如图，在平面直角坐标系中，已知点A（1，2），B（3，2），C（4，3），D（2，6），E （3，5）且以点D、E、F为顶点的三角形与△ABC全等，那么点F的坐标为 .题四：题面：已知Rt△ABC与Rt△ADE中，△ACE≌△ABD且AB=AC，AD=AE．求证：BD⊥CE．题面：如图，已知△ABC中，AB=AC=6cm，∠B=∠C，BC=4cm，点D为AB的中点．如果点P在线段BC上以1cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，△BPD与△CQP是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD 与△CQP全等？课后练习详解重难点易错点解析题一：答案：4个.详解：根据全等三角形的性质可知：全等三角形的形状相同，①正确；全等三角形的周长和面积相等，②正确；若两个钝角三角形全等，则两个钝角所对应的边是对应边，③正确；两个全等形不论怎样改变位置，都能够完全重合，④正确．所以说法正确的个数有4个．题二：答案：60°．详解：如图，∵△ABE≌△ADC≌△ABC，∴∠BAE=∠1=150°，∠DCA=∠E，∴∠2=360° ∠1 ∠BAE=360° 150° 150°=60°，∴∠DFE=180° ∠α ∠E，∠AFC=180° ∠2 ∠DCA，∵∠DFE=∠AFC（对顶角相等），∴180° ∠α ∠E=180° ∠2 ∠DCA，∴∠α=∠2=60°．金题精讲题一：答案：3.详解：∵△ACE≌△DBF，∠E=∠F，AD=8，BC=2∴AC=BD，即AB+BC=CD+BC∴AB=CD∴AB=(AD BC)÷2=(8 2)÷2=3.题二：答案：n=7．详解：n 1，n+1，n+3中n+3是最长边，∵这两个三角形全等，∴10=n+3，解得n=7．题三：答案：F1（2，8），F2（0，6），F3（5，5），F4（3，3）．详解：设点F的坐标是（x，y）．∵A（1，2），B（3，2），C（4，3），D（2，6），E（3，5），题四：答案：BD⊥CE．详解：如图，BD与CE交于点P，BD交AE于点O，∵△ACE≌△ABD，∴∠CEA=∠BDA，∵∠AOD=∠POE，∴∠OPE=∠OAD=90°，∴BD⊥CE．思维拓展答案：△BPD≌△CPQ；1.5cm/s.详解：①全等，理由如下：∵t=1秒，∴BP=CQ=1×1=1厘米，∵AB=6cm，点D为AB的中点，∴BD=3cm．又∵PC=BC BP，BC=4cm，∴PC=4 1=3cm，∴PC=BD．又∵AB=AC，∴∠B=∠C，∴△BPD≌△CPQ；相信自己，就能走向成功的第一步教师不光要传授知识，还要告诉学生学会生活。

信达初中数学试卷1.如图，已知△ABC 为等边三角形，点D 、E 分别在BC 、AC 边上，且AE=CD ，AD 与BE 相交于点F ． (1)求证：ABE ≌△CAD ；(2)求∠BFD 的度数．2.如图，在△ABE 中，AB ＝AE,AD ＝AC,∠BAD ＝∠EAC, BC 、DE 交于点O. 求证：(1) △ABC ≌△AED ； (2) OB ＝OE .3.如图，在△ABC 和△DCB 中，AB = DC ，AC = DB ，AC 与DB 交于点M ．（1）求证：△ABC ≌△DCB ；（2）过点C 作CN ∥BD ，过点B 作BN ∥AC ，CN 与BN 交于点N ，试判断线段BN 与CN 的数量关系，并证明你的结论．B CA DMN信达4.在⊿ABC 中，∠ACB 的平分线交AB 于E ，过E 点作BC 的平行线交AC 于F ，交外角∠ACD 的平分线于G 。

求证：F 为EG 的中点。

5.在⊿ABC 中，∠B ＝60。

，∠BAC 和∠BCA 的平分线AD 和CF 交于I 点。

试猜想：AF 、CD 、AC 三条线段之间有着怎样的数量关系，并加以证明。

18.在直角⊿ABC 中，CA ＝CB ，BD 为AC 上的中线，作∠ADF ＝∠CDB ，如图，连结CF 交BD 于E ，求证：CF ⊥BD 。

（提示：作AC 的中线CO ）GOEFDBCA20. 以⊿ABC 的边AB 、AC 为边向形外作等边⊿ABM 、⊿CAN ，BN 和CM 交于一点P 。

试判断：∠APM 、∠APN 的大小关系，并加以证明。

21. 在∆ABC 中，AB=AC ，DE ∥BC.（1）试问∆ADE 是否是等腰三角形，说明理由. （2）若M 为DE 上的点，且BM 平分ABC ∠，CM 平E MD CBA第5题第18题分ACB∠，若ADE∆的周长20，BC=8.求ABC∆的周长.26. 如图, 已知: 等腰Rt△OAB中,∠AOB=900, 等腰Rt△EOF中,∠EOF=900, 连结AE、BF. 求证:(1) AE=BF; (2) AE⊥BF.27.如图，△ABC中，D是BC的中点，过D点的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF交AB于点E，连接EG。

个性化教学辅导教案1．如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=°．2．如图所示，AB=AC，AD=AE，∠BAC=∠DAE，∠1=25°，∠2=30°，则∠3=．3．如图，已知：AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则①BF=DF，②DF=BC，③∠ADF=∠C=∠ABE，④FD∥BC，⑤∠CAB=∠CBE=∠DFE，其中正确（只填序号）．1．如图，已知：∠B=∠DEF，BC=EF，现要证明△ABC≌△DEF，若要以“SAS”为依据，还缺条件；若要以“ASA”为依据，还缺条件，若要以“AAS”为依据，还缺条件．2．已知：如图，AE⊥BC，DF⊥BC，垂足分别为E，F，AE=DF，AB=DC，则△≌△（HL）．精准突破一: ASA、AASASA﹣﹣两角及其夹边分别对应相等的两个三角形全等．AAS﹣两角及其中一个角的对边对应相等的两个三角形全等．在△ABC 和△DEF⎪⎩⎪⎨⎧∠=∠=∠=∠FCDFACDA△ABC ≌△DEF在△ABC 和△DEF中⎪⎩⎪⎨⎧=∠=∠∠=∠EFBCFCDA△ABC ≌△DEF例题讲解：1．下列各组条件中，能确定△ABC≌△DEF的是（）A．∠A=∠D，∠B=∠E，∠C=∠F B．∠A=∠D，∠C=∠F，AC=DFC．∠A=∠D，∠C=∠F，AC=EF D．AB=DE，BC=EF，∠A=∠D2．如图，已知AB，CD相交于点0，△ACO≌△BD0，CE∥DF，求证：CE=DF．练习：1．如图，AB=AC，∠B=∠C，求证：△ABD≌△ACE．证明：在△ABD和△ACE中，∴≌．2．已知：如图，AD∥BC，∠B=∠D．求证：△ADC≌△CBA．3．如图：已知：∠1=∠2，AC=AF，∠C=∠F．求证：△ABC≌△AEF．极限挑战：1．如图，AC⊥AB，BD⊥AB，CE⊥DE，CE=DE．求证：AC+BD=AB．2．如图，在等腰Rt△ABC中，D是斜边BC的中点，以D为顶点的直角的两边分别与边AB，AC交于点E，F．当∠EDF绕顶点D旋转时（点E不与A，B重合），试判断DE与DF 的数量关系，并证明．精准突破二：：HL﹣﹣斜边与直角边对应相等的两个直角三角形全等．HL﹣﹣斜边与直角边对应相等的两个直角三角形全等．AA DB C E F 在RT△ABC 和RT△DEF中⎩⎨⎧==DFACDEABRT△ABC ≌RT△DEF例题讲解：1．下面关于两个直角三角形全等的判定，不正确的是（）A．斜边和一锐角对应相等的两个直角三角形全等B．两条直角边对应相等的两个直角三角形全等C．斜边和一条直角边对应相等的两个直角三角形全等D．两个面积相等的直角三角形全等2．如图，已知AD，AF分别是两个钝角△ABC和△ABE的高，如果AD=AF，AC=AE．求证：BC=BE．练习：1．如图，在Rt△ABC与Rt△DEF中，∠B=∠E=90°，AC=DF，AB=DE，∠A=50°，则∠DFE=．2．如图，AD是△ABC的高，且AD平分∠BAC，请指出∠B与∠C的关系，并说明理由．3．如图，OB⊥AB，OC⊥AC，垂足为B，C，OB=OC，证明：AO平分∠BAC．4．如图，H是△ABC的高AD、BE的交点，且AD=BE，则下列结论中正确的有①AE=BD，②AH=BH，③EH=DH，④∠HAB=∠HBA（）A．1个B．2个C．3个D．4个极限挑战：1．如图，AC=BC，∠ACB=90°，D为BC的中点，BE⊥BC，CE⊥AD，垂足分别为B、G，那么AD=CE，BD=BE．这个结论对不对？为什么？1．如图，∠ACB=90°，AC=BC，AD⊥CE于D，BE⊥CD于E，AD=2.4cm，DE=1.7cm，则BE 的长度为．2．如图，AB∥CF，E为DF中点，AB=20，CF=15，则BD=．3．如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF，AB=6，AC=10，则AE=．4．已知：如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，点B，D，E 在同一直线上，AF⊥BE于点F，那么线段BE，CE，AF三者之间的数量关系是．5．已知：如图所示，△ABC中，∠BAC=90°，AB=AC，分别过点B、C作经过点A的直线L的垂线段BD、CE，垂足分别D、E．（1）求证：DE=BD+CE．（2）如果过点A的直线经过∠BAC的内部，那么上述结论还成立吗？请给出你的结论，并画出图形予以证明．6．如图，△ABC中，AB=AC，BE⊥AC于点E，AD⊥BC于点D，∠ABE=45°，AD与BE交于点F，连接CF．求证：（1）∠DAC=∠EBC；（2）△BEC≌△AEF；（3）AF=2BD．7．如图，BC⊥CA于点C，DC⊥CE点C，∠ACE=∠DCB，BC=CA，DC=CE，直线BD与AE 交于点F，交AC于点G，连接CF．（1）求证：△ACE≌△BCD；（2）求证：BF⊥AE；（3）请判断：∠CFE∠CAB，并说明理由．8．如图，四边形ABCD中，BC∥AD，BC=AB，∠BAD=90°，∠D=45°，E是BC上一点，F 是CD上一点，（1）若EF⊥AE，求证：AE=EF．（2）若AE=EF，求证：EF⊥AE．1．全等三角形的判定与性质（1）全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．（2）在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．——出门测评分_____1．如图所示，AD是∠BAC的平分线，∠B=∠C，则图中全等的三角形有（）A．3对B．1对C．5对D．6对2．如图，已知∠ACB=90°，AC=BC，BE⊥CE，AD⊥CE于点D，AD=2.5cm，DE=1.7cm，则BE=（）A．1cm B．0.8cm C．4.2cm D．1.5cm3．如图，已知∠B=∠C，添加一个条件使△ABF≌△ACE（不标注新的字母，不添加新的线段），你添加的条件是．4．如图，AE⊥BD于C，AB=ED，AC=EC，则AB与ED的位置关系是．——课后作业1．如图所示，已知∠1=∠2，∠C=∠D，AC=3，BC=2，则AD+BD等于（）A．3B．4C．6D．52．如图，已知AD平分∠BAC，要使△ABD≌△ACD，根据“SAS”需要添加条件；根据“ASA”需要添加条件；根据“AAS”需要添加条件．3．已知：如图，∠1=∠3，∠2=∠4，则△≌△．4．补充一个条件，使推理完整，在△DEF和△MNP中，∠D=∠M，，DF=MP，∴△DEF≌△MNP（AAS）如图，AB=AC，若利用“ASA”来证明△ABE≌△ACD，需补充的一个条件是．6．如图，已知AB∥DC，AD∥BC，AM=CN，图中全等三角形有对．7．如图，CD⊥AB于D点，BE⊥AC于E点，BE，CD交于O点，且AO平分∠BAC．求证：OB=OC．8．如图，E是AC上的一点，∠1=∠2，∠3=∠4，求证：EB=ED．9．完成下面的证明过程：如图，已知：AB是∠CAD的平分线，∠C=∠D．求证：BC=BD．证明：∵AB是∠CAD的平分线，∴∠=∠．在△ABC和△ABD中，∠=∠，∠ABD=∠，AB=．∴△ABC≌△ABD（ASA）∴=．10．如图，已知：∠1=∠2，∠ABC=∠DCB．求证：AC=DB．11．如图在△CDE中，∠DCE=90°，DC=CE，DA⊥AB于A，EB⊥AB于B，试判断AB与AD，BE之间的数量关系，并证明．12．已知：如图，CE⊥AB，BF⊥AC，CE与BF相交于D，且BD=CD．求证：（1）△BDE≌△CDF；（2）AE=AF．。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题（每空xx 分，共xx分）试题1:如图，已知AD是△ABC的边BC上的高，下列能使△ABD≌△ACD的条件是（）A.AB=ACB.∠BAC=90°C.BD=ACD.∠B=45°试题2:已知一等腰三角形的腰长为5，底边长为4，底角为β．满足下列条件的三角形不一定与已知三角形全等的是（）(A)两条边长分别为4，5，它们的夹角为β(B)两个角是β，它们的夹边为4(C)三条边长分别是4，5，5(D)两条边长是5，一个角是β试题3:如图所示，AB=DB，∠ABD=∠C BE，请你添加一个适当的条件，使ΔABC≌ΔDBE． (只需添加一个即可)评卷人得分试题4:如图所示，已知点A、D、B、F在一条直线上，AC=EF，AD=FB，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是．（只需填一个即可）试题5:如图，点D，E分别在线段AB，AC上，BE，CD相交于点O，AE=AD，要使△ABE≌△ACD，需添加一个条件是（只需一个即可，图中不能再添加其他点或线）．试题6:如图，E、F是四边形ABCD的对角线BD上的两点，AE∥CF，AE=CF，BE=DF．求证：△AD E≌△CBF．试题1答案:A．详解：添加AB=AC，符合判定定理HL．而添加∠BAC=90°，或BD=AC，或∠B=45°，不能使△ABD≌△ACD．故选A．试题2答案:D．详解：(A)由SAS知两三角形全等；(B)由ASA知两三角形全等；(C) 由SSS知两三角形全等；(D) 当顶角为β时，两三角形不一定全等．故选D．试题3答案:∠BDE=∠BAC（答案不唯一）。

详解：根据∠ABD=∠CBE可以证明得到∠ABC=∠DBE，然后根据利用的证明方法，“ASA”“SAS”“AAS”分别写出第三个条件即可：∵∠ABD=∠CBE，∴∠ABD+∠ABE=∠CBE+∠ABE，即∠ABC=∠DBE。