方差分析中多重比较标记字母法的实现_潘沈元

多重比较字母标记法例题讲解
多重比较字母标记法是一种在统计学中常用的方法，用于比较多个样本的平均数差异。

这种方法使用不同的字母来表示各组之间的差异，以简化比较过程。

以下是一个多重比较字母标记法的例题讲解：
题目：比较四组实验数据的平均数差异。

数据如下：
组别数据1 数据2 数据3 数据4
A 10 15 20 25
B 8 12 16 22
C 6 9 12 18
D 4 6 8 14
首先，我们需要对每组数据进行排序，以便进行比较。

排序后的数据如下：
组别数据1 数据2 数据3 数据4
A 10 15 20 25
B 8 12 16 22
C 6 9 12 18
D 4 6 8 14
接下来，我们使用多重比较字母标记法对各组数据进行比较。

根据排序后的数据，我们可以得出以下结论：
组A的平均数高于组B、C和D。

组B的平均数高于组C和D。

组C的平均数高于组D。

根据上述结论，我们可以使用字母来表示各组之间的差异。

由于组A的平均数最高，所以用字母A表示，然后依次为B、C和D。

因此，这四组数据按照平均数大小排列的顺序为：A、B、C、D。

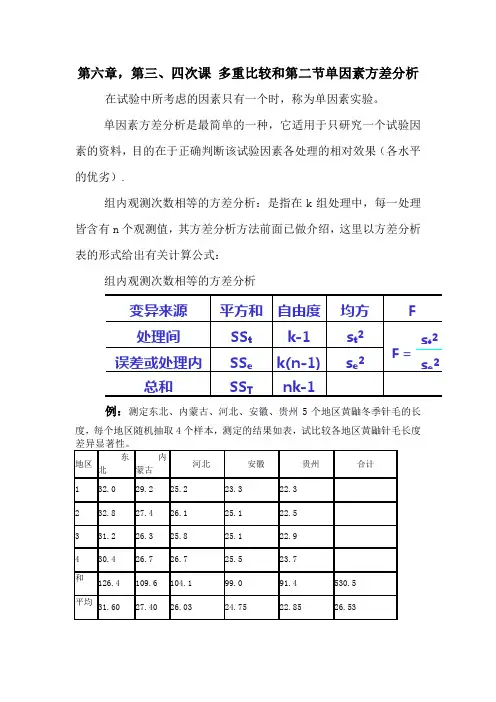
第六章，第三、四次课 多重比较和第二节单因素方差分析在试验中所考虑的因素只有一个时，称为单因素实验。

单因素方差分析是最简单的一种，它适用于只研究一个试验因素的资料，目的在于正确判断该试验因素各处理的相对效果（各水平的优劣）.组内观测次数相等的方差分析：是指在k 组处理中，每一处理皆含有n 个观测值，其方差分析方法前面已做介绍，这里以方差分析表的形式给出有关计算公式：组内观测次数相等的方差分析例：测定东北、内蒙古、河北、安徽、贵州5个地区黄鼬冬季针毛的长度，每个地区随机抽取4个样本，测定的结果如表，试比较各地区黄鼬针毛长度s e 2k(n-1) SS e 误差或处理内nk-1SS T总和s t2 k-1 SS t处理间 F 均方 自由度 平方和 变异来源 F ＝ s t 2 s e21）分解平方和和自由度＝186.7-173.71＝12.99作方差分析F 测验 查F 值表，得F0.05 (4,15) ＝3.06， F0.01 (4,15) ＝4.89，故F >F0.01 ，P < 0.01，说明5个地区黄鼬冬季针毛长度差异极显著。

不同地区黄鼬冬季针毛长度方差分析表为了确定各个地区之间的差异是否显著，需要进行多重比较。

这里用最小显著差数法（LSD ）进行检验。

查t 值表，当dfe =15时，t0.05 ＝2.131，t0.01 ＝2.947，于是有：LSD0.05 = 2.131 ×0.658 =1.402 LSD0.01 = 2.947 ×0.658 =1.939本例中各组内观测数相等，而且组内方差均为0.866，故任何两组的比较均可用LSD0.05 及LSD0.01。

在进行LSD0.05 及LSD0.01比较时各组间差数 > LSD0.01，说明两地间差异极显著，标以不同的大写字母；LSD0.01 >各组间差数>LSD0.05 ，说明两地间差异显著，标以不同的小写字母；51.14071455.53022=⨯==nk T C 7.18651.1407121.142582=-=-=∑C x SS T C T n SS i t -=∑2171.17351.14071)4.916.1094.126(41222=-+++⨯= t T e SS SS SS -=43.43471.1732===tt t df SS s 866.01599.122===e e e df SS s 15.50866.043.4322===e t s s F平均数多重比较表结果表明，东北与其它地区，内蒙古与安徽、贵州，河北与贵州黄鼬冬季针毛长度差异均达到极显著水平，安徽与贵州差异达到显著水平，而内蒙古与河北、河北与安徽差异不显著。

第一章复习1.解释以下概念：总体、个体、样本、样本容量、变量、参数？1.总体是具有相同性质的个体所组成的集合，是指研究对象的全体。

2.个体是组成总体的根本单元。

3.样本是从总体中抽出的假设干个个体所构成的集合。

4.样本容量是指样本个体的数目。

5.变量是相同性质的事物间表现差异性的某种特征。

6.参数是描述总体特征的数量。

7.统计数是描述样本特征的数量。

8.因素是指试验中所研究的影响试验指标的原因或原因组合。

2.统计数、因素、水平、处理、重复、效应、互作、试验误差？1.水平是指每个试验因素的不同状态(处理的某种特定状态或数量上的差异)。

2.处理是指对受试对象给予的某种外部干预(或措施)。

3.重复是指在试验中，将一个处理实施在两个或两个以上的试验单位上。

4.效应是由处理因素作用于受试对象而引起试验差异的作用。

5.互作是指两个或两个以上处理因素间的相互作用产生的效应。

6.试验误差是指试验中不可控因素所引起的观测值偏离真值的差异，可以分为随机误差和系统误差。

3.随机误差与系统误差有何区别?随机误差也称为抽样误差或偶然误差，它是由于试验中许多无法控制的偶然因素所造成的试验结果与真实结果之间的差异，是不可防止的。

随机误差可以通过试验设计和精心管理设法减小，但不能完全消除。

系统误差也称为片面误差，是由于试验处理以外的其他条件明显不一致所产生的带有倾向性的或定向性的偏差。

系统误差主要由一些相对固定的因素引起，在某种程度上是可控制的，在试验过程中是可以防止的。

4.准确性与精确性有何区别?准确性也称为准确度，是指在调查或试验中某一试验指标或性状的观测值与真值接近的程度。

精确性也称为精确度，是指调查或试验中同一试验指标或性状的重复观测值彼此的接近程度的大小。

准确性是说明测定值对真值符合程度的大小，用统计数接近参数真值的程度来衡量。

精确性是反映屡次测定值的变异程度，用样本中的各个变量问的变异程度的大小来衡量。

填空1.变量按其性质可以分为〔连续〕变量和〔非连续(离散型)〕变量。

基于R语言的七种多重比较方法一花视界百家号10-1403:18多重比较的方法很多，根据试验设计的目的不同有不同的应用。

若试验设计之初，便明确要比较某几个组均数间是否有差异，称为事前比较。

常用的事前比较方法有LSD、Bonferroni和Dunnett法。

若研究目的是方差分析有统计学差异后，想知道哪些组间的均数有差异，便是事后比较。

事后比较的常用方法有SNK、Turkey、Scheffe 和Bonferroni法。

本文仅介绍7种方法及R语言函数，可解决绝大部分多重比较问题。

1.LSD法LSD法即最小显著差法；该法一般用于计划好的多重比较。

它其实只是t检验的一个简单变形，并未对检验水准做出任何校正，只是为所有组的均数统一估计了一个更为稳健的标准误。

LSD法比较效果较为灵敏，在R语言中可利用agricolae包中的LSD.test函数实现，其调用格式为：LSD.test(y, trt, DFerror, MSerror, alpha = 0.05, p.adj=c(&quot;none&quot;,&quot;holm&quot;,&quot;hommel&quot;,&quot;hochberg&quot;, &quot;bonferroni&quot;, &quot;BH&quot;, &quot;BY&quot;, &quot;fdr&quot;), …)其中y为方差分析对象，trt为要进行多重比较的分组变量，p.adj可以选定P值矫正方法。

当p.adj=”none”时，为LSD法，p.adj=&quot;bonferroni&quot;时为Bonferroni法。

R代码：library(agricolae)# sweetpotato为agricolae自带数据集data(sweetpotato)#进行方差分析，分组变量为virusmodel#进行多重比较，不矫正P值out &lt;- lsd.test(model,&quot;virus&quot;,=&quot;&quot; p.adj=&quot;none&quot; )#结果显示：标记字母法out$group#可视化plot(out)程序运行结果：从运行结果看，四个处理，oo和ff处理无差异，与cc和fc彼此差异显著。

第六章 方差分析第五章所介绍的t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验，但在生产和科学研究中经常会遇到比较多个处理优劣的问题，即需进行多个平均数间的差异显著性检验。

这时，若仍采用t 检验法就不适宜了。

这是因为：1、检验过程烦琐 例如，一试验包含5个处理，采用t 检验法要进行25C =10次两两平均数的差异显著性检验；若有k 个处理，则要作k (k-1)/2次类似的检验。

2、无统一的试验误差，误差估计的精确性和检验的灵敏性低 对同一试验的多个处理进行比较时，应该有一个统一的试验误差的估计值。

若用t 检验法作两两比较，由于每次比较需计算一个21x x S ，故使得各次比较误差的估计不统一，同时没有充分利用资料所提供的信息而使误差估计的精确性降低，从而降低检验的灵敏性。

例如，试验有5个处理，每个处理重复6次，共有30个观测值。

进行t 检验时，每次只能利用两个处理共12个观测值估计试验误差，误差自由度为2(6-1)=10；若利用整个试验的30个观测值估计试验误差，显然估计的精确性高，且误差自由度为5(6-1)=25。

可见，在用t 检法进行检验时，由于估计误差的精确性低，误差自由度小，使检验的灵敏性降低，容易掩盖差异的显著性。

3、推断的可靠性低，检验的I 型错误率大 即使利用资料所提供的全部信息估计了试验误差，若用t 检验法进行多个处理平均数间的差异显著性检验，由于没有考虑相互比较的两个平均数的秩次问题，因而会增大犯I 型错误的概率，降低推断的可靠性。

由于上述原因，多个平均数的差异显著性检验不宜用t 检验，须采用方差分析法。

方差分析(analysis of variance)是由英国统计学家，把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度，进而获得不同变异来源总体方差估计值；通过计算这些总体方差的估计值的适当比值，就能检验各样本所属总体平均数是否相等。

在处理数据中遇到多重比较字母标记的问题，搜索过后，各个说法不一，难以判断。

因此查阅资料后，向大家分享。

查阅生物统计书明确，多重比较的标记字母法
2015年2月3日
1、此法首先将各个处理平均数由大到小，自上而下的排列。

2、当显著水平为0.05时，在最大平均数后标记小写拉丁字母a，直到某一个与其差异显著的平均数标记字母b 为止。

3、再以标有字母b的平均数，与上方比它大的各个平均数比较，凡与其差异不显著着，一律再加标字母b，直到差异显著不加标字母b为止。

4、再以标记有字母b的最大平均数，与其下面各个未标记字母的平均数相比较，凡与其差异不显著者，继续标记字母b，直到某一个与其差异显著的平均数标记为c为止。

·························
如此重复下去，直到最小的平均数被标记、比较完毕。

这样，各个平均数间凡有一个相同字母的，为差异不显著；凡无相同字母的，为差异显著。

当显著水平为0.01时，则用大写拉丁字母A、B、C等表示多重比较结果。

统计学多重比较结果标记字母法例题一、概述在统计学中，多重比较是指对于多个处理组进行比较的情况。

在进行多重比较时，我们需要考虑到由于进行多次比较而可能带来的错误率增加的问题。

为了解决这一问题，统计学家们提出了各种多重比较方法，其中最常见的就是标记字母法。

二、问题描述假设有一个实验，共包括4个处理组。

我们想要比较这4个处理组的均值是否存在显著差异。

我们对实验结果进行了方差分析，并得到了F 检验的显著性水平为0.05。

接下来，我们希望利用标记字母法对各个处理组进行两两比较，并标记出显著差异的组别。

三、数据处理我们首先需要计算各个处理组的均值和标准差，然后进行多重比较。

假设处理组的均值分别为20、25、30和35，标准差分别为5、6、7和8。

接下来，我们将进行多重比较的计算。

四、多重比较的进行根据方差分析的结果，我们知道F检验的显著性水平为0.05。

在进行多重比较时，我们需要设定一个整体的显著性水平，通常取α=0.05。

接下来，我们可以使用标记字母法进行多重比较。

标记字母法是一种对处理组进行两两比较的方法，其基本思想是对于均值差异显著的组别，用不同的字母进行标记。

五、结果呈现根据标记字母法的计算结果，我们得到了四个处理组的比较结果。

假设经过计算后，我们得到了处理组1、2、3、4的标记分别为a、b、ab、c。

这样，我们就可以清晰地看出，处理组1与2之间的均值差异显著，处理组3与4之间的均值差异显著，而处理组2、3之间的均值差异不显著。

六、讨论与结论通过标记字母法的多重比较，我们得出了各个处理组之间的显著差异情况。

这样的结果对于我们正确地进行实验结果的解释和后续分析具有重要意义。

标记字母法的使用也充分展现了统计学在实际应用中的重要作用。

七、总结在统计学中，多重比较是非常重要的一部分。

而标记字母法作为多重比较的一种常用方法，能够清晰地展现出各个处理组之间的差异情况。

在实际应用中，我们需要谨慎地选择适合的多重比较方法，并根据实验情况进行合理的解释和分析。

统计实验设计中的方差分析与多重比较方法方差分析（ANOVA）和多重比较方法是统计学中常用于研究实验设计的重要工具。

方差分析用于比较多个组别之间的均值是否有显著差异，而多重比较方法则用于确定哪些组别之间存在差异。

本文将介绍方差分析和多重比较方法的原理、应用以及相关注意事项。

一、方差分析（ANOVA）的原理方差分析是用于比较两个或多个组别之间差异的一种统计方法。

它基于总体均值之间的方差来判断各组别之间是否存在显著差异。

方差分析的核心思想是将总体方差分为组内方差与组间方差，并通过比较两者的大小来判断组别之间的差异是否显著。

在进行方差分析时，需要满足以下假设：各组别之间的样本来自于正态分布的总体，各组别的方差相等，样本之间独立。

对于一个因变量和一个自变量，可以使用单因素方差分析；对于一个因变量和多个自变量，可以使用多因素方差分析。

方差分析的结果通常通过F统计量来体现。

F统计量是组间方差与组内方差的比值，如果F值足够大，就可以认为组别之间存在显著差异。

如果显著性水平小于设定的阈值（通常是0.05），则可以拒绝无差异的假设，认为组别之间存在显著差异。

二、多重比较方法当我们得出方差分析结果显示组别之间存在显著差异时，接下来需要进行多重比较以确定具体差异在哪些组别之间。

多重比较方法可以帮助我们进行两两组别之间的比较，以确定哪些组别之间存在差异。

常见的多重比较方法包括Tukey方法、Bonferroni方法和Duncan方法等。

这些方法的原理和步骤有所不同，但基本思想是进行多次假设检验，并通过控制错误率来确定具体差异是否显著。

Tukey方法是一种常用的多重比较方法，它通过计算各组别之间的平均差异和置信区间来判断是否存在显著差异。

Bonferroni方法则是将显著性水平除以比较的次数，以控制整体错误率。

Duncan方法是利用多重范围检验校正标准来确定差异的存在。

三、方差分析与多重比较方法的应用方差分析和多重比较方法在统计实验设计中有广泛的应用。

第六章 方差分析第五章所介绍的t 检验法适用于样本平均数与总体平均数及两样本平均数间的差异显著性检验，但在生产和科学研究中经常会遇到比较多个处理优劣的问题，即需进行多个平均数间的差异显著性检验。

这时，若仍采用t 检验法就不适宜了。

这是因为：1、检验过程烦琐 例如，一试验包含5个处理，采用t 检验法要进行25C =10次两两平均数的差异显著性检验；若有k 个处理，则要作k (k-1)/2次类似的检验。

2、无统一的试验误差，误差估计的精确性和检验的灵敏性低 对同一试验的多个处理进行比较时，应该有一个统一的试验误差的估计值。

若用t 检验法作两两比较，由于每次比较需计算一个21x x S ，故使得各次比较误差的估计不统一，同时没有充分利用资料所提供的信息而使误差估计的精确性降低，从而降低检验的灵敏性。

例如，试验有5个处理，每个处理重复6次，共有30个观测值。

进行t 检验时，每次只能利用两个处理共12个观测值估计试验误差，误差自由度为2(6-1)=10；若利用整个试验的30个观测值估计试验误差，显然估计的精确性高，且误差自由度为5(6-1)=25。

可见，在用t 检法进行检验时，由于估计误差的精确性低，误差自由度小，使检验的灵敏性降低，容易掩盖差异的显著性。

3、推断的可靠性低，检验的I 型错误率大 即使利用资料所提供的全部信息估计了试验误差，若用t 检验法进行多个处理平均数间的差异显著性检验，由于没有考虑相互比较的两个平均数的秩次问题，因而会增大犯I 型错误的概率，降低推断的可靠性。

由于上述原因，多个平均数的差异显著性检验不宜用t 检验，须采用方差分析法。

方差分析(analysis of variance)是由英国统计学家，把观测值总变异的平方和及自由度分解为相应于不同变异来源的平方和及自由度，进而获得不同变异来源总体方差估计值；通过计算这些总体方差的估计值的适当比值，就能检验各样本所属总体平均数是否相等。

多重比较的‎字母标记法‎本届答辩刘‎老师反复指‎出多重比较‎字母标记法‎的问题，大部分人都‎是一头雾水‎，特查了一下‎具体标记方‎法。

*******************1）将全部平均‎数从大到小‎顺序排列，然后在最大‎的平均数上‎标上字母a‎；2）将该平均数‎依次和其以‎下各平均数‎相比，凡差异不显‎著的都标字‎母a，直至某一个‎与之相差显‎著的平均数‎则标以字母‎b。

3）再以该标有‎b的平均数‎为标准，与上方各个‎比它大的平‎均数比，凡不显著的‎也一律标以‎字母b；4）再以标有b‎的最大平均‎数为标准，与以下各未‎标记的平均‎数比，凡不显著的‎继续标以字‎母b，直至某一个‎与之相差显‎著的平均数‎则标以字母‎c；5）……如此重复下‎去，直至最小的‎一个平均数‎有了标记字‎母为止。

这样各平均‎数间，凡有一个标‎记相同字母‎的即为差异‎不显著，凡具不同标‎记字母的即‎为差异显著‎。

在实际应用‎时，一般以大写‎字母 A.B.C…… 表示α=0.01显著水‎平，以小写字母‎a.b.c……表示α=0.05显著水‎平。

胡乱编一个‎例子，假设差值大‎于10显著‎，小等于10‎不显著，则100与‎80显著，80与70‎不显著。

100 a80 b79 b78 b70 bc60 cd50 d30 e29 e100标a‎，100与8‎0显著80‎标b，80与79‎不显著79‎标b，80与78‎不显著78‎标b，80与70‎不显著70‎标b，80与60‎显著60标‎c，60与70‎不显著70‎标c，60与78‎显著78已‎经和60不‎同不标，70与50‎显著50标‎d，50与60‎不显著60‎标d，50与70‎显著70已‎经和50不‎同不标，60与30‎显著30标‎e30与29‎不显著29‎标e。

多重比较的字母标记法
本届答辩刘老师反复指出多重比较字母标记法的问题，大部分人都是一头雾水，特查了一下具体标记方法。

*******************
1）将全部平均数从大到小顺序排列，然后在最大的平均数上标上字母a；
2）将该平均数依次和其以下各平均数相比，凡差异不显著的都标字母a，直至某一个与之相差显著的平均数则标以字母b。

3）再以该标有b的平均数为标准，与上方各个比它大的平均数比，凡不显著的也一律标以字母b；4）再以标有b的最大平均数为标准，与以下各未标记的平均数比，凡不显著的继续标以字母b，直至某一个与之相差显著的平均数则标以字母c；
5）……如此重复下去，直至最小的一个平均数有了标记字母为止。

这样各平均数间，凡有一个标记相同字母的即为差异不显著，凡具不同标记字母的即为差异显著。

在实际应用时，一般以大写字母A.B.C…… 表示α=0.01显著水平，以小写字母a.b.c……表示α=0.05显著水平。

胡乱编一个例子，假设差值大于10显著，小等于10不显著，则100与80显著，80与70不显著。

100 a
80 b
79 b
78 b
70 bc
60 cd
50 d
30 e
29 e
100标a，
100与80显著80标b，
80与79不显著79标b，
80与78不显著78标b，
80与70不显著70标b，
80与60显著60标c，
60与70不显著70标c，
60与78显著78已经和60不同不标，70与50显著50标d，
50与60不显著60标d，
50与70显著70已经和50不同不标，60与30显著30标e
30与29不显著29标e。

方差分析中的多重比较在stata软件中的实现中国卫生统计1996年第13卷第2期计算机应用?,中,(,方差分析中的多重比较在stata软件中的实现ff了;?t-鞴室在方差分析中,stata提供了三种多重比较的方法:Bonferroni法,Seheffe法和S~dak法.Bonferroni法的校正公式为P=min(1.g?P)其中P是校正前概率值,尸是校正后的概率值;g是多重比较的检验总数.Scheffe法的校正公式为P一rob(r一1,一r,￡/(r一1))其中t=(r～1)F(1一P,r一1,～r)fpro6(af,,,)是分子自由度为,分母自由度为af,F值为,的F分布的累积概率函数,r是因素的水平数.Sidak法的校正公式为P一min(1,1一(1一,))多重比较的结果是看校正后的概率值尸是否大于给定的检验水平n,如果P&lt;.,则认为该多重比较的结果在统计学意义上有显着性差异,反之,则无显着性差异.如果仅考虑单因素方差分析两两比较的情况+Stata软件给出了一个非常简单的命令实现,即在oneway命令后加bonferron[或scheffe或sidak选择项便可得到经上面三种方法校正后的概率值.现以Bonferroni法为侧,说明单因素方差分析两两比较的结果.例l,数据集sysage.dta是一组有关心『姥收缩压(systolic),疾病种类(disease),用药种娄(drug)和年龄(age)的数据调用s3Isage.dta数据后,输入命令onewaysystolicdrug,bonferroni将得到以下两两比较的结果(表1)表1各药物组收缩压变化值的两两比较在以上两两比较的结果中,第2行第1例的值一17.32表示用药为第一种类型和第三种类型时平均收缩压的差别,其bonferroni法校正概率值为0.001.若以0.05为检验水平,则认为第一种类型的药物和第三种类型的药物对收缩压的影响在统计上有显着性意义.其他结果解释类推.两两比较除了用oneway命令实现外,也可用anova命令加上test命令实现.anova命令及test命令还可以进行其他多重比较检验. 例2,仍以sysage.dta数据为例,给定下列多重比较的检验假设B:下uIq-u~=丁uaq-u~A:≠%下ulq-ua—u下2+u,A2:≠B:uTt+uz4-u~一"A:≠".003a原假设日.:nB.备择假设H一UA首先输入anova命令,得到有关方差分析的结果.命令如下;Ⅱndsystolicdrug.reg方差分析结果;52表2方差分析结果来僻SSd{MS模型31332鼬5l31044.41柏4残差总计;9340.1551787163.862371观察投=58F&lt;3.54)一9.09P,&gt;F=00001R0—0.33fi5枝正R一0.2985离均差平方根一10721其次用test命令求出校正前各概率值P. 以及t值.命令格式及结果如下:testb[drug:1)+一b[drug(2]一rug(333+b(drug[4]](1)drug[1]+drug(2]一drug(33一drug (43—0.0F(1,54)=26.85Pr&gt;F一0.0000testb[drug[1]]+.b(drug(333一一brug(2]]+6rug[4]](1)drug[1]--drug(23+r"g(33一drug (43—0.0F(1.54)一0.55Prob&gt;F一0.4599testb(dnug[1]]4-b[drug[2]]+b[drugb(313一b(drug(4]]*3F(1+54)=4.40Prob&gt;F一0.0406Bonferroni法:在本侧中,多重比较的检验总数g一3. Bonferroni法校正后概率值P分别为P一rain(1,3×0.0000)一0.0000P2一m[n(1,3×0.4599)一1P一rain(1,3×0.0406)一0.1224 Sacheffe法:在本例中三组比较的t(F)值分别为26.85,0.55和4.40,drug水平数r一4,由fprob函数可求得Scheffe法校正概率值P, P,P,结果如下:genPt—fprob(3,54,26.85/3)genP'z=fprob(3,54,0.55/3)genP3=fprob(3,54,4.40/3)HstPl—P3in1PlP!P31.0.00006560.907273l0.2338896Sidak法:在本例中,多重比较的检验总数g一3.P=min(1,1一(1—0.0000))一0.0000P=min(I,1一(1—0.4599))一0.8531P=mln(1,1一(1—0.0406))一0.1170如果以0.05为检验水平,那么根据前三种多重比较的结果可以看出,只有第一组检验的结果在统计学上具有显着性差异,其他两组检验的结果均无统计学上的显着性差异.讨论1.用Bonferroni法校正概率值较Scheffe法简捷,但检验总数g较大时,其校正后的概率值往往偏大,所以当检验总数较大时,不宜用Bonfferron法.2.Bonferroni法和Sidak法的校正结果与检验总数有关,而Scheffe法却与之无关.对校正后概率值的解释有所差异,由Bonfferroni法和Sidak法校正后概率值作出的判断是指对g 个检验假设同时作出判断,而由Scheffe法校正后的概率值作出的判断是指对所有假设同时作出判断.因此Scheffe法是一种相对保守的多重比较法.3.Bonfferroni法和Sidak法在多因素方差分析及协方差分析模型中皆保持不变,而Scheffe法则需做一些修改.如在协方差分析中,其公式改为:声=rob(r一1,n—r一1,t2/(r一1))其中—1)F(1一声,T-m1,H—r一1).参考文献1.JohaNeteeets1.AppliedLinear~tatlst[calModels.Regres—sion.AnalysisofV ariance.sndExperimentalDcsigns.1985|973--593z.辐维双,等.多元统计舟析.北京-高等教育出版社.1989 390—3263王建民.马林茂.Stata软件手册.1991;i9i一9i6.373—379.SlB一5204陈希描.等.近代回归分析.台肥:安敬教育出版杜,198724 —42感谢)&lt;车文承蒙丰宣盘水高老师和薛禾生老师的指导.谨此婴儿死亡漏报调查方法上海市卫生防疫站宋挂香根据我市多年的工作经验,我们认为单靠常规登记工作难以反映婴儿实际死亡术平的真实情况,必颓充实调查方法.用常规登记与抽样调查相结台,采用以下几种调查方法.一,每年进行婴儿死亡漏报检查检查形式方法不一.区县防疫站,妇幼保健院对本地区的医疗单位半年检查一次,全市性抽样检查每年一次.在市区.采取区与区之同对rl或循环检查.区内医院之间的检查.郊县+县与县之间对口或县内医院,乡卫生院对口检查.或由市卫生局抽一些人员组成一十检查组.检查内容:首先检查产房接产登记,出生时评分在2分以下,死产,死胎,新生儿死亡的婴儿,全部查看病史I查看婴儿室死亡登记,儿科病房死亡登记,门(急) 诊死亡登记,随机抽看产科病史棱对.各级医院产科及儿科等有关科室做好婴儿,新生儿死亡,死产,死胎登记情况.每月填写《婴儿,新生儿死亡.死产.死胎一览表》,该表作为卫生统计法定上报报表,由医院病案室报告所在地区卫生防疫站,由防疫站调查,按实.代报出生,死亡.二,怀孕结局调查怀孕结局调查是以怀孕妇女为对象,跟踪到妊娠结柬,掌握胎儿的击向.以地区妇幼保健,计翊生育部f]建立的孕卡为基础资料.核实数据.以专业人员为主体.组织计划生育专职干部,产后家访下段医生,一起进行现场十寰调查,核实胎儿击向——活产,死亡.死胎.死产.大月龄自然流产等.三,畸形儿追踪调查将接产登记中注明畸形的婴儿.如腭裂,唇裂,先心等.这些婴儿是死亡的高危对象.遂十上门调查.查看婴儿存活情况.四,现场调查不定期的整群分层随机抽样,每次抽取一十街道,一十乡上仃调查,将调查到的死亡资料与防疫站常规性死因登记资料桉对.多年来我们采用了上述几种调查方法,娶儿死亡漏报逐年下降,1973年为lm32%,1980年为1.97%, 1985年为1.21%.1994年为0.22%.调查结果表明:这种婴儿死亡漏报调查方式是可行的,能反映出本地区的实际水平.。

方差分析（ANOVA）、多重比较（LSDDuncan）、q检验（student）方差分析（ANOV A）、多重比较（LSD Duncan）、q检验(student)实际研究中，经常需要比较两组以上样本均数的差别，这时不能使用t检验方法作两两间的比较（如有人对四组均数的比较，作6次两两间的t检验），这势必增加两类错误的可能性（如原先a定为0.05，这样作多次的t检验将使最终推断时的a>0.05）。

故对于两组以上的均数比较，必须使用方差分析的方法，当然方差分析方法亦适用于两组均数的比较。

方差分析可调用此过程可完成。

Least-significant difference(LSD)：最小显著差法。

a可指定0~1之间任何显著性水平，默认值为0.05；Bonferroni：Bonferroni修正差别检验法。

a可指定0~1之间任何显著性水平，默认值为0.05；Duncan’s multiple range test：Duncan多范围检验。

只能指定a为0.05或0.01或0.1，默认值为0.05；Student-Newman-Keuls：Student-Newman-Keuls检验，简称N-K检验,亦即q 检验。

a只能为0.05；(以前都以SNK法最为常用，但研究表明，当两两比较的次数极多时，该方法的假阳性非常高，最终可以达到100%。

因此比较次数较多时，包括SPSS和SAS在内的权威统计软件都不再推荐使用此法。

) Tukey’s honestly significant difference：Tukey显著性检验。

a只能为0.05；Tukey’s b：Tukey另一种显著性检验。

a只能为0.05；Scheffe：Scheffe差别检验法。

a可指定0~1之间任何显著性水平，默认值为0.05。

根据对相关研究的检索结果，除了参照所研究领域的惯例外，一般可以参照如下标准：如果存在明确的对照组，要进行的是验证性研究，即计划好的某两个或几个组间（和对照组）的比较，宜用Bonferoni(LSD)法；若需要进行的是多个平均数间的两两比较（探索性研究），且各组样本数相等，宜用Tukey法，其他情况宜用Scheffe法。

多重比较中字母标注方法
显著性检验：采用SPSS或其它数据统计软件进行，得到任意两个平均值间的显著性关系。

字母标注：
1. 首先将所有平均值由大到小排序。

2. 在最大的平均值后标字母a；
3. 以最大的平均值与居于第二的平均值对比，如显著，则标字母b（即不同字母），不显著，标字母a（即相同字母）；
4. 当标不同字母时，再以标有不同字母的平均值为标准，与大于该平均值的平均值从小到大依次比较，差异不显著者标相同字母，到所有不显著的平均值中最大者时停止（即比显著者小的最大平均值）；
5. 以标有相同字母的最大平均值为基础，向小的平均值变小方向比较，如差异不显著，标相同字母，差异显著，标不同字母。

当出现标不同字母时，按4中方法继续朝平均值变大方向比较。

6. 如此反复进行，直到最小的一个平均值标有字母为止。

一般地，当在0.05水平上显著时，标小写字母；当在0.01水平上显著时，标大写字母。

[精品]多重比较的字母标记法多重比较的字母标记法是一种用来比较多个相关样本平均值的统计方法。

这种方法旨在确定哪些样本之间存在显著差异，以及哪些样本之间的差异可能是由于偶然因素引起的。

在使用这种方法时，我们通常会使用字母标记来表示不同样本之间的显著差异。

这种方法的基本思想是，我们首先对所有样本进行排序。

然后，从最小的平均值开始，对每个平均值分配一个字母标记。

对于具有相同平均值的样本，它们应该被分配相同的字母标记。

如果相同平均值的样本的数量超过了可用的字母，那么它们应该被分配相同的标记，并用括号括起来。

然后，我们将比较每对相邻标记的差异是否显著。

如果这些差异不显著，那么它们应该被分配相同的字母标记。

否则，它们应该被分配不同的字母标记。

一个例子可以更好地说明这个方法的应用。

假设我们有三个组的数据，每个组的平均值和标准误如下所示：组1：平均值=10，标准误=1首先，我们对这些组的平均值进行排序，并按顺序分配字母标记。

由于组2的平均值最大，所以它被分配字母“A”。

由于组1的平均值没有达到显著水平，所以它和组2被分配相同的字母标记“A"，组3的平均值超过了组2，所以它被分配字母“B”。

然后，我们将比较相邻的标记之间的差异是否显著。

在这种情况下，标记“A"和标记“B”之间的差异是显著的，因此它们被分配不同的字母标记。

因此，我们可以将这些结果汇总为：通过这种方法，我们可以确定哪些组之间存在显著差异，以及哪些组之间的差异可能仅是由于偶然因素引起的。

同时，通过使用字母标记，我们可以在结果中提供一个简单的视觉表示，以便更容易地理解和传达结果。