年中考冲刺之选择填空压轴题

1 （2011湖南岳阳）如图，把一张长方形纸片ABCD 沿对角线BD 折叠，使C 点落在E 处，BE 与AD 相交于点F ，下列结论：①22ABADBD ②△ABF ≌△EDF ③AFEF ABDE ④AD=BD ·cos45°，其中正确的一组是（）A ．①②B ．②③C ．①④D ．③④2（2012四川达州）将矩形纸片ABCD ，按如图所示的方式折叠，点A 、点C 恰好落在对角线BD 上，得到菱形BEDF.若BC=6，则AB 的长为 .3 （2011安徽，22，12分）在△ABC 中，∠ACB=90°，∠ABC=30°，将△ABC 绕顶点C 顺时针旋转，旋转角为（0°＜＜180°），得到△A ′B ′C ．（1）如图（1），当AB ∥CB ′时，设A ′B ′与CB 相交于点D ．证明：△A ′CD 是等边三角形；（2）如图（2），连接A ′A 、B ′B ，设△ACA ′和△BCB ′的面积分别为S △ACA ′和S △BCB ′．求证：S △ACA ′：S △BCB ′1：3；（3）如图（3），设AC 中点为E ，A ′B ′中点为P ，AC=a ，连接EP ，当=°时，EP 长度最大，最大值为．4 .（2012山东东营）（1）如图1，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF ＝BE ．求证：CE ＝CF ；（2）如图2，在正方形ABCD 中，E 是AB 上一点，G 是AD 上一点，如果∠GCE ＝45°，请你利用（1）的结论证明：GE ＝BE ＋GD ．（3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD 中，AD ∥BC （BC ＞AD ），∠B ＝90°，AB ＝BC ，E 是AB 上一点，且∠DCE ＝45°，BE ＝4，DE=10, 求直角梯形ABCD 的面积．ABFCDEAθA ′B ′BCA ′AB B ′CE PθABBC Aθ（第23题图1）AEBCDF（第23题图3）BCADE（第23题图2）AEBCDG5.（2012湖南益阳，21，12分）已知：如图1，在面积为3的正方形ABCD 中，E 、F 分别是BC和CD 边上的两点，AE ⊥BF 于点G ，且BE=1．（1）求证：△ABE ≌△BCF ；（2）求出△ABE 和△BCF 重叠部分（即△BEG ）的面积；（3）现将△ABE 绕点A 逆时针方向旋转到△AB ＇E ＇（如图2），使点E 落在CD 边上的点E ＇处，问△ABE 在旋转前后与△BCF 重叠部分的面积是否发生了变化？请说明理由．6.（2012山东泰安）如图，菱形OABC 的顶点O 在坐标原点，顶点A 在x 轴上，∠B=120°，OA=2，将菱形OABC 绕点O 顺时针旋转105°至OA B C 的位置，则点B 的坐标为（）A.(2,2) B.(2,2) C.(2,2) D.(2,2)7.（2012河北省）9、如图4，在□ABCD 中，∠A=70°，将□ABCD 折叠，使点D ，C 分别落在点F ，E 处，（点F ，E 都在AB 所在的直线上），折痕为MN ，则∠AMF 等于（）Ａ．70° Ｂ．40° Ｃ．30°Ｄ．20°8如图，A ，B 的坐标为（2，0），（0，1），若将线段AB 平移至A1B1，则a+b 的值为（）A.2B.3C.4D.59..如图，在直角坐标系中，矩形ABCO 的边OA 在x 轴上，边OC 在y 轴上，点B 的坐标为（1，3），将矩形沿对角线AC 翻折，B 点落在D 点的位置，且AD 交y 轴于点 E.那么D 点的坐标为（）A.B. C. D.10.如图，平面直角坐标系中，OB 在x 轴上，∠ABO=90°，点A 的坐标为（1，2），将△AOB 绕点A 逆时针旋转90°，点O 的对应点C 恰好落在双曲线（x ＞0）上，则k 的值为（）A.2B.3C.4D.611.如图，在扇形纸片AOB 中，OA=10，∠AOB=36°，OB 在桌面内的直线l 上.现将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA 落在l 上时，停止旋转.则点O 所经过的路线长为（）A.12πB.11πC.10πD.12（2011湖北黄冈）如图，把Rt △ABC 放在直角坐标系内，其中∠CAB=90°，BC=5，点A 、B 的坐标分别为（1，0）、（4，0），将△ABC 沿x 轴向右平移，当点C 落在直线y=2x －6上时，线段BC 扫过的面积为（）ABAC DBGFD'B CF'E E图2图1A ．4B ．8C ．16D ．8213.（2011山西）将一个矩形纸片依次按图（1）、图的方式对折，然后沿图（3）中的虚线裁剪，最后头将图（4）的纸再展开铺平，所得到的图案是（）14（2011福建泉州）如图，如果边长为1的正六边形ABCDEF 绕着顶点A 顺时针旋转60°后与正六边形AGHMNP 重合，那么点B 的对应点是点，点E 在整个旋转过程中，所经过的路径长为（结果保留）.15（2011广西贵港）如图所示，在边长为2的正三角形ABC 中，E 、F 、G 分别为AB 、AC 、BC 的中点，点P 线段EF 上一个动点，连接BP 、GP ，则△BPG 周长的最小值是。

1．（深圳）如图，已知四边形ABCD为等腰梯形，AD∥BC，AB=CD，AD=，E为CD中点，连接AE，且AE=2，∥DAE=30°，作AE∥AF交BC于F，则BF=（）A．1B．3﹣C．﹣1D．4﹣2A．B．C．D．A．6B．12C．32D．644．（深圳）如图，∥ABC与∥DEF均为等边三角形，O为BC、EF的中点，则AD：BE的值为（）A．：1B．：1C．5：3D．不确定1 / 95．（深圳）如图所示，点P（3a，a）是反比例函数y=（k＞0）与∥O的一个交点，图中阴影部分的面积为10π，则反比例函数的解析式为（）A．y=B．y=C．y=D．y=6．（深圳）如图，已知点A，B，C，D均在已知圆上，AD∥BC，AC平分∥BCD，∥ADC=120°，四边形ABCD A．cm2B．（π﹣）cm2C．cm2D．cm28．（宝安区二模）如图，将半径为6的∥O沿AB折叠，与AB垂直的半径OC交于点D且CD=2OD，则折痕A．B．C．6D．2 / 9A．B．C．D．210．（鄂州）已知直角梯形ABCD中，AD∥BC，AB∥BC，AD=2，BC=DC=5，点P在BC上移动，则当PA+PDA．B．C．D．3边且在AD的右侧作正方形ADEF，CF交DE于点P．若AC=，CD=2，则线段CP的长（）A．1B．2C．D．A．2B．4C．2D．43 / 9∥b＞2a；∥ax2+bx+c=0的两根分别为﹣3和1；∥a﹣2b+c＞0．你认为其中正确的有（）A．4个B．3个C．2个D．1个15．（宝安区一模）如图，已知抛物线与x轴分别交于A、B两点，顶点为M．将抛物线l116．（深圳）如图，下列图形是将正三角形按一定规律排列，则第5个图形中所有正三角形的个数有_________．17．（深圳）如图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有5个正方形；…按这样的规律下去，第6幅图中有_________个正方形．4 / 918．（深圳）如图，Rt∥ABC中，∥C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为_________．19．（深圳）如图，∥ABC的内心在y轴上，点C的坐标为（2，0），点B的坐标是（0，2），直线AC的解析式为，则tanA的值是_________．20．（深圳）刘谦的魔术表演风靡全国，小明也学起了刘谦发明了一个魔术盒，当任意实数对（a，b）进_________．22．（坪山新区模拟）如图，已知直线l：y=x，过点A（0，1）作轴的垂线交直线l于点B，过点B作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线l的垂线交y轴于点A2；…按此作法继续下去，则点A2014的坐标为_________．（提示：∥BOX=30°）23．（龙岗区模拟）如图，在平面直角坐标系中，Rt∥OAB的顶点A在x轴的正半轴上．顶点B的坐标为（6，），点C的坐标为（1，0），点P为斜边OB上的一个动点，则PA+PC的最小值为_________．5 / 924．（宝安区二模）如图，直角梯形ABCD中，AD∥BC，AB∥BC，AD=4，BC=6．将腰CD以D为旋转中心逆时针旋转90°至DE，连接AE，则∥ADE的面积是_________．25．（深圳一模）如图，一段抛物线：y=﹣x（x﹣4）（0≤x≤4），记为C1，它与x轴交于点O，A1：将C1绕点A1旋转180°得C2，交x轴于点A2；将C2绕点A2旋转180°得C3，交x轴于A3；…如此进行下去，直至得C10，若P（37，m）在第10段抛物线C10上，则m=_________．26．（宁波）正方形的A1B1P1P2顶点P1、P2在反比例函数y=（x＞0）的图象上，顶点A1、B1分别在x 轴、y轴的正半轴上，再在其右侧作正方形P2P3A2B2，顶点P3在反比例函数y=（x＞0）的图象上，顶点A2在x轴的正半轴上，则点P3的坐标为_________．27．（福田区一模）如图所示，在∥O中，点A在圆内，B、C在圆上，其中OA=7，BC=18，∥A=∥B=60°，6 / 928．（宝安区一模）四边形ABCD、AEFG都是正方形，当正方形AEFG绕点A逆时针旋转45°时，如图，连接DG、BE，并延长BE交DG于点H，且BH∥DG与H．若AB=4，AE=时，则线段BH的长是_________．29．（深圳二模）如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=．下列结论：∥∥APD∥∥AEB；∥点B到直线AE的距离为；∥EB∥ED；∥S∥APD+S∥APB=1+；∥S正方形ABCD=4+．其中正确结论的序号是_________．30．（宝安区二模）如图，梯形ABCD中，AD∥BC，BE平分∥ABC，且BE∥CD于E，P是BE上一动点．若BC=6，CE=2DE，则|PC﹣PA|的最大值是_________．7 / 98 / 933．（深圳）如图1，直线AB过点A（m，0），B（0，n），且m+n=20（其中m＞0，n＞0）．（1）m为何值时，∥OAB面积最大？最大值是多少？（2）如图2，在（1）的条件下，函数的图象与直线AB相交于C、D两点，若，求k的值．（3）在（2）的条件下，将∥OCD以每秒1个单位的速度沿x轴的正方向平移，如图3，设它与∥OAB的重叠部分面积为S，请求出S与运动时间t（秒）的函数关系式（0＜t＜10）．9 / 9。

中考数学选择填空压轴题 Modified by JEEP on December 26th, 2020.
中考数学：选择、填空压轴题
百题冲刺
编辑：XXXX（不告诉你）
花了很长时间整理的
肯定要卖贵点
嘿嘿嘿
目录：
专题一数与式
专题二方程、不等式与函数
专题三图形的性质与变换
专题四圆
专题五点的运动路径
专题六几何最值问题
专题七探究型几何问题
专题一数与式
【定义新运算】
【定义新运算：与高中知识有关】
【定义新概念】
【流程图】
【等差数列】【等差数列求和】【等比数列】【等比数列求和】
【二阶等差数列】
【循环型规律】
【递进型规律】
专题二方程、不等式与函数专题三图形的性质与变换
专题四圆
专题五点的运动路径
专题六几何最值问题
专题七探究型几何问题。

中考冲刺之填空选择压轴题精选1.(2024福田中考一模)直角三角形ABC 中，∠C=90°，BD 是AC 边上的中线，若AC=4，∠A=2∠DBA ，则AB 的长为_______解：在AB 上取点E ，使EB=ED ，连接EC ，设∠ABD=α，则∠BAD=2α，同时∠BDE=α，得∠AED=2α，故DE=DC=DA=2，故∠AEC=90°(若一个三角形一边的中线等于这边的一半，那这个三角形为直角三角形)，由射影定理有AE ·AB=AC 2，设AE=m,则有m(m+2)=16,得m=117-，故AB=117+2.(2024深中模拟)如图，矩形ABCD 的CD 边上取一点E ，将BCE 沿BE 翻折至BFE 的位置，如图，当点F 落在矩形ABCD 内部时，连接CF 并延长，交AD 于点G ，若AB=12，BC=15，DG=5，则GF 的长度为____解：设∠DCG=ɑ，易知sinɑ=135,易知∠CBE=ɑ，CH=BCsinɑ=1375，由折叠的性质知CH=FH=1375，CG=13，故GF=13-1375-1375=13193.(2024南山模拟)如图，在四边形ABCD 中，对角线AB 、CD 交于点O ，∠ACB=90°，BD=CD 且sin ∠DBC=53,若∠DAB=2∠ABC ，则ABAD 的值为________解：取AB 的中点E ，连接CE ，DE ，易知CE=BE=AE ，同时∠AEC=2∠ABC,而∠DAB=2∠ABC ，故AD||CE ；由EC=EB 知点E 在BC 的垂直平分线上，BD=CD,故DE ⟂BC ，而∠ACB=90°，故DE||AC ，故ACED 为平行四边形，故AD=CE ，故21AB AD (此题明显有条件多余)4.(2024宝安一模)如图，矩形ABCD 的长BC=15，将矩形ABCD 对折，折痕为PQ ，展开后，再将∠C 折到∠DFE 的位置，使点C 刚好落在线段AQ 的中点F 处，则折痕DE ＝．解：过点F 作MN ⊥BC ，设MF=m ，则FN=3m,DC=4m,DF=4m,由勾股定理可得m=0.5，而△DMF~△FNE ，得NE=1015，于是可得EF=5152，故DE=51045.(2024武汉3月中考模拟)如图，在△ABC 中，AB=AC ，点D 是AC 的中点，将△BCD 沿BD 折叠得到△BED ，连接AE ，若DE ⊥AB 于点F ，BC=10，则AF 的长为__________解：作AG ⊥BC 交BD 于点H,连接CE ，易知AG||BE ，由DE=DA=DC 得∠AEC=90°，而BD ⊥EC ，得AE||BH ，故AEBH 为平行四边形，得AH=BE=10，故AB=510，易知∠EAH=45°，而tan ∠BAG=31,故tan ∠EAF=21,得AF=2106.(2024南山实验)在锐角△ABC 中，AD 、BE 分别为△ABC 的中线和角平分线，AD=BE ，且AD ⊥BE ，则BC AC =______解：BE 平分∠ABC ，AD ⊥BE ，故△ABD 为等腰三角形方法一：过点F 作AF||BC 交BE 于点F ，易知∠AFB=∠ABG ，故AF=AB ，而AB=BD ，故AF ：BC=1：2，设EF=2m ，则BE=4m,而G 为AD 的中点，故EG=m ，BG=3m ，又BE=AD 得AG=DG=2m ，故AC=35m,BC=213m ，故26653BC AC =方法二：过点D 作DG||AC 交Be 于点G ，易知F 为AD 中点，故EF=FG ，而D 为BC 的中点，故GE=GB ，设EF=m ，则BF=3m ，AF=DF=2m ，DG:AC=1：3，AE=5m,AC=35m,BD=13m,BC=213m,故26653BC AC =7.如图，在等边△ABC 中，过点C 作射线CD ⊥BC ，点M 、N 分别在边AB 、BC 上，将△ABC 沿MN 折叠，使点B 落在射线CD 上的点B′处，连接AB′，已知AB=2，当AB′⊥CD 时，MN=_________解：方法一：连接BB′，作MG ⊥BC,设CN=m ，则BN=BN=4-m ，在△CB′N 中，由勾股定理得22)4(3m m -=+得m=41,得BN=47，而BB′=7，BH=27，于是NH=421，tan ∠CBB′=23,设BG=a ,则MG=23a ,GN=23a ,BN=a +23a =47,得a =107,GN=2021，故MN=21207(另法如右图，可再次利用方程求解)8.如图，在矩形ABCD 中，E 是AB 的中点，作EF ⊥DE 交BC 于点F ，对角线AC 分别交DE 、DF 于点G 、H ，当DH ⊥AC 时，则EFGH 的值为_________解：方法一：作EI ⊥DF 于点I,易知△ADE~△BEF ，得AD ：BE=AE:BF,而AE=BE 得AD:AE=BE ：BF ，故ADE=EDF ，故△DEA ≌△DEI ，得EI=EA ，设AE=1，AD=m ，则BF=m 1，CF=mm 1-，同时有△CDF~△DAD ，得AD CD CD CF =得m=5,于是EF=530，而GH=32，得930EF GH =(另法可参考下右图)9.如图所示，在Rt △BCD 中，∠BCD=90°，CB=CD ，过点D 作DH||BC ，点F 在线段DH 上，连接CF 、CH 、BF ，且BF 交CD 于点K ，3DH=2CK ，∠BKC=2∠DCH ，DK=1，则CH 的长为__________解：过点C 作CG ⊥BF 于点G ，易知△BCK ≌△CDG ，设DH=2m ，则CK=3m ，DG=3m ，同时设∠DCH=α，则∠H=90°-α，∠BKC=2α，得∠GCH=90°-α，GC=GH=5m ，得DC=4m,即有4m=3m+1,得m=1，故CH=2510.如图，矩形ABCD 中，AB=4，BC=8，点E 在BC 边上，连接EA ，EA=EC ，将线段EA 绕点A 逆时针旋转90°，点E 的对应点为F ，连接CF ，则cos ∠ACF 的值为_________解：设EA=m ，则EC=m,则BE=8-m ，由勾股定理得222)8(4m m =-+得m=5;过点F 作FG ⊥AD 于点G ，易知△ABE ≌△AGF ，故FG=3，AG=4；易知FG||CD ，DG=4，GM ：DM=3：4，故GM=712，DM=716得AM=740；同时易sin ∠CAD=55,cos ∠CAD=552,NM=AMsin ∠CAD=758,AN=AMcos ∠CAD=7516,又AC=45，得CN=7512，CM=7654，cos ∠ACF=1313311.已知二次函数)0(122≠+-=a ax ax y 经过点(-1，m )(1,n )和(3,p ),若在m 、n 、p 这三个实数中，只有一个是正数，则a 的取值范围为___________解：易知抛物线的对称轴为直线x =1,与y 轴的交点坐标为(0,1),后分两种情况进行讨论1.若a >0时，如图所示，此时m>0,n<0,p ≤0,即有3a +1>0,a -2a +1<0,9a -6a +1≤0，无解；2.若a <0时，如图所示，此时m ≤0,n>0,p ≤0,即有3a +1≤0,a -2a +1>0,9a -6a +1≤0,得31-≤a12.如图，在正方形ABCD 对角线AC 上取一点E ，使得AE=2CE ，连接BE ，将△BCE 沿BE 翻折得到△BFE ，连接DF ，若BC=4，则DF 的长为_______解：连接CF ，延长BE 交CD 于点G ，AE ：EC=2：1，得AB:CG=2:1,故G 为CG 的中点；同时由对称可知BG ⊥CF ，H 为CF 的中点，故GH||DF,得∠CFD=90°，易知sin α=55，∠DCF=α，故DF=CDsin α=55413.如图，在△ABC 中，∠B=90°，D 是BC 边上一点且满足∠C=2∠BAD ，CD=3BD ，E 是AC 边上一点且满足∠ADB=∠ADE ，连接BE 交AD 于点F ，则BFEF=______解：第一步：设∠DAB=α，则∠C=2α，取点D 关于AB 的对称点G ，连接GB 、GA ，易知∠G=90°-α，∠CAG=90°-α，故CA=CG ；第二步：设BD=m ，则CD=3m ，GB=m ，CG=5m ，于是CA=5m ，于是AB=3m ；同时∠ADB=∠ADE=90°-α，于得∠CDE=2α，EC=ED ；第三步：作EH ⊥CD 于点H ，CH=23m,cosC=54,即有EC m 2354EC CH ==得m 815EC =，在△BDE 中，DF 平分∠BDE ，由角平分线定理可得815BD DE BF EF ==14.如图，D 是等边三角形ABC 外一点，连接AD 、BD 、CD ，若BD=219，CD=23，AD=8，则△ABD 的面积为________方法一：将△ACD 绕点A 顺时针旋转60°得△ABE,连接DE ，作AF ⊥BE 于点F ，易知△ADE 为等边三角形，AE=DE=AD=8，BE=CD=23，而BD 2=BE 2+DE 2，故∠BED=90°，而∠AED=60°，故∠AEB=30°，AF=4，EF=43，S △ABD =S 四ABED -S △BDE =S △ADE +S △ABE -S △BDE =123方法二：将△BCD 绕点B 逆时针旋转60°得△BAE ，延长DC 、EA 交于点F ，连接BF ，易知AE 2+AD 2=DE 2，故∠DAE=90°，而∠FEB=∠FDB ，故E 、F 、B 、D 共圆，故∠AFD=60°，AF=338，DF=3316，CF=3310；由模型知FB+FA=FC ，故FB=332得GF=33，故AG=33，S △ABD =S △ADG =12315.四边形ABCD 中，∠ABC+∠BCD=90°，AB=CD ，AD=1，BC=5，连接BD ，∠ADB=45°，则BD=_____解：延长BA 、CD 交于点E ，过点B 、C 作AD 的垂线于F 、G ，易知△ABF ≌△CDG ，设AF=m ，则BF=DG=m+1，CG=m ，作CH ⊥BF 于点H ，易知BH=1,得m=6-1,故BD=2316.如图，在△ABC 中，∠A=60°，BC=7，点D 、E 分别在边AC 、AB 上，连接CE 、DE ，若BE=CD ，∠CED=30°，CE=5，则DE=_________17.如图，在△ABC 中，∠BAC=60°，D 是BC 边上的一点，∠ADC=30°,BD=1,BC=7,则AD=______解：引△ABC 的外接圆，圆心为O ，易知∠BOC=120°，OA=OB=OC=321,连接OA ，作AE ⊥BF 于点E ，延长AO 交AE 于点G ，易知AB||AG ，OB||AF ，故ADBG 为平行四边形，故AG=BD=1，设OE=m,则EG=3m ，由勾股定理得222321()13(=++m m 得m=63，EG=33，故AD=3321+18.如图，在矩形ABCD 中，AB<BC ，点E 、F 分别在CD 、AD 边上，且△BCE 与△BFE 关于直线BE 对称，点G 在AB 边上，GC 分别与BF 、BE 交于P 、Q 两点，若54AB =BC ，CE=CQ ，则=CQGP ______解：设AB=4，则BC=5，BF=5，则AF=3，DF=2，设CE=m ，则EF=m,DE=4-m,由勾股定理得222)4(2m m =-+得m=25，由CE=CQ 知∠CEQ=∠CQE ，而∠BEF=∠CEQ ，∠BQG=∠CQE ，故CG||EF ，BP ⊥GC ，故tan α=2,设PQ=m ，则PB=2m ，同时tan ∠GBP=43,GP=m 23,由射影定理知BP 2=PG·PC ，即有)25(234+=m m m ，m=3,故59CQ GP =19.如图，在正方形ABCD 中，O 为对角线AC 的中点，E 为正方形内一点，连接BE ，BE=BA ，连接CE 并延长，与∠ABE 的平分线交于点F ，连接OF ，若AB=2，则OF 的长度为_______解：D ，连接AF ，BF 为∠ABE 的角平分线可知∠ABF=∠EBF ，又AB=BE ，BF=BF 得△ABF ≌△EBF ；设∠ACF=α，则∠BEC=45°+α，∠BAF=∠BEF=135°-α，于是∠CAF=90°-α，故∠CAF+∠ACF=90°，而O 为AC 的中点，故OF=220.如图，在Rt △ABC 中，∠ACB=90°，过点B 作BD ⊥AB ，交∠ACB 的平分线于点D ，AB 与CD 相交于点E ，若BE=310，BD=610，则AC 的长为_______解：方法一：作BF ⊥CD 于点F ，易得DE=152，BF=62，EF=32，CE=32，作BG ⊥BC 交CD 于点G ，可得FG=6，而BG||AC ，得BG ：AC=EG:CE=1：3，得AC=4方法二：设∠ABC=α，得∠DEB=45°+α，tan(45°+α)=2,得tanα=31,即有AC:BC=1：3，由角平分线定理得AE:BE=1：3，得AE=10，故AC=421如图，已知∠B=90°，AD=CE ，∠DEA=15°，DE=2，AC=7，则AE=_________解：方法一：作等腰直角三角形AEF ，且∠AEF=90°，作FG ⊥BC 于点G,连接FC 、FE ，易得△ABE ≌△EFG ，又AD=CE ，得△ADE ≌△ECF ，故∠CFE=∠AED=15°，CF=DE=2；作CG ⊥AF 于点G,∠GFC=60°，得GF=1，AG=2，故AE=223方法二：作等腰直角三角形AEM，作MN⊥AB于点N，连接MA、MD、MC，易得△AMN≌△EAB得BE=AN，又AD=CE，得DN=BC，得△DMN≌△CAB，得DM=AC=7；作DI⊥EM，∠DEI=60°，得EI=1，MI=2，即EM=3，故AE=22322.如图，在正方形ABCD中，AB=6，点E是边AB上一点，且AB=3BE，点F是对角线BD上一点且BF=BE，过点F作∠EFG=90°，边FG交直线AD于点G，则AG的长为___________方法一：一线三角相似过点F作MN||BC，作GN⊥MF于点N，易知△EFM~△FGN，MF=2，ME=2-2，而GN=6-2，得FN=72-8，故AG=82-8方法二：对角互补相似过点F作FH、FI分别垂直于AB、AD，易知△EFH~△GFI，EH=2-2，FI=6-2，HF=2，故GI=72-8，故AG=82-8方法三：利用特殊角的三角函数值易知△DFG=22.5°，tan22.5°=2-1,设GM=m，则DM=m，FM=(2-1)m，可得2m=14-82,故AG=82-823.如图，在△ABC中，∠C=90°，点D、E在BC上，连接AD、AE，AD=BD，∠CAE=∠B，AD=13，AE=413，则BC=______解：方法一：取AB 的中点F ，连接CF ，AD=BD 得∠DFA=90°，∠BAD=∠B ，而∠B=∠CAE 得∠CAE=∠DAF ，故△ACE~△AFD ，得AC:AF=4：13，设AC=4m ，则AF=13m,故AC=213m ，由此可得BC=6m ，得CD=6m-13,由勾股定理得22213)136()4(=-+m m 得m=6，故BC=18方法二：在BC 的延长线上取点F 使CF=CE ，设∠B=α，则∠ADF=2α，∠F=∠FAD=90°-α，故DF=AD=13，设CD=t,则CF=13-t ，AF=AE=413，由勾股定理可得222213)13()134(t t -=--得t=5，故BC=1824.点A 在反比例函数xk y =上，OA=2，OA 的垂直平分线与双曲线相切，则k =_______解：如图，作AD ⊥x 轴，BF ⊥y 轴，设A(a,b ),易知△OEM~△OAD ，得OE·OD=OM·OA=2，OE=a 2；同时由双曲线切线的性质可知B 为CE 的中点；△COE~△ODA 得OD·OE=OC·AD=2，得OC=b 2，故可得B(a 1,b 1)，于是ab b a =⋅11,得ab =1,故k =1(下证双曲线切线的性质)如下图，设MN ：y=mx+b,反比例函数x k y =，联立得02=-+k bx mx ，相切时，0=∆即有m b x x m b k mk b 24,042122-==-==+，，由此可得B(2,2b m b -)同时M(0,b),N(0,m b -)，故B 为MN 的中点.25.如图，在△ABC 中，∠BAC=45°，D 是BC 上一点，21BD CD =，过点D 作DE ⊥AB 交AB 于点E ，若BE=2，∠BAD=2∠BDE ，则_____BE AC =26.如图，A 、B 在反比例函数xk y =图像上，OA=AB=2，OB=6，则k =_____解：取AB 的中点C ，由中线长公式可得2(OC 2+CB 2)=OA 2+OB 2,代入数据得2(OC 2+1)=4+6,得OC=2；由AD=BE()可知C 为BD 的中点，故CD=CE=OC=2，故AD=BE=1，作OH ⊥AB 于点H ，得AH=CH=21得OH=215，于是OD=6，OE=10，此处还有△AOD ≌△ACB ，作AM ⊥OD 于点D ，AM||OE ，得AM=410，OM=463，于是k =815327.在四边形ABCD 中，AB=AD ，∠BAD=60°，∠DAC=150°，过点D 作DH ⊥BC ，垂足为H ，若DH=2，则AC 的最小值为____________方法一：取BC 的中点E ，同时作等边△BEF ，连接AF 、BD 、DE 、FC ，易知△ABF ≌△DBE ，而∠BDC=90°，DE=EB=EC=AF=m,则明显2≥m ,而FG=r 23，GC=r 23，FC=r 3，而AC>AF+FC,当A 、F 、C 共线时取最值，最值为232+方法二：作等边三角形△BCE ，同时取BC 的中点F ，易知△ABC ≌△DBE ，AC=DE>DF+EF,当D 、F 、E 共线时，取最小值，最小值为232+28.如图，已知矩形ABCD 中，点E 、F 、P 分别在线段AD 、BC 、DC 上，BP 交EF 于点M ，∠EMP=45°，AD=12，AB=6，BF=ED=4.5,则PC=________解：方法一：相似作BI||EF，同时在DC的延长线上取点H使CH=CB=12，DG=CD=6，易知△ABI~△CBG，故∠ABI=∠CBG，故∠PBG=45°，而∠H=45°，故△PBG~△PHB，故PB2=PG·PH,即有(m+6)(12+m),又PB2=144+m2,即有(m+6)(12+m)=144+m2，得m=4,故PC=4方法二：半角模型补全正方形AMND，同时作MI||EF，BH||EF，MO||BP，易知∠OMI=45°，由半角模型的结论可知AI+ON=OI，设ON=m，则OI=6+m，DO=12-m，在ODI中，由勾股定理可得62+(12-m)2=(6+m)2得m=4，故PC=4方法三：12345原理作BM||EF得AM=3，tan∠ABM=1/2,∠ABM+∠CBP=45°，故tan∠CBP=1/3，故PC=429.如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作DF⊥AB于点F，交AC于点E，已知AE=4，EC=6，则BF OE 的值为________AC=AE+EC=10,得OA=OC=5，OE=1，OC=5，由射影定理得OD 2=OE·OC ，OD=5，得CD=30，由△DBF~△ABO 得BF=330，于是1030BF OE 30.(2023-2024深圳中考适应性考试第15题)如图，在四边形ABCD 中，AB=BC=6，∠ABC=60°，∠ADC=90°，对角线AC 与BD 相交于点E ，若BE=3DE ，则BD=____36____方法一：作BF ⊥AC 、DG ⊥AC ，BF||DG ，易知BF=33，得DG=3，由射影定理得DG 2=AG ·CG ，设AG=x ，则CG=6-x ,得x (6-x )=3,得x =3+6,于是FG=6，可得BE=643得BD=36；或者作BG ⊥DG 于点H ，BH=6，DH=43，得BD=36方法二：作BF ⊥AC ，DG ⊥BF 于点G ，易知F 为AC 的中点，故DF=3，同时FG=3，于是BD=36。

中考专题复习之多命题类选择填空压轴题备考练习试卷简介:全卷共12道题，8道选择题，4道填空题，每题10分，共120分。

本专题精选08到10的多命题判断类选择题，填空压轴题，分为数据图表分析类，几何题类，二次函数类三种，做针对性练习，帮助您冲刺中考，做好填空选择压轴题。

学习建议:中考中填空选择各有一道难度较高的题目，近几年多命题判断类题目频繁出现在填空选择压轴题中，本专题精选此类题目，分为三个小类别，专项突破。

这类题目也有一些解题技巧，本专题立足于解决问题，冲刺满分，做了深入的解析，同学们可以在应用技巧解题的同时关注下问题的解决过程。

一、单选题(共8道，每道10分)1.随着经济的发展，人们的生活水平不断提高．上图分别是某景点2007—2009年游客总人数和旅游收入年增长率统计图．已知该景点2008年旅游收入4500万元．下列说法：①三年中该景点2009年旅游收入最高；②与2007年相比，该景点2009年的旅游收入增加[4500×(1+29%)－4500×(1－33%)]万元；③若按2009年游客人数的年增长率计算，2010年该景点游客总人数将达到(280+280*)万人次。

其中正确的个数是（）A.0B.1C.2D.3答案：C解题思路：从年增长率图中我们可以看出，2007-2009年三年的年增长率都是正的，所以2009年的旅游收入是三年中最高的，①正确；由年增长率图我们可以得到2007年的旅游收入为万元，2009年的旅游收入为[4500×(1+29%)]万元，所以与2007年相比，该景点2009年的旅游收入增加[4500×(1+29%)－]万元，②错误；由旅游人数增长图来看，2009年旅游人数相对2008年增长了*100%，所以2010年旅游人数为(280+280*)万人次，③正确。

综上所述，答案选C。

易错点：对年增长率的理解出错，增长率下降并不表示今年的游客总人数比去年低，而是今年的增长幅度比去年小了，增长率>0，则今年的游客总人数>去年的游客总人数。

中考冲刺之选择填空压轴题（探索规律类）一、单选题(共10道，每道10分)1.意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，根据这组数的规律第10个数是（）A.57B.55C.89D.1442.刘老师设计了一个计算程序，输入和输出的数据如下表，那么，当输入数据是7时，输出的数据是（）A.B.C.D.3.观察下列单项式：，，，…，，，…，从中我们可以猜想出第2012个单项式是（）A.B.C.D.4.观察下列等式：①1＝12；②2＋3＋4＝32；③3＋4＋5＋6＋7＝52；④4＋5＋6＋7＋8＋9＋10＝72；…请你根据观察得到的规律判断下列各式正确的是（）A.1005＋1006＋1007＋…＋3016＝20112B.1005＋1006＋1007＋…＋3017＝20112C.1006＋1007＋1008＋…＋3016＝20112D.1007＋1008＋1009＋…＋3017＝201125.填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是（）A.152B.168C.144D.1586.将1、、、按如下方式排列．若规定（m，n）表示第m排从左向右第n个数，则（5，4）与（15，7）表示的两数之积是()．A.B.C.D.7.在下表中，我们把第i行第j列的数记为（其中i，j都是不大于5的正整数），对于表中的每个数，规定如下：当时，＝1；当时，＝0.例如：当，时，＝＝1.按此规定，计算：的值为（）A.1B.0C.2D.38.如图下面是按照一定规律画出的一行“树形图”，经观察可以发现：图比图多出了2个“树枝”，图比图多出了4个“树枝”，图比图多出了8个“树枝”，…，照此规律，则图比图多出“树枝”()A.28个B.56个C.60个D.124个9.如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……，如此进行下去，得到四边形AnBnCnDn.下列结论正确的有（）①四边形A2B2C2D2是矩形；②四边形A4B4C4D4是菱形；③四边形A5B5C5D5的周长是；④四边形AnBnCnDn 的面积是A.①②B.②③C.②③④D.①②③④10.2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形，中间的阴影部分是一个小正方形的“赵爽弦图”．若这四个全等的直角三角形有一个角为30°，顶点、、、…、和、、、…、分别在直线y=-和轴上，则第个阴影正方形的面积为()A.B.C.D.。

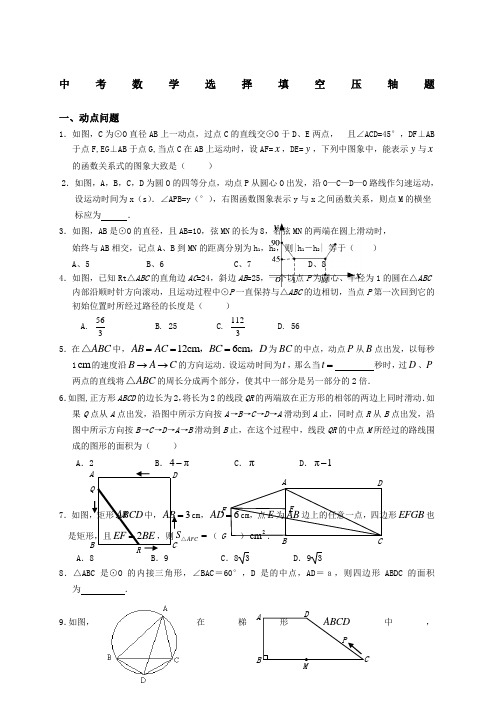
中考数学选择填空压轴题一、动点问题1．如图，C 为⊙O 直径AB 上一动点，过点C 的直线交⊙O 于D 、E 两点， 且∠ACD=45°，DF ⊥AB 于点F,EG ⊥AB 于点G,当点C 在AB 上运动时，设AF=x ，DE=y ，下列中图象中，能表示y 与x 的函数关系式的图象大致是（ ）2．如图，A ，B ，C ，D 为圆O 的四等分点，动点P 从圆心O 出发，沿O —C —D —O 路线作匀速运动，设运动时间为x （s ）．∠APB=y（°），右图函数图象表示y 与x 之间函数关系，则点M 的横坐标应为 ．3．如图，AB 是⊙O 的直径，且AB=10，弦MN 的长为8，若弦MN 的两端在圆上滑动时， 始终与AB 相交，记点A 、B 到MN 的距离分别为h 1，h 2，则|h 1－h 2| 等于（ ） A 、5 B 、6 C 、7 D 、84．如图，已知Rt △ABC 的直角边AC =24，斜边AB =25，一个以点P 为圆心、半径为1的圆在△ABC 内部沿顺时针方向滚动，且运动过程中⊙P 一直保持与△ABC 的边相切，当点P 第一次回到它的初始位置时所经过路径的长度是（ ） A.563 B. 25 C. 1123D. 565．在ABC △中，12cm 6cm AB AC BC D ===，，为BC 的中点，动点P 从B 点出发，以每秒1cm 的速度沿B A C →→的方向运动．设运动时间为t ，那么当t = 秒时，过D 、P 两点的直线将ABC △的周长分成两个部分，使其中一部分是另一部分的2倍．6．如图,正方形ABCD 的边长为2，将长为2的线段QR 的两端放在正方形的相邻的两边上同时滑动．如果Q 点从A 点出发，沿图中所示方向按A→B→C→D→A 滑动到A 止，同时点R 从B 点出发，沿图中所示方向按B→C→D→A→B 滑动到B 止，在这个过程中，线段QR 的中点M 所经过的路线围成的图形的面积为（ ）A ．2B ．4π-C ．πD ．π1-7．如图，矩形ABCD 中，3AB cm ，6AD =cm ，点E 为AB 边上的任意一点，四边形EFGB 也是矩形，且2EF BE =，则AFC S =△（ ）2cm ． A ．8 B ．9 C ．8 3 D ．9 38．△ABC 是⊙O 的内接三角形，∠BAC＝60°，D 是的中点，AD ＝ａ，则四边形ABDC 的面积为 ．在梯形ABCD中，9．如图，A B CQRM DADCE F G B AB D BP BBBB B90614AD BC ABC AD AB BC ∠====∥，°，，，点M 是线段BC 上一定点，且MC =8．动点P 从C 点出发沿C D A B →→→的路线运动，运动到点B 停止．在点P 的运动过程中，使PMC △为等腰三角形的点P 有 个10．如图在边长为2的正方形ABCD 中，E ，F ，O 分别是AB ，CD ，AD 的中点，以O 为圆心，以OE 为半径画弧是上的一个动点，连结OP ，并延长OP 交线段BC 于点K ，过点P 作⊙O 的切线，分别交射线AB 于点M ，交直线BC 于点G . 若3=BMBG，则BK ﹦ . 二、面积与长度问题1．如图，△ABC 是直角边长为a 的等腰直角三角形，直角边AB 是半圆O 1的直径，半圆O 2过C 点且与半圆O 1相切，则图中阴影部分的面积是（ ）A ．2367a π- B ．2365a π- C ．2367a D ．2365a2．如图，在x 轴上有五个点，它们的横坐标依次为l ，2，3，4，5．分别过这些点作x 轴的垂线与三条直线y=ax ，y=(a+1)x ，y=(a+2)x 相交，其中a>0．则图中阴影部分的面积是( ) A ．12．5 B ．25 C ．12．5a D ．25a 3．如图，在反比例函数2y x=（0x >）的图象上，有点1234P P P P ，，，，它们的横坐标依次为1，2，3，4．分别过这些点作x 轴与y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为123S S S ，，，则123S S S ++= ．4．已知, A 、B 、C 、D 、E 是反比例函数16y x=（x>0）图象上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图5所示的五个橄榄形（阴影部分），则这五个橄榄形的面积总和是 （用含π的代数式表示）5．如图，在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====，xyOP 1P 2P 3P 41 234AODBFKE GM C KyxO P 1P 2P 3 P4P 5A 1 A 2 A 3 A 4 A 5ADEPBC ABCDN M过点A 1、A 2、A 3、A 4、A 5分别作x 轴的垂线与反比例函数()20y x x =≠的图象相交于点P 1、P 2、P 3、P 4、P 5，得直角三角形(阴影部分)并设 其面积分别为12345S S S S S 、、、、，则5S 的值为 ．6．如图，把一个棱长为3的正方体的每个面等分成9个小正方形，然后沿每个面正中心的一个正方形向里挖空（相当于挖去了7个小正方体），所得到的几何体的表面积是（ ） A ．78B ．72C ．54D ．487．如图，平行于y 轴的直线l 被抛物线y ＝2112x +、y ＝2112x -所截．当直线l 向右平移3个单位时，直线l 被两条抛物线所截得的线段扫过的图形面积为平方单位．8．如图，在Rt ABC △中，9042C AC BC ===∠°，，，分别以AC 、BC 为直径画半圆，则图中阴影部分的面积为 ．（结果保留π）9．如图，Rt ABC △中，90ACB ∠=o，30CAB ∠=o，2BC =，O H ，分别为边AB AC ， 的中点，将ABC △绕点B 顺时针旋转120o 到11A BC △的位置，则整个旋转过程中线段OH 所扫过部分的面积（即阴影部分面积）为（ ） A ．77π338- B ．47π338+ C ．π D ．4π33+ 10．如图，正方形ABCD 的面积为12，ABE △是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD PE +的和最小，则这个最小值为（ ） A ．23 B ．26C ．3D ．6图，在锐角ABC △中，11．如4245AB BAC =∠=，°，BAC ∠的平分线交于点D M N ，、分别是AD和AB 上的动点，则BCBM MN +的最小值是___________ ．12．如图，在矩形ABCD 中，AB =3，AD =4，点P 在AD 上，PE ⊥AC 于E ，PF ⊥BD 于F ，则PE +PF 等于（ ） Ａ．75 Ｂ．125 Ｃ．135 Ｄ．145中，E 是BC 边上一点，形ABCD 13．正方以E 为为半径的半圆与以A 为圆圆心、ECAH BO C ADBC E FPA D FCＢＯＥEFD CBA心，AB 为半径的圆弧外切，则sin EAB ∠的值为（ ）A ．43B ．34C ．45D ．3514．在Rt △ABC 内有边长分别为,,a b c 的三个正方形，则,,a b c 满足关系式 ． 15．一张等腰三角形纸片，底边长l5cm ，底边上的高长22．5cm ．现沿底边依次从下往上裁剪宽度均为3cm 的矩形纸条，如图所示．已知剪得的纸条中有一张是正方形，则这张正方形纸条是( ) A ．第4张 B ．第5张 C.第6张 D ．第7张16．如图，等腰△ABC 中，底边a BC =，︒=∠36A ，ABC ∠的平分线交AC 于D ，BCD ∠的平分线交BD 于E ，设215-=k ，则=DE （ ） A ．a k 2B ．a k 3C ．2k aD ．3ka17．如图，直径分别为CD 、CE 的两个半圆相切于点C ，大半圆M 的弦AB 与小半圆N 相切于点F ，且AB ∥CD ，AB=4，设弧CD 、弧CE 的长分别为x 、y ，线段ED 的长为z ，则z （x+y ）= .三、多结论问题1．如图，在Rt△ABC 中，AB AC =，D 、E 是斜边BC 上两点，且∠DAE =45°，将△ADC 绕点A 顺时针旋转90︒后，得到△AFB ，连接EF ，下列结论：①△AED ≌△AEF ； ②△ABE ∽△ACD ； ③BE DC DE +=； ④222BE DC DE +=其中一定正确的是（ ） A ．②④ B ．①③ C ．②③ D ．①④2．如图，在等腰Rt△ABC 中，∠C =90o ，AC =8，F 是AB 边上的中点，点D 、E 分别在AC 、BC 边上运动，且保持AD =CE ，连接DE 、DF 、EF 。

中考选择填空压轴题专题：函数1．如图所示，A1（1，3），A2（32，32），A3（2，3），A4（3，0）．作折线A1A2A3A4关于点A4的中心对称图形，再做出新的折线关于与x轴的下一个交点的中心对称图形……以此类推，得到一个大的折线．现有一动点P从原点O出发，沿着折线一每秒1个单位的速度移动，设运动时间为t．当t＝2020时，点P的坐标为（）A．（1010，3）B．（2020，3）C．（2016，0）D．（1010，3）1【答案】A【解析】由题意OA1＝A3A4＝A4A5＝A7A8＝2，A1A2＝A2A3＝A5A6＝A6A7＝1，∴点P从O运动到A8的路程＝2+1+1+2+2+1+1+2＝12，∴t＝12，把点P从O运动到A8作为一个循环，∵2020÷12＝168余数为4，∴把点A3向右平移168×3个单位，可得t＝2020时，点P的坐标，∵A3（2，3），168×6＝1008，1008+2＝1010，∴t＝2020时，点P的坐标（1010，3），故选：A．2．甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙出发沿同一路线行走．设甲乙两人相距（米），甲行走的时间为（分），关于的函数函数图像的一部分如图所示，下列说法：①甲行走的速度是30米/分；②乙出发12．5分钟后追上甲；③甲比乙晚到图书馆20分钟；④甲行走30．5分钟或38分钟时甲、乙两人相距360米；其中正确的个数是（）A．1个B．2个C．3个D．4个【答案】B【解析】①甲行走的速度：150÷5=30（米/分）；故正确；②由图象知，第12.5分钟时乙追上甲，甲出发5分钟后，乙出发沿同一路线行走，所以乙出发7.5分钟后追上甲，故不正确；③由图象知，第12.5分钟时乙追上甲，所以乙出发7.5分钟后追上甲，此时甲走了375米，故乙的速度为375÷7.5=50米/分，当t=35时，甲行走的路程为：30×35=1050（米），乙行走的路程为：（35-5）×50=1500（米），∴当t=35时，乙已经到达图书馆，甲距图书馆的路程还有（1500-1050）=450米，∴甲到达图书馆还需时间；450÷30=15（分），所以甲比乙晚到图书馆20分钟不正确；④当乙追上甲时点的坐标为（12.5，0），当12.5≤t≤35时，设解析式为：s=kt+b，把（35，450），（12.5，0）代入可得：12.5k+b＝0，35k+b＝450，解得：k＝20，b＝-250，∴s=20t-250，当35＜t≤50时，由于甲比乙晚到图书馆15分钟，所以函数图象过点（50，0），补全函数图象如图，设解析式为s=k1x+b1，把（50，0），（35，450）代入得：50k1+b1＝0，35k1+b1＝450，解得：k1＝-30，b1＝1500，∴s=-30t+1500，∵甲、乙两人相距360米，即s=360，解得：t=30.5，t1=38，∴当甲行走30.5分钟或38分钟时，甲、乙两人相距360米．故正确，故选B.专题：一次函数1如图，直线y＝12x﹣2与x轴交于点A，以OA为斜边在x轴上方作等腰直角三角形OAB，将△OAB沿x轴向右平移，当点B落在直线y＝12x﹣2上时，则△OAB平移的距离是_____．【答案】6【解析】y＝12x﹣2，当y＝0时，12x﹣2＝0，解得：x＝4，即OA＝4，过B作BC⊥OA于C，∵△OAB是以OA为斜边的等腰直角三角形，∴BC＝OC＝AC＝2，即B点的坐标是（2，2），设平移的距离为a，则B点的对称点B′的坐标为（a+2，2），代入y＝12x﹣2得：2＝12（a+2）﹣2，解得：a＝6，即△OAB平移的距离是6，故答案为6．2如图，已知直线MN：y＝kx+2交x轴负半轴于点A，交y轴于点B，∠BAO＝30°，点C 是x轴上的一点，且OC＝2，则∠MBC的度数为（）A．75°B．165°C．75°或45°D．75°或165°【答案】D【解析】由一次函数y=kx+2可得，OB=2由已知可得：∠MBC=120°．如图，分两种情况考虑①当点C在x轴正半轴上时，∠C1BO=45°，∠MBC1=120°﹣45°=75°；②当点C在x轴负半轴上时，∠MBC2=120°+45°=165°．故选D．3如图，AB⊥y轴，垂足为B，∠BAO＝30°，将△ABO绕点A逆时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y x上，再将△AB1O1绕点B1逆时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y＝－x上，依次进行下去…若3点B的坐标是（0，1），则点O2020的纵坐标为___________．【答案】【分析】观察图象可知，O2、O4、O6、...O2020在直线y＝－x上，OO2＝ABO3的周长=（+2），OO4=2（+2），OO6=3（+2），依次类推OO2020=1010（+2），再根据点O2020的纵坐标是OO2020的一半，由此即可解决问题．【解析】观察图象可知，O2、O4、O6、...O2020在直线y上，∵∠BAO＝30°，AB⊥y轴，点B的坐标是（0，1），∴OO 2＝ABO 的周长=（+2），∴OO 4=2（+2），OO 6=3（ +2），依次类推OO 2020=1010（+2），∵直线y 与x 轴负半轴的交角为30°∴点O 2020的纵坐标=12O O 2020=故答案为： 专题；反比例函数1如图，点A 在双曲线y ＝kx的第一象限的那一支上，AB 垂直于x 轴与点B ，点C 在x 轴正半轴上，且OC ＝2AB ，点E 在线段AC 上，且AE ＝3EC ，点D 为OB 的中点，若△ADE 的面积为3，则k 的值为_____．【答案】163. 【解析】如图，连接DC ，∵AE=3EC ，△ADE 的面积为3，∴△CDE 的面积为1.∴△ADC 的面积为4.∵点A 在双曲线y ＝kx 的第一象限的那一支上， ∴设A 点坐标为 (x,kx).∵OC ＝2AB ，∴OC=2x.∵点D 为OB 的中点，∴△ADC 的面积为梯形BOCA面积的一半，∴梯形BOCA的面积为8.∴梯形BOCA的面积=11(2)3822k kx x xx x+⋅=⋅⋅=，解得16k3=.2如图，菱形OABC的一边OA在x轴的负半轴上，O是坐标原点，tan∠AOC=43，反比例函数y=﹣12x的图象经过点C，与AB交与点D，则△COD的面积的值等于_____；【答案】10．【解析】作DE∥AO，CF⊥AO，设CF=4x，∵四边形OABC为菱形，∴AB∥CO，AO∥BC．∵DE∥AO，∴S△ADO=S△DEO，同理S△BCD=S△CDE．∵S菱形ABCO=S△ADO+S△DEO+S△BCD+S△CDE，∴S菱形ABCO=2（S△DEO+S△CDE）=2S△CDO．∵tan∠AOC=43，∴OF=3x，∴OC=5x，∴OA=OC=5x．∵S菱形ABCO=AO•CF=20x2．∵C（﹣3x，4x），∴12×3x×4x=6，∴x2=1，∴S菱形ABCO=20，∴△COD的面积=10．故答案为10．3如图，平面直角坐标系中，A（﹣8，0），B（﹣8，4），C（0，4），反比例函数y＝的图象分别与线段AB，BC交于点D，E，连接DE．若点B关于DE的对称点恰好在OA 上，则k=___1解：过点E作EG⊥OA，垂足为G，设点B关于DE的对称点为F，连接DF、EF、BF，如图所示：则△BDE≌△FDE，∴BD＝FD，BE＝FE，∠DFE＝∠DBE＝90°易证△ADF∽△GFE∴，∵A（﹣8，0），B（﹣8，4），C（0，4），∴AB＝OC＝EG＝4，OA＝BC＝8，∵D、E在反比例函数y＝的图象上，∴E（，4）、D（﹣8，）∴OG＝EC＝，AD＝﹣，∴BD＝4+，BE＝8+∴，∴AF＝，在Rt△ADF中，由勾股定理：AD2+AF2＝DF2即：（﹣）2+22＝（4+）2解得：k＝﹣124如图，点A、B为直线y=x上的两点，过A、B两点分别作y轴的平行线交双曲线y=1x（x＞0）于C、D两点. 若BD=2AC，则4OC2-OD2的值为________.解：设A （a ，a ），B （b ，b ），则C （a ，1a ），D （b ，1b ）AC =a -1a ，BD =b -1b， ∵BD =2AC ，∴b -1b =2（a -1a ）4OC 2-OD 2=4（a 2+21a ）-（b 2+21b） =4[(a -1a )2+2]-[(b -1b )2+2]=4(a -1a )2+8-4(a -1a)2-2=6．故答案为：6． 5如图，O 为原点，A （4，0），E （0，3），四边形OABC ，四边形OCDE 都为平行四边形，OC =5，函数y =kx（x ＞0）的图象经过AB 的中点F 和DE 的中点G ，则k 的值为________．解：∵A （4，0），E （0，3），∴OE =3，OA =4，由□OABC 和□OCDE 得：OE ∥DC ，BC ∥OA 且DC =OE =3，BC =OA =4， 设C （a ，b ），则D （a ，b +3）、B （4+a ，b ），∵AB 的中点F 和DE 的中点G ， ∴G （2a ，62b +），F （82a +，2b ） ，∵函数y =kx（x ＞0）的图象经过点G 和F ， 则2a ×62b +=82a +×2b ，3a =4b ，a =43b ，∵OC =5，C （a ，b ）， ∴a 2+b 2=52，243b ⎛⎫ ⎪⎝⎭+b 2=52，b =±3，∵b ＞0，∴b =3，a =4，∴F （6，32）， ∴k =6×32=9.故答案为：9．专题：二次函数1廊桥是我国古老的文化遗产如图，是某座抛物线型的廊桥示意图，已知抛物线的函数表达式为，为保护廊桥的安全，在该抛物线上距水面AB 高为8米的点E ，F 处要安装两盏警示灯，则这两盏灯的水平距离EF 是___________米精确到1米【答案】 【解析】由于两盏E 、F 距离水面都是8m ，因而两盏景观灯之间的水平距离就是直线y=8与抛物线两交点的横坐标差的绝对值．故有，即，，所以两盏警示灯之间的水平距离为：2二次函数2y ax bx c =++（,,a b c 是常数，0a ≠）的自变量x 与函数值y 的部分对应值如下表：且当12x =-时，与其对应的函数值0y >．有下列结论：①0abc >；②2-和3是关于x 的方程2ax bx c t ++=的两个根；③0m <203n +<．其中，正确结论的个数是 A ．0B ．1C ．2D ．3【答案】C 【解析】∵由表格可知当x =0和x =1时的函数值相等都为-2，∴抛物线的对称轴是：x =-2b a =12， ∴a 、b 异号，且b =-a ，∵当x =0时y =c =-2，∴c 0<，∴abc >0，故①正确； ∵根据抛物线的对称性可得当x =-2和x =3时的函数值相等都为t ，∴2-和3是关于x 的方程2ax bx c t ++=的两个根；故②正确；∵b =-a ，c =-2，∴二次函数解析式：22y ax ax =--，∵当12x =-时，与其对应的函数值0y >．∴3204a ->，∴a 83>，∵当x =-1和x =2时的函数值分别为m 和n ，∴m =n =2a -2，∴m +n =4a -4203>，故③错误，故选C ．3．已知：二次函数y =ax 2+bx +c （a ≠0）的图象如图所示，下列结论中：①abc ＞0；②2a +b＜0；③a +b ＜m （am +b ）（m ≠1的实数）；④（a +c ）2＜b 2；⑤a ＞1，其中正确的项是（ ） A ．①⑤B ．①②⑤C ．②⑤D ．①③④【解析】①∵抛物线的开口向上，∴a ＞0，∵与y 轴的交点为在y 轴的负半轴上，∴c ＜0，∵对称轴为x=-2ba ＞0，∴a 、b 异号，即b ＜0，又∵c ＜0，∴abc ＞0，故本选项正确； ②∵对称轴为x=-2b a ＞0，a ＞0，-2b a＜1，∴-b ＜2a ，∴2a+b ＞0；故本选项错误； ③当x=1时，y 1=a+b+c ；当x=m 时，y 2=m （am+b ）+c ，当m ＞1，y 2＞y 1；当m ＜1，y 2＜y 1，所以不能确定；故本选项错误； ④当x=1时，a+b+c=0；当x=-1时，a-b+c ＞0；∴（a+b+c ）（a-b+c ）=0，即（a+c ）2-b 2=0，∴（a+c ）2=b 2，故本选项错误； ⑤当x=-1时，a-b+c=2；当x=1时，a+b+c=0，∴a+c=1，∴a=1+（-c ）＞1，即a ＞1；故本选项正确；综上所述，正确的是①⑤．故选A ．4如图，y ＝ax2+bx+c 的图象经过点（﹣1，0），（m ，0）；有如下判断：①abc ＜0；②b ＞3c ；③1m ＝1﹣bc；④|am+a| ）A ．1个B ．2个C ．3个D ．4个【解析】抛物线开口向下．则a ＜0，对称轴在y 轴右侧，a 、b 异号，有b ＞0，与y 轴交于正半轴，则c ＞0，因此abc ＜0，故①正确；y ＝ax 2+bx+c 的图象经过点（﹣1，0），则a ﹣b+c ＝0，即：b ＝a+c ，又a ＜0，c ＞0，所以b ＜c ，因此b ＞3c 不正确，即②不正确；x 1＝﹣1，x 2＝m 是方程，ax 2+bx+c ＝0的两个根，则有x 1•x 2＝﹣m ＝c a ，所以a c ＝﹣1m， 又∵a ﹣b+c ＝0，c ＞0，∴a c ﹣b c +1＝0，即：1﹣b c ＝﹣a c ＝1m ，因此③正确； ∵x 1＝﹣1，x 2＝m 是方程，ax 2+bx+c ＝0的两个根，∴x 11，x 2m ，∴x 1﹣x 2＝2b a -+﹣2b a-＝﹣1﹣m ，a ﹣am |am+a|，因此④正确；综上所述，正确的结论有3个，故选：C ．5函数y=x 2+bx+c 与y=x 的图象如图所示，有以下结论：①b 2﹣4c ＞0；②b+c+1=0；③3b+c+6=0；④当1＜x ＜3时，x 2+（b ﹣1）x+c ＜0． 其中正确的个数为A ．1B ．2C ．3D ．4【答案】B 【解析】∵函数y=x 2+bx+c 与x 轴无交点，∴b 2﹣4c ＜0；故①错误。

冲刺专题6：第12和18题专题训练一、工具法例1.如图，将正方形ABCD折叠，使顶点A与CD边上的一点H重合（H不与端点C，D重合），折痕交AD 于点E，交BC于点F，边AB折叠后与边BC交于点G．设正方形ABCD的周长为m，△CHG的周长为n，则的值为（）A．B． C．D．随H点位置的变化而变化例1 变式1变式1：点P是正方形ABCD边AB上一点（不与A、B重合），连接PD并将线段PD绕点P顺时针旋转90°，得线段PE，连接BE，则∠CBE等于（）A．75° B．60° C．45° D．30°二、极值法例2.若对于任意非零实数a，抛物线y＝a（x+2）（x﹣1）总不经过点P（x0﹣3，x0﹣5），则符合条件的点P（）A．有1个B．有2个C．有3个D．有无穷多个变式2：在平面直角坐标系xOy中，已知点M，N的坐标分别为（﹣1，2），（2，1），若抛物线y＝ax2﹣x+2（a＜0）与线段MN有一个交点，则a的取值范围是（）A．a≤﹣1 B．﹣1＜a＜0 C．a＜﹣1 D．﹣1≤a＜0三、特殊值法例3.若实数a，b满足ab＝1，设M＝，N＝，则M，N的大小关系是（）A．M＞N B．M＝N C．M＜N D．不确定变式3：无论m为何值，二次函数y＝x2+（2﹣m）x+m的图象总经过定点．四、特殊位置法：特殊点，特殊线，特殊角，特殊模型例4.如图，已知点A（12，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD＝AD＝8时，这两个二次函数的最大值之和等于（）变式4：（1）如图，在菱形ABCD和菱形BEFG中，点A、B、E在同一直线上，P是线段DF的中点，连接PG，PC．若∠ABC＝∠BEF＝60°，则＝（）A． B． C． D．（2）如图，E是边长为4的正方形ABCD的对角线BD上一点，且BE＝BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BR于点R，则PQ+PR的值是（）A．2B．2 C．2D．五、排除法例5.如图，△ABC中，∠ACB＝90°，AB＝10，tanA＝．点P是斜边AB上一个动点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP＝x，△APQ的面积为y，则y与x之间的函数图象大致为（）A．B．C．D．例5 变式5变式5：如图，直线y＝kx+b（k≠0）与抛物线y＝ax2（a≠0）交于A，B两点，且点A的横坐标是﹣2，点B的横坐标是3，则以下结论：①抛物线y＝ax2（a≠0）的图象的顶点一定是原点；②x＞0时，直线y＝kx+b（k≠0）与抛物线y＝ax2（a≠0）的函数值都随着x的增大而增大；③AB的长度可以等于5；④△OAB有可能成为等边三角形；⑤当﹣3＜x＜2时，ax2+kx＜b，其中正确的结论是（）A．①②④B．①②⑤C．②③④D．③④⑤六、转化法例6.如图，△ABC中，AB＝AC＝10，tanA＝2，BE⊥AC于点E，D是线段BE上的一个动点，则CD+BD 的最小值是．（1）如图，在△ABC中，∠BAC＝60°，∠ACB＝75°，AB＝2，D是线段BC上的一个动点，以AD为直径画⊙O分别交AB、AC于点E、F，连接EF，则线段EF长度的最小值为．（2）如图，在Rt△ABC中，∠ACB＝90°，将△ABC绕顶点C逆时针旋转得到△A′B′C，M是BC的中点，P是A′B′的中点，连接PM，若BC＝2，∠BAC＝30°，则线段PM的最小值是．例6变式6（1）变式6（2）七、综合分析法例7.已知抛物线y＝ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：①该抛物线的对称轴在y轴左侧；②关于x的方程ax2+bx+c+2＝0无实数根；③a﹣b+c≥0；④的最小值为3．其中，正确结论的个数为（）A．1个B．2个C．3个D．4个变式7：如图，正方形ABCD的边长为4，点E、F分别从点A、点D以相同速度同时出发，点E从点A向点D运动，点F从点D向点C运动，点E运动到D点时，E、F停止运动．连接BE、AF相交于点G，连接CG．有下列结论：①AF⊥BE；②点G随着点E、F的运动而运动，且点G的运动路径的长度为π；③线段DG的最小值为2﹣2；④当线段DG最小时，△BCG的面积S＝8+．其中正确的命题有．（填序号）八、特征分析法例8．如图，在平面直角坐标系中，OA＝AB，∠OAB＝90°，反比例函数y＝（x＞0）的图象经过A，B 两点．若点A的坐标为（n，1），则k的值为（）A．B．C．D．变式8：如图，两个反比例函数y＝和y＝﹣的图象分别是l1和l2．设点P在l1上，PC⊥x轴，垂足为C，交l2于点A，PD⊥y轴，垂足为D，交l2于点B，则三角形PAB的面积为（）A．3 B．4 C．D．5例8变式8。

中考冲刺之选择填空压轴题（探索规律类）一、单选题(共10道，每道10分)1.意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，根据这组数的规律第10个数是（）A.57B.55C.89D.144答案：B试题难度：三颗星知识点：整数类2.刘老师设计了一个计算程序，输入和输出的数据如下表，那么，当输入数据是7时，输出的数据是（）A.B.C.D.答案：B试题难度：三颗星知识点：分数类3.观察下列单项式：，，，…，，，…，从中我们可以猜想出第2012个单项式是（）A.B.C.D.答案：D试题难度：三颗星知识点：单项式类4.观察下列等式：①1＝12；②2＋3＋4＝32；③3＋4＋5＋6＋7＝52；④4＋5＋6＋7＋8＋9＋10＝72；…请你根据观察得到的规律判断下列各式正确的是（）A.1005＋1006＋1007＋…＋3016＝20112B.1005＋1006＋1007＋…＋3017＝20112C.1006＋1007＋1008＋…＋3016＝20112D.1007＋1008＋1009＋…＋3017＝20112答案：C试题难度：三颗星知识点：等式类5.填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值是（）A.152B.168C.144D.158答案：D试题难度：三颗星知识点：表格类6.将1、、、按如下方式排列．若规定（m，n）表示第m排从左向右第n个数，则（5，4）与（15，7）表示的两数之积是()．A.B.C.D.答案：D试题难度：三颗星知识点：周期循环类7.在下表中，我们把第i行第j列的数记为（其中i，j都是不大于5的正整数），对于表中的每个数，规定如下：当时，＝1；当时，＝0.例如：当，时，＝＝1.按此规定，计算：的值为（）A.1B.0C.2D.3答案：A试题难度：三颗星知识点：定义新运算类8.如图下面是按照一定规律画出的一行“树形图”，经观察可以发现：图比图多出了2个“树枝”，图比图多出了4个“树枝”，图比图多出了8个“树枝”，…，照此规律，则图比图多出“树枝”()A.28个B.56个C.60个D.124个答案：C试题难度：三颗星知识点：多个变化类图形9.如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，顺次连接四边形ABCD各边中点，得到四边形A1B1C1D1，再顺次连接四边形A1B1C1D1各边中点，得到四边形A2B2C2D2……，如此进行下去，得到四边形AnBnCnDn.下列结论正确的有（）①四边形A2B2C2D2是矩形；②四边形A4B4C4D4是菱形；③四边形A5B5C5D5的周长是；④四边形AnBnCnDn 的面积是A.①②B.②③C.②③④D.①②③④答案：C试题难度：三颗星知识点：单个图形10.2002年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形，中间的阴影部分是一个小正方形的“赵爽弦图”．若这四个全等的直角三角形有一个角为30°，顶点、、、…、和、、、…、分别在直线y=-和轴上，则第个阴影正方形的面积为()A.B.C.D.答案：B试题难度：三颗星知识点：系列图形变换。

选填压轴题选集一．选择题（共16小题）1．函数y=和y=在第一象限内的图象如图，点P是y=的图象上一动点，PC⊥x轴于点C，交y=的图象于点B．给出如下结论：①△ODB与△OCA的面积相等；②PA与PB始终相等；③四边形PAOB的面积大小不会发生变化；④CA=AP．其中所有正确结论的序号是（）A．①②③B．②③④C．①③④D．①②④2．如图，在直角坐标系中，直线y1=2x﹣2与坐标轴交于A、B两点，与双曲线y2=（x＞0）交于点C，过点C作CD⊥x轴，垂足为D，且OA=AD，则以下结论：①S△ADB=S△ADC；②当0＜x＜3时，y1＜y2；③如图，当x=3时，EF=；④当x＞0时，y1随x的增大而增大，y2随x的增大而减小．其中正确结论的个数是（）A．1B．2C．3D．43．如图，A、B是双曲线上的点，A、B两点的横坐标分别是a、2a，线段AB的延长线交x轴于点C，若S△AOC=6．则k的值为（）A．1B．2C．4D．无法确定4．如图，是二次函数 y=ax2+bx+c（a≠0）的图象的一部分，给出下列命题：①a+b+c=0；②b＞2a；③ax2+bx+c=0的两根分别为﹣3和1；④a﹣2b+c＞0．其中正确的命题是（）A．①②B．②③C．①③D．①②③④5．如图（1）所示，E为矩形ABCD的边AD上一点，动点P，Q同时从点B出发，点P沿折线BE﹣ED﹣DC运动到点C时停止，点Q沿BC运动到点C时停止，它们运动的速度都是1cm/秒．设P、Q同时出发t秒时，△BPQ的面积为ycm2．已知y与t的函数关系图象如图（2）（曲线OM为抛物线的一部分），则下列结论：①AD=BE=5；②；③当0＜t≤5时，；④当秒时，△ABE∽△QBP；其中正确的结论是（）A．①②③B．②③B．①③④D．②④6．如图是二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为x=，且经过点（2，0），有下列说法：①abc＜0；②a+b=0；③4a+2b+c＜0；④若（0，y1），（1，y2）是抛物线上的两点，则y1=y2．上述说法正确的是（）A．①②④B．③④C．①③④D．①②7．如图，已知A、B两点的坐标分别为（﹣2，0）、（0，1），⊙C 的圆心坐标为（0，﹣1），半径为1．若D是⊙C上的一个动点，射线AD与y轴交于点E，则△ABE面积的最大值是（）A．3B．C．D．48．图1是用钢丝制作的一个几何探究工具，其中△ABC内接于⊙G，AB是⊙G的直径，AB=6，AC=2．现将制作的几何探究工具放在平面直角坐标系中（如图2），然后点A在射线OX上由点O开始向右滑动，点B在射线OY上也随之向点O滑动（如图3），当点B滑动至与点O重合时运动结束．在整个运动过程中，点C运动的路程是（）A．4B．6C．4﹣2D．10﹣49．如图，AB为半圆O在直径，AD、BC分别切⊙O于A、B两点，CD切⊙O于点E，连接OD、OC，下列结论：①∠DOC=90°，②AD+BC=CD，③S△AOD：S△BOC=AD2：AO2，④OD：OC=DE：EC，⑤OD2=DE•CD，正确的有（）A．2个B．3个C．4个D．5个10．如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（）A．B．C．D．2B．11．如图，⊙O的半径为2，AB、CD是互相垂直的两条直径，点P是⊙O上任意一点（P与A、B、C、D不重合），经过P作PM⊥AB于点M，PN⊥CD于点N，点Q是MN的中点，当点P沿着圆周转过45°时，点Q走过的路径长为（）B．C．D．A．B．12．一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形，边长都为1，则扇形和圆形纸板的面积比是（）A．5：4B．5：2C．：2D．：13．如图，在平面直角坐标系中，⊙O的半径为1，点P在经过点A（﹣4，0）、B（0，4）的直线上，PQ切⊙O于点Q，则切线长PQ的最小值为（）A．B．2C．3D．414．如图1，在矩形ABCD中，动点E从A出发，沿AB→BC方向运动，当点E到达点C时停止运动，过点E做FE⊥AE，交CD于F点，设点E运动路程为x，FC=y，如图2所表示的是y与x的函数关系的大致图象，当点E在BC上运动时，FC的最大长度是，则矩形ABCD的面积是（）B．5C．6D．A．15．如图，在平面直角坐标系中，四边形OBCD是边长为4的正方形，平行于对角线BD的直线l从O出发，沿x轴正方向以每秒1个单位长度的速度运动，运动到直线l与正方形没有交点为止．设直线l扫过正方形OBCD的面积为S，直线l运动的时间为t（秒），下列能反映S与t之间函数关系的图象是（）A．B．C．D．16．如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为（）A．B．C．D．二．填空题（共7小题）17．如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=的图象上，若点A的坐标为（﹣2，﹣2），则k的值为．18．如图，已知点A，C在反比例函数y=（a＞0）的图象上，点B，D在反比例函数y=（b＜0）的图象上，AB∥CD∥x轴，AB，CD在x轴的两侧，AB=3，CD=2，AB与CD的距离为5，则a﹣b的值是．19．如图，在平面直角坐标系xOy中，四边形ODEF和四边形ABCD都是正方形，点F在x 轴的正半轴上，点C在边DE上，反比例函数y=（k≠0，x＞0）的图象过点B，E．若AB=2，则k的值为．20．如图，点A1，A2依次在y=（x＞0）的图象上，点B1，B2依次在x轴的正半轴上．若△A1OB1，△A2B1B2均为等边三角形，则点B2的坐标为．21．如图，若双曲线y=（k＞0）与边长为3的等边△AOB（O为坐标原点）的边OA、AB 分别交于C、D两点，且OC=2BD，则k的值为．22．如图，在平面直角坐标系xOy中，△OAB的顶点A在x轴正半轴上，OC是△OAB的中线，点B，C在反比例函数y=（x＞0）的图象上，则△OAB的面积等于．23．如图，已知点A1，A2，…，A n均在直线y=x﹣1上，点B1，B2，…，B n均在双曲线y=﹣上，并且满足：A1B1⊥x轴，B1A2⊥y轴，A2B2⊥x轴，B2A3⊥y轴，…，A n B n⊥x轴，B n A n+1⊥y 轴，…，记点A n的横坐标为a n（n为正整数）．若a1=﹣1，则a2015=．2018年06月02日445****3977的初中数学组卷参考答案一．选择题（共17小题）1．C；2．C；3．C；4．C；5．C；6．A；7．B；8．D；9．C；10．A；11．A；12．A；13．A；14．B；15．D；16．B；二．填空题（共7小题）17．4；18．6；19．6+2；20．（6，0）；21．；22．；23．2；。

中考冲刺之选择填空压轴题（确定函数图象类）一、单选题(共10道，每道10分)1.（2011重庆綦江）小明从家中出发，到离家1.2千米的早餐店吃早餐，用了一刻钟吃完早餐后，按原路返回到离家1千米的学校上课，在下列图象中，能反映这一过程的大致图象是（）A.B.C.D.答案：B试题难度：三颗星知识点：行程类—单2.甲、乙二人从山脚开始爬山，到达山顶后立即下山返回，已知甲上山的速度比下山的速度慢，乙上山的速度比甲上山的速度慢，但乙的下山的速度比甲下山的速度快，即使如此，乙还是在甲之后回到山脚，如果甲、乙两人同时从山脚出发，下列图象中，①、②分别描述甲、乙二人离山脚的距离S（米）和从山脚出发的时间t（分）之间的函数关系，其中大致正确的是（）A.B.C.D.答案：C试题难度：三颗星知识点：行程类—双3.如图，某工厂有两个大小相同的蓄水池，且中间有管道连通．现要向甲池中注水，若单位时间内的注水量不变，那么，从注水开始，水池乙水面上升的高度h与注水时间t之间的函数关系的图象可能是（）A.B.C.D.答案：C试题难度：三颗星知识点：注水4.（11河北）如图4，在长方形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱.设矩形的长和宽分别为y和x，则y与x的函数图象大致是（）A.B.C.D.答案：A试题难度：三颗星知识点：利用数学公式类5.（哈尔滨市）下列各图中，能表示函数y=k(1-x)和y=(k≠0)在同一平面直角坐标系中的图象大致是（）A.B.C.D.答案：D试题难度：三颗星知识点：多函数交叉类6.如下图，在平行四边形ABCD中，∠DAB＝60°，AB＝5，BC＝3，点P从起点D出发，沿DC、CB向终点B匀速运动。

设点P所走过的路程为x，点P所经过的线段与线段AD、AP 所围成图形的面积为y，y随x的变化而变化。

在下列图象中，能正确反映y与x的函数关系的是（）A.B.C.D.答案：A试题难度：三颗星知识点：单动点7.如图，在梯形ABCD中，AB=BC=10cm，CD=6cm，∠C=∠D=90°，动点P、Q同时以每秒1cm 的速度从点B出发，点P沿BA、AD、DC运动，点Q沿BC、CD运动，P点与Q点相遇时停止，设P、Q同时从点B出发x秒时，P、Q经过的路径与线段PQ围成的图形的面积为y（cm2），则y与x之间的函数关系的大致图象为（）A.B.C.D.答案：C试题难度：三颗星知识点：双动点8.如图，直线l0过正方形ABCD的顶点B，且l0∥AC，当直线l从l0开始在平面内向左上方向匀速平移（经过点D止）时，它扫过的正方形内阴影部分的面积S是时间t的函数，这个函数的图象大致是（）A.B.C.D.答案：C试题难度：三颗星知识点：动线9.已知如图，等腰三角形ABC的直角边长为a，正方形MNPQ的边为b（a＜b），C、M、A、N在同一条直线上，开始时点A与点M重合，让△ABC向右移动，最后点C与点N重合．设三角形与正方形的重合面积为y，点A移动的距离为x，则y关于x的大致图象是（）A.B.C.D.答案：B试题难度：三颗星知识点：动面10.（2011北京）如图在Rt△中，∠ACB＝90°，∠BAC＝30°，AB＝2，D是AB边上的一个动点（不与点A、B重合），过点D作CD的垂线交射线CA于点E.设AD＝x，CE＝，则下列图象中，能表示y与x的函数关系的图象大致是（）A.B.C.D.答案：B试题难度：三颗星知识点：无解析式类。

机密★启用前密密 封 线 内 不 得 答 题1．如图，在矩形纸片ABCD 中，AB ＝3，BC ＝5，点E 、F 分别在线段AB 、BC 上，将△BEF 沿EF 折叠，点B 落在B ′ 处．如图1，当B ′ 在AD 上时，B ′ 在AD 上可移动的最大距离为_________；如图2，当B ′ 在矩形ABCD 内部时，AB ′ 的最小值为______________．2．如图，乐器上一根弦固定在乐器面板上A 、B 两点，支撑点C 是靠近点B 的黄金分割点，若AB＝80cm ，则AC ＝______________cm ．（结果保留根号）3．已知抛物线y ＝ax 2－2ax －1＋a （a ＞0）与直线x ＝2，x ＝3，y ＝1，y ＝2围成的正方形有公共点，则a 的取值范围是___________________．4．如图，7根圆柱形木棒的横截面圆的半径均为1，则捆扎这7根木棒一周的绳子长度为_______________． 5．如图，已知A 1（1，0），A 2（1，－1），A 3（－1，－1），A 4（－1，1）， A 5（2，1），…，则点A 2010的坐标是__________________．6．在Rt △ABC 中，∠C ＝90°，AC ＝3，BC ＝4．若以C 点为圆心，r 为半径所作的圆与斜边AB 只有一个公共点，则r 的取值范围是_________________．7．已知⊙A 和⊙B 相交，⊙A 的半径为5，AB ＝8，那么⊙B 的半径r 的取值范围是_________________．8．已知抛物线F 1：y ＝x 2－4x －1，抛物线F 2与F 1关于点（1，0）中心对称，则在F 1和F 2围成的封闭图形上，平行于y 轴的线段长度的最大值为_____________．A DB C B ′ E 图1A DBCB ′E图29．如图，四边形ABCD 中，AB ＝4，BC ＝7，CD ＝2，AD ＝x ，则x 的取值范围是（ ）．10．已知正数a 、b 、c 满足a 2＋c 2＝16，b 2＋c 2＝25，则k ＝a 2＋b 2的取值范围是_________________．11．如图，在△ABC 中，AB ＝AC ，D 在AB 上，BD ＝AB ，则∠A 的取值范围是_________________．12．函数y ＝2x 2＋4|x |－1的最小值是____________．13．已知抛物线y ＝ax 2＋2ax ＋4（0＜ a ＜3），A （x 1，y 1），B （x 2，y 2）是抛物线上两点，若x 1＜x 2，且x 1＋x 2＝1－a ，则y 1 __________ y 2（填“＞”、“＜”或“＝”） 14．如图，△ABC 中，∠A 的平分线交BC 于D ，若AB ＝6，AC ＝4，∠A ＝60°，则AD 的长为___________． 15．如图，Rt △ABC 中，∠C ＝90°，AC ＝交AC 于E ，DF ⊥AB 交BC 于F ，设AD ＝x 于x 的函数解析式为_____________________．16．两个反比例函数y ＝x k 和y ＝x 1在第一象限内的图象如图所示，点P 在y ＝xk的图象上，PC ⊥x 轴于点C ，交y ＝x 1的图象于点A ，PD ⊥y 轴于点D ，交y ＝x 1的图象于点B ，当点P 在y ＝xk的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化；③PA 与PB 始终相等；④当点A 是PC 的中点时，点B 一定是PD 的中点． 其中一定正确的是_________________．（把你认为正确结论的序号都填上，少填或错填不给分）．17．如图，△ABC 中，BC ＝8，高AD ＝6，矩形EFGH 的一边EF 在边BC 上，其余两个顶点G 、H 分别在边AC 、AB 上，则矩形EFGH 的面积最大值为___________．Ax DB C74 2CC机密★启用前密密 封 线 内 不 得 答 题18．已知二次函数y ＝a (a ＋1)x 2－(2a ＋1)x ＋1，当a 依次取1，2，…，2010时，函数的图像在x 轴上所截得的线段A 1B 1，A 2B 2，…，A 2010B 2010的长度之和为_____________．19．如图是一个矩形桌子，一小球从P 撞击到Q ，反射到R ，又从R 反射到S ，从S 反射回原处P ，入射角与反射角相等（例如∠PQA ＝∠RQB 等），已知AB ＝8，BC ＝15，DP ＝3．则小球所走的路径的长为_____________．20．如图，在平行四边形ABCD 中，点E 、F 分别在AB 、AD 上，且AE ＝31AB ，AF ＝41AD ，连结EF 交对角线AC 于G ，则ACAG＝_____________．21．已知m ，n 是关于x 的方程x 2－2ax ＋a ＋6＝0的两实根，则(m －1)2＋(n －1)2的最小值为_____________．22．如图，四边形ABCD 和BEFG 均为正方形，则AG : DF : CE ＝_____________． 23．如图，在△ABC 中，∠ABC ＝60°，点P 是△ABC 内的一点，且∠APB ＝∠BPC＝∠CPA ，且PA ＝8，PC ＝6，则PB ＝________．24．如图，AB 、CD 是⊙O 的两条弦，∠AOB 与∠C 互补，∠COD 与∠A 相等，则∠AOB 的度数是________．25．如图，一个半径为2的圆经过一个半径为2的圆的圆心，则图中阴影部分的面积为_____________．C DA PBC OC D ABB A BCGDEF123426．如图，在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，AC ＝2．作△ABC 的高CD ，作△CDB 的高DC 1，作△DC 1B 的高C 1D 1，……，如此下去，则得到的所有阴影三角形的面积之和为__________．27．已知抛物线y ＝x 2－(2m ＋4)x ＋m 2－10与x 轴交于A 、B 两点，C 是抛物线顶点，若△ABC 为直角三角形，则m ＝__________．28．已知抛物线y ＝x 2－(2m ＋4)x ＋m 2－10与x 轴交于A 、B 两点，C 是抛物线顶点，若△ABC 为等边三角形，则该抛物线的解析式为___________________________．29．已知抛物线y ＝ax 2＋(34＋3a )x ＋4与x 轴交于A 、B 两点，与y 轴交于点C ．若△ABC 为直角三角形，则a ＝__________．30．如图，在直角三角形ABC 中，∠A ＝90°，点D 在斜边BC 上，点E 、F 分别在直角边AB 、AC 上，且BD ＝5，CD ＝9，四边形AEDF 是正方形，则阴影部分的面积为__________．31．小颖同学想用“描点法”画二次函数y ＝ax 2＋bx ＋c （a ≠0）的图象，取自变量x 的5个值，分别计算出对应的y 值，如下表：由于粗心，小颖算错了其中的一个y 值，请你指出这个算错的y 值所对应的x ＝__________．32．等边三角形ABC 的边长为6，将其放置在如图所示的平面直角坐标系中，其中BC 边在x 轴上，BC 边上的高OA 在y 轴上。

1 （2011湖南岳阳）如图，把一张长方形纸片ABCD 沿对角线BD 折叠，使C 点落在E 处，BE 与AD 相交于点F ，下列结论：①22AB AD BD += ②△ABF ≌△EDF ③AFEFAB DE =④AD=BD ·cos45°，其中正确的一组是（ ）A ．①②B ．②③C ．①④D ．③④2（2012四川达州）将矩形纸片ABCD ，按如图所示的方式折叠，点A 、点C 恰好落在对角线BD 上，得到菱形BEDF.若BC=6，则AB 的长为 .3 （2011安徽，22，12分）在△ABC 中，∠ACB =90°，∠ABC =30°，将△ABC 绕顶点C 顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A ′B ′C ． （1）如图（1），当AB ∥CB ′时，设A ′B ′与CB 相交于点D ．证明：△A ′CD 是等边三角形；（2）如图（2），连接A ′A 、B ′B ，设△ACA ′ 和△BCB ′ 的面积分别为S △ACA ′ 和S △BC B′．求证：S △ACA ′ ：S △BC B′1：3；（3）如图（3），设AC 中点为E ，A ′B ′中点为P ，AC =a ，连接EP ，当θ= °时，EP 长度最大，最大值为 ．4 .（2012山东东营）（1）如图1，在正方形ABCD 中，E 是AB 上一点，F 是AD 延长线上一点，且DF ＝BE ．求证：CE ＝CF ；（2）如图2，在正方形ABCD 中，E 是AB 上一点，G 是AD 上一点，如果∠GCE ＝45°，请你利用（1）的结论证明：GE ＝BE ＋GD ． （3）运用（1）（2）解答中所积累的经验和知识，完成下题：如图3，在直角梯形ABCD 中，AD ∥BC （BC ＞AD ），∠B ＝90°，AB ＝BC ，E 是AB 上一点，且∠DCE ＝45°，BE ＝4，DE =10, 求直角梯形ABCD 的面积．AB FCDEAθA ′B ′BCA ′AB B ′CE PθABBCAθ（第23题图1） C D F （第23题图3） B CA DE （第23题图2） A E C D G5.（2012湖南益阳，21，12分）已知：如图1，在面积为3的正方形ABCD 中，E 、F 分别是BC 和CD 边上的两点，AE ⊥BF 于点G ，且BE =1． （1）求证：△ABE ≌△BCF ；（2）求出△ABE 和△BCF 重叠部分（即△BEG ）的面积； （3）现将△ABE 绕点A 逆时针方向旋转到△AB ＇E ＇（如图2），使点E 落在CD 边上的点E ＇处，问△ABE 在旋转前后与△BCF 重叠部分的面积是否发生了变化？请说明理由．6.（2012山东泰安）如图，菱形OABC 的顶点O 在坐标原点，顶点A 在x 轴上，∠B=120°，OA=2，将菱形OABC 绕点O 顺时针旋转105°至OA B C '''的位置，则点B '的坐标为（ ）A.(2,2)-B.(2,2)-C.(2,2)-D.(2,2)-7.（2012河北省）9、如图4，在□ABCD 中，∠A=70°，将□ABCD 折叠，使点D ，C 分别落在点F ，E 处，（点F ，E 都在AB 所在的直线上），折痕为MN ，则∠AMF 等于 （ ）Ａ．70° Ｂ．40° Ｃ．30° Ｄ．20°8如图，A ，B 的坐标为（2，0），（0，1），若将线段AB 平移至A1B1，则a+b 的值为（ ）A.2B.3C.4D.59. .如图，在直角坐标系中，矩形ABCO 的边OA 在x 轴上，边OC 在y 轴上，点B 的坐标为（1，3），将矩形沿对角线AC 翻折，B 点落在D 点的位置，且AD 交y 轴于点E.那么D 点的坐标为（ ）A. B. C. D. 10 .如图，平面直角坐标系中，OB 在x 轴上，∠ABO=90°，点A 的坐标为（1，2），将△AOB 绕点A 逆时针旋转90°，点O 的对应点C 恰好落在双曲线（x ＞0）上，则k 的值为（ ）A.2 B.3 C.4 D.611.如图，在扇形纸片AOB 中，OA=10，∠AOB=36°，OB 在桌面内的直线l 上.现将此扇形沿l按顺时针方向旋转（旋转过程中无滑动），当OA 落在l 上时，停止旋转.则点O 所经过的路线长为（ ）A.12πB.11πC.10πD.12（2011湖北黄冈）如图，把Rt △ABC 放在直角坐标系内，其中∠CAB=90°，BC=5，点A 、B 的坐标分别为（1，0）、（4，0），将△ABC 沿x 轴向右平移，当点C 落在直线y=2x －6上时，线段BC 扫过的面积为（ ）ABACDB GFD'B CF 'E E图2图1A ．4B ．8C ．16D ．8213.（2011山西）将一个矩形纸片依次按图（1）、图的方式对折，然后沿图（3）中的虚线裁剪，最后头将图（4）的纸再展开铺平，所得到的图案是（ ）14（2011福建泉州）如图，如果边长为1的正六边形ABCDEF 绕着顶点A 顺时针旋转60°后与正六边形AGHMNP 重合，那么点B 的对应点是点 ，点E 在整个旋转过程中，所经过的路径长为 （结果保留π）.15（2011广西贵港）如图所示，在边长为2的正三角形ABC 中，E 、F 、G 分别为AB 、AC 、BC 的中点，点P 线段EF 上一个动点，连接BP 、GP ，则△BPG 周长的最小值是 。

中考冲刺之选择填空压轴题（第一部份函数图象的综合应用）一、单项选择题(共5道，每道20分)1.（2020四川乐山）如图，直线交x轴、y轴于A、B两点，P是反比例函数图象上位于直线下方的一点，过点P作x轴的垂线，垂足为点M，交AB于点E，过点P作y轴的垂线，垂足为点N，交AB于点F．那么AF*BE=（）D.2.（2020江苏无锡）如图，抛物线y=x2+1与双曲线y=的交点A的横坐标是1，那么关于x的不等式+x2+1＜0的解集是（）＞1 ＜－1 ＜x＜1 D.－1＜x＜03.（2020山东聊城）某公司草坪的防护栏是由100段形状相同的抛物线形构件组成的，为了牢固起见，每段护栏需要间距加设一根不锈钢的支柱，防护栏的最高点距底部(如图)，那么这条防护栏需要不锈钢支柱的总长度至少为（）4.(2020江苏南京)如图，在平面直角坐标系中，⊙P的圆心是（2，a）(a＞2)，半径为2，函数y=x的图象被⊙P截得的弦AB的长为，那么a的值是（）A. B. C. D.5.（2020山东烟台）在全民健身环城越野赛中，甲乙两选手的行程y（千米）随时刻（时）转变的图象（全程）如下图.有以下说法：①起跑后1小时内，甲在乙的前面；②第1小时两人都跑了10千米；③甲比乙先抵达终点；④两人都跑了20千米.其中正确的说法有（）个个个个中考冲刺之选择填空压轴题（第二部份面积周长类）一、单项选择题(共9道，每道11分)1.如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°，∠C=60°，BC=2AD=，点E 是BC边的中点，△DEF是等边三角形，DF交AB于点G，那么△BFG的周长为（）.A.+ C.2.如图1，两个等边△ABD，△CBD的边长均为1，将△ABD沿AC方向向右平移到△A′B′D′的位置，取得图2，那么阴影部份的周长为（）．++3.已知两个相似三角形的一对对应边长别离是35cm和14cm且它们的周长相差60cm，那么较大的三角形的周长是（）cm．4.如图是一个几何体的三视图，那个几何体的全面积为()．A. B. C. D.5.如图，在△ABC中，AB＝AC＝10，CB＝16，别离以AB、AC为直径作半圆，那么图中阴影部份面积是（）A. B. C. D.6.如图，在△ABC中，∠ACB＝90°，AC＞BC，别离以AB、BC、CA为一边向△ABC外作正方形ABDE、BCMN、CAFG，连接EF、GM、ND，设△AEF、△BND、△CGM的面积别离为S一、S二、S3，那么以下结论正确的选项是（）＝S2＝S3 ＝S2＜S3 ＝S3＜S2 ＝S3＜S17.如图，△ABC的面积为63，D是BC上的一点，且BD:CD＝2:1，DE∥AC交AB于点E，延长DE到F，使FE:ED＝2:1，那么△CDF的面积为（）．8.如图，反比例函数的图象与直线的交点为A，B，过点A作y轴的平行线与过点B作x轴的平行线相交于点C，那么△ABC的面积为（）9.如图，已知△ABC是面积为的等边三角形，△ABC∽△ADE，AB＝2AD，∠BAD＝45°，AC与DE相交于点F，那么△AEF的面积等于（）.A. B. C. D.中考冲刺之选择填空压轴题（第三部份多情形、多结论类）一、单项选择题(共8道，每道12分)1.如图，△ABC内接于⊙O，D为线段AB的中点，延长OD交⊙O于点E，连接AE，BE，那么以下五个结论①AB⊥DE,②AE=BE,③OD=DE,④∠AEO=∠C,⑤,正确结论的个数是（）2.已知：二次函数y=ax2+bx+c（a≠0）的图象如下图，以下结论中：①abc＞0；②2a+b＜0；（m≠1）；④（a+c）2＜b2；⑤a＞1．其中正确的项有（）个③a+b＜m（am+b）3.如图．直线与双曲线交于A、B两点，连接OA、OB，AM⊥y 轴于M，BN⊥x轴于N.有以下结论：①OA=OB；②△AOM≌△BON；③假设∠AOB=45°，那么；④当AB=时，ON-BN=1.其中结论正确的个数为（）4.已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．假设AE＝AP＝1，PB＝．以下结论：①△APD≌△AEB；②点B到直线AE的距离为；③EB⊥ED；④S△APD＋S△APB＝1＋；⑤S正方形ABCD＝4＋．其中正确结论的序号是（）A.①③④B.①②⑤C.③④⑤D.①③⑤5.如图，在Rt△ABC中，AB=CB，BO⊥AC，把△ABC折叠，使AB落在AC上，点B与AC上的点E重合，展开后，折痕AD交BO于点F，连结DE、EF．以下结论：①tan∠ADB=2；②图中有4对全等三角形；③假设将△DEF沿EF折叠，那么点D不必然落在AC上；④BD=BF；⑤S四边形DFOE=S△AOF，上述结论中正确的个数是（）个个个个6.如下图，在平面直角坐标系中，直线OM是正比例函数y＝－x的图象，点A的坐标为(1,0)，在直线OM上找点N，使△ONA是等腰三角形，符合条件的点N的个数是（）个个个个7.如图，⊙O1的半径为1，正方形ABCD的边长为6，点O2为正方形ABCD的中心，O1O2垂直AB于P点，O1O2＝8．假设将⊙O1绕点P按顺时针方向旋转360°，在旋转进程中，⊙O1与正方形ABCD的边只有一个公共点的情形一共显现（）次次次次8.在等腰Rt△ABC中，∠C=90°，AC=1，过点C作直线l∥AB，F是l上的一点，且AB=AF，那么点F到直线BC的距离为（）．A. B. C. D.或中考冲刺之选择填空压轴题（第四部份几何三大变换类）一、单项选择题(共8道，每道12分)1.如图，A，B的坐标为（2，0），（0，1），假设将线段AB平移至A1B1，那么a+b的值为（）2.如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A、B的坐标别离为（1，0）、（4，0），将△ABC沿x轴向右平移，当点C落在直线y=2x-6上时，线段BC扫过的面积为（）D.3.如图，在直角坐标系中，矩形ABCO的边OA在x轴上，边OC在y轴上，点B的坐标为（1，3），将矩形沿对角线AC翻折，B点落在D点的位置，且AD交y轴于点E.那么D点的坐标为（）A. B. C. D.4.如图，已知边长为5的等边三角形ABC纸片，点E在AC边上，点F在AB边上，沿着EF折叠，使点A落在BC边上的点D的位置，且，那么CE的长是（）A. B. C. D.5.如图，在矩形ABCD中，AB=8，BC=4，将矩形沿AC折叠，那么重叠部份△AFC的面积为（）6.如图，平面直角坐标系中，OB在x轴上，∠ABO=90°，点A的坐标为（1，2），将△AOB 绕点A逆时针旋转90°，点O的对应点C恰好落在双曲线（x＞0）上，那么k的值为（）7.如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°至DE，连接AE，那么△ADE的面积是（）8.如图，在扇形纸片AOB中，OA=10，∠AOB=36°，OB在桌面内的直线l上.现将此扇形沿l按顺时针方向旋转（旋转进程中无滑动），当OA落在l上时，停止旋转.那么点O所通过的线路长为（）πππ D.中考冲刺之选择填空压轴题（第五部份探讨规律类）一、单项选择题(共10道，每道10分)1.意大利闻名数学家斐波那契在研究兔子繁衍问题时，发觉有如此一组数：1，1，2，3，5，8，13，…，依照这组数的规律第10个数是（）2.刘教师设计了一个计算程序，输入和输出的数据如下表，那么，当输入数据是7时，输出的数据是（）A. B. C. D.3.观看以下单项式：，，，…，，，…，从中咱们能够猜想出第2021个单项式是（）A. B. C. D.4.观看以劣等式：①1＝12；②2＋3＋4＝32；③3＋4＋5＋6＋7＝52；④4＋5＋6＋7＋8＋9＋10＝72；…请你依照观看取得的规律判定以下各式正确的选项是（）＋1006＋1007＋…＋3016＝20202 ＋1006＋1007＋…＋3017＝20202＋1007＋1008＋…＋3016＝20112 ＋1008＋1009＋…＋3017＝202025.填在下面各正方形中的四个数之间都有相同的规律，依照这种规律，m的值是（）6.将一、、、按如下方式排列．假设规定（m，n）表示第m排从左向右第n个数，那么（5，4）与（15，7）表示的两数之积是()．A. B. C. D.7.在下表中，咱们把第i行第j列的数记为（其中i，j都是不大于5的正整数），关于表中的每一个数，规定如下：当时，＝1；当时，＝0.例如：当，时，＝＝1.按此规定，计算：的值为（）8.如图下面是依照必然规律画出的一行“树形图”，经观看能够发觉：图比图多出了2个“树枝”，图比图多出了4个“树枝”，图比图多出了8个“树枝”，…，照此规律，那么图比图多出“树枝”()个个个个9.如图，四边形ABCD中，AC=a，BD=b，且AC⊥BD，按序连接四边形ABCD各边中点，取得四边形A1B1C1D1，再按序连接四边形A1B1C1D1各边中点，取得四边形A2B2C2D2……，如此进行下去，取得四边形AnBnCnDn.以下结论正确的有（）①四边形A2B2C2D2是矩形；②四边形A4B4C4D4是菱形；③四边形A5B5C5D5的周长是；④四边形AnBnCnDn的面积是A.①②B.②③C.②③④D.①②③④年在北京召开的世界数学大会会标图案是由四个全等的直角三角形围成的一个大正方形，中间的阴影部份是一个小正方形的“赵爽弦图”．假设这四个全等的直角三角形有一个角为30°，极点、、、…、和、、、…、别离在直线y=-和轴上，那么第个阴影正方形的面积为()A. B. C. D.中考冲刺之选择填空压轴题（第六部份确信函数图象类）一、单项选择题(共10道，每道10分)1.（2020重庆綦江）小明从家中动身，到离家千米的早饭店吃早饭，用了一刻钟吃完早饭后，按原路返回到离家1千米的学校上课，在以下图象中，能反映这一进程的大致图象是（）..2.甲、乙二人从山脚开始登山，抵达山顶后当即下山返回，已知甲上山的速度比下山的速度慢，乙上山的速度比甲上山的速度慢，但乙的下山的速度比甲下山的速度快，即便如此，乙仍是在甲以后回到山脚，若是甲、乙两人同时从山脚动身，以下图象中，①、②别离描述甲、乙二人离山脚的距离S（米）和从山脚动身的时刻t（分）之间的函数关系，其中大致正确的选项是（）3.如图，某工厂有两个大小相同的蓄水池，且中间有管道连通．现要向甲池中注水，假设单位时刻内的注水量不变，那么，从注水开始，水池乙水面上升的高度h与注水时刻t之间的函数关系的图象可能是（）4.（11河北）如图4，在长方形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，恰好能组合成圆柱.设矩形的长和宽别离为y和x，那么y与x的函数图象大致是（）5.（哈尔滨市）以下各图中，能表示函数y=k(1-x)和y=(k≠0)在同一平面直角坐标系中的图象大致是（）6.如以下图，在平行四边形ABCD中，∠DAB＝60°，AB＝5，BC＝3，点P从起点D动身，沿DC、CB向终点B匀速运动。

中考复习选择填空压轴题（精选二）1.任意实数a，可用[a]表示不超过a的最大整数，如[4]=4，[]=1，现对72进行如下操作：72→[]=8→[]=2→[]=1，这样对72只需进行3次操作后变为1．类似地：对数字900进行了n次操作后变为1，那么n的值为（）A．3 B．4 C．5 D．62.对于实数x，我们规定[x]表示不大于x的最大整数，例如[1.2]=1，[3]=3，[﹣2.5]=﹣3，若[]=5，则x的取值可以是（）A．36 B．40 C．45 D．463.如图，正方形OABC，ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数y=（x＞0）的图象上，则点E的坐标是（）A．（+1，﹣1） B．（3+，3﹣） C．（﹣1，+1） D．（3﹣，3+）4.如图，已知∠B=90°，AB=3cm，BC=cm，点D是线段BC上的一个动点，连接AD，动点B′始终与点B关于直线AD对称，当点D由点B位置向右运动至点C位置时，相应的点B′所经过的路程为（）A．3cm B．πcm C．2cm D．2πcm5.如图，在△ABC中，AB=3，AC=2．当∠B最大时，BC的长是（）A．1 B．C．D．56.如图，已知平行四边形ABCD中，AB=5，BC=8，cosB=，点E是BC边上的动点，当以CE为半径的圆C与边AD不相交时，半径CE的取值范围是（）A．0＜CE≤8 B．0＜CE≤5 C．0＜CE＜3或5＜CE≤8 D．3＜CE≤57.如图，已知抛物线y=x2+2x﹣3，把此抛物线沿y轴向上平移，平移后的抛物线和原抛物线与经过点（﹣2，0），（2，0）且平行于y轴的两条直线所围成的阴影部分的面积为s，平移的距离为m，则下列图象中，能表示s与m的函数关系的图象大致是（）A． B． C． D．8.在平行四边形ABCD中，点P从起点B出发，沿BC，CD逆时针方向向终点D匀速运动．设点P所走过的路程为x，则线段AP，AD与平行四边形的边所围成的图形面积为y，表示y与x的函数关系的图象大致如下图，则AB边上的高是（）A． 3 B． 4 C． 5 D． 69.如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB面积的最大值是．10.如图，△ABC为等边三角形，点E在BA的延长线上，点D在BC边上，且ED=EC．若△ABC的边长为4，AE=2，则BD的长为．11.若直线y=m（m为常数）与函数y=的图象恒有三个不同的交点，则常数m的取值范围是．12.如图，在正方形ABCD中，AB=1，E、F分别是BC、CD边上的点，（1）若CE=CB，CF=CD，则图中阴影部分的面积是；（2）若CE=CB，CF=CD，则图中阴影部分的面积是（用含n的式子表示，n是正整数）．。